Talk:Monty Hall problem/Archive 13

Archive 10

Archive 11

Archive 12

Archive 13

Archive 14

Archive 15

→

Archive 20

Building Consenus - Mediation

At day's end, it will be 7 days since Rick requested comments from all the editors we could think of who had shown an interest in the MHP, plus a general request to the WikiProject Mathematics page. Three days ago, Rick requested mediation assistance. To date there have been no volunteers.

How and when do we keep moving forward toward a consensus? Glkanter (talk) 13:56, 9 December 2009 (UTC)

If you look at the list of pending cases at Wikipedia:Mediation Cabal, the oldest was opened on Nov 20. I don't know if they treat the backlog as a strict FIFO queue, but it seems like 2-3 weeks might be a fairly reasonable amount of time to wait for a response. -- Rick Block (talk) 14:42, 9 December 2009 (UTC)

Rick, based on the following, I don't see this procedure as being any help whatsoever to this particular group of editors. Is there some other benefit to this that I do not understand? What other path can the clear consensus take toward gaining 'permission' from the minority view to move forward with editing the article?

"The Mediation Cabal is a bunch of volunteers providing unofficial, informal mediation for disputes on Wikipedia. We do not impose sanctions or make judgments. We are just ordinary Wikipedians who help facilitate communication and help parties reach an agreement."

http://wiki.riteme.site/wiki/Wikipedia:Mediation_Cabal

You made some claim a couple of days ago about this legitimately created good faith consensus violating NPOV, which I'm sure each member of the consensus would dispute strongly. Is this the issue you want mediated? The claim seems far fetched, certainly, to me. Or is this still an issue from your point of view? Glkanter (talk) 13:01, 10 December 2009 (UTC)

I have two concerns that I believe mediation may help:

1. I am less than convinced that the users Martin has identified as "for change" agree with what you and Martin are thinking they agree with. For example, in the section below Colincbn says that the Solution section of this version "seems to have nothing in it about the conditional solution at all". I believe you and Martin disagree with this. So, is Colincbn for the change you're suggesting or not? To some extent, I think many of us are talking past each other and not necessarily understanding what others are saying.

That point is rather more easily resolved. Why not ask those in the list if they are in the right section. I have asked people to sign to confirm that they are in the right section or to move themselves if they are not. You are free to ask any editor to check that they are in the right section if you think that I have got it wrong. Martin Hogbin (talk) 22:20, 10 December 2009 (UTC)

Rick, re: 'talking past each other', I sure would appreciate some closure on the very first section I started when I returned: 'Is The Contestant Aware?' You're last response was 'yes, but', and I've asked you to clarify, as neither of us wants me mis-interpreting your intent. Thank you. Glkanter (talk) 04:45, 11 December 2009 (UTC)

Martin - this is a perfect example. You seem to not be understanding my point, but I'm puzzled how to make it more clear. If I try to clarify I suspect you'll think I'm arguing with you about the "consensus". A mediator presumably wouldn't have this issue and might be able to convey the point I'm making in a way that you wouldn't take as an argument. Actually, I'm saying the same thing I've said in some other threads lately which is that without talking about specific changes it's very easy to miscommunicate. -- Rick Block (talk) 03:56, 11 December 2009 (UTC)

Be sure to consider all the 'invitees' who consented to the proposals by remaining silent. Glkanter (talk) 22:26, 10 December 2009 (UTC)

2. I personally have been trying to play two roles here, i.e. as a proponent for one "side" in this discussion (per my comment above, I'm not sure there are only two sides) and (since I am an administrator) as an authority on Wikipedia policies and procedures. You, in particular, seem to believe I am not acting in good faith and that everything I say reflects an advocacy of a POV.

Well, it's evident now why these discussions take 6 years and never get anywhere. Rick, under who's auspices were you alone chosen to act "...as an authority on Wikipedia policies and procedures" for purposes of these discussions? Were the other editors advised of your dual role? I sure wasn't, and I am greatly distressed by this revelation. Is this common to have an entrenched protagonist also serve as some sort of 'junior mediator'? I can see all kinds of conflict from this, and have personally witnessed and been the recipient of this conflict of interest in your discussions for 14 months. Have you considered not continuing this dual role? More than ever, I'm certain we need to move beyond the mediator cabal level to declare the consensus in favor of the proposals. Glkanter (talk) 16:25, 12 December 2009 (UTC)

Both of these are areas where I think an uninvolved mediator could help. -- Rick Block (talk) 17:26, 10 December 2009 (UTC)

Why not be upfront? Neither you, myself or Nijdam are going to budge. This cabal can do nothing for us. Let's get whatever issues you have in front of someone who can escalate this, asap. Glkanter (talk) 17:32, 10 December 2009 (UTC)

Please do not attribute motivations to me or Nijdam or anyone other than yourself. I am plenty willing to budge and have done so in the past. Whether you are willing to budge is up to you. Informal mediation is the next step in the dispute resolution process, see Wikipedia:Dispute resolution. Formal mediation comes next, but my understanding is informal mediation is generally treated as a prerequisite. -- Rick Block (talk) 17:58, 10 December 2009 (UTC)

When I first read MHP and the explanations, in the first follow-up column in "Ask Marilyn" years ago, I believed she was right about the answer, but thought her explanations were ridiculous. The best apparent solution offered was to use a simulation--for example, with playing cards. I immediately grabbed a deck of cards and tried the simulation, and within a few minutes saw that it was obvious that the simulation would lead to a 1/3 stay, 2/3 switch ratio for winning over the long run. Obvious, obvious! That was obviously because, of the 2/3 cases in which the prize was not card #1 (i.e., behind door #1), it would be card #2 half the time, and card #3 half the time. So obvious!

This explanation was very unsatisfactory because in the actual tricky puzzle, the actual door opened is actually identified. Door #3 is opened! What then? The simulation (like other explanations) did not specifically address this scenario, but instead included alternate scenarios in which a completely different door (#2) was opened. Sure, we can agree that if either of the non-chosen doors might be opened, the odds of switching are double the odds compared to staying--but what is true once one of the non-chosen doors is actually opened? That is what makes the puzzle an interesting, tricky puzzle! That's why people much smarter than I got fooled!

Eventually I worked out a reasonable solution + explanation (c) and let it go. This Wikipedia article brought the irritation back. I contributed with some silly stuff, got bored, and left.

I'm back in for a minute to argue:

(a) even though Morgan et. al. are very wrong and beside the point overall, they ought not be ignored, because they made a nice (misguided, but nice) argument that the player can't be sure the odds of switching are 2-to-1, since for all we know, a host choosing between two losing doors might prefer one to the other. They rightly acknowledge that you should still switch. They don't add a lot to the discussion beyond that. Their contribution is mostly "too clever by half" and not useful. It is reasonable for the player to play with the assumption that the host is no more likely to open one losing door than another.

(b) the usual explanations given for why you double your odds by switching are worded as if the actual puzzle said something like this:

Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1. You know at least one of the other two doors has a goat behind it. The host, who knows what's behind the doors, opens one of the other two doors (No. 2 or No. 3),showing you a goat. He then says to you, "Do you want to switch to the closed door you didn't orignally pick?" Is it to your advantage to switch your choice?

I don't enjoy the fact that this is treated as an argument about"conditional" versus "unconditional" thingies. Those words seem too complicated to me. Too, I believe Morgan et. al. are fundamentally wrong. But given all that, Rick Block is closer to reality on this topic than is the average person who fundamentally understands the problem. The usual explanations given are not explanations that fit the actual puzzle as it was actually worded! That matters! Simple31415 (talk) 03:24, 13 December 2009 (UTC)

I agree with some of your ideas, disagree with some. Mainly whether "The usual explanations given are not explanations that fit the actual puzzle as it was actually worded! That matters!" As an analyst (problem solver), I'm always looking for shortcuts. And that strictly means find 'differences that make no difference'. I think the open door fits that description. Please look at the section I recently created, Let's Say Some Huckleberry Played Repeatedly and tell me where the contestant did not properly maximize his situation using a simple solution. Glkanter (talk) 05:17, 13 December 2009 (UTC)

Fascinating! Is there any particular reason why you returned now to say, 'Rick Block is closer to reality on this topic than is the average person who fundamentally understands the problem? Perhaps you could tell us which aspect of his argument you support, particularly in view of your comment that Morgan's contribution is mostly, "too clever by half", which I agree with totally although I might add, 'and, in fact wrong'.

Also, there is no "the question", although it is true that the most often quoted problem statement is that by Whitaker. Perhaps you should read it, it says, '...the host, who knows what's behind the doors, opens another door, say No. 3...'. Note the words that I have put in italics. It is quite obvious that it is not intention of the questioner to ask about the probability given that the host opens a specific door but to ask about the probability when he opens one of the other doors to reveal a goat. The door numbers quoted throughout the question are just examples. Nobody can imagine that Whitaker wanted to know about only the specific case where the player chooses door 1 and the host opens door 3!

In fact the MHP is, as we say in the article, a probability puzzle. Its main interest is that it is a simple problem that nearly everyone gets wrong. We should therefore treat the problem and solution simply without even mentioning the terms conditional/unconditional, at least for the first section of the article. Martin Hogbin (talk) 10:26, 13 December 2009 (UTC)

I don't think the informal mediation is going to be of any value. It requires a volunteer mediator, of which none have come forward yet. It could takes weeks before one comes forward, it could be never. Whatever the mediator comes up with is non-binding. It has no teeth. In the meantime, all sorts of edits are being made to the article without any discussions whatsoever.

I suggest we request Mediation immediately, recognize the consensus for the proposed changes, and stop being hostages to this 6 year long filibuster. Glkanter (talk) 14:40, 14 December 2009 (UTC)

I just read about Informal Mediation. If I read it correctly, any Wikipedia editor can offer to mediate. No prior approval of the volunteer mediators occurs. I just don't see where continuing to wait, perhaps forever, for this is of any benefit. Glkanter (talk) 14:46, 15 December 2009 (UTC)

There's A Difference Between A Logical Argument and OR

The first section I created after my return is called 'Is the Contestant Aware'. http://wiki.riteme.site/wiki/Talk:Monty_Hall_problem#Is_The_Contestant_Aware.3F

All I ask is this:

"Has it been agreed by the editors of this article that regardless of how Monty handles the 'two goats remaining' situation, the contestant has no knowledge of the method?"

It's a pretty simple, straightforward, and incredibly relevant question.

But neither Rick or Nijdam have given me a straight 'yes' or 'no'.

So, we're asking for mediation, but we haven't even stated our underlying reasons for disagreement. Because without their responses, any logical argument I might make to a mediator can be refuted, for most any reason.

And, as the section name indicates, using your noggin is not the same as OR. But that seems to be the reason for not replying.

So, enough of the 'well, I didn't say that per se', and let's get to the bottom of this. No mediator can help us if we're not being forthright. Glkanter (talk) 05:11, 11 December 2009 (UTC)

Despite your claim to the contrary, this has already been answered. See, for example #Is The Contestant Aware?, above. And again (for what is it the 4th time?) this is a question for the /Arguments page, not here. Whether the editors of this article agree or don't agree about this should have no bearing whatsoever on what the content of the article should be. In fact, from a Wikipedia policy perspective an unreferenced logical argument is precisely WP:OR. The content of the article must be based only on what reliable sources say. Would it help if a mediator said this rather than me? -- Rick Block (talk) 06:25, 11 December 2009 (UTC)

We disagree. And your choosing to not respond to my very relevant talk page questions is seen, by me, as dodging the truth. You interpret what all these Wikipedia policies & guidelines mean one way, sometimes I'll interpret them another. So, no, it will take the 'formalist' of procedures to convince me that 'endorsing wrongness' is a Wikipedia policy. The source material has conflicts. Editors resolve conflicts of content all the time in the real world. I'm just saying sometimes these conflicts are resolved using logic, often known as common sense. OK. Don't answer. Let's just move the process forward, and the mediation cabal has nothing to offer me. Can we move on to the next level? Glkanter (talk) 08:54, 11 December 2009 (UTC)

"Is the Contestant Aware?" is part of the English language method of conveying the mandatory symmetry for this story. Which is contrary to Morgan. Which, if I understand, means unconditional and conditional must be equal. Glkanter (talk) 09:20, 11 December 2009 (UTC)

Rick, despite your claims to the contrary, you have never answered the question. You have argued for why it shouldn't be answered based on Wikipedia policy, and why you think (and this is your POV) it doesn't matter, but you have not answered the question. Part of that is that it isn't quite the right question, but you have been evasive about why that is so. That is also POV.

No reference uses non-standard, specific knowledge of the game protocol (whether a door is always revealed, and if it always reveals a goat), or a specific asymetric probability for the two uncertainties (car placement and host choice between two goats) to answer the question posed by the MHP. This cannot be denied. (Rick - feel free to try: just point out such a reference. If you don't, it validates my statement.) The so-called "conditional solution" includes terms to represent those concepts, but whenever they use that result to answer the question, they make at least three assumptions: A door is always opened, a goat is always revealed, and the car placement is treated as a uniform choice. For good reason - the question cannot be answered "yes" or "no" without those three assumptions. A brain teaser that asks a "yes/no" question has to have a "yes/no" answer. The fourth assumption - that the choice of the door to open is treated as a uniform choice - is made in some references, but not others. But those others don't use any knowledge of that probability to answer the question, either. They say it is irrelevant to the question. Either way, no knowledge that is not explicitly in the possession of the contestant is used. This is the point you need to agree to, or not: that every reference eliminates any reliance on knowledge that is neither specifically stated nor clearly assumable, before answering the question "should she switch?"

Once you admit to that, and I don't see how you can deny it, we can see that the so-called "conditional solution" is only a tool that is used to generalize the MHP; it is not the MHP problem itself. Because the aspects unique to it are always removed before answering the MHP. Yes, this seems to contradict some sources (but not all, or even the majority - just those that try for a rigorous approach, and make a debatable interpretation about the meaning of door numbers). My point - and I hope Glkanter's, although he isn't phrasing it the same way - is that it only seems that it contradicts these sources. And that assuming there is a contradiction is POV because the sources do not (again, just find me one that uses it to answer the MHP, and I'll back off of this) use specific knowledge not available to the contestant. They either use the contestant's (assumed) knowledge, or say it is irrelevant.

So it is not OR, or inconsistent with any source, to say the problem has to be addressed in the SoK of the player only. All of the sources do the same thing, after they have created that more general tool. They just don't come out and phrase explicitly that "We are now putting the solution into the SoK of the contestant because that is the only useful SoK." They just do it. All of them. The false impression that specific doors are meant never factors into any source's answer of the MHP itself. It never factors into any explanation about why the common intuition, that the remaining doors should be equivalent, is incorrect. So the conditional solution does not aid our readers in understanding why switching is the correct strategy, and it is not necessary to use it to explain the result. It does add extra depth to the various possibilities, but only after the reader has understood that revealing a door places conditions on the remaining door but not on the chosen door. It is not the MHP. It will not be diminished, or ignored, by moving it to after the discussion of alternate strategies. But it does get in the way of understanding, on an intuitive level, why switching works. JeffJor (talk) 18:02, 11 December 2009 (UTC)

Nice job, JeffJor. But not quite perfect from my POV.

Morgan uses some hazy allusion to contestant awareness to discredit the reliably sourced published 'simple' solutions. This is the nucleus of all of Rick's arguments, that Morgan says the 'simple solutions' are inadequate. No published source directly refutes Morgan, so, ipso facto, Morgan is the Uber Reliable Source. Which in Rick's world is a neutral POV. So, Morgan is relying on the contestant having some aura of knowledge. As someone else wrote on this problem, elsewhere in Wikipedia, 'I choose not to discuss a problem where the host and contestant are mind reading or are in collusion'.

I get tired of typing it, and you guys have to be tired of reading it, but any 'host behaviour' is the opposite of the problem statement, 'Suppose you're on a game show...'. Now, you're on a street with a hustler and a card table, some shells and a pea. It is meaningless vis-a-vis the MHP paradox.

There's little point in repeating and continuing the arguments. Both Rick and Nijdam have not given a straight answer to 'Is the Contestant Aware'. Which by the way, Mr. JeffJor, is phrased perfectly fine for my needs, thank you. I think I've asked courteously and tried to explain why it's important. When we get in front of someone to argue for the consensus, I am prepared to explain that this refusal to answer forthrightly (remember the 'meow, meow' answer to this very question?) is consistent with the filibustering, personal attacks on my grasp of the subject matter (Even got one of those from Rick just today. Everyone knows this has been decided in our favor for weeks, and he still says I don't know what I'm talking about. What does that tell you about his grasp of the subject matter, or perhaps his intellectual honesty?) and other passive-aggressive discussion techniques I've experienced personally for 14 months, and countless editors have put up with for 6 years or so. Glkanter (talk) 23:55, 11 December 2009 (UTC)

Excuse me, but what question are you thinking I haven't answered? I answered Glkanter's questions about a week ago (with this edit), in the section I linked to above.

If what I wrote before is not clear, what I think is that the contestant knows what is given in the problem statement, no more and no less. The specific problem statement varies, so what the contestant knows also varies. If, for example, we're given the K&W statement of the problem but without the host's protocol for choosing between two goats (I believe this is precisely the problem Morgan et al. call the "vos Savant scenario"), the contestant does not know the host's choice is uniform. This means a specific player who has initially chosen door 1 and has seen the host open door 3 does not have enough information to know her precise probability of winning by switching. It is something between 1/2 and 1, and it is unconditionally 2/3. I agree there is a sense in which this means the probability is 2/3, but I think this is actually the answer to a different question than what nearly everyone interprets the MHP to actually be asking and that this is the precise reason the MHP is a paradox. I also agree that most people who ask the question intend the answer to the "conditional" question (the one that most people think the question is asking) also be 2/3. IMO, this means the host's preference for choosing between two goats should be specified as part of the problem statement.

However, in addition to the above I also believe that for editing purposes Wikipedia doesn't give a damn what I think and insisting that this question is important or that anyone answer such a question demonstrates a profound misunderstanding of Wikipedia's fundamental content policies.

JeffJor - One reference is Morgan et al. Another one that uses exactly the same approach and makes exactly the same points is Gillman. Another one that distinguishes the "unconditional" and "conditional" questions is Grinstead and Snell. I definitely do not claim that the host preference must be treated as a variable (are you thinking I'm insisting on this?), but that the "Solution" section is really not complete without an analysis using conditional probability and that the distinction between conditional and unconditional probabilities is a central issue at the heart of the MHP. Martin has argued for a long time that a conditional probability analysis would be inaccessible to most readers - essentially that we need to "dumb down" the article. Per Wikipedia:Make technical articles accessible, we should start with an unconditional explanation, proceed with a conditional explanation, with a picture. Hmmm. This sounds exactly like the Solution section in this version. You have seemingly ignored the questions I asked you above at the end of #What "the conditional problem" and "the unconditional problem" mean. I am interested in your response. -- Rick Block (talk) 04:53, 12 December 2009 (UTC)

The above is a great summary of how much I disagree with Rick on most everything that is open to interpretation, or that to most people isn't open to interpretation. I suppose, however, that the time stamp is accurate. Glkanter (talk) 05:37, 12 December 2009 (UTC)

Rick: Saying "Yes we are limited to the player's knowledge BUT the player can wonder about knowledge she doesn't have as though it were useful" is a non-answer. It is straddling the fence on exactly the point you refuse to acknowledge, by answering it both ways. If, for example, Morgan's formula had turned out to be 3/(4+3q) instead of 1/(1+q)? Such "wondering" would not be useful. Switching would be helpful with only some possible qs, but the question as it was asked would still have a definite answer. By assuming q=1/2 and P(C1)=P(C2)=P(C3)=1/3 because the player cannot assume anything else for them.

Morgan, et al, say "In general, we cannot answer the question ... unless we know the host's strategy." So they don't answer the MHP question based on their (incomplete - ignoring P(C1)) formula. The only answer to the MHP question that they give is based on what they call "the vos Savant scenario" and the fact that q doesn't matter. Gillman wrote the assumtion of symmetry for car placement into their problem statement - at least they didn't ignore it like Morgan - but also only provide an answer to the MHP question based on standard game protocol and ignoring q. Grinstead and Snell don't address the MHP's question when they present the so-called conditional solution. So you have not provided the referencecs I asked for. Once again, there is no source that uses the unique properties of the so-called conditional solution to answer "Should the contestant switch?" Those properties only become important if non-standard game rules apply, or if assymetric probabilities are known by the contestant to exist.

The article version you linked is still treating the possibility, that the doors could be treated differently, as something the player could use. It says "A subtly different question is which strategy is best for an individual player after being shown a particular open door." That answer is also "switch, based on an assumed q=1/2 and P(C1)=P(C2)=P(C3)=1/3" in every source that addresses it. Because they don't say that there are other values of those parameters that can be used. Any mention of it belongs after mentioning variants, and providing the "bayesian" solution. Because they don't address, in any way, the issues that make the MHP controversial. They only address ways that variations of the MHP, from what was intended by vos Savant and Selvin, can become more intersting as a mathematic (as opposed to logic) problem. JeffJor (talk) 20:46, 12 December 2009 (UTC)

Jeff - Are you saying you consider any analysis using conditional probability to be a variant? Again, for about the 4th time in the last few days, I'm NOT saying we need to include the host preference (q) generalization in the initial analysis. I'm happy moving that to a variant section (I don't think there's anyone arguing against this, so maybe I'll do that right now). What I'm not happy with is introducing a POV which favors an unconditional solution by omitting any mention of conditional probability. A conditional solution assuming uniform car placement and random host selection between two goats belongs in the initial Solution section. Not doing this is what I'm saying would be counter to NPOV. IMO, the figure in the existing 'Probabilistic solution" section showing the symmetry belongs in the initial solution section. I think there should also be an explanation that there is a difference between the "conditional" question and the "unconditional" question very early, although perhaps not necessarily in the initial Solution section. -- Rick Block (talk) 00:31, 13 December 2009 (UTC)

Rick - I never said that using conditional probability was a variant. I clearly said that using different probabilities based on door numbers is the variant. The problem can be solved with conditional probability, but by the tree G&S use as their figure 4.4. Morgan's criticism of the solutions from the Parade affair are mostly wrong, since they apply to the variant where different probabilities can be considered. Solutions that do not use conditional probability ARE NOT WRONG, as Morgan says; they are only wrong FOR MORGAN'S VARIANT WHICH IS NOT THE MHP. And those solutions Moragn dismissed, which are correct, are easier for lay people to understand. There is no need for G&S's conditional solution early, but it can be included. I don't think it helps anybody who needs to rely on the initial section. But there is no place for Morgan's formulation there.

About my recent edits: It is you who is not sticking to what the sources actually said. MvS did not say that "letting the host choose a door with the car" was the only strategy that was not a part of her problem. She said it was the most significant, of of all the conditions she assumed were defined by her answers. That also incldues anything that would prevent her 2/3 answer from being correct. Every single one of her answers makes the assumptions that render Morgan's formula useless. You have to realize that she needs to compact her column into very few words, and so is not addressing the problem rigorously. And shouldn't be expected to. The only mention of anything having to do with assymetric probabilities CAN ONLY APPEAR in the "variants" section.

Morgan, at al, do not, EVER, claim that their formula answers the question in the MHP. In fact, they say it doesn't. With emphasis added: "In general we cannot answer the question 'What is the probability of winning if I switch...' unless we either know the host's strategy of are Bayesians with a specified prior." This is why the question you keep refusing to give a direct answer to is important. It says we don't "know the host's strategy" and are not "are Bayesians with a specified prior." The direct answer you shodl give means that, by their own admission, MORGAN DOES NOT APPLY. Anything they conclude applies only to their variant, and only then if one of these conditions they describe holds. It does not help to "wonder" what the possibilities might be, except in the case where every answer to that wondering says "switch." WHICH WAS MORGAN'S THESIS. JeffJor (talk) 18:08, 14 December 2009 (UTC)

Glkanter: I've given up on getting Rick to stop using Morgan. It is a reference, and it claims to address the MHP (it doesn't, it addresses what they changed the MHP into), so he will forever stand behind his "Wikipedia Policy" arguments to say it must be included. (I can find an internet reference that claims the answer is 4/9 and has not been discredited, mainly becasue it can't be understood, but we won't quote it because we know what is wrong with it. Why we can't do the same with Morgan, since they misquoted the problem into something which is documented to be not the intent, I can't fathom.) The fact is, it is an interesting treatment, but of a variation. And the only reason I said your question wasn't well-asked, was because it allowed Rick to give his non-answer. We need to include the fact that it is only useful to "wonder" about other knowledge if the contestant can actually get it. And just one last comment for Rick: although you will say this is OR that contradicts Gillman, it isn't. It is a fact that Gillman glosses over because of the altered nature of his MHP. The q=1/2 approach is not just the equivalent to "announcing the switch strategy before a door is opened," it is equivalent to "announcing the switch strategy without knowledge of how the host chooses a door." Under Gillman's modificaiton, "before" is the time that is not known, at least until he assumes q=1/2 so that he can answer the question. JeffJor (talk) 21:06, 12 December 2009 (UTC)

JeffJor, oh, yeah, you've made the right decision. We have clearly demonstrated a consensus. Rick is going to use every method he can devise to extend his filibuster. There have been a lot of folks prior to us who ultimately made the same decision, to quit arguing with Rick. But we have proven the argument unlike anyone before us. "Suppose you're on a game show..." End of discussion on who's POV for the doors, and no more host behaviour. They used to argue 'little green men from space's' POV as being the MHP. I kid you not. And, no more host behaviour means no more Morgan. Of course, kmhkmh is still arguing the definition of a game show, but won't answer the 'Is The Contestant Aware?' question.

As far as the details, Morgan and his ilk get mentioned, they're published. But no more bad mouthing the Devlin solutions. Did you read my Huckleberry section? Please re-read my modified proposal. So, we just have to navigate Wikipedia's consensus processes. Rick is the king of that crap, so we'll learn as we go up the chain, whatever it is. Do you have any experience with that? So, a few of us will continue working together the straight path to improving the article. Glkanter (talk) 22:53, 12 December 2009 (UTC)

Moved conditional analysis involving host preference q to variant section

I think this is at least one of the changes that has been argued for, and I haven't seen anyone argue against it (and those of you who think this is what I have been arguing against are simply incorrect), so I've moved the paragraph about the Morgan/Gillman generalization introducing the host preference as a variable q to the Variants section. If anyone is arguing about this, feel free to revert. -- Rick Block (talk) 00:51, 13 December 2009 (UTC)

I think that is a good move but it still does not address the fundamental issue that many people here are concerned about, which is that the Monty Hall problem is a simple problem that most people get wrong. This article needs to reflect that fact, based on the many reliable sources that treat the problem simply (I am not going to mention the c-word). Martin Hogbin (talk) 17:50, 13 December 2009 (UTC)

I understand your point, but based on other comments there seems to be some confusion about what those of us who favor presenting a "conditional approach" as an equally valid POV are saying. Rather than argue generalities, I think it is helpful to see specific changes. My stance is that a single solution section, more or less like (and about as long as) this one is sufficient. I think it would be very helpful if you (or anyone) could draft a specific proposal (not just an outline, but actual content). With the amount of text on this page, we could have 5 or 10 specific proposals by now. -- Rick Block (talk) 18:45, 13 December 2009 (UTC)

Rick, you wrote this above: "..."conditional approach" as an equally valid POV...".

That's incorrect. It's an equally valid way to develop a problem statement. Unnecessarily complex, but valid. It is not, however an equally valid way to solve and explain the paradox. Glkanter (talk) 19:21, 13 December 2009 (UTC)

Hey Rick, we talked about this before:

"...The total probability must be 100%, and before the host opens a door it's surely 1/3 player's door vs. 2/3 for the other two doors (so 2/3 of the players who decide to switch before the host opens a door will win) but the only thing that keeps it that way after the host opens a door is that pesky equal goat door constraint. The best way I know to show that it CAN change is to contrast the problem as stated with a different problem (i.e. the aforementioned "host opens lowest numbered door possible" variant)...Rick Block (talk) 00:24, 27 October 2008 (UTC)"

"False. The only thing 'keeping it that way' is that pesky law of probabilty that the outcomes must = 100%. Glkanter (talk) 03:46, 27 October 2008 (UTC)"

The more things change, the more they stay the same, eh? Still using some so-called 'variant' to explain away the simple solutions. That doesn't even make sense from a mathematical standpoint. Oh, but now (per your paragraph above) you say they're 'equally valid'.

By now, your only remaining argument is that 'people could get confused', because the MHP only works with the particular set of premises given. The part about why it works may be true. The part about confused readers is your personal interpretation, and not supported by at least one editor who includes the problem in his course work. And it's certainly not Wikipedia's job to teach probability in the MHP Paradox article. Anything like that belongs in what I call the 'Diversions' section, if at all.

And there is no point whatsoever in creating mock articles until the consensus for the proposals has been 'certified' to your satisfaction. They are not ambiguous in any way regarding the minimal value of the 'conditional' approach. Anything else is just a waste of time, and feeds your filibuster. Glkanter (talk) 12:46, 14 December 2009 (UTC)

Proposed unified solution section

Here's a proposal for a unified solution section that I suggest replace the current two solution subsections. I offer this partly as an example of what I mean by a specific suggestion, and partly to show what I think would be a sufficient, NPOV, solution section.

---

According to the problem statement above, a car and two goats are arranged behind three doors and then the player initially picks a door. Assuming the player's initial pick is Door 1 (vos Savant 1990):

• The player originally picked the door hiding the car. The game host must open one of the two remaining doors randomly.
• The car is behind Door 2 and the host must open Door 3.
• The car is behind Door 3 and the host must open Door 2.

Players who choose to switch win if the car is behind either of the two unchosen doors rather than the one that was originally picked. In two cases with 1/3 probability switching wins, so the probability of winning by switching is 2/3 as shown in the diagram below. In other words, there is a 2/3 chance of being wrong initially, and thus a 2/3 chance of being right when changing to the other door. This result has been verified experimentally using computer and other simulation techniques (see Simulation below).

Combining doors solution

Player's pick has a 1/3 chance while the other two doors have a 2/3 chance.

Player's pick has a 1/3 chance, other two doors a 2/3 chance split 2/3 for the still unopened one and 0 for the one the host opened

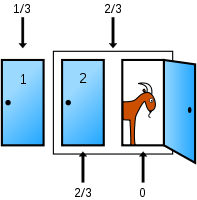
Another way to understand the solution is to consider the two original unchosen doors together. Instead of one door being opened and shown to be a losing door, an equivalent action is to combine the two unchosen doors into one since the player cannot choose the opened door (Adams 1990; Devlin 2003; Williams 2004; Stibel et al., 2008).

As Cecil Adams puts it (Adams 1990), "Monty is saying in effect: you can keep your one door or you can have the other two doors." The player therefore has the choice of either sticking with the original choice of door, or choosing the sum of the contents of the two other doors, as the 2/3 chance of hiding the car hasn't been changed by the opening of one of these doors.

As Keith Devlin says (Devlin 2003), "By opening his door, Monty is saying to the contestant 'There are two doors you did not choose, and the probability that the prize is behind one of them is 2/3. I'll help you by using my knowledge of where the prize is to open one of those two doors to show you that it does not hide the prize. You can now take advantage of this additional information. Your choice of door A has a chance of 1 in 3 of being the winner. I have not changed that. But by eliminating door C, I have shown you that the probability that door B hides the prize is 2 in 3.'"

Car hidden behind Door 1		Car hidden behind Door 2	Car hidden behind Door 3
Player initially picks Door 1
Probability 1/3		Probability 1/3	Probability 1/3
Host randomly opens either goat door		Host must open Door 3	Host must open Door 2
Switching loses		Switching wins	Switching wins

Tree showing the probability of every possible outcome if the player initially picks Door 1

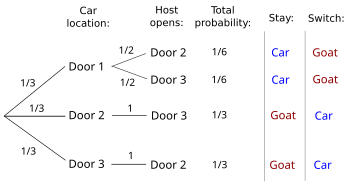
Another way to analyze the problem is to determine the probability in a specific case such as that of a player who has picked Door 1 and has then seen the host open Door 3, as opposed to the approach above which addresses the average probability across all possible combinations of initial player choice and door the host opens (Morgan et al. 1991). This difference can also be expressed as whether the player must decide to switch before the host opens a door or is allowed to decide after seeing which door the host opens (Gillman 1992). The probability in a specific case can be determined by referring to the expanded figure below (note the case where the car is behind Door 1 is now the middle column) or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138). Considering only the possibilities where the host opens Door 3, switching loses with probability 1/6 when the player initially picked the car and otherwise wins with probability 1/3. Switching wins twice as often as staying, so the conditional probability of winning by switching for players who pick Door 1 and see the host open Door 3 is 2/3—the same as the overall probability of winning by switching. Although these two probabilities are both 2/3 for the unambiguous problem statement as presented above, depending on the exact formulation of the problem the conditional probability may differ from the overall probability and either or both may not be able to be determined (Gill 2009b), see Variants below.

A formal proof that the conditional probability of winning by switching is 2/3 using Bayes' theorem is presented below, see Bayesian analysis.

Car hidden behind Door 3	Car hidden behind Door 1		Car hidden behind Door 2
Player initially picks Door 1
Host must open Door 2	Host randomly opens Door 2	Host randomly opens Door 3	Host must open Door 3
Probability 1/3	Probability 1/6	Probability 1/6	Probability 1/3
Switching wins	Switching loses	Switching loses	Switching wins
If the host has opened Door 3, this case has not happened		If the host has opened Door 3, switching wins twice as often as staying

---

I have tried to remove any POV-ish statements in the above. If there's anything left that does not sound NPOV please either just fix it or discuss here. The idea is to present both a plainly correct unconditional solution (it's basically vos Savant's from her second column) as well as a plainly correct conditional solution, without expressing a preference for either treatment. -- Rick Block (talk) 19:12, 14 December 2009 (UTC)

And I don't think you did a good job of removing your POV, Rick. It's all through the second paragraph, as you try to make it sound like what we want while leaving Morgan in it. My criticisms will address that, and hopefully suggest NPOV corrections, soon.

The 3-point options at the start, and the following diagram, present the unconditional solution (e.g., Door #2 gets opened in some cases), yet seemingly claim to follow from the K&W statement. To use this approach (which we should), this part needs to attribute it to the MvS statement, and not use door numbers. (This is consistent with MvS's answer, which refers to "the first door" and "the second door".) The following preserves her use of examples while not requiring door numbers:

According to the Parade problem statement, a car and two goats are arranged behind three doors. The player initially picks one, and the host always opens a different door with a goat, choosing at random if necessary (Seymann). (Aside: Seymann does not say the MvS problem statement is ambiguous, as the article currently claims. Seymann says the assumptions should be inferred from intent, and intent is quite clear from her solutions and following columns. Seymann is chastising Morgan, et al, for not using this clear intent. Seymann does say the host chooses randomly, as an "agent of chance".)

Car hidden behind chosen door		Car hidden behind first unchosen door	Car hidden behind second unchosen door
Host randomly opens either goat door		Host must open second unchosen door	Host must open first unchosen door
Probability 1/6	Probability 1/6	Probability 1/3	Probability 1/3
Switching loses	Switching loses	Switching wins	Switching wins
Switching loses half as often as it wins		Switching wins twice as often as it loses

The second paragraph does not match the decision tree it says it matches. It is trying to address the conditional solution without assymetric probabilities, yet duplicates the diagram's unconditional treatment. So, it should cite G&S only, not Morgan, because this "symmetric conditional" treatment is far closer to their treatment than Morgan's. I'm not going to try to draw a tree, but it is in G&S as Figure 4.4 (the existing tree misrepresents it). We can include the "disallowed" options that the existing tree does, opening Door #2, by making it clear how they are disallowed by G&S. Make them a different color, add a column that says "didn't happen." Alternately, it could just trim the diagram down, like G&S trim thier tree down.

Another way to analyze the problem is with conditional probability, as the specific case where the player has picked Door 1 and the host has opened Door 3. This contrasts with the approach above which addresses the average probability across all possible combinations of initial player choice and door the host opens. The probability in this specific case can be determined by referring to the decision tree as (will be) shown to the right (Grinstead and Snell 2006:137-138). Considering only the possibilities where the player chooses Door #1 and the host opens Door 3, switching loses with probability 1/18 and wins with probability 1/9. But these possibilities comprise only 1/6 of the total possibilities, so their probabilities must be divided by 1/6 in accordance with Bayes Rule. Thus we get the same overall probability of winning by switching as before. And while these two probabilities are both 2/3 for the problem statement as presented above, if there is reason to beleive that the host prefers to open one door over another, the conditional probability may differ from the average probability that disregards which doors are chosen (Grinstead and Snell 2006:137-138, see Variants below.

I left it as "there is reason to believe" rather than the correct "the player has reason to believe" to keep what Rick thinks is POV out. The content of this section now matches G&S in every way, except it is a paraphrasal. G&S is aimed at students of probability, where we want to aim at non mathematicians. JeffJor (talk) 16:17, 15 December 2009 (UTC)

The problem is that the diagram is still complicated by the fact that it shows the host opening one of two doors. You are stuck in the world of door numbers. I would prefer this diagram (with pretty pictures) and some explanation:

1/3		1/3		1/3
You choose a goat		You choose a goat		You choose a car
The host opens a door to reveal a goat		The host opens a door to reveal a goat		The host opens a door to reveal a goat
You Stick	You Swap	You Stick	You Swap	You Stick	You Swap
You get a Goat	You get a Car	You get a Goat	You get a Car	You get a Car	You get a Goat

Martin Hogbin (talk) 19:38, 14 December 2009 (UTC)

So, you're OK with the words but not the diagram? Comments from other might be nice, but one thing I like about the diagram is that it SHOWS the symmetry (the diagram is symmetric). -- Rick Block (talk) 19:52, 14 December 2009 (UTC)

I think this whole thing is a nightmare giant step backwards into an abyss. How did the Combined Doors solution get eliminated? Why? There is no need to include 1/6 in any explanation of the paradox. 'Simulations' as 'proofs'? Please. And I don't understand why editing is being discussed prior to the consensus being recognized. Just more filibustering. Enough, already! Glkanter (talk) 20:45, 14 December 2009 (UTC)

Glkanter - Where did combined doors go? Well, I think vos Savant's solution is clear enough for nearly anyone. Most of the folks who talk about "combining doors" offer it as an aid to understanding, so it could certainly go there (and, let me just say, for one who is so against variants of the problem, your attachment to this explanation is incredibly incongruous). 1/6 is included because it is what the unconditional probability of the player's initially selected door becomes in the cases where the host opens each door, just like the sources say (the probability tree is directly from Chun, 1991). The forward reference to the Simulation section is there because some people trust simulations more than logic. If you don't want it, let's just delete it and see if anyone objects. I'm trying to work toward a specific compromise we can all live with. -- Rick Block (talk) 02:58, 15 December 2009 (UTC)

Binary choices don't offer 'compromise'. The simple solutions are more than sufficient. Let's get the Formal Mediator to acknowledge the consensus to make the proposed changes. I think a lot of what is taking place lately does not represent a good faith effort at recognizing the consensus that clearly exists. Did Huckleberry get it right or not? Is the contestant aware? These are direct yes/no questions, not 'yes, but'. You are THE LAST person who should be leading the editing effort. Maybe you haven't accepted it yet, but your 6 year crusade was misguided. Simply wrong. Just like I've been trying to tell you for 14 months. I'd appreciate it if you'd stop all this mis-direction, and let the consensus edit the article as proposed, finally. Glkanter (talk) 03:25, 15 December 2009 (UTC)

Any other comments? I'm particularly interested in comments from the folks Glkanter is considering part of the "consensus", i.e. JeffJor, Colincbn, Boris, and Melchoir. -- Rick Block (talk) 14:29, 15 December 2009 (UTC)

Which of your various roles are you in when you ask this question, Rick? Editor, Owner, FA Shepard, or Junior Moderator? Glkanter (talk) 14:37, 15 December 2009 (UTC)

Glkanter - I see you've edited in the combining doors solution. Does this mean you're more or less OK with a single solution section? I'd prefer for the combining doors bit to be in an aid to understanding section (it's even phrased that way "Another way to understand the solution ..."). Do you consider this a deal breaker? I'm curious what others think about this. -- Rick Block (talk) 19:33, 15 December 2009 (UTC)

Jeff - Aside from some minor quibbles (which I don't have time to enumerate at the moment - I will later, although perhaps not until tomorrow), I'm more or less OK with your version of the conditional analysis. Not minor - I assume you don't mean for the aside to be in the article. Please say what you think about including the "combining doors" bit in the solution section. -- Rick Block (talk)

Martin - Is Jeff's version of the image more to your liking? -- Rick Block (talk) 19:33, 15 December 2009 (UTC)

Anyone else have any comments about all of this? -- Rick Block (talk) 19:33, 15 December 2009 (UTC)

Rick, you continue to be confused. There are no 'deals'. And you are NOT the deal maker. You chose to not be part of the consensus. It makes no sense, then, for you to be proposing what the consensus wants. I wish I had a way to just make you stop. I don't, of course. I have, over 14 months used the Combined Doors solution as the published simple solution to support my agrument with you and the others. You all continue to post, even today, that I don't understand the problem, or worse, actually. But, Devlin's solution was right and proper all along. And it's in the article that way now. Only YOU would think of removing it. Certainly not me. And I don't foresee a 'Unified solution' section, or a 'disclaimer' of any sort. It's not correct. That's why I proposed a brief section summarizing the 6 years and soon-to-be 10 archives of arguments, and why the consensus supports the simple solution. Glkanter (talk) 19:56, 15 December 2009 (UTC)

Here's my interpretation of Wikipedia policy, speaking as an admin. Consensus applies to changes to articles (even specific changes), not to groups of editors. No editor is more or less a part of the consensus for any individual change than any other editor. Trying to cut off discussion about a specific suggested change is classic disruption. -- Rick Block (talk) 21:09, 15 December 2009 (UTC)

But Rick, you are not part of the consensus. You are against the proposals. Or has that changed, and mediation is no longer required? Glkanter (talk) 21:30, 15 December 2009 (UTC)

And if you honestly believe I am attempting to violate disruption, I suggest you follow the procedures necessary to stop me. Otherwise, I'll consider the threat just one more of your endless filibustering techniques, not offered by you in good faith. Glkanter (talk) 21:40, 15 December 2009 (UTC)

Martin's suggestion

I would like to see 'combining doors' back at the start of the article along with my suggestion above. I think that most people will agree that these are the most convincing explanations of the basic problem (where the issue of conditional/unconditional is deferred to a later section). These diagrams should be accompanied by new wording specifically relevant to the explanations shown in the diagrams. This should be followed by 'Aids to understanding' and 'Sources of confusion' relating to the simple solutions - this is what the Monty Hall Problem is all about.

After the above we should explain why some formulations of the problem are, strictly speaking, conditional (with reference to the Morgan paper) and why this fact is not so important for the symmetrical case.

Then we should have a section on variants, the most important of these being 'the host chooses any unchosen door randomly', but including the Morgan scenario, 'we are aware of the host door opening policy'. We can then have more on sources of confusion etc as it relates to the more complex cases. That is what I would like to see. Who agrees? Martin Hogbin (talk) 15:18, 15 December 2009 (UTC)

Just to add, I would not object to a brief and mildly worded disclaimer at the start of the simple solution to the effect that some academic sources insist the problem must be treated conditionally but, for simplicity and clarity, these issues are discussed in a later section. Martin Hogbin (talk) 15:22, 15 December 2009 (UTC)

The so called "combining doors solution" is in a certain sense the worst of all. Let me try to make this clear to you. Choose door 1 and start from this situation: then with prob. 1/3 the car is behind door 2 and also with 1/3 behind door 3. Formally: P(C=2)=P(C=3)=1/3. That's why we can say: P(C=2 or C=3) = 2/3 (doors combined). But there is no immediate logical reason why this should lead to the prob. 2/3 that the car is behind door 2 when door 3 is opened. We know P(C=3|H=3)=0, but this does not imply that P(C=2|H=3)= 2/3. Only if one reasons that from symmetry it follows that {H=3} is independent of {C=2 or C=3}, one may conclude that also P(C=2 or C=3|H=3) = P(C=2 or C=3) = 2/3, and hence P(C=2|H=3) = 2/3. Even then as you may note is the prob, of interest the conditional prob. I'm pretty sure however most of the readers do not understand this independency, but simply have no idea of the different prob.s and follow a wrong way of reasoning. BTW also some referred sources do! Nijdam (talk) 22:25, 15 December 2009 (UTC)

I accept what you are saying. The issue is addresses in words by Adams, who says (without proof) '...as the 2/3 chance of hiding the car hasn't been changed by the opening of one of these doors'.

On the other hand, three sources use this approach and I think it is intuitively acceptable to many people. What about having footnotes for the two simple solutions saying something along the lines of, 'There are some important complicating issues here which are discussed later but, as it happens, if the host chooses randomly they do not affect the result'. This has the advantage of not affecting the simplicity of the explanation but drawing attention the the complication issues for those interested. Again, this approach is not uncommon in maths text books. Martin Hogbin (talk) 10:00, 16 December 2009 (UTC)

Being a lay person, I'm curious, what was the outcome of all the work Boris did? He said his mission here was finished. Devlin, Adams, etc. are published, and a consensus is that their approach has NOT been mathematically refuted by Morgan and the others. There's no complication with the MHP, the complication is with the 4 confused sources which do NOT address the MHP. I've suggested a brief paragraph after the simple (only) solutions that summarizes the lengthy discussions that have taken place as the appropriate way to recognize Morgan and the others. Glkanter (talk) 11:29, 16 December 2009 (UTC)

Again, I'm not sure where to insert comments. (1) On my "aside": Yes, Rick, it was meant to be left here, not included in the article. That's why it is an aside. I didn't want you to change the text again to match your POV of what Seymann says, or to continue thinking than nobody had ever refuted Morgan's assertion that the door numbers were intended. That was refuted when Morgan published. (2) I'm not a great fan of the "combining doors" explanation, because it is a (very slightly) different problem. But not anywhere close to as different as Nijdam claims. The only difference is that you shold get the better of the two prizes, not both. (For Nijdam: the Host's required behavior, revealing an unchosen door with a lesser prize, is logically equivalent to the switching player receiving the better prize of the two unchosen doors. That is indeed an "immediate logical reason" for the 2/3 probability applied to the combination. But Carol Merrill should lead a goat out of the combined doors, in such a way that you don't know where it came from, for it to be the same problem. It is when we translate the combined-door probability back to the original, unopened Door #2 that it can be associated with one door only). I just don't know of a source that explains it my way. Delvin comes close, since he used empty doors instead of goats. But it is a good way over the intuition bubble, as Delvin explains; so the only reason to not use it is if we have too many explanations. I'm not sure which we are proposing keeping. We need at least one basic solution (as I did above), and one explanation for why it works (like combining doors). I don't consider the conditional probability one I listed "basic," but I'm not going to fight including it. That does, however, limit what other "basic" solutions we could use, because we lose readers if we over-explain. (3) We need a disclaimer with the full Morgan conditional statement. Not before. The disclaimer is that some advanced treatments consider it a Door 1/Door 3 issue; but that that was never the intent of the originators, has been denied by the originators, and is not even universally accepted. Then add that even those who use it remove the dependency on those door numbers before addressing "Should the contestant switch?" Essentially, the full conditional solution is a tool only. JeffJor (talk) 17:17, 16 December 2009 (UTC)

@JeffJor: Show me the way you interpret the problem (with reference), and give me the solution in proper terminology. Nijdam (talk) 11:05, 17 December 2009 (UTC)

Nijdam, how does this question differ from the issue you and Boris analyzed? Boris declared his mission finished. I'm beginning to think that like Rick, you are simply using various filibustering techniques to avoid recognizing the legitimate consensus for the proposed changes. Why don't you ever answer my questions? I imagine Socrates would have. Glkanter (talk) 12:08, 17 December 2009 (UTC)

OH MY GOD!!!

Holy cow. I went camping this weekend and I woke up in the tent in 33 degree F. cold trembling in a cold sweat, having a nightmare about goats and shiny cars and numbered doors and a genetic-cross monster whose body was that of a water buffalo and the head was that of Thomas Bayes, and everyone was throwing food about and nobody knew whether everything or anything is random or predetermined and people were capriciously changing their minds in the middle of the game conditionally and unconditionally, and I decided that I would just run off and try to re-read "Kant's Critique of Pure Reason", and then maybe shoot myself. That might be easier. :o) Worldrimroamer (talk) 02:04, 15 December 2009 (UTC)

OK, folks ... please don't fuss at me. I was only kidding. Worldrimroamer (talk) 02:08, 15 December 2009 (UTC)

Why Wait To Edit The Article & FAQs As Per The Proposals Supported By The Consensus?

There's plenty of editing of the article currently taking place, including by Rick Block, who is not part of the consensus.

Why couldn't the consensus just go ahead and begin fixing the article, so that it is in line with the proposals? Glkanter (talk) 11:51, 15 December 2009 (UTC)

I think the article is OK through the Popular solution. Then the Probabilistic solution begins all the trouble with the gibberish and double talk about Morgan's stuff.

Let's put a paragraph right after the Popular solution that discusses why the Morgan solution, while published, is considered to be discussing a different problem.

Then we replace nearly all the text of the Probabilistic solution, and replace it with how to do the conditional solutions.

Beyond that, it's just chatter, that hopefully most readers won't need. Unless there's something in all that which denigrates the Popular solutions, I would just let it be for now. Glkanter (talk) 12:17, 15 December 2009 (UTC)

The article is not protected. Anyone can make whatever change they'd like, and to a large extent making a change and seeing that it is not reverted is how consensus is demonstrated (see WP:BRD). I think you should also really read WP:BATTLE. -- Rick Block (talk) 14:46, 15 December 2009 (UTC)

How do we resolve the inconsistency between the Contestant's POV in the MHP, and the "unknowns'" POV in all the host variant stuff? Especially that large table. The whole thing makes no sense to me. Glkanter (talk) 15:08, 15 December 2009 (UTC)

Are you suggesting this section is not a neutral recounting of what reliable sources say? Or is your problem that you don't understand it? -- Rick Block (talk) 15:40, 15 December 2009 (UTC)

Like many things in the article it is inconstant from a logical standpoint. The MHP, as you know, is from the contestant's POV. All these so-called 'variants' are solved from some 'unknown' person's POV. So that's inconsistent. Even worse, since it's not the contestant's POV, it's not the MHP. I just don't see much value there. Maybe a section with links, and that's it.

I understand the problem just fine, thank you. I'm just waiting for you to (finally) cry 'uncle'. I think you should also really read WP:BATTLE. Glkanter (talk) 16:05, 15 December 2009 (UTC)

I'm Ready for Formal Mediation

I suggest we quit waiting around for the informal mediation. There may never be a volunteer.

Formal Mediation is the next step, then arbitration.

Is there a second to my motion? Glkanter (talk) 15:26, 16 December 2009 (UTC)

Is Rick's diff out of control consistent with our efforts to find an unbiased informal mediator? Or has he made that impossible?

"==Please help==

"The situation at talk:Monty Hall problem is really getting out of control..." Rick Block (talk) 15:34, 15 December 2009 (UTC)"

Glkanter (talk) 20:22, 16 December 2009 (UTC)

I've asked the chair of the mediation committee what a reasonable length of time to wait for an informal mediator might be before proceeding with a formal mediation request. See User talk:Ryan Postlethwaite#Mediation question. -- Rick Block (talk) 02:06, 17 December 2009 (UTC)

Wiki-Ego

I can see why someone who has a great deal of time, effort and pride invested in Wikipedia would be protective of his work. Especially if the only Featured Article which he personally 'sheparded' through the review process was at risk of being dramatically revised. Revised so much, that the FA designation would likely be at risk.

But there is a difference between understanding and condoning. In addition to all the filibustering that takes place on the talk pages, these phrases were used when requesting (supposedly) un-biased assistance as per Wikipedia policy:

"...This is a featured article that has been through 2 FARCs..." - Request to Mediation Cabal

"...The situation at talk:Monty Hall problem is really getting out of control..." - 2nd request to Mediation Cabal

"...At least one of the other editors involved is agitating to proceed with formal mediation..." - 3rd request, sent to Ryan Postlethwaite, Chairperson of the Mediation Committee

So, I can see why an owner of an article would reject all good faith efforts at improved clarity. I just don't agree with the continual passive-aggressive intellectual dishonesty that I have witnessed throughout the 14 months I've been active on this article. I've got a lot of time, effort and pride invested in this article, too. And I'm part of a legitimate consensus for making the proposed changes. That's why I point out, without hesitation, when I think another editor is not behaving in good faith. These aren't personal attacks. They are a recognition of why the article has been so wrong, for so long, despite the efforts of so many 'agitating' editors who disagree with the "shepard's" POV.

Some people will argue that this discussion is out of line. But everything I wrote is supported by diffs. Why fear the truth? I would reply that the criticisms would come from those who favor the status quo for the article. Glkanter (talk) 13:05, 17 December 2009 (UTC)

This rant is nothing but another in your continuing series of disruptive edits. Please stop. -- Rick Block (talk) 13:43, 17 December 2009 (UTC)

Call it 'disruptive' if you want. I call it honest. There's been no edit warring by anybody. No profanity on the article's various talk pages. Nothing disruptive at all, other than your endless filibusters, despite a consensus to proceed. Just things you find uncomfortable. All these discussions show good faith by many people that they're looking for a proper Wikipedia solution. The only 'disruption' was Dicklyon's unprovoked savage violation of my MHP talk page new section. I noticed you didn't admonish him at the time. Not a peep out of you, the self-appointed Monty Hall problem Admin and Mediator. But you told a buddy, whom you may have been trying to recruit to mediate this dispute, that 'I chased him away'. Dicklyon takes no responsibility whatsoever for his own reprehensible actions, and you defend him. That's intellectually dishonest. And you know it. Glkanter (talk) 15:12, 17 December 2009 (UTC)

Kanov Is Wrong

The article states (without citation) that Kanov stated that in the "Ignorant Monty" case, swapping still yields a 2/3 chance of winning - but a quick simulation of all cases reveals this to be wrong: suppose I pick door 1, and Monty opens door 2 without knowing what is there but reveals a goat (all other permutations are equivalent to this): the car will now be behind either door 1 or door 3 with a 1/2 probability. --New Thought (talk) 09:44, 19 December 2009 (UTC)

You are quite right. Because of all the argument here nobody has noticed a simple error. There seems to be a section based on a the supposed opinion of a mysterious Kanov. I will remove this unless someone can explain why I should not. Martin Hogbin (talk) 10:54, 19 December 2009 (UTC)

I've wondered about this, going back to the summer. If I recall correctly, Marilyn vos Savant says it's 1/2 because of the plays that get eliminated by Monty revealing a car. I might suggest that once the contestant is faced with the two doors and a revealed goat, it's the same 1/3, 2/3 as the original MHP. Then I have to figure out how this is consistent with Deal or no Deal, which says there is no advantage to switching.

Vos Savant is correct. If Monty chooses any unchosen door randomly you have to decide what to do if he reveals a car, asking the player whether she wants to change after a car has been revealed is pointless. Easiest would be to replay those games from the start. Games where Monty reveals a car are therefore discounted. These games can only be ones where the player has originally chosen a goat because, if the player has originally chosen the car, the host cannot reveal it. Thus in the 'Ignorant Monty' case we remove some games where the player originally chose a goat but none where she originally chose the car, thus her chance of having originally chosen the car goes up. Martin Hogbin (talk) 18:56, 19 December 2009 (UTC)

Martin - I don't think you're addressing the issue. I believe the confusing scenario is a specific show, say last Tuesday's, where Glkanter was the contestant. On this show, he's initially picked a door, say Door 1, and Monty has forgotten where the car is. He says "Oh dear, I've forgotten where the car is. I hope this works out OK - Carol, please open a random unchosen door". And, fortuitously, the door that is opened, say Door 3, reveals a goat. There is no decision about what to do if the car is revealed, because the car simply wasn't revealed. Glkanter's initial choice has a 1/3 chance of having been correct. The chance the car is behind the open door is clearly 0. The other one must have a 2/3 chance.

That is the issue I addressed. I explained why the probability that the player has chosen the car increases when Monty reveals a goat by chance. Even for the one-off case the fact that Monty has chosen randomly but in fact revealed a goat means that the player is more likely to have chosen the car. Martin Hogbin (talk) 20:15, 19 December 2009 (UTC)

Glkanter - is this more or less what you're thinking? -- Rick Block (talk) 19:41, 19 December 2009 (UTC)

Did you really do a simulation? Glkanter (talk) 14:15, 19 December 2009 (UTC)

The original sources are correct. "Kanov" is presumably the name of the anonymous editor who put this in the article (yesterday). I've reverted this change.

Glkanter - the probability this is talking about is precisely the one applying to the contestant faced with two doors and a revealed goat (in a case where the host has randomly, but successfully, opened a door revealing a goat). Perhaps Martin or JeffJor could explain to you why the "combining doors" solution (or any of the other unconditional solutions) do not apply, and why the probability is indeed 1/2 in this case. This is not a sarcastic suggestion - I could try to explain it but I doubt that you'd be willing to listen to me. -- Rick Block (talk) 17:24, 19 December 2009 (UTC)

It's a different problem, what you call a 'variant'. I offered my two cents on a talk page. I figured I might regret it. Glkanter (talk) 17:42, 19 December 2009 (UTC)

Even though this problem is always described as "counter-intuitive", I find it interesting that EVERYONE on Earth understands the problem intuitively if you look at it another way: When you watch Deal or No Deal, the only reason it's suspenseful is because the person opening a case does NOT know if there's a big number inside that case. If you were on a Monty Hall Problem game show, and picked door #1, and the host said "I'm going to open a door now... hmmm... number 2" (ignorant monty - or at least from the player's POV, you must assume ignorant monty), you would be worried and suspense-filled that he might open the door with the car. When he doesn't, you feel relief. However, if Monty said, "Now, let me open a door with a goat in it... number 2" you would feel no suspense. He has told you the door has a goat, you know it's a goat, and it has no suspense. This is because there is no risk in him opening a door. He will always open a goat door. If your odds of having a goat behind your original selection improved, you'd be excited after he revealed a goat, but because he knows it's a goat, you feel no more excited about your first choice than before he opened the good. This is an example of how people DO intuitively understand this, but then don't recognize the ramifications of this feeling when offered the choice to switch observe below:

Interesting. Martin Hogbin (talk) 20:19, 19 December 2009 (UTC)

Here is an analysis of all cases when the car is behind Door number 3 (logic dictates that there are tables for the car behind behind doors 1 and 2 that have identical probabilities (for the appropriate doors). The number at left is the door you choose; the number at the top is the door Ignorant Monty opens. The result is whether you should switch ("y" or "n"). "c" represents Monty revealing the car.

	1	2	3
1		y	c
2	y		c
3	n	n

1,1 2,2 and 3,3 are greyed out, because he can't open the door you chose. As you can see, there are two cases where switching nets you a car, and two cases when it does not. There are also two cases where he reveals the car ("c") and you are (presumably) not offered a choice, as the car location is now known. Ignorant Monty has a 1/3 chance of revealing a car and ending the game. ONCE that does not happen, there are four possible cases left, 1/2 of which require switching to win, 1/2 of which require keeping to win. This is the conditional probability of "What is the probablity that switching will win GIVEN that Montry did not reveal the car?" The absolute probability is absolutely true - even with ignorant Monty, switching will win you the car 1/3 of the time - 1/3 of the time staying will win, and 1/3 of the time Monty will reveal the car, and you will not get the option.

Regular Monty has 0 chance of revealing a car. While regular monty has a decision to make SOMETIMES (if you select the car, he must pick which goat to reveal), as long as his pick is random, the result of his pick are both the same: you should still not switch, (so the conditional probability of winning by switch IF monty randomly selects one door or the other is 0 in both cases - you can't win by switching). Thus, if you picked right the first time, don't switch. If you picked wrong the first time, DO switch. Therefore, 1/3 of the time, don't switch, 2/3 of the time, switch.

This is true in the ignorany monty case also: If you picked wrong (2/3), do switch. If you picked right (1/3) don't switch. However, half of the time when you pick wrong (half of 2/3 = 1/3), Monty reveals the car, and you don't get to make a choice. Therefore, IF you get the option to switch (only 2/3 of the time will you get this far), then the odds are even between keeping (1/3) and switching (1/3) (the other third is monty reveals the car). TheHYPO (talk) 19:47, 19 December 2009 (UTC)

As a PS: I thought I'd explain the difference in why one is conditional and one is not: remember that if you have four cases: in order to say that any of them has a 1 in 4 chance of occuring, there MUST be an equal chance of each occuring. In the original monty hall problem (let's say car is behind door 3):

1. If you pick door 1 (1/3 chance), he MUST open door 2 100% of the time (thus, also 1/3 chance).
2. If you pick door 2 (1/3 chance), he MUST open door 1 100% of the time (thus, also 1/3 chance).
3. If you pick door 3 (1/3 chance), he could open doors 1 or 2 (if he picks randomly, 50% chance of either).

As you can see, your choice of doors all have an equal 1/3 chance of occuring, there are four 2nd step cases ([you:1 monty:2], [you:2, monty:1], [you:3, monty:1], [you:3, monty:2] with DIFFERENT probabilities of occuring (1/3 each for the first two - both of which say "switch", 1/6 each for the second two - both of which say "don't switch"). Thus some people claim that logically, two of those four 2nd step cases say "switch" and two say "stay" - that's 50/50. But two cases occur half has often has the other two. In the Ignorant Monty problem, all 6 cases in my table above are equal probability (1/6). This is because when you pick a "wrong" door, he has two options, not one. so your 1/3 choice results in two 1/6 choices for Ignorant Monty (one of which reveals the car and ends the game). If he DOESN'T reveal a car, you're left with four cases with initial probability of 1/6, and thus, each case NOW has a 1/4 chance (two win by switch, two lose by switching, thus 1/2 chance of winning by switching.) TheHYPO (talk) 20:08, 19 December 2009 (UTC)

Technology required new section.

I believe I correctly summarized vos Savant.

Let's re-apply some things we've learned: 'Suppose you're on a game show...' Still true? Contestant's SoK? 'Random' would equal Deal or No Deal. 'He's drunk' or 'forgetful' might not be communicated to the contestant. Then it's still the MHP from the contestant's SoK.

What exactly is the revised problem statement? —Preceding unsigned comment added by Glkanter (talk • contribs) 20:04, 19 December 2009 (UTC)

The probability from the contestant's point of view depends on the contestant's knowledge of the game rules. If the contestant is told the host knows what is behind the doors and will always choose a goat then the probability of winning by switching is 2/3 from the contestant's POV (SoK). If the contestant knows the host is choosing another door randomly (and then is relieved to see a goat revealed - see comment above) the probability of winning by switching is now 1/2. Is that your understanding? Martin Hogbin (talk) 20:28, 19 December 2009 (UTC)

By 'random' I mean 'car or goat revealed by Monty'.

I don't thìnk your summary or Rick's summary reflect my thoughts on this puzzle. Have I been obtuse? Why summarize me at all? —Preceding unsigned comment added by Glkanter (talk • contribs) 21:03, 19 December 2009 (UTC)

It was meant to be an explanation of why the probability of winning by switching is 1/2 if the host chooses an unchosen door randomly (that is to say he might choose a car or a goat). You seemed uncertain as to whether you agree with this statement. Do you agree? Martin Hogbin (talk) 21:16, 19 December 2009 (UTC)

If the contestant is informed (that is, it's a premise of the puzzle) that the host is opening doors randomly, and may reveal a car, then it's Deal or No Deal. Rick had a very elaborate scenario for the 'drunk' or 'forgetful' Monty. What is communicated to the contestant prior to his decision? Is this still a game show, then? How is it stated as premises?

I'm just pointing out that 'random', or 'forgetful' still require 'formalized' problem statements, which may be different. Absent that, either, or any answer may be correct. I'm not real good at multi-tasking. I just had some thoughts that could have developed into something. But until we have the underlying MHP squared away, I find this personally distracting. Glkanter (talk) 21:27, 19 December 2009 (UTC)

Summary of opinions

I have added names to the sections below based on comments above. If I have got it wrong please move yourself.
Please do not make comments in this section.
Editors are invited to sign against their names to confirm that they are in the right section. Martin Hogbin (talk) 11:29, 5 December 2009 (UTC)

Martin, What exactly do you mean by "for change" and "against change"? Dicklyon and JeffJor's opinions (for example) seem very different to me. By categorizing them both as "for change" I think you may be misrepresenting the situation. It would be better to be more specific about what change you're talking about, i.e. Glkanter's suggestion (remove any mention of conditional probability and any host behavior variants) Eliminate all 'host behaviour, etc' influenced discussion, save for the Wikipedia minimum necessary references to Morgan and his ilk, JeffJor's suggestion (separate articles - basically Glkanter's suggestion plus create a new article for the "conditional" treatment), your suggestion (I'm not exactly sure precisely how to summarize yours). In addition, rather than "against change" the other alternative should probably be described in terms of what it is for, which I think could be described as "present both unconditional and conditional solutions without taking a POV about the validity of either one". And, I'll note that for the article to say that Morgan et al. criticize the unconditional solutions is not the same as taking that POV. You do understand this difference, don't you? -- Rick Block (talk) 16:52, 5

Although there may be some discussion over the details it is fairly clear that several people would like to see the simple/unconditional solution/problem given more prominence here. This is the change that I am referring to. 'Against change' is fairly self explanatory Martin Hogbin (talk) 16:58, 5 December 2009 (UTC)

For change

Colincbn
Martin Hogbin Martin Hogbin (talk) 11:29, 5 December 2009 (UTC)
Glkanter Glkanter (talk) 12:16, 5 December 2009 (UTC)
JeffJor
Melchoir
Dicklyon
Boris Tsirelson Boris Tsirelson (talk) 15:27, 5 December 2009 (UTC)
Gill110951 (talk) 13:28, 20 December 2009 (UTC)

Against change

Rick Block
Nijdam
kmhkmh
Glopk

Unable to classify

Please move your name to the correct section if appropriate. Martin Hogbin (talk) 11:24, 5 December 2009 (UTC)
Henning Makholm
Chardish (I object to summary classification of my comments. - Chardish (talk) 00:59, 11 December 2009 (UTC))

Repeated text

Why does the entire Krauss and Wang text appear twice in the first bit of the article? Isn't the article long enough without this repetition? RomaC (talk) 14:48, 10 December 2009 (UTC)

Please see WP:Lead section. The lead is meant to be a concise, standalone overview of the entire article. The K&W problem definition was added to make the problem description unambiguous (even in the lead). I would be fine with deleting it and presenting only the Parade description. I predict others will object to this. -- Rick Block (talk) 15:44, 10 December 2009 (UTC)

Actually I kind of like the FARC lead better, it clearly states that the problem as stated in Parade is ambiguous. The K&W problem is in the beginning of the Problem section as an example of an unambiguous way of stating the problem anyway so I don't think it is entirely necessary in the lead. But I would rather work on consensus of the other suggested changes above before diving into those waters... Colincbn (talk) 16:10, 10 December 2009 (UTC)

Now I'm curious. Has Selvin's original statement been considered for the article? I've never read it. vos Savant made the MHP famous, but Selvin made it. Glkanter (talk) 16:16, 10 December 2009 (UTC)

Oohh, that might be a great idea. It would prevent repeating both the vS and K&W versions. of course there would also need to be a bit of rewording to make sure the information about the Parade article can stay in the lead and still make sense... Colincbn (talk) 16:27, 10 December 2009 (UTC)

Unlike the Parade statement of the problem, Selvin's statement is not very well known. It's also considerably longer. Because Jstor makes the first page of any reference available as a preview, it can be viewed online here. -- Rick Block (talk) 17:39, 10 December 2009 (UTC)

I like the solution though. Selvin's answer is published in a reliable source and I would like to see it in the article (but in the form of a pretty diagram). It treats the opening of either of the two unchosen boxes by the host as equivalent. Martin Hogbin (talk) 22:28, 10 December 2009 (UTC)

Isn't it funny how we've argued so much about vos Savant's failings and intents with the problem statement, and we never, since I've been around, discussed Selvin, et al's. I'm going to go read that page right now! I guess collaboration really can work. Who knew? Rick, thank you very much for the link! Glkanter (talk) 22:37, 10 December 2009 (UTC)

It says it all - it gives a simple solution (showing that the contestant has a 1/3 chance of winning if they stick and a 2/3 chance if they swap) and notes that the contestant's chance of having the car in their original box is unchanged at 1/3 after Monty has opened a door. Not only that but it was published in the same peer-reviewed journal as Morgan but it is not followed by a highly critical comment. Looks like a winner to me. Martin Hogbin (talk) 23:43, 10 December 2009 (UTC)

From a sourcing perspective, it is important to note that this is a letter to the editor, not an article. Articles from peer reviewed journals are usually the most reliable sources. Letters to the editor are more like primary sources. -- Rick Block (talk) 17:18, 11 December 2009 (UTC)

You might also be interested in Selvin's second letter in vol 29 #3. I can't find a pdf of the journal page online, but there's what appears to be a faithful copy here. Although I haven't compared it to the copy I have of the printed journal page, it's clearly missing a "/" on the 4th line of the conditional probability expansion. BTW - references to both of these have been in the article for several years. -- Rick Block (talk) 05:35, 11 December 2009 (UTC)

Thanks for that. It does not, in my opinion, discount the solution given the his original letter. The interesting point, when you look at that history of the problem, is that Monty actually never offered the swap and, if Selvin's account is accurate, it was the contestant who suggested it. Martin Hogbin (talk) 09:56, 11 December 2009 (UTC)

The other point which becomes apparent is that Monty, who was the only person who knew for sure his door opening policy, has clearly stated that he knew the contestants chance of holding the car remained at 1/3 after he had opened his door. That seems to me to rule out Morgan's conjecture that he might have had a preference for one door or the other. Martin Hogbin (talk) 09:56, 11 December 2009 (UTC)

Thanks, Rick, for finding a solution that resolves my concern (an overly long intro) Butwhatdoiknow (talk) 00:02, 21 December 2009 (UTC)

The Mathematics Rule I Am Properly Applying

Way back in junior high, we did some proofs or problems or something to do with absolute values. That's all I can remember.

But the thing I do remember is that after you 'solved' the problem, you had to go back and check each of the results to make sure it didn't violate the original problem statement in some way.

That's all I'm saying about Morgan and the rest. When you check your work with some 'host behaviour' variant, it no longer meets the original problem statement, "Suppose you're on a game show..." Go ahead and argue. Better you should save your breath. Hosts don't tell contestants where the car is.

So, as an encyclopedia, Wikipedia will properly refer to reliably published sources like Morgan. And Devlin. No problem.

But, as a self-appointed 'explainer' of all things MHP, I think the article improperly gives the conditional solutions way too much emphasis. Because it doesn't match the original problem statement any longer. Glkanter (talk) 21:47, 6 December 2009 (UTC)

Often one solves a problem by saying something like "let x be the distance travelled". One converts the problem to algebra, and finds a solution "x=-2 or x=3". Lazy students quit there. But good students think. We go back and remember that we wanted a distance and it had to be positive, so the real answer is x=3. This is a fine problem solving strategy. One solves a relaxation of the problem, that is to say one solves the problem while forgetting about some of the constraints, finds some answers, and then looks to see if any satisfy the original problem. But I wouldn't call this strategy a "mathematics rule". I'm not sure it applies in this case, where the original problem is somewhat ambiguous. It turns out that there are a number of interesting MHPs. Gill110951 (talk) 05:19, 22 December 2009 (UTC)

What I'm saying is that the so-called 'variants' do not satisfy the original problem. As I see it, the contestant being aware of any host bias is mutually exclusive with 'Suppose you're on a game show'. That's why the question the 'opposed' editors refuse to answer, 'Is the Contestant Aware...' is so pivotal to these discussions. A game-breaker, really. Glkanter (talk) 05:32, 22 December 2009 (UTC)

The Meta Paradox of The Monty Hall Problem Paradox

Selvin poses the MHp. He solves it unconditionally at 2/3 vs 1/3 if you switch. The problem is hailed as a great paradox.

vos Savant prints a letter inspired by Selvin in a general interest USA Sunday newspaper supplement. She solves it unconditionally at 2/3 vs 1/3 both when you made your choice, and when the switch is offered. Because Monty's actions don't impart usable knowledge to the contestant. It's a sleight of hand. Nothing happened.

All heck breaks out. Tens of thousands of letters, including over 1,000 from PhDs tell her she's wrong. And they are certain!

vos Savant soothes the savage beasts with logic and smarts. The unconditional solution carries the day. The problem is, again, hailed as a great paradox.

This group, "J. P. Morgan, N. R. Chaganty, and M. J. Doviak are Associate Professors and R. C. Dahiya is Professor, all in the Department of Mathematics and Statistics, Old Dominion University, Norfolk, Virginia" (284 The American Statistician, November 1991, Vol. 45, No. 4 (C 1991 American Statistical Association) develops the argument that the problem is only properly solved using a conditional problem statement. Their criticisms, etc. rest on this: That when faced with 2 goats, the host must decide which goat to reveal. This rests on the assumption (presumption, invention) that the contestant might somehow gain usable information as to the location of the car in this particular instance of the game by Monty's actions. It's left unstated whether Monty's actions would be shared with the contestant. And if they are shared, what method is used. But it's clear: in this instance of game play they claim, the subject contestant could be armed with more useful information that the average contestant.

The only problem is, their 'assumption' is not consistent with the first words of the MHP problem statement: "Suppose you're on a game show...", as Hosts don't tell contestants where the car is hidden. Actually, some Wikipedia editors have found a math error in the paper, and are in communication with the publication. Oh, and "Richard G. Seymann is Professor of Statistics and Business Administration, School of Business, Lynchburg College, Lynchburg, VA 24501" (1991 American Statistical Association The American Statistician, November 1991, Vol. 45, No. 4 287) wrote a paper that spoke only about Morgan's paper. It was included in the very same issue of the journal. It's weird. Is it a disclaimer, a clarifier? It's sure not an endorsement.

Others come out with papers supporting Morgans criticisms, including Gillman in 1992 and Grinstead and Snell 2006.

Others continue publishing unconditional papers. (It seems likely that if 3 Wikipedia editors plus Seymann find fault with the paper, so too would members of the Professional Mathematics Community. And as professionals, they don't make a big stink about it. They just ignore the paper and continue publishing articles that rely solely on the unconditional problem statement.)

So, has the Professional Mathematics Community decided that Morgan is right, and Selvin was a hack? I don't think so. Before, during and after Morgan's paper, respected, credentialed reliable Mathematics professionals continued to publish articles solving the MHP unconditionally. I don't know that any of these professionals in either camp have attacked or counter-attacked anyone else's paper. It looks to me, that in the Professional Mathematics Community nothing happened. No usable information was gained. Perhaps Morgan's paper, like Monty revealing a goat is just sleight of hand, imparting no usable knowledge? It's possible. Most published MHP articles say nothing of Morgan or conditionality.

Which brings us, finally, to the Meta Paradox. The Wikipedia editors are arguing, essentially, over whether or not solving the unconditional problem is 'enough'.

Suppose you are given a story problem about a game show. The Professional Mathematics Community agrees heartily that this is a delightful paradox which can be 'proved' or 'solved' using an unconditional problem statement. Maybe not even requiring formal probability notation. Symbolic notation is often used. Then "J. P. Morgan, N. R. Chaganty, and M. J. Doviak are Associate Professors and R. C. Dahiya is Professor, all in the Department of Mathematics and Statistics, Old Dominion University, Norfolk, Virginia" come forth and say it must be solved conditionally, based on the arguments set forth in their paper. You are then offered to stay with the unconditional solution being complete, or you may switch to the conditional solution.

Many people are fooled by this paradox, and accept the switch. Because they don't realize that like Monty revealing the goat, no new usable information has been revealed by this paper. Nothing happened. Glkanter (talk) 18:27, 8 December 2009 (UTC)

I like this way of looking at things! Except that there is no law against studying conditional Monty Hall problems, and quiz-players should also realize what they get when they go with the unconditional solution. So I think that something useful did come of the Morgan et al. contribution. Now we just need a reputable mathematician to publish a peer reviewed paper on the Monty Hall paradox paradox, and then wikipedia editors can write articles on it. Gill110951 (talk) 05:36, 22 December 2009 (UTC)

Glad you like it, thanks! It's a free country. They can do what they want. It just adds no value to those simply wanting to understand the MHP paradox. As the article is written, quite the opposite! There's an old salesperson's saying, 'Don't close past the sale' (it may actually be 'Don't sell past the order'). I may have had a professor say something like, 'Don't over-solve the test problems. Solve it and move on'.

Maybe you could look at my 'Huckleberry' section and tell me how his approach was insufficient, and how his results would have been improved by someone explaining to him the 'equal goat door constraint'? Glkanter (talk) 05:48, 22 December 2009 (UTC)

A comment from a newcomer to this discussion

Wow, this thread is long! And I haven't even looked at the archive(s?). I thought it might be worthwhile to make a comment as a person who has not been following this thread before now. I just, in the last couple of days, read the article and a big portion of the discussion.

My comment is simple: Please, I am not attacking anyone; I am just making a general, honest, respectful IMO comment. (And yes, I am schooled in mathematics.) I agree with those that say the article is too long, very unwieldy, and often downright confusing. I think the article as it now stands is almost worthless. I agree with those who say: Just state the "standard" problem as most people assume it is stated, and give a simple explanation as to why it is correct. Then meander off into the conditional and unconditional ponderings, the Bayesian statistics, etc.

I started out reading the article, with expectation of fun. I was already familiar what the "Monty Hall problem", and I understood it, at least in its more obviously stated form (based on the generally accepted assumptions). As I read on I thought, "Whaaa???" Much of the -- sorry, but most -- of the article is a murky mess, and even those who are somewhat probabilistically astute I think would have difficulty making sense of some of it. I'll cite just one example: The section titled "Popular Solution" is, IMHO, poorly written and confusing. Frankly, it's not clear what the author is meaning to get across in several places (even though I understand exactly what it is that he/she is intending to say). It needs to be rewritten, as does much of the rest of the article. Not tweaked, but rewritten. This sort of muddled presentation is just not necessary, and it is not worthy of the standards of Wikipedia. This stuff is not string theory or Gödel's incompleteness theorems in ZFC. This is introductory-level probability, albeit a very subtly tricky example of it.

I never seen an article on Wikipedia that has created such a WikeWar as this article has. It apparently has no resolution in sight. Anyway, I'm all out of suggestions -- if I have even made any.

Finally, just for fun, I wanted to mention a somewhat similar conditional-probability problem which I haven't seen anyone else mention. (It is not relevant to this article, nor should it appear in it; it's just related.) You play a "flip three coins game". The person I am gambling with shakes up three fair coins in a canister and spills them onto the table top. I am not allowed to see the coins initially before I make my choice; the canister shaker (my opponent) hides the coins from me. The rules are, the shaker peeks at the coins on the table and he has to tell me what the "majority" coin is. There will be either a majority of heads (3 heads or 2 heads) or a majority of tails (3 tails or 2 tails). Then, having been told what the majority is, I must guess what the third coin is -- heads or tails. If I get it right I get paid a dollar by the shaker; if I get it wrong, I pay him two dollars. Most people would think this a stupid gamble on my part; they will assume that the guess as to the heads-tails of the third coin has a 50-50 chance of being right. But it's easy to see (though it is initially counter-intuitive to many people) that if you always guess the opposite of the majority, you will win 3/4 of the time. Just write down all combinations: HHH, HHT, HTH, THH, HTT, THT, TTH, TTT, and it's obvious. That would make a cool bar game. Even offering your opponent the 2-to-1 payoff, you would still win, on average, in the long run 25 cents per play:

   1/4*(-2) + 3/4*(1) = 1/4 of a dollar per coin-shake, in the long-run average.

Good luck with your little war. Worldrimroamer (talk) 23:53, 8 December 2009 (UTC)

There's no war. Just good faith disagreement. Likely to end soon, anyways. Is there any reason this editor's comments should not be reflected in our quorum building? Glkanter (talk) 01:18, 9 December 2009 (UTC)

I'm afraid I don't understand what you mean. Who is the "this editor" to whom you refer? I tried to state at the outset that I was not targeting my comments at any particular person. I did not compile a ledger of who wrote what. I was just making general comments, in the hopes that they might be a small but helpful contribution. —Preceding unsigned comment added by Worldrimroamer (talk • contribs) 03:10, 9 December 2009 (UTC)

Er... the obvious guess is that the third coin is the same as the majority, which is a bloody good guess: it is correct 3/4 of the time, both conditionally on the majority being heads, and conditionally on the majority being tails, and unconditionally on the nature of the majority. I shall try this in the pub to see if my population is smarter than Worldrimroamer's. Gill110951 (talk) 05:45, 22 December 2009 (UTC)

Sorry for being so cryptic. 'The editor' is you. As we try to bring this discussion to a close, we are attempting to build a Wikipedia Consensus to make changes very much as you described. So, I was asking the other editors if there is any reason your opinion should not be considered as part of the 'let's change the article' consensus, of which I am a part. It's all good. I think you'll find the discussion of the last few weeks most meaningful. Some extra Wikipedia Mathematics Project people have begun contributing, by request, and it's helped move things forward a great deal. Again, sorry for being unclear. Glkanter (talk) 03:27, 9 December 2009 (UTC)

Glkanter, thanks for your reply. I understand now what you meant. And by referring to "editing wars" I did not mean to be denigrating. Perhaps I should have used a different term. I just thought it was very interesting that this "simple" little topic has stirred up so much discussion. It does my heart good to see that there are people that care about esoterica like this (at least, in the eyes of the general public it would seem like esoterica). Best regards to all ... Worldrimroamer (talk) 17:48, 9 December 2009 (UTC)

Worldrimroamer, thanks for you contribution. New thought is always welcome here. One thing I might explain is that the article as it is now (more or less) in not the end result of the pages of discussion that you have seen. It is little changed in principle from the original FA version.

There are basically two broad factions of editors here. Those who want to keep the article as it is (or perhaps as it was about a year ago) and those who want to change the article to reflect more or less what you say, namely that The Monty Hall Problem is a simple mathematical puzzle that most people get wrong. What the article needs (according to the pro-change editors) is an initial section that concentrates on a simple description of the puzzle with normal 'puzzle assumptions' (all choices are random unless specified etc). This should be followed by some simple, convincing solutions that show why the player has a 2/3 chance of winning by switching.

The anti-change editors believe that the proposed changes are not justified by the available sources and that making them would jeopardise the article's FA status. Of particular importance is a paper by Morgan et al. which claims that the problem must be treated as one of conditional probability. This has the effect of changing the simple problem that most people get wrong to a complicated problem that most people are bored by. I strongly dislike the Morgan paper, you should get a copy and see what you think.

It the moment, apart from a few minor changes, the article is still built around the Morgan paper. The editors who want change have refrained from drastic editing as fought to get a consensus for change here. So far although there is a majority for change there is far from general agreement.

There are some things that are generally agreed on such as the game rules (the host always offers the swap and always opens a unchosen door to reveal a goat) the fact that overall the player has a 2/3 chance of winning by switching, and that it is assumed that the player has not studied replays of old shows to gain statistical information. I might add that, although there are strong opinions on both sides discussion has generally remained civil and there has been no edit warring. Martin Hogbin (talk) 11:57, 9 December 2009 (UTC)

Thanks, Martin. Yes, I understand what you mean about the basic disagreement. It sounds like a rather intractable situation to me. I hope you guys can work something out. As I told Glkanter in the post immediately above, I should perhaps not have used the term "edit wars". I just meant that it was impressive how much intense interest has been evidenced in this discussion. I think that's a good thing. I just wish that the article were not so ... opaque? IMO, Wikipedia should be accessible both to the experts in the field, as well as to the (curious and smart) not-so-expert people. There's room for both. I'll butt out now and wish you luck. You may need it. :o) Best regards. Worldrimroamer (talk) 17:48, 9 December 2009 (UTC)

__________________________________________________ —Preceding unsigned comment added by Worldrimroamer (talk • contribs) 17:51, 9 December 2009 (UTC)

The links are at the top of this talk page - as of the last FARC the article looked like this. Since then the "Solution" section (that arguably took the POV that the "unconditional" solution does not address the question as asked) has been split into a "popular solution" and "probabilistic solution" in a more NPOV manner. Saying this is "relatively unchanged" understates the situation fairly dramatically. What this extended discussion is about is furthering this change, to make the article effectively take the POV that a "conditional solution" is an unnecessary nuisance - i.e. that the POV presented by the aforementioned Morgan et al. paper is invalid. Saying the article in its current form, or even as of the last FARC is "built around the Morgan paper" is (IMO) factually false.

No article is ever finished and improvements are always welcome. This extended discussion is about whether additional changes are necessary to undo the POV some editors think was present in the version at the last FARC. -- Rick Block (talk) 15:35, 9 December 2009 (UTC)

What has to be considered the MHP??

I very much like this question to be answered first. (BTW several sources mention the MHP to be equivalent to the three prisoners problem.) Nijdam (talk) 22:35, 15 December 2009 (UTC)

I created a "construction" site, where we may step by step build the article, until we come at a point we don't find agreement on. —Preceding unsigned comment added by Nijdam (talk • contribs) 16:41, 16 December 2009 (UTC)

Nijdam, have you joined the consensus? Is mediation still necessary? What conclusions did you and Boris reach? Please address my points from this diff Huckleberry & Awareness and these questions before we invest all the time and effort. Glkanter (talk) 16:51, 16 December 2009 (UTC)

I think everyone would like an answer to that question but it is unlikely that there will be agreement on the subject. I would say that there are several formulations of the problem. I would personally like the MHP be treated initially as a mathematical puzzle, formulated in such a way as to make the solution simple and not depend on conditional probability. In my opinion the MHP is fundamentally a simple problem that most people get wrong, this is undoubtedly its most notable aspect. This was obviously Gardner's intention with the TPP although you might still argue that this problem is still, strictly speaking, conditional. The difficulty with implementing my preferred approach here is that there are no sources that specifically treat the problem in that way, unless we can find one.

Without doubt, the most notable problem statement is Whitaker's but, as you are well aware, this leaves so much unsaid that it can be interpreted in many different ways. In my opinion vos Savant answered the question correctly (but failed to make clear exactly what the question was) whilst Morgan interpreted the question too strictly (and still ambiguously) and then answered their interpretation (for the most part) correctly.

The only unambiguous problem formulation that I know of in the literature is the Krauss and Wang version that we quote. This is exactly equivalent to the TPP but this suffers the problem that, although the effect of conditionality is negated by the host's random choice, it can still be argued (as you do) that the problem is still strictly one of conditional probability and thus, unfortunately, it is not amenable to a simple solution.

So, I regret that I have failed to answer your very important question. The lack of an answer is the cause of much of the argument here. I think we just have to argue it out as best we can to create the best article possible. Martin Hogbin (talk) 11:00, 16 December 2009 (UTC)

Here is the Monty Hall problem:

"Suppose you're on a game show..."

The symmetry is a premise. And needs no disclaimer or footnoting. Anybody that disagrees should tell me what's wrong with Huckleberry's approach and must answer, incorrectly, that 'the contestant is aware' to Is The Contestant Aware? Glkanter (talk) 11:22, 16 December 2009 (UTC)

From Wikipedia's perspective, the MHP is whatever reliable sources say it is. WE don't need to (in fact, we don't get to) decide. What we do need to do is say what reliable sources say about whatever they consider it to be.

As I thought I made clear above, reliable sources do not answer the question of what exactly is the MHP. We have at least Selvin's original statement, Whitaker's question, vos Savant's partial formulation, Morgans misiquotation and subsequent incomplete formulation, and several formulations in K&W. The only one that is unambiguous is the one we quote from K&W, but K&W make no claim that this is The MHP. Thus reliable sources do not answer the question and we must decide what the subject of our own article is to be here.

Martin - you keep saying it's a simple problem that most people get wrong and that approaching it as a conditional probability problem is (more or less) a nuisance. If it's so simple, why (in your opinion) do most people get it wrong? My answer to this is that they try to solve it conditionally (what was it in the K&W experiment - 35 out of 36 subjects consider only the case where the player has picked Door 1 and the host has opened Door 3), which means to me that we can't fully explain it without addressing this issue.

Yes we can, there is no evidence anywhere that anyone considers it important which door the host opens. K&W's main point is that giving door numbers just confuses the issue, and I agree. Martin Hogbin (talk) 18:14, 16 December 2009 (UTC)

Regardless of the above, since reliable sources address it both ways the article must also. Not to do so would imply a POV that the "unconditional" approach is better or more correct. Avoiding this POV is the reason I'm suggesting we go back to a single Solution section. JeffJor seems to be OK with this (since he's engaged in editing a proposal for such a suggestion). I can't tell if Glkanter is OK with this or not. You (Martin) are at least currently saying you're not OK with this (is that right?). So, directly, would both of you (Nijdam, too) be OK with a single solution section more or less like JeffJor's suggestion? -- Rick Block (talk) 15:04, 16 December 2009 (UTC)

Rick, I didn't realize I hadn't made my position clear. The 'Solution section' will contain simple solutions only. No disclaimers, no footnotes, no 'buts'. This is what the consensus has agreed to. Your NPOV threats are just that. They are intimidation, and an attempt at prior restraint. Just more filibustering, as usual. And Rick, nobody is buying your NPOV act. The current article has such a heavy Rick Block/Morgan bias it's laughable. The FAQs alone make me want to vomit. Just getting to NPOV from your extremes will be an accomplishment. I can't conceive of the article ever being so POV-ed in the other direction as great as you have accomplished. I agree, as you posted on the Mediation Cabal page, this discussion is totally out of control. How many times does the consensus have to tell you your interpretations are inconsistent with the consensus? Glkanter (talk) 15:20, 16 December 2009 (UTC)

Whoa, whoa, whoa. Rick, you have a sad way of imnposing your own POV in every possible way that lets you keep it in the article. It is downright insulting. I am not "OK" with considering the Morgan "conditional" approach as addressing the MHP. It does not. Seymann says it does not. Nobody, not even Morgan, says it does address the actual question. But I am a realist, and I recognize that you will not let it be separated AS IT SHOULD BE, because you feel justified in your POV because your misread those sources and think they say something they do not.

So I am "OK" with trying to improve the article in a way that can be accomplished. That means inculding your un-intended, not-MHP, POV in the article. Specific door numbers were never intended to be important, and any possible importance implied by the "reliablle sources" you quote, who demonstratably misrpresented the MHP, was for rigor only. It gets removed by those sources before actually addressing the MHP with their formula. IT HAS NOTHING TO DO WITH THE MHP. IT IS NOT REPRESENTATIVE OF THE MHP. IT DOES NOT HELP IN UNDERSTANDING WHY THE MHP IS CONTROVERSIAL. All it does is extend the thought problem, in a way that is interesting only to mathematicians. The body of the article needs to address the problem as seen by the general populace, not pedantic mathematicians who proved one assumption (of two similar ones that are normally made) was unnecessary. While interesting, being unnecessary doesn't explain the unintuitive nature of the problem. JeffJor (talk) 22:46, 16 December 2009 (UTC)

It seems like we must not be talking about the same thing here. I'm talking about a conditional probability analysis, like the one you wrote above (the paragraph starting "Another way to analyze the problem ..."). Which I think is exactly the way the general populace, not pedantic mathematicians, see the problem. What are you talking about? -- Rick Block (talk) 23:07, 16 December 2009 (UTC)

Rick, this is exactly why you and Nijdam cannot be the self appointed 'lead editors' for the consensus in favor of the change proposals. You do not understand the paradox in the same way as the consensus does. Glkanter (talk) 23:25, 16 December 2009 (UTC)

Hear! Hear! Glkanter (talk) 22:53, 16 December 2009 (UTC)

Except for the 'giving in to Rick and Nijadm' to the detriment of the honesty of the article part. Glkanter (talk) 22:58, 16 December 2009 (UTC)

Jeff - if you can reply I would appreciate it. My assumption was that since you wrote the above paragraph that you would be OK with putting it (or something like it) in the article. If that was not your intent I'm sorry to have misinterpreted. -- Rick Block (talk) 01:53, 17 December 2009 (UTC)

Rick - Just to be clear, there are four categories that different sources have used to approach the MHP. I will call them "Unconditional Approach," "Symmetric Conditional Approach," "Asymmetric Conditional Approach," and "Reduced Asymmetric Conditional Approach." UA, SCA, ACA, and RACA for short. And there can be different kinds of RACAs, depending on what gets "reduced," by which I mean eliminating the importance of a condition.

The UA supports either MvS's explanation, or Devlin's combined doors, or anything similar. It really doesn't utilize the doors in any specific way. It can be done rigorously (G&S do it in their first solution not attributed to MvS), but usually isn't. Non-rigorous solvers use symmetry to reduce G&S's twelve cases to four. The SCA looks at specific doors, but assumes that any uncertainty must be uniformly assigned as in G&S's second solution. Some UAs - those that mention door numbers - look like SCAs but are really using numbers only as examples. The "tree" version as it currently exists did this. You can tell because it has four cases that sum to P=1, not twelve cases as in G&S. ACA is stated in K&W (not Morgan, Gillman, or G&S since all ignore car placement bias) as Equation 1. But it is not useable to answer the question "Should she switch?" because of the placement bias. Morgan, Gillman, and G&S use an RACA where they make one reduction - they eliminate placement bias by assumption. K&W discuss several ways of reducing ACA by assumption - their no/one/two door solutions. Morgan's thesis is not that ACA is proper (although they mistakenly assume it), but that you don't need to assume anything to reduce the importance of host choice. They reduce it by making it unimportant to the quesiton, and that is still a reduction. Eventually, every source that considers an ACA reduces it to a question (not a probability value) that is answered independent of door numbers.

So, what I think is that UA needs to be the primary focus of the article. SCA can be used, or not; but if you insist on it, it needs to be done properly as G&S did. That's why I changed the probabilities in the discussion I wrote of it. I don't think you will let anybody take it out of the body completely, so I left it and did my best to improve it. But it really does not help non-students of probability. They don't understand that conditional probability depends as much on what is removed as what is left. The terms in the SCA formula can show this, but the non-student will not understand how to read such a formula. So it really doesn't help them, it just makes the article look like a textbook that they don't want to read. And any ACA is addressing a variant of the MHP where asymetric probabilites need to be considered. Few people think the problem says that, and fewer still think they can be used. Certainly not any of the references, who always reduce ACA completely. So I don't see any benefit from that to the general public. There is benefit to students of probability, but that benefit is not directly related to the MHP itself. It only shows how you don't have to make assumptiosn to reduce all of the conditiosn that might affect a strategy. So it can be included AS LONG AS IT IS CLEARLY SEPARATED FROM THE ACTUAL MHP DISCUSSION. And it needs to be made clear that it is a non-standard interpretation of the problem, and that the parts that make it diffewrent are never used directly to answer the MHP.

I hope this helps you and Nijdam. It is the ACA and RACA that belong as a variant. The SCA is "better" solution in the sense of rigor only; but it does not satisfy any need the article has, except rigor. Since the reason the MHP is enigmatic at all has nothing to do with rigor, but with intuition, we really should pay more attention to the issues that surround intuition. JeffJor (talk) 15:35, 17 December 2009 (UTC)

I don't need help. What you call UA, suggesting an approach to the MHP, is just a solution of a specific simple version, not the K&W-formulation, and in my opinion also lacking the characteristics of the MHP. This is also admitted by G&S: This very simple analysis, though correct, does not quite solve the problem that Craig posed. The SCA and ACA are both solutions to the MHP (K&W version). Nijdam (talk) 12:55, 20 December 2009 (UTC)

(1) Nijdam, elsewhere you had asked for my interpretation. When I "hoped it helped" you, I meant "helped you understand my interpretation." (2) But you apparently do need my help, because you think something other than UA/SCA is "the MHP." As has been clearly demonstrated through references,UA/SCA is indeed what was intended as "the MHP" by the originators, whether or not some others misinterpreted it. And all of the controversy in the general public surrounding those puplications stem directly from, and only from, it. Anything else is a distraction. The fact that some sources disagree on this point only proves that we need to handle that disagreement by separating the issues. Craig's problem can solved, as written. This is clearly admitted by Seymann. It is G&S's alternate interpretation that cannot be solved. They only supply a solution to an isolated example that they do not claim is as a valid solution the problem itself. And in fact, G&S is the model for how to do this. They separate their approaches the exact same way. JeffJor (talk) 13:04, 21 December 2009 (UTC)

You know what, JeffJor? Formulate in correct terminology what you consider to be a possible version of the MHP and add an appropriate solution. Nijdam (talk) 14:07, 21 December 2009 (UTC)

Nobody can solve the problem that Craig posed because it is not clear exactly what it is. Morgan interpreted it in one particular way that makes the problem clearly conditional. In fact he probably just wanted to know, 'What is the probability you win if your strategy is to switch?', as Morgan put it. Martin Hogbin (talk) 15:32, 20 December 2009 (UTC)

Incorrect, Martin. Read Seymann's comment to Morgan. It was not supposed to be a rigorous prob=l;em statement, it was a "fun" puzzle in a newspaper. And there are clear assumptions that can, and should, be made; which were reinforced by MvS herself. The controversy had nothing to do with any of those possible ambiguities. JeffJor (talk) 20:55, 20 December 2009 (UTC)

Jeff it would probably help our cause if you were to stop jumping down my throat at the first opportunity. I was the first, I believe, to bring to the attention of editors here Seymann's commentary, which points out that the problem can be interpreted in different ways. I am agreeing with you that Whitaker probably just wanted the simple unconditional problem answered, with normal 'puzzle' assumptions (as correctly made by vos Savant). That is why I quoted from Morgan's example of an unconditional statement of the problem. Even that 'most reliable of sources' gives the problem to which the simple solutions, including vos Savants are the answer; that is what I have quoted from. Martin Hogbin (talk) 21:23, 20 December 2009 (UTC)

It would help if we were all on the same page. Any ambiguity in the Parade statement is unimportant to what makes the MHP controversial. Considering such is what leads some people to think the Morgan analysis should be part of the main issue. The point is, that the Whitiker statement is sufficient for the vehicle in which it was published. Seymann does not say it "can be interpreted in different ways." He says, and I quote, "Simply put, and quite clear considering her suggestions for simulation procedures in her two later columns, the host is to be viewed as nothing more than an agent of chance who always opens a losing door, reveals a goat, and offers the contestant the opportunity to switch to the remaining, unselected door." There is nothing vague about this. Craig's problem can be solved, without having to allow for any alternate host strategies.

Rick (and others) keeps trying to inject his POV by suggesting Seymann thought it was ambiguous, and Seymann did not. And MvS said explicitly that the vast majority of the controversy in the letters had nothing to do with such possibilities. Your comment came in the middle of an "edit battle" where Rick reworded the article to inject that POV, and I removed it. As long as they keep trying, NPOV requires it be squelched. It is only this way that we can eliminate POV from the article. JeffJor (talk) 23:11, 20 December 2009 (UTC)

I will leave you to your lone battle as you seem determined to pick fights with those who essentially agree with you. I was arguing that Craig's question should be treated in a manner sympathetic to its origin long ago. Martin Hogbin (talk) 00:12, 21 December 2009 (UTC)

I'll note that I didn't "reword" anything. Butwhatdoiknow's complaint was the length of the lead. There was a pending suggestion on the talk page to drop the K&W problem statement in favor of the Parade problem statement. He dropped the Parade one. I simply flipped this to the (existing) paragraph about the (much better known) Parade one, with one minor change to make it less POV (in the same direction as JeffJor's subsequent edit). Here's a diff to an earlier version [1]. -- Rick Block (talk) 05:32, 21 December 2009 (UTC)

Rick said "I didn't 'reword' anything ... with one minor change to make it less POV same direction as JeffJor's subsequent edit." Ignoring the self-contradiction, your rewording was in the opposite direction. You added "Some of the controversy was because the Parade version of the problem leaves certain aspects of the host's behavior unstated." You said this as though it was a significant portion of the controversy, which is what MvS specifically denied and what you have no support for. The only thing that contributes to the controversty soem have called "The Parade affair," which is the controversy meant here, is the unintuitive result. You left out the parts that said the problem statement was perfectly clear for the forum in which it was published, which is the "direction of my edits." JeffJor (talk) 12:46, 21 December 2009 (UTC)

I have also had many discussions with Rick where I find his interpretations of events that we both witnessed as they occurred, or of Mathematical concepts, or of WP policies to be 180 degrees apart from mine. Glkanter (talk) 12:56, 21 December 2009 (UTC)

Sorry, wrong diff. The version I started with was this one. This is the correct diff [2]. I changed "A well-known, though ambiguous (Seymann 1991), statement of the problem was published in Parade magazine:" to "A well-known statement of the problem was published in Parade magazine:". The "Some of the controversy" sentence is in both what I started with and your subsequent edit. In general, references do not belong in the lead (see WP:LEADCITE). -- Rick Block (talk) 15:09, 21 December 2009 (UTC)

I don't care what the diff is, Rick. If you edit a paragraph that has two known flaws in it, and take out only one flaw, you are tacitly approving the other. There is no documented evidence that the MvP statement generated that controversy. She denied it was a signifcant factor. Others inserted the possibility (not the controversy), by failing to interpret the Whitiker statement as it was clearly intended. That means no alternate host strategies, and no probabilities that differ by door number alone. So you can solve the problem by UA/SCA, which are equivalent as G&S said. The only place where any controversy has arisen surrounding anything besides UA/SCA is HERE. That isn't NPOV. It is OR. It does not come from any of your references, because they never said what q was. They only said there ewas a potential for it to make a difference, but it didn't affect the answer. JeffJor (talk) 17:29, 21 December 2009 (UTC)

I agree intuition is the problem and that rigor is not the answer. IMO (this is WP:OR) the problem statement deliberately forces the reader to think about the specific conditional case where door 1 has been picked and the host has opened door 3, so the player is now looking at two specific closed doors and an open door. And, yes, this case is used as an example.

The salient features of this case (which apply to any other) are 1) the player doesn't know where the car is with certainty, and 2) there are only two possible choices. The "equal probability" assumption (cf. Falk or Fox and Levav) strongly leads people to the conclusion that the odds must be 50/50 in this case, and therefore any other equivalent case. Note that this reasoning starts with a specific conditional case, and then extends to the unconditional answer not the other way around.

The unconditional solutions ignore the specific conditional case the problem statement has forced the reader to think about, and jump straight to the (correct) unconditional answer. However, they NEVER reconnect back to the original conditional case—that is, these solutions do not address the mental model most people construct which led them so convincingly to their initial 50/50 conclusion. This is basically a bait and switch approach, leaving people with two choices - trust their "equal probability" intuition, or believe a solution that seems to be true but doesn't specifically address why or how their intuition failed. I think this is precisely what leads to many of the arguments over this problem. Most people are very reluctant to abandon what they see as an intuitively obvious answer. The unconditional solution approach tries to lead people to a different mental model. The other alternative is to address the conditional case head-on, and explain why even in this case the odds are 1/3:2/3. I would like the article to do both of these, in one solution section. As Boris says "The coexistence of the conditional and the unconditional can be more peaceful". -- Rick Block (talk) 21:27, 19 December 2009 (UTC)

Many more words

Until now only Boris has shown the derivation of a solution in formulas, using symmetry. This leads to the conclusion - as I BTW showed a million comments ago - that the conditional probability we are interested in is equal to the unconditional and hence may be easily calculated. It doesn't show the conditional probability is not needed. All others come with words, words, .... Nijdam (talk) 17:25, 20 December 2009 (UTC)

Yes, Nijdam, too many words. How about your signature agreeing to Formal Mediation? Glkanter (talk) 17:33, 20 December 2009 (UTC)

There are so many words here because people don't explicitly state the assumptions they use to get their solution. Conditional and unconditional probabilies are equal and easy to find by symmetry in a special, nice, symmetric case. I took a look at the Selvin paper. I like the intro very much indeed, I don't like the solution. He does not say in advance what assumptions he is making, you can only guess them by studying his proof. He enumerates the cases and solves the problem by counting. This means that he is assuming that all cases are equally likely. This means that he is assuming the car-key is hidden uniformly at random, that the quiz-player chooses a box uniformly at random independently of the location of the key, and that the quiz-master opens a box uniformly at random out of those available to him, given the previous two choices. Why I don't like Selvin's solution? Because it depends on his strong assumptions. We only need to assume that the first box you pick has 1/3 probability of having the key, in order to guarantee that always switching gives you 2/3 probability of ending with the key. Proof: everytime you would have got the key without switching you don't get it with switching, and vice-versa. I guess that most players think that they have a 1/3 chance of picking the right box first time. Whether or not this is true could be empirically verified. This is both real and theoretical game theory. Gill110951 (talk) 06:06, 22 December 2009 (UTC)

Words, words, ... Gill, why don't you show me your assumptions and proof in proper terminology? May be the terminology I proposed somewhere above. Nijdam (talk) 19:21, 23 December 2009 (UTC)

How About A Temporary Editing Freeze On The Article

I don't understand why all this article editing is taking place without being discussed.

While we 'old guys' are working towards a formal WP solution, newer people are editing at will.

This seems unproductive, not good for the article or readers, and distracting.

Any support for a temporary freeze? Is this even plausible? Thanks. Glkanter (talk) 12:25, 21 December 2009 (UTC)

I think it would be wise for editors to wait, as after mediation there may well be major changes (I hope) and they would the be wasting all their effort. Martin Hogbin (talk) 15:31, 21 December 2009 (UTC)

I guess I am "a newer person, editing at will". My excuse: when I see factual incorrectness or incompleteness in the existing article I make small edits - I don't touch the main structure. I obviously won't/can't object if those contributions get thrown out later. What I do like is the draft construction page, http://wiki.riteme.site/wiki/Talk:Monty_Hall_problem%5CConstruction That seems to me to be a very useful step: make a fresh start aiming to accomodate the various opinions which are around. It is precisely because there are so many different ways to formulate a Monty Hall problem that it is so attractive. Gill110951 (talk) 19:35, 21 December 2009 (UTC)

Why not use the current version as the starting point for the construction page? Then all edits will be in a clear audit trail for all to see. Glkanter (talk) 20:02, 21 December 2009 (UTC)

Rick Just Filed This RfC On Me

RfC Glkanter

He's expecting Dicklyon to 2nd it. I see a lot of unintended irony here. I had just created a new section on the talk page with 3 edits. Then, here's what I call Dicklyons's unprovoked vandalism on my talk page edits:

(Reverted 1 edit by Glkanter; Obviously incorrect, pointy addition, bordering on vandalism.

declutter a bit

*Roughly*

It's all right here: Is This Chronology Correct?

So, if anybody wants to put in a good word for me, I'd be much obliged. Please note, I'm pretty sure I will get this promptly dismissed, but any support is appreciated. Glkanter (talk) 04:25, 22 December 2009 (UTC)

Anyone unfamiliar with this process might want to review Wikipedia:Requests for comment/User conduct/Guidance2. It is certified now which means it won't be closed until the criteria at Wikipedia:Requests for comment/User conduct/Closingis met. Anyone is welcome to comment. -- Rick Block (talk) 05:41, 22 December 2009 (UTC)

On this RfC/U, Rick Block and Dicklyon are trying to make a case that I am disruptive, don't edit the article often enough(?),incivil, interrupt consensus building, chase other editors away, contribute nothing of value, too aggressive with my POV, have bad breath, etc. I'm holding my own on the RfC. It's gotten pretty ugly. So, if anybody would like to drop a supportive word about good ol' Glkanter, now would be a good time. By reading the RfC, you will also learn a lot about the inner thought processes of some well known editors. Thanks. Glkanter (talk) 22:22, 26 December 2009 (UTC)

Please see this new section on the Arguments Page

Huckleberry Opportunity

Thank you. Glkanter (talk) 15:10, 23 December 2009 (UTC)

I'll Bet That 'Paradox' and 'Game Theory' Are Mutually Exclusive And Opposites

I think there are 2 POVs regarding how to 'cherish' the MHP paradox.

Some of us, including myself, love the simplicity. Nothing happens. Heated Arguments over 1/2 vs 2/3 ensue. More than once, even.

Other people like the complexity, and 'what ifs' that the MHP could be with just a little tweaking. The permutations can approach Game Theory scenarios.

Since it was a great paradox before Morgan and conditional, I consider the 'simplicity' people the ones who accurately support how Selvin's MHP paradox should be presented in the Wikipedia Article. Glkanter (talk) 15:35, 23 December 2009 (UTC)

There's Only 2 Things Being Debated Anymore

1. The simple solutions are not solving the correct problem.

2. Morgan's paper, published in 1991, can claim to recognize and describe the Monty Hall Problem Paradox, first published by Selvin in 1975, equally as well (and equally importantly) as Selvin's original paper, which relied only on simple solutions.

I'd like to see the people arguing in support of those 2 arguments come out and directly say it. Once you clearly state your positions, the other editors, using reliably published sources can then address your objections to the proposed changes. Glkanter (talk) 18:32, 23 December 2009 (UTC)

I Guess I'd Better Start Editing The Article

In the RfC that Rick Block and Dicklyon filed on me RfC Glkanter one of the 'complaints' was that I argue on the MHP talk pages too much, at the expense of actually editing the MHP article. The associated 'remedy' was that I modify the MHP article more frequently and discuss my reasons for doing so less often.

Now, that's no reason to slap me with an RfC, but the point is well taken. I've asked for a 'freeze' on the article of some sort at least twice in the last couple of weeks. Meanwhile, some editors just make edits without discussing them first.

So, consistent with my stated understanding of the various literature on the MHP, and in accordance with Rick's criticism/suggestion as conveyed via Wikipedia's formal RfC procedure, I will begin to thoughtfully edit the article as I understand the consensus has approved. Glkanter (talk) 15:51, 24 December 2009 (UTC)

How about I start with the FAQs on the talk page? That looks like pure Morgan POV, a clear violation of NPOV. Anybody want to clean it up, or should I just delete it? Glkanter (talk) 16:47, 24 December 2009 (UTC)

I'm sorry, but how do you find the FAQ a "clear violation of NPOV"? Would it help if it said "according to these sources" a couple of times? There is no particular requirement that talk page FAQs adhere to NPOV, but I'd be happy to work with you to make this more NPOV if it bothers you (which it clearly seems to). -- Rick Block (talk) 17:39, 24 December 2009 (UTC)

No thanks. I'm going to use the RfC as an opportunity to learn. Since you feel I should be sanctioned because I've only made '6 article edits out of about 1000 talk page edits', I'll go it alone, without all that 'discussing' you find so offensive from me. Glkanter (talk) 22:39, 24 December 2009 (UTC)

The first two lines address FAQs. The rest is yet another lengthy defense of Morgan. NPOV is not a requirement for FAQs? That seems to contradict Wikipedia's bedrock policy. Can you provide a link that supports your POV? Glkanter (talk) 14:13, 25 December 2009 (UTC)

Here's another one. Id like to change the 'Simple solution' heading to something like 'Original Paradox explanation' or 'Selvin's Proof' or 'vos Savant's Popular Solution'? I'd like to get the point across concisely that it was this level of understand from which all the excitement about the paradox came. Not to be confused with the 'conditional solution' or, non-solution without the equal goat door constraint being equal to exactly 1/2, that came out some 15 years later. Glkanter (talk) 16:03, 25 December 2009 (UTC)

Then a transition section that says 'For many people, this is all the understanding they need, and was Selvins and vos Savant's point. Others may want to continue further into this article...' And as long as there's no bad-mouthing the 'original' solutions, you 'conditional' guys can pretty much do what you want with the article from there. Glkanter (talk) 16:10, 25 December 2009 (UTC)

Editing the MHP FAQs

Rick, the current text includes this:

"The point of introducing this variant is to show the difference between the unconditional and conditional questions. In this variant, these questions have different answers exposing the difference between unconditional and conditional solutions."

I still disagree that using a different problem is a means of challenging a particular problem. Originalists would argue that all you've demonstrated is the difference between puzzles with different premises. I would further argue that with the contestant being aware of Monty's left door bias, this is no longer the MHP about a game show that Selvin and vos Sovant made so famous. Glkanter (talk) 06:38, 27 December 2009 (UTC)

OK, I'm Paraphrasing slightly...

When asked how he was able to sculpt the venerated 'David', Michelangelo replied, 'It was easy really. I removed everything that didn't look like David'. —Preceding unsigned comment added by Glkanter (talk • contribs) 23:51, 8 December 2009 (UTC)

FAQ page boilerplate

This is most of the 'greeting' to the talk page of the FAQs. Probably only seen by other editors.

"This page is an FAQ about the corresponding page Monty Hall problem."

"It provides responses to certain topics being brought up again and again on the talk page, sapping many editors' time and energy by forcing them to respond repeatedly to the same issues. The FAQ addresses these common concerns, criticisms, and arguments, and answers various misconceptions behind them."

I think this can be improved. Anybody mind if I take a shot at it? Glkanter (talk) 23:32, 26 December 2009 (UTC)

This is standard boilerplate from Template:FAQ page. Are you suggesting changing the standard boilerplate (used on over 100 pages) or replacing the standard message with something custom for this page? -- Rick Block (talk) 00:29, 27 December 2009 (UTC)

I guess this is why we discuss things. I don't like the phrasing. Maybe the words in the box were only meant as an example? Glkanter (talk) 01:12, 27 December 2009 (UTC)

It's a variant of template:FAQ, one of many templates intended for use on talk pages. See Wikipedia:Template messages/Talk namespace. Template:FAQ2 is another version. - Rick Block (talk) 01:58, 27 December 2009 (UTC)

The 2 FAQ templates don't strike me as civil. Is there a rule against changing the text inside the box? Maybe it was just sample text? Glkanter (talk) 02:36, 27 December 2009 (UTC)

No, there is no rule against changing the text in templates. I'm sure there are plenty of people who have these templates on their watchlists. If you make a change anyone objects to they'll revert it. Whatever change you make will show up on every talk page the template is used on, so don't change the text to be less generic. -- Rick Block (talk) 05:01, 27 December 2009 (UTC)

You're saying that by changing the text in the MHP FAQ text box template, this will back-propogate to all users of that template? I wouldn't have expected that. Is that theory, or experience that informs you? Glkanter (talk) 06:26, 27 December 2009 (UTC)

I'm saying if you edit template:FAQ page the text will appear on any page that transcludes this template (anything marked as "transclusion" here). This is a feature of the MediaWiki software used to run this site. This is both theory (in the sense that it is a known feature of the software) and something I have personally experienced, many hundreds of times. -- Rick Block (talk) 18:50, 27 December 2009 (UTC)

I appreciate your help with this, Rick. I'm suggesting we would edit this. What then? Glkanter (talk) 19:27, 27 December 2009 (UTC)

If you edit Talk:Monty Hall problem/FAQ and change

<noinclude>{{FAQ page}}</noinclude>

to something else, e.g.

<noinclude>blah blah blah</noinclude>

"blah blah blah" will only show up on the MHP FAQ page. However, because the text you're talking about is inside the "noinclude" tags it does not appear when you're viewing this page (Talk:Monty Hall problem), even if you click the "show" link at the top of this page (scroll up to the top of this page and try it!). The bottom line is you only see this text if you're editing the FAQ page (and previewing your edit), or directly viewing the FAQ page as opposed to the talk page (there's no link to it, so I'm not sure how this would happen). I might suggest that whatever you think of this text, it's not worth worrying about. -- Rick Block (talk) 19:56, 27 December 2009 (UTC)

Variants

Variants - Slightly Modified Problems section.

Since the MHP is from the contestant's POV, there should be some narrative about what the POV's in this whole section represent. Are they the contestant's? Is it a premise in each different problem that it's no longer the contestant's POV? What about addressing the Monty Hall problem from 'not-the-contestant's POV' for comparison purposes? This would be beneficial to the readers, I believe. Glkanter (talk) 16:55, 27 December 2009 (UTC)

Can we call this "state of knowledge", not "POV" (to distinguish from the local Wikipedia meaning of POV)? In all cases what is meant is the probability given everything included in the problem statement. This is perhaps most literally the SoK of the puzzle solver, but presumably matches the contestant's SoK as well. The "MHP" is also from the puzzle solver's SoK, so there's really no difference. If this is not clear it wouldn't hurt to try to clarify it, but I don't think anyone should be confused about this since it is how mathematical word problems are universally treated. If it's important to the problem to take some particular perspective, the problem says to. For example, in vos Savant's "little green woman" scenario [3] if the player has picked door 1 and the host has opened door 3 we (the puzzle solver) know the probabilities are split 1/3 (door 1) and 2/3 (door 2) but the question is what are the little green woman's chances of randomly picking the door with the car, not what is the probability the car is behind door 1 or door 2. -- Rick Block (talk) 19:28, 27 December 2009 (UTC)

In Selvin's and vos Savant's MHP, what the reader knows and what the contestant knows are both consistent with "Suppose you're on a game show..." Every host/producer decision is described as 'random'. That's no longer true with the 'variants' where the reader becomes aware of some host bias. The contestant, of course, cannot. Hence, I disagree with your above explanation.Glkanter (talk) 19:37, 27 December 2009 (UTC)

Are there 3 published solutions?

Selvin's - simple: 2/3 & 1/3, always switching doubles your likelihood of getting the car
Morgan's - conditional, no symmetry: between 1/2 and 1 (?), never to your disadvantage to switch
Morgan's - conditional, with symmetry: 2/3 & 1/3, always switching doubles your likelihood of getting the car

Have I summarized the above properly? Glkanter (talk) 11:03, 27 December 2009 (UTC)

If so, maybe the article could transition from:

Simple, to conditional - with symmetry (they are equivalent), to conditional - no symmetry (leftmost door variant). Glkanter (talk) 11:30, 27 December 2009 (UTC)

This is the current structure of the article, so I don't get what you're suggesting (change the article to be like the article?). The conditional with symmetry solution dates to Selvin as well. -- Rick Block (talk) 20:24, 27 December 2009 (UTC)

Rick, rather than make controversial changes or deletions to the article's text, I am trying to make it clearer to the reader how the whole 'Morgan' controversy started. I thought Morgan's whole point was that Selvin and vos Savant overlooked something? So, I'm just suggesting to actually add a 3rd solution section, for increased overall clarity. Glkanter (talk) 20:41, 27 December 2009 (UTC)

Is the term 'Variant' as used in the MHP a common usage?

I disagree with your recent reverts to the article, Rick.

I just checked the Morgan paper, and they do not use the word 'variant' or any derivative of it when describing the problems.

I think this is an uncommon usage, and does not clearly indicate to the reader exactly what is being described. I don't think adding 'Slightly Modified Problem' to a heading, and replacing 1 instance of 'variant' in the article also with 'slightly modified problem' is 'pointy'. Different than your POV, perhaps, but that does not necessarily make it, or any other edits I may make in good faith, 'pointy'. Glkanter (talk) 19:45, 27 December 2009 (UTC)

Yes, "variant" is common usage. Pointy was referring to the dates. Sevlin's 2nd letter has a conditional solution, so saying the "probabilistic" solution dates from 1991, or is not the "original" solution, or addresses only a variant is a clear attempt to diminish this solution which is not only a violation of NPOV but is factually false. I would appreciate it if someone (anyone) would revert this change. If Glkanter reverts again without further discussion here I'll report him to Wikipedia:Administrators' noticeboard/Edit warring for edit warring. -- Rick Block (talk) 20:15, 27 December 2009 (UTC)

Some questions for you all

In an attempt to see exactly who thinks what I have set up some questions on User:Martin_Hogbin/Monty_Hall_problem/dissenters. Everyone is welcome to add their answers. Please comment briefly only in the comment section and have discussions about the questions on the associated talk page.

Whether we have external mediation or not I am sure it will help if everyone answers the questions on this page. I am trying to determine of we have two distinct camps, a single axis of opinion, or just randomly scattered views on the subject. Are there any other questions that editors feel will help sort out the differences of opinion here? I have just added a few extra ones. Martin Hogbin (talk) 11:36, 28 December 2009 (UTC)

What's Wrong With Adding Dates For Clarity?

Explain the problem to me please. Glkanter (talk) 01:45, 28 December 2009 (UTC)

Per above, the date you're adding for the conditional solution is simply wrong. Both the "popular" (unconditional) and conditional solutions date to 1975, both to Selvin. If you're going to add dates, you need to add 1975 for both which makes it completely redundant. You seem to be trying to insert your completely made up chronology (#Is This Chronology Correct?) into the article. -- Rick Block (talk) 04:31, 28 December 2009 (UTC)

So this whole time 'conditional v unconditional' has really been 'Selvin v Selvin'? No way. That's never been your stated intent. Or the way your POV article is written. It's always been 'Morgan v Selvin/vos Savant'. Adding two simple dates to two headings makes it clear where it all started. And it wasn't with Morgan. So the dates help the reader, and do not hurt the article. Your response is not credible based on your previous arguments for many years. Glkanter (talk) 12:56, 28 December 2009 (UTC)

Rick, you have already acknowledged a Pro-Morgan POV in the article. And offered to help me edit. Why must you continue to confound my very modest efforts at improving the article by removing this POV? Clarifying what a so-called 'variant' is and adding dates are non-antagonistic efforts to improve the article. They just happen to be different than your preference. Your actions, especially calling out to 'anyone' for 'revert' help seem to show ownership issues. Just let me edit out the POV in good faith, OK? Glkanter (talk) 13:20, 28 December 2009 (UTC)

This whole time, conditional v unconditional has always been different. In Selvin's second letter (which I've previously pointed you to, to refresh your memory there's a copy here), he says he received "a number of letters" including several who "claim my answer is incorrect". Like vos Savant, he says "The basis to my solution is that Monty Hall knows which box contains the keys" but unlike vos Savant he goes on to say "and when he can open either of two boxes without exposing the keys, he chooses between them at random" (emphasis added). Also unlike vos Savant he goes on to present a solution using conditional probability which he calls an "alternative solution" to the solution in his first letter "enumerating the mutually exclusive and equally likely outcomes".

The issue Morgan et al. address is that vos Savant's solution, and her subsequent defense of it, and the popular discussion at the time (1990 and 1991), completely overlooked the critical assumption that makes the unconditional and conditional solutions the same, i.e. that the host must choose between two boxes (two goats doors) randomly. Selvin knew this and acknowledged it in his second letter. Martin Gardner knew this and addressed it in his version of the Three Prisoners problem. vos Savant blew it, and both Morgan et al. and Gillman called her on it. That's what the "Morgan controversy" is about. Morgan et al. and Gillman both examine the consequences of omitting this assumption, in the process showing why it's critical and how the unconditional and conditional solutions are different. The unconditional solution is NOT saying that every player who switches has a 2/3 chance of winning, but that the average across all players is 2/3. The conditional solution shows that the chances are the same (2/3) for each player only if the "equal goat" assumption is made. Even without it, players who switch will win on average 2/3 of the time (and if they switch they're never worse off), but to say a player who picks door 1 and sees the host open door 3 has a 2/3 chance of winning by switching is a conditional statement and requires this assumption. The assumption can be explicitly part of the problem description (as per the Krauss and Wang version) or implicitly assumed because of symmetry or the principle of indifference, but the statement is still a conditional statement. I don't think ANYONE here (other than you) has ever argued against any of this.

What I said was "I'd be delighted to work toward a more NPOV treatment". This is not saying that I think the article has a pro-Morgan POV, but that I'm acknowledging that you think it does and I'd be happy to work with you to make it address whatever concerns you have. Adding dates (even if they weren't wrong) is not improving the article or addressing any POV concern. What you seem to be doing is trying to introduce an anti-Morgan POV. That's not how it works. Please read WP:NPOV again, specifically WP:STRUCTURE. You have said repeatedly [4] you want an unconditional solution first and foremost, followed by a disclaimer like "The Monty Hall problem is unconditional. That is the whole paradox; the rest is the explanation; go and learn." This would be sort of the exact opposite of editing out POV. -- Rick Block (talk) 19:08, 28 December 2009 (UTC)

Let the readers decide amongst the published papers. Just don't cloud the story with unnatural euphemism's like 'variant'. The 3 separate solution sections approach accomplishes my goal, along with dates clearly highlighting the history and clarifying what the heck a 'variant' is. That's not a POV, that's shedding light on the controversy. It just weakens your POV, so you demonize it.

But anyway, you argue whatever side of the coin is convenient for you each day. What's the point in going around further?

Editing delayed is editing denied! Glkanter (talk) 19:32, 28 December 2009 (UTC)

I've asked user:K10wnsta to drop by and say what he might be able to do as an informal mediator. I'll wait to see what he says. Do not in any way take the fact that I haven't reverted your change (again) to mean I accept it or agree with it. I think it might be helpful if some other folks would comment on this specific change as well. -- Rick Block (talk) 23:39, 28 December 2009 (UTC)

Changes suggested by JeffJor, Martin Hogbin, and Glkanter

If you're here because you've been invited to comment, there are ,two,. three (related) suggestions.

• #Glkanter's suggestion: Eliminate all 'host behaviour, etc' influenced discussion, save for the Wikipedia minimum necessary references to Morgan and his ilk, as the 'conditional' problem is the converse of "Suppose you are on a game show."

If nobody minds, I'd like to revise my proposal to make it more reflective of the literature: 3 Sections to the article: The unconditional MHP, A brief discussion on why Morgan and the 'conditional variants' are not the MHP, and 'diversions' - which includes 'variants', etc.

• #JeffJor's suggestion: The so-called conditional problem needs to be a separate article, with "conditional" in its title.

• #Martin Hogbin's suggestion: This article should concentrate on the unconditional solution with the Morgan's conditional solution in a variations section.

Please indicate in subsections below whether you favor or oppose each of these suggested changes.

The intent is to try to determine whether there is community consensus for any of these changes. I would suggest one subsection per user who is commenting, and to avoid endless arguments, restricting your comments to your own section (this is modeled after the process used at Wikipedia:Arbitration Committee). I've precreated sections for everyone I've explicitly invited to comment. -- Rick Block (talk) 15:31, 2 December 2009 (UTC)

Discussion about setting up this section and inviting folks to comment

In this section please summarize the changes you're suggesting. I'll be asking the set of folks I mentioned to Glkanter above to come here and offer their opinions, so please keep it as brief as possible. Please let me know when you think this section is ready for others to comment on. -- Rick Block (talk) 01:07, 1 December 2009 (UTC)

Rick, have you invited Boris Tsirel, William Connolley, or C S to contribute their opinions? What sort of time frame do you have in mind before 'In essence, silence implies consent' as per Wikipedia policy? Glkanter (talk) 15:47, 2 December 2009 (UTC)

I haven't invited anyone yet. The list of folks is the set of users I added below, plus I'll post something at Wikipedia:WikiProject Mathematics. I can specifically invite Boris, William, and C S if you'd like. As far as the timeframe, I was thinking maybe something like a week or two. -- Rick Block (talk) 15:53, 2 December 2009 (UTC)

I posted on Boris' page earlier this morning. Otherwise, don't do anything 'special' on my account. It just looked like you had sent out 'request for comments' by the way you set things up. Glkanter (talk) 16:02, 2 December 2009 (UTC)

I was going to, but had an edit conflict with Martin as he added his new section below. We need to straighten this out first. -- Rick Block (talk) 16:06, 2 December 2009 (UTC)

Yes, please include the 3 editors I mentioned. Thank you. Glkanter (talk) 16:11, 2 December 2009 (UTC)

kmhkmh was active for a while, too... Glkanter (talk) 16:54, 2 December 2009 (UTC)

Gill110951 perhaps? Glkanter (talk) 17:09, 2 December 2009 (UTC)

And Friday as well. Glkanter (talk) 17:27, 2 December 2009 (UTC)

I've notified all (including Wikipedia:WikiProject Mathematics) using template:please see referring them to this section. -- Rick Block (talk) 04:20, 3 December 2009 (UTC)

Glkanter's suggestion

This is from the section above.

Each instance in the article (and the various FAQs) of a host behaviour, or host bias, or host prejudice is indicative of a reliance on Morgan's paper. Regardless of what is being illustrated, this topic only exists among Morgan and a few others.

Since the problem statement of both vos Savant (Whitaker) and Krauss & Wang begins with: "Suppose you are on a game show", we know that this host behaviour will not be shared with the contestant, whose State of Knowledge is the only one asked for in The Monty Hall problem.

So, while Morgan is published, his argument is irretrievably flawed. The moment the problem is restated to rely on a host behaviour, it's no longer the Monty Hall problem. The problem statement becomes: 'Suppose you are not on a game show'. Which is the exact opposite of how both Monty Hall problem statements in the article begin: "Suppose you are on a game show". Morgan's criticism and his solutions are not relevant to the Monty Hall game show problem, which is the subject of this article.

Only because it's been published, Morgan should be referenced, but with such an obviously erroneous argument, it hardly deserves the great emphasis it currently enjoys. All other references to host behavior, etc., 'conditional vs unconditional', 'variants', and the Popular solutions being in any way inadequate should be removed from the article.

A second section would explain why Morgan and 'conditional variants' are not the Monty Hall problem

A final section on 'diversions' would include 'variants' and whatever else.

JeffJor's suggestion

Rick, I've changed my mind on one thing. The so-called conditional problem needs to be a separate article, with "conditional" in its title. It can be linked to the MHP, but it is not the MHP. For justification, see (and cite in the article) [url=http://www.jstor.org/stable/187880] Maya Bar-Hillel's article "How to Solve Probability Teasers," Philosophy of Science, Vol. 56, No. 2 (Jun., 1989), pp. 348-358. That addresses several points critical to the problem, that are quite specific to all of the arguments we have had here, incuding documented evidence. Specifically: (1) It's just a puzzle. It isn't supposed to present a rigorously-defined mathematical problem, (2) The simple assumptions implied by the informal problem statement are intended, and almost universally accepted by anyone who isn't expecting such a rigorously-defined mathematical problem, (3) Even when presented with alternate wordings that explicitly include elements of host strategy, the general audience does not take that strategy into account in their solutions, and (4) the clear majority of respondents get the wrong answer (1/2) that is based on naive intuition rather than a formal solution.

By separating the articles this way, Wikipedia can clearly present both problems in a fair and uncluttered manner, allowing any reader who wants to depend on the more formal approach to do so, and allowing those who do not see that formalism as necessary to limit themselves to the information that is of interest to them. JeffJor (talk) 15:03, 1 December 2009 (UTC)

Martin Hogbin's suggestion

We should take the current K & W statement as our starting definition of the MHP.

I suggest that we give the Whitaker statement first then say that the K & W statement is how this is generally interpreted. The K & W paper itself supports this view.

The primary solution and explanation should not use conditional probability

Although it can be argued that, even in the case where the host is defined to choose a legal door randomly, conditional probability should still be used because the action of choosing a particular door reduces the sample set and thus the opening of a specific door represents a conditioning of the sample set, it is clear that this is a trivial condition that it is not necessary to consider. This is quite evident either from the symmetry of the problem or from the fact that the revealing of random information tells us nothing. I am sure that we can find reliable sources to support this view.

The Morgan paper clearly does not answer the question as stated in the article and thus should not be regarded as our ultimate reliable source.

The Morgan paper introduces a parameter q for something that is defined by the article problem statement to have only the value of 1/2. The Morgan paper thus answers a different problem (I suggest that we call it the Morgan scenario) from that posed in the article. In the Morgan scenario it is known that the host might have some preference for one of the legal goat doors.

The Morgan solution should be introduced in a later section of the article that deals with variations of the problem.

There are many variations of this problem and the Morgan Scenario is just one of many.

Colincbn's comments

(referring to JeffJor's suggestion)

Hear, hear!! Colincbn (talk) 15:09, 1 December 2009 (UTC)

(referring to Glkanter's suggestion)

I really don't know jack about probability and whatnot, but I still tend to agree with Glkanter's points. I came to this article through looking up various paradoxes and this was a really neat one that I got to try out in the real world (see simulation question above). As I understand it the "Monty Hall problem" states that the host chooses randomly, so any other discussion about host behavior should be limited to the "Variants" section under "Other host behaviors". Just my 2 cents, Colincbn (talk) 02:41, 1 December 2009 (UTC)

• Just to clarify, I think a mention of the Host behaviour/Conditional problem should be made in a subsection of this article, such as the Variants section, with a "main article" link (ie: {{main|MHP Conditional solution}} ) to a separate article that goes into Morgan's conditional problem in detail. I figure this will give the casual reader all the info he/she is looking for with an easy way to delve into the mathematics more deeply if they want. (also thanks to Rick for maintaining this section!) Colincbn (talk) 01:07, 3 December 2009 (UTC)

Martin Hogbin's comments

I agree that this article should concentrate on the simple and notable interpretation of the MHP, namely the version in which a conditional solution is an unnecessary complication. Morgan's academic problem could be a section of this article or could form a new one. Martin Hogbin (talk) 22:02, 1 December 2009 (UTC)

Glkanter's comments

By my count, that's 4 in favor of the proposed changes, and 0 against. I've been championing these changes since October, 2008, Martin prior to that, and countless other editors for about 5 years. When can we declare an end to the pointless filibustering, acknowledge a consensus, and move on? Rick, will you be offering your comments? Have you contacted the others? Glkanter (talk) 22:29, 1 December 2009 (UTC)

About Martin Hogbin's suggestion - :I agree 100% with your proposed changes. I would like to add my 2 cents to the rationale, however. Morgan is criticizing and solving something other than the Monty Hall game show problem in the article. The introduction of the contestant being aware of any 'host behaviour' when selecting from 2 remaining goats changes the Problem Statement of both vos Savant/Whitaker and Karauss & Wang from "Suppose you are on a game show" to the converse, "Suppose you are not on a game show". Individual contestants on game shows are never provided more information than the 'average' contestant will have. There can be no 'condition'. It's illogical. Glkanter (talk) 15:33, 2 December 2009 (UTC)

JeffJor's comments

[Repeated in part from comments below]

The point of separating the articles is not to eliminate any POVs. It is to emphasize them. To not let one facet of the MHP (simple solution w nonintuitive result) become overpowered by the other (good teaching tool for conditional probabilites). If we don't physically separate them, we need to more clearly divide the article. The first part should be about the classic (unconditional) MHP, as stated by MvS (not K&W), and listing the set of assumptions she has said (and 99.9% of readers agree) are implied: interchangable doors, and any kind bias becomes irrelevant because of interchangeable doors. Then a section about game protocals (part of what some call host stratgies) such as always opening a door or revealing a goat, WITHOUT mention of bias or conditional problems. This mostly exists. Finally, you can cite Gillman (not Morgan) as a reference that introduces the possibility that the conditional problem is intended, but matters only if there is a bias. Use the K&W statement here, not Gillman's misquote. Gillman is better than Morgan because it is clearer, includes placement bias, and does not launch into possibilities that we are never told how to use. I think this is pretty consistent with Martin's suggestion. JeffJor (talk) 17:44, 4 December 2009 (UTC)

Rick, no paper that uses q<>1/2 is addressing the K&W problem. They allow for it as a very specific variant of what they are addressing. But make no mistake: they are treating the problem statement we are supposed to be working with as the variant. That is wrong. There is nothing wrong with addressing their solutions as the variant, because it is a (more general) variation of what the article is supposed to be about. It isn't even a variant that is supposed to be used: no references use it, they just present it and say you don't need to use it. And I feel you have been just as much as stone wall on points relating to this as you accuse others of being. Meow. JeffJor (talk) 17:56, 4 December 2009 (UTC)

Rick, you keep treating the Morgan POV as though it is involiate. It is not. Morgan misquotes the MvS problem statement, and so their claim that "the conditional problem is intended" cannot be taken as a reliable interpretation of the MHP. It is just a possible interpretation. Any reference that derives from Morgan is similarly suspect. Gillman misquotes, too, but in different ways. Bar-Hillel's survey proves that few (she found none) readers think of the conditional problem. More references exist that ignore it completely, than that address it. Krauss and Wang admit what the mis-quoters do not - I'll repeat it since when I said it before, it was apparently in cat language before - "Semantically, Door 3 in the standard version is named merely as an example." Grinstead and Snell separate the problem in the exact same two ways I suggested (and in fact, were a model for the suggestion). In short, it is a very minor POV that the conditional problem is meant, and it is based on citable misquotation and misinterpretation. JeffJor (talk) 18:24, 4 December 2009 (UTC)

Rick Block's comments

As a matter of fundamental Wikipedia policy, articles MUST be written from a neutral point of view. What the proponents of these changes are essentially suggesting is that this article take the POV that the interpretation of the problem described by a significant number of reliable sources (the Morgan et al. reference and others) is invalid. Even if this were a stance taken by reliable sources (which, as far as I know, is not the case), by relegating the "Morgan" interpretation to a "variant" subsection or splitting it into a POV fork this article would then be taking the "anti-Morgan" POV. I've made this point to these editors numerous times before, but yet they keep tendentiously arguing that the "Morgan" POV is wrong, or the Morgan et al. reference has errors, or (most recently) that the Morgan POV is NOT about the "real" Monty Hall problem (as if by convincing me that their POV is "correct" I would then agree with the changes they're suggesting).

I sincerely hope the "consensus" from this process is against making these changes, because even if there is a consensus for these changes they cannot be implemented - doing so would violate Wikipedia policy. -- Rick Block (talk) 04:01, 3 December 2009 (UTC)

You all realize Martin's proposal implies the article will not even mention conditional probability except in a "variant" section, don't you? How anyone can think this is not a blatant POV issue escapes me. -- Rick Block (talk) 20:19, 3 December 2009 (UTC)

And why so dramatic, Rick? We've all disagreed with you on this forever. Glkanter (talk) 22:02, 3 December 2009 (UTC)

Yes Rick, all three proposals are consistent that way. It's based on this very recent and brief section of this talk page (following long and lengthy discussions on various 'talk' and 'argument' pages), 'Is The Contestant Aware?':

http://wiki.riteme.site/wiki/Talk:Monty_Hall_problem#Is_The_Contestant_Aware.3F

I started this section at 11:28, 29 November 2009 (UTC). You responded with 2 vague, filibuster-style questions, and at 23:02, 1 December 2009 (UTC) I wrote this:

"Rick, I have directly asked you this question many times, and have never seen a direct 'yes or no' answer from you. As this is a crucial element of the consensus that has been built, it is essential that we understand your reasons if you do not agree with the paragraph above:

"Has it been agreed by the editors of this article that regardless of how Monty handles the 'two goats remaining' situation, the contestant has no knowledge of the method?". [This question was ommitted when I asked Rick the 3rd time. I include it here for clarity]

""It seems to me that this is a (unstated) premise of the problem, as both vos Savant (Whitaker) and Krauss and Wang begin the problem statement with: 'Suppose you're on a game show'. I read this as clearly stating it is only the contestant's point of view we are concerned about. And, being a game show, the host is prohibited from divulging to the contestant either where the car is, or where the car is not.""

To date, at 20:36, 3 December 2009 (UTC), you have still not responded directly to this question. Glkanter (talk) 20:36, 3 December 2009 (UTC)

I have to state the opposite view, which is that you have taken a ridiculously pro-Morgan POV. There are many reliable sources that relate to the MHP and not all of them have a host door choice parameter. Those that do generally quote Morgan as the source for this.

The article already takes a problem statement from a reliable source (K & W) and that same source confirms that this is how most people view the problem. In that statement, the host is defined to choose a legal goat door randomly. It is thus a simple matter of fact that the Morgan paper does not address that problem in so far as it allows a door choice parameter where none is permitted by the problem statement.

The Morgan paper clearly addresses a scenario where where the player is somehow aware of the host's policy for choosing a legal goat door. This rather bizarre scenario is not the one described by our problem statement and thus it should be viewed as a variant of the MHP as it is most commonly understood. Martin Hogbin (talk) 21:30, 3 December 2009 (UTC)

I thought I made it clear we were to use arbcom style rules here, which are that you only comment in your own section (it really does help keep the threads from getting absurdly long). However, since you've been rude enough to post here I'll respond to each of you, BUT please do not continue this as a thread here.

Glkanter asks why so dramatic? The argument has shifted from "present an unconditional analysis first (and don't criticize it)" to "exclude the conditional analysis completely (except as a variant)". This is a huge difference.

Glkanter asks why I haven't responded about his "Is The Contestant Aware?" question. Why should I? Glkanter has repeatedly demonstrated a complete lack of comprehension of nearly everything I've ever said. It's like trying to explain something to a cat. At some point you just have to give up. However, I'll give it another go. Meow, meeeow, meow, meowww. I'm not sure I have that quite right since I don't speak cat, but it's probably about as comprehensible to him as anything else I could say.

Martin (incorrectly) claims again that the Morgan et al. paper does not address the K&W version of the problem. Quote from the paper: "Incidentally, Pr(W_s | D3) = 2/3 iff p = q = 1/2". This is the solution to the K&R version of the problem statement. The Morgan et al. paper (and the Gillman paper and many, many others who approach the problem conditionally) absolutely address the K&R version. Because they also address other versions doesn't mean they don't address the K&R version.

In the K & W statement q=1/2 by definition thus any problem in which q might not be equal to 1/2 must be a different problem. It is that simple. Martin Hogbin (talk) 19:04, 4 December 2009 (UTC)

Martin and Glkanter are both apparently completely incapable of understanding the main point of the Morgan et al. paper (and the Gillman paper, and what Grinstead and Snell have to say) which is that the MHP is fundamentally a conditional probability problem and that there's a difference between an unconditional and conditional solution. What these sources are saying is that a conditional solution clearly addresses the MHP (as they view the problem), but an unconditional solution doesn't unless it's accompanied by some argument for why it applies to the conditional case as well (and there are many valid arguments, but no argument at all which is what is generally provided with most unconditional solutions is not one of them). The fact that the problem can be (and typically is meant to be) defined in such a way that unconditional and conditional solutions have the same numeric answer in no way invalidates what these sources say. To have the article take the stance that the conditional solution is invalid (which would be truly absurd), or that the criticism these sources make of unconditional solutions is incorrect, or that a conditional solution applies only to a "variant" is making the article take a POV. This would be a direct violation of a FUNDAMENTAL Wikipedia policy. -- Rick Block (talk) 01:53, 4 December 2009 (UTC)

Glopk's comments

Delayed response (am not a very active editor at all these days), but here it is.
Statement

I support Rick Block's statement as expressed above, and am in favor of keeping the article more or less in the state in which it passed the last FA review, with minor edits where needed. I am in strong disagreement with all three suggestions above (JeffJor, Glkanter, Martin Hogbin). In particular, I am in strong support of keeping the language that differentiates between the conditional (Bayesian) interpretation of the problem and the unconditional (elementary) one.

Motivation. The purpose of an encyclopedia is to present a "best" selection from the body of knowledge about each topic, being POV neutral as well as reader-neutral. --glopk (talk) 18:53, 29 December 2009 (UTC)

Chardish's comments

Thanks for the invitation to comment. In my opinion, Martin Hogbin's suggestion seems the post prudent. The Monty Hall problem as popularly explained doesn't rely on conditional probability, and the Whitman explanation seems sufficient for anyone who is not a mathematician. Wikipedia is a general-purpose encyclopedia, and as such main articles should focus on explaining topics as they are popularly understood, with specific scientific analysis relegated to separate articles.

And, to be honest, the article as it stands is much harder to read and understand (as a layperson) than it was several years ago. NPOV isn't "pleasing everyone equally"; don't let efforts towards neutrality wind up hurting the article. - Chardish (talk) 02:53, 6 December 2009 (UTC)

Melchoir's comments

Just from reading the present Wikipedia article, I agree with Martin Hogbin's suggestion, because I don't see why allowing the host to prefer one goat over the other is a more relevant generalization than allowing the host other behaviors. Melchoir (talk) 06:47, 3 December 2009 (UTC)

Nijdam's comments

I fully support Rick's view. Nijdam (talk) 10:34, 3 December 2009 (UTC)

To make my position crystal clear: there is no such as an unconditional solution. There are different problems: an unconditional problem and a conditional one. The latter generally being called the MHP. Nijdam (talk) 22:24, 3 December 2009 (UTC)

Please read my proposal. I do not claim that the MHP is an unconditional problem. What I say is that in the problem definition given in the article the host is taken to choose a legal goat door randomly. Morgan address the case where this choice is non-random,thus they do not address the problem as defined in this article. Martin Hogbin (talk) 22:39, 3 December 2009 (UTC)

I'm in the audience looking at the stage. I see three doors and a player pointing to one of them. From the two remaining doors one is opened and shows a goat. That's what I call the MHP. (And I know of the random placement of the car and the random choice of the host.) Nijdam (talk) 22:50, 3 December 2009 (UTC)

Quite, and that is not the problem that the Morgan paper addresses. The Morgan paper addresses the case where the host door choice is not random. Thus the Morgan paper addresses a variation on what we all agree is the MHP. Martin Hogbin (talk) 23:28, 3 December 2009 (UTC)

Quite, but that is not the problem we are continuously arguing about. Even "our" MHP needs conditional probabilities. Nijdam (talk) 15:04, 4 December 2009 (UTC)

The problem that you and K & W describe, which is the problem addressed by this article, is one in which q=1/2 by definition. Therefore, any problem in which there is a possibility that q might not equal 1/2 must be a different problem. Morgan clearly consider a problem in which it is possible for q to have a value other than 1/2. The problem they consider therefore must be different from that in which q is defined to be 1/2. Morgan do indeed address a (bizarrely) more general problem than the one we are considering but it is, for sure, a different problem. Martin Hogbin (talk) 19:35, 4 December 2009 (UTC)

Dicklyon's comments

I haven't been watching this article for a while; glad to see the K&W treatment up front; that looks like the most sensible article I've seen on it. As for the Morgan conditional approach, I think it's an unnecessary distraction, but it's out there in mainstream reliable sources about the topic, so we ought to cover it in the article. I think Martin Hogbin's proposal sounds best. Dicklyon (talk) 05:01, 3 December 2009 (UTC)

I agree with Rick Block that the other two proposals essentially violate WP:NPOV; but I disagree that moving the conditional stuff to a more minor position is a problem; his heavy promotion of the conditional approach violates WP:UNDUE in my opinion. Dicklyon (talk) 16:29, 3 December 2009 (UTC)

Henning Makholm's comments

I have long since given up on following these discussions, and am not even a very active editor these days. However, since somebody went to the length of creating a heading for me, here are my general recommendations -- for whatever they are worth:

1. The article absolutely should discuss assumptions about the host's behavior. It is impossible to derive a valid answer without making some assumptions, and differences in which assumptions are implicit are one of the main reasons why smart people can disagree on the solution when the problem is stated sloppily. It would be a sorry encyclopedia that purported to treat the Monty Hall problem without explicitly pointing out this kind of confusion.
2. The analysis that involves conditional probabilities and the one that considers whole-game expectations under different player strategies are both valid ways of approaching the problem, each with its own advantages and disadvantages. The article should present both, and must not suggest that one of them is inherently better or more correct than the other. (For this reason I would oppose splitting one of the analyses into a separate article, suggesting that it solves a fundamentally different problem, rather than being an alternative way of approaching the same problem).
3. There has been far too much microlinguistic analysis about precise wordings of the problem in this source or that one, trying to argue that this analysis or that one is the one that most directly addresses the question being asked (implying that the other is a detour via a different but non-canonical presentation of the problem). Which analysis one chooses depends depends far more on which properties (besides being valid) one wants of it. For example, raw convincing power for a lay audience would favor the whole-game analysis, whereas a more in-depth discussion of the effect of different assumptions of the host's behavior is most easily done using conditional probabilities.
4. Editors should keep in mind that Wikipedia is an encyclopedia, not a textbook, an question-and-answer database, or a Court of Public Opinion. The goal of an encyclopedia article is not to answer one particular question but to present a body of knowledge. Therefore the amount of energy spent on negotiating "the" question that this article should be about answering is fundamentally misspent. The body of knowledge the article ought to present encompasses several different but related questions (some of which are sometimes mistaken for each other), and several different way of approaching some of them. An approach that restricts ourselves to discussing just one of them would fail to cover the topic encyclopedically.
5. I have no strong opinion about which analysis should be first in the article, as long as it is not being touted as inherently superior or inferior by virtue of its position. However, the general principle of progressing from the "quick and easily understood" to the "more complex but also more general and (possibly) enlightening" would seem to suggest starting with the whole-game analysis.

–Henning Makholm (talk) 07:13, 3 December 2009 (UTC)

Most people, including Rick, think that the problems should be addresses from the player's point of view (state of knowledge). As has been pointed out by many people, it is extremely unlikely that the player would have any knowledge of the host's door opening policy, thus from the player's point of view the host policy must be taken as random (within the rules).

I have no objection to the Morgan scenario (in which the payer is assumed to know the host's policy) as well as the more simple case being presented here provided that it is made clear exactly what case this applies to.

What you call, 'microlinguistic analysis about precise wordings of the problem' was started by Morgan et al. who added a pointless layer of obfuscation to a simple puzzle that most people get wrong.

The point is that the simple/symmetrical/non-conditional problem is the notable one and therefore it should come first. More complex versions should come later for the few that are interested in such complications. Martin Hogbin (talk) 22:36, 4 December 2009 (UTC)

Boris Tsirelson's comments

I summarize my position in two points:

• 1. The symmetric case is more important for an encyclopedia than the general case. (Likewise, a circle is more important for an encyclopedia than an arbitrary curve.)

• 2. The coexistence of the conditional and the unconditional can be more peaceful. (Not just "numeric coincidence" in the symmetric case; see #Not just words and #Formulas, not words.)

Boris Tsirelson (talk) 06:44, 9 December 2009 (UTC)

Being invited by Glkanter, I quote here some paragraphs of a discussion that happened on my talk page on February 2009. As far as I understand, my position is close to that of JeffJor. Boris Tsirelson (talk) 17:20, 2 December 2009 (UTC)

Why split? Because of different importance. The "conditional" article will be, say, of middle importance, while the "unconditional" article – of high importance. We surely have our point of view about importance (rather than content). Boris Tsirelson (talk) 05:54, 4 December 2009 (UTC)

The quotes follow.

Each time giving the course "Introduction to probability" for our first-year students (math+stat+cs) I spend 20-30 min on the Monty Hall paradox. I compare two cases: (a) the given case: the host knows what's behind the doors, and (b) the alternative case: he does not know, and it is his good luck that he opens a door which has a goat. Im addition I treat the case of 100 (rather than 3) doors (just like Monty Hall problem#Increasing the number of doors). And, I believe, students understand it.

I have no idea, why some people spend much more time on the Monty Hall paradox (and even publish papers). (Boris Tsirelson)

This simple little problem is deeper than it might appear, and likely well worth more than 20-30 mins of lecture time. Perhaps even worth revisiting once or twice during a term to explore its more subtle aspects. (Rick Block)

Deeper than it might appear? OK, why not; but still, for now I am not enthusiastic to deep into it. Tastes differ. I find it more instructive, to restrict myself to the simpler, symmetric case, and compare the two cases mentioned above.

If an article leaves many readers puzzled, why it is unnecessarily complicated, it is a drawback. (Boris Tsirelson)

If a problem that appears so simple to me, like the Monty Hall problem, is not sufficiently solved using my unconditional proof, in what circumstances is the unconditional proof appropriate? Thank you. (Glkanter)

The unconditional argument shows that "always switch" is better than "never switch". This is what it can do. Let me add: if you (that is, the player) are not informed about possible asymmetry then you cannot do better than these two strategies, either "always switch" or "never switch". (Boris Tsirelson)

Well, I gotta ask. Do you still prefer JeffJor's proposal among the 3 proposals put forth? Glkanter (talk) 07:19, 9 December 2009 (UTC)

Really, I have nothing to add to the two points that summarize my position (above). Any move toward them is good for me. My resolution power, and my acquaintance with the literature, are too low for choosing between different proposals; I leave this matter to more informed (and less lazy) editors. Boris Tsirelson (talk) 08:22, 9 December 2009 (UTC)

kmhkmh's comments

I'll start with a clear statement and give some more detailed information afterwards:

I strongly disagree with any of the 3 suggestions (JeffJor, Glkanter, Martin Hogbin) and aside from minor difference fully support Rick Block's approach

If one surveys the available literature literature/publications on the topic, you pretty much get an relatively obvious outline for the article: original problem (in vos savant's column), unconditional solution (basically vos savant and/or various math sources), conditional solution (Morgan and almost in any math source), various problem variation and caveats, history of the problem, application of the problem outside the math domain. Which is essentially for the most part, what we already had and what Rick managed to maintain. In that context I fully agree with Henning Makholm's comments above, who puts it fairly well. The article wouldn't have such problems if all participants would follow that rationale.

The fuzz over quality or minor mistakes in Morgan's paper is a somewhat ridiculous distraction, since Morgan's paper is not needed to argue the conditional solution or caveats to the unconditional solution at all. There is plenty of other math literature dealing with the problem in more or less the same manner.

My personal advice would be to pass the article for final thorough review and modification to the math or a science portal. During that review neither of the 4 disagreeing authors (JeffJor, Glkanter, Martin Hogbin, Rick Block) are allowed to participate/edit. After that review the article should be fully protected for good.

I've seen what happened to the German version, that had similar problems (without a Rick Block around to constantly remain some standard). So we had a lot of people with a somewhat fanatic approach constantly pushing for their favoured explanation and constantly ignoring wiki standards, common sense and more important the available literature on the subject. As result mathematicians and scientists basically dumped the article and gave up on improving it.An effect this article has partially seen as well.--Kmhkmh (talk) 16:45, 4 December 2009 (UTC)

Kmhkmh, no one is proposing a reduction in the quality of this article but you miss some essential points out in your outline. We should have: 'original problem (in vos savant's column), unambiguous problem definition (K&W), solution to the unambiguous problem (which is trivially conditional but need not be treated so, basically vos savant and/or various math sources), the Morgan scenario (in which the player knows host door choice policy) the conditional solution (Morgan). Martin Hogbin (talk) 19:46, 4 December 2009 (UTC)

I don't quite see how that is "missing" in my outline above nor do I see any particular reason to give (K&W) a preferred treatment, such an approach does not reflect the publications on the topic.--Kmhkmh (talk) 20:11, 4 December 2009 (UTC)

I am not proposing that we give K&W and preference but must have a clear and unambiguous problem statement before we (or anyone else) can attempt to answer the problem. Morgan do not have such a statement in their paper so we must use one from another reliable source, in this case another published paper. Note that the lack of clear problem statement in the Morgan paper is not just my opinion, that same point is made clear in the comment by Prof Seymann published in the same journal immediately after the Morgan paper. Martin Hogbin (talk) 20:20, 4 December 2009 (UTC)

I'm really not interested in repeating now here the discussion that you're pushing for almost over a year now and which frankly from my perspective is entirely pointless and misguided. The original problem in vos Savant's column was ambiguous and hence various articles on the topic and its variations provide their own specifications. As pointed out above already Morgan doesn't really matter in that regard. What the Wikipedia article has to do, is to describe the all various specification and not arbitrarily picking one like K&W as the "right" one. I'd recommend you to reread Henning Makholm's comments carefully. Or to put it rather bluntly - you asked for my comment here it is: Leave the article alone.--Kmhkmh (talk) 21:46, 4 December 2009 (UTC)

Actually I did not ask for your comment here and I certainly did not ask for, and do not need, your permission to edit Wikipedia. Neither did I pick K&W as the 'right one' as you put it, somebody else put it in the article as a clear and unambiguous description of the problem. As it happens I agree with whoever did this as K & W is the only published paper to seriously address the question of how most people interpret the MHP. It is therefore an excellent place to start the article. Martin Hogbin (talk) 22:25, 4 December 2009 (UTC)

Gill110951's comments

No comment right now. But a lot of Christmas break reading to do here, to catch up. Happy Wikipedia Christmas, everyone! Gill110951 (talk) 13:27, 20 December 2009 (UTC)

Methods of numbering doors

(I welcome you all back to my screen. This article has improved a lot over the last year.)

Morgan et al. (1991) seem to assume that the doors are statically numbered, having the same numbers through repeated experiment. Vos Savant however writes in her column: "You pick a door, say #1, and the host opens another door, say #3". This may mean that after a door is picked, we (always) call it #1, while the opened door is (always) called #3. Such dynamic numbering can make it easier to discuss and calculate the given options. The consequences of the assumption of Morgan et al. are further explained in this article under "Probabilistic solution - 1991".

The Morgan paper classifies solution F5 as "incorrect because it does not use the information in the number of the door shown". This is only true assuming statical numbering. In this context it is questionable why Morgan et al. quote vos Savant wrongly, writing "You pick door No. 1, and the host opens No. 3". Heptalogos (talk) 14:11, 30 December 2009 (UTC)

The show the problem clearly refers to (Let's Make a Deal, hosted by Monty Hall) had doors with numbers on them. Here's a screenshot [5]. You could assume the doors are numberless and the numbers magically appear on them as they are used, but the question for editing purposes is what reliable sources say about the problem. Are you suggesting this "numberless door" interpretation is the predominant one used by reliable sources - or is this more like your own original research? If the latter, I'd suggest moving or continuing this thread at the #Arguments subpage. -- Rick Block (talk) 18:00, 30 December 2009 (UTC)

The Morgan paper is not about Monty Hall, but about a question in a column of vos Savant, starting with "Suppose you're on a game show". All exact information is, of course, in the paper, so no other sources are relevant. Heptalogos (talk) 19:44, 30 December 2009 (UTC)

So, again, are you talking about what reliable sources say (if so, references would be helpful), or something you've thought of on your own (if so, please use the #Arguments page)? -- Rick Block (talk) 19:56, 30 December 2009 (UTC)

The source I mention, "Morgan et al. (1991)", is probably the most argued source in this article. It is in the article reference list mentioned as: "Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). "Let's make a deal: The player's dilemma," American Statistician 45: 284-287." Heptalogos (talk) 20:11, 30 December 2009 (UTC)

If you're suggesting to move or continue discussion about the specific arguments used in the Morgan source, to or on the arguments subpage, then that's fine with me. But I'm doing more than that, namely introducing a new element to the global dilemma, which is the method of numbering doors. Heptalogos (talk) 20:43, 30 December 2009 (UTC)

I think the point that you are making is already covered by considering the player's initial choice to be random. In other words we can take it that either the Morgan paper refers 'only to the specific door numbers shown or that all the door numbers including the door opened by the host are examples only. Martin Hogbin (talk) 21:03, 30 December 2009 (UTC)

The Morgan paper is quite clear about the disctinction between conditional and unconditional. I quote: the unconditional problem, which may be stated as follows: "You will be offered the choice of three doors, and after you choose the host will open a different door, revealing a goat. What is the probability that you win if your strategy is to switch?" The distinction is made by opening a specific door, instead of "a different door". This is mentioned elsewhere in the paper several times. I agree that No. 3 is an example and might be No. 2 as well, but the paper assumes that there is an essential difference between "the open door" and "door No. x, which is open". To my opinion these are only labels which don't make any difference, unless of course one assumes that a specific door is labelled the same through repeated experiment. Heptalogos (talk) 21:40, 30 December 2009 (UTC)

Yes, they're clearly assuming distinguishable doors with persistent numbering. Is the topic you're introducing, specifically "the method of numbering doors", discussed in reliable sources or is this a topic you're introducing based on your own personal knowledge? Once again, only in the former case is this an appropriate topic for this page. If this is the case, please provide references to sources that discuss this topic. There are plenty of disagreements here without delving into original research. -- Rick Block (talk) 22:47, 30 December 2009 (UTC)

I want this article to explain how the conditional probability could actually differ from the overall probability (I refer to chapter "Probabilistic solution - 1991"), when the distinction between both is made by information (a door number) which seems to have no statistic dependency or influence on the requested probability. To my opinion, the average intelligent reader of this paradox, who has no mathematical skills, still doesn't understand the necessicity of using the relatively complex method of conditional solution. I agree that the discussion about the necessicity itself should preferably be held elsewhere, but an elementary explanation key in the article should be, I guess, in the idea of a static door position through repeated experiment, whatever it means. The meaning of that I would like to be explained. Heptalogos (talk) 23:45, 30 December 2009 (UTC)

I would actually prefer a combined solution section, like the one above (#Proposed unified solution section). It presents a conditional approach as an alternative, with a brief explanation of the difference between the conditional probability and the average probability, with a forward reference to the "Variants" section (at the moment called "Variants - Slightly Modified Problems"). Is this version more clear? -- Rick Block (talk) 01:02, 31 December 2009 (UTC)

I propose adding a link in external references

I propose adding an external link to http://www.opentradingsystem.com/quantNotes/Monty_Hall_problem_.html

The link in question contains derivation of solution in a general context developed on other examples. —Preceding unsigned comment added by Kaslanidi (talk • contribs) 20:27, 30 December 2009 (UTC)

I object, per WP:ELNO points 1, 4, and 11. - MrOllie (talk) 20:32, 30 December 2009 (UTC)

Yes, I Have A 'POV'.

My 'POV' is that this paradox twists peoples' brains a lot, just the way it is. Whatever 'is' means.

So a sequenced roll out of how the problem became published, then controversial twice would help the interested reader. What could make more sense then to describe the events roughly as they occurred, and beliefs/understandings changed, or maybe they didn't.

Let the reader decide for himself, or herself.

Yes, 'sequenced roll out' really means 'chronological'. Forgive me.

Pretty radical, eh? Just tell the story as the sources do, and let the reader draw his own conclusions. Whoda thunk it? Glkanter (talk) 20:35, 30 December 2009 (UTC)

I'm not sure I understand what you're suggesting. There is already a "history" section. Are you suggesting pitching the entire article and starting over with a strictly chronological accounting that would be sort of an expanded version of the "History" section? Or are you simply saying the same thing you said above as your position in the "Mediation" section, i.e. that you want to see 3 solution sections? -- Rick Block (talk) 01:37, 31 December 2009 (UTC)

Same thing. Or 1 Solution section with 3 sub-headings.Glkanter (talk) 02:02, 31 December 2009 (UTC)

This Is Why They Can't Be Represented in the Article 'Equally'.

Simple solution is not a solution at all

"This is the same topic discussed in more detail three sections down (about the subtly different question), and indeed Morgan et al. argue the "simple" solution is not a solution at all." -- Rick Block (talk) 16:28, 26 October 2008 (UTC) —Preceding unsigned comment added by Glkanter (talk • contribs)

Many sources do give simple solutions but you try to use one source to veto all others by saying, 'Morgan et al. argue the "simple" solution is not a solution at all'. This is your POV but it is not what sources (note the plural) all say. Some sources give the simple solution as the correct one. These sources should be properly represented in the article. Martin Hogbin (talk) 13:42, 24 December 2009 (UTC)

I have no idea why Glkanter reposted this old quote. I think we all agree the POV of the article should not be that the unconditional solutions are incorrect. On the other hand, the article does need include the POV expressed by Morgan et al., and Gillman, and Grinstead and Snell (this is their POV - and whether any editor here agrees with it or not is completely irrelevant) that the unconditional solutions are addressing a slightly different problem than what they think the problem is. I think the only question here should be how best to do this in an NPOV manner. What I hear you (and Glkanter and Jeff) arguing is that they're wrong (sorry, per WP:OR and WP:V Wikipedia doesn't care what you think about their POV), or that their POV should be excluded (sorry, per WP:NPOV Wikipedia must include all significant views). I'd be delighted to work toward a more NPOV treatment. -- Rick Block (talk) 17:27, 24 December 2009 (UTC)

Is it typical for a FA article to need a '...more NPOV treatment.'?

You've always denied the Morgan-centric POV exists until now. How did this POV get into the article? How do we make sure this doesn't happen again? Shouldn't somebody be in big trouble for editing in these violations of WP:NPOV? Glkanter (talk) 18:03, 24 December 2009 (UTC)

This is yet another example of exactly the kind of disruptive behavior Wikipedia:Requests for comment/Glkanter is about. I'm offering to help you achieve your goal. What would you say you're doing? I'd call it trolling. I can't speak for anyone else, but I'm extremely tired of it. Please stop. -- Rick Block (talk) 19:53, 24 December 2009 (UTC)

Actually, Rick, this is another example of you claiming whatever fits your current needs. Here you sound the alarm about the potential for the article to have a POV Last Paragraph. As if the Wikipedia world as we know it would collapse if that happened. But, when you acknowledge that the article currently has a Morgan POV (above), you're not quite as concerned about fixing it in a timely manner. Glkanter (talk) 22:47, 24 December 2009 (UTC)

@Rick, you seem to be putting up an Aunt Sally (Strawman argument). You seem to be implying that I want to remove the POV of Morgan and others who agree with them from the article. That is not the case. I have always suggested that the article should start with the simple non-conditional solutions and then, after discussing these thoroughly, move on to the conditional case discussed by Morgan and others. It is clear, from your reposted quote above (I had not noticed that it had been reposted) that you believe that the Morgan paper should somehow veto or overrule all other sources no matter what they say. Martin Hogbin (talk) 22:54, 26 December 2009 (UTC)

Am I somehow not being clear here? What I believe is that the article should represent as a POV what it is that Morgan et al. (and Gillman, and Grinstead and Snell) say. What they all say is that the unconditional solutions don't exactly address the problem. Morgan et al. go so far as to say the "simple" solution is a "false" solution. In the quote above, I'm saying that Morgan et al. say this, not that I think this POV should veto or overrule all other sources. Whether you agree with what they say or not, do you at least agree that this is what these sources say? I assume you understand that saying that these sources say the simple solution is no solution is not the same as the article taking this as its POV. -- Rick Block (talk) 00:21, 27 December 2009 (UTC)

I am fine with Morgan's POV in the appropriate place but not in the simple solution section. Martin Hogbin (talk) 17:51, 3 January 2010 (UTC)

There's a huge dichotomy between what you write above, Rick, and how you've edited and protected Morgan's POV throughout the article, even down to the FAQs. Plus, it contradicts your long standing and still existing arguments that Morgan's, as the sole peer-reviewed source, is the prevailing POV, and deserves prominence in the article. Plenty of sources apparently don't find Morgan's arguments all that convincing, as they keep publishing simple solutions. I'm not publishing them, professionals are publishing them. It's not my POV, it's the sources' POV. That's why there is an 'editing' function required more so for some articles than others. Editing means more than proper footnoting. And sometimes it means telling a story as it happened, chronologically. That's not POV, that's editing. Glkanter (talk) 18:18, 3 January 2010 (UTC)

Any support for Arbitration?

I think Rick Block and Nijdam are fillibustering and ownershipping against beneficial changes to this article.

I see no point in waiting for either form of mediation unless Nijdam indicates he will accept the findings.

Rick filed an RfC against me last week, the first item of which is 'only edited the article 1 time.' Now, as you've seen yesterday, every edit I make, he or Nijdam at his request, reverts.

If at least 2 people are with me, I'll proceed. Glkanter (talk) 17:31, 28 December 2009 (UTC)

Be aware that mediation does not produce "findings". Its purpose is diplomatic -- to help the parties to find points of agreement. In the best of cases, the parties can agree upon a full course of action, thereby resolving the dispute.

I am almost certain that the Arbitration Committee would not accept the case, since this is primarily a content dispute, and ArbCom rejects content disputes flat out. Just FYI.--Father Goose (talk) 06:20, 29 December 2009 (UTC)

Father Goose, this is from the Formal Mediation page:

"Mediation cannot take place if all parties are not willing to take part. Mediation is only for disputes about Article Content, not for complaints about user conduct."

Since I asked on December 18th if there were objections, and would everyone indicate their agreement to take part, Nijdam has not responded. I felt that rendered the exercise useless.

The arbitration request would allege that Rick Block and Nijdam are using various filibustering and ownershipping techniques (for example, not replying to the Formal Mediation question) against beneficial changes to the MHP article, as desired by the consensus of editors many weeks ago. I fear some of them have lost interest because of the filibustering. Glkanter (talk) 11:01, 29 December 2009 (UTC)

I think you will find that what Father Goose says is still true. They are unlikely to even consider the case. Martin Hogbin (talk) 19:12, 5 January 2010 (UTC)

Mediation

Case link
I've re-opened the case at MedCab and volunteered to assume the role of mediator in a discussion aimed at resolving an on-going dispute here. Additionally, I've issued invitations to participate in the discussion to all involved parties listed in the mediation request. While anyone is welcome to offer input, I ask that those who participate do their best to be concise and refrain from assumption/presumption regarding other's perspectives.

As mediator, my primary goal is to step in as an uninvolved party and help find some common ground from which to proceed. It is not my task to pass judgment on anyone's opinion in the discussion and there is no 'right' or 'wrong' beyond that which is dictated by Wikipedia policy.

I have read the article and understand its subject matter and all it details. As I begin delving through the talk page archives, I'll open the discussion with a call for opening statements. If you feel any archived passages are significant in summarizing the situation, it would help to include links, but please conclude your first post with a Summary of Position (your opinion as it relates to the matter). And remember...concise ;-)
-- (talk) 05:28, 29 December 2009 (UTC)

K10wnsta, what exactly are you trying to facilitate? The original ruckus which led to the request was that perhaps 3 editors were not willing to allow a large consensus to change the article. Their reasons have been debated extensively, and imho, found wanting.

Rick wrote this on his informal mediation request:

What would you like to change about this?

"I would like the endless discussions to be settled. I would like the article to remain a featured article."

What most of us want is some measure of the three change proposals to be reflected in the article in a prompt fashion, via consensus. Is this what you are working towards? In what way? Do you have agreement from all parties that they will honor whatever comes out of this? What form will the outcome of this mediation take? Glkanter (talk) 14:24, 3 January 2010 (UTC) Glkanter (talk) 17:05, 3 January 2010 (UTC)

Nijdam's position

I want the article clearly mention the remark made by some sources that the so called "simple solution" is not complete. It doesn't need initially mentioning the technical term "conditional probability". To make my point clear: the following resoning:

The player, having chosen a door, has a 1/3 chance of having the car behind the chosen door and a 2/3 chance that it's behind one of the other doors. Hence when the host opens a door to reveal a goat, the probability of a car behind the remaining door must be 2/3.

is not complete and better should read:

The player, having chosen a door, has a 1/3 chance of having the car behind the chosen door and a 2/3 chance that it's behind one of the other doors. When the host opens a door to reveal a goat, this action does not give the player any new information about what is behind the door she has chosen, so the probability of there being a car remains 1/3. Hence the probability of a car behind the remaining door must be 2/3.

Something alike holds for the so called "combined doors solution" and most of the other simple ways of understanding. That's all.Nijdam (talk) 08:36, 29 December 2009 (UTC)

I'd like to add that the (a) MHP always involves enumerated doors and a decision to switch offered to the player after a door is opened, seen by the player who has to decide. This is in my opinion and of many (most) sources the only relevant problem.Nijdam (talk) 11:48, 31 December 2009 (UTC)

Martin Hogbin's position

The MHP is essentially a simple mathematical puzzle that most people get wrong. At least the first part of the article should concentrate on giving a simple, clear, and convincing solution that does not involve conditional probability. All diagrams and explanations in this section should not show or discuss the possible difference that the door opened by the host might make, although I would be happy to include, 'this action does not give the player any new information about what is behind the door she has chosen' as in Nijdam's second statement above. The first section should give aids to understanding and discuss why many people get the solution wrong, without the use of conditional probability. The first section should be supported by sources which do not mention conditional probability

The simple solution section should be followed by an explanation of why some formulations of the problem require the use of conditional probability, with reference to the paper by Morgan et al. and other sources. It should also include the various variations of the basic problem and other, more complex, issues. Martin Hogbin (talk) 10:19, 29 December 2009 (UTC)

Glkanter's position

I want the article to clearly mention that the remarks made by some sources, that the so called "simple solution" is not complete, is not shared by all sources. It need not mention "conditional probability" beyond saying that due to the symmetry forced by being a game show, the simple solution is equivalent to the symmetric 'conditional solution'.

I think I agree with Nijdam on the text, although they are both OR. It's consistent with my 1st talk page edit, using an IP address in October, 2008:

Monty's Action Does Not Cause The Original Odds To Change.

When Monty opens a door, he doesn't tell us anything we didn't already need to know. He always shows a goat. It makes no difference to this puzzle which remaining door he shows. So it starts out as 1/3 for your door + 2/3 for the remaining doors = 100%. Then he shows a door, but we knew in advance that he was going to show a goat. The odds simply haven't changed following his action. They remain 1/3 for your door + 2/3 for the remaining doors (of which there is now just 1).

I'd like to see 3 solution sections: Selvin's simple solution of 1975, transitions to Selvin's symmetrically equivalent conditional solution of 1975 (where the discussion of the simple solution's criticisms occurs), transitioning to Morgan's conditional non-solution of 1991.

I'd like to see the word 'variant' either stricken, or augmented by 'slightly different problem'.

I'd like to see a lot of 'blather' removed from the article. Too much time and effort is spent in the various remaining sections explaining the conditional solution, for no real reader benefit. Glkanter (talk) 10:39, 29 December 2009 (UTC)

And the 'Variants - Slightly Modified Problems' section needs work. The MHP is from the contestant's state of knowledge (SoK). The versions in this section are not. This needs to be normalized for the reader in a few possible ways: An explicit statement that the contestant is aware of these new conditions (in which case these are no longer game show problems), or the explicit statement these problems are not from the contestant's SoK, and a comparison of the MHP from a non-contestant's SoK. Glkanter (talk) 13:14, 29 December 2009 (UTC)

Rick Block's position

First, I think the basic issue is an NPOV issue. The primary question is whether the article currently expresses a "pro-Morgan" POV, i.e. takes the POV of the Morgan et al. source that "unconditional" solutions are unresponsive to the question and are therefore "false" solutions - and, if so, what should the remedy be.

There are a variety of sub-issues we need to discuss but I think the main event is how the solution section is presented. I strongly object to splitting the solution section into separate sections (this was done some time ago, well after the last FARC), which inherently favors whatever solution is presented in the first such section. I mildly object to including the "combining doors" explanation in the solution section rather than in a subsequent "aid to understanding" section.

What I would like is for the article to represent in an NPOV fashion both a well-sourced "unconditional" simple solution (e.g. vos Savant's or Selvin's) and a well-sourced conditional solution of the symmetric case (e.g. Chun's, or Morgan et al.'s, or Gillman's, or Grinstead and Snell's) in a single "Solution" section, more or less like the suggestion above (see #Proposed unified solution section - somewhat modified just now). This follows the guidelines at Wikipedia:Make technical articles accessible, specifically most accessible parts up front, add a concrete example, add a picture, and do not "dumb-down".

Once we address this basic issue I think the other issues will be easier. -- Rick Block (talk) 19:43, 29 December 2009 (UTC)

---

Overview

So, let's start at the very beginning...based on my analysis of the archives (*whew*), the positions stated here, and the current article lead, am I correct in understanding everyone agrees on defining the core Monty Hall problem as the one presented in Parade magazine in 1990 that reads:

Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?

--K10wnsta (talk) 22:01, 1 January 2010 (UTC):

I'm not sure what you mean by "core". This is certainly a well known statement of the problem, but it is not very precise. What the the standard analysis is based on (per Barbeau) and how people generally interpret it (per Krauss and Wang) is consistent with the more explicit Krauss and Wang version from the "Problem" section of the article. In particular, the initial placement of the car is assumed to be random (and/or the player's initial choice is assumed to be random) and the host is constrained to always open a door deliberately revealing a goat, choose between two goats randomly, and always make the offer to switch. The effect of changing or omitting various of these assumptions is discussed in the "Variants" section. -- Rick Block (talk) 22:54, 1 January 2010 (UTC)

That is the most often quoted and the most notable statement but, as Rick says, it leaves a lot out. Martin Hogbin (talk) 22:57, 1 January 2010 (UTC)

I started a concept here taking the Parade version and K&W into account. If everyone agrees, we may proceed from there.Nijdam (talk) 12:30, 2 January 2010 (UTC)

Hello K10wnsta. There are several editors here keen to get on with improving this article. Are you still intending to mediate? Martin Hogbin (talk) 10:08, 4 January 2010 (UTC)

Yes, and I apologize for the delay. I have written and rewritten and deleted probably ten thousand words worth of questions, answers, and ideas to offer here and always end up backtracking and starting over because, honestly, you guys have covered every imaginable nuance and detail of the issue in past discussion here. It is not a decision I came to lightly, but I must wash my hands of this. This is an issue that I cannot help you to resolve.

Prior to stepping away and recommending formal mediation (actually, I would recommend some binding arbitration, but we'll follow procedure), I would like to present to you my own perspective (or a third opinion) on the state of the article (and this is boiled down from three lengthy paragraphs):

I was intrigued by the problem. Reading the article, I had the same reaction most people have when the problem is initially presented ('it must be a 50-50 chance'). The actual solution seemed outlandish. Once I read the explanation with the door diagrams, a light bulb went on and it made sense - it was better to switch. Much like the birthday problem, it's an intriguing solution that seems to defy logic. Once explained, it makes sense, and the novelty no longer exists. Everything else in the article is over-analysis, largely because it goes about solving variations of a problem that, once varied, lack the same novelty response that makes the Monty Hall problem notable to begin with.

Again, I'm sorry for the delay in posting this, but it was something I really didn't want to give up on. I wish I could offer more than just an opinion on the state of things, but you guys are so far out in left field in your analysis of this, I just can't wrap my head around it. Sorry I let you down.
--K10wnsta (talk) 01:04, 5 January 2010 (UTC)

BEST WISHES TO YOU ALL

And a fruitful start (continuation) in 2010! Nijdam (talk) 11:45, 31 December 2009 (UTC)

I would like to echo the last comment: Best wishes to all! And a fruitful start (continuation) in 2010. Gill110951 (talk) 19:36, 3 January 2010 (UTC)

What If Morgan Had Used A Different Variant?

Say, the 'forgetful' Monty?

Marilyn vos Savant says this is really a 'random' Monty, who might reveal a car.

I expand this to say, if it's random, then anyone, including the contestant could open the doors.

And if it's the contestant, then we're really talking about 'Deal Or No Deal'.

Does it makes sense to criticize the original solutions to the MHP based on an analysis of Deal or No Deal? Not in my book. Glkanter (talk) 17:21, 1 January 2010 (UTC)

If Monty *might* reveal a car nothing much is changed: the player always switches (only she should be sensible about which door to switch to). If Monty might *not open a door at all* then of course things do change, though under some conditions they don't. Game theory solves this case. If Monty might or might not open a door, and if he might reveal a goat or a car when he does (he does know where the car is), then the minimax solution is the very boring game: the car is hidden uniformly at random, and Monty never opens a door; the player chooses her door uniformly at random, and thereafter never switches. With those strategies the player is guaranteed at least a probability of 1/3 of winning the car; the quiz-team is guaranteed a probability of at most 1/3 of losing the car. So this solution is the saddle-point or Nash equilibrium. (von Neuman's theorem says that there certainly is a saddle-point). I think the solution is unique too: if the player would use any other strategy then the quiz-team could decrease their car-losing probability from 1/3, and if the quiz-team would use any other strategy then the player could increase her car-winning probability from 1/3. Gill110951 (talk) 19:46, 3 January 2010 (UTC)

I'm more interested in the idea that one can critique puzzle 'B', and find fault with puzzle 'A'. Which is what Morgan do, and every time I ask Rick to critique the simple proofs, much as I asked him about Huckleberry, he replies with a critique of a different puzzle. I don't get it. I think it's baseless. Glkanter (talk) 20:26, 3 January 2010 (UTC)

Is Morgan et al. a reliable source by Wikipedia standards? Does this article say If, regardless of the host's action, the player's strategy is to never switch, she will obviously will the car 1/3 of the time. Hence, the probability that she wins if she does switch is 2/3. ... F1's beauty as a false solution is that it is a true statement! It just does not solve the problem at hand.?

Is Grinstead and Snell a reliable source by Wikipedia standards? Does this book say This very simple analysis [as a preselected strategy, staying wins with probability 1/3 while switching wins with probability 2/3], though correct, does not quite solve the problem that Craig posed.

Is Gillman a reliable source by Wikipedia standards? Does this article say This is an elegant proof [vos Savant's solution], but it does not address the problem posed, in which the host has shown you a goat at #3.

Perhaps you don't understand or don't agree with what they're saying, but the beauty of Wikipedia is that it doesn't matter whether you understand it or agree with it so long as what the article says is NPOV and verifiable against a reliable source. We have 3 reliable sources here which all say nearly exactly the same thing. -- Rick Block (talk) 22:34, 3 January 2010 (UTC)

So, did you check the sources of the popular solution? They are quite contradictory. Heptalogos (talk) 23:17, 3 January 2010 (UTC)

Yes, I have checked. They present an unconditional solution without mentioning conditional probability as if the solution is responsive to the question that is asked. So, we have reliable sources that say one thing and other reliable sources that say the first bunch is not quite addressing the problem. I'm open to any reasonable suggestion for how to present this in an NPOV fashion, but not ignoring the second bunch of sources because some editors disagree with what they say. -- Rick Block (talk) 00:19, 4 January 2010 (UTC)

I'm very sorry, you are right. I lost the context because I sometimes find it hard to understand Glkanter. The article is quite good on the solutions, very NPOV (without irony). Now let's hope some scientist attacks Morgan, Grinstead and Gillman in a very irrelevant, but reliable manner. Heptalogos (talk) 20:52, 4 January 2010 (UTC)

Another Straw Man from Rick. Both sides go in the article. Why not chronologically? I've been saying this for a week. Your's and Morgan's POV not dominating the current article? Don't make me laugh. Now, why not answer for yourself, as a sentient being, what does "Suppose you're on a game show...' mean? Without hiding behind Wikipedia's policies. It's OK, we're on a talk page. Glkanter (talk) 01:16, 4 January 2010 (UTC)

Kind of ironic that you're complaining about straw men in a section titled "What If Morgan Had Used A Different Variant?", don't you think? I've asked you before, but where exactly do you see Morgan's POV dominating the article? As far as I can tell the only mention of this POV is in the "Probabilistic solution" section, the 4th paragraph in "Sources of confusion" and a paragraph in "Variants". -- Rick Block (talk) 02:53, 4 January 2010 (UTC)

All is right with the world. As we enter our 15th month of this argument, I disagree with you on the meanings of both 'Straw Man' and 'ironic'. Your POV? It's in every word except the intro and the Simple solution section. You just don't see it for some reason. Glkanter (talk) 06:19, 4 January 2010 (UTC)

And, of course, you avoided the question I asked you. Glkanter (talk) 06:20, 4 January 2010 (UTC)

What question is that? What does "assume you're on a game show" mean? I've answered this before. It provides a context for what is meant by "host" and "contestant" and "door". -- Rick Block (talk) 15:26, 4 January 2010 (UTC)

Maybe The Host Has A Bias Towards Pretty Women?

So, by watching, you realize he nods his head at where the car is. Now the female contestant has a 100% likelihood of selecting the car.

This is equivalent to Morgan's argument about a left-most door bias. It's published, but pretty darn stupid.

There is no contestant, or viewer, awareness of a host bias on a game show. And the puzzle begins, 'Suppose you're on a game show...' Glkanter (talk) 17:20, 5 January 2010 (UTC)

Equivalent, except your scenario is NOT published in a well known peer reviewed statistics journal. And, in the extreme, if it were published (and there were multiple confirming sources) we should include it.

These little sections you keep adding that suggest no specific change to the article at best belong at /Arguments. Please stop posting them here. -- Rick Block (talk) 19:23, 5 January 2010 (UTC)

Glkanter's point, which I agree might be better in the argument page, is that even in a real-life scenario the player is unlikely to know much about the host's door choice and would therefore be reasonably expected to treat it as random. As this is, in fact, a mathematical puzzle, as the article makes clear at the start, it would be perfectly normal to take an unknown initial distribution as uniform. This makes the conditional answer exactly equal to the unconditional answer and the issue of conditionality somewhat irrelevant to explaining to a typical reader of this article why the answer is 2/3 and not 1/2. This is the improvement to the article that many of us here want. Martin Hogbin (talk) 23:51, 5 January 2010 (UTC)

Thanks for the support? My point is that this Pretty Woman variant is just as likely as the left-most door variant that Morgan (or Rick?, I've lost track and interest) uses to stigmatize the probability/logic solutions. They're both made from whole cloth. Mine is just less opaque in it's ridiculousness. I would not strike the keys of my keyboard to discuss the initial distribution. Although, I have spent 15 months arguing over a host bias. Glkanter (talk) 06:17, 6 January 2010 (UTC)

What is the Morgan scenario?

I have now shown that in order to get an answer (probability of winning by switching) of anything other than 2/3, Morgan have had to assume that we know that the producer places the car randomly, but we do not know that the host opens a legal door randomly. Is there anyone here who can justify that odd POV.? Martin Hogbin (talk) 10:12, 4 January 2010 (UTC)

Yes. There will be at least one editor who will attempt to justify that odd POV. Glkanter (talk) 13:10, 4 January 2010 (UTC)

It's not "Morgan's scenario", but Morgan's interpretation of vos Savant's scenario - perhaps "Morgan's vos Savant scenario" would be a better way to refer to it. It exactly matches the rules she sets up for the experiment she describes in her 3rd column, see [6]. I assume this is the "false simulation" they refer to in the introduction to their paper. The cups are labeled #1, #2, and #3. The host randomizes where the penny is placed. The contestant randomizes her pick. Then the host "purposely lifts up a losing cup from the two unchosen" (no mention of randomization in the case where the host can lift up either unchosen cup, even though both the initial placement and the player's pick are explicitly randomized). What is counted is overall success when not switching and overall success when switching, rather than success when not switching and success when switching for players who have picked cup #1 and have seen the host reveal what's under cup #3. This experiment is explicitly addressing the unconditional probability of winning by switching rather than the conditional probability - in a setup where they might actually be different (since the host is not required to randomize his choice of cup to lift up in the case where there is a choice). -- Rick Block (talk) 15:14, 4 January 2010 (UTC)

It really is unfair to try to blame vos Savant for failings in the Morgan paper. Sure Morgan mention vS at the start of their paper, they also mention the "prisoner's dilemma" (where the warden does secretly toss a coin), and Mosteller's' solution. Later on they state that vS took it that the host never reveals a car, and it is clearly this rule that they describe as the vos Savant scenario.

Regardless of what vos Savant or anyone else assumed, Morgan are under an obligation to firstly make consistent assumptions (for example that all unstated distributions are to be taken as random) and then to make clear the assumptions that they have made. They conspicuously fail in both of these respects.

Morgan claim to have 'an elegant solution that assumes no additional information', clearly referring to the Whitaker's original question, rather than vos Savant's interpretation. Their solution does not live up to this claim.

Finally, regardless of reasons or motives, Morgan do in fact consider the scenario that we know the producer places the car randomly but we do not know that the host chooses a legal door randomly. Their answer of 1/(1+q) is based on this scenario. This is not a reasonable or consistent assumption thus their answer of anything other than 2/3 is not valid. Martin Hogbin (talk) 16:11, 4 January 2010 (UTC)

Rick, you are still misrepresenting MvS's statements, and that is an example of how you inject your POV into everything you write. Please stop taking her statements out of context. "Anything else is a different question" refers to all of the assumptions she made in her approaches to the solution. That includes random car placement and random host selection (if needed), and excludes any dependence on Door #1/Door #3 that you think is included. Her shell game analogy did not number the shells, yet she said it was the same problem. As you yourself point out, the cup experiment does not mention picking cup #1 or lifting cup #3. You can't treat that part as an error; it, too, has to be part of any "exact match to the rules she sets up." So Morgan's interpretation does not qualify.

In the literature, there are two camps that do not agree with each other, and that never reconcile their differences (well; actually, MvS does - she said Morgan's is a different problem). Those that follow Morgan's "conditional problem" and those who agree with Seymann, that "the host is to be viewed as nothing more than an agent of chance who always opens a losing door, reveals a goat, and offers the contestant the opportunity to switch to the remaining, unselected door." Insisting that only the former group is correct is POV, and that is what I mean when I say you inject your POV. I will only stop saying it, when you stop doing it. Morgan's POV can be handled in the article; but it clearly is not the problem MvS intended. That fact is acknowledged in literature. So the article needs to first address the problem she said was intended, and then add the second opinion in as a variant, and clearly label it as a variant. That is the NPOV approach.

Martin, I firmly believe that Morgan never intended to introduce theirs as a "variant" problem, or to avoid making assumptions like the one about car placememt. All they ever say, is that one of the assumptions MvS made is not necessary to answer the question "should we switch?" They misspoke when they said "assumes no additional information," they quite clearly meant "assumes no unnecessary information," since they did make assumptions. And their answer to the Monty Hall Problem does not use the 1/(1+q) result, it only shows that no specific value is needed. It was an intellectual excersize only, and is not intended to be the MHP. So yes, it would be inconsistent to give an answer that includes q but not P(C₁), P(C₂), and P(C₃). My point here is that they don't - but they also fail to make it clear to their readers that they don't. JeffJor (talk) 17:14, 4 January 2010 (UTC)

Jeff, I agree, the Morgan paper is not entirely without interest or value. They show how, in a more general case, the host behaviour is important, firstly in never showing a car, then in choosing which door to open, but the player can never do worse by swapping. The problem is that they make such a bad job of what they do that it is hard to work out exactly what their main point is, except to criticise others.

My main point is that there is no justification for saying that in the MHP, with standard rules, the action of the host is important. There are only two logical and consistent ways to look at Whitaker's question. Take it as a real world question about the actual probabilities on hypothetical TV show, in which case it depends on so many factors that the answer is indeterminate, or take it as a mathematical puzzle, in which the normal mathematical puzzle assumptions are made, undefined distributions are taken as random etc. Anything else is, as you say, just an intellectual exercise. Martin Hogbin (talk) 18:11, 4 January 2010 (UTC)

I disagree on 1 point, Martin. "Suppose you're on a game show..." means the car placement and host choice, as far as the contestant is concerned, are random. This is true whether it's a hypothetical game show, or a mathematical puzzle. Because that is the host/contestant relationship on a game show. And it's every bit as much a premise of this math puzzle as '1 car and 2 goats' which is clearly stated. Because 'Suppose you're on a game show...' has also been clearly stated. Glkanter (talk) 18:44, 4 January 2010 (UTC)

It depends on the presumed state of knowledge of a contestant on the hypothetical show. Maybe the contestant has watched the show and discovered that the car is most often behind door 1. I do agree that a natural assumption would be that a contestant would have no knowledge of how the car might be placed or the host would choose but in real life this might not be the case. I am not seriously pushing the real life option, just stating that it is the only logical alternative to the 'puzzle' option. Martin Hogbin (talk) 20:01, 4 January 2010 (UTC)

Martin, this is not about "real life." It is a thought puzzle, only. No biases, or unrandom occurrences, can be assumed unless specifically stated. But this has nothing (directly) to do with "Suppose you are on a game show..." It has to do with its not being mentioned. You must assume any unmentioned options have to be random between the possibilities (and so this is another reason the conditional solution can't be used.) JeffJor (talk) 20:32, 4 January 2010 (UTC)

Jeff you are the hardest person in the world to agree with sometimes. As I said to Glkanter, the real world scenario is the other consistent option, but I agree that the real one in the 'puzzle' option. Martin Hogbin (talk) 20:40, 4 January 2010 (UTC)

Martin, you have a problem because you don't acknowledge the fact that it is your argument, not your conclusion, that I disagree with. There is no supportable definition for what "suppose you are on a game show" means, so it is pointless to try to argue for a meaning behind it. There also is no justification for trying to place the problem in a real-world setting, which is one of the problems with Morgan. (Just like "What is the probability that the woman I met yesterday, who has two children, has two boys?" The real-world answer is 100%, because she does have two boys. The intent of the question, as a puzzle, is 25%; and the real-world scenario is completely irrelevant.) So I view any arguments based on eithar as being counter-productive. JeffJor (talk) 17:31, 6 January 2010 (UTC)

Jeff - I'm merely suggesting where Morgan et al. got the "odd" scenario from. MvS explicitly said lots of things, but never (as far as I know) explicitly said anything about how the host chooses when given the chance (at least not before the Morgan et al. paper was published). This is NOT "my" POV, but Morgan's POV (that I seem to be the only one representing here). I'm FINE with treating this specific scenario as a variant (it's already been moved to the variant section), but I don't think it means that a conditional solution must also be deferred to a variant or that a discussion of whether the question refers to the unconditional probability or the conditional probability must be deferred to a variant. The unconditional and conditional probability for the fully explicit version (including "host picks randomly if given the chance") are the same - we all agree about this - but I think clarifying that these are different questions and which approach addresses which question should be part of the initial "Solution" section. -- Rick Block (talk) 19:12, 4 January 2010 (UTC)

Rick - I'm not saying that your agreeing with Morgan, per se, is POV. I'm saying that disagreeing with MvS on the same subject, where she disagrees with Morgan, is POV. You said "[Morgan's interpretation] exactly matches the rules [Marilyn vos Savant] sets up for the experiment she describes in her 3rd column." It does not - why do you ignore that part of what I said? It exactly matches what Morgan said her set of rules was, a set she explicitly denied was her intent. There are two parts to that difference, and it requires both of them to make Morgan's interpretation applicable to anything: There is the question about whether Door numbers are important (they aren't, and she explicitly made that clear because she does not use the numbers in her two analogies), and there is the question about how the host treats door numbers if they are important (which MvS doesn't mention, but doesn't need to: as per Seymann, the host is only an AGENT OF CHANCE and so everything he does must be goverened by chance alone. That is the statement you are missing. But even if that is not accepted, since the door numbers are not important, no such bias can be used. You yourself pointed that out, because her experiment was "explicitly addressing the unconditional probability of winning by switching rather than the conditional probability." Those are what her rules are, according to her.)

To say there is a match requires that you ignore MvS's comments and accept only Morgan's. We simply have to beleive MvS's statements of what her intent was, over Morgan's. That's what makes their treatment a variant, and what makes disagreeing with her "set of rules" POV even if you find sources for support. Plus, you misinterpret Morgan (I still must be speaking in cat whan I say this): They do not present a solution to the MHP that includes q. They show that if the MHP is CHANGED (they don't call it a change, but MvS does, so we have to treat it as one to be NPOV), then you get the same answer ("switch") no matter what q is. But they ignore placement bias the exact same way MvS does, because it does affect the answer, and is part of being an "agnet of chance."

There is no justification for saying the host's preferences for opening one door over another matters, because the MHP is about the strategy, not the doors. Any mention of it belongs with the variants, and even then we have to say that you can't use it unless you know it. JeffJor (talk) 20:25, 4 January 2010 (UTC)

Jeff - How do the rules of Morgan's vos Savant scenario not match the experiment she described? As far as I can tell, the difference is whether you're ignoring the conditional question and intending to answer the unconditional question (like vos Savant does) or whether you understand there may be a difference and are intending to answer the conditional question (like Morgan et al. says is what the question asks). Which specific comments of MvS's (from her columns) did they ignore? It sounds like you're claiming the quote "Anything else is a different problem" applies to anything you'd like it to apply to. Here's the full quote:

Rick - I can keep repeating this as often as you ignore it: Morgan assumes that the door numbers were intended to be used as part of the problem, and not meant as examples. MvS does not. That is, Morgan addresses what you call "the conditional proeblem," which is part of what MvS calls "a different problem." As I said twice yesterday, this is clear because the two analogies she uses do not use those door numbers in the solution, not even the one (and only one) that includes them in the description. So how can you ask this question? Her experiment that does not use door numbers, and that you said "exactly matches" a treatment that does. So I'm not "ignoring" the conditional problem, I'm saying (1) It isn't there to be ignored, (2) teh conclusion that it is comes from a misreading of the problem (K&W say the door numbers are sematically just examples) (3) MvS has denied it is intended, which allows us to ignore it and still be NPOV (4) Seymann acknowledges it is not how the problem shoud be read, and (5) The vast majority of sources that address what they call the MHP, especially in popular literature where the controversy exists, do not consider it at all. Selvin, Savant, Gardner, Tierney, Delvin, Mlodinow, and others all either ignore door numbers, or uses them as examples and treat them as though they represent "without loss of generality" selections. JeffJor (talk) 17:25, 5 January 2010 (UTC)

Morgan et al. assume the door numbers are persistent and the problem pertains to a player who has initially selected a specific door and has seen the host open another specific door. They use the example case of door 1 and door 3 as representative of any other (equivalent) case. Selvin (2nd letter), Morgan, Gillman, Grinstead and Snell, Chun, Falk, and others all approach the problem this way using this case "without loss of generality". -- Rick Block (talk) 19:48, 5 January 2010 (UTC)

Only partially right, Rick. Not all use the phrase "without loss of generality." Those that do, are acknowledging that they are using single cases to represent all of the symmetric cases. Those that never consider "host strategies" other than random selection - like Selvin in what he calls an alternate solution - are implicitly doing the same thing. It is the insistence that the problem [i]must[/i] be solved with conditional problility AND that this solution must consider p!=q that we object to. Once you remove that second possibility, there is no need to use specific doors. You can change "Door #1" to "the chosen door," "Door #3" to "the opened door," and "Door #3" to "the remaining door." There is no way apply the parameters p and q this way. Doing so removes a level of complication that obfuscates the MHP to the casual reader, and so makes the article more readable. JeffJor (talk) 17:22, 6 January 2010 (UTC)

So let's look at it again, remembering that the original answer defines certain conditions, the most significant of which is that the host always opens a losing door on purpose. (There's no way he can always open a losing door by chance!) Anything else is a different question.

You're telling me you're absolutely sure "anything else" here does not refer specifically to the host opening a losing door on purpose but to all the "certain conditions" that she hasn't enumerated (and, so, anything she might need to justify her solution is included). Furthermore, you're telling me that in spite of explicitly labeling the cups she never meant the labels to mean anything (!?), and in spite of explicitly randomizing the initial distribution of the penny under the cups as well as the contestant's initial choice but saying nothing about the host's choice when the host has a choice she clearly meant the host to choose randomly as well (?).

What is "anything else" comparing? Questions. What is the subject of the paragraph? Conditions that are defined for her question, by her answers. "Anything else" means anything other than the conditions she describes - those stated in her original problem OR implied by her solution. And it is quite clear in "opens a losing door" is just one example of a condition she means, and yes it is quite clear there are others. So absolutely, positively, can't mean just that one specific condition. JeffJor (talk) 17:25, 5 January 2010 (UTC)

I think we both know she simply wasn't thinking of the conditional case at all - which is precisely what Morgan et al. criticize her for since in their view the question is clearly what is the chance of winning by switching in a specific case (such as the player has picked door 1 and the host has opened door 3). The chance is the same as the unconditional chance only in "certain conditions" one of which is that the host choose randomly when able to choose - or, less realistically, you can't tell the difference between the doors - or, more pedantically, you're restricting the solution to the player's SoK and assuming the player has no way to know about a host preference (essentially a sophisticated way of saying you can't tell the difference between the doors). You're saying MvS clearly understood this and clearly meant this to be one of the conditions of the problem. Fine. You're certainly entitled to your opinion, but since she never explicitly mentioned it in her columns (or, BTW, even in her rejoinder to Morgan et al.) it seems like there's a pretty good argument that she overlooked this condition. It was one of the first things Selvin mentioned in his second letter about the problem in response to the letters he got. It's not a "throwaway" detail. What I'm saying is that this article should not treat it as a throwaway detail either.

And how is "not thinking of" different from "not intending?" JeffJor (talk) 17:25, 5 January 2010 (UTC)

As far as my POV, what I'm saying is that there is a difference between a solution that inherently addresses only the unconditional probability and a solution that is able to address the probability in a specific case. I would like BOTH to be presented, as equally valid solutions to the fully specified, symmetric, problem (where the answer is the same). Based on how violently you're objecting to this are you arguing that a conditional solution is somehow wrong? -- Rick Block (talk) 01:07, 5 January 2010 (UTC)

There is no "specific case." It is an example. Here's another one: A woman I met at random yesterday has two children. What is the probability she has two boys? Answer, for the specific case: 100%. Answer clearly intended by the question: 1/4. It's a puzzle that uses an example to describe the random process. The example is not intended, and never is in such questions unless specifically included. And it has to be so, because probabilities do not apply to specific cases. They only apply to random processes. JeffJor (talk) 17:25, 5 January 2010 (UTC)

Since I can enumerate the specific cases (player picks door 1 and host opens door 2, player picks door 1 and host opens door 3, etc.) your claim that there is no specific case seems rather curious. Bottom line, you're saying "yes" a conditional solution is wrong? -- Rick Block (talk) 19:48, 5 January 2010 (UTC)

And once again, you insist on ignoring the point so that you can justify including Morgan. The numbers are not a part of the problem, they are only examples used to illustrate the problem. Stop me if you've heard this before: "Say," when used as an adverb like that, means "for example." The problem statement without examples is "Suppose you're on a game show, and you're given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door ... and the host, who knows what's behind the doors, opens another door ... which has a goat. ... Is it to your advantage to switch your choice of doors?" The parts I removed are simply not part of the question that is being asked. Period. We also know MvS intended it that way, because the statement as I just worded it is the only statement that is equivalent to Marilyn's two experiments. The only source that addresses why we should, or shouldn't, use the so-called "conditional problem" is K&W. All others merely assume one or the other (some implicitly and some explicitly, but still an assumption) without justifying why. And when they present that argument, K&W say the door numbers are not semantically part of the question. So by the Wikipedia guidelines, the only problem we can consider "the" MHP is the unconditional one. Morgan's treatment of it does not address her problem, because they changed the wording in the quote to insert the door numbers into the actual problem. So we cannot use Morgan as a source that addresses our main problem, and any solution they depends on specific door numbers must be relegated to the section on the variant they created. (Note that Selvin's conditionl solution does not depend on the door numbers, as it sets all probabilities by the assumption of uniformity. I've always agreed it can be used as a solution, but not with q != 1/2. And it doesn't help explain the controversy.) JeffJor (talk) 16:41, 7 January 2010 (UTC)

Let's continue this during mediation if you don't mind. -- Rick Block (talk) 19:41, 7 January 2010 (UTC)

JeffJor, I'm with you on this 100%. So, living with the requirement that since they're published, Morgan and its ilk must be included in the article, how would you apply your argument to the article? Bear in mind, imho, the conclusion that 'Morgan's paper does not address the MHP' is, unfortunately, OR. Unless you have a source? Seymann just couldn't quite say it. Glkanter (talk) 18:03, 7 January 2010 (UTC)