Talk:Monty Hall problem/Archive 11

Archive 5

←

Archive 9

Archive 10

Archive 11

Archive 12

Archive 13

→

Archive 15

Bayesian approach

I’ve added a link in “See also” to the discussion at Bayes' theorem. I see that Bayesian approaches (etc.) have occasioned controversy (in this talk page); my feeling is that:

• while the Monty Hall problem is a good illustration of Bayesian probability, and thus warrants discussion (under “Bayesian probability”),
• for readers just wanting to understand the Monty Hall problem, Bayesian analysis likely confuses matters, and shouldn’t be on the Monty Hall page itself – the simple analysis (1/3 right at first, switching reverses these) is plenty, and clearly is confusing enough as is.

For comparison, see this paper on variants – which essentially gives a Bayesian/Principle of Indifference approach:

• Monty Hall, Monty Fall, Monty Crawl, by Jeffrey Rosenthal

—Nils von Barth (nbarth) (talk) 01:54, 23 April 2009 (UTC)

I’ve linked Rosenthal’s paper from the variants he mentions, as it’s available online and the statements (why half the time?) may be confusing – which he elaborates and clarifies – but I’ve made no mention of Bayesian approaches vs. enumeration, leaving that to the references.

—Nils von Barth (nbarth) (talk) 02:11, 23 April 2009 (UTC)

I've just restored the formal Bayesian approach that had been in the article for a long time and deleted fairly recently by user:Nijdam. IMO, the article is incomplete without it. -- Rick Block (talk) 04:44, 23 April 2009 (UTC)

I only deleted it, because I replaced it with a much shorter formulation, as part of the probabilistic approach. In my opinion it should not be called a Baysian approach, as it hardly has anything to do with Bayesian analysis. It is plain probability theory, using Bayes' law, that all. Nijdam (talk) 08:21, 23 April 2009 (UTC)

Hi Rick – I agree that the Bayesian analysis is informative; thanks!

One may argue that the section is a bit long, and may be technical for readers unfamiliar with probability, though putting it as the last section seems to address that.

To Nijdam – it seems reasonable that some mention of Bayes' law should be made, whether it be framed as a Bayesian analysis or not, no?

The distinction between a frequentist/probabilistic statement of applying Bayes' law vs. a Bayesian statement seems to me to turn on whether one should say “1/3 of the time the car will be behind each door” vs. “By the principle of indifference, one should assign a prior probability of 1/3 to each door,” – and similar framings for the inference/likelihood.

The Bayesian interpretation of probability is widespread and valued, which argues for an explicitly Bayesian statement of this interpretation; in how much detail might be argued about though.

So does it seem reasonable to both explicitly mention Bayes' law and to give a (brief or detailed) discussion from the Bayesian perspective?

—Nils von Barth (nbarth) (talk) 11:15, 23 April 2009 (UTC)

I have no objection of mentioning Bayes' law, on the contrary. But it has nothing to do with a Bayesian type of analysis, as some people seem to think as soos as they happen to hear the name Bayes. My problem is the naming of "Baysian approach" as one and further the quite heavy formulation. It is no more than the needed formulation for the solution, and it can be written down quite easy as I did in my formulation of the "probabilistic approach", which alas has been deleted recently. Nijdam (talk) 14:47, 23 April 2009 (UTC)

Hi Nijdam,

I’ve made some changes to your formulation (formatting and linking Bayes' law).

Substantively, I’ve also mentioned that the Bayesian interpretation of P(Car behind door 1)=1/3 is as the principle of indifference (prior belief), as opposed to the frequentist “Model as a uniform distribution/In the long run 1/3 of the time it will be”, as this is an important philosophical point as I understand it.

(I imagine there may be some more back-and-forth on how best to discussion Bayesian interpretations, as per Rick’s comments.)

—Nils von Barth (nbarth) (talk) 15:51, 23 April 2009 (UTC)

Well to be honest, I don't like it. According to the rules the car is placed randomly, so why complcate things in mentioning notions of Baysian approach. The interested reader has nothing to gain from it. Nijdam (talk) 20:41, 23 April 2009 (UTC)

At least at first glance it seems to me, that it might be wise to keep the probability/statistic schools (frequentists vs bayesians) out of the problem at the elementary. Because to the average reader and probably even the average mathematician this might be rather confusing then helpful. If analyzing the problem from the 2 different philosophies provides some useful insight (I'm not knowlegdable there) it should be treated in a separate section with more detail and not mixed with the "elementary" Bayes solution section.--84.174.195.210 (talk) 11:35, 1 May 2009 (UTC)

The point of the previous section was that it is a rigorous proof, referenced to a published source. To be rigorous it needs to be in the context of a specific formalism - yes, it is quite elementary and only uses Bayes' law, but it is a formal proof unlike the "replacement" section which is informal and unreferenced (making it effectively WP:OR). I'm not going to edit war about this, but I vastly prefer the more formal treatment. -- Rick Block (talk) 16:07, 23 April 2009 (UTC)

I don't necessarily prefer formal over informal, but always we must prefer sourced over unsourced. If there's an alternative people want to consider, they need to show a source that analyzes the problem that way. Dicklyon (talk) 17:23, 23 April 2009 (UTC)

I won't consider my formulation as WP:OR; it is merely a better readable translation of the former so called Bayesian approach, which, as I indicated, is hardly Baysian. Nijdam (talk) 20:41, 23 April 2009 (UTC)

Nijdam - your version is an entire section without a reference, which is pretty much a no-no for a featured article. And, why would you say the former version is "hardly Bayesian"? It's simple, but precisely follows the formalism - which has the advantage of being mathematically rigorous. I've asked user:Glopk (the primary author of the section you've replaced) to comment. -- Rick Block (talk) 14:12, 24 April 2009 (UTC)

I just reformulated the formal derivation as can be found in Morgan etc. Bayesian statistics is typical concerned with parameter estimation, using prior distribution of the parameter in achieving specific estimators. Although Bayesian methods use Bayes' law, not every use of this law is a Bayesian method. Bayes' law is a simple rule in probability theory as you know. Nijdam (talk) 16:01, 24 April 2009 (UTC)

I haven't even read the section in question, but just want to point out that "reformulating" can be a problem. Given the controversial nature of this problem, we'd do best to stick very close to just reporting the analyses that are in sources. Dicklyon (talk) 16:23, 24 April 2009 (UTC)

I am reverting this edit. The derivation is much less clear than the original one, and the typesetting is an ugly mixture of ASCII and inline math images. We may argue on whether the section should be titled "Bayesian Analsys" or just "Formal Probabilistic Analysis", but the replacement of its content with the current one is just bad.glopk (talk) 19:48, 27 April 2009 (UTC)

I'm strongly against reverting. If it is the ugliness, may be you may enhance the beauty of the section. But the former section was way to long and used a much to complicated notation. Not only should it not be named 'Bayesian approach', it also should not mention anything of this kind in the text. Nijdam (talk) 21:51, 27 April 2009 (UTC)

[outindent]Nijdam, please re-check your priorities and onus assignment. The previous "Bayesian Analysis" section was well-referenced, complete as any elementary proof should be, and used a standard mathematical notation (the notation of most modern probability theory textbooks that I am aware of). Its graphical editing was well up to par with other articles of mathematical content. Because of the above, it has passed two FA reviews along with the rest of the article. Now you are replacing it with something concise to the point of being almost a link, unreadable for the non-mathematically initiated, and using an ugly mashup of ASCII and LaTeX notation. Now think again and answer: on whom does the onus of "enhancing the beauty" of the section fall, you or me? This new section is going away as soon as I have a few minutes to unravel the pile of **** you have larded upon it. Man, are you on a mission to ruin this article?glopk (talk) 22:35, 27 April 2009 (UTC)

I don't know if I can helpfully moderate here, but before this gets more heated I just want to mention that (unlike many who choose to comment on this page) you are both math professors and should treat each other with due respect. Per my previous comments above I favor the original treatment. -- Rick Block (talk) 23:29, 27 April 2009 (UTC)

And, to be clear, I'm definitely NOT saying that only folks who are self-identified math professors should be treated with respect. Since you really don't know who you might be interacting with here, it's best to treat everyone as a colleague (even though in reality they might be dogs). -- Rick Block (talk) 00:24, 28 April 2009 (UTC)

Well, very glad to hear that, since I am not a math professor (where did you get the idea ? :-)

Generally speaking, and to begin with, I have a hard time respecting the arguments of someone who starts with a strawman. A few paragraphs above Nijdam states: "Bayesian statistics is typically concerned with parameter estimation". This is inane in general, but particularly so when referring to a section that had absolutely nothing to do with statistics - its very first sentence stated: "An analysis of the problem using the formalism of Bayesian probability theory". If Nijdam does not understand the difference between Statistics and Probability Theory, I surmise that he has no business arguing about either. Further, it is really baffling to replace an FA-quality section with one so poorly edited, and then invite a critic to "enhance its beauty". Seriously? Are we talking about editing a reference resource that people have come to rely upon, or is it the faculty bocce-ball club newsletter? Surely prof. Nijdam would not ask the same of a reviewer of one of his academical papers, and I expect he should treat his WP reviewers with as much respect.

More to the point of his criticism. Those who attended the last two FA-reviews will remember that both points - article length and formalism - were discussed at lenght, and the consensus was that the article in the then-current form, inclusive of the Bayesian Analysis section, were more than acceptable. Nijdam is not presenting any argument that hasn't been already rehashed and found wanting.glopk (talk) 03:38, 28 April 2009 (UTC)

My problem with this section is that it is not of interest for the average interested reader of an encyclopedia. It is a very formal way of Bayesian terminology, which is not appropriate for this problem, at least not for the presentation in Wikipedia. The (common) solution of the MHP asks for the calculation of conditional probability that can be straightforward done. It involves using Bayes' law, that's all. This simple derivation, as found in many text books is now nowhere found in the article. Nijdam (talk) 07:42, 28 April 2009 (UTC)

outindented)See i.e. Behrends, Ehrhard (2008). I'll just use some other symbols.

---

The solution may be given in terms of the following events:

$\!\;C_{i}$, the car is placed behind door No. i,

and:

$\!\;H_{i}$, the host opens door No. i.

The car is placed randomly behind the doors, hence every door has the same probability of hiding the car:

$\!\;P(C_{i})={\tfrac {1}{3}}.$

Let us assume the player has initially chosen door No. 1. From the rules of the game it follows:

$\!\;P(H_{1})=0.$ (The chosen door is never opened)

$P(H_{2}|C_{1})=P(H_{3}|C_{1})={\tfrac {1}{2}}.$ (If the car is behind the chosen door, the host chooses randomly to open one of the other doors.)

$\!\;P(H_{3}|C_{2})=P(H_{2}|C_{3})=1.$ (The host only reveals a goat)

If the host has opened door 3, the probability of the car being behind door 2 may be calculated using Bayes' law:

$P(C_{2}|H_{3})={\frac {P(H_{3}|C_{2})P(C_{2})}{P(H_{3}|C_{2})P(C_{2})+P(H_{3}|C_{1})P(C_{1})}}={\frac {1\cdot {\frac {1}{3}}}{1\cdot {\frac {1}{3}}+{\frac {1}{2}}\cdot {\frac {1}{3}}}}={\tfrac {2}{3}}.$

---

This is all there is to it. Plain, straightforward, found in many textbooks. Nothing my own research, simple, easy to understand for someone familiar with the basics of probability theory, nice lay out, etc. etc. What do we want more.Nijdam (talk) 13:08, 28 April 2009 (UTC)

Let's see, I count at least 3 POV statements in your last (indented) paragraph above, which is OK since this is a discussion. What is not OK is your uncritical application of them to the article. Face it: you are not the mythical "average interested reader" - a non-existent construct of imagination until someone show the results of a controlled poll of readers on a well-defined set of questions. However, from our experience with students (BTW, yes, years ago I did teach elementary prob. theory at both undergrad and grad level), and from the history of editing a long-lived article such as this, it is possible to draw some suggestive conclusion. Feel free to call them my POV's, if you wish. One is that a reader that is curious and conversant with math, but not (yet) a student of particular math discipline, favors a proof in which as many steps as possible are clearly spelled out, from first principles and hypotheses to thesis. Call it "The average reader dislikes jumps" principle. This, of course, is possible only for elementary proofs that are only a few theorems removed from the axioms - but guess what, we are exactly in this situation here, and - ri-guess what, that's exactly why a good author like Gill puts the problem and this solution in the first chapter of his textbook. Of course the calculation can be done in a straightforward manner, but that is precisely NOT the point of this section.

On your repetition of the formulation above. Yes, absolutely, it is plain, easy, quick. It is also un-readable unless you already know very well what the symbols mean, why you are allowed to combine them in this manner, and how they relate (if at all) to the MHP. I think you just proved my point, thanks. On the other hand, the Bayesian analysis section as it stands now (I put it back, as you can see) is self-contained, except for pointers to more general topics, and uses standard textbook notation as well. It just take several lines more in order to spell out all the logical steps, but not so many as to become a treatise unto itself.glopk (talk) 15:05, 28 April 2009 (UTC)

Seemes you missed the words: with some extra text, which I added to indicate it's needed to make my suggestion readable to this mythical average reader. The formulation above, as a framework, is just for this discussion. Nijdam (talk) 16:35, 28 April 2009 (UTC)

I'll complete the text. Nijdam (talk) 16:48, 28 April 2009 (UTC)

Seems you have forgotten what your (now deleted) section in the article looked like - there wasn't any "extra text" in there either, yet you were "strongly against" reverting it. I'll be happy to see it - in a proposal page or section of this discussion page, rather than on the main article until it's ready (if ever). Please avoid defacing the article again. glopk (talk) 16:57, 28 April 2009 (UTC)

Question: What more do you want? Nijdam (talk) 10:01, 29 April 2009 (UTC)

Question: Why won't you leave this section alone? You have three users already (me included) telling you it's fine and informative as it is. Your arguments for changing it are either old and already refuted (length, symbols) or specious ("average reader", a foggy notion of what Bayesian probability theory is about). If not, propose changes that make sense AND keep this article at FA-level. And please use a fine brush and leave the jackhammer home, because - believe it or not - noone likes to drive a steamroller over your edits. glopk (talk) 15:13, 29 April 2009 (UTC)

Simply because the explanation in words, may (even should) be followed by a formal mathematical dervation. And that's what the proposed part is. Special attention to Bayesian probability theory is not the purpose of this article. Nijdam (talk) 10:28, 30 April 2009 (UTC)

Let's first dispose of this new variant of your "Bayesian, boooh!" strawman. Exactly how does Bayesian probability theory get special attention in this article? If you bothered to count words, you'd notice that the vast majority of the article's content reflects a frequentist view of probability. More, the lede is a frequentist "Popular solution". Recent edits (by you and others) even managed to beat into a small pulp of packed text and inline ASCII formulae Rick Block's elegant presentation of the "conditional" (i.e. Bayesian) interpretation of the problem. Besides, your whole point is bizantyne: BPT is simply used in this section as an explanatory tool, and in this sense no more "special attention" is given to it than the top figure gives to Cartoon Graphics. Are you going to argue next for removing the figures because the purpose of the article is not to give special attention to cartoons?

Second, the position of the formal derivation in the article. This section was at one point higher up, above the "History", and part of a wider "Aids to understanding" section. It was moved to the bottom of the article when revised for a past FA review. The reasoning went, give or take, like this: only a quite small fraction of readers is conversant with mathematical symbolism and willing to read a formal proof (*any* formal proof), therefore let's do something akin to the way in which, in many journal articles, math proofs are placed in appendices. The interested readers will find and enjoy it, while those not interested won't be distracted. So no harm is done to anyone, and the "flow" of the article is enhanced. glopk (talk) 16:05, 30 April 2009 (UTC)

Imho the current version fine and I agree that Nijdam's edit/revert was problematic for several reasons you've outlined above (independent of the question which version one personally consider as nicer). I do however have some questions/possible about the current title and the references to Bayesian statistics. My understanding so far is, that frequentists and Bayesians alike do use Bayes' formula on an elementary level and they would both model/explain the MHP problem as stated here. So assuming I'm not mistaken here, the terminology bayesian as well as the references, as they are used now, can create a misleading impression (in particular that this analysis would only be valid from bayesian viewpoint and frequentists may decline it). Hence overall I prefer the current solution and I agree with your criticism of Nijdam's actions. However I do think some of the wording/title should be revised nevertheless for the reason i just outlined.--Kmhkmh (talk) 12:11, 1 May 2009 (UTC)

I partially agree with your points above. Indeed the solution of the "conditional" interpretation of the problem would be similarly written in any sane formulation of probability theory, but there are non-trivial differences in the conceptualization of both hypotheses and result. Yes, we could shove these differences under the "purely philosophical" carpet, and come up with a text neutral with respect to probability interpretation. However, I believe that doing so would be a disservice to the reader, for (at least) the following reasons: (1) What a waste of an excellent opportunity to offer the reader a complete and self-consistent treatment, rather than a bunch of pointers. (2) WP editing rules strongly discourage using "weasel expressions" in text, so why accept them in math?
Consider, for example, Nijdam's text above. It starts with the sentence "The solution may be given in terms of the following events", which of course begs the question of what is an "event" in the context of the MHP. And if we are going to make the terminology precise, why not do it the "right" way, that is, introducing the theoretical context of the formulation and proceeding within it?
So, if you stipulate (at least for the sake of argument) that a formal treatment of the MHP should be written with explicit (if abbreviated) reference to a specific interpretation of probability, well, then we have to choose one: frequentist, bayesian, measure-theory (Kolmogorov), ...? Well, the bayesian interpretation is particularly attractive for a puzzle of logic because it needs not introduce any extraneous concepts ("sample space", "ensembles of identically-prepared random experiments", etc.). Rather, probabilities are defined as numbers measuring a degree of belief in the truth of propositions - i.e. of assertions that are unequivocally true or false, and thus subject to the rules of boolean logic. Cox's genius was to show that such an assignment of numbers to propositions cannot be arbitrary and must follow the standard product and sum rules of probability, under penalty of logical inconsistency (see Dutch book). glopk (talk) 03:50, 4 May 2009 (UTC)

Well, this is an encyclopedia, not a higher level math textbook. Any student who just has learned something of probability theory, may (or even will) be confronted with the MHP. The formal solution is no more than an application of Bayes' law, which the student has just met in his course. No Bayesian approach for him. And if the formal solution is presented, in its simple form, the so called Bayesian approach is superfluous. Actually I don't see what it contributes to the article. Nijdam (talk) 22:07, 10 June 2009 (UTC)

So you are not answering any of my points, but are saying that the level of the article should be as directed to someone who as "just has learned something of probability theory". I believe this sort of "soft bigotry of low expectations" is adequate for Conservapedia, not here. glopk (talk) 22:57, 14 June 2009 (UTC)

The key approach to comprehension of the MHP problem

As experience shows, the fact is not so intuitively and easily observable, that a group of 2 doors that – as per the rule – must inevitably contain one goat at least, one goat that even can be shown later on – can have a chance of winning=2/3. And, "even because" one door must contain a goat, the "other" door quasi automatically consolidates the whole chance of winning of the group, from the beginning, as soon as the player made his choice. That means that the chance of that "other" door is even twice as high as the chance of winning for the single door that the player has individually selected from 3 doors. Of course, actually the simple logic says so, but even mathematicians often have difficulties in recognizing this fact intuitively. And, instead, they look for some mathematical proof, and for this purpose they are making probabilistic evaluations, that always show the same result, however.

A group of 2 doors inevitably contains at least 1 door with a goat that is already guaranteed by the rule. It must contain a goat, as to the rule, thus, from the beginning, without any chance of winning. And this group of 2 gates nevertheless has a chance of winning of 2/3 (???) - There are two doors. Can the door that, as per the rule, contains a goat and no car, can this door have a chance of winning of 1/3? It hardly can. Even "because" of the fact that one door is to contain a goat, and does contain a goat, it has no chance of winning at all. And even "because" of this fact the "other" door has a consolidated chance of the whole group.

I made that edit in the article (unfortunately as IP 62.47.250.187) Gerhardvalentin (talk) 07:40, 30 April 2009 (UTC)

Lacking references, this amounts to original research which is prohibited (see WP:OR). All Wikipedia content must be verifiable against reliable sources. -- Rick Block (talk) 13:46, 30 April 2009 (UTC)

Sorry, Rick, everyone can add 1+1=2. Source? Yes, this explanation is the result of my endless discussion abt exactly this approach in German WP. The discussion wasn't successful at all, he refuses to get the point. But by and by, over the months, my perception zeroed in on the point, more and more. And this discussion already did last since February. This contribution in the article was created me alone, by me alone and by nobody but me alone. I did put it in the German WP last night. And I do not guess it is possible than anyone else has formulated this model of approach in similar words. Otherwise it would not be possible that nobody ever made reference to at least a similar view in similar words: "Because of an imperative goat" (in any group of any two doors) - all chance of the group "therefore" is consolidated by the other door that automatically imperatively must have the chance of the whole group. No "theory", but a matter of fact that everyone can see, if he just might glance at this end.
No WO:OR therefore, as it is the result of my very own research. Ask Nijdam, he knows more about the history of my phrasing, as I tried and tried to explain my point of view, initially in Februar, 2008 in German WP.
But I regret Nijdam deleted my contribution "The key approach to comprehension of the MHP" without any comment. I'm going to put it on the page, again. Please comment my point of view, am very interested in first comments. Thank you. Gerhardvalentin (talk) 14:19, 30 April 2009 (UTC)

Something that is the result of your very own research is the definition of WP:OR. I'm deleting this section again. If it is not your own research and you want to add it again, please find a reference. If it is your own research this is not the place for it. -- Rick Block (talk) 03:20, 1 May 2009 (UTC)

Broken figure position

Help, WP-fu black belt needed to please fix the position of the second "goat" figure. It now spans the boundary between two sections (see attached screenshot). This happens in both Firefox 2 and Chrome, with several window sizes. I have tried some obvious tricks, but can't seem to get it right. I think it should be entirely contained withing the "Popular solution" section. glopk (talk) 15:06, 4 May 2009 (UTC)

I had placed the first figure on the left side of the text. That solved the problem. Someone didn't like it, so they put it back as you see it now. Glkanter (talk) 15:19, 4 May 2009 (UTC)

Don't bother about this picture, it is wrong, and there is already a better, correct one. Nijdam (talk) 21:04, 4 May 2009 (UTC)

Mutually Exclusive Published Reliable Sources

Much (most) of our arguing revolves around the conditional/unconditional solutions of the problem. There are published reliable sources that claim any unconditional solution is false, and there are published reliable sources that solve the MHP using an unconditional solution.

So, we get into arguments about which source is more reliable, or who is asking the 'right' question.

Since the two viewpoints can't both be right, we should be able to find the error in one or the other party's logic. I would think in this case OR would have to be acceptable in order to pick the more appropriate alternative.

These are the five previously agreed upon premises:

car is randomly placed

initial pick is random

host must show a goat (and, hence, knows where the car is)

host must make the offer to switch

player decides after the host opens a door

To these I propose adding:

the puzzle is to be solved from the contestant's point of view

the hosts behaviour cannot provide information to the contestant as to the car's location

As I have posted frequently in the last month or so, this is due to both the definition (nature) of game shows, and in the US, it is forbidden by law.

Of course, I will start with Morgan. Here is the first paragraph following the introduction:

"1. TO SWITCH OR NOT TO SWITCH

We begin by enumerating and discussing the most appealing of the false solutions. To avoid any confusion, here is the situation: The player has chosen door 1, the host has then revealed a goat behind door 3, and the player is now offered the option to switch. Thus is the player having been given additional information, faced with a conditional probability problem. The event of interest is "win by switching"; both "lose by switching" and "win by not switching" are complements of this event. For clarity and equality, we refer to the host as "he" and the player as "she.""

What is this 'additional information' they speak of? The only information of any value would be to be told where the car is. Is that what Morgan is saying? That because Monty has given me information as to the location of the car, this is now a conditional problem? I'll call this Case A.

Or is he saying that showing me a goat behind a numbered door in and of itself is 'additional information' that makes this a conditional problem? I'll call this Case B.

Case A: This violates one of the premises, and is eliminated

Case B: As Monty cannot divulge any information as to the whereabouts of the car when he opens the door, his actions can be considered 'random'. When Monty acts in a random manner, the probabilities are exactly equal for the conditional and the unconditional solutions.

Here's Morgan's description of the unconditional problem:

Solution Fl. If, regardless of the host's action, the player's strategy is to never switch, she will obviously win the car 1/3 of the time. Hence the probability that she wins if she does switch is 2/3.

Here's Morgan's argument against the unconditional solution:

Fl is immediately appealing, and we found its advocates quite reluctant to capitulate. Fl's beauty as a false solution is that it is a true statement! It just does not solve the problem at hand. Fl is a solution to the unconditional problem, which may be stated as follows: "You will be offered the choice of three doors, and after you choose the host will open a different door, revealing a goat. What is the probability that you win if your strategy is to switch?" The distinction between the conditional and unconditional situations here seems to confound many, from whence much of the pedagogic and entertainment value is derived.

Conclusion: Since Case: A is eliminated, that leaves only Case: B. For Case: B, since the conditional and unconditional probabilities will always be equal, we may use an unconditional solution to correctly determine the probabilities of the Monty Hall problem. This contradicts Morgans criticism of the unconditional solution. Therefore, Morgan's criticism of the unconditional solutions is invalid, and the article should be corrected accordingly. Glkanter (talk) 12:33, 3 June 2009 (UTC)

I assume by "corrected" you mean deleting what Morgan et al. have to say from the article. Morgan et al. is a paper specifically about the Monty Hall problem published in a peer reviewed math journal that has not been discredited in any way in any published source. As such, it meets Wikipedia:Verifiability and Wikipedia:Reliable sources and whether you like what it has to say or not is irrelevant. It would be a violation of Wikipedia:Neutral point of view to omit what this paper says fom the article. -- Rick Block (talk) 13:19, 3 June 2009 (UTC)

I would hope that a consensus would be reached whereby the following changes are affected:

Unqualified recognition of the validity of the unconditional solutions would, of course, diminish Morgan's claim as the only 'true' solution. Noteworthy, perhaps, but not due the emphasis it currently enjoys. There are numerous citations in the article of the unconditional solutions being false, etc., and these would be removed. Extensive discussion of 'variants' would also be less important, as 'host behaviour' would no longer be a necessary component in understanding the solution. I believe these changes would result in a more concise article, leading the reader to a better comprehension of the Monty Hall problem.

Do you agree that the continued publication of unconditional solutions from reliable sources indicates professional disagreement as to the validity of the unconditional solutions? Do you not see this as being a paradox? How can both be right? Who decided that Morgan was 'most' right? Or do you claim that Morgan is 'uniquely' right? Perhaps you could indicate where my analysis is flawed? Or do you believe it is correct? Glkanter (talk) 13:39, 3 June 2009 (UTC)

Don't bother about the US law. It has no jurisdiction in mathematical problems. These are the agreed upon premises:

1. car is randomly placed
2. initial pick is independent of the position of the car
3. host never shows the car
4. "random" strategy of the host
5. initial pick is door 1
6. host opens door 3
7. host offers to switch
8. player decides after the host opened a door
9. what 'probability' does the player have winning the car?

Now what??Nijdam (talk) 22:42, 3 June 2009 (UTC)

Why can't you just respond to what I posted? Glkanter (talk) 23:27, 3 June 2009 (UTC)

Your questions:

Do you agree that the continued publication of unconditional solutions from reliable sources indicates professional disagreement as to the validity of the unconditional solutions?

Not necessarily, and since there has been no "followup paper" anyone has offered that directly contradicts Morgan et al. (and Gillman, and Grinstead and Snell, and Falk) per WP:NPOV the best approach is to present what all "sides" have to say.

Do you not see this as being a paradox?

See what? That a peer reviewed paper in a math journal says one thing and then "reliable" popular sources and some (but by no means all) subsequent academic sources say something else? No, I don't see this as a paradox.

How can both be right?

As a matter of policy (WP:NPOV), as long as they're all published in reliable sources Wikipedia doesn't care. If you want to discuss this in a personal sense, feel free to do so at the Talk:Monty Hall problem/Arguments.

Who decided that Morgan was 'most' right?

No one. The article currently presents both views (right?). I don't see the emphasis you're objecting to.

Or do you claim that Morgan is 'uniquely' right?

If this is a personal opinion question, please take it to Talk:Monty Hall problem/Arguments.

Perhaps you could indicate where my analysis is flawed? Or do you believe it is correct?

This is another topic for the arguments page and has no relevance here (hint: there's a difference between presenting an unconditional solution as if it addresses the conditional question that is asked, and presenting an argument that the conditional and unconditional solutions must be equal and then presenting an unconditional solution). -- Rick Block (talk) 00:44, 4 June 2009 (UTC)

Just comment on the original dilemma posed at the beginning of this section. From WP's standpoint it should be clear that in doubt if there differing reputable sources, then WP has to mention them both. If we decide to peer review/validate/judge various publication on our own, we are performing OR, which is normally a big no no. Also note, that in such problem as Monty Hall the tricky part is coming up with an appropriate model and there might be more than one appropriate model. The only certain way to exclude a model is , when it yields false predictions, however all models yield correct predictions for the original goat problem.--Kmhkmh (talk) 01:20, 4 June 2009 (UTC)

Rick, I have suggested removing the following from the 'Sources of Confusion' more than once:

"According to Morgan et al. (1991) "The distinction between the conditional and unconditional situations here seems to confound many." That is, they, and some others, interpret the usual wording of the problem statement as asking about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability. These are mathematically different questions and can have different answers depending on how the host chooses which door to open when the player's initial choice is the car (Morgan et al., 1991; Gillman 1992). For example, if the host opens Door 3 whenever possible then the probability of winning by switching for players initially choosing Door 1 is 2/3 overall, but only 1/2 if the host opens Door 3. In its usual form the problem statement does not specify this detail of the host's behavior, making the answer that switching wins the car with probability 2/3 mathematically unjustified. Many commonly presented solutions address the unconditional probability, ignoring which door the host opens; Morgan et al. call these "false solutions" (1991). Others, such as Behrends (2008), conclude that "One must consider the matter with care to see that both analyses are correct.""

You have not been in favor of that change to the article. Despite the Behrends quote at the end of the paragraph, this strikes me as a POV that Morgan is right. This was already addressed in the Probabilistic solution section. Why repeat it here? I have advocated for the removal of the 3rd paragraph as well, for essentially the same reason.

The first item in the 'Aids to understanding' section says:

"This difference can be demonstrated by contrasting the original problem with a variation that appeared in vos Savant's column in November 2006. In this version, Monty Hall forgets which door hides the car. He opens one of the doors at random and is relieved when a goat is revealed. Asked whether the contestant should switch, vos Savant correctly replied, "If the host is clueless, it makes no difference whether you stay or switch. If he knows, switch" (vos Savant, 2006)."

If, as I propose, there is agreement that the host must act randomly, then a valid 'editorial' decision could be made to remove this. Why discuss a problem with a different premises that couldn't happen? Why not include a 4 door variant as well? I don't see it as an aid to understanding at all. Besides, as we have discussed, Marilyn describes in this scenario that Monty could reveal the car. So that's a second changed premise. Of course, if Monty reveals a car, there can be no offer to switch, a third changed premise. Now it's Deal or No Deal, with the Host selecting randomly rather than the contestant. Glkanter (talk) 06:43, 4 June 2009 (UTC)

Take a look at the FAQ for this page. Would anyone agree with me that there is a pro-Morgan POV at work here? Glkanter (talk) 14:38, 4 June 2009 (UTC)

By the way, Morgan's entire objection to the unconditional solutions is that it answers the wrong question. I've read numerous comments from what I presume are knowledgeable people that if the host acts randomly, the conditional and unconditional solutions are equivalent. I think I proved he must act randomly, and as Nijdam included this as one of his premises in his response, I guess I'm right.

So it's not just "chocolate is better than vanilla". But I'm sure this "correct vs published" argument gets very old, very fast. Glkanter (talk) 16:01, 4 June 2009 (UTC)

We've previously discussed deleting the paragraph you dislike from the "Sources of confusion section", twice in fact (see #How about we delete the 4th paragraph of the Sources of Confusion section? and #Once more, How about we delete the 4th paragraph of the Sources of Confusion section?). Is there anything different now that would warrant reconsidering this?

The "Aids to understanding" section was butchered a while ago since the bulk of it was not referenced. It used to look like this. What remains is essentially an introduction to a section that no longer exists (it was vaguely based on [1], which is not a reliable enough source for a featured article). That this section needs some work does not seem like a reason to delete it.

Do I understand correctly that you're complaining that the FAQ response explaining the issue you're complaining about is not NPOV? And you're not joking? -- Rick Block (talk) 19:01, 4 June 2009 (UTC)

Yes, Rick, as you know, I believe your POV is not a NPOV as it relates to the MHP. And that this has a negative affect on the content and utility of the article and the FAQ. There's no point in you and I debating this further. I'm more interested in what other editors have to say. Glkanter (talk) 19:09, 4 June 2009 (UTC)

Well, no point in debating with me then, because I totally agree with Rick (and Morgan, except for his minor miscalculation). My advice: study the analysis I gave on Talk:Monty Hall problem/Arguments#Analysis and feel challenged to react. Nijdam (talk) 22:04, 4 June 2009 (UTC)

Certainly, I agree. Why would I argue with someone who claims a NPOV, then advocates for a POV? Glkanter (talk) 23:36, 4 June 2009 (UTC)

Remove the First Item In the 'Aids to understanding' Section

Here's What It Says:

"Aids to understanding"

""Why the probability is not 1/2"

"This difference can be demonstrated by contrasting the original problem with a variation that appeared in vos Savant's column in November 2006. In this version, Monty Hall forgets which door hides the car. He opens one of the doors at random and is relieved when a goat is revealed. Asked whether the contestant should switch, vos Savant correctly replied, "If the host is clueless, it makes no difference whether you stay or switch. If he knows, switch" (vos Savant, 2006)."

I'm not sure which readers will find this an 'Aide to Understand' of 'Why the probability is not 1/2'. There are three changed premises:

Host does not always reveal a goat

Host does not always offer a switch

Contestant does not always decide after the door is open

So, while this new puzzle may indeed have a 1/2 probability, I don't see how it answers why the subject puzzle is not 1/2. Further, this puzzle is already included in the 'Variants' section. I suggest it be deleted. Glkanter (talk) 20:50, 5 June 2009 (UTC)

No one has any comments? Would anyone revert my edit if I deleted the paragraph? Glkanter (talk) 11:24, 7 June 2009 (UTC)

(repeating from immediately above) The "Aids to understanding" section was butchered a while ago since the bulk of it was not referenced. It used to look like this. What remains is essentially an introduction to a section that no longer exists (it was vaguely based on [2], which is not a reliable enough source for a featured article). That this section needs some work does not seem like a reason to delete it. (end of repeat)

How about if you or someone else works on expanding this section to explain why in the "classic" MHP the probability is 2/3, but in this version the probability is 1/2? The only one of the three premises you claim are changed in this vos Savant "host forgets" version (relative to the version she originally discussed) is rather than the host must reveal a goat the host has revealed a goat. The situation is all the normal rules apply, except the host momentarily forgets which door the car is behind. Since the show must go on, he guesses and opens a door anyway. This door turns out not to reveal the car. Just like the regular version, the player has picked door 1, door 1 and door 2 are closed, and door 3 is open showing a goat - and we're asked what are the player's chances of winning by staying vs. switching. From the player's viewpoint, it's identical.

Why the probability is 1/2 in this version but not 1/2 in the "regular" version seems to me to be exactly relevant and should be in this article. There are dozens of sources which contrast these two versions. -- Rick Block (talk) 14:57, 7 June 2009 (UTC)

This is the link you referenced: http://www.parade.com/articles/web_exclusives/2007/02-04-2007/Marilyn-Readers-Respond

This is a direct quote from MvS:

"Here’s one way to look at it. A third of the time, the clueless host will choose the door with the prize, and the game will be over immediately. In our puzzle, that didn’t occur. So we’re considering the two-thirds of the time when either: 1) You have chosen the door with the prize; or 2) The prize is behind the unopened door. Each of these two events will occur one-third of the time, so you don’t gain by switching."

I do not understand how you can disagree that 3 premises have been changed. This statement:

"From the player's viewpoint, it's identical."

is especially egregious. The way you look at it, why bother giving the contestant any rules (problem premises) at all?

You wrote:

"That this section needs some work does not seem like a reason to delete it."

and

"How about if you or someone else works on expanding this section to explain why in the "classic" MHP..."

The way I read it, you agree it's not an 'Aid to understanding' in its current form. As I have demonstrated, with 3 premise changes, it is valueless in this section. That's why I have suggested removing it, rather than adding more diarrhea to the article. Glkanter (talk) 16:43, 7 June 2009 (UTC)

Suggestion

While the discussion may continue forever, I would suggest to edit the article. I would like to start the "solutions" with a correct one, and made the following concept.

---

Solution

When the player is offered to switch, a new situation has arisen, in which Door 3 has been opened by the host. To make the right decision the player calculates the probability in this new situation of winning the car by switching to Door 2. This probability is a conditional probability (Morgan et al. 1991; Gillman 1992; Grinstead and Snell 2006:137).

Tree showing the probability of every possible outcome if the player initially picks Door 1

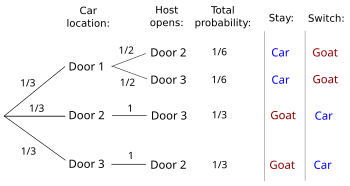
The conditional probability of winning by switching given Door 3 has been opened by the host can be determined by referring either to the figure below or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138), or by the use of Bayes' theorem as in the Bayesian analysis section below. For example, if the host opens Door 3 and the player switches, the player wins with overall probability 1/3 if the car is behind Door 2 and loses with overall probability 1/6 if the car is behind Door 1 — the possibilities involving the host opening Door 2 do not apply. Hence, by switching to Door 2 the player will win the car twice as often as when sticking to the original choice of Door 1. The conditional probability of winning the car by switching, given the player picks Door 1 and the host opens Door 3, is therefore (1/3)/(1/3 + 1/6), which is 2/3.

Player initially picks Door 1
Car hidden behind Door 3	Car hidden behind Door 1		Car hidden behind Door 2
Host must open Door 2	Host randomly opens either goat door		Host must open Door 3
Probability 1/3	Probability 1/6	Probability 1/6	Probability 1/3
Switching wins	Switching loses	Switching loses	Switching wins
As the host has opened Door 3, this didn't occur		Switching wins twice as often as staying

---

Discussion

• So, 'host behaviour' is out? Calling the unconditional solution 'incomplete' or 'false' is out? This is a dramatic improvement over the current 'Probabilistic solution' section. Glkanter (talk) 17:19, 7 June 2009 (UTC)

• I would imagine at least Glkanter and Martin Hogbin will never agree to this, so unless there is overwhelming support from other editors constituting a consensus in spite of these two dissenting opinions this change should not be made. I don't know how many editors watch this page, but I think it might be helpful if everyone who does watch this page can make a brief comment here indicating whether they would support or oppose such a change. I would support such a change, but only if we can amicably resolve what to do with the "Popular solution" section. One possibility might be to simply switch the order of what is currently the "Probabilistic solution" and "Popular solution" sections. -- Rick Block (talk) 17:28, 7 June 2009 (UTC)

I don't think I've ever exhibited a shyness towards expressing my own opinion, thank you. You need not 'imagine' anything, nor make presumptions as to what I may or may not do, on my behalf. I'll thank you, in advance, for not to setting me up as a straw man. Did you read my comment, above? Is "This is a dramatic improvement over the current 'Probabilistic solution' section." ambiguous in some way? Glkanter (talk) 17:48, 7 June 2009 (UTC)

Just to be clear, Nijdam is suggesting this new text come before (or perhaps even instead of) the current "Popular solution" section. Are you saying you'd be OK with this? -- Rick Block (talk) 17:57, 7 June 2009 (UTC)

Have I missed something here? What is the suggested change? Martin Hogbin (talk) 18:35, 7 June 2009 (UTC)

Nijdam suggests starting a "Solution" section with the text above (see #Suggestion), presumably instead of following the "Problem" section with the current "Popular solution" section. -- Rick Block (talk) 19:54, 7 June 2009 (UTC)

Thank you, that wasn't clear at all. Entirely remove the unconditional solution from the Solutions? I don't know if I'm on board with that so much. I mean, we wouldn't want the article not to have a NPOV would we? Wouldn't this ignore all the reliable published sources that use the unconditional solution? Glkanter (talk) 18:38, 7 June 2009 (UTC)

Nijdam hasn't said what he'd propose doing with the "Popular solution" section. So far, he's suggesting only that there be a "Solution" section, and that it start with the above text. Perhaps Nijdam might flesh this proposal out in a little more detail. -- Rick Block (talk) 19:54, 7 June 2009 (UTC)

Again, thanks Rick, for clarifying. I don't know how I could've interpreted this:

"Just to be clear, Nijdam is suggesting this new text come before (or perhaps even instead of) the current "Popular solution" section."

as at least one of you suggesting the removal of the unconditional solution from the article. Glkanter (talk) 20:40, 7 June 2009 (UTC)

• About the image: the image shows outcomes where the host has opened both Door 2 and Door 3. The problem statement only talks about the Door 3 outcome, so the entire left half of the image does not apply. That's what "As the host has opened Door 3, this didn't occur" means. This is what it means to be a conditional probability problem. We're not talking about all cases where the player has picked Door 1, only the subset of these cases where the player has picked Door 1 and the host has opened Door 3. It is in this subset of cases where the player is standing on a stage with Door 1 and Door 2 closed and Door 3 open showing a goat. The paradox is that the host has opened a door (say Door 3) leaving only two doors, but yet the probabilities of these two doors are not the same. These probabilities, the ones in effect after the host has opened the door, are conditional probabilities. -- Rick Block (talk) 19:54, 7 June 2009 (UTC)

(out) Indeed, my first suggestion is no more than to start the explanation of the problem with this (correct) solution. Feel free BTW to make suggestions to the text. Nijdam (talk) 09:05, 8 June 2009 (UTC)

With Nijdam's newly proposed conditional solution, there is no further need for two separate solution sections. They no longer conflict one another. So, why not:

Rename the 'Popular solution' section as 'Solution'

Add Nijdam's new conditional solution to this renamed section

Eliminate the existing 'Probabilistic solution' section

Glkanter (talk) 10:04, 8 June 2009 (UTC)

Add Nijdam's text at the beginning of the renamed section? And what about the text (and figures) in the existing 'Popular solution' section? -- Rick Block (talk) 12:54, 8 June 2009 (UTC)

It all stays, of course. Wasn't that clear? You are familiar with Wikipedia's NPOV policy, I assume? Being as we just discussed this exact same issue yesterday on this very same page.Glkanter (talk) 13:04, 8 June 2009 (UTC)

As to your other vital concern, which solution comes first: Maybe we should throw you a bone here. I mean, after 4 years and 9 archives, the following aspects of your precious Morgan's paper have been discredited:

The unconditional solutions are false

The host may exhibit a behaviour which indicates to the contestant where the car is

Misquotes Whitaker: "the host, who knows what's behind the doors, opens another door, say No. 3." becomes "the host, who knows what's behind the doors, opens No. 3," —Preceding unsigned comment added by Glkanter (talk • contribs) 22:55, 8 June 2009 (UTC)

There's a mathematics error in the article

His conclusion - "In general, we cannot answer the question "What is the probability of winning if I switch, given that I have been shown a goat behind door 3?" unless we either know the host's strategy or are Bayesians with a specified prior. Nevertheless, in the vos Savant scenario we can state that it is always better to switch. The fact that Pr(W | D3) - 1/2, regardless of the host's strategy, is the key to the solution."

So, I guess from your point of view, Morgan merits top billing. Sorry, I don't see it that way. I would go with Marilyn vos Savant's solution first, which has been supported by countless reliable published sources subsequent to Morgan's article. Given that vos Savant single handedly popularized the MHP in contemporary American culture, I see no reason why her solution wouldn't go first. And please be certain to note: Morgan belongs in the article as it is a reliable, published source. That's in keeping with Wikipedia's NPOV policy. Glkanter (talk) 14:04, 8 June 2009 (UTC)

It's okay with me if the "popular solution" stays first, as long as the text is a little improved: The player, having chosen a door, has a 1/3 chance of having the car behind the chosen door and a 2/3 chance that it's behind one of the other doors. It is assumed that when the host opens a door to reveal a goat, this action does not give the player any new information about what is behind the door she has chosen, so, after a door has been opened, the probability of the car behind the chosen door will also be 1/3. And therefore the probability of the car behind the remaining door must be 2/3 (Wheeler 1991; Schwager 1994). Switching doors thus wins the car with a probability of 2/3, so the player should always switch (Wheeler 1991; Mack 1992; Schwager 1994; vos Savant 1996:8; Martin 2002). Like it?Nijdam (talk) 14:26, 8 June 2009 (UTC)

Well, I actually are not very happy with the "assumed'. Let me change it into: From the symmetry in the problem it may be proven that when the host opens a door to reveal a goat, this action does not give the player any new information about what is behind the door she has chosen. Nijdam (talk) 10:46, 9 June 2009 (UTC)

I realize it's in the current article, but I don't think the 'assumed' in "It is assumed that when the host opens a door..." is necessary. You and I disagreed on the word 'also' in "...so, after a door has been opened, the probability of the car behind the chosen door will also be 1/3." on the arguments page. I think the word 'still' or 'remains' is more appropriate, for the reasons I put forth there. You didn't mention it, does the 'Combining Doors' solution remain in your proposed 'Solution' section? It does in mine. Glkanter (talk) 15:54, 8 June 2009 (UTC)

I agree with Glkanter. Why 'assumed'. It is no more assumed than many other things in the problem. It is quite obvious that no information is given to the player about what is behind the door she has chosen when the host has opened a door. Anyone who disagrees please answer this question. You have chosen door 1, the host now opens door 3 to reveal a goat. What information does this give you about what is behind the door you have chosen? To be more specific, is the probability that you have chosen a car now more or less than 1/3? Martin Hogbin (talk) 19:32, 8 June 2009 (UTC)

Actually there is information given to the player and whether or not that results in a modification of the probailities depends on certain assumptions. This is the scenario which was outlined by Morgan and Rosenthal (see under the section other host behaviour in the article). Also the phrasing of the question is no quite accurate. Since the question is not simply "What is the probability for the car being behind door 1?", but rather "What is the probability for the car being behind door 1 under the condition that the host has shown you a goat behind door 3?". At first glance that condition might not matter, however a more detailed modelling of the situation with a P-space constructed from a 3 step experiment (placing the car,select a door, showing a goat) reveals that the condition does matter and only under the assumption that the host select randomly the answer will be 1/3.--Kmhkmh (talk) 21:05, 8 June 2009 (UTC)

OK, I have chosen door 1. I think that we all agree that, if the car was intitially randomly placed, the probability that I have chosen the car is 1/3 before any door has been opened. The host then opens door 3 to reveal a goat. Is the probability that I have chosen a car now more or less than 1/3? Martin Hogbin (talk) 21:19, 8 June 2009 (UTC)

The exact answer depends on the specified host behavior, but let's assume that if the host has the option to choose from 2 goats, he would always go for door 3. In that case the probability for the car behind door 1 under the condition of having being shown a goat at door 3 is 1/2, so greater than 1/3. --Kmhkmh (talk) 22:09, 8 June 2009 (UTC)

That is a ridiculous answer. You just claimed that information is given to the player that results in modification of the probabilities. I have just given you the exact same information that the player would have received, namely that door 3 has been opened. Kindly tell me what your revised probability is. Martin Hogbin (talk) 22:25, 8 June 2009 (UTC)

I think you misunderstood my point or I misunderstood the intend of your question. The revised probability is 1/3 in the original problem, i.e. it stays the same. However my point was, that this is not something we can take for granted (hence the example with a revised host begaviour as an illustration, which might not have been helpful for you here). The important argument here is the following. It is a general feature of probility theory that additional information or conditions can change probabilities (basicly the concept of conditional probabilities). That is just a general fact completely independent from the problem at hand. Now being aware of this general fact, we need to assure that in our particular case (the MHP as posed by Vos Savant) the probabilities do not change. We can do that either by assuming it (as it seems reasonable in this oarticular case) or by proving it (doing the actual computation with conditional probabilities and getting as a result that they do indeed not change in this particular case). Since we are looking for an explanation without conditional probablities the proof option is not available and we need to use the assumption instead. That is why the "assumed" wording in the article is justified.--Kmhkmh (talk) 00:10, 9 June 2009 (UTC)

I have not misunderstood anything, I asked a simple question which you cannot answer, you are just waffling. This page is really for discussion on how to improve the article. I will be happy to continue this discussion on the Arguments page. Martin Hogbin (talk) 09:29, 9 June 2009 (UTC)

It's not an 'assumption' at all. It's part of the definition of a 'game show'. So, the sentence would say, "Based on the rules of game shows...". But why would that qualification be necessary at all? Glkanter (talk) 23:48, 8 June 2009 (UTC)

It is an assumption for the mathematical analysis (i.e. the game show regulation translates into an assumption for the simplified undontional math model). Also note however that original MHP afaik did not bother with game show regulations. Furthermore you cannot assume an average WP reader to be aware of specifics of US gameshow rules & regulations or legal issues even. In short such things cannot be taking for granted and should be stated explicitly. P.S. I somehat revised my posting to Martin to make the point more clear I hope, while you were posting your answer.--Kmhkmh (talk) 00:10, 9 June 2009 (UTC)

Yes, it's been debated ad nauseum on this talk page and on the arguments page whether the host is required to choose randomly when faced with two goats. This phrase from Whitaker, which comes very early in the Wikipedia article, brought that debate to a standstill:

"Suppose you're on a game show..."

Game show hosts don't reveal the whereabouts, or give clues as to the whereabouts, of the prize in a game like this. In the US, that would be illegal, as evidenced by the Quiz Show scandals of the 1950s. By virtue of this being a puzzle about a game show, from the contestant's point of view, it is therefore a premise that Monty acts randomly. At this point, based on his proposal, I believe Nijdam agrees. Maybe, Rick, too. I can't really be sure about either of them. Maybe they will volunteer what their views are. Glkanter (talk) 21:37, 8 June 2009 (UTC)

The above response is only in regard to the word 'assumed' in the unconditional solution. I have stated earlier that I understand that Morgan should be included in the article as per Wikipedia NPOV, as for the time being anyway, it is regarded as a reliable published source. Glkanter (talk) 21:49, 8 June 2009 (UTC)

Well it is a consequence of the conditional solution (or more precisely of a more detailed/accurate model in which you use conditional propabilities), that you need to use the word "assumed" in the unconditional solution. Anyhow in case the editors cannot agree on the exact wording here, then one obvious solution would be to ask the math portal for review/3rd opinion on the wording in question. It is in general a good idea, when doing (bigger) edits on a "difficult" article with the editors disagreeing, to make sure independent experts (best source for that in WP is the math portal) do review it.--Kmhkmh (talk) 22:09, 8 June 2009 (UTC)

As for whether 'still' or 'remains' is preferable to 'also', I reference Nijdam's response on the arguments page http://wiki.riteme.site/w/index.php?title=Talk:Monty_Hall_problem/Arguments&diff=294935860&oldid=294935109. Glkanter (talk) 22:09, 8 June 2009 (UTC)

Can we please return to the original issue. Nijdam has proposed some major changes, I have further defined how I would like to see his proposed changes implemented. Glkanter (talk) 23:51, 8 June 2009 (UTC)

I'm not sure I understand the proposal at this point. Is it essentially:

1. replace the content currently under "Probabilistic solution" with the text above
2. delete the heading "Probabilistic solution"
3. change the heading "Popular solution" to "Solution"

This basically deletes the first and third paragraphs in the "Probabilistic solution" section. Is this the substance of the proposal? -- Rick Block (talk) 01:53, 9 June 2009 (UTC)

So close, Rick! You got 2 out of 3! Here's what I'm suggesting:

Change the heading "Popular solution" to "Solution"

Add Nijdam's new conditional solution to this renamed section

Delete the "Probabilistic solution" section

This will result in a a single 'Solution' section Glkanter (talk) 03:51, 9 June 2009 (UTC)

I don't see how this is different from what I said, but in any event I think the third paragraph in the existing "Probabilistic solution" section (the 1/1+q solution) should go somewhere and the bit in the first paragraph explaining the difference between conditional and unconditional should go somewhere as well. I'm not sure Nijdam was suggesting deleting these. To make this more concrete, I've created a version with the suggested changes at User:Rick Block/Monty Hall problem (draft). -- Rick Block (talk) 12:51, 9 June 2009 (UTC)

Not bad at all. I'm anxious to hear what Nijdam's intentions are for paragraphs 1 & 3. I assumed they were deleted. Glkanter (talk) 13:34, 9 June 2009 (UTC)

I have formulated on User: Nijdam/conceptMHP my ideas about the beginning of the solution section. On second thoughts I left the simple solution as 'simple explanation' as I mentioned above at the start. Nijdam (talk) 15:02, 9 June 2009 (UTC)

You know, I only took an editor's interest in this problem because the way the solution was presented when I first looked at the article, I would not have been able to use the article to get paid off on a bar bet. Now, with Rick's version, I am certain I would get paid. With Nijdam's I think I would get paid. But it would be easier with either or both of the unconditional images and some related text. So, as long as 'host behaviour' is nowhere near the 'Solution' section, and the single obligatory mention of 'Morgan says the unconditional solution is false' is somewhere else in the article (not in the Solutions section) and is immediately followed by the statement, 'this viewpoint is not shared universally in the professional community' I'm good. Glkanter (talk) 15:50, 9 June 2009 (UTC)

Here's a direct question. Rick, will you be part of a consensus that de-emphasizes 'host behaviour' and 'the unconditional solution is false'? While staying true to the spirit of Wikipedia NPOV? Do you support Nijdam's proposed changes? Glkanter (talk) 19:58, 9 June 2009 (UTC)

What I support is any version that meets Wikipedia:Featured article criteria (which explicitly includes all policy requirements, like WP:NPOV). Do you seriously think the version you're suggesting is better than, say, this version, which is how it looked after the last WP:FAR? The solution section in that version says the answer is 2/3, using both an unconditional and conditional approach (introducing the conditional solution as answering a "subtly different question"). The conditional solution in that version (which, as I recollect, you violently disliked) seems strikingly similar to Nijdam's version (which you seem to be OK with). Frankly, I'm puzzled. -- Rick Block (talk) 03:33, 10 June 2009 (UTC)

Well, since that version starts with this incredible blunder:

"The overall probability of winning by switching is determined by the location of the car.", I don't like it at all.

But essentially, as I expected, this is just another of your stalling techniques. The only real comparison worth making is between the article as it is today, versus what Nijdam is proposing. But you know that. So, your stalling, and delaying, and obfuscating continues unabated. You put up pages so other editors will waste time on various drafts, with no honest intention of being part of a consensus to actually implement these changes. That shows a great disrespect for us other editors. Why not answer my direct questions above, instead? Glkanter (talk) 04:02, 10 June 2009 (UTC)

No, the only real comparison worth making is the state of the article now (or with any proposed change) to when it was last reviewed by the broader community. Are you trying to goad me into some incivility here? It won't work, so you might as well stop. My answer to your questions is what I said above. I'll support any version that meets WP:FACR. So, as long as de-emphasizing "host behavior" and the criticisms of the unconditional solution doesn't violate criteria 1b, and so long as the new version is WP:NPOV (this is a given), and so long as what's deleted from Nijdam's version ends up somewhere (that pesky 1b thing again), I'm good. This is what I meant. In comparison to the version I mention, I think the current and proposed versions don't measure up regarding 1a (and 3), either. -- Rick Block (talk) 04:42, 10 June 2009 (UTC)

Rick, what is your personal opinion, given that Whitaker starts "Assume you're on a game show...", can the problem be interpreted any way other than 'Monty acts randomly when faced with two goats'? Glkanter (talk) 06:31, 10 June 2009 (UTC)

yes it can. Aside from the fact that many publications on the subject actually do consider different host behaviours you cannot assume readers to be aware of the specific game show regulations, which in theory might (legally) enforce Monty to pick randomly.--Kmhkmh (talk) 09:16, 10 June 2009 (UTC)

I didn't ask if it needed to be clearly stated as a premise, I asked approximately 'since this is a story problem about a game show, can it be interpreted any other way?' And I'm limiting this question to the MHP as presented by Marilyn vos Savant. I have little interest in different puzzles with different premises. But, no offense, I am primarily interested in Rick's point of view, as his concurrence is essential in reaching a consensus. Glkanter (talk) 09:31, 10 June 2009 (UTC)

Yes it can, the original formulation by vos Savant made no statement regarding the host behaviour. Hence strictly speaking the question as posed by Vos Savant gives already rise to different variations and they are not simply different but related puzzles. From Vos Savants suggested solution however you can conclude, that it was to be understood that way, that the host picks randomly if he can. This is not just an issue regarding Rick but it has to do with factual correctness, meaning the answer to your posed question is yes (no matter Rick) whether personally sees it that way or not). In fact you just have to read the problem paragraph of current article to see that the answer is yes.--Kmhkmh (talk) 03:11, 11 June 2009 (UTC)

Please address the salient point. The MHP is a story problem about an American game show. That the host cannot give out info on the car's location is already a premise in that it's a game show. It's counter-intuitive to think the host would give out this info. If he did, they would stop filming, and start over. The host giving out info on the location of the car is eliminated because its a game show. Glkanter (talk) 04:10, 11 June 2009 (UTC)

I think there is a misunderstanding. There are variations of the host behaviour, where the host does not reveal the car, but can distort the probabilities nevertheless. This exactly what Morgan explained in his paper. In other words you can assume that the host never reveals the car (because it is a game show), but you cannot automatically assume that the host picks randomly when he can choose between 2 goats.--Kmhkmh (talk) 19:22, 11 June 2009 (UTC)

Rick, would something close to this satisfy FACR 1b in your mind: 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.'? Glkanter (talk) 06:43, 10 June 2009 (UTC)

what is to be understood under professional community here? Mathematicians/Statisticians? Scientist? Any person publishing on the subject (including non science publications)?--Kmhkmh (talk) 09:16, 10 June 2009 (UTC)

Well, this guy http://wiki.riteme.site/wiki/Keith_Devlin would be part of it. He published this unconditional solution http://www.maa.org/devlin/devlin_07_03.html in 2003. There's plenty more. How many more than 1 reliable sources that are a Consulting Professor in the Department of Mathematics at Stanford University, do I need for the above statement to be true, correct, valid and, most importantly, be in the spirit of FACR 1b? Glkanter (talk) 09:39, 10 June 2009 (UTC)

Ok, so i guess professional community then means scientists which would be ok by me. I took a look at Devlin's column and I agree that Devlin is a quotable source. However but imho it doesn't really prove your claim. To be more precise, what Devlins show that some mathematicians consider the simply unconditional as ok. However it doesn't really make statement regarding conditional solution and its potential superiority (or lack thereof), this means you cannot really tell from that column wether Devlin explicitly disagrees with Morgan or not.--Kmhkmh (talk) 03:11, 11 June 2009 (UTC)

Would Devlin, or any reliable source, publish an unconditional solution if they (without even knowing of Morgan) thought it was 'false'? Of course not. The statement 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.' is nothing more than a statement of fact. And I made no inference whatsoever to the relative merits of the different solutions. Neither should anyone else. Glkanter (talk) 04:10, 11 June 2009 (UTC)

It is not that simple. Devlin (or similar resources) do allow to describe the simple solution as correct, however the article does that already in a proper fashion (Morgan et al. call these "false solutions" (1991). Others, such as Behrends (2008), conclude that "One must consider the matter with care to see that both analyses are correct."). In more general terms the assessment of "true" and "false" is question of the perspective under which the problem is analysed. Basically you have 2 models to explain/describe a real world problem: A (complex,conditional, Morgan et et al) and B (simple, unconditional, Devlin et al). Both models describe the problem nicely and predict the empiric result correctly. In that sense both solutions are correct and following Ockham's razor you can argue to prefer B. However A is the more powerful theory that allows you to treat problem generalizations and variations as well - in particular different host behaviours. From that perspective you can consider A as "better" or "more correct", because it provides a "deeper insights" and allows you to understand why B fails for other host behaviours. To pick a crude analogon from physics it is like arguing whether newtonian or einsteinian mechanics are correct or more precisely whether newton is "false" since we know Einstein. As far as the article is concerned it needs to contain both solutions and describe them both as correct. However it also should note Morgan's perspective that from a more a more general perspective B is "false" (or more friendly put inferior and providing less inside than A). Note that the quotes in "false" are absolutely essential, because false is to be understood as described in the brackets and not as plain false. This description in italic follows exactly from the sources and is already described in the current article as it is.--Kmhkmh (talk) 19:10, 11 June 2009 (UTC)

You wrote: "From that perspective you can consider A as "better" or "more correct", because it provides a "deeper insights" and allows you to understand why B fails for other host behaviours." Yes, I'm familiar with the opinion that this article should be treated as a primer in Logic and Probability, rather than solely addressing the MHP. I don't agree with that viewpoint. And NPOV says we should not judge which might be better. Glkanter (talk) 19:26, 11 June 2009 (UTC)

We don't judge, but we paraphrase Morgan's publication (i.e. there is no NPOV issue here). And when addressing the MHP it is a fact, that the unconditional solution only models one interpretation of the MHP (as stated by vos Savant) correctly, while the conditional solution models other interpretations correctly as well. That is not a viewpoint but a fact. We don't have to use the term "better", but we can (and should) paraphrase Morgan (or similar sources) and we can (and should) state the fact given in italic the line before.--Kmhkmh (talk) 21:05, 11 June 2009 (UTC)

Kmhkmh, you wrote this above:

"To be more precise, what Devlins show that some mathematicians consider the simply unconditional as ok."

You agree Devlin is a reliable source, meeting your standard as a member of the professional community. Can Devlin say it is both "ok" and "false" at the same time?

How can you still take issue with this simple, NPOV statement: 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.'? Glkanter (talk) 18:47, 11 June 2009 (UTC)

yes he can because the answer is depending on context/perspective (see explnanation) above. Meaning Devlin argues from the context of giving the most simple explanation for most commonly assumed host behaviour and in that context the unconditional solution is correct. But Devlin makes no statement whatsoever regarding a advanced persptective from which you could consider the unconditional solution as false, in that sense he does not contradict Morgan at all. As far as the formulation goes false needs to be in quotes and I don't like the term professional community, since it is ambiguous to me. The current formulation (Morgan et al. call these "false solutions" (1991). Others, such as Behrends (2008), conclude that "One must consider the matter with care to see that both analyses are correct.") is imho better and more correct since after all wie just repeat the takes of a few mathematicians rather than the mathematical community at large. --Kmhkmh (talk) 19:10, 11 June 2009 (UTC)

Alas it is not that simple. Morgan is absolute right when he states that the unconditional solution, of course not for the numerical answer, but for its way of reasoning, is false, wrong. And, as far as I know, none of the advocates of the unconditional solution has commented on Morgan's paper. The big problem is, it spreads illogical thinking, and as it sounds very attractive, it is adopted by many people, among them, as I mentioned before, pupils, teachers and students, who should being taught better. So it is my goal, within the rules of Wikipedia, to set this straight.Nijdam (talk) 19:33, 11 June 2009 (UTC)

(outindented)The quote from Behrends must not be considered out of its context. Here is the complete end of the chapter, of which the first part is completely concerned with the correct treatment in calculating the conditional probabilities (and especially the introduction of the concept for this purpose). Behrends made his last remark after being tipped by a German professor:

Actually as far as WP is concerned it is rather simple - descriptions of reputable sources are repeated here, the rest stays out. Devlin is such reputable source, therefore considering unconditional solution in WP as correct is ok. And Devlin is by far not the only reputable mathematician stating it that way, Henze (statistics professor at the university of Karlsruhe) gives more or less the same treatmeant in his German probability textbook Stochastik für Einsteiger (Vieweg 1997), further examples are in the sources of the WP article). So to be rather clear : There is nothing to be set straight here. The unconditional solution is neither false nor illogic and students or teachers picking it up do correctly though. However it is true that the unconditional is inferior from a general perspective, that however is not really a question of true or false. --Kmhkmh (talk) 20:51, 11 June 2009 (UTC)

So, Kmhkmh says "So to be rather clear : There is nothing to be set straight here. The unconditional solution is neither false nor illogic..." but continues to support Morgan's statement that 'The unconditional solution is false".

No offense, but you need to make up your mind, whether you want to quote out of context to score rhetoric points or whether you want to argue content. Above i explained rather clearly that the notion of "false" and "true" depends on the perspective/context under which the problem is analyzed. And again Devlin is not contradicting Morgan (directly) since he is arguing from a different perspective and he is not making Morgan obsolete or superseeding him. Both Morgan and Devlin are correct from their given perspective, both are reputable sources and both can and should be quoted in the article.--Kmhkmh (talk) 15:32, 12 June 2009 (UTC)

Nijdam says of Devlin (a Consulting Professor in the Department of Mathematics at Stanford University), who actually took the time and effort to publish an article on the MHP, "Well Devlin may be a source, as a source on the MHP he is not reputable." Somehow, however, Nijdam proclaims himself the ultimate arbiter of who is reliable, and finds he is he.

Nijdam is wrong here regarding Devlin however that doesn't make you right. Imho you would both do the article a favour if you keep your respective condtional-probilities- are-just-an-academic-distraction and everything-must-be-explained-by-conditional-probabilities agendas out, since neither is appropriate nor backed up by all of the reputable sources.--Kmhkmh (talk) 15:32, 12 June 2009 (UTC)

I have been recently been reminded that it is insanity to repeat the same steps over and over, expecting different results. I chose sanity. Glkanter (talk) 02:59, 12 June 2009 (UTC)

It looks like Kmhkmh agrees with me, We have essentially two formulations and solutions. The simple (unconditional) and the academic(conditional). We currently have both of these in the article, which I support. The only change that I would like to see is greater separation of these two formulations, so that each has its own sources of confusion and aids to understanding sections. My suggestion is that those who favour the unconditional solution should contribute mainly to the unconditional section and vice versa. Martin Hogbin (talk) 19:59, 12 June 2009 (UTC)

I don't know on what there might be agreement. Let me say I also agree with you, if that's what you mean, that one may formulate a problem, to be called 'unconditional problem', to which the simple explanation is the solution. It reads in short: 3 doors, random car, pick a door, what is the probability you pick the car, or if you prefer: what is the probability you did not pick the car. Interesting? The MHP deals with the extra of opening a door.

You seem to be at odds with everyone else here. Rick, Glkanter, Kmhkmh, myself, and Morgan all agree that the full MHP (in which a door is opened by the host) can be formulated unconditionally. Morgan give an unconditional formulation of the problem in their paper. Martin Hogbin (talk) 21:57, 13 June 2009 (UTC)

Speak for yourself. IMO, the MHP is a conditional problem. Period. Full stop. I'm going to start a new thread on this below since this thread is already too long. -- Rick Block (talk) 22:59, 13 June 2009 (UTC)

This argument can be refined a bit. Let p1, p2, p3 denote the probabilities that the auto is hidden behind door 1, door 2, door 3. Then if door 1 is chosen, the probability of "the car is won without switching doors" is equal to p1, and the probability of "the car is won in switching doors" is equal to p2 + p3.

It is possible that some readers might be puzzled by the fact that in the second analysis the actions of the quizmaster apparently play no role. One must consider the matter with care to see that both analyses are correct.

In the first analysis the initial situation was given thus: Door 1 is chosen, door 3 (with the goat) is opened. And from this one has to determine the relevant probabilities.

In the second analysis the situation was different. The action of the quizmaster was irrelevant, and one should switch in any case. Nevertheless, it is intuitively difficult to see that this different information is responsible for the different probabilities.

Note already the problem he gets: p3 = 1/3, but also p3 = 0?! Then see what he says about both the situations: the situations are different. Nijdam (talk) 21:41, 11 June 2009 (UTC)

It is true that Behrens states that the 2 solutions strictly speaking adress slightly different problems. However despite the subtle differences both can be understood as valid solutions to the MHP with all its ambiguities. So in that sense current current description in the article is still ok imho. However if you feel the quote or description of Behrens argument is somewhat misleading, you could use Devlin or Henze instead. I don't think any of the referenced mathematicians for the unconditional solution can be understood as contradicting Morgan or the "superiority" of the conditional solution, they do however apparently consider the unconditional solution as a "good enough" explanation and so should we as far the description in WP goes.--Kmhkmh (talk) 00:18, 12 June 2009 (UTC)

You're right in that it's a "good enough" explanation, and so it should be presented, but as a solution it's wrong. I hope the mathematicians, not always probabalists, are well aware of this fact. Although I have my doubts as turned out in discussions with some of them. Nijdam (talk) 10:49, 12 June 2009 (UTC)

Let me ask you straight: are you able to formulate, in correct mathematics, an "unconditional solution" to the MHP (as stated above)? If so, I very much like to see it. If not, don't doubt your math skills, no-one can. That's my drive in the discussions here and elsewhere. Nijdam (talk) 21:25, 13 June 2009 (UTC)

(outindented)Well Devlin may be a source, as a source on the MHP he is not reputable. That is a problem for Wikipedia, not every source is reliable. And as we have to mention this type of so called solution as Devlin's, which BTW is definitely false and illogic, we may do it in confrontation with Morgan's, telling that in his paper such a solution is called false.Nijdam (talk) 21:49, 11 June 2009 (UTC)

Let us not put too much emphasis on Devlin. He may be mentioned, but with a critical note referring to Morgan. Devlin just wrote about the problem in his popular column, and what he wrote was mainly a paraphrasing of Marylin's popular explanation. I emailed Devlin about it, but he prefers to stay low. The 'plenty more' is not an argument pro, it mainly shows how most people easily get confused and do not think for themselves. Nijdam (talk) 11:06, 10 June 2009 (UTC)

Those are interesting opinions you have. Are you suggesting Devlin has retracted this work publicly? Would you also discount every other equally qualified source I provided for the same reasons? Is this consistent with FACR 1b? How is disregarding a reliable, published source like Professor Devlin's, because your opinion is "it mainly shows how most people easily get confused and do not think for themselves" remotely consistent with NPOV? Rick, you're pretty big on NPOV, what are your thoughts on this? Glkanter (talk) 11:12, 10 June 2009 (UTC)

Glkanter - you've asked several questions:

Given that Whitaker starts "Assume you're on a game show...", can the problem be interpreted any way other than 'Monty acts randomly when faced with two goats'? In the context of this page (talk page for the article), the only thing that matters is what reliable sources say. Plenty of reliable sources interpret it in other ways, so yes. If you're asking what I think the Truth is, this is a question for the Arguments page, not here, but I think the answer is yes.

Would something close to this satisfy FACR 1b in your mind: 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.'? This phrasing is problematic from several viewpoints. First, it's not NPOV, but stated in a way that casts doubt on Morgan's claim. Second, it says something the sources you're referring to don't actually say which is a WP:V issue. You could say "Subsequent sources present unconditional solutions", but that's not quite the same (you see the difference?). Third, this is not enough to explain the conditional vs. unconditional issue so if this is all the article says about it 1b is not satisfied either. There should be an explanation like the first paragraph in the current version of the "Probabilistic solution" section somewhere.

Would Devlin, or any reliable source, publish an unconditional solution if they (without even knowing of Morgan) thought it was 'false'? Of course not. The statement as I presented it is nothing more than a statement of fact. Glkanter (talk) 02:11, 11 June 2009 (UTC)

(paraphrased) How do we treat Devlin and others who have presented unconditional solutions subsequent to Morgan et al. in an NPOV manner? Like anything else, we must say what they say, no more and no less. Many of them say things Morgan et al. discredits, but none of them (as far as I know) specifically say anything about the issue Morgan et al. brings up. We can't invent a response to Morgan et al. on their behalf. We can't assume they've seen Morgan et al. or are aware of the central issue raised unless they reference it in some way. The closest I've ever seen is vos Savant's letter to the editor (American Statistician, Nov 1991, pp 347-348) following the publication of Morgan et al., in which she says "Pure probability is the paradigm, and we published no significant reason to view the host as anything more than an agent of chance who always opens a losing door and offers the contestant the opportunity to switch". This can be taken to mean she considered the host to pick randomly when faced with two goats to pick from, but does not address the central criticism raised by Morgan et al. which is that the problem is inherently conditional and an unconditional solution is therefore a "false" solution. The NPOV approach is we say what Devlin says, and we say what Morgan et al. (and Gillman, and Grinstead and Snell, and others) say as well. Since Morgan et al. (and the rest) say the question is inherently conditional we say that. But since the unconditional "side" says nothing in response we can't put words in their mouths. -- Rick Block (talk) 01:20, 11 June 2009 (UTC)

I don't like your paraphrasing. Please respond to the thread as posted. Do you support Nijdam's response? Is that consistent with your understanding of Wikipedia NPOV? Glkanter (talk) 02:11, 11 June 2009 (UTC)

Sources of confusion

The current section 'Sources of confusion' is, to say the least, confusing. It attempts to address at least three issues at once. These are:

1) People get the answer wrong even in the unconditional problem.

2) The rules of the game are uncertain.

3) The issue of conditional probability and the added confusion that this adds to an already difficult problem.

I suggest that 2 is dealt with earlier in the article so that here we are dealing only with the 'standard rules' version.

1 and 3 could either be dealt with in the same sections as their related solutions or should have sub-headings within this section.

Any comments? Martin Hogbin (talk) 21:32, 8 June 2009 (UTC)

As I read it the section addresses the major reasons why so many people get the answer wrong. It says:

1. people get the answer wrong
2. people answer what they think the question says rather than what it actually says (this is quite different from the rules being uncertain)
3. people think N unknowns each have probability 1/N whether this is the case or not
4. people think revealing something that is already known cannot affect conditional probabilities whether this is the case or not
5. people are unaccustomed to dealing with conditional probabilities (sort of a generalization of the previous two)

All of these are meticulously sourced. Distributing them throughout the article rather than keeping them together in one section seems like a strange idea. -- Rick Block (talk) 01:41, 9 June 2009 (UTC)

I am trying to fine some kind of compromise between the views of Glkanter and myself that the notable Monty Hall problem is the simple (unconditional if you like) formulation and the conditional formulation is, at best, an academic diversion; and the views of yourself and Nijdam that the conditional formulation is the only correct one. Both sides are supported by reliable sources and I do not think that the conflict will be resolved by a 'battle of the sources'. My suggestion is that the article remains much as it is with the two solutions given, both properly sourced, but with their own sections on confusion and understanding. I suggest that it might be generally better to allow the supporters of each formulation to decide the wording in that section. Of course, this does not stop anybody from commenting or editing anywhere. Martin Hogbin (talk) 17:10, 9 June 2009 (UTC)

Concept

I mentioned this before: I have formulated on User: Nijdam/conceptMHP my ideas about the beginning of the solution section. On second thoughts I keep the simple solution as 'simple explanation'. What has to follow, like the different host strategy, may be dicussed later on. Please mention your comment or just your approval. Nijdam (talk) 11:17, 10 June 2009 (UTC)

Perhaps you and Rick would first agree on whose document we should be working on. I prefer Rick's, in that it has the entire article, so that issues like 'where to discuss host strategy' can be fleshed out. Glkanter (talk) 11:22, 10 June 2009 (UTC)

Can we draw a line in your version of the article up to the point were we agree on the text. As you may have seen in my concept, I don't want to change the introduction. I like to start the solutions with explicit naming the simple explanation. I changed the "assumed", to put more weight on the fact that some proof is omitted. Further I'm not happy with the accompanying picture, as it doesn't meet the conditions of the problem. In the problem formulation Door 1 is chosen, and the picture shows different chosen doors. Actually I would not put much emphasis on the simple explanation. Nijdam (talk) 22:26, 10 June 2009 (UTC)

I forgot to say we may work on Rick's version, and consider my concept just as a proposal. Nijdam (talk) 22:29, 10 June 2009 (UTC)

Nijdam, while I am enthusiastic to contribute, I have a concern. Will we be following the established protocols of Wikipedia, especially NPOV and FACR, or will be expected to operate according to your personal opinions regarding the reliable, published sources that use the unconditional solution? Here's an example:

"Let us not put too much emphasis on Devlin. He may be mentioned, but with a critical note referring to Morgan. Devlin just wrote about the problem in his popular column, and what he wrote was mainly a paraphrasing of Marylin's popular explanation. I emailed Devlin about it, but he prefers to stay low. The 'plenty more' is not an argument pro, it mainly shows how most people easily get confused and do not think for themselves. Nijdam (talk) 11:06, 10 June 2009 (UTC)"

How do you feel about this, Rick? Glkanter (talk) 23:51, 10 June 2009 (UTC)

Nijdam clearly has an opinion about what is "correct" (as do you, Glkanter). Similar to Wikipedia:Autobiography, it is sometimes difficult for experts to write in a way that is truly based on cited sources rather than what they know to be true. This is not at all to say that experts shouldn't write in their own field. Just that experts need to be particularly careful about injecting their own opinions into what they are writing. The way to tell whether this is going on is to look at each sentence and figure out specifically what reference it came from (and where). I haven't checked all the references, but I sort of doubt the second sentence in Nijdam's "Simple solution" came from one of them. BTW - this general structure looks promising to me and other than this one sentence seems very good. -- Rick Block (talk) 01:50, 11 June 2009 (UTC)

I take the liberty to have my own opinion on this talk page. How far this will influence my suggestions about the article will depend on the sources that support my opinion. At least we have Morgan and as a other sources (the numbers doesn't matter in fact) are not in line with this, it seems to me not sufficient just mentioning them both, leaving the readers in uncertainty. BTW I changed the questionable second sentence. Nijdam (talk) 10:19, 11 June 2009 (UTC)

Since there are reliable, published sources on both sides of the 'unconditional solution' question, of course the reader will be left with uncertainty. How could it be otherwise, without violating NPOV? The question is, how much time and text should be spent addressing it? And while your opinion may be interest, when you use it to 'win' arguments by violating Wikipedia standards, then not so much. To deny Devlin equal stature in this article as Morgan? Because you disagree with him, and think him lazy? Horse feathers! Glkanter (talk) 11:10, 11 June 2009 (UTC)

In response to this question:

"Will we be following the established protocols of Wikipedia, especially NPOV and FACR, or will be expected to operate according to your personal opinions regarding the reliable, published sources that use the unconditional solution?"

You appear to have replied:

"How far this will influence my suggestions about the article will depend on the sources that support my opinion."

Should I interpret that as "We will only follow established protocols of Wikipedia, such as NPOV and FACR, when it is to my liking?" Glkanter (talk) 11:35, 11 June 2009 (UTC)

Variation where Monty doesn't know

Extract from reverted edit:

"However, after a door opened and a goat revealed, the outcomes and the probabilities immediately shifted back to those of the classical Monty Hall problem. The correct decision, at this stage, would be switching doors."

Before anybody reinstates it, I shall explain why this is nonsense. It seems the editor has assumed that, just because the set of possible game states is the same, the relative probabilities of them are the same.

Let's compare them. WLOG suppose the contestant picks door A.

In the standard Monty Hall problem, there are four possible outcomes:

1. Car is behind A, Monty opens B (prob 1/6)
2. Car is behind A, Monty opens C (prob 1/6)
3. Car is behind B, Monty opens C (prob 1/3)
4. Car is behind C, Monty opens B (prob 1/3)

a probability of 1/3 that the car is behind A, i.e. the contestant has chosen the correct door in the first place, therefore it's advantageous to switch.

If Monty doesn't know which door conceals the car, then there are six possible outcomes:

1. Car is behind A, Monty opens B (prob 1/6)
2. Car is behind A, Monty opens C (prob 1/6)
3. Car is behind B, Monty opens B (prob 1/6)
4. Car is behind B, Monty opens C (prob 1/6)
5. Car is behind C, Monty opens B (prob 1/6)
6. Car is behind C, Monty opens C (prob 1/6)

If Monty reveals a goat, outcomes 3 and 6 are ruled out. This doesn't alter the probabilities of the remaining outcomes relative to each other, so it becomes

1. Car is behind A, Monty opens B (prob 1/4)
2. Car is behind A, Monty opens C (prob 1/4)
3. Car is behind B, Monty opens C (prob 1/4)
4. Car is behind C, Monty opens B (prob 1/4)

a probability of 1/2 that the car is behind A, so switching and sticking are equally favourable options.

There's an ambiguity in this variation, in that there's no comment on what the contestant is allowed to do if the car is revealed, but that's outside the case being considered. -- Smjg (talk) 13:05, 11 June 2009 (UTC)

Yes, this is known as the game show 'Deal or No Deal'. The contestant reveals suitcases randomly, but it could be a host acting randomly as well. It's not all that relevant to the MHP problem, however, where the host knowingly always reveals a goat. Glkanter (talk) 13:16, 11 June 2009 (UTC)

Conditional vs. unconditional for the umpteenth time

(sort of continuing from the ridiculously long thread above) What the most reliable sources about the MHP say is that it is a conditional probability problem. Period. Full stop. There are related unconditional problems, but (IMO) the related problems are distinctly not what most people think of as the MHP or what most people "solving" the MHP using an unconditional solution mean to be solving. Rather than argue about this, we should focus on what the sources say. As far as I know, those sources presenting only an unconditional solution never rigorously say what problem they're solving but simply present a "solution" to "the MHP" (usually something very similar to the Parade version). There are numerous reliable sources that do this (including Devlin). Again as far as I know, every source examining what the problem actually means (including Morgan et al., Gillman, Falk, and Grinstead and Snell) says the problem is a conditional probability problem. It is certainly possible to invent a related problem for which the unconditional solution is the appropriate solution (Morgan et al., and Gillman, and Grinstead and Snell all do this). The question is what do we do with this?

The NPOV way to handle this is clear. We present the problem. We present one or more referenced unconditional solutions. We then present the published criticism of the unconditional solutions, and a conditional solution. All using reliable sources. This approach may seem to favor the POV of Morgan et al. (and Gillman, and Falk, and Grinstead and Snell), but it simply says what the sources say. Specifically, unless someone can find a source that defends the validity of an unconditional approach against the published criticisms, e.g. says specifically what unconditional problem some unconditional solution is addressing, or specifically how their unconditional solution addresses the commonly understood conditional problem, the article must not provide any such defense. Lacking any published response (and not just a subsequent regurgitation of an unconditional solution) from the "unconditional side" this is a completely NPOV approach.

It's well past time to stop with the WP:OR and personal opinions, and instead stick to what reliable sources actually say. Numerous reliable sources unequivocally say the MHP is a conditional probability problem and that unconditional solutions address a slightly different problem. Are there any sources that directly contradict this viewpoint? -- Rick Block (talk) 01:57, 14 June 2009 (UTC)

I completely agree. However what the article still could do better, is to explicitly state the differences between "MHP related problem" ([1], where the unconditional solution is correct and complete) and the "MHP stated by Whitman" ([2], where unconditional solution is incomplete or requires assumption, that strictly speaking would have to proved via conditional probabilities). And we have a reputable source for this difference as well - Behrens, so instead instead of giving an abbreviated quote ("both solutions are correct"), he should be quoted in full, where he points out the differences. This is also important because [1] can be understood as correct and complete solution, if you phrase MHP somwhat differently.--Kmhkmh (talk) 14:30, 14 June 2009 (UTC)

Just my idea! Nijdam (talk) 06:16, 14 June 2009 (UTC)

I am not against what you propose. The only thing I would like is for the simple solution to stand in it own right. By this I mean two things. Firstly, there should be no suggestion in the simple (unconditional) solution section that this approach is wrong. Suggestions that the problem must be treated conditionally should be reserved for the academic (conditional) section, where they can be appropriately referenced.

Secondly, even when given a clearly unconditional formulation (or perhaps the issue of conditionality is not fully appreciated) most people still get the answer wrong. For this reason, I believe that the unconditional sections should have its own 'Aids to understanding' and 'Sources of confusion' section, which should come before the conditional section. This is not unlike the approach used by Krauss and Wang, who do not bring up the issue of conditional probability until some way through the paper.

Finally, we need some neutral, balanced, and understandable names for the two sections. 'Popular' and 'Academic', for example, but disagreement on this detail need not prevent us from making progress on the content. Martin Hogbin (talk) 10:30, 14 June 2009 (UTC)

You're basically suggesting that there are two problems both known at the "Monty Hall problem" and that we should treat them separately. What source is there that says there are two different problems? I would suggest there's only one problem, and we structure the article as follows:

<lead as in the current article>

Problem

<as in the current article>

Solutions

<some short introduction that essentially says there are multiple approaches to solving the Monty Hall problem>

1/3 + 2/3 = 1

<a description of the 1/3 + 2/3 = 1 solution, with File:Monty closed doors.svg and File:Monty open door chances.svg, sourced to Devlin, Wheeler, etc.>

Analysis of the chances of winning by switching versus staying

<a description of the switch/stay case analysis with vos Savant's table of outcomes, sourced to vos Savant, Grinstead and Snell, etc>

Conditional probability analysis

<a description of the conditional solution including the criticism of the unconditional approaches and both the 2/3 and 1/1+q answers with File:Monty tree door1.svg and the large image currently in User:Rick Block/Monty Hall problem (draft), sourced to Morgan et al., Gillman, etc.>

Formal proof using Bayes' theorem

<the proof currently in the "Bayesian analysis" section>

I believe this structure follows the guidelines at Wikipedia:Make technical articles accessible. I'll work on a draft of this at User:Rick Block/Monty Hall problem (draft) so that it is very clear what I'm suggesting. -- Rick Block (talk) 14:56, 14 June 2009 (UTC)

Well, Rick, no offense, but I'm not very happy with your draft and I can hardly imagine you are yourself. Month of discussion here seems to be wasted. The sole purpose of my intervening here was to edit the article in such a way that (within the possibilities of Wikipedia) no one would get the idea the simple explanations are complete. So what was wrong with my formulation of the simple solution? At least it made clear that some extra proof was needed, according to Morgan, Behrends, and definitely more. The I wouldn't call the solution "conditional prob, analysis". Just call it "probabilistic analysis", that's what it is. Also, as you may know, I don't much like the so called Bayesian approach. It is needless complicated where it should only be the formal proof in mathematical terms. Nijdam (talk) 21:40, 14 June 2009 (UTC)

No offense taken. The point is to let the sources speak for themselves. I think the two unconditional solutions that are presented are faithful to the sources they're drawn from (and, on very careful reading, don't say anything that is actually incorrect). Whether the other section is called "conditional probability analysis" or "probabilistic analysis" is not that important but what are the others if not "probabilistic"? The fully formal nature of the Bayesian approach is possibly overkill, but I think there's value in precisely following a specific formalism. Would you be willing to live with something close to this if Glkanter and Martin would be OK with it? -- Rick Block (talk) 23:07, 14 June 2009 (UTC)

Nijdam, you seem to be moving more to an extreme view here in insisting that simple explanations are always incomplete. There are, in principle, three ways the problem can be formulated. It can be formulated as an unconditional problem, as Morgan do when they give the question that they consider vos Savant to be answering. It can also be formulated in a way that must be treated conditionally if, for example the host is stated to open an identified door non-randomly. Finally there is a grey area in between, for example, where the host action is considered random or the door opened by the host is not identified. This is where most of the argument here has occurred. Martin Hogbin (talk) 12:16, 15 June 2009 (UTC)

As you notice yourself, any solution belongs to the appropriate problem. That's why I'm reluctant to present fundamental different explanation to the "same" problem. So to be specific: the simple explanations are incomplete as an explanation to your second mentioned version of the MHP (which I consider the MHP, BTW). I can't imagine you may differ in opinion with me here. Nijdam (talk) 12:43, 15 June 2009 (UTC)

In the context of this page (the talk page for the article) the focus should be on what the sources actually say. Martin - do any of the sources presenting an "unconditional solution" clarify how they're interpreting the problem, or do they simply quote or paraphrase the Parade version and proceed? If this is what they do we simply don't know what problem they think they're addressing and we certainly can't clarify this on their behalf. Unless they're rooted in what sources say, discussions about what the problem means do not belong here but on the Argument subpage. Nijdam - given there are reliable sources that do not share your POV about this, we must follow an WP:NPOV approach where the article says what the various sources say - no matter how "wrong" what they say might seem to you. The POV that the unconditional solutions are incomplete cannot be "Wikipedia's POV" but can certainly be a POV presented in the article attributed to one or more specific sources. -- Rick Block (talk) 14:39, 15 June 2009 (UTC)

Well Devlin uses the Parade version (using letters for the doors instead of numbers), Behrens kinda states 2 versions a conditional and an unconditional and points out the difference (though somewhat compressed), Henze (a german book for introduction into probability from 1997, exact reference in the german interwiki) states the problem as in parade and suggest an conditional (like morgan) and an uncoditional solution (like devlin) without giving a clear preference.--Kmhkmh (talk) 00:58, 16 June 2009 (UTC)

I should also add that Krauss and Wang consider the reasons that people get the answer wrong without mention of conditional probability (which comes later). In fact they appear to consider the issue of door identification something of a distraction to clear thinking. Note that even Morgan refer to their approach as dealing with the problem, 'in one form'. I think we therefore have sufficient reason to deal with the unconditional case as a problem in its own right, with its own 'Sources of confusion' and 'Aids to understanding' sections. The reason that I want to do this is to help people who are struggling with the basic problem (that is to say most people) without confusing them further with potentially irrelevant subtleties of the problem formulation. Martin Hogbin (talk) 08:47, 16 June 2009 (UTC)

One more comment regarding the suggested new structure by Rick. The section history and problem variants seem to be missing. Does that mean they stay as they are or do you had in mind to delete them? In any case I'd consider them an important part of the article.--Kmhkmh (talk) 14:31, 16 June 2009 (UTC)

The proposed outline above is only for sections through the solution. The remaining sections would remain the same. This draft has a complete version of the article (with two alternatives for the solution section).

Ok then it is basically fine with me, though as pointed out above i would suggested to quote Behrens more thoroughly compared to the current version.--Kmhkmh (talk) 00:00, 18 June 2009 (UTC)

Martin - do you mean essentially splitting the article into two articles, one about the probabilities involved when always switching (or always staying with the original choice) and the other about the conditional probabilities in the situation where Door 1 is initially picked and Door 3 is opened? I still think there's only one problem, and most of the sources that mention both interpretations clearly state the "unconditional" one does not reflect a normal wording of the MHP. I would consider Morgan et al., Gillman, Grindstead and Snell, Falk, and even Behrends in this camp. I don't read German, so can't comment on the Henze book. -- Rick Block (talk) 15:34, 17 June 2009 (UTC)

I read the chapter in Norbert Henze's book 'Stochastik für Einsteiger'. He only discusses the "combined doors" explanation, in words, without any formal proof, repeating other sources. So no independent source, and without his own comment. Unimportant. Nijdam (talk) 17:01, 17 June 2009 (UTC)

I'm with you, Nijdam, 110%. This Henze fellow is even lazier and stupider than that hack, Devlin. Glkanter (talk) 19:16, 17 June 2009 (UTC)

Excuse me? Henze is a tenure professor for statistics at the university of Karlsruhe and the book is regular primer for probability theory. The source is "independent" as any standard textbook is. And of course he doesn't give a "formal" proof, since in the unconditional approach there isn't really much to prove formally. Also it clearly discusses the MHP in more detail then Grinstead/Snell do and is not giving "only" the combined door solution, but the complete conditional solution as well.

Mea maxima culpa! You're right, I didn't read further after I had seen section with the problem in chapter 7. He does use the problem in ch. 15 as an example of the use of Bayes' law, but I have to add, without comparing it with the "solution" in ch.7. So he doesn't shed any new light. Nijdam (talk) 09:16, 18 June 2009 (UTC)

@rick Yes the unconditional approach is an "incomplete" solution for the normal wording of the MHP (which explicitly uses standing on door one and getting shown a goat at door 3 - that scenario is a conditional probability). But if you state it without explicit doors and moreover you simply ask, whether staying or switching is a better strategy, that you could answer with an unconditional argument, which can be considered as "complete". And again the source explaining that is Behrens.--Kmhkmh (talk) 23:57, 17 June 2009 (UTC)

Let me get this straight: A German university-level textbook, written by Henze, used as a primer for probability theory includes prominently the 'combining doors' solution and a Bayesian solution for the MHP. But this 'combining doors' solution, which concludes with an open door #3 with a goat standing behind it, is not a sufficiently-reliable/good/complete/thorough/non-false/robust enough solution, on its own, for Wikipedia's readers? Glkanter (talk) 15:05, 18 June 2009 (UTC)

This kinda hard to follow. First you dismiss Henze without any real argument and now you want to use him to back up your claim? In any case if you read Henze carefully, you will see that he essentially the same argument as Behrens. Meaning you can make a correct and complete unconditional argument, if you rephrase the MHP somewhat differently as Henze does in his unconditional solution. I've pointed out already earlier it might be useful to give a more thorough account of Behrens. However this is not really changing rick's general suggestion (which is ok), just an addon to it.--Kmhkmh (talk) 17:01, 18 June 2009 (UTC)

Excuse me? I "dismiss Henze without any real argument"? I agreed 110% with Nijdam's dismissal of Henze (and previously, Devlin) without any real argument. That's all the 'real argument' guys like me and Nijdam need. We're not so different, he and I. We get it. We're not brainiacs on the nerd patrol. We're not members of the factinista. We go straight from the gut, right Nijdam? That's where the truth lies, right down here in the gut.

And you have the NERVE to say I "dismiss Henze without any real argument"? How DARE YOU, sir! Glkanter (talk) 04:01, 19 June 2009 (UTC)

Rick, no I do not suggest splitting the article into two articles. I suggest we deal with two interpretations of the same problem, as the article currently does. The first is the notable one, the one that made the problem famous and the one that was answered correctly by vos Savant. There are reliable sources for this interpretation thus we should include it. You can call this unconditional if you like, you could call it the interpretation in which the conditional aspect is considered unimportant or irrelevant. The second is the conditional interpretation.

The most reliable source for interpreting a question in a popular general interest magazine is vos Savant; that was her job. Academics have chosen to interpret the problem differently because that made it interesting for them. The normal hierarchy of reliability of sources does not apply here since the problem is one of interpreting the meaning of a question from a member of the public.

There are ample sources for an unconditional section (which we already have). These include vos Savant, Devlin, Krauss and Wang, and, some say, Behrends and Henze. So my point is this. If we stick to our current format of two interpretations, there is absolutely no point in having one 'Sources of confusion' and one 'Aids to understanding' section since some of the sources of confusion only apply if the problem is taken to be conditional. Martin Hogbin (talk) 21:32, 17 June 2009 (UTC)

Well imho do Morgan and vos Savant answer the same problem, i.e. the normal wording for which the unconditional solution is "incomplete" (or more precisely requires the unspoken assumption that showing the goat does not change the original probability) and of course is Morgan and the "academic analysis" here the primary source and not vos Savant. This is not to devalue vos Savant's contributions, but it should be rather obvious that peer reviewed science journals are more reputable sources than (arbitrary) magazin columns. As far as i'm concerned (and i'm sure there a broad consensus among WP editors) there is no room for discussion ont that, i.e. that peer reviewed science journals overrule non science magazines can be considered a "WP-Axiom".--Kmhkmh (talk) 23:57, 17 June 2009 (UTC)

How might this mythical "WP-Axiom" be applied in the following case: An allegedly peer-reviewed article with it's very own cautionary comment by Seymann versus a professionally-edited University-level textbook used as a primer for probability theory? One says unequivocally that the unconditional solutions are 'false', the other solely(?) and unrepentantly uses the 'combining doors' solution. Which brings up the question: Who decided that the 'combining doors' solution is unconditional? The 2nd image clearly shows door #3 open with a goat revealed. Glkanter (talk) 13:26, 18 June 2009 (UTC)

Rick, I think it was you who originally (or most recently) said the 'combining doors' solution falls into the category of Morgan's 'F1', which Morgan says is "false due to being unconditional." Perhaps you would respond to the above question: "Who decided that the 'combining doors' solution is unconditional?." Glkanter (talk) 22:23, 19 June 2009 (UTC)

Kmhkmh, you seem to adopting the strange position that the answer is the same regardless of the question. I agree that academic sources are more reliable within their area of expertise but this is not necessarily so otherwise. Would you take Morgan as a reliable source in the area of, say, veterinary medicine? Of course not. As experts giving an answer to a well-posed probability problem Morgan are to be considered reliable but as interpreters of what a member of the public actually wanted to know in a question in a popular general interest magazine they are no more reliable than anyone else, and less so than vos Savant, whose job it was to answer such questions. Martin Hogbin (talk) 16:41, 19 June 2009 (UTC)

The area of expertise here is probability & statistics - period. And you cannot argue using vos Savant's columns as a source over a peer reviewed science journal for any well or ill posed math problem. If you want to focus non-mathematical aspects of reading/perceiving a problem then the authoritative resource would be an article in some psychology related journal (maybe something like Krauss- Wang) and again not vos Savant. If we were talking about veterinary medicine, then the authoritative source would be some academic journal for veterinary medicine.--Kmhkmh (talk) 21:16, 19 June 2009 (UTC)

"The area of expertise here is probability & statistics - period." Maybe not. Is the 'by switching, you always get the opposite' solution an example of Probability Theory? Or is it Logic and Symbolic Notation?

So, since a Logic and Symbolic Notation solution is valid, is the very first sentence of the article incorrect: "The Monty Hall problem is a probability puzzle..."?

I could argue that the only 'issues of probability' in the problem are the placement of the car, the contestant's selection, and the host's two-goat choice. All of which are random. What could possibly be less interesting, or less complex? Glkanter (talk) 22:07, 19 June 2009 (UTC)

To give a specific example, imagine a reader who is trying to understand why people are confused about the popular (unconditional) formulation. What sense can they make of, '..interpret the usual wording of the problem statement as asking about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability'? I am not saying that the quote from Morgan is wrong, just that it is completely unhelpful to someone who sees the problem as an unconditional one. Martin Hogbin (talk) 21:37, 17 June 2009 (UTC)

Be that as it may - for an encyclopedia correctness is more important than "optimal access" for laymen. The reader should learn from the article that in the standard wording MHP is indeed about conditional probabilities.--Kmhkmh (talk) 00:09, 18 June 2009 (UTC)

Surely we should aim for both. There is no standard formulation of the MHP, nor even a standard wording. All you are referring to is Morgan's interpretation of the most common problem statement, that by Whitaker. However, it is possible to formulate the problem as a clearly unconditional one, just as it is possible to formulate the problem as one which must be treated conditionally. In the current article we give both solutions. It is possible to argue (wrongly in my opinion) that the unconditional solution should not be there, but it makes no sense at all to present the unconditional solution and then give aids to understanding for the conditional solution without any indication to the reader of what it is that you are trying to help them understand. If the unconditional solution had its own 'Aids to understanding' section, referring specifically to the unconditional formulation and solution, this would be easier for the reader to follow and be perfectly correct. Martin Hogbin (talk) 17:25, 19 June 2009 (UTC)

Martin - we're talking about what sources say, not personal opinions. From Barbeau's Mathematical fallacies, flaws, and flimflam (in the references of the article): "The standard analysis of problem M [the Monty Hall problem] is based on the assumption that after the contestant makes the first choice, the host will always open an unselected door and reveal a goat (choosing the door randomly if both conceal goats) and then always offer the contestant the opportunity to switch." So, yes, there is a standard analysis and it includes the constraints present in the Krauss and Wang explicit version (which I believe you agree is conditional, right?). If you're going to keep arguing that the "unconditional problem" is the "notable" or popular one, I would really like you to provide a source that says something similar to this claim, or even a source that presents the problem using an unconditional phrasing (and by this I don't mean a source like Morgan et al. or Gillman that suggests an unconditional phrasing for purposes of contrast). Similarly, if you want any content in an "Aids to understanding the unconditional solution" section you'll need to find sources that clearly say that they're talking about the "unconditional" problem. -- Rick Block (talk) 19:06, 19 June 2009 (UTC)

Rick, Henze wrote a university-level primer textbook on probability theory which includes the 'combining doors' solution. What more do you want? I get the feeling that since Henze did not specifically write: "Here's where I disagree with Morgan:", you consider him either 'uninformed' or perhaps 'agnostic' relative to Morgan. Why not just take him at his printed word, which he puts his entire professional reputation behind? He used the 'combining doors solution.' Glkanter (talk) 22:07, 19 June 2009 (UTC)

Are you saying you read German and Henze presents "combining doors" as a correct solution to the MHP, or are you simply referring to Nijdam's and Kmhkmh's comments above? Looking at the Google books preview, the first appearance of the problem (first occurrence of "vos Savant") is in chapter 7 and the full solution is not given until chapter 15. Again, I don't read German, but my guess would be that the first mention in chapter 7 is before conditional probability has been introduced and uses only concepts introduced to that point - and is revisited in Chapter 15 after the necessary foundations have been established. I would be quite interested in an exact translation. On the other hand, since this is the English Wikipedia and there is no shortage of references in English I think we can safely ignore this particular reference.

My request for Martin (and you if you'd like) is some source, any source, that says anything remotely like "the probability in question in the MHP is the overall probability of winning by switching". -- Rick Block (talk) 16:37, 20 June 2009 (UTC)

Your quotation of what Barbeau call the standard analyis is simply a statement of the game rules, which we all agree. It does not include a question. Does Barbeau mention a standard question and, if so, on what basis does he describe it as such?

We already have a section on the popular/unconditional problem and solution including some explanation of solution. This is well-sourced (Wheeler 1991; Mack 1992; Schwager 1994; vos Savant 1996:8; Martin 2002Adams 1990; Devlin 2003; Williams 2004; Stibel et al., 2008)). All I am pointing out is that at present there is no way for the reader to tell which parts of, 'Aids to understanding' and 'Sources of confusion' apply to this section. This makes the situation even more confusing. So why not put the bits of these sections together with the solutions to which they apply rather than leaving it to the reader to work out by themselves which sources of confusion apply to which formulation Also, much of Krauss and Wang's explanation of why people get the problem wrong clearly applies to the unconditional case and could be added. Martin Hogbin (talk) 21:31, 19 June 2009 (UTC)

We have a section on popular solutions, not a section on a separate "unconditional" problem. Are you suggesting that these solutions are intended to address a different problem than the one that is clearly conditional (e.g. Whitaker's phrasing, where the player picks Door 1 and the host opens Door 3 and the host then asks the player to decide whether to switch) and that people find this (other) problem confusing? What I'm saying is that unless there are sources that clearly say they are solving some theoretical "unconditional" version of the MHP there is really only one problem involving a first choice, the host opening a door, and then a second choice given the knowledge of the originally chosen door and the door the host opens. There are indeed plenty of published unconditional solutions, and they do indeed end up with the correct answer (given the "standard" interpretation of the problem), but if any of these solutions clarify the problem to be the "unconditional" problem please let me know which ones. If there's really only one problem then there's no need for separate sections as you suggest. -- Rick Block (talk) 16:37, 20 June 2009 (UTC)

Where do we stand?

I think we discussed almost anything there is to discuss on the MHP. I try to sum up the different positions we encounter here and ask the discussiants to take position.

A
MHP = K&W formulation, and the only solution is the one with conditional probabilities. Other explanations are incomplete for this MHP, but may address other formulations, which are of less interest.

Nijdam

B
MHP = K&W formulation, which may be solved with conditional probabilities. Other explanations, like the simple explanation, also may solve the problem.

C
MHP has different formulations. One is the K&W formulation, another is the original Parade version. K&W needs conditional probabilities, Parade not.

D
MHP has different formulations. One is the K&W formulation, another is the original Parade version. Both may be solved with or without conditional probabilities.

E
??

This may help us in finding the necessary form of edits to the article. (I hope.) Nijdam (talk) 11:15, 20 June 2009 (UTC)

I think it would be far more helpful to categorize what sources say, rather than identify what various editors think, since what editors think doesn't actually matter. It should be easier to agree as well. I think the sources fall into one of the following categories:

• The MHP is the Parade version with the additional assumptions that the car is uniformly distributed and the host always reveals a goat and always makes the offer to switch - with no explicit mention of how the host decides what door to open in the case the player initially selects the car. An unconditional solution showing the probability of winning by switching is 2/3 is presented without clarifying whether the problem is conditional or unconditional.

  vos Savant, Devlin, and most "popular" sources

• The MHP is as above but is clearly conditional, and since there is no constraint on the host in the case the player initially selects the car the host's preference in this case must be treated as an unknown variable q. Unconditional solutions (such as vos Savant) address a slightly different problem for which the answer is 2/3. The answer to the problem as stated is 1/(1+q), which is 2/3 only if q is 1/2.

  Morgan et al., Gillman, Rosenthal

• The MHP is as above but with the additional constraint that the host choose randomly if the player initially selects the car (e.g. the Krauss and Wang version, i.e. the same as immediately above with q=1/2). An unconditional (2/3) solution is presented without clarifying whether the problem is conditional or unconditional.

  Mueser and Granberg, Krauss and Wang

• The MHP is the Krauss and Wang version but is clearly conditional. Unconditional solutions say the answer is 2/3 (which is the correct numeric result) but answer a slightly different question.

  Grinstead and Snell

I keep hearing Martin suggest another but I am not aware of any sources that present it this way:

• The MHP is the Parade version, but the probability of interest is explicitly the overall probability of winning by switching as opposed to the conditional probability faced by a player who has picked Door 1 and has seen the host open Door 3 (or, alternatively, a variant where the player must decide whether to switch before the host opens a door - "I'm going to open a door and show you a goat, decide now if you'd like to keep Door 1 or switch to the door I don't open").

  Can anyone provide a source for this specific interpretation?

Behrens and Henze do that if you read them carefully. They do not state the MHP differently, but in their suggested unconditional solutions, they rephrase the problem somewhat in such way, i.e. they state explicitly that they compute the probabilities for staying versus switching regardless which door was chosen by the player and which was opened by the host.--Kmhkmh (talk) 03:10, 21 June 2009 (UTC)

Again, what I think matters here is not what we each think about the problem but what sources actually say. If you'd like to add more sources in each of the categories above please feel free. If you'd like to suggest another interpretation that other sources use, also feel free. -- Rick Block (talk) 17:46, 20 June 2009 (UTC)

There is a problem with a strict 'cut-and-paste' attitude to reliable sources, which is that people do not usually state all the things they do not do. In other words, sources that treat the problem as essentially unconditional may not specifically mention that they do not treat the problem as one requiring the use of conditional probability just as they do not mention other techniques that they do not use to solve the problem. It seems clear to me, however, that any sources that treat the problem unconditionally after the publication of Morgan do so because they consider this approach is valid. (I inserted this response before Glkanters as I think the two make more sense that way. I hope this is OK) Martin Hogbin (talk) 13:46, 21 June 2009 (UTC)

Normally I would mind, but since my post is a hijack anyways, what difference does it make? And, you re-inforce, perhaps in a more erudite manner, this point: Absent this statement in any published source, "Here's where I disagree with Morgan:", I think Rick views all other author's viewpoints as either 'uninformed' or 'agnostic' regarding Morgan. Your statement "...(they) do so because they consider this approach is valid." is, of course, the most reasonable interpretation. Glkanter (talk) 14:38, 21 June 2009 (UTC)

I'm sure nobody minds me re-hijacking this discussion...

Why is the 'Combining Doors' solution considered 'unconditional'? It clearly shows an open door #3 with a goat behind it? Rick, I think you most recently labeled it as such, perhaps you could address this?

Where does Devlin's reliable-sourced article stand in this discussion? What about similar articles from sources of equal reliability? Will Nijdam's casual blow-off become the defacto policy for this article? Is there a consensus that Morgan's article carries more weight than Zehne's textbook or Devlin's column? There are at least 5 errors in Morgan's paper. Other than not concurring with Morgan that 'the unconditional solutions are false', how many errors are in Devlin's paper, or Zehne's textbook?

How much emphasis in the article will 'non-random host behaviour' continue to receive? Will it be part of the 'conditional' solution section, or will it appear elsewhere?

Will something like this statement appear in the article: 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.'? Glkanter (talk) 13:17, 21 June 2009 (UTC)

@Martin - Most of the sources we're talking about are popular, not academic, and I think we have very little reason to expect them to be aware of Morgan et al. or Gillman. I've suggested this before, but if anyone wants to survey what academic sources say that cite Morgan et al. it's not that hard (although would probably require an afternoon in a university library). Here's a link from Google Scholar of (currently 52) sources that cite this paper [3]. Suggesting that any source published after Morgan et al., or Gillman, was likely to be aware of them, and by not saying anything about the conditional vs. unconditional issue they both bring up is saying they disagree seems like an absurd stance. My stance is if some later source doesn't actually reference either of these papers we simply don't know whether the later source was aware of them or not. It seems pretty obvious that we shouldn't invent an argument where there is none.

@Glkanter - The combining doors solution is unconditional because it doesn't say anything about how the host decides what door to open in the case where the player initially picks the car. Another way you can tell is to apply the same solution to a variant where the conditional answer differs from the unconditional answer (for example, host always opens Door 3 if possible). Combining doors still says the answer is 2/3, when the actual answer (for this variant) is 1/2.

Devlin's article is as reliable as Gillman's. They are both essentially columns written by math professors in general math sources, so they are both reliable sources by Wikipedia's standards. On the other hand, Morgan et al. is a paper in a peer reviewed statistics journal making it more reliable by Wikipedia's standards (which reflect normal academic standards as well). There are not 5 errors in Morgan et al. and although I'm not entirely sure I think continuing to repeat this could be considered to be libelous. I strongly suggest you (and Martin) stop saying this. Wikipedia's WP:libel policy applies to talk pages as well as articles. Saying you think there might be an error in a source is certainly fine. Incessantly repeating this as if it were an established fact is not.

How much emphasis the article places on non-random host behaviors should reflect how much emphasis this aspect of the problem receives in the published literature. I wouldn't expect it to be mentioned in a section discussing an unconditional solution, but I think it is entirely relevant to sections discussing conditional solutions, variants of the problem, and sources of confusion.

Your wording "Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community." is problematic for the reasons I already mentioned above (in the #Discussion thread), i.e. it's not NPOV and it's not verifiable to any specific source. In response you said it's simply a statement of fact, but it's not - it's a conjecture. What is a verifiable fact is that subsequent sources have published unconditional solutions. -- Rick Block (talk) 16:58, 21 June 2009 (UTC)

Rick, it's not conjecture, at all. Watch how a logical argument works:

Morgan published a paper that says 'the unconditional solution is false.'

Devlin and Zehne, two members in good standing of the relevant professional community, published papers under their own names using an allegedly 'unconditional solution'.

Devlin and Zehne would not put their names and reputations on a published paper they disagreed with.

Therefore, Devlin and Zehne have reliably published that they believe the unconditional solution is not false.

Therefore, the viewpoint that 'the unconditional solution is false' is not by shared Devlin and Zehne, two members of the relevant professional community.

In conclusion, "Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community." is a true AND valid statement, supported by the reliably published sources.

But this has been instructive. The reason that these talk pages go on endlessly for 5 years is that you apparently do not understand how to parse a logical argument. Sue me. Glkanter (talk) 02:28, 22 June 2009 (UTC)

Please read WP:SYNTHESIS. "This viewpoint is not shared universally in the professional community" is a statement of opinion (specifically your opinion). It is not based on what any particular source says, meaning from a Wikipedia policy standpoint it is original research. -- Rick Block (talk) 19:22, 22 June 2009 (UTC)

No, Rick. It is a conclusion derived from the facts as enumerated in the logical argument presented above. What you would need to do is indicate which statement is not a fact, or how the conclusion doesn't follow from the factual statements. Then I would have a flawed argument, but still, not an opinion. Do you understand the difference? Glkanter (talk) 10:44, 23 June 2009 (UTC)

This is Morgan's argument against 'F1':

Here is the first paragraph following the introduction:

"1. TO SWITCH OR NOT TO SWITCH

We begin by enumerating and discussing the most appealing of the false solutions. To avoid any confusion, here is the situation: The player has chosen door 1, the host has then revealed a goat behind door 3, and the player is now offered the option to switch. Thus is the player having been given additional information, faced with a conditional probability problem. The event of interest is "win by switching"; both "lose by switching" and "win by not switching" are complements of this event. For clarity and equality, we refer to the host as "he" and the player as "she.""

Here's Morgan's description of the unconditional problem:

Solution Fl. If, regardless of the host's action, the player's strategy is to never switch, she will obviously win the car 1/3 of the time. Hence the probability that she wins if she does switch is 2/3.

Here's Morgan's argument against the unconditional solution:

Fl is immediately appealing, and we found its advocates quite reluctant to capitulate. Fl's beauty as a false solution is that it is a true statement! It just does not solve the problem at hand. Fl is a solution to the unconditional problem, which may be stated as follows: "You will be offered the choice of three doors, and after you choose the host will open a different door, revealing a goat. What is the probability that you win if your strategy is to switch?" The distinction between the conditional and unconditional situations here seems to confound many, from whence much of the pedagogic and entertainment value is derived.

But this does not describe the 'combining doors' solution, as the 'combining doors' solution clearly shows door #3 open with a goat revealed. I think Rick's personal interpretation (similar to OR) of Morgan's criticism is incorrect. There is no mention of any so-called 'host-behaviour'. Morgan does not specifically call the 'combining doors' solution 'false'. Glkanter (talk) 21:51, 21 June 2009 (UTC)

Is this is a response to something I said above? I don't see how. Combining doors is unconditional because it does not say anything about the host's strategy in the case the player initially picks the car and because it gives the wrong answer for the conditional variant I suggest. Morgan's F1 is clearly equivalent. If you can't see this, I'm not sure I can help you. -- Rick Block (talk) 23:56, 21 June 2009 (UTC)

We're discussing what the world's most reliable source says about the 'Combining Doors' solution, which in your opinion, based on Morgan's F1, is unconditional. Morgan, as shown above, says nothing of the sort. So, it is nothing more than your OR (or 'opinion') until you show a reliable published source that says the 'Combining Doors solution is unconditional'. And, please, no conjecture. 'Host's strategy' has nothing to do with 'conditional vs unconditional'. Why, Nijdam proposed a 'conditional' solution just last week which made no mention whatsoever of 'host's strategy'. Further, in another demonstration of your lack of understanding of how logical arguments work, 'because it gives the wrong answer for the conditional variant I suggest.' is not a valid method of dis-proving a solution. It is nothing more than something you invented out of whole cloth. Right, Nijdam? Glkanter (talk) 10:44, 23 June 2009 (UTC)

I'm sorry Glkanter, the 'combined doors' is just a way of refrasing the 'simple solution'. You of all, with your continuing appeal on logic, should understand this. May be tomorrow someone will call it the 'restgroup solution'. There is of course no mention in Morgan's paper of it, but .... (guess what, use your logic). Nijdam (talk) 16:26, 23 June 2009 (UTC)

Yes, continue to 'label' it rather than address the actual solution. It makes a proper and valid Logical Argument, and it addresses the 'after revealing door 3 issue.' In the form that Devlin and Zehne have published it, it is perfectly complete, valid, and instructive. And, you concur that Morgan does not even mention it. To claim that Morgan does, must be Rick's personal opinion. So, as a professor, what 'grade' would you give Rick's 'method of disproving the 'Combining Doors' solution. You know, where he posted "...and because it gives the wrong answer for the conditional variant I suggest."? I guess Zehne and Devlin didn't realize that (Of course they didn't. It's nonsensical drivel.). So, is it a failing grade? Or D- for 'creativity' and 'stick-to-it-ness'? Glkanter (talk) 19:52, 23 June 2009 (UTC) Glkanter (talk) 00:01, 25 June 2009 (UTC)

Yes, continue to 'label' it rather than address the actual solution.

>>What the h... do you mean?

It makes a proper and valid Logical Argument, and it addresses the 'after revealing door 3 issue.' 

>>What does?

In the form that Devlin and Zehne have published it, it is perfectly complete, valid, and instructive.

>>Definitely not!

And, you concur that Morgan does not even mention it.

>>What do I?

To claim that Morgan does, must be Rick's personal opinion.

>>There is no such.

So, as a professor, what 'grade' would you give Rick's 'method of disproving the 'Combining Doors' solution.

>>A+

You know, where he posted "...and because it gives the wrong answer for the conditional variant I suggest."?

>>Do I have to?

I guess Zehne and Devlin didn't realize that (Of course they didn't. It's nonsensical drivel.).

>>I'm not sure whether they do realize anything.

So, is it a failing grade? Or D- for 'creativity' and 'stick-to-it-ness'?

>>Do you want to know your grade?Nijdam (talk) 17:56, 24 June 2009 (UTC)

Glkanter (talk) 19:52, 23 June 2009 (UTC)

Rick, I will address the sensible content of your latest post later but please come back to Earth and stop being silly about libel. Martin Hogbin (talk) 22:45, 21 June 2009 (UTC)

I'm absolutely serious about libel. If you or Glkanter persist in posting unsubstantiated claims about Morgan et al., I will ask an uninvolved admin to review your posts. From Defamation: [Libel is] the communication of a statement that makes a claim, expressly stated or implied to be factual, that may give an individual, business, product, group, government or nation a negative image. This seems to be your precise intent. You're saying Morgan et al., and Morgan in particular, published an article containing numerous factual errors. If I were to post at some newsgroup that you don't frequent that Martin Hogbin in his professional capacity as a physicist had published articles containing numerous factual errors would you not consider this to be libelous? I really am serious about this. You really do need to stop it. -- Rick Block (talk) 23:56, 21 June 2009 (UTC)

No doubt we will also be burnt at the stake as heretics too. You make yourself look foolish by sticking to such an absurd line. In fact you have lost all credibility with me and, I would think, most other editors here.

Just to make my position on the subject absolutely clear. I believe that the paper by Morgan et al (which for brevity I often refer to as Morgan, although I have no idea which author contributed which bit) contains a number of errors. Firstly there is the error in the calculation of the probability of winning by switching given a uniform prior distribution of q. This is a basic and obvious error in which the authors fail to take account of the information revealed by the opening of a door by the host. A letter pointing out this error has been sent to the journal and is being given due consideration. Unsurprisingly, their response did not include threats of legal action for libel.

I also believe that there are a a number of other serious mistakes in the paper of a somewhat more philosophical nature. Firstly the authors interpret Whitaker's question in a overly literal manner, considering its origin. This is alluded to in Seymann's comment at the end of the paper. Secondly the authors do not apply the principle of indifference consistently to the stated question, resulting is a spurious result in which a host choice parameter assumes undue significance. Finally the authors fail state explicitly in their paper the assumptions that they have actually made.

I would welcome the opportunity to have the truth of the above claims examined in court but unfortunately I doubt that I will get the opportunity to do so. Martin Hogbin (talk) 09:12, 22 June 2009 (UTC)

Are you really not understanding what I'm saying or are you just pretending to be stupid? You can certainly think whatever you'd like, and say what you think, but an assertion like Glkanter's above ("There are at least 5 errors in Morgan's paper.") is not OK. "Martin thinks there are at least 5 errors in Morgan's paper" would be fine. Criticize all you want, but don't malign. -- Rick Block (talk) 19:10, 22 June 2009 (UTC)

I suggest we drop this ludicrous topic. I will not enter into any more discussion about it. Martin Hogbin (talk) 21:42, 22 June 2009 (UTC)

Rick, since I've written 'repeatedly' that "There are at least 5 errors in Morgan's paper.", I wonder if you could tell me, what status as a plaintiff does Morgan's paper have in a US court of law? And, now I'm done with this ludicrous topic. Glkanter (talk) 10:44, 23 June 2009 (UTC)

Refereed paper agreeing with Morgan et al.

Looking through some of the sources that reference Morgan et al. I ran into [4]. This is a paper apparently (I haven't actually seen it in the journal, but I trust that it is there) published in the Spring 2000 edition of Teaching Statistics, a refereed journal. From the "Controversy" section (referring to vos Savant's columns):

Adding to the confusion, vos Savant then gave `a dubious analogy . . . [and] went on to defend her original claim with a false proof and also suggested a false simulation as a method of empirical verification' (Morgan et al. 1991, p. 284). Consequently, what could and should have been a correct and enlightening answer to the problem was made unconvincing and misleading. Subsequent work by Gillman (1992) and Falk (1992) applied the correct Bayesian mathematics to derive the general solution, but several other authors continued to perpetuate the `no news' argument, which at best relies on an unstated assumption.

This is a published article in a refereed journal, which completely agrees with Morgan et al.

To be completely fair, I also ran into [5] (as far as I can tell, a pre-publication draft of a chapter of The Remarkable Story of Math's Most Contentious Brain Teaser ), which has a largely critical account of the exchange between Morgan et al. and vos Savant (but, curiously, seemingly agrees with Morgan et al. "there was a subtle shift from the correspondent’s initial question, in which the host always opens door three, to the listing of the scenarios given by vos Savant, in which it was assumed only that the host always opens a goat-concealing door"). Unlike the source above, this one is not published in a refereed journal but it (or presumably something very much like it) is published by a reputable publisher (Oxford University Press).

I think the bottom line here is that Morgan et al. are clearly correct, but there is room for quibbling on the other side. -- Rick Block (talk) 23:07, 21 June 2009 (UTC)

Your first source seems to agree with Morgan but the second (Rosenhouse)says this, 'But for all of that it seems clear that vos Savant successfully apprehended all of the major points of the problem, and explained them rather well considering the forum in which she was writing. Her intent was not to provide an argument of the sort a mathematician would regard as definitive, but rather to illuminate the main points at issue with arguments that would be persuasive and comprehensible. In this she was successful'. Of Morgan's comments on vos Savant he says, 'Rather strongly worded, wouldn't you say? And largely unfair...' and continues to defend her by saying, '... continuing with their lengthy essay makes clear that their primary issue with vos Savant is her shift from what they call the \conditional problem," as posed by her correspondent (in which it is stipulated that the contestant always chooses door one and the host always opens door three) to the \unconditional problem," in which we stipulate only that after the contestant chooses a door, the host opens one of the goatconcealing doors. She did, indeed, make this shift, but this was hardly the point at issue between vos Savant and her angry letter-writers'.

In fact, as I read more, Rosenhouse is rapidly becoming one of my heroes as he (bravely risking legal action) refers the Morgan paper as, a 'bellicose and condescending essay'. Finally Rosenhouse provides a quote from vos Savant showing that the simple (unconditional) version is the one that everybody cares about, 'Nearly all of my critics understood the intended scenario, and few raised questions of ambiguity. I personally read nearly three thousand letters (out of many more thousands that ultimately arrived and found virtually every reader, from university lectern to kitchen table, insisting simply that because two options remained, the chances were even'. Martin Hogbin (talk) 22:03, 22 June 2009 (UTC)

Sorry Martin, I don't like partial quotations. Let me add:

Certainly vos Savant’s arguments are not mathematically rigorous, and we can surely point to places where her phrasing might have been somewhat more precise. Her initial argument based on the million door case is pedagogically effective, but mathematically incomplete (as we shall see). And there was a subtle shift from the correspondent’s initial question, in which the host always opens door three, to the listing of the scenarios given by vos Savant, in which it was assumed only that the host always opens a goat-concealing door.

and about Morgan et al.:

They, at least, were mathematically correct in their substantive points.

Nijdam (talk) 22:25, 22 June 2009 (UTC)

Martin - how are you getting that the vos Savant quote shows "that the simple (unconditional) version is the one that everybody cares about"? I believe what she's saying people understood were the unstated assumptions about 1) the uniform distribution of the car, 2) the host always making the offer to switch, and 3) the host never revealing the car - these are points of ambiguity that some (not very many) folks raised and has nothing to do with whether the problem is conditional or not. I believe (notice the wording here - "I believe", not "it is a fact that") vos Savant meant to be answering the conditional question but completely overlooked that the unconditional and conditional answers might be different. While she is indeed very smart, she's not a mathematician. -- Rick Block (talk) 01:23, 23 June 2009 (UTC)

There is no way of telling exactly question vos Savant intended to answer but she said this, 'virtually every reader...insisting simply that because two options remained, the chances were even'. In other words the issue that caused all the interest was the fact that people think the answer is 1/2 when it is in fact 2/3. This is the Monty Hall problem in a nutshell. There is no mention of conditional probability or host preference.

To get back to improving the article, we already have a section describing the simple solution, followed by a section describing the conditional solution. All I am asking is that we have some way of indicating to the reader which sources of confusion and which aids to understanding apply to which section. I believe we have ample reliable sources to do this. Martin Hogbin (talk) 17:51, 23 June 2009 (UTC)

Isn't it completely obvious that most people think the answer is 1/2 because they're thinking about the case the problem asks them to, where the player has picked a door, say Door 1, and the host has opened a door showing a goat, say Door 3, at which point there are only 2 closed doors - i.e. the conditional problem? Specifically, they're not thinking about the unconditional solution because the problem statement asks them not to. Doesn't this make the central source of confusion that people attempt to solve the problem conditionally, but do so incorrectly? Krauss and Wang's comments on this in the early section of their paper are interesting - they say that people who see the "correct" solution tend to have a 3 part mental model (following all possible locations of the car) and mostly simply ignore what they consider to be an extraneous fact that the host has opened Door 3. This means of course that these people are actually solving the unconditional problem, not the conditional problem. On the other hand if most people (those who end up with the 1/2 answer) actually see the problem in its conditional form shouldn't the primary focus of the article be on this interpretation? In any event, I think the sources of confusion about the unconditional and conditional interpretations are sufficiently intertwined that it makes little sense to try to specify which pertain to which interpretation. -- Rick Block (talk) 14:29, 24 June 2009 (UTC)

We have reliable sources that treat the subject without making it conditional. We have sources that explain reasons for confusion and give aids to understanding based on the simple (unconditional or conditionality ignored) treatment of the problem. It seems to me that we are back where we started when I responded to the original RfC. Despite many editors taking a much less hard line on conditionality, a small number of editors are refusing to allow change to the page to make it more useful to the average reader. Martin Hogbin (talk) 17:46, 26 June 2009 (UTC)

However that is imho somewhat of a mischaracterization of what we actually have. Almost all scientific sources (Devlin being the only exception) treat the problem with conditional probabilities, some of them explicitly criticizing the unconditional solution. 2 sources give an unconditional and conditional a solution without giving a clear pference but pointing out that the unconditional solution strictly speaking solves a slightly different problem (Henze, Behrens). Also there was never an argument of not offering the unconditional solution and making it less useful ro the average reader. However suppressing the criticism of the uncodintional solution is mischaracterization of the problem(and its treatment in reputable sources) and hence no service to the average reader at all.--Kmhkmh (talk) 22:28, 26 June 2009 (UTC)

That is your opinion, but some sources, such as vos Savant, Devlin and to a large degree Krauss and Wang treat the problem non-conditionally, that is to say that the issue of which door the host opens is not considered important. Most 'scentific' treatments start by assuming a particular formulation of the problem, that the questioner wishes to know what the probability of winning by switching is after a specific sequence of events has occurred. This assumption is criticised in Seymann's commentary at the end of the Morgan paper. There is no reason that 'scientific' sources should be considered better at interpreting the precise intent of the question than popular sources are, If anybody is, vos Savant is the expert in this respect. It may be that 'non-scientific' sources take the question to be more general in nature, or that they consider the 'condition' that the host opens a random door to be self-evidently irrelevant.

There nothing wrong with "non scientific" fources looking at a "more general" (or rather simpler) scenario und use that as an heuristic argument as well, but there is something wrong with suppressing the known and published caveats of that view. Frankly put such an attempt is a distortion of the facts we have.--Kmhkmh (talk) 11:21, 27 June 2009 (UTC)

What is clear, however, is that we have reliable sources that treat the problem conditionally and reliable sources that treat the problem non-conditionally, including giving aids to understanding and causes of confusion. It is the non-conditional formulation and solution that makes this problem famous and a clear non-conditional treatment of the problem should be given in the article. Martin Hogbin (talk) 09:12, 27 June 2009 (UTC)

Now you are trying to pull the same thing again simply equating all sources. That is a logical fallacy, which btw is related to MHP ittself or another fanous problem from statistics the Simpson Paradox. It is possible that from a more general/less detailed perspective you can draw a seemingly obvious solution, which however turns out to be false in some of the more detailed (sub)scenarios. Breaking that down regarding your argument we have variety of sources stating undconditional solution without stating any caveats, so from that that "general" perspective the unconditional solution might appear almost as good as conditional one. But if we examine the source in more detail and rank them by reputation/expertise then the picture looks rather different and we get a clear preference for the conditional solution, in particular having only 1 out of many scientific sources stating the unconditional solution without caveats.--Kmhkmh (talk) 11:21, 27 June 2009 (UTC)

From where you get the idea that fame of the problem is based on the unconditinal solution is somewhat uncomprehensible to me. The fame of the problem is clearly based on the original 1/2 vs 2/3 controversy (and vos Savant being correct with 2/3) and later within the science domain as well known example for conditional probabilities and failing intuition.--Kmhkmh (talk) 11:21, 27 June 2009 (UTC)

There is no universally agreed formulation of the MHP. Before we can provide a definitive solution we must decide many things including the game rules (on which there is general agreement) which distributions are to be taken as random, whether the doors opened are specified and finally what question we are going to ask. Until all those (and probably other) points have been decided there can be no single correct solution. Perhaps you could tell be in what order you would rank the available sources for reputation/expertise in deciding what question is being asked. Martin Hogbin (talk) 15:10, 27 June 2009 (UTC)

yes, but there is a original formulation of the MHP (the one in parade) and for none of its possible interpretations is Vos Savant's explanation "complete". Strictly speaking it "merely" provides a reasonable heuristic. Vos Savants explanation is only complete for answering the question: "Is switching in general better than staying", that however is strictly speaking not among the possible interpretations of the original MHP. As far as ranking of sources go, it should be something like this: 1.) peer reviewed science journals (Morgan, Gillman, ...) 2.) science publications (books, non peer reviewed journals or columns) by reputable science institutions, reputable science publishers, reputable science individuals (Devlin Henze, Snell/Grinstead, various other math books). 3.)reputable general publications (New York Times, Parade) 4.)reputable general individuals/"pundits" (on record outside their publication) (vos Savant, gero von randow,...)--Kmhkmh (talk) 17:12, 27 June 2009 (UTC)

I am not going to argue that Whitaker's was not the most notable statement of the problem but we need to understand what it was. It was a question from a member of the public in a popular general interest magazine about a TV show. It was not intended to be used as a question in a statistics exam. You say that vos Savant's answer is only complete for answering the question: "Is switching in general better than staying". That is almost certainly what Whitaker actually wanted to know. Do you really think he wanted to know the chances of winning by switching given that a particular door had been opened by the host? It was a TV show and Whitaker clearly wanted to know if was generally better to switch or stick, or to put it another way, what would be the players best strategy if they found themselves in the situation just described (bearing in mind that the player would have no idea of the host's strategy, if any) and how much better is this strategy. The conditional formulation and solution is clearly irrelevant to this situation.

As far as the math goes, it is is not about intent, but about what was actually stated. As far as speculating or examining potential intent goes, the authoritative source would be a peer reviewed journal for psychology. Concerning your claims about Whitaker's intent, personally I believe he wanted to know what's best for the candidate in the stated situation and he probably was not looking for a "complicated" explanation involving conditional probabilities. From that point of view you can consider vos Savants answer as perfectly alright. However we are not writing a private explanation for Whitaker in particular nor a Parade article in general, we are writing an encyclopedic article on the problem. Hence we need to provide an explanation, that has to be correct rather than being only adequate for Whitaker (or Parade readers). Being slightly polemic and picking up you last line above: Conditional explanation might be irrelevant to Whitaker, however whether it is or not is rather irrelevant for us (=WP).--Kmhkmh (talk) 20:06, 27 June 2009 (UTC)

Why should peer reviewed journals be better at interpreting the precise intent of Whitaker's question that a very intelligent person whose job it was to answer such questions? Martin Hogbin (talk) 18:18, 27 June 2009 (UTC)

The wikipedia is about the actual stated problem and what is known/publsihed about it in reputable sources. It is not about speculative or fictious "intent". Moreover even if we were to take a different intent for granted the result is kinda the same. The WP article still needs to point out the problems with vos Savant's explanation aplpied for the stated problem (no change there). Then it would need to state the "intended problem" (as far as resources for that exist) and explain how vos Savant argument correctly explains the "intended version". Also we would have to state the exact differences between the intended and the actually stated version and that most literature refers to the actually stated version and it variants.--Kmhkmh (talk) 19:39, 27 June 2009 (UTC)

There is no 'stated problem'. Whitaker's problem cannot be solved at all without many details being added. It is generally accepted principle in statistics that no problem can be solved until it is properly defined. For example I found this quote, 'Every statistic is the product of many human decisions about what the statistic is supposed to describe'. This is a fundamental principle of the science of statistics. Most arguments in statistics come from failing to define the question properly. To answer a statistics question properly it is necessary to consider what the questioner actually wants to know, but do not take my word for this, read the comment by Prof Seymann at the and of Morgan's paper, where this point is made abundantly clear.

Adding the details that must be decided upon to get a well-defined problem is not 'speculative' or 'fictitious' it is an important part of statistics. The one thing that is essential, however, in any answer in which details have been filled in is to make absolutely clear the assumptions on which your answer is based. The most conspicuous failure to do this is in the paper by Morgan et al, where a form of solution is assumed at the start without most of the assumptions made being stated. Martin Hogbin (talk) 09:27, 28 June 2009 (UTC)

Much (most?) of the problem's fame came from vos Savant. vos Savant did not discuss 'conditional' solutions or 'host behaviour'. It seems to be a logical fallacy then, that the 'confusion' would be based on either of these items. Why do you guys keep bringing up 'variants' and 'sub-scenarios'? They are not relevant to the vos Savant MHP. Of course, adding or changing assumptions/premises could change the solution. What's that got to do with anything? And your statement that there is 'only 1 out of many scientific sources stating the unconditional solution without caveats.' is false. Everyone, except Morgan, Gillman, and what, 2 or 3 others uses the 'unconditional' solution. So that's hundreds of reliable sources. And the 'combining doors' solution is not unconditional. It shows that Monty revealed a goat behind door #3. Glkanter (talk) 16:23, 27 June 2009 (UTC)

Nobody disagrees with most of the publicity coming from Vos Savant (however Martin above referred to Vos Savants explanation not Vos Savant in general and that difference matters). Also you seem to misunderstand the argument above, the use of the "subscenario" above is not refering to MHP variants, the argument is about MHP itsself and a fallacy in Martin's argument. The basic idea here is that, some statistical property that holds for the overall population, does not have to be true for various subpopulations (="subscenarios"). For crude analogon, it is true that 50% of the population is male, however if i look at the subpopulation of people wearing skirts, it is not true that 50% of them are still male. Meaning additional information matters! While it is true, that in 2/3 of all cases switching wins, it does not necessarily mean that, when sitting on door X and knowing about a goat on door Z, that switching wins in 2/3 of the cases as well. --Kmhkmh (talk) 16:53, 27 June 2009 (UTC)

As far as my statement regarding the scientific sources, strictly speaking it should have been, all scientific sources I'm aware of (>4 math papers, >7 math books). However your claim, that "hundreds of Scientific sources" (except devlin) do otherwise, seems to be rather unfounded to me. However please feel free to prove me wrong and share those sources with us.--Kmhkmh (talk) 16:53, 27 June 2009 (UTC)

Are you saying that Monty revealing a goat provides useful information to the contestant? The contestant is indifferent as to which door may have the car. Glkanter (talk) 17:11, 27 June 2009 (UTC)

I'm saying whether the goat info turns out to be useful or not in this particular, is something that to be proven/checked and not just to be assumed either way. --Kmhkmh (talk) 19:39, 27 June 2009 (UTC)

There are simple, if not immediately obvious, arguments showing the revealing of a goat does not provide any useful information to the contestant. Even more so if the door opened by the host is defined to be random. Martin Hogbin (talk) 09:30, 28 June 2009 (UTC)

And the point is without actually making one of these arguments the solution does not actually address the case where a player is deciding whether to switch while standing in front of two closed doors (which is presumably how most people interpret the problem). -- Rick Block (talk) 16:34, 28 June 2009 (UTC)

And to say 'only Probability professors are reliable sources' is FALSE. The 'Combining Doors' solution, and many others, rely on Logic. A perfectly acceptable science to utilize for this problem. Glkanter (talk) 16:23, 27 June 2009 (UTC)

Nobody says "only probability professors are reliable sources". I do say however that probability professors are the higher ranked sources on probability problems. Logic by no means leads to the conclusion that the unconditional solution is without caveats.--Kmhkmh (talk) 19:39, 27 June 2009 (UTC)

What about my statement "And to say 'only Probability professors are reliable sources' is FALSE. The 'Combining Doors' solution, and many others, rely on Logic. A perfectly acceptable science to utilize for this problem."? Glkanter (talk) 17:11, 27 June 2009 (UTC)

What do the sources actually say

Can we get back to what the sources actually say. Two threads above, I listed 4 POVs and some sources that take each and conjectured a 5th (which I think matches Martin's) that Kmhkmh claims Behrens and Henze take. Sorry for repeating them but I think it's helpful not to have to dig them out of the thread above (which got rather violently sidetracked). In this thread I would like the discussion to be limited to what sources say as opposed to arguments about the problem. If anyone would like to suggest additional POVs that other sources take, please do so.

• "vos Savant": The MHP is the Parade version with the additional assumptions that the car is uniformly distributed and the host always reveals a goat and always makes the offer to switch - with no explicit mention of how the host decides what door to open in the case the player initially selects the car. An unconditional solution showing the probability of winning by switching is 2/3 is presented without clarifying whether the problem is conditional or unconditional.

vos Savant, Devlin, and most "popular" sources

• "Morgan et al.": The MHP is as above but is clearly conditional, and since there is no constraint on the host in the case the player initially selects the car the host's preference in this case must be treated as an unknown variable q. Unconditional solutions (such as vos Savant) address a slightly different problem for which the answer is 2/3. The answer to the problem as stated is 1/(1+q), which is 2/3 only if q is 1/2.

Morgan et al., Gillman, Rosenthal

• "Krauss and Wang": The MHP is as above but with the additional constraint that the host choose randomly if the player initially selects the car (e.g. the Krauss and Wang version, i.e. the same as immediately above with q=1/2). An unconditional (2/3) solution is presented without clarifying whether the problem is necessarily conditional or unconditional.

Mueser and Granberg, Krauss and Wang

• "Grinstead and Snell": The MHP is the Krauss and Wang version but is clearly conditional. Unconditional solutions say the answer is 2/3 (which is the correct numeric result) but answer a slightly different question.

Grinstead and Snell

• "Martin": The MHP is the Parade version, but the probability of interest is meant to be the overall probability of winning by switching as opposed to the conditional probability faced by a player who has picked Door 1 and has seen the host open Door 3 (or, alternatively, a variant where the player must decide whether to switch before the host opens a door - "I'm going to open a door and show you a goat, decide now if you'd like to keep Door 1 or switch to the door I don't open").

Kmhkmh suggests Behrends, Henze

I'd consider Behrends actually to be closer to Grinstead and Snell since the conditional solution is presented first and the unconditional solution is described as addressing a different problem. Behrends doesn't exactly take a definitive stance, but immediately after saying both analyses are correct he says "In the second analysis the situation was different." (which sounds an awful like Grinstead and Snell's "This very simple analysis, though correct, does not quite solve the problem that Craig posed"). Like I've said I don't read German so can't really comment on Henze, but a conditional solution is presented so the POV is not "Martin" but perhaps

• "Henze": The MHP is the Parade version. An unconditional solution is presented as well as a conditional solution (one that assumes q=1/2) without taking a stance on whether the problem is necessarily conditional.

Henze

The point of all of this is that I'm finding remarkably little support (possibly none at all) for what I'm calling the "Martin" POV. I believe Martin (the user, not the POV) considers vos Savant, and Devlin, and most popular sources to be taking the "Martin" POV above but I don't think this is actually supported by what they say. I think there's as much evidence (i.e. none) for the "Martin" POV as there is for the following "Block" POV

• "Block": The MHP is the Parade version with an unstated (and unacknowledged) assumption that q=1/2 (i.e. it is the Krauss and Wang version) and is clearly conditional. An unconditional solution is presented under the unstated (and unjustified) assumption that the conditional and unconditional solutions must be the same.

There is, of course, no published support for the "Block" POV either. Since they don't say, we simply don't know whether sources presenting unconditional solutions think they're solving an "unconditional" version of the MHP (per the "Martin" POV) or think their unconditional solution is addressing the conditional problem (per the "Block" POV). Rather than put words in their mouths, I think we have to consider these sources as taking the "vos Savant" POV - i.e. we don't know what exact problem they think they're addressing.

What we do have are sources that say the unconditional and conditional interpretations are different problems and (with the possible exceptions of Behrends and Henze) every single source that identifies these as different problems explicitly saying the MHP is the conditional one. Treating these as equally valid interpretations doesn't seem to be supported by the sources. -- Rick Block (talk) 17:17, 27 June 2009 (UTC)

Henze (and Devlin) offers the 'Combining Doors' solution, which clearly shows a goat behind door #3. How is this unconditional? Is there a reliable published source you can provide who says it's 'unconditional'? Glkanter (talk) 17:43, 27 June 2009 (UTC)

Henze gives it as an unconditional solution. He treats it under a chapter 7 (laplace models) and conditional probabilities are introduced in chapter 16, where the treatment of MHP with bayes follows.--Kmhkmh (talk) 01:24, 28 June 2009 (UTC)

Does Henze describe this chapter 7 solution as 'false' in any way? Glkanter (talk) 06:58, 29 June 2009 (UTC)

In my reading Behrens and Henze do consider the conditional and unconditional solution as solutions to slightly different problems. But they consider the unconditional solution however as a good heuristic argument for switching in the original MHP (as long as no better analysis is vailable). The rationale behind this that, you usually assume statistical properties of the total population to be true for subpopulation as well as long as you have no clear indication to believe otherwise. So if switching wins overall in 2/3 of the cases, you take that as an indicator that switching will win in the candidate's specific situation as well. That of course is a heuristic argument and a such it might fail. In that sense you can see the unconditional solution as a valid heuristic argument for switching rather than a valid rigorous proof (using all infos/details being available). I agree with your comment regarding Martin POV vs Block's POV, in my eyes Martin's perception of the sources is somewhat distorted (see comments above) and it does not reflect the true source situation appropriately.--Kmhkmh (talk) 18:00, 27 June 2009 (UTC)

Kmhkmh, From what you say above Behrens actually seems to support my argument for treating the non-conditional solution as a good one. Is there an English translation of it anywhere? Martin Hogbin (talk) 23:49, 27 June 2009 (UTC)

Behrens is in English, the link is in the article. Or did you mean Henze? Henze is only available in German. You can find most of Henze online here: [6]. That pages also contains an extensive collection of scientific sources in english and german that are available online. As is said above in my view Behrens and Henze both give the unconditional solution, stating that the probabilities belong to a slightly different problem, but that they can be used as a heuristic argument for the original MHP. None of them can be understood as disagreeing with Morgan et al.--Kmhkmh (talk) 01:17, 28 June 2009 (UTC)

Rick, Comments on the sources below.

I would prefer to call the vos Savant solution non-conditional. We do not know whether she considered the question to be an unconditional one (what is the best strategy for the player), whether she considered the host to choose randomly and thus the condition that one particular door is opened to be irrelevant or whether she did neither of these. Her subsequent comments suggest she considered the door opened to be irrelevant. What we do know is that conditionality does not enter into her solution and that we have a section in the article that treats the problem the same way and that she gave aids to understanding and causes of confusion that specifically relate to her solution.

What we do know is that her solution addresses the overall chance of winning by staying vs. switching (which other sources call unconditional, not "non-conditional"), and that her explanation includes cases where the car is behind Door 3 in apparent violation of the problem statement. We don't know whether she thought the same solution pertains to the specific (conditional) case mentioned in the problem statement (i.e. player picks Door 1 and host opens Door 3) or not. We might infer that she thought so, but then the criticism that her solution does not exactly address this case is completely valid. Are the aids to understanding you're referring to the million door variant and the experiment she suggested? I'm not aware of any causes of confusion she's discussed. My issue with providing aids to understanding and sources of confusion in a separate section including the "unconditional" solutions is that we don't exactly know what problem these solutions are talking about. I think you're assuming those offering these solutions interpret the problem statement to be about the overall chance of winning by switching vs. staying, but since the problem statement they use (e.g. the Parade version) doesn't clearly say this (IMO, it pretty clearly specifies the conditional probability is the one of interest, but in any event it certainly never mentions anything about the unconditional probability) I don't think we can change the problem statement on their behalf. Just out of curiosity, how would you introduce such a separate section? -- Rick Block (talk) 17:30, 28 June 2009 (UTC)

I am using the term 'non-conditional' on this talk page to mean the any solution which does not treat the problem conditionally, for whatever reason, in other words the 'simple' solution. I accept that it is not a standard term and I am not necessarily advocating its use in the article.

I would introduce the non-conditional section exactly as we do now but just move the relevant aids to understanding and causes of confusion to that section.

Pretty well nobody, including Morgan, makes clear exactly what question they are answering. It is always possible to make maths problems more complicated by adding extra complexity and then treating the simple problem as a special case of a more complex one. In some cases this may be instructive but generally it is a good idea to make solutions as simple as possible. The MHP may be treated non-conditionally for a variety of formulations and many reliable sources do this. It may not always be clear exactly what problem they are addressing and why they are not treating the problem conditionally, but nevertheless they do treat the problem unconditionally and they do give the correct answer.

When an expert answers a question from a non-expert member of the public they have a duty to try to determine what it is that the questioner actually wants to know rather than just answering the question as asked, not doing this is the kind of thing that gives statisticians a bad name For the question to be conditional we must take it that Whitaker considered that which door was opened by the host was relevant to the decision to be made. I very much doubt that this was the case. Martin Hogbin (talk) 09:50, 29 June 2009 (UTC)

I will not repeat my views on the Morgan paper except to point out again that Seymann considered that they may have been answering the wrong question. I may put my many criticisms on the Morgan paper on a page in my user space so that I can link to them rather than repeating them. Now done, here is my comprehensive criticism of the Morgan paper

I agree with you description of Krauss and Wang's paper and note that they also give causes of confusion for the non-conditional solution. In fact they suggest that too much information, such as the number of the door that the host opens, to be one of the reasons that people get the answer wrong. This again supports having a separate 'Causes of confusion' section fot the non-conditional solution that we already have.

With the "Grinstead and Snell" (which I have not read) solution we are back to asking what 'the question' is and who is best qualified to judge this. Martin Hogbin (talk) 23:49, 27 June 2009 (UTC)

Why haven't you read Grinstead and Snell yet? The PDF is linked from the article, all you have to do is click it and then search for "Monty Hall". Their discussion starts at the bottom of page 136, in the chapter on "Discrete Conditional Probability" (kind of hint about what kind of problem they think it is) - it's less than 3 pages. With regard to who is best qualified to judge what the question is, what exact question would you say vos Savant answers (and how do you know this)? -- Rick Block (talk) 17:30, 28 June 2009 (UTC)

Actually, when I looked at it I had seen G & S before. Like many others their treatment seems to be based on the Morgan paper. Vos Savant answered the question where the player chooses after a door has been opened but the host chooses randomly. I know this because she says so. The condition in this case becomes a pointless complication since it clearly makes no difference to the answer as G & S say. Martin Hogbin (talk) 21:47, 29 June 2009 (UTC)

"Seems to be based on the Morgan paper" is pure conjecture on your part (we're talking here about what the sources actually say, remember?). vos Savant says (in her response to Morgan's paper published in American Statistician, Nov 1991, p 347) "In the original column, no additional stated conditions appeared important to a general apprehension of the problem because circumstances in default are reasonably considered random." - but her explicit experimental procedure described in one of her followup Parade columns makes no mention of the host's choice in the case the player initially selects correctly (even though she explicitly randomizes both the initial car placement and the player's initial choice) and (as far as I know) she never exactly clarified if she was intending that her answer apply to the specific case mentioned in the problem statement (player picks Door 1 and host opens Door 3) or not. In Morgan et al.'s rejoinder to vos Savant they say "One of the ideas put forth in our article, and one of the few that directly concerns her responses, is that even if one accepts the restrictions that she places on the reader's question, it is still a conditional probability problem."

G&S certainly do not say the condition becomes a pointless complication or that it clearly makes no difference. What they do say (after clarifying the host's choice is random in the case the player initially picks the car and presenting both an unconditional and conditional solution) is "At this point, the reader may think that the two problems above are the same, since they have the same answers." and then proceed to show how they are indeed different problems that may have different solutions by assigning a probability other than 1/2 to the host's choice in the case the player initially picks the car. This seems to be the exact opposite of what you're saying, i.e. they're saying it is a necessary assumption and it clearly does make a difference. -- Rick Block (talk) 13:16, 2 July 2009 (UTC)

We seem to be going over the same old ground again. We both read the same sources and come to different conclusions. I came here in response to an RfC in which it was said that a group of editors were claiming ownership of the article. I am not sure how to proceed now, I am convinced that the article currently does the average reader a massive disservice in that it fails to address what is commonly thought of as the MHP, but am not allowed to change this.

I suggest that I ask some of the recent editors to come back and give their views again on how the problem should be presented. Martin Hogbin (talk) 15:58, 8 July 2009 (UTC)

Simple Solution

I don't understand why the solution in the article has to be so long? It's quite simple really.

According to the traditional description of the game the host cannot show you the car if you picked a goat. Therefore, if you picked a goat the host will always eliminate the other goat. Thus when you switch you are basically betting that you picked a goat. The only time switching loses is when you picked the car in the first place. Thus when you don't switch you are basically betting that you picked the car. It's trivial to say that there's a 2/3 probability you pick a goat and only a 1/3 chance you pick the car. Thus, betting you picked a goat, and therefore switching, will win more often since you will more often, randomly choose a goat. 167.6.247.204 (talk) 19:57, 10 July 2009 (UTC)

I agree with you, but unfortunately some academics (Morgan et al) decided that the problem was too simple for them and that it need to be made more complicated. They managed to convince people that it somehow mattered which door the host opened when the player had initially chosen the car, thus making the problem one which required the use of conditional probability to solve. Martin Hogbin (talk) 20:16, 10 July 2009 (UTC)

Isn't this what the "popular solution" section says? What Martin is referring to is the fact that this solution doesn't always work. What the "academics" say is the answer always depends on how the host chooses which door to open if you've initially picked the car. The simple solution works only if the host randomly picks which door to open in this case - a reasonable assumption but the fact the solution depends on this assumption is not readily apparent. The easiest way to see it does matter how the host decides in this case is to force the host to decide some other way (like always opening the rightmost door if the player initially picks the car). With this way of deciding, if you pick door 1 and the host opens door 3 you have a 50/50 chance of winning by switching. What the academics say is if the host opens the door with probability p (in the case the player's door hides the car) your probability of winning by switching is 1/(1+p). The only way this works out to 2/3, is if p is 1/2. -- Rick Block (talk) 23:54, 10 July 2009 (UTC)

The complicated solution is only required if you make a number or arbitrary and unjustified assumptions. This has been argued many times on this page but if you are interested in my criticism of the 'academic' solution the look here. Martin Hogbin (talk) 09:31, 11 July 2009 (UTC)

Also see the FAQ at the top of this page. -- Rick Block (talk) 13:15, 11 July 2009 (UTC)

new book

There is a new book out, The Monty Hall Problem: The Remarkable Story of Math's Most Contentious Brain Teaser by Jason Rosenhouse, Oxford University Press 2009, ISBN 9780195367898. I'm surprised the wikipedia article doesn't reference it. 67.117.147.249 (talk) 19:04, 1 August 2009 (UTC)

Thanks. I added a link on the Arguments page. Glkanter (talk) 09:45, 2 August 2009 (UTC)

There is discussion of this book's account of the exchange between Morgan et al. and vos Savant above (#Refereed paper agreeing with Morgan et al.). The book is not used as a reference so is not cited. Per WP:SOAP, Wikipedia is not to be used for advertising, so unless there is a legitimate reason to reference something from this book it should not be mentioned, just as http://www.amazon.com/Monty-Hall-Problem-Beyond-Closed/dp/1847530788 is not mentioned. One difference is that the Deaves book does not satisfy Wikipedia's criteria for WP:reliable sources since it is self-published. The Rosenhouse book is published by Oxford University Press, so could be used as a reference if it has anything to say that is not already covered in the article. -- Rick Block (talk) 15:11, 2 August 2009 (UTC)

My explanation (the average joe way)

This is how I understand it: Right off, everyone can say you have a 2/3 chance of picking the goat. Well, what most people are forgetting is the host *has to show you another goat* (at least in the "usual" way this problem is told). That means in the same 2/3 cases, the host will be *forced* to pick the other goat you didn't pick. Both you by choice and the host by force eliminate the goats 2/3 times without even realizing it. So 2/3 you should switch and get the car since it was the only thing not eliminated in this 2/3 world.

But, an astute person will feel cheated thinking there's only 3 possibilities. In reality, there's 12 moves you and the host could make, but in 8 of these switching is a winner. So 8/12 is just 2/3.

Trying to explain it with pictures or examples doesn't make much sense at least for me (And I'm in upper division college math). —Preceding unsigned comment added by 150.135.245.202 (talk) 09:13, 28 August 2009 (UTC)

"Monty Fall"

In two sections of the article-- Why the probability is not 1/2 (under Aids to understanding), and Other host behaviors (Monty Fall), it is stated that the probablity of winning by switching becomes 1/2 instead of 2/3 if Monty reveals a goat accidentally instead of intentionally. This is seemimgly wrong and absurd, since it asserts that probability can be dictated by intent. Perhaps the phrasing needs to be udpated to indicate whether the door opened can include the door the player initially picked, which would indeed drastically change the odds. Or maybe I'm wrong, and am missing some obscure mathematical subtlety of the Monty Fall problem. In either case, this example most certainly did NOT "aid my understanding", and rather served only to make an already-confusing problem even more confusing. Clayhalliwell (talk) 17:25, 6 September 2009 (UTC)

As far as the quality of explanation goes, I agree with you to some degree, but that is another matter.

Regarding your point, the host never picks the door chosen by the player but, if the host chooses randomly, the player's chances of winning by switching are indeed reduced to 1/2. How can this be? You first need to note that if the host chooses randomly he will sometimes choose the car. What happens to these games? We can only assume that they are declared void as there is no point in offering the player a swap as they know they will lose either way. Of the remaining games, the ones that have not been voided, the player has a 1/2 chance of winning by swapping. This has changed from the original 2/3 chance for the following reason. If the player has originally chosen the car the they will obviously lose by swapping, but in this case the host cannot reveal the car, because the player has it. If, on the other hand, the host has initially chosen a goat, and would therefore win by swapping, the host could possibly open a door to reveal the car thus voiding the game.

So to sum up, some of the games (half of them) in which the player would have won the car by swapping will be voided if the host chooses randomly but none of the games in which the player would have lost by swapping car will be voided. This gives the payer only a 1/2 chance of winning by swapping overall. Martin Hogbin (talk) 17:56, 6 September 2009 (UTC)

The "Why the probability is not 1/2" section was butchered a while ago since the bulk of it was not referenced. It used to look like this. What remains is essentially an introduction to a section that no longer exists (it was vaguely based on [7], which is not a reliable enough source for a featured article). There was a previous suggestion to delete this section, although the fact that it admittedly needs some work does not seem like a reason to delete it. -- Rick Block (talk) 00:09, 7 September 2009 (UTC)

Another way to think about it is that we need to know why the host chooses to open his particular door if we are going to extract useful information from observing his choice. If the host chose a door randomly (and got lucky), we can't get the same information out as if the host chose a door because he knew it contained a goat. In the standard problem, the host is giving us a bit of information: of the two doors he can choose, he chose -this- one and not the other one. It's not perfect information, but it still helps (and it's how we improve our chances of winning in the swap from 1/2 to 2/3). However if Monty is forgetful and simply got lucky (by revealing a goat door, at random), he isn't imparting even partial information to us. He could just as easily have revealed the car. You might be able to think of other strategies that Monty could employ, and observe how they will give the player different probability estimates for winning by swapping. In summary, knowing why the host chooses his door is vital if we are to interpret his choice in our analysis. Maelin (Talk | Contribs) 02:55, 7 September 2009 (UTC)

Well, honestly, the door-opening in both cases doesn't provide ANY information, since the problem functionally distills down to choosing one door, or two doors. Whether you get to see behind one of the two doors first should be statistically irrelevant. Clayhalliwell (talk) 17:00, 21 September 2009 (UTC)

Perhaps you're confusing unconditional and conditional probabilities - which many explanations of this problem don't exactly explain very clearly. For example, one fairly popular solution says something like "your original chance of picking a door hiding a car is 1/3, so if you ignore what the host does and don't switch you'll win the car 1/3 of the time". Given that the host must open a door and won't ever reveal the car this is a true statement, but it doesn't really address the situation given in the problem statement which is that the player has picked a door and then the host has opened a door revealing a goat. The probability the car is behind the door the player initially picks, say door 1, is generally considered the unconditional probability. This probability is clearly 1/3 and stays 1/3 regardless of anything that later happens. The probability the car is behind the door the player picks given something has later happened, like say the host has opened some other door and has revealed a goat, is a conditional probability and may or may not be the same as the initial 1/3 probability. In the problem as usually presented no outcomes are excluded and all outcomes are equally likely so this conditional probability is the same as the initial unconditional probability. In the host forgets variant, all outcomes are equally likely but outcomes where the host opens a door and accidentally reveals the car are excluded. This allows the conditional probability to be different than the original (unconditional) 1/3. -- Rick Block (talk) 03:58, 22 September 2009 (UTC)

Simulations show 50%?

Unfortunately, every time I have I have attempted to simulate this problem, I have consistently achieved the 50% result. This makes it very difficult for me to believe the extensive rationales offered on this Wikipedia page. I'm willing to try again based on the deck-of-cards example, but I'm highly skeptical that the result will differ given my many past attempts. When experimentation agrees with intuition, it's time to suspect a math error. 173.48.171.191 (talk) 03:08, 1 October 2009 (UTC)

How, exactly, are you simulating the problem? -- Rick Block (talk) 03:30, 1 October 2009 (UTC)

What usually causes confusion in this type of a conditional probability problem, especially when you claim "proof by simulation," is the problem setup itself. Your simulation will get the correct answer to the wrong problem if you are not careful. Specifically, what other possibilities could have happened, but didn't in the specific instance of the experiment you simulate? For example, under "Monty Fall" above, Clayhalliwell observed: "It is stated that the probablity of winning by switching becomes 1/2 instead of 2/3 if Monty reveals a goat accidentally instead of intentionally. This is seemimgly wrong and absurd, since it asserts that probability can be dictated by intent." It isn't intent that changes the probability in that case, it is the fact that some possibilities are included in the case that leads to "2/3," while the same possibilities are excluded in the case that leads to "1/2." When the host intentionally reveals a goat, every single case must be included in your sample space. Because every time the host runs that game, he can reval a goat. If the host chooses randomly, then the host sometimes reveals the car, and those cases must be dismissed in your simulation because they do not match the problem description. If your simulation gets the answer 1/2, then you are dismissing some cases which you should not. That is why Rick Block asked how you are simulating the problem. --JeffJor (talk) 13:23, 1 October 2009 (UTC)

Simulation

How to correctly simulate the problem? If it is given that the player picks door 1 and the host opens door 3 (as described in the problem statement), then take for example 3 cards, ace of spades (car), 2 of hearts and 2 of diamonds (goats). Shuffle them and lay them out next to each other (face up!). Their position, left to right, represents the door number 1-3 (from left to right). Keep two tallies: win by switching (lose by staying) and win by staying (lose by switching). If the ace (car) is at the right, start again, because this event did not occur (this would mean the host must have opened door 2, but we're given the player picked door 1 and the host opened door 3!)- i.e. do not count this as a win either by staying or by switching. If the ace (car) is in the middle, add one to the tally of wins by switching. If the ace (car) is at the left, flip a coin representing the host's choice of which door to open in the case the car is behind the player's initially selected door (door 1). If the coin shows heads (host opens door 3), add one to the tally of wins by staying; if tails (host opens door 2, but since we're given the host opens door 3 this did not occur) nothing is done - i.e. do not count this as anything at all. Repeat as often as you like, but at least 20-30 times. You may already predict the outcome. Nijdam (talk) 21:50, 3 October 2009 (UTC) [edited by Rick Block (talk) 23:45, 3 October 2009 (UTC)]

This procedure simulates the conditional problem as described, specifically the case where the player has selected door 1 and the host has opened door 3 (randomly choosing to open door 2 or door 3 if the player has initially selected the car). Simulations where all outcomes are counted, for example the one suggested by vos Savant [8] involving two people with one playing the "host" and the other taking the role of the "player", ignore the potential effect of the host's choice when the car is behind the player's initially selected door. In this unconditional problem (which might be described as what is the chance of winning for a player who decides to switch before seeing what door the host opens) there is a 2/3 chance of winning by switching regardless of how the host picks which door to open if the car is behind the player's initially selected door. The probability is the same in the conditional problem as described (where it is given the player picks door 1 and the host opens door 3) only if the host must choose between the two remaining doors equally often when the car is behind the player's initially selected door. -- Rick Block (talk) 23:45, 3 October 2009 (UTC)

What keeps the first choice from being entirely unrelated? The choice is being made by the player (who has no information as to what's behind the doors) on a set of three doors. Then, they are allowed to remake their choice (that is, theoretically a choice of the same weight) on a reduced set of two doors. Why is the probability of the second choice multiplied by the probability of the first, when the player makes the second choice between two options with no information? To put it another way, let's say we have N boxes and one contains a bunny. We are allowed two choices. Assuming that we don't find the bunny the first time and the known empty box is then removed, why is the chance of bunny not now 1/(N-1)? —Preceding unsigned comment added by 142.205.213.254 (talk) 20:51, 14 October 2009 (UTC)

Do you mean "What keeps the second choice from being unrelated to the first? The fact that it isn't a new choice of a door at all. It is a choice to keep the first-chosen door, or change to the remaining closed door which represents the best prize of the two doors you didn't choose. To see what I mean, consider the "calling" of a simple flip of a coin instead of this game. Before the coin is revealed, you call "heads" or "tails." Then you are told what the coin did not land on, giving you some (actually, in this example, all) of the information in the event. Say you are then offered the chance to change your call, or keep your original call. If you choose "heads" or "tails" randomly (i.e., you make a second choice "unrelated" to the first), you will be right 50% of the time. But why would you do that? You know by elimination how the coin landed. The Game Show problem is different only in that you are given partial information rather than complete information. Before a door is open, you know that the two doors you didn't choose, between them, have a 2/3 chance of hiding the car. And that the host knows which one of them hides the goat. He can open that one without changing anything. Your choice to change isn't a new choice of a door, it is a choice to keep what you had first (a 1/3 chance) or change to a 2/3 chance. JeffJor (talk) 00:31, 15 October 2009 (UTC)

If the host opens a door he changes something, don't you agree?! Nijdam (talk) 11:31, 25 October 2009 (UTC)

The only thing that changed is that you stop using "unconditional probability," and start using "conditional probability." Anybody who insists there is no benefit to switching is refusing to recognize this. Before the host opens the door, there is no "conditional probability." There is only the "unconditional probability" that a car is behind a particular door. It is 1/3 for each. After he opens a door, you have to integrate the added information into your probabilities. But the added information only affects the two doors you didn't choose, never the one you did. This is because the host cannot choose that one, so it is unaffected by any action he take that does not eliminate all of the unchosen doors. Its (conditional) probability stays at 1/3, the door the host opens goes to 0 (because you know it doesn't have the car) and the "unconditional probability" it used to have is transfered to the remaining door, making its conditional probability 2/3.JeffJor (talk) 22:13, 25 October 2009 (UTC)

The probability of the player's initially selected door happens to not change in the problem as generally understood, but this is not some immutable fact caused by the rule that the host cannot open this door. Frequent readers of this talk page may find this sort of example tiresome, however consider a host who never opens the door the player chooses (i.e. if the player chooses a goat the host opens the other goat door) but does not choose with equal probability if the player has initially chosen the car. For example, in this case let's say the host picks the leftmost door 1/3 of the time and the rightmost door 2/3 of the time. With this host, if the player picks door 1 and the host opens door 3, the conditional probabilities are NOT 1/3 for the player's initial door and 2/3 for door 2 but rather 2/5 and 3/5, respectively. The point of this example is not to say that the solution saying the player's chances of winning double by switching is wrong - but that the explanation that says "the added information only affects the two doors you didn't choose" is not quite right. The added information means the conditional probabilities must be calculated.

The conditional chance of the door the player doesn't pick is 1/3 out of (1/3 + X), where X is 1/3 times the chance the host opens door 3 when the player picks door 1 and the car is behind door 1. Assuming the host picks equally when the player initially picks the car, this chance is 50% so X is 1/6 and the chance the car is behind door 2 is therefore (1/3) / (1/3 + 1/6), which is 2/3. Similarly, the chance the car is behind door 1 is X / (1/3 + X), which (still assuming the host picks equally) is (1/6) / (1/3 + 1/6) - i.e. 1/3.

Saying "the player's initial chance doesn't change because the host cannot open the player's initially selected door" misses another critical condition - which is that the host also must choose equally if the player initially selects the car. Without this additional constraint, the statement is simply not true. BTW - I'm quite sure Professor Nijdam is not saying it doesn't matter if you switch but rather that the probabilities of the player's door and the remaining unopened door are always both affected by the host opening a door. -- Rick Block (talk) 23:43, 25 October 2009 (UTC)

Rick? That action you described lets the host "eliminate all of the unchosen doors" 1/3 of the time, by revealing the car 1/3 of the time. Maybe I didn't phrase it as well as you would have liked, but I do understand this problem and I am on your "side" of the arguments. As long as the host CAN, BY ANY POSSIBLE OUTCOME OF HIS STRATEGY, ONLY REVEAL INFORMATION ABOUT WHERE THE CAR IS NOT, (a better choice of words), the a posteriori probability that the car is behind the chosen door remains 1/3 (or 1/N if you have N doors and one car), the same as the a priori probability. That condition happens if the host CAN reveal a car, or if he reveals all of the unchosen doors. You allowed him to reveal a car 1/3 of the time.

Yes, the a posterioi of any unopened, unchoosen door changes from what its a priori probability was. My point was that the significant change is bewteen using a priori and a posteriori probabilities. Under the conditions I meant (Host can't reveal the car and can't reveal all unchosen doors), the a posteriori probability for the chosen door is always the same as its a priori porbability, while the a posteriori probability of any unopened, unchosen door is always greater than its a priori probability (assuming the host opens some number of a doors, that is).JeffJor (talk) 15:24, 26 October 2009 (UTC)

The host action I'm suggesting never reveals the car. The change from the typical analysis is only in the case where the host has a choice (the case where the player's initially selected door hides the car). In this case, if the host's preference for the door that is opened is expressed as a probability p, the player's initially chosen door hides the car with probability p / (1+p) - and the other door's probability is 1 / (1+p). These are 1/3 and 2/3 only if p is 1/2, so the conditional probability of the player's initial selection changes from 1/3 to something else under all conditions except if the host makes an evenly random choice (when the host can choose). The Parade version of the problem doesn't specify how the host chooses if a choice is available. Many people (quite sensibly) take this to mean p should be assumed to be 1/2. However, in a mathematically pedantic sense, if it's not specified it should be left as a variable. Note you're never worse off switching, regardless of what p is. This is (more or less) the central point of both the Morgan et al. and Gillman papers. -- Rick Block (talk) 19:21, 26 October 2009 (UTC)

I apologize; I didn't read it all - just enough to see that you said the probability changed, which it CAN NOT DO unless the contestant knows the host's strategy is biased as you said. It has to be an axiom that the contestant does not know it, if it is biased toward one door or the other. That represents additional information that is not in the problem statement. Think of it this way - the contestant can mentally name the doors Tom, Dick, and Harry. It is only if he can associate these names with the host's "left" and "right" that your biased strategy affects the conditional probability to contestant sees. Otherwise, when he choses Tom the chances are 1/2 that the host opens Harry or Dick. It isn't that P is assumed to be 1/2, it is that the contestant has a 1/2 chance of being right about which door is favored, and 1/2 chance of being wrong. So again, the a posteriori probability of the original choce DOES NOT CHANGE unless the host gives away information about where the car is, or how he is choosing, in a way that contradicts the problem statement. [Oops - I keep forgetting to log in before I sign with four tildas] JeffJor (talk) 22:31, 26 October 2009 (UTC)

Is the question what the contestant knows, or is the question what the probability is? This gets into discussions that have been held at length on the /Arguments page. If the host chooses equally if given the choice and an alien lands at the point the player is deciding whether to switch and is told only that one door hides a car and the other hides a goat, what are the probabilities? From the player's perspective it's still 1/3 vs. 2/3 even though the alien has a 50/50 chance of picking the door hiding the car. Morgan et al. (1991) and Gillman (1992) solve for the probability, regardless of whether the contestant knows it. Perhaps the contestant isn't aware of the host's preference (like the alien isn't aware of the full problem set up), but not knowing the host's preference doesn't mean it has no effect on the actual probabilities. -- Rick Block (talk) 00:53, 27 October 2009 (UTC)

The only possible question is what the contestant knows, since the question is about whether the contestant should switch. There in no such thing as an "absolute" probability for a particular instance of the game, as you insinuate here. Only probabilities based on the various perspectives. Since the actual problem is based on "What should the contestant do?," it has to be evaluated from his perspective. (The correct resolution to the arguments you refer to, which I have not read, is that "probability" does not apply to the specific instance of the game. Probability only applies to a process. The instance given to us merely demonstrates that process from the contestant's perspective.) But even if you consider the wrong perspective, since the problem does not say which door was opened, you need to consider all possibilities. And that still makes the answer P(switch to car)=2/3. Even the alien you refer to, when it switches doors, it wins 2/3 of the time; and when it keeps the original door, it wins 1/3 of the time. Since it actually switches half of the time, it wins (1/2*2/3+1/2*1/3)=1/2 of the time.

For example, the car is behind one door that is known to the host. From the host's persepctive, the probability of switching to a car is either 0 or 1, because he knows where the car is. But those two cases don't happen in equal numbers. Regardless of his strategy, as long as he always opens one door with a goat, the probability that the original door had the car is 1/3 so that is the probability of getting a goat by switching. This answer does not depend on how the host choose what door to open.

From the show's producer's standpoint (she doesn't know where the car is, but does know the host's strategy), which is what you attempted to calculate, there are four possibilities. Using a notation where CCOL means "contestant Choose Car, host Opened Leftmost door," they have probabilities P(CCOL)=1/9, P(CCOR)=2/9, P(CGOL)=1/3, and P(CGOR)=1/3. The conditional probability when when the host opened the leftmost door is P(switch to car|opened leftmost)=P(CGOL)/[P(CCOL)+P(CGOL)]=(1/3)/(1/9+1/3)=(1/3)/(4/9)=3/4. The conditional probability when when the host opened the rightmost door is P(switch to car|opened rightmost)=P(CGOR)/[P(CCOR)+P(CGOR)]=(1/3)/(2/9+1/3)=(1/3)/(5/9)=3/5. I presume the latter is what you calculated? More generally, these are 1/(1+P) and 1/(2-P), respectively, which does nto seem to be what you calculated. But, what you got is only part of what you needed to calculate, since it only represents the cases where the host opened the rightmost door. In actuality, P(swith to car)=P(CGOL)+P(CGOR)=1/3+1/3=2/3. Or you could use the Law of Total Probability to say P(switch to car)=P(swith to car|opened leftmost)*P(opened leftmost)+P(switch to car|opened rightmost)*P(opened rightmost)=(1/(1+p))*((1+p)/3)+(1/(2-P))*((2-P)/3)=2/3. Unless tyhe problem states "The host opened the rightmost door," that is the answer you need to use. The generality I made is correct.JeffJor (talk) 12:52, 27 October 2009 (UTC)

In the typical problem statement, specifically the one from Parade, aren't we told to consider the case where the player picks door 1 and the host opens door 3? By computing the "total probability" you're actually computing the unconditional, a priori, probability not the conditional probability in a particular case. The point of introducing p is not to address a host with a specific rightmost or leftmost preference, but any preference for the door that has been opened. The conditional probability given the player picked door 1 and the host opened door 3 is P(CGO3) / [ P(CCO3)+P(CGO3) ]. Please show me how you would solve this without making an assumption about the probability of the host opening door 3 in the case the car is behind door 1. BTW - you might find the Morgan et al. paper interesting. And, since we're really not talking about changes to the article here should we move this thread to #Arguments? -- Rick Block (talk) 14:36, 27 October 2009 (UTC)

No, we are not really told that the player opened a specific door. In the Parade quote (which is an ambiguous formulation), it is "You pick a door, say No. 1." The number is an example used to establish a way to distinguish the doors in the description, without saying which has a car or goat. The wording we are supposed to be using makes that even clearer by actually describing the process and naming the doors only at the end, in an example of the process. Neither gives a right-to-left ordering of doors, so your example is useless. And even if it was a specific door, it only matters (to the player) if the player knows how the host favors the specific doors, which most definitely is not in either problem statement. And the reason you can't use the calculation you asked for, is that it assumes the host's strategy is known to the player. [Added: But to avoid any confusion here, and when reading Morgan, just assume that the player and the host have each assigned their own sets of numbers, at random, to the three doors. The two sets are independent of each other. That is the problem intended. JeffJor (talk) 16:03, 27 October 2009 (UTC)]

"A priori" and "a posteriori" are terms that apply relative to the gaining of some information. "Total" refers to the a set of probabilities that comprise the entire set of possibilities for the information you have (e.g., this is why you divide by the sum of all probabilities that meet the condition in Bayes' Theorem). So you can use "total probability" on both sides of gaining the information, as long as it uses the proper information. The set of a priori, total probabilities are 1/3 for each door, no matter what you use to designate them. If the information is "Player chooses one door, Host opens an unchosen door that he knows has a goat, chosing BY SOME MEANS UNKNOWN TO THE PLAYER if both have a goat," then the a posteriori, total probability is 1/3 for the door the player chose, 2/3 for the unopened door, and 0 for the opened door. There may be different information that goes into the host's assessment of a posteriori probabilities, and those use the contestant's a posteriori probabilities as their a priori probabilities, since the two sets are on opposite sides of the strategy information.

I have read Morgan, but it was long ago. AFAIK, nothing I have said is contradicted there, and it should not be. But they may talking about these concepts in a different way. And yes, this should move - I just don't know how. JeffJor (talk) 15:57, 27 October 2009 (UTC)

Ok, I went and perused Morgan. They misquoted the problem. They based everything on the assumption that the contestant always opens a door that is clearly labeled "Door #1" to both the player and the host. That not what the article they are referring to said (http://www.marilynvossavant.com/forum/viewtopic.php?t=64). Most of the solutions they said are "wrong" are still "wrong" for some very pedantic reasons, but most are trivial to correct. For example, F1 is "wrong" because it fails to equate P(win)=P(lose|switch to D2)*P(switch to D2)+P(lose|switch to D3)*P(switch to D3) and then set P(switch to D3) to 0, since the contestant will never do that. The point is that there can be differnet models set up to solve a probability problem, and theirs may not be the easiest. JeffJor (talk) 16:36, 27 October 2009 (UTC)

Jeff, there is actually rather more than that wrong with the Morgan paper, including a rather surprising error. Have a look at User_talk:Martin_Hogbin/Morgan_Criticism Martin Hogbin (talk) 22:26, 27 October 2009 (UTC)

-- thread continues at /Arguments#JeffJor's comments to your redirection here from the MHP discussion page. -- Rick Block (talk) 20:19, 28 October 2009 (UTC)

Problem in opening should be changed

It doesn't mention you "win" by getting the car. Fafas (talk) 01:07, 22 October 2009 (UTC)

The problem statement in the lead is a quote. I've added "[that is, booby prizes]" following the initial reference to "goats". Good enough? -- Rick Block (talk) 02:14, 22 October 2009 (UTC)

It's better now. Fafas (talk) 21:22, 22 October 2009 (UTC)

One more simulation question

If one was to write a program to simulate this problem would the same rules apply or would the ratio of win/losses be 50-50 because the programing would not be choosing to switch or not like a human would but simply randomly choosing one of the remaining two doors after one of the initial three non-win doors was dropped?

Granted I'm not a computer programmer but it seems to me the program would run something like this:

1. Choose a random number between 1~3, set that number as WIN.
2. Again choose a random number between 1~3 set that number as CHOICE.
3. Discard one non-WIN non-CHOICE number (randomly chosen if there are two possibilities).
4. Randomly choose one of the remaining two numbers (this represents staying or switching).
5. Log and graph results.

Is this an accurate simulation?

If this has been addressed somewhere referenceable can someone point me to it? Thanks! Colincbn (talk) 12:31, 12 November 2009 (UTC)

If a person or a program randomly chooses whether to switch, they'll win 50% of the time - but this is not what the problem is asking. In either case (person or program) you should keep track of how many times you switch and win, how many times you switch and lose, how many times you don't switch and win, and how many times you don't switch and lose. The ratio of (switch and win) to (switch and lose) is the chance of winning by switching and will be about 2:1 (2/3). The ratio of (don't switch and win) to (don't switch and lose) is the chance of winning by not switching and will be about 1:2 (1/3). These two ratios must add up to 1. If you randomly pick whether to switch or not the ratio of switch (win + lose) to don't switch (win + lose) will be about 1:1, and the ratio of (switch and win) to (don't switch and win) will be about 2:1. This doesn't mean the chance of winning by switching is 50%, but that the chance of winning by making a random choice between switching and not is 50%. Regardless of how you choose whether to switch or not, if you switch your chance of winning is 2/3 and if you don't your chance of winning is 1/3.

Specific numbers might help. If you do this 600 times, and always switch you'll win about 400 times and lose about 200 times. Similarly, if you never switch you'll win about 200 times and lose about 400 times. However if you randomly pick whether to switch, you'll switch about 300 times and not switch about 300 times. Of the times you switch, you'll win about 200 and lose about 100. Of the times you don't switch, you'll win about 100 and lose about 200. Overall, because you're randomly picking whether to switch or not, you'll win about 300 times.

There is source code for some simulations (in various languages) at http://en.wikibooks.org/wiki/Algorithm_Implementation/Simulation/Monty_Hall_problem. -- Rick Block (talk) 20:19, 12 November 2009 (UTC)

BTW - the discussion above contrasts the probability of winning if you choose to switch randomly vs. the probability of winning by switching. There's another layer to the problem as usually stated which is that you're asked to imagine having chosen door 1 and the host having opened door 3. Opinions differ about whether this is significant, but most simulations, and many solutions to the problem, don't address this particular situation (or any other specific combination of player pick and door the host opens) but rather what might be called the overall probability of winning by switching assuming (usually without an explicit justification) that this overall probability must be the same as the conditional probability of winning by switching given the player picks door 1 and the host opens door 3. If you're actually interested in the conditional probability of winning by switching given that you've chosen some particular door (like door 1) and the host has then opened some other particular door (like door 3), the simulation should be more like the one suggested above by Nijdam where you only record cases where the player initially chooses door 1 and the host opens door 3.

Again, specific numbers might help.

If you run 600 simulations (initially picking door 1 each time) we'd expect the car to be behind each door about 200 times. So if you switch every time, you'll win about 400 times meaning the probability of winning by switching is 2/3. However, how many times will the host open door 3, and how many of those times will you win if you switch? The host has to open door 2 if the car is behind door 3. This should happen about 200 times. And the host has to open door 3 if the car is behind door 2 - which also should happen about 200 times. If the car is behind door 1 the host can open either door. If he picks which door to open randomly (in this case) he'll open each of doors 2 and 3 about 100 times. In total, the host opens door 3 about 300 times - all 200 times the car is behind door 2 but only 100 of the times the car is behind door 1. So if you switch given you've chosen door 1 and the host has then opened door 3 you'll win about 200 out of 300 times (i.e. 2/3 of the time).

Keeping track of it this way also lets us figure out the probability of winning by switching if the host doesn't pick which door to open randomly (in the case the car is behind the door the player picks). For example, if the player picks door 1 and the host opens door 3 with probability p when the car is behind door 1 (the player may or may not know what p is), in the 200 times the car is behind door 1 the host opens door 3 200p times. These are all cases where switching loses, so switching wins about 200 times out of a total of 200+200p times. Expressed as a fraction this is 200/(200+200p) which simplifies to 1/(1+p). Since p can theoretically be anything between 0 and 1, this means the probability of winning by switching given the player picks door 1 and the host opens door 3 could be anything between 1/2 and 1, depending on p. Again, the player may not know what p is. Many folks (on this page) insist the player CANNOT know what p is and therefore p MUST be taken to be 1/2, which leads to the 2/3 answer. Note that if all you're interested in is the overall chance of winning by switching, p doesn't matter at all. Staying with the numbers we've been using all along, if you always switch you'll win about 400 out of 600 times no matter what p is. If you're interested in the chances given the player picks door 1 and the host opens door 3 (or given any other specific combination, where p refers to the probability that the host opens the door he's opened in the case the car is behind the player's chosen door), then p does matter. -- Rick Block (talk) 02:51, 13 November 2009 (UTC)

Thanks for the link, that is exactly what I was looking for!

As far as I understand the p problem (hehe, "p problem" hehe...) this only applies in real world situations where "Monty" has some kind of preference when choosing goats, and that in any "true" random pattern of choosing this never comes into play (I realize that there is a different problem with whether or not there is such a thing as "true" randomness but for our purposes computer generated "system clock randomness" is most likely sufficient). But where the conditional/unconditional argument comes into play is if someone spent everyday of their adult life watching Let's Make A Deal then got invited on the show; that person might have a better than 2/3 chance given that they have a better understanding of Monty's preference of goat choosing, is this an accurate simplification?

On a side note I actually ran through this in a pub last night with my sister in-law. At first she was always staying but after I explained the math (using mainly the Cecil Adams approach) she started switching and winning much more (about twice as much as it were). We used a deck of cards (ie: red twos and the ace of spades), and my randomizer was shuffling under the table and me trying not to think about it if I had to choose between two "goats". It was an interesting way to spend twenty minutes while guzzling Guinness and I would recommend it to anyone. Colincbn (talk) 07:11, 13 November 2009 (UTC)

Even If it's not stated, the host MUST choose randomly between two goats contestant's assesment of the host's choice must be that it appears random to her.

You do have to treat p as 1/2 unless you are told what its value is, and which doors it relates to. Many people, even those who should know better, forget that "probability" is not a property of the specific result, it is a property of the random process that led to the result. As Kreyszig said on page 714 of his famous book (mine is the 1972 edition), "For this reason we now postulate the existence of a number P(E) which is called the probability of the event E in that random experiment. Note that this number is not an absolute property if E but refers to a certain sample space S, that is, to a certain random experiment."

Here's my favorite example of the difference: Suppose I draw a card at random. I look at it by myself and see that it is the Queen of Hearts. I tell Ann that it is red, Bob that it is a heart, Carl that it a face card (that means TJQKA), and Dee that its value is even. I ask each what the probability is, that it is the Queen of Hearts. Ann says 1/26, Bob says 1/13, Carl says 1/20, and Dee says 1/24. But I know that this "probability" is actually 1/1. Since all the answers are different, who is wrong?

Answer: Nobody. The probability is not about the card, it is about the process. And each person sees a different process, one that leads to the specific piece of information I gave to them. Since each piece is different, the process each is evaluating is different. In the Monty Hall problem, the card represents one particular day's broadcast of this game show. The probability we are trying to evaluate is not a property of this broadcast, but of all possible broadcasts. Even ones where Monty might change how he picks.

Those people who think you can use a p other than p=1/2 to get an answer are wrong, by their own arguments. Consider that Monty might vary how he chooses p. He might choose p=1/3 when he is wearing white underwear, and p=3/4 when he is wearing colored underwear. But only Monty knows what kind of underwwear he randomly selected that day, or what mix exists in his wardrobe. So even if you track many games, and think you know what p is, you will still be wrong every time you use that p. It is never the value Monty uses. The assumption that p can be something other than 1/2 in the solution to the problem, leads to the contradiction that you have to know every factor that goes into determining what p is before you can use it. JeffJor (talk) 17:41, 13 November 2009 (UTC)

What those who say p is important (e.g. Morgan et al. 1991, and Gillman 1992) actually say is

• unless you're told the host picks randomly if given the chance then assuming p is 1/2 is an unwarranted assumption [note the randomization procedure Gardner included in his version of the Three Prisoners problem)
• in this case (not being told what p is) the probability given a specific initial player choice and door the host has opened does not have a single numerical answer and the best we can say is that it is in the range [1/2, 1]
• if you're saying the answer is 2/3, either you're not addressing the conditional probability in a specific case of initial player pick and door the host has opened or you've assumed p is 1/2

I think you disagree with them, but do you at least agree that this is what these sources say? -- Rick Block (talk) 20:36, 13 November 2009 (UTC)

• Those who say p is important are addressing a different problem than the one this article is about. So what they say isn't appropriate here. But their problem is actually unsolvable by the methods they use, since nothing can be assumed about the value of p by those methods. Especially not a "uniform distribution" of p. Those references should be dropped from this article, regardless of what you think they say about p.

• There are references that say p=1/2 is the only valid option, even when addressing Morgan's problem. That includes Gardner's version of the Three Prisoners problem. Gardner's assumption that p=1/2 is not part of the problem statement, it is part of his solution. It comes after he says "Now assume, by renaming the prisoners if necessary, that A is the one questioning the warden, and B the one the warden names as executed" which actually necessitates that p=1-p since the solution's treatment toward B (assume a value of p_B) and C (which has p_C=1-p_B) has to be the same. Or just look up the Principle of Indifference.

• If you think you need to solve "the case of not being told what p is, then you are addressing the probability of a particular instance of the random experiment (e.g., The show that aired on March 27, 1993), not the random experiment itself. You are essentially saying that there is one, and only one, correct answer to my card problem about the Queen of Hearts. Which person do you think gave the one correct answer? Why is that person's answer "better" than the others? Or, just see my reference about probability being about the samples space - the set of possibilities - not E itself.

• I am saying the one, and only, possible answer to the problem this article is about, is 2/3. Many more references support this solution than the fradulent Morgan, et al, treatment. The 2/3 solution applies if the player picks a specific door (which isn't part of the problem) and the host also picks a specific door (also not part of the problem), AS LONG AS THE PROBLEM STATEMENT DOES NOT SPECIFY ANY BIAS IN HOW THEY WERE CHOSEN. If you can find such information in the problem statement, the answer might not be 2/3. But you can't speculate about it - you need to be told a value for p to use it. See the Principle of Indifference, particularly the parts about names not being useable as identification. JeffJor (talk) 14:36, 14 November 2009 (UTC)

The real problem, Jeff, is that Morgan et al managed to get their paper published in a respectable journal. You know their paper is wrong and I know it is wrong but unfortunately that counts for nothing here, we must rely on 'reliable' sources. Their most serious error was that pointed out by Professor Seymann in his comment, published in the same journal. This is that Morgan do not make clear exactly what question they are answering. In the circumstances this is inexcusable. Martin Hogbin (talk) 18:24, 14 November 2009 (UTC)

My point was to try to shift this discussion from an argument about what you or I or anyone else thinks the Truth(tm) might be, to a discussion about what the sources say. The former topic is a fine topic for the /Arguments page, but really has no relevance to the content of this article.

And that is fine. Morgan, et al, and Gillman, do not address the problem that this article is about. Regardless of anybody's POV, THOSE REFERENCES DO NOT BELONG HERE. You are wrong whan you say they are references about this problem. Now, secondary to that, it is POV (and quite provable, which is a property that can be used to ignore a reference), that their treatment is wrong even for the problem they address. That is not the reason to remove the references, although it is a good reason to ignore them.

The Eisenhauer reference you give acknowledges that what Morgan and Gillman handle is a different problem. All it does is acknowledge that the contestant still does better by switching in that different problem; it does not attempt to say what the probability is. So it does, indeed, supercede both Morgans's and Gillman's conclusions about the problem the article addresses. JeffJor (talk) 15:20, 15 November 2009 (UTC)

The claim that Morgan et al. 1991, and Gillman 1992 (and Grinstead and Snell 2006, and Falk 1992) are addressing a different problem than the one this article is about is directly contradicted by what these sources say. For example, they all reference the problem statement from Parade.

Morgan misquoted the problem, and misinterpreted what they misquoted. And (to comment to what you said next) no, Gardner does not state p=1/2 explicitly. He states that you flip a coin, and in his solution implicitly through the Principle of Indifference assumes that the probability of the two outcomes are each 1/2. The same principle could be applied if he didn't say to flip a coin, so that part is irrelevant in the problem statement. It just makes it more apparent to the masses who do not realize the same Principle applies to "The warden chooses between B and C" and "The warden flips a coin to choose between B and C." Or that whan a problem says "flip a coin" it really means "Assume the Principle of Indifference applies." JeffJor (talk) 15:20, 15 November 2009 (UTC)

Gardner's description of the Three Prisoners problem (as published in Scientific American, Oct 1959) includes the following:

"Then tell me", said A, "the name of one of the others who will be executed. If B is to be pardoned, give me C's name. If C is to be pardoned, give me B's name. And if I'm to be pardoned, flip a coin to decide whether to name B or C."

There's no appeal to the principle of indifference. His problem description unambiguously specifies p=1/2.

I agree there are plenty of references that say the answer is 2/3. However, (as far as I know) nearly all of these are not in peer reviewed math journals. Without sources to back up it up, the opinion that the Morgan et al. treatment is "fradulent" is irrelevant to the content of this article. From wp:reliable sources: Academic and peer-reviewed publications are usually the most reliable sources when available. However, some scholarly material may be outdated, superseded by more recent research, in competition with alternate theories, or controversial within the relevant field. The Morgan et al. paper is specifically about this problem, and it appears in a peer reviewed math journal. Is it outdated or superseded by more recent research? On the contrary, it is directly supported by a subsequently published paper (also in a peer reviewed journal) (see #Refereed paper agreeing with Morgan et al., above). Is it controversial within the relevant field? Rosenhouse's recent book (The Monty Hall problem, Jason Rosenhouse) doesn't like the tone, but even he goes on to say They, at least, were mathematically correct in their substantive points. Is it in competition with alternate theories? There are plenty of popular sources that perpetuate vos Savant's solution, or other solutions directly criticized by Morgan et al. To consider this treatment to be in competition with alternate theories, I would expect there to be academic sources that reference Morgan et al. and directly dispute it. I think the academic response has been to clarify the problem description, consistent with the Krauss and Wang version presented in the article. In this version, the constraints on the host behavior explicitly force p to be 1/2 so that the answer is unambiguously 2/3 even if the problem is interpreted as Morgan et al. do.

Anyone can personally have whatever POV he or she would like about this problem. On the other hand, the article needs to reflect what reliable sources say regardless of whether you or I or anyone else agrees with them. -- Rick Block (talk) 19:52, 14 November 2009 (UTC)

Jeff - So, your claim is that Morgan et al., and Gillman (and presumably Grinstead and Snell, and Falk, and Eisenhauer) do not address the problem this article is about. Your opinion about this clearly reflects your POV, and is worth much less than a published opinion like (for example) Barbeau's - see either Barbeau 1993 or Barbeau 2000. Martin has previously suggested trying to split the article into sections about two different problems, what he considers the "notable" one (which I think is consistent with what you seem to consider to be the one, true, interpretation) and an explicitly conditional version. The issue with this approach is finding appropriate sources. Many sources treat the problem unconditionally even though the usual form of the problem statement is fairly clearly conditional. You're saying even though it's conditional the probability of the host's choice (in the case the host has a choice) must be treated as 1/2 because of the principle of indifference. Do you know of a source that explicitly (not implicitly) treats it this way? -- Rick Block (talk) 19:02, 15 November 2009 (UTC)

Rick - have you noticed that this article explicitly says "If both remaining doors have goats behind them, he chooses one randomly?" All those references EXCEPT MORGAN (and I just found a copy of Gillman today) acknowledge that they are talking about a different problem when that allow p<>1/2, and solve for a probability based on the parameter p THAT THE CONTESTANT HAS ACCESS TO (example, from Gillman: "In the extreme case of q=1, the host's opening of door #3 'gives you no information [emphasis added]. It is not inforrmation ONLY IF YOU KNOW q=1.) They all - EXCEPT MORGAN - acknowledge that the probability they give is based on the contestant's knowledge of p. Those treatments are correct. Only Morgan takes the additional, and quite incorrect, step of saying you can solve for a probability when p is not known or implied, even parametrically. Essentially, Morgan is claiming lat ln(2) is an answer to the unconditional problem, and it is not. If you don't know pp, the probability is 2/3 if you switch AND NOTHING IS CONTRADICTED if somebody who does know p claims a different probability. The two peoepl are answering different problems.

And no, regardless of how many people treat the original problem conditionally, it is not. Definitely not this article's problem, and not Parade's, either. The door numbers used were examples (for a similar case, look at Grinstead & Snell's problem #7 on page 13. Are you suggesting that Roulette only allows people to bet on a 17, or that the correct answer needs to include whether the roulette wheel is unbalanced toward a 17? Or does every book on probabiltiy need to be re-written to make their exampels into conditions?). Those people are just grabbing onto a more interesting problem, one that shows that "switch" is a good strategy even if you allow for biases. JeffJor (talk) 18:01, 16 November 2009 (UTC)

On thing that is undoubtedly true about Morgan is that they do not make clear exactly what question they are attempting to answer. This is not just what I say on my Morgan criticism page but it is what Prof Seymann says in his comment in the same peer-reviewed journal that Morgan were published in. Martin Hogbin (talk) 23:11, 16 November 2009 (UTC)

To start with, is there anyone who can tell me whether Morgan are answering the problem from:

1. The point of view (state of knowledge) of the player.
2. The point of view (state of knowledge) of the audience.
3. Only on the information given in Whitaker's question.
4. Only on the information given in Morgan's restatement of the question.
5. Some other basis - please specify.

This is not a minor detail but something that is universally accepted as an essential requirement in statistics - that the question being asked is clear. Martin Hogbin (talk) 11:32, 17 November 2009 (UTC)

Reply added at the /Arguments page. JeffJor (talk) 19:17, 17 November 2009 (UTC)

Martin - you know perfectly well what problem Morgan et al. are answering (we've been over this innumerable times before). To save any newcomer to this argument the trouble of looking back through this thread, Morgan et al. answer the question based on the information given in Whitaker's version of the question, as printed in Parade (which they trivially misquote) which is the same as the point of view of the player and the audience. They interpret the question to be about a game show (involving physically identifiable, distinguishable doors) and, in this game show, the probability of winning by switching given that the player has initially selected a door (an identified door) and then the host has opened another (identified) door. They work through the example situation suggested in the problem statement where the player has picked door 1 and the host has then opened door 3 as a straightforward application of conditional probability. Their analysis covers a variety of host protocols (what JeffJor is calling different problems), including the one vos Savant's published clarifications suggest she was attempting to solve where nothing is said about the host's choice if the player initially selects the car (which means the conditional probability equation contains an unspecified variable) as well as the Krauss & Wang version where the host is known to select equally randomly in this case. I'll reply to JeffJor's comments at the /Arguments page there. -- Rick Block (talk) 02:13, 19 November 2009 (UTC)

Rick, you know perfectly well that Morgan did not use Whitiker's version of the problem. They edited it into a different form that more closely resembled the problem they misinterpreted it for - and were ambiguous about (more below) in their solution. In Whitiker's version, the contestant chose a door (not "door No. 1"), and "#1" was given as an example in an aside that in no way implied it was meant to be a condition of the problem. The host opens a door (not "door #3), and "#3" was given as an example. Do you know what "a" means in English? It is an indefinite article, "used before a singular noun not referring to any specific member of a class or group" according to my Random House dictionary. The literal meaning of Whitiker's problem is nonspecific doors. I know you don't agree, but those newcomers might. And that difference doesn't actually matter, and isn't what Martin was referring to. Newcomers should know that, too.

If you would read Martin's comment, it is plainly obvious he wasn't talking about the difference between "the conditional problem" and "the unconditional problem" as you are. He is asking "From whose point of view is the probability calculated?" Yes, if the conditional problem is intended, both the audience and the contestant can include that information in their point of view. IT CHANGES NOTHING. It does not matter if the doors are phsycially identifiable (see the Principle of Indifference), because the contestant has no way to know how the host uses such distinctions on this particular day. ANY NAMES ATTACHED TO THE DOORS CANNOT MATTER. And if it could matter? Moragn's entire analysis is invalid because they must assign a similar set of parameters to the probabiltiy that the car is placed behind the specific door numbers. Neither Whitiker's problem, nor Morgan's, ever say the car is placed randomly. That fact is just as implicit (or not implied, as Morgan assumes) as any bias the host has about opening a specific (by name) door.

There is no absolute-correct probability for the two remaining doors, in either the conditional or unconditional problem. Because all of the random elements of the problem have already been determined at the time the decision is to be made. The car 'is behind one of the two doors. Any probability that can be assigned is a only measure of the information you assume is avaliable to calculate it, not a measure of that door's worth. If the contestant has only the information available to Marilyn's Little Green Woman, that probability is 1/2 (yes, I know that is less information than the problem says the contestant has). If the contestant has only the information that the problem says she has, the probability is 2/3 EVEN IF THE CONDITIONAL PROBLEM IS CONSIDERED. And if you are going to assume the contestant has more information than the problem says - i.e., that she knows the host has a bias measured by a parameter q - you might as well assume the contestant also knows everything that the host knows. Because only the host really knows how his q was determined on this particular day. Even if he is consistent with past games, and we assume the contestant knows all that history (which the problem does not allow), there could be unseen factors that influence the actual q so that on that day, it is not what this omniscient contestant thinks it is. The only virtue in considering a possible q, is that whatever its value is, it is never detrimental to switch. JeffJor (talk) 13:16, 19 November 2009 (UTC)

Yes, that is my main point. Rick, you say that the question is being answered from the point of view (state of knowledge) of the contestant (or the audience, which I agree is likely to be the same). What Morgan have done, in that case, is to arbitrarily dis-apply the principle of indifference to the host's choice of goat door. As Jeff says, the player has no more idea of the host's door opening policy than she does of the car's initial position, yet Morgan tacitly take the car's initial position to be random (which is quite reasonable as the player is presumed to have no information on its whereabouts) but they take the host's door choice to be non-random and described by the parameter q, even though the player has no information about the host's strategy. Thus, as I have said all along, Morgan add an artificial layer of complexity and obfuscation to what should be a simple (but very unintuitive) problem. Martin Hogbin (talk) 17:01, 19 November 2009 (UTC)

I'll try one last time, but this is a tiresomely repetitive argument. I think everyone (more or less) agrees the problem should be answered from the state of knowledge of someone who knows what is given in the problem statement (which we could assume is the player's SoK). I also think everyone (more or less) agrees the principle of indifference applies to the player's initial selection since, even if the player suspects the initial distribution is not random, the player has no way to know what the distribution is and is therefore making a random initial choice. In her followup columns, vos Savant removes any doubt about this explicitly saying the car is meant to be randomly located. I think so far, everyone is on the same page.

Now, the host comes into the picture.

The Parade problem statement says only "the host, who knows what's behind the doors, opens another door" and shows a goat. To make a decision about whether she should switch, the player now needs a little more information about the host's intent not specified in the Parade problem statement. Does the host always open a door showing a goat and make the offer to switch, or is this perhaps a one-time attempted swindle being offered only because the player's initial choice hides the car or even is the host opening a random other door which (this time) happens to not reveal the car? In her followup columns, vos Savant makes it very clear (even though these conditions are not in the problem as originally stated in Parade) the problem is meant to be interpreted that the host always opens a door, never reveals the car, and always makes the offer to switch. Even to this point I think everyone (more or less) still agrees.

So, back to the state of the knowledge of the player. The player knows

1. The initial distribution is explicitly 1/3:1/3:1/3 (and, even if it isn't, can be assumed to be because of the principle of indifference)
2. The host is compelled to open a door showing a goat and make the offer to swtich, and is not acting randomly because doing so would involve the chance of revealing the car

Sounds like a simple conditional probability problem to me. If we take a specific case (like the one mentioned in the problem statement, where the player initially picks door 1 and the host opens door 3), the probability of winning by switching is

P(car is behind door 2) / (P(car is behind door 1)*X + P(car is behind door 2))

where X is the probability the host opens door 3 in the case the car is behind door 1. This equation is well within the SoK of the player to come up with (and, by renumbering the doors, applies to any specific player's case), and would now (I think) lead the player to wonder about X. What exactly does this X mean? Is there anything in the player's SoK (i.e. the problem statement) that constrains it? The player definitely knows the host is not acting completely randomly, but should she assume the host is acting randomly in this subcase? Note that it's not the player who's choosing between these doors, but the host. Does the principle of indifference apply here?

This is the point where opinions differ. Morgan et al. have an opinion, that they published in a peer reviewed journal. Gillman published his opinion, which agrees with Morgan et al. Grinstead and Snell finesse the issue, by explicitly requiring the host to choose randomly in this case (while acknowledging the difference between the unconditional and conditional problems and the effect of X in the conditional case).

We can, and seemingly may, argue about this forever, but the bottom line is that from the state of knowledge of a Wikipedia editor Morgan et al. is a wp:reliable source and any arguments about what it says that are not based on equally reliable sources are simply wp:original research that has absolutely no bearing on the article content (by Wikipedia policy). -- Rick Block (talk) 19:27, 21 November 2009 (UTC)

Yes, Rick, it is quite tiresome. The reason is that you won't even consider the validity of arguments that disagree with the approach taken by Morgan, et al, or Gillman. The Principle of Indifference applies equally to the initial car placement and the host's choice of doors to open. It is inconsistent for "all to agree" it should be applied to one, and accept it for that choice, while insisting you can ignore it for the other. To paraphrase you, the player has no way to know what the distribution of the Host's bias is, and therefore it must be treated as a random choice. And before you try to deny this, apply the exact same argument you intend to use to the car placement.

You used the argument that "vos Savant [in later columns] removes any doubt about [the randomness of the car placement by] explicitly saying the car is meant to be randomly located." She also makes it clear in later columns that the host's choice is random. You can't apply these arguments differently to the two sources of uncertainty. Again, apply the same arguments to both choices.

And nobody is claiming the host's choice is random between the unchosen doors. It is well established that the host knows where the car is, and where the goats are. This provides a way, not based on names, for the host to distinguish all three doors in some cases. So the host's choice is random between the set of unchosen doors with goats, which are the ones the Principle of Indifference applies to from his SoK. A choice can still be considered random, by the Principle of Indifference, when n=1." Your point #2 above does not apply to any situation in the problem - if it did, the host would also open the contestant's chosen door 1/3 of the time. The implicit assumption vos Savant makes is that the host opens a random unchosen goat door.

Morgan's analysis is not an "opinion." It is a solution to a problem that is never stated in any of the traditional forms. Never. It does not belong in the article. JeffJor (talk) 20:37, 21 November 2009 (UTC)

I'm perfectly willing to consider the validity of arguments that disagree with the approach taken by Morgan et al., or Gillman. However, to be relevant to the article content it takes a published argument. I did a search on Google Scholar for "Monty Hall problem" and "principle of indifference". As far as I can tell, none of the hits say anything about applying this principle to the issue we're talking about. Including this argument in the article would require a published source - whether it's valid or not is a secondary issue and, unless there's a source making this argument, from Wikipedia's perspective it doesn't matter if it's a valid argument.

Do I personally agree that it's a valid argument? If you're attempting to justify 2/3 as the answer, sure - but I definitely don't agree that this means the approach Morgan et al. take is invalid. What I actually believe is that the approach Morgan et al. take applies to a broader range of specific wordings of the problem, and is therefore more useful, than an approach targeted at one and only one interpretation of the problem statement. In particular, the Morgan et al. approach addresses (among others) what might be called the current "standard form" (e.g. the K&R version with explicit constraints on the host including random pick between two goats if it comes up), and the "Monty forgets" variant (that vos Savant has mentioned in the last year or so in her column), as well as the "host might have a preference" generalization of the standard form. As has been previously mentioned, they don't do it but their approach also easily extends to an analysis where the initial probabilities are not 1/3 for each door. I know opinions about this differ, but I think the explicit conditional approach is an extremely clear and utterly convincing way to present the solution (even the 2/3 solution!).

Separately, your repeated assertion that Morgan's analysis does not belong in this article is (quite frankly) bizarre. It is I believe the first (and perhaps only) paper in a peer reviewed math journal specifically about the mathematical intricacies of the Monty Hall problem in its usual form. Google Scholar lists 60 citations. The article would not be complete without this reference. -- Rick Block (talk) 23:11, 21 November 2009 (UTC)

Rick you seem to want to confuse the issue in question by bringing up things that we all agree about. We all agree that (in the standard rules) the host always offers the swap and we all agree that the host knows where the car is and never opens a door to reveal it. The point is that, where the host has a choice of which door to open in other words in the case that the player has initially chosen the car, the player has no information on which to decide how the host will make this choice and thus we must take it that, in this case, the choice is random. This is not what Morgan do, they take it that this choice is not random and assign it a host door choice parameter.

I think that the article needs to concentrate much more on the simple problem. This is the notable problem. The simple fact is that the answer (chance of winning on swapping) is 2/3 but nearly everybody thinks otherwise. Th article should concentrate on explaining why this is so.

Regarding reliable sources and scholarly discussion, there are many reliable sources on this subject and there is no reason that we must use Morgan as the guiding light in our article. Although the paper was published in a peer-reviewed journal it has been the subject of much criticism, starting with Seymann's comment in the same publication. I suggest that the article should be based more of the article on K & W, for example, who actually start to address the reason that so many people get the answer wrong. If we take it that The Monty Hall Problem is the fully defined problem as stated by K & W (as we seem to do in the article now) then the Morgan paper is irrelevant as it does not address this problem, where the host choice is defined to be random.

Although the article should be based on reliable sources there is some latitude to decide which sources are most relevant to the problem being addressed. I have seen more of a consensus to use sources other than Morgan or those based on it. Martin Hogbin (talk) 12:16, 22 November 2009 (UTC)

Martin - please read the "comprehensive" and "well-researched" criteria from WP:FACR. Omitting significant references because they don't address what you think is the "notable" problem is contrary to both of these. You and Jeff have both asserted your opinion that if the host preference is not constrained by the problem statement then it must be taken to be random, citing principle of indifference. Since there are reliable sources for this specific problem (including a peer reviewed paper co-authored by 4 members of the faculty of a university math and statistics department!) that don't do this, your opinion is apparently wrong. Moreover, your opinion doesn't matter here - what does matter is what reliable sources say. Find a reliable source that explicitly makes this argument about this problem, ideally directly referencing Morgan et al. or Gillman or some similar source, and then we'll talk. Until then, what you're saying is simply WP:OR.

And, I think you're absolutely incorrect about what the consensus is. As far I as I remember, you, Jeff, and one or two others we haven't heard from in a while are the only ones in favor of dropping Morgan et al. and similar sources, while Nijdam, I, and at least as many others we haven't heard from in a while (I think it's actually far more than one or two) are not in favor of this. I think the discussion on this page is so tiresomely repetitive that many, many folks have simply checked out, so trying to gauge consensus based on current participation is not likely to be very accurate. -- Rick Block (talk) 20:09, 22 November 2009 (UTC)

Rick, I corrected your header for this section. The mistake you made in naming it points out the issues that you are misintpreting. Morgan does not take a broader view of the problem's various wordings, it is a narrower view in the sense of approaching a solution. It is narrower because the simpler wordings, that Morgan deny, allow some assumptions to be made. Assumptions that are traditioanlly made in word problems. I.e., if you can draw N balls out of a bag, the problem does not need to state that each has a probability 1/N. Morgan disallows such assumptions, but only where the "conditional" solution can still provide an answer to the question "should you switch?" They aren't calcualting a probability, they are showing that whatever the calculation could produce, switching is a good idea.

I agree that published work, and not our opinions, must be the basis for the article. But the theses of Morgan, et al, and Gillman, are not about the general problem this article is about. Morgan, et al, even say "In general, we cannot answer the question 'What is the probability of winning if I switch, given that I have been shown a goat behind door #3?' unless we ... know the host's strategy ..." So Morgan is not answering the "general" problem, they are answering one where p₁₃ takes on a specific value that is unknown ot the contestant, p₂₂=p₃₃=0, and (the assumption they make but don't state) p₁₁=p₂₁=p₃₁=0. So they explicitly state that their solution applies to just one variation of the unknown Host's Strategy. Essentially, they solved a variation of the general problem that is interesting because you can get an answer without making the usual assumptions for one part of that strategy, but do for others. And that is where they are inconsistent. The article is flawed because it suggests someone did calulate a probability.

If their approach belongs at all, it should be moved to below the discussion about alternate Host stratgeies. It applies - according to the authors - only if the contestant knows the host's stragtegy except for the exact value of p₂₃. And they also say that if the contestant does not know the host's strategy, that the best appraoch gives "the popular answer" of 2/3. (Note: there is a typo in their article. They gave the wrong value for that part, 1/2 instead of 2/3. And I think that proves that any oversight of their article treated it more as a curiosity, than as a scholarly work to be checked for accuracy.)

About the Principle of Indifference. It is so basic a principle in probability, that it never is listed as the reason whan it is applied. Authors just go ahead and state that they are applying an even distribution to the indistinguishable items, and it is universally understood why. Morgan does it, for the car's palcement. The only reason I brought it up (by name) at all is because it says the door numbers don't distinguish the doors unless there is some other known reason to treat them differently based on the numbers. When there is not, the solution treats them equally even if they are not. And so gets a correct answer that reflects how any possible bias could favor either door.

Finally, and you seem to keep ignoring this, the Parade version of the problem, and the K & W one this article is based on, do not describe the so-called "conditional" problem. Morgan misinterpreted it, and I have shown you exactly how their problem statement is different. The vast majority of peopel who see teh word puzzle do not even consider the "conditional" problem. But even in Morgan, they admit the "conditional" answer only applies when the host's strategy is known to fit within certain boundaries, that include knowing p₂₃. Several times, Gillman points out that not knowing it makes the answers to his Game I and Game II equivalent. This is why they deserve to be a sidebar, at best, in the article. It simply is not "about the mathematical intricacies of the Monty Hall problem in its usual form." Their problem is just an interesting fact about one possible variation of what everybody sees the the usual form of the puzzle to be. JeffJor (talk) 19:25, 23 November 2009 (UTC)

Do Morgan et al. address 'The Monty Hall Problem'

I have added a heading here for ease of editing.

Rick, I see nothing in WP:FACR that tells us that we must use an academic paper that does not address the problem as stated in the article. As Jeff has said above, the problem statement given in the article, namely that from K & W, clearly states that the host door choice is random (subject to the agreed rules) and the initial car placement is random. The Morgan paper clearly refers to the specific case where the initial car placement is random (even though this is not explicitly stated) but the host door choice is not random. Thus the paper by Morgan et al is not relevant to the article, except as a special, and rather unrealistic, variation of the basic problem. Martin Hogbin (talk) 22:42, 23 November 2009 (UTC)

No, they don't. And just to make it clear, this article is about the variation where these are the defining points of the problem:

1. The car is placed randomly.
2. The contestant can choose any door.
3. The host must open a door that is randomly selected from all unopened doors that hide goats (this could be a choice of one door only).

This is the "K&W" problem. It is what the casual reader feels any version (unless explicitly contradicting some part of it, which Parade's version does not do) means. (Documentation: some of the scholarly references listed in the article are not as much about the Mathematics, as about the perception of the problem by readers. Falk and Fox & Levav, to name two.) It is teh problem Marilyn vos Savant (who is notorious for expressing problems in an amgiguous way, but assuming peoepl will only see one) assumed people would see, and so is what she answered. But the most general case, using Morgan's approach for what makes for a more "general" problem, has these defining ponts:

1. The car can be placed with a bias.
2. The contestant always chooses Door #1 (chosing other doors is a similar problem, but with different paramater values based on point #5 below).
3. The host can open an unchosen door with the car. If he does, the game ends immediately.
4. The host can open the contestant's door. If he does, the game ends immediately. (Note that revealing Door #3 has the car in the previous point is the same as revealing Door #1 has a goat here.)
5. The host has a set of biases that depend on the car placement and the contestant's choice.
6. The contesant knows this bias exists, but not what it is.
7. In the case of interest, the host actually reveals a goat behind Door #3.

Morgan and Gillman do not address this most general case, because the question "should the contestant switch" cannot be answered for it. Instead, they apply (whether they say so or not) the Principle of Indifference to the placement of the car, because to not apply it is "unlikely to correspond to a real playing of the game." I take that to mean either (A) that the car's placement cannot be observed to be biased in the past history of the game show, or (B) even if it could, the contestant's choice is uninformed about that history. Either criterion makes the Principle of Indifference apply.

They ignore point #4 but not point #3 which is essentially the same thing. And finally, they ignore the Principle of Indifference for how the contestant evaluates the host's choice, even though that is just as "unlikely to correspond to a real playing of the game." The host would no more want to (A) exhibit a bias than the stagehands would in placing the car, and (B) the contestant is just as uninformed about whether he is biased. So Morgan's problem is:

1. The car is placed randomly (Morgan assumes it, Gillman actually edited this into the problem he claimed "appeared in the Ask Marilyn column in Parade.)
2. The contestant always chooses Door #1 (chosing other doors is a similar problem, but with different paramater values based on point #5 below).
3. The host can open an unchosen door with the car. If he does, the game ends immediately.
4. The host cannot open the contestant's door.
5. The host has a set of biases that depend on the car placement and the contestant's choice.
6. The contesant knows this bias exists, but not what it is.
7. In the case of interest, the host actually reveals a goat behind Door #3.

The interesty in this "conditional problem" is that it restricts (not eliminates) the host's ability to trick her into switching, thereby reducing the probability she will win the car. Specifically, he can trick her if his strategy included the option to end the game without offering the choice to switch. Otherwise, her probability after switching goes up to at least 1/2 (from the 1/3 it was before he applied his strategy), and possibly more. It goes to 2/3 if she does not have any idea how he is biased. It goes to somewhere in the range of 1/2 to 1 if she thinks she knows something of his bias, and is trying to out-guess him.

These conclusions are not OR, they are contained in both Morgan's, and Gillman's, paper. They just are hard to read in the text because the authors were focused more on addressing the interesting issues, than on the problem from the contestant's point of view. The wiki article does a poor job (i.e., not at all currently) in separating out those issues. "The" answer to the probabiltiy after switching is 2/3 based on the K&W problem the article is about. JeffJor (talk) 17:08, 24 November 2009 (UTC)

Jeff, I am puzzled by your point 3 above - The host can open an unchosen door with the car. If he does, the game ends immediately. This possibility is excluded in what they call the vos Savant scenario. Martin Hogbin (talk) 17:34, 24 November 2009 (UTC)

Jeff is listing the range of problems the Morgan et al. paper addresses. Although it briefly mentions the possibility of the host opening a door and revealing the car, the majority of the paper addresses a problem (their interpretation of what vos Savant intended, based on her clarifications in Parade prior to the publication of their paper) which could perhaps be more simply expressed as having these defining characteristics:

1. The car is placed randomly.
2. The contestant has initially chosen a door (which we'll call door 1).
3. The host has opened a different door (which we'll call door 3) revealing a goat and is not precluded from having a bias if given a choice between two "goat doors".
4. The contestant, knowing which door was initially selected and now seeing two unopened doors and one open door showing a goat, can switch to the other unopened door.

I believe this differs from the K&R version only in that the K&R version adds the explicit constraint that the host must choose randomly between two goats if this comes up.

The main point of the Morgan et al. paper is that this is a conditional probability problem and should be approached as such. They use the unspecified host bias mostly to show that there is a difference between solving for the unconditional probability of winning by switching vs. the conditional probability of winning by switching given knowledge of which door was initially picked and which door the host opened. I believe most people understand the door 1/door 3 combination to be representative of the general solution, and (whether they realize it or not) erroneously evaluate the conditional probability in this case using the "equal probability" assumption (as described by Falk, and Fox and Levav). Whether the host has a bias or not, the probability of interest is the conditional probability. If you're an expert in probability theory, you can perhaps immediately see that unless the host has a bias the unconditional and conditional solutions must be the same - but (IMO) most people do not understand that these are different questions and consequently find an unconditional solution not very convincing since they're actually trying to solve the conditional problem.

The root question the article needs to address is WHY the 1/3 probability of the car being behind door 1 remains the same AFTER the player sees the host open door 3. The first step to understanding this is to understand that the probability after the host opens door 3 is a conditional probability. The second step is either to understand that this conditional probability is the same regardless of which door the player initially picks and which door the host opens and that this means the conditional probability (whatever it is) must be the same as the unconditional probability (which is trivial to compute), or to understand how to actually compute the conditional probability.

IMO, the article would be more clear if we explained the difference between the unconditional and conditional questions up front, and (perhaps) said the Monty Hall problem as generally interpreted intends for these two different questions to have the same answer. The problem is most published unconditional solutions make no mention of the unconditional and conditional questions, and only implicitly equate them (leaving open the question of what exact problem they are addressing).

Jeff - do you agree given more or less any set of Monty Hall rules that asking what is the (unconditional) probability of winning by switching is a different question than asking what is the (conditional) probability of winning by switching given which door the player picks and which door the host opens? If so, which question do most people think the Monty Hall problem asks? -- Rick Block (talk) 20:36, 24 November 2009 (UTC)

Martin, that point represents the parameter Morgan call p₂₂. They never use it explicitly in their results, but they do use p₂₃ and the identity 'p₂₂+p₂₃=1. So anytiem they discuss, p₂₃, they are using that point.

So, in Morgan's terminology, the scenarios are:

Marilyn vos Savant's actually-intended scenario: p₂₃=1 and p₁₃=1/2. Marilyn clarified both parts of that.

Their pedantic misinterpretation of Marilyn vos Savant's scenario: p₂₃=1.

Their general scenario: no restrictions of their stated paramaners.

The actual general scenario, alluded to in their conclusion, incldues a non-zero p₁₁.

Rick, I don't know how many different ways I can try to say this, but it is not getting through to you. The "given knowledge of which door was initially picked and which door the host opened" is useless to the contestant unless she knows both the value of q and which door is favored. Morgan's conclusions DO NOT use any such knowledge as a given. They only use the fact that, whatever q is in what they call the "vos Savant scenario," that specific strategy can't make the probability less than 1/2 by switching. They only answer teh quesiton "shoudl she switch," not "what is the exact probability if she switches?"

And the "door 1/door 3" combination IS REPRESENTATIVE OF the general solution, even if the the host is biased, because the contestant does not know which door is favored. Look at it this way: suppose the host says to the contestant "I am using Moragn's stratgey based on a q of..." and names a value. "But," he adds, "I won't tell you which of the two doors, #2 and #3, is favored this way." From the contestant's SoK, WHICH IS THE ONLY ONE RELEVANT TO THE PROBLEM, the exact probability of winning is 2/3. Fporm the host's SoK, it is either 1 or 0, since he knows where the car is. Nobody possesses the SoK where the probabiltiy is 1/(1+q). That wasn't Morgan's point.

I've got to go now - I'll get back later. JeffJor (talk) 21:21, 24 November 2009 (UTC)

We all seem to have fairly entrenched positions here so let me suggest that we leave the issue of conditional/unconditional for the moment. I agree that even if the host goat door choice is taken to be random, the problem can be treated as one of conditional probability. Whether this is necessary or desirable is another matter, which I suggest we leave for the moment.

This leaves the point that Jeff makes above, which is the same point that I made at the start of this conversation when I came here in response to the RfC. If we are answering the question from the state of knowledge of the player, and the player does not know the host door choice strategy (the value of the parameter q) then we must take host the choice of door (from those permitted by the rules) to be random. Rick, do you accept this? Martin Hogbin (talk) 23:11, 24 November 2009 (UTC)

I'll accept that if your goal is to determine a single numerical answer for the probability it is most sensible to take the host's choice (from those otherwise permitted by the rules) to be random, and that most people who pose this problem intend this to be the case. On the other hand, must is too strong. It's perfectly legitimate to leave this as a variable and to express the probability as a function of this variable. It is, in fact, helpful since (as Jeff notes) it can be used to show a specific player's chances never decrease. Saying the answer is "2/3" and saying it is "1/(1+q) for some unknown value of q" do not contradict each other. Both answers are right.

In Jeff's example above where the contestant knows q but not which door it pertains to, I'd say the exact probability is either 1/(1+q) or 1/(2-q). The total probability works out to 2/3 since the probability that it's 1/(1+q) is (1/3)(1+q) and the probability that it's 1/(2-q) is (1/3)(2-q), but saying you can simply ignore q in this case takes an argument of some form. If you're given conditions in the problem statement that you're ignoring, you really need to say why it's OK to ignore them. Ignoring them because you simply "know" they have no effect on the answer doesn't cut it.

Similarly, expressing the probability in terms of something that it depends on but is not constrained by the problem statement is not wrong but (I'd say) is actually a better answer. From the formula you can derive what the numeric average should be for a random set of trials, but it also can lead you to other factors that you could observe that might be important. -- Rick Block (talk) 01:42, 25 November 2009 (UTC)

No, Rick, "must" is not too strong. The ultimate question is "should the player switch," and that can only be evaluated in the player's SoK. And let me reiterate that there is no SoK where the probability is 1/(1+q), because the only SoK that includes any knowledge of a value for q - that is, the host's SoK - also includes the exact knowledge of where the car is. In that SoK, the probability is not a choice between 1/(1+q) and 1/(2-q), it is between 1/1 and 0/1.

Let me try another example by tweaking the problem to get certain results that might re-focus you. Suppose before the initial choice, the host says "The car has 50% chance to be behind #1, and a 25% chance to be behind #2 or #3." The contestant, naturally enough, chooses #1. The host then says "I will now open one of the other doors that does not have a goat. If both have goats, I will choose with a 75%/25% bias - but I won't tell you which is favored. You can then either keep your initial choice, or switch to the other closed door." He then flips two coins behind his back, and opens #3. Should the contestant switch? If my math is right, by your approach the chances are either 40% that switching will win, or 66.7%. In one possibility, the chances of winning go down; in the other, they go up, but by more than the other case's chances went down. But still, the player should switch. The possible probabilities 40% and 66.7% are not what is important to the contestant when making this decision, only the combined probability of 53.3%. (And incidentally, I did not say whether the assignment of the bias by the host is itself biased - it doesn't matter.)

The so-called "conditional solution" is only useful to answer the question "should the contestant switch" if every possible value that q could take (in my example, I made two possibilities) is weighted (as I did with the weights 25% and 75%), and the corresponding values for P(W_s|D3) are averaged. This is not possible to do, in general, as Morgan correctly points out. We can't know the weights. But since every P(W_s|D3) is at least 1/2 when the car is randomly placed, regardless of q, they can conclude that the weighted average is also at least 1/2, regardless of the weights. That means the player should switch regardless of any value q could take. Not because of a q, regardless of it. (And if you check my unbalanced scenario, it has the same property as long as neither door is associated with a q, even though some qs do make for a lower probability.)

Rick, you asked, given a specific host strategy, (1) if I thought whether asking for the "conditional" answer was different that asking for the "unconditional" answer, and (2) which one most people see in the Monty Hall problem. The fact that you have to ask either question shows that you haven't understood anything I've said. First off, I had just explicitly said that K&W, Marilyn vos Savant, the cited researchers who did psychological studies, and most people all see the problem, all see the only the "unconditional" problem unless it is explicitly stated how the "conditional" scenario applies. It IS the Monty Hall Problem. Anything else is a variation.

Second, there really is no difference between the two problems. The apparent difference is created by whatever boundaries are placed on what you want to call "one" specific host strategy. What you call "the unconditional solution" does allow for the host to have a bias, but it does not specify which door the host favors with that bias. So whatever q may be, the contestant sees two host strategies in your one: one with a split of q:(1-q) for the two unchosen doors, and one with a split of (1-q):q for the same doors. But the contestant sees them as equally likely, where you want to see only one as possible. Since these two strategies are indistinguishable to the contestant, the Principle of Indifference says they must have equal weights in the solution. So the contestant can replace those two host strategies with one, where she averages the two weights given to any specific door. The average of q and (1-q) is 1/2. So whether or not the host is biased, unless the contestant is told which door is favored, the contestant must treat the host as being unbiased.

Morgan, et al, and Gillman, and any others who address what you call "the conditional problem," are all adding additional boundaries to the host's startegies. By doing so, they create a set of strategies that cannot be used directly when answering the question. Their entire thesis is that no matter which of the strategies that fit in their boundaries is actually the case, the answer is still "switching is best." And now my entire argument can be encapsulated in one statement, so I will set it apart:

The formula that Morgan, et al, give for P(W_s|D3) is not an answer to the Monty Hall Problem. It is

the complete set of possible answers based on certain assumptions. Any one of them could be

the correct answer, keeping within their assumptions, if the contestant had more information.

But every answer that is correct, within their assumptions, is in that set. And every answer is

at least 1/2. So regardless of what additional information the contestant could gain, again keeping

within their assumptions, it will always be advantageous to switch.

They state, several times, that there is no need to assume the host is unbiased. They fail to recognize that, although that is one possible way to view the assumption being made, it isn't the actual assumption. The assumption, derived directly from the fact that the problem statement does not say which door could be favored, is that the contestant is unbiased in how she treats each door. Just like if you always choose "rock" in "rock, paper, scissors," but I don't know that and choose randomly, I have a 50% chance of winning. You are biased, by my assessment of your possible choices must be unbiased so I consider it a 1/3 chance that you will pick any of the three. The solution to the actual Monty Hall problem has to do the same. Even if the host is biased in opening doors, the contestant does not know how and so treats the host as unbiased. This isn't the same as saying he is unbiased.

And they make similar assumptions, in order to get their set of possible soluitions. Just not about the host's choice. They assume the car is randomly placed, which vos Savant never said, and whcih is similarly unnecessary It must be treated as unbiased because the contestant will choose any one with equal likelihood.

JeffJor (talk) 16:38, 25 November 2009 (UTC)

Rick, I agree with you that [my italics] "if your goal is to determine a single numerical answer for the probability it is most sensible to take the host's choice (from those otherwise permitted by the rules) to be random", but I am not sure what other goal one might have for a probability question. Of course it is possible to produce a general answer where we do not apply the principle of indifference to the choices about which we are given no information. If we represent all the unknown choices by parameters we simply find that the probability of winning by switching is from 0 to 1, depending on where the car was initially placed and which door the player chooses. Not a very interesting result. Martin Hogbin (talk) 17:04, 25 November 2009 (UTC)

Jeff - I believe I understand what you're saying perfectly well. I am on the other hand less than certain that you're understanding what I'm saying. Your opinion (or Martin's, or mine) about what IS the Monty Hall problem, no matter how fervently you believe it, is (from Wikipedia's perspective) original research and is not relevant to the content of the article. What is relevant is what reliable sources say. We have (of course) already discussed this on this page, and it's not even archived yet (see above, #What do the sources actually say).

Rick, I am not basing what I think the MHP "is" on OR. It is the expressed opinion of those who wrote it (MVS specifically), it is explicitly contained in the problem statement this article is based on, and it is what is used by many of the references. Do you disagree? With what? In all those versions, the car is placed randomly, the host's strategy is to always open a door, with a goat, and to pick randomly. They may not explain why they think "randomly" is included in there either once or twice; but they all do at least once, including Morgan and Gillman (who edited it into what he claimed was a quote). They never explain why. You may think my providing the reason for them is OR, but it is not. I'm just explaining what they assumed was so implicit they did not need to say it.

The question is never "what is the probability of winning?", it is "should the contestant in the problem switch?" Morgan answers that question IN STRAWMAN FASHION under a set of assumptions that they (not quite clearly) state, which include "car is placed randomly" and "host's strategy is to always open a door, with a goat, and to pick with a parametric bias based on door numbers." All they concluded is that under those conditions, switching is either a neutral choice or it improves the odds. They did not address how the contestant should know what q, becasue their conclusion did not require knowing q. Or say that their answer is "correct" for the MHP in general. And look at the second paragraph of their conclusions. They imply they are solving "the unconditional problem," but if you compare it to Grinstead and Snell, you will see that they are not. They are taking the two possible "unconditional" solutions and combining them is a way that becomes transparent to the contestant not knowing which door is favored; which is to say, they are putting the conditional solution into the SoK of the contestant. The answer they give for that SoK is 2/3.

And read that Grinstead and Snell. They state quite clearly that the probability for both the conditional and unconditional MHP, as stated, is 2/3. They just require different solution methods. To illustrate that, they apply a specific q=3/4 and so it is a different problem. It is a problem based on the MHP, but it not the MHP itself. The "before" and "after" bit you refer to is a red herring. The timing isn't what is important, it is the knowledge. If the contestant chooses to switch "before the host opens a door" = "without any knowledge of how the host may use door numbers to pick" then the probability is 2/3. That's what establishes the difference. Morgan implies this is the important difference when they talk about their anlysis only affecting "informed players." JeffJor (talk) 19:49, 25 November 2009 (UTC)

Martin - Strawman arguments are not helpful. The sources that introduce q don't "represent all the unknown choices by parameters", but rather a specific interesting one that highlights the difference between variants of the problem where the player might as well choose to switch before the host opens a door from those where the player specifically chooses after. IMO (to be clear, this is my opinion - not something from a published source) the difficulty most people have with the MHP is precisely because the point of decision is after the host has opened a door meaning most people treat it as a conditional probability problem. I definitely agree with Morgan et al. that whether the host is explicitly constrained to pick randomly between two goats, or whether we treat this choice as random because we don't know q, or whether we know q and which door it applies to "it [the MHP] is still a conditional probability problem". -- Rick Block (talk) 18:16, 25 November 2009 (UTC)

Rick, I thought we had agree to drop the conditional/unconditional argument for the moment. Yes. Morgan have, for reasons known only to themselves, chosen to address a specific interesting problem. But, as you have already agreed, there is only a difference between the case where the player chooses whether to swap or not before a door is opened and the case where they chose after it has been opened if the player knows the host door opening strategy. If the player does not know this, even though they may have seen which door was opened, '...it is most sensible to take the host's choice (from those otherwise permitted by the rules) to be random'. This gives exactly the same probability of winning by switching as in the case where the player chooses whether to switch or not before the door has been opened. Do you not agree?

What you call my strawman argument was intended simply to show the natural result of dis-applying the principle of indifference consistently. Martin Hogbin (talk) 19:34, 25 November 2009 (UTC)