Talk:Szilassi polyhedron
| This article is rated Start-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||||||||||||
| |||||||||||||||||||||
Photo
[edit]I have one of these, but I can't find it or my camera. Photo when both issues are resolved. All the best: Rich Farmbrough, 15:23, 26 June 2015 (UTC).
Genus in infobox
[edit]In the infobox, it says e.g. "Properties Nonconvex", but nowhere does it say "genus 1" or the like - wouldn't that be sensible?--Noe (talk) 09:53, 23 November 2008 (UTC)
- Go for it (as in WP:BB). Mhym (talk) 17:58, 23 November 2008 (UTC)
- I swapped out the template table so new rows can be added. I guess there's not many torus polyhedra on wikipedia, so the genus isn't given anywhere else I can think of immediately. Tom Ruen (talk) 00:56, 24 November 2008 (UTC)
- That's fine. I thought an other way would be to add it in the "Properties" box.--Noe (talk) 12:14, 24 November 2008 (UTC)
- The problem was there's about 100 polyhedra which use that template, so adding a field would have all the other copies blank. (I think there's tricks to smarter templates, but I only know simple ones like the one that was here.) Tom Ruen (talk) 01:27, 25 November 2008 (UTC)
- This is what I meant (see source, or see infobox on this talk page):
| Szilassi polyhedron | |
|---|---|
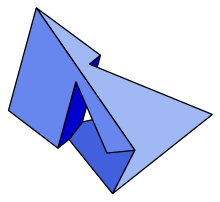 | |
| Faces | 7 hexagons |
| Edges | 21 |
| Vertices | 14 |
| Euler char. | 0 (Genus 1) |
| Vertex configuration | 6.6.6 |
| Symmetry group | ? |
| Dual polyhedron | Császár polyhedron |
| Properties | Nonconvex; Genus 1 |
--Noe (talk) 07:46, 25 November 2008 (UTC)
#Disputed
[edit]The section on complete face adjacency states that it is an open problem whether there is any polyhedron with the complete face adjacency property, other than the tetrahedron and the Szilassi polyhedron itself. Some quick searching, however, turns out the following website, which describes the faces of the duals of two other such polyhedra: [1]. I checked them myself, and after dualizing, I was only able to construct shapes with self-intersecting faces, but surely this doesn't exclude them from being valid geometric representations (and if it does, we should specify it).
Furthermore, one of them (the one with 9 faces) is non-orientable, and attains a fractional value of h = 2.5. The article seems to suggest that h must necessarily be a positive integer.
Surely these factual gaps could be filled if we had an actual citation to this section. Unfortunately, I can't find any. Hopefully someone else can make the claim on which polyhedra we know of with this property more precise. – OfficialURL (talk) 16:51, 22 August 2020 (UTC)
- Those are not geometric polyhedra, and your lack of knowledge of a different solution does not constitute an inaccuracy in the article's statement that no other solution is known. —David Eppstein (talk) 18:04, 22 August 2020 (UTC)
- (edit conflict) The phrase "realized geometrically" is undoubtedly meant to exclude self-crossings (and so also non-orientable surfaces) -- I think it is instructive to compare with the discussion at Polyhedron#Definition. There is no question that the link you gave does not answer the open problem. I agree with you that the sourcing of this article could be both better and more explicit. --JBL (talk) 18:06, 22 August 2020 (UTC)


