Talk:Monty Hall problem/Archive 16

This is an archive of past discussions about Monty Hall problem. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page.

Archive 10

←

Archive 14

→

A genuine attempt at compromise.

My POV is the Morgan paper is no more that a minor academic distraction from the real MHP, which is a mathematical puzzle in which the host is defined to open a legal door randomly and the issue of conditional probability is insignificant. However, in the interests of compromise, I will put this view to one side and adopt the position that conditional probability and, in particular, the host's choice of door when the player has originally chosen the car, is essential to a proper understanding of the problem. I will also accept that this view is fully supported by a multitude of reliable sources.

The question now becomes, 'How do we explain this position to our readers?'. I suggest that we should follow the model of many mathematical and technical text books and, bearing in mind how hard most people find any version of this problem when they first see it, start with a simplified (and possible strictly incorrect) solution and explanation of the problem. Note carefully that I am not suggesting that we start with a unconditional formulation of the problem because, even mention of the two possibilities that the player chooses after the host has opened a door or before he has done so, adds another layer of conceptual complication to the problem. What I am suggesting is that we ignore this point completely to start with. Nobody at first sight finds the legal door opened by the host to be significant.

Again, I draw the parallel with text books. Mathematicians can be as rigorous and pedantic as you like when they put their minds to it but if they adopted this approach in books on most mathematical topics the intended readers would not get beyond the first page before giving up. Strictly speaking, Newtonian physics is wrong, but it is still taught in all schools and colleges. I am not against trying to use the K&W paper to help us or trying to keep the errors and omissions to a minimum, but not at the expense of clarity. Let me add that many books have a page of problems after the first introductory chapter to ensure that the reader has understood so far. We should do similarly and have a 'Aids to understanding' section before discussing complicating issues.

Now you may see this as a dirty trick to get my own way by subterfuge but actually it is a way that works for everybody. We have what is undoubtedly one of the world's most difficult simple puzzles, which even famous mathematicians have got wrong. Do we really want to start our article by making the problem harder? Martin Hogbin (talk) 13:34, 12 May 2010 (UTC)

And my genuine attempt at a compromise is the following proposal which I think satisfies what you're suggesting (other than the "aids to understanding" - more on this below). It starts with two simplified explanations of the solution to the problem, both ignoring a precise definition of the problem, almost exactly like the presentation in Grinstead and Snell (a textbook). It doesn't say these simplified explanations are wrong, but it does attempt to say what it is that they actually say. Is this what you object to about this proposal?

Why I object to putting the "aids to understanding" section between the simple solutions and the conditional solution is that it implies, by the structure of the article (see WP:STRUCTURE), that the "simple" solutions are correct and undisputed. You say you're willing to put your POV aside and "adopt the position that conditional probability and, in particular, the host's choice of door when the player has originally chosen the car, is essential to a proper understanding of the problem" - but then what you're suggesting doesn't do this. Instead, it puts the simple solutions and the conditional solution on unequal footing, separated by a lengthy "aids to understanding" section. Unless the "other" view is contextually nearby, whatever view is presented first (more or less) becomes the de facto view of the article. This is apparently a common enough POV issue that it's even mentioned in the NPOV policy page. You might think I'm raising NPOV as a dirty trick to get my way - but I'm already not getting my way (my actual preference would be to start with a conditional solution and put all the simple solutions in "aids to understanding"). Treating this as a POV issue seems to me like the most reasonable compromise.

I understand your concern about the understandability of the simple solutions, but I think it is misplaced. No one fails to understand what these solutions literally say. What people fail to understand is how these solutions connect to their mental image of picking door 1 and then standing in front of two closed doors after the host has opened door 3. The fact is the simple solutions simply do not address this case (but the conditional solution does

), i.e. it's not understanding these solutions that's difficult, it's mentally redefining the problem so these solutions apply (specifically that the overall chance of winning by switching, which the simple solutions clearly show is 2/3, must be the same as the chance in any individual case). So, again, my suggested compromise is we present both kinds of solutions, as neutrally as we can manage, but immediately adjacent. My strong preference is to have them in a single "Solution" section, like below. This is changed slightly from the previous version in an attempt to connect the simple solutions to the mental image most people create based on the problem description. -- Rick Block (talk) 16:25, 12 May 2010 (UTC)

Proposed text

Solution

Different sources present solutions to the problem using a variety of approaches.

Simplest approach

The player initially has a 1/3 chance of picking the car. The host always opens a door revealing a goat, so if the player doesn't switch the player has a 1/3 chance of winning the car. Similarly, the player has a 2/3 chance of initially picking a goat and if the player switches after the host has revealed the other goat the player has a 2/3 chance of winning the car. (some appropriate reference, perhaps Grinstead and Snell)

What this solution is saying is that if 900 contestants all switch, regardless of which door they initially pick and which door the host opens about 600 would win the car. Assuming each specific case is like any other, this means a player who initially picks Door 1 and sees the host open Door 3 wins the car with a 1/3 chance by not switching and with a 2/3 chance by switching.

Enumeration of all cases where the player picks Door 1

If the player has picked, say, Door 1, there are three equally likely cases.

Door 1	Door 2	Door 3	result if switching
Car	Goat	Goat	Goat
Goat	Car	Goat	Car
Goat	Goat	Car	Car

A player who switches ends up with a goat in only one of these cases but ends up with the car in two, so the probability of winning the car by switching is 2/3. (some appropriate reference, perhaps vos Savant)

What this solution is saying is that if 900 contestants are on the show and roughly 1/3 pick Door 1 and they all switch, of these 300 players about 200 would win the car. Assuming the cases where the host opens Door 2 or Door 3 when the player picks Door 1 are the same, this means a player who initially picks Door 1 and sees the host open Door 3 wins the car with a 1/3 chance by not switching and with a 2/3 chance by switching.

The probability of winning by switching given the player picks Door 1 and the host opens Door 3

This is a more complicated type of solution involving conditional probability. The difference between this approach and the previous one can be expressed as whether the player must decide to switch before the host opens a door or is allowed to decide after seeing which door the host opens (Gillman 1992).

The probabilities in all cases where the player has initially picked Door 1 can be determined by referring to the figure below or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138 presents an expanded tree showing all initial player picks). Given the player has picked Door 1 but before the host opens a door, the player has a 1/3 chance of having selected the car. Referring to either the figure or the tree, in the cases the host then opens Door 3, switching wins with probability 1/3 if the car is behind Door 2 but loses only with probability 1/6 if the car is behind Door 1. The sum of these probabilities is 1/2, meaning the host opens Door 3 only 1/2 of the time. The conditional probability of winning by switching for players who pick Door 1 and see the host open Door 3 is computed by dividing the total probability of winning in the case the host opens Door 3 (1/3) by the probability of all cases where the host opens Door 3 (1/2), therefore this probability is (1/3)/(1/2)=2/3.

Although this is the same answer as the simpler solutions for the unambiguous problem statement as presented above, in some variations of the problem the conditional probability may differ from the average probability and the probability given only that the player initially picks Door 1, see Variants below. Some proponents of solutions using conditional probability consider the simpler solutions to be incomplete, since the simpler solutions do not explicitly use the constraint in the problem statement that the host must choose which door to open randomly if both hide goats (multiple references, e.g. Morgan et al., Gillman, ...).

What this type of solution is saying is that if 900 contestants are on the show and roughly 1/3 pick Door 1, of these 300 players about 150 will see the host open Door 3. If they all switch, about 100 would win the car.

A formal proof that the conditional probability of winning by switching is 2/3 is presented below, see Bayesian analysis.

Car hidden behind Door 3	Car hidden behind Door 1		Car hidden behind Door 2
Player initially picks Door 1

Host must open Door 2	Host randomly opens either goat door		Host must open Door 3

Probability 1/3	Probability 1/6	Probability 1/6	Probability 1/3
Switching wins	Switching loses	Switching loses	Switching wins
If the host has opened Door 3, these cases have not happened		If the host has opened Door 3, switching wins twice as often as staying

I like the concept of your first solution although I might want to change the wording little. The 'explanation' of the explanation (second paragraph) is in my opinion confusing and pointless. Why mention which door the host opens. By mentioning this you actually bring attention to the thing you want to ignore. It is like saying, 'ignore for the moment that the host says the word "door"', it leaves the reader wondering why they should ignore that fact. More later. Martin Hogbin (talk)

The point of the second paragraph (and there's something like this for each) is to clarify what each of the solutions is saying (in frequency probability terms - using the same sample space of 900 contestants who make their initial pick randomly) and to connect the solution to the example situation described in the problem statement where the player has picked door 1 and the host has opened door 3. For example the first one says nothing about what door the player picks or what door the host opens. It therefore applies to the entire sample space, so the probability it's talking about is literally the average probability of winning by switching. However it also applies to the example case given in the problem description if you assume symmetry, i.e. any individual case is the same as any other individual case (we really shouldn't say this without a reference, but it's certainly true). If you're thinking about the example situation from the problem statement, without this paragraph this solution sounds like a non sequitur. It's like a zen lightbulb joke - Q: How many zen masters does it take to change a lightbulb? A: A tree in a golden forest. It's perhaps not quite this extreme, but the connection between this solution and the example case is far from obvious. The intent is to make the connection explicit. -- Rick Block (talk) 04:32, 13 May 2010 (UTC)

If your aim is to show how well we all understand the subtleties of the problem then you idea may have some merit but I believe that our aim should, in the first instance, be to explain clearly to the reader why the answer is 2/3 and not 1/2. At this stage we really do not want to confuse the reader by comparing the sample spaces of different problem formulations. You seem determined to go straight into Morgan's argument, or at the very least prepare the reader at the start for it.

Regarding your comment about structure, I agree that to put an 'Aids to understanding' section immediately after a section which describes only the simple problem gives the impression that the simple solution is the only solution and the complete solution. At least it would if we did not state clearly in the next section that this is not the case. In this case, the subtle impression given by the structure is obviously overruled by the clear statement that we later make. Martin Hogbin (talk) 07:05, 13 May 2010 (UTC)

The new 'improvements' seem to have mangled your formatting, Rick. Martin Hogbin (talk) 07:05, 13 May 2010 (UTC)

By the mangling you mean issues (with the large table/figure at the end?) due to the new skin? Looks OK to me. What browser and OS are you using?

Seems OK now. Martin Hogbin (talk) 22:26, 13 May 2010 (UTC)

Regarding aim - a simple question for you. Can we convince the reader the answer is 2/3 vs 1/2 with a simple solution without also convincing the reader the POV the simple solution is based on is the "right" POV? Seems like this might be part of the fundamental source of our conflict. If we're treating the approach to the solution as a POV issue, I think all we actually need to convey is what the sources say - as inarguable facts, e.g. "vos Savant says the answer is 2/3 because ..." - and let readers draw their own conclusions. This is a subtle difference in presentation. We're not stating facts (the speed of light is 186212 miles per second) which are then referenced to a source, we're describing what different sources say more like what they say are opinions. Convincing someone vos Savant says the answer is 2/3 should be fairly easy. Convincing someone vos Savant's answer is factually correct might be considerably more difficult, but frankly why would we care? -- Rick Block (talk) 20:45, 13 May 2010 (UTC)

I think you want to treat this page more like a literature survey than an encyclopedia article. We can structure the article the way that we think best serves the purpose of convincing the reader, provided that the solutions are based on reliable sources. Martin Hogbin (talk) 22:25, 13 May 2010 (UTC)

No, since we're not apparently going to agree on what the "truth" is I've concluded the only feasible approach is to treat it like a POV issue. This is the approach I'm aiming for with the proposal above. Different sources say different things, some sources say <the first thing>, some say <the second thing>, some say <the third thing>. The article is not picking which one is "right" - and the reader doesn't have to either. Anyone can verify the article actual says what the sources say. Whether they find the explanation some source gives convincing or not is really irrelevant. Maybe they'll understand the problem the way vos Savant explained it. Maybe they'll agree that a conditional view is a better match for how they're thinking of the problem. Not forcing the article (or the reader) to agree with the content is a fairly standard technique to achieve NPOV. Treating a math problem this way feels very odd, but I think it may be the only choice we have. -- Rick Block (talk) 05:04, 14 May 2010 (UTC)

I have already said that, for the sake of this discussion, the 'truth' is what many academic sources say, which is that the door number opened by the host when the player has originally chosen the car is important. Even so, it would seem to me that, as editors, we can choose to structure the article with the simplest (but strictly speaking wrong) solutions first. There can be do doubt that the biggest problem that most readers will have is understanding why the answer (in any formulation or from any POV) is 2/3. We should therefore start by making sure that the reader fully understands this fact before complicating the issue with host legal door choice. Some readers may stop reading after reading about the simple solution. That would be their choice and has nothing to do with my POV. Martin Hogbin (talk) 10:05, 14 May 2010 (UTC)

Right, you've said this but you're unwilling to act on it. You're not even willing to give this POV equal treatment. Instead, you want the article to convincingly say the answer is 2/3, based on a simple solution, forcing (with great difficulty, per K&W) the reader to change their mental model of the problem from one where they're imagining having picked door 1 and having seen the host open door 3 (consistent with a conditional answer) to one where what's important is the overall chance of winning by switching. Something like:

The problem's simple - just ignore the part about picking door 1 and seeing the host open door 3 and focus instead on the overall probability of winning by switching. When you initially pick a door you have a 1/3 chance of picking the car. If you don't switch you win the car 1/3 of the time. You have a 2/3 chance of initially pick a goat, in which case if you switch you win the car (2/3 of the time). So you win the car 1/3 of the time if you don't switch and 2/3 of the time if you do switch. What could be simpler?

If you're conceding the door number opened by the host when the player has originally chosen the car is important, the initial intuitive solution could be more like this:

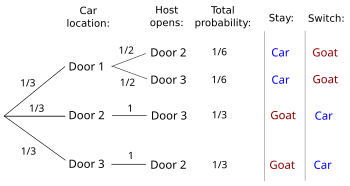
When you initially pick door 1 you have a 1/3 chance of picking the car. If the car is behind door 1 the host can open door 2 or door 3, so the chance the car is behind door 1 and the host opens door 3 is only half of the chance the car is behind door 1, i.e. 1/6. On the other hand if the car is behind door 2 the host must open door 3, so the chance the car is behind door 2 and the host opens door 3 is same as the chance the car is behind door 2, i.e. 1/3. So, if you've seen the host open door 3, you win the car 1/6 of the time if you don't switch and 1/3 of the time if you do switch. Similarly, if you've seen the host open door 2, you win with a 1/6 chance if you don't switch and a 1/3 chance if you do. No matter which door you see the host open, you win twice as often by switching - with probability 2/3 rather than 1/3.

Well, I can follow that because I have been discussing the problem for years but the average reader who is not familiar with the problem is going to find that hard going. Martin Hogbin (talk) 17:24, 14 May 2010 (UTC)

I'm not insisting we omit the "ignore the example case" kind of solution. However, I will offer the observation that we know people resist this sort of solution. If your primary goal is to convince people the answer is 2/3, starting with a solution that requires them to ignore the example case they're almost certainly thinking about may not be the best approach. The fact that you see these solutions as simple doesn't mean someone who may not be understanding the problem the same way you do can easily grasp them. In particular, your assertion that paying attention to the door numbers is an unnecessary complication seems to me to be rooted in the way you're understanding the problem. -- Rick Block (talk) 15:23, 14 May 2010 (UTC)

I looks like we both see K&W's paper differently. They say: Note that participants are only able to provide the intuitive solution (see Figure 1) if the specific number of the door that Monty Hall actually opens is not taken into account. The easiest way to make sure that the participants' reasoning processes are not impeded by knowing which door Monty opens is simply not to give them this information. Figure 1 does not show door numbers. Martin Hogbin (talk) 17:24, 14 May 2010 (UTC)

Exactly. They're talking about presenting the problem (not the solution) in a way that naturally leads to the "simple" solution. The way the problem is usually phrased includes the example where you've picked door 1 and the host has opened door 3. What they're saying is when presented this way (the usual way), the participants are not able to provide the "intuitive" solution. By the time they even start thinking about the problem, it's too late (because the typical wording includes the example). The simple solution is not simple to grasp if you start with the usual wording of the problem. -- Rick Block (talk) 21:36, 14 May 2010 (UTC)

Then that is what we need to do here, provide a simple version of the problem (no door numbers) followed by a simple solution (as you in fact do). This is what people understand most easily. Probably we need several simple solutions to the simple problem, but then we need to make absolutely sure that they have understood the solution by having an 'Aids to understanding' section.

After we have done this we can say something along the lines of ' Some sources take the question to refer to specific identifiable doors ...' and move on the the Morgan interpretation. This could have its own 'Aids to understanding section' to explain the issues raised by Morgan. Martin Hogbin (talk)

It seems to me that you are determined to keep the article as it is whatever the evidence or logic for changing it. Clearly this attempt at compromise is not going to work. Martin Hogbin (talk) 17:24, 14 May 2010 (UTC)

Now wait a minute. I'm suggesting we make a major change (from the current article) and incorporate both "simple" and conditional solutions in one combined, NPOV, solution section, and have drafted at least two rewrites. You're suggesting we re-order a couple of sections to keep the conditional solution further away from our simple minded readers who won't be able to understand it. I'm very unhappy with the article as is. Saying I'm determined to keep the article in its current form couldn't be further from the truth. I think we both agree it should be changed. What we disagree about is how. -- Rick Block (talk) 21:36, 14 May 2010 (UTC)

Yes, we do both want to change the article but it would seem in completely incompatible ways. I as a compromise, I have suggested that we start with a complete section using only simple solutions, with no complications of the legal door number chosen by the host and then move on to discuss the conditional case. I was hoping for a quick win (for both sides) but it looks a though that is not going to happen. Martin Hogbin (talk) 10:39, 15 May 2010 (UTC)

In what way is what you are suggesting a compromise? What I'd actually prefer is to start with a main solution that explicitly addresses the (conditional) case where the player picks door 1 and the host opens door 3 (per the Parade version of the problem statement) and move the simple solutions to the "aids to understanding" section. I'm willing to compromise and put both simple solutions and a conditional solution in the same solution section in an NPOV manner. If what you're suggesting is a compromise, what is your actual (non-compromise) preference? -- Rick Block (talk) 19:06, 15 May 2010 (UTC)

I would like to see Morgan's solution relegated to a section on academic diversions. This is a long-held view of mine which is explained in detail on my Morgan criticism page.

Imho, "... and this simple solution distributes equally over any and all door selection and door revealed pairings." does address the conditional problem. Glkanter (talk) 15:11, 16 May 2010 (UTC)

Yet another draft of an NPOV solution

I've drafted yet another version of a merged solution section, see User:Rick Block/MH solution. Again, the intent is to be scrupulously NPOV. The suggestion is to replace both the "Popular" and "Probabilistic" solution sections, with other content from both of these sections moved elsewhere. -- Rick Block (talk) 22:29, 16 May 2010 (UTC)

This seems to be just your usual idea. Confuse the reader with conditional probability as soon as possible. Martin Hogbin (talk) 22:48, 16 May 2010 (UTC)

No, the idea is to present an understandable simple solution (specifically vos Savant's), but to mention right up front that it's not the one and only way sources approach the problem. Is there additional text you think is necessary to make vos Savant's solution more convincing, or the conditional solution less confusing? Suggest away. As long as you keep it to a paragraph or two I think I'll be fine with it although I've tried to reduce both approaches to their essence without any unnecessary fluff. If the simple solution requires pages and pages of explanation to make it understandable, then I think we should defer the explanation to an "aids to understanding" section (and, BTW, if this is the case in what universe would we regard this as a "simple" solution?). -- Rick Block (talk) 23:56, 16 May 2010 (UTC)

The References!!!

While I agree with a lot of what Martin has said, I would not go so far as to say that Morgan is just a diversion. I do however feel that people are misinterpreting the effect Morgan's paper had on the academic world. I feel that Morgan's paper drew a lot of attention not because of his math, but because of his psychology. in the papers that cite Morgan almost all refer to his handling of the psychology of the MHP, not his math. I think this is a point that got buried during the "mediation". While I agree that the conditional approach has produced references and genuine scholarly discussion, and therefore should remain in the article, I feel it is demonstrably much less than the unconditional version. "well then demonstrate it!" you say? OK, Read the first ten, no twenty, papers brought up by google when you search for papers that cite Morgan and count how many cite Morgan as a reference for the psychological response to the unconditional version and how many cite him while discussing the conditional version. better yet, check all the papers that mention the MHP at all and count how many are psychology papers discussing the reasoning people use based on the unconditional version. you will see that those papers, together with the mathematics papers that deal solely with the unconditional version, far outweigh those that deal with, or even mention, the conditional version!

This has been my problem with this discussion from the beginning, far too much impetus is put on the math. WP enforces its guidelines and policies based on the amount of coverage a topic receives in scholarly papers and trusted news sources whenever they are available. If you look at scholarly papers and trusted news articles that discuss the MHP the vast majority refer to the unconditional version, because the psychology papers and news articles count too! The math is irrelevant! It does not in anyway matter who is right mathematically, all that matters is the weight of popular coverage. That being the case, the fact that the unconditional version should be the version most covered by this article is, as far as I am concerned, indisputable. Colincbn (talk) 15:09, 16 May 2010 (UTC)

One of the problems of this discussion is that apparently false points get iterated over and over in different nuances and evidence to the contrary is simply ignored. The claim that "unconditional only" treatments by far outweigh the others is simply not true, at least not as far as reputable/academic resources are concerned (the rest is irrelevant for WP). The main psychological paper used in the article deals extensively with the conditional solution. And of course are not all generally somewhat reputable sources treated in the same manner, but their area of expertise and the domain matters greatly. We are not writing articles on science subjects based on what most reputable newspapers might write about the subject, but we use scholarly science literature of the concerned domain instead. That means as far as this article is concerned, that for the math part/aspects we mainly rely on scholarly math literature and for the psychological aspects, we rely on scholarly psychology papers. But we do not take the math form the psychology papers and the psychology from the math papers, that's essentially a no go. This is an encyclopedia and not a popularity contest or the yellow press.
The overemphasis of math in article has obviously something to do with the nature of the problem. However nobody is kept from writing sections dealing with other aspects than that (psychology, social sciences, economics, etc.) in fact it was suggested several times that this could/should be done. But that has nothing to do with the core disagreement that's being discussed here ad nauseam.

--Kmhkmh (talk) 16:19, 16 May 2010 (UTC)

Kmhkmh, you say The claim that "unconditional only" treatments by far outweigh the others is simply 'not true, at least not as far as reputable/academic resources are concerned. Do a Google search on the MHP and you will see that the simple treatment is far more common than the 'conditional only' treatment. Of course if you restrict your search to academic sources only you get, unsurprisingly, only answers to the academic ('conditional only') question. WP is based on reliable sources, most of the sources found by a Google search are reliable by normal WP standards. You have imposed an arbitrary restriction on sources to get the answer that you want. Martin Hogbin (talk) 16:28, 16 May 2010 (UTC)

First of of all a plain Google search (aka websearch) produces ton of unreliable sources and is utterly useless in that regard. Google Scholar or Google Books searches however have some merit and contain at least a large percentage of reputable sources. Second there is nothing arbitrary here, I explained above that the domain matters. You cannot simply assess sources by some general notability notion independent of the domain. We do not use the New York Times as a primary source for a physics article, just we because the New York Times is a reputable newspaper in general, instead we use scholarly physics literature (textbooks, monographies, journal publications, etc.) on subject. Similarly we do not use a reputable scholarly social science publication as a primary source for the physics article either. Putting forward the notion, that the domain doesn't matter is imho an utter misrepresentation of the WP guidelines and defies common sense as well. In the context of this discussion it is most likely just a smokescreen to justify POV-pushing. In any case a domain unaware treatment of sources is a nogo and there there isn't really anything to argue or negotiate on that issue. It's simply unacceptable for an encyclopedia - plain and simple.--Kmhkmh (talk) 17:19, 16 May 2010 (UTC)

I don't agree that you get only "conditional" papers from an academic search. You get a mountain of psychology papers that use the unconditional version, and some math papers that reference both, and a very small number that use the conditional version only. What is "The MHP" is the problem we have been having. I propose that it is not a question defined solely by mathematics but by psychology as well. And more importantly by the academic papers that discuss it, regardless of the field the papers are written in (Oh and the myriad of trusted news articles that most readers will have come to learn about the problem from). Also I think many of the articles that are being considered as "covering the conditional problem" are in fact only giving and example of the unconditional version, such as: "for example, you chose door b/ the red door/ the square door/ door one/ etc. and the host chooses...", but this can be easily explained by using Glkanter's sentence "... and this simple solution distributes equally over any and all door selection and door revealed pairings" after the unconditional explanation. And may I say that neither your nor I can pick and choose what sources we use as long as they all fall under WP guidelines for reliable sources, that is the heart of NPOV, and is why Morgan and those who cite him must be represented. Colincbn (talk) 16:53, 16 May 2010 (UTC)

First of all I did not suggest (and would not since it is false) that you get only "conditional papers" from academic research. I merely pointed out that your claim was false. Of course it is not a problem that's only defined by math, but again usually we do not use psychology papers for the math part but for psychological aspects instead. You can basically use all academic papers on MHP and of course consider/describe non math aspects or treatments of MHP, but you need to consider their domains as well. A domain unaware usage of sources is, as said above already, an utter misrepresentation of the WP guidelines and unacceptable for an encyclopedia - period. --Kmhkmh (talk) 17:19, 16 May 2010 (UTC)

I wrote the my last paragraph before reading the sentence Kmhkmh added to the end of the paragraph above (which is totally fine). You are of course correct that math papers should be used when discussing math, and that is why I have always maintained that the article must contain information about the conditional version as represented by Morgan. However I am much less concerned with the math than with how the MHP is defined in the academic world at large. I do not think it is solely the domain of mathematics, and as far as I can see the simple version is by far the most common one cited in reliable academic sources. Colincbn (talk) 17:34, 16 May 2010 (UTC)

Yes it is not only in the math domain and as i said there's no problem with describing other aspects of the problem. It is also possible to describe the treatment in the academic at large as long as it doesn't turn into WP:OR. However the article needs to be clear what it is talking about at a given time, i.e. it should not pretend to the reader to talk math while it in fact talks psychology or something else.--Kmhkmh (talk) 17:56, 16 May 2010 (UTC)

What is meant by "version"? The statement of the problem that is by far most often cited is the Parade version. No argument. Whether "unconditional" solutions (solutions that mathematically solve P(win by switch|player picks door 1) as opposed to P(win by switch|player picks door 1 AND host opens door 3)) are "by far" most often offered is less clear. Are you (Colincbn) claiming you've actually surveyed the literature and have observed unconditional solutions are "by far the most common cited" in academic literature? It seems to me the last time we talked about how many and which sources say what, the general agreement was most popular sources present an unconditional solution, most academic sources present either only a conditional solution or both unconditional and conditional solutions, and a significant number of academic sources (not just Morgan et al.) explicitly criticize unconditional solutions. The best way to handle this in an NPOV manner is I think what we should be talking about. Having the article be dominated by what popular sources say doesn't seem to me to even remotely reflect a "neutral point of view, representing fairly, proportionately, and as far as possible without bias, all significant views that have been published by reliable sources" (as required per WP:NPOV). -- Rick Block (talk) 18:18, 16 May 2010 (UTC)

It seems that in the term "popular sources" you include the "reliable academic sources that are not specifically papers written about the math", but I argue that reliable third party sources, regardless of what field or domain they come from, show how the question and solution are defined by the academic world as a whole. You said "Having the article be dominated by what popular sources say doesn't seem to me to even remotely reflect a "neutral point of view"", but have you forgotten NPOV#Undue weight and NPOV#Balance? It is unbalanced and biased to define the MHP based solely on the math (and only the math you happen to agree with for that matter) instead of looking at the broader picture of how the MHP is defined by the entire academic world. Because, as I said above, the psychology and news articles count too, all reliable sources do, picking and choosing only the ones you like, or that agree with your arguments is the very definition of POV pushing. Colincbn (talk) 03:05, 17 May 2010 (UTC)

Again, have you surveyed the literature? I'm well aware of undue weight and balance. I think we simply disagree about the prevalence of sources presenting each kind of solution, and I'm not including non-math academic sources in "popular sources". -- Rick Block (talk) 03:52, 17 May 2010 (UTC)

Yes, yes I have. And I am not suggesting we remove any content from the article. I am simply pointing out that the majority of academic sources, and this of course includes non-maths sources, use the simple/unconditional version of the problem and never bring up conditional probability. Therefore this simple version should be more prominent in the article. Conditional probability can come later, not to hide or bury it, but to put it in the most logical place considering what the most accepted form of the problem is. Besides there is no page on 1+1=2, or 1+2=3, the only reason there is an MHP is because of the psychology of why people get it wrong, therefore if anything the psychology should take the lead in defining the problem. Colincbn (talk) 04:09, 17 May 2010 (UTC)

Just for the record, the impression you've gotten from your surveying of the literature does not at all match my impression from surveying the literature. In particular, I dispute your claim that the number of sources that "deal solely with the unconditional version, far outweigh those that deal with, or even mention, the conditional version". At one point Martin said he'd accept that the conditional version is as mainstream as the unconditional if I could produce 100 references (he has since said he'd concede this point "in the interests of compromise"). Would that be enough to convince you as well? Rather than 100, how about as many sources that present an unconditional solution as you can find? Or how about if we agree that squabbling about this is silly, that both approaches are common, and that if one is used in (say) 200 sources and the other in only (say) 100 that they're still both common? -- Rick Block (talk) 23:38, 17 May 2010 (UTC)

Ok if I can find more that use the simple solution will you stop blocking the advancement of this article? I'll do that. However I feel that after I do you will simply try to discount the sources I use.Colincbn (talk) 00:17, 18 May 2010 (UTC)

Like I say in a thread below, and like Kmhkmh says above in this thread, NPOV is about more than counting references. I wasn't seriously suggesting we compare source counts. I was seriously suggesting that this would be silly and that we should agree both approaches are common. If you're not willing to agree with this then I suggest we ask the mediator for help. Another possibility would be to get some opinions at Wikipedia:Neutral point of view/Noticeboard. -- Rick Block (talk) 02:42, 18 May 2010 (UTC)

I honestly think we might have to count references eventually. Unless you agree that the simple/popular solution is more common in relaiable sources, if you include non-maths sources. Colincbn (talk) 02:59, 18 May 2010 (UTC)

NPOV is sometimes difficult to get right. You might be interested in Wikipedia:NPOV tutorial#Expertise. This is what Kmhkmh is referring to above. Sheer number of references aren't generally a good way to determine weight, although the fact that significant numbers of sources all take the same POV is sufficient to show that a POV is not crackpot (which is essentially how Martin has been characterizing what he calls the "Morgan POV" for several years). I'm fine with presenting a "simple" solution first. All of my draft proposals do this. What I"m not fine with his Martin's insistence that the conditional viewpoint be marginalized and that the article endorse the POV he favors. -- Rick Block (talk) 04:40, 18 May 2010 (UTC)

I suppose our only real disagreement is that I don't think it is marginalizing to place the conditional solution into a separate section dealing with the math on a more in-depth level. I realized long ago that using the term "variants" or anything else that implies that there is "one true solution" is unacceptable. And I realize that the wording of the article must be thoroughly thought out in order to avoid promoting one version of the math over any other. I just feel that explaining the math simply and leading with the paradoxical nature of the problem first makes the most sense structurally. I don't even have a problem with letting people know before the simple explanation that there are several ways to look at the math. Colincbn (talk) 06:26, 18 May 2010 (UTC)

Logical Fallacy

Not Agreeing With Rick = Violation of Wikipedia NPOV

Glkanter (talk) 04:52, 18 May 2010 (UTC)

It's No Longer 'Which Problem?' It's 'Which Solution?'

With the symmetrical conditional solution being provided by the 'unconditional', or 'omniconditional' solution, which could include "...and this simple solution distributes equally over any and all door selection and door revealed pairings", the debate is no longer about which MHP is being solved. They're both the same.

The question is how to best present the material. Glkanter (talk) 23:52, 16 May 2010 (UTC)

Yes, and "best" includes "fairly, proportionately, and as far as possible without bias, all significant views that have been published by reliable sources" (quote from WP:NPOV). Ignoring or otherwise marginalizing sources which present solutions based on conditional probability isn't representing their view fairly, or proportionately. -- Rick Block (talk) 00:09, 17 May 2010 (UTC)

Of course. That goes without saying. I have never insisted that any reliable source should be excluded. And no editor owns a monopoly on NPOV. We're all capable, and have demonstrated so, of editing in such a manner. And I suggest there should be no further presumption of 'guilt/intent of violating NPOV' being bandied about without cause. Glkanter (talk) 00:15, 17 May 2010 (UTC)

Do you have an opinion on User:Rick Block/MH solution? -- Rick Block (talk) 00:56, 17 May 2010 (UTC)

Fully concur with Martin's response. Glkanter (talk) 01:32, 17 May 2010 (UTC)

Alright. Same question for you that I asked Martin. Is there additional text you think is necessary to make vos Savant's solution more convincing, or the conditional solution less confusing? Please suggest away. -- Rick Block (talk) 02:43, 17 May 2010 (UTC)

Once again I agree with Glkanter. I feel the page Rick made above at User:Rick Block/MH solution shows the MHP Problem in a nutshell. You have defined the popular/simple/unconditional version of the MHP in two short sentences with only a small table as a visual aid. This is a good thing. It is concise and easy for anyone, even those of us who are not mathematicians, to follow. Well done. You then go into a long two paragraph explanation of the conditional version that serves to confuse the hell out of anyone who is not familiar with probabilistic maths. Thereby making the article almost totally inaccessible to those who came to it through reading about paradoxes(like me), psychology, bar games, or any other of the many areas that use the MHP. When all you really needed to do was to add Glkanter's sentance: "...and this simple solution distributes equally over any and all door selection and door revealed pairings" after your simple explanation. Colincbn (talk) 03:21, 17 May 2010 (UTC)

Another explanation of my proposed NPOV solution

The concept shown on Rick's solution is fine, but it does not go nearly far enough. Let me repeat a line from the lead of this article: 'Even when given a completely unambiguous statement of the Monty Hall problem, explanations, simulations, and formal mathematical proofs, many people still meet the correct answer with disbelief'. We need to give the new reader as much help, and as little unnecessary complication, as possible in order to overcome this problem. Thus my proposed NPOV organisation would be

The lead

Fine as it is.

Simple solution section

This must make every effort to convince the new reader that the answer to the problem is 2/3 and not 1/2 by using a variety of simple solutions, (all supported by sources).
There must be no confusion of the reader with statements along the lines that these solutions are incomplete, or do not answer the question as asked, or answer only the unconditional formulation of the question (even if we accept that this is the case).
There must be no mention of the fact that the host has a choice of door when the player has originally chosen the car, this choice should not be shown in any diagrams.

Aids to understanding

Much as it is now, this section must concentrate on the helping the reader understand why the simple solution is correct, in particular, why the fact that the host knows what is behind the doors matters.

Again there must be no confusion of the reader with statements along the lines that these solutions are incomplete, or do not answer the question as asked or answer only the unconditional formulation of the question (even if we accept that this is the case)

Academic solution

Here we give Morgan's solution and fully and completely explain the issues involved and exactly why some sources consider that the simple solution is incomplete, does not answer the question as asked, or deals only with the unconditional formulation.

There is no attempt to bury or hide the points raised by Morgan and other sources.
The prevalence of this solution in certain types of reliable source can be made clear.
Equal space and prominence (including an additional 'Aids to understanding' section if desired) to the simple solutions section will be given to this section. Martin Hogbin (talk) 10:46, 17 May 2010 (UTC)

Discussion

The above proposal successfully answers all my issues with the article. Colincbn (talk) 11:30, 17 May 2010 (UTC)

I have added a point to the simple solution section. Are you still happy with this? Martin Hogbin (talk) 11:57, 17 May 2010 (UTC)

I think it's well supported by logic, fact, universally recognized educational practices and the sources. I suggest you commence to editing the article. Glkanter (talk) 12:49, 17 May 2010 (UTC)

I agree with point 3 of the simple solution as long as the host's choice is brought up in the academic section. I agree with Kmhkmh we should mention this in the mediation and see if there is discussion there before making any significant changes though. We have waited this long, I think a few hours or even days for the sake of transparency and good faith is called for. Colincbn (talk) 13:37, 17 May 2010 (UTC)

Yes, of course the host's door choice should be mentioned in the academic section, I am not trying to hide anything, just defer the complications until the reader has understood the simple stuff. Martin Hogbin (talk) 15:20, 17 May 2010 (UTC)

Well I'm not really happy with point 2 & 3 of the simple solution, but i'd still consider it as acceptable (in connection with the rest). I suggest to move this over to the mediation and see whether it can be revived with that approach.--Kmhkmh (talk) 13:20, 17 May 2010 (UTC)

Martin - Are you suggesting deleting the existing "Problem" section, or is this an oversight? Either way, what you are suggesting is the article wholeheartedly endorse the POV of those sources presenting "simple" solutions, completely ignoring the alternate POV until a section titled "Academic solution". Your bullet in this section "There is no attempt to bury or hide the points raised by Morgan and other sources" is funny, because this is apparently exactly your intent with the structure you're proposing. If one POV is so hard to understand that it takes multiple sections to explain (and, ironically, you're suggesting the "simple" solution requires an extensive discussion to be convincing), then to be even remotely NPOV the fact that there are two main approaches needs to made clear before delving into details. I'd be OK with a structure like:

Lead

As is.

Problem

As is.

Solution

Wording that makes it clear there are two main solution approaches, perhaps like this:

There are two main approaches to solving the Monty Hall problem based on a subtle difference in interpretation of the problem statement. Most popular sources present simple solutions based on the overall probability of winning the car by switching versus staying with the player's initial choice. The other main approach to solving the problem, used primarily in academic sources, is to treat it as a conditional probability problem.

Solutions based on the overall probability of winning by switching versus staying

Solutions based on conditional probability

But without some kind of lead-in that says another solution is coming, in my book what you're suggesting is not NPOV. -- Rick Block (talk) 14:32, 17 May 2010 (UTC)

Three sentences of preamble. That's the difference between unacceptable POV and NPOV? Who knew? Glkanter (talk) 15:11, 17 May 2010 (UTC)

I'll wait for the mediator. In any case I'm not pleased with points 2 and 3 in the simple solution section. It doesn't seem appropriate to convince someone with false arguments. We may as well convince the reader in this way that the solution is 50-50. Nijdam (talk) 15:38, 17 May 2010 (UTC)

The mediator is not going to help us here. Due to his own schedule he has not contributed to this discussion for some weeks now. We have to decide this amongst ourselves.

We have to agree to disagree about exactly what arguments are false or not but the view that the earlier arguments are 'false' and exactly why some people think them so can be made clear later in the article. I am not trying to hide anything or push my POV. We might be close to agreement.Martin Hogbin (talk) 16:00, 17 May 2010 (UTC)

Second attempt

You are right Rick, I did overlook the 'Problem section', sorry folks, let me try again:

The lead

Fine as it is.

The problem

As it is with but without the paragraphs starting: 'Without a clear understanding...', and 'Suppose you’re on a game show...'. These start to complicate the problem and could be included in the 'Academic solution' section

What???? You're suggesting deleting both vos Savant's problem description and the one from K&W, so the Problem section would not include ANY statement of the problem? Surely you jest. -- Rick Block (talk) 18:01, 17 May 2010 (UTC)

Simple solution section

No lead-in which says that the simple solution is wrong, or one of several versions of the problem, or says anything about conditional/unconditional probability, this can all come later.
This must make every effort to convince the new reader that the answer to the problem is 2/3 and not 1/2 by using a variety of simple solutions, (all supported by sources).
There must be no confusion of the reader with statements along the lines that these solutions are incomplete, or do not answer the question as asked, or answer only the unconditional formulation of the question (even if we accept that this is the case).
There must be no mention of the fact that the host has a choice of door when the player has originally chosen the car, this choice should not be shown in any diagrams.

Aids to understanding

Much as it is now, this section must concentrate on the helping the reader understand why the simple solution is correct, in particular, why the fact that the host knows what is behind the doors matters.

Again there must be no confusion of the reader with statements along the lines that these solutions are incomplete, or do not answer the question as asked or answer only the unconditional formulation of the question (even if we accept that this is the case)

Academic solution

Here we give Morgan's solution and fully and completely explain the issues involved and exactly why some sources consider that the simple solution is incomplete, does not answer the question as asked, or deals only with the unconditional formulation.

Further details about the problem and its possible interpretations
A clear note about conditional probability stating why some consider the simple version to be incomplete/incorrect
There is no attempt to bury or hide the points raised by Morgan and other sources.
The effect of various host door choice policies must be considered here.
The prevalence of this solution in certain types of reliable source can be made clear.
Equal space and prominence (including an additional 'Aids to understanding' section if desired) to the simple solutions section will be given to this section. Martin Hogbin (talk) 10:46, 17 May 2010 (UTC)

Discussion

I really cannot be what is POV about the above. There are two POV's represented but one comes first because that format makes it easier for the reader to understand the basic problem before learning abut host behaviour etc. Nothing implies that the first approach is the one true solution.

There will no doubt be some readers who lose interest after reading the simple solution. They will probably be the same people who lose the plot right at the start of the article currently. Martin Hogbin (talk) 15:54, 17 May 2010 (UTC)

I agree with this layout. Colincbn (talk) 16:36, 17 May 2010 (UTC)

Martin - If you think what you're suggesting is NPOV, as a thought experiment how about if we switch the order and start with a conditional solution that is entirely convincing and then (some time later) introduce the "simple" solution - sort of the way calculus is usually taught (you don't learn the simple way to differentiate polynomials until after you understand the limit based approach). Still feel NPOV? Why are you so against a preamble that says other sources approach the problem using conditional probability?

In case it's not obvious, I strenuously object to this suggested layout. And, rather than pussyfoot around any more with suggestions that are vague enough to be entirely misinterpreted I think it's well past time you drafted a more or less complete version of what you are talking about so we can all see what you would consider NPOV - i.e. put up or shut up. -- Rick Block (talk)

But Rick, Wikipedia isn't a textbook for a calculus course. It's a general interest encyclopedia, just the same as Parade Magazine, which published vos Savant's famous MHP columns, is a general interest Sunday newspaper supplement.

And I, as a reasonable editor, see no violation of NPOV in Martin's proposal. Quite the contrary. As has been the rule since I started posting on this topic, you and I, Rick, see matters 180 degrees differently. It seems obvious to me that it is YOU who are the proponent of a POV, abetted by Nijdam. Glkanter (talk) 18:30, 17 May 2010 (UTC)

The order of solutions is not based on my POV it is based on the most common way of teaching almost any subject; start with the simple (possibly even oversimplified to the degree that it is strictly incorrect) then proceed to the complex. School students are initially taught a subject called mechanics. It is in fact Newtonian mechanics which, in the light of relativity and quantum mechanics is, in fact, incorrect, but nobody tell the students at that stage that what they are learning is wrong because to do so would completely put them off the subject. Later on, the same subject may be referred to as Newtonian mechanics, this may give some students a clue that there may be other kinds of mechanics. At university, physics students learn that Newtonian mechanics is a weak-field, low-speed, macroscopic-scale approximation. Strictly speaking it is wrong, but it is still incredibly useful. In many college courses, one of the earliest, and often most memorable, lectures goes along the lines of, 'everything you have learned so far is wrong'. My order is the standard for nearly any subject and is not dependent on my POV.

In the case of the MHP the simple problem is still plenty hard enough for nearly everybody. The last thing we want to do is make it harder by quibbling about door numbers. Martin Hogbin (talk) 19:01, 17 May 2010 (UTC)

Rick, regarding 'your put up or shut up' comment it is not my intention or desire to produce the whole simple solution on my own. I prefer to work with other editors by cooperative editing to produce a result that is better than and single editor could have done. I think most editors here realise what I am getting at and once we are past this impasse we can all get on with improving the article. Martin Hogbin (talk) 19:08, 17 May 2010 (UTC)

I said "as a thought experiment" (meaning I'm not actually suggesting this, but just wanted you to think about whether the result would feel NPOV to you). As usual, you are completely missing the points I'm raising. Perhaps I misread Glkanter's earlier comment about 3 sentences of preamble being the difference between POV and NPOV, but I thought it meant he was OK with adding this preamble. You (Martin) seem to be arguing against this. Why? And, in your latest "structure" suggestion (above) you slipped in that you'd delete the problem descriptions from the section called "Problem". Frankly, I doubt most people noticed this which is why I'm asking you to actually write out what you're talking about (as a first draft). You continue to object to anything I write. Fine. But, so people can tell what you're actually talking about please create a draft. It doesn't have to be camera ready copy - but without seeing proposed content it's really not very clear how your "bullet points" would affect things. -- Rick Block (talk) 19:23, 17 May 2010 (UTC)

I do not see any need to expand on my bullet points. They simply mean what they say. Nobody wants to waste any more time on sandbox solutions, we want to edit the article. Regarding a preamble, I would not object to a very subtle preamble to appease the sensibilities of those who think that to initially show a simple, and wrong, solution will harm their self respect and mathematical image, so long as it does not confuse the reader with the things mentioned in my bullet points. For example, we could maybe (assuming other dissident editors agree) we say something like, 'The simple solution given below addresses the formulation of the problem assumed by most non-specialist sources'. Martin Hogbin (talk) 19:50, 17 May 2010 (UTC)

Yes or no - are you suggesting deleting the problem statements from the section called "Problem"? -- Rick Block (talk) 19:54, 17 May 2010 (UTC)

Sorry, I forgot that two statements start with the same words. I would delete just the K&W problem statement but keep Whitaker's. Martin Hogbin (talk) 21:31, 17 May 2010 (UTC)

Maybe we could find a sourced 'puzzle' statement (that is to say, no door numbers) to add. That might resolve the argument. Martin Hogbin (talk) 21:35, 17 May 2010 (UTC)

Resolve what argument? You're going to present a "door number less" solution as the main solution to the MHP using a variant description where the example involving the player picking door 1 and host opening door 3 has been deleted? Right. That's the most common approach and not at all POV.

Martin - what you're describing is nearly the recipe for POV. Let me paraphrase your suggestion and first set of bullets:

We must start with a solution (that matches my POV).
Before delving into the solution (that matches my POV) we must not even mention any other POVs exist (well, ok, you've relented as long as it's "very subtle preamble" with a suggested wording that marginalizes any other solution as "specialist"), and (God forbid) we certainly can't say half a dozen published papers take exception to this POV.
The initial section (matching my POV) must be long enough and detailed enough to convince others it is The Truth.
It must not have any critical words (that would contradict or in any way criticize my POV) - not even anything that attempts to describe what (my preferred) solution says.
This solution must ignore the very aspect of the problem that causes (my preferred) solution to be correct, i.e. that the host must choose randomly between two goats if given the chance.

Pretty much in every case, to be NPOV, we MUST do the exact opposite. You've been ignoring the line from WP:NPOV I've quoted a couple of times. Here's another (emphasis added): An article should clearly describe, represent, and characterize all the disputes within a topic, but should not endorse any particular point of view.

"Endorse". Nice word. This is EXACTLY what you're asking for. -- Rick Block (talk) 23:19, 17 May 2010 (UTC)

And I feel that you have ignored what I have been saying about undue weight and balance in order to push your own POV. Although I accept that you don't see it that way. But the fact is that when you count the trusted news sources and psychology papers that use the MHP they the number of sources that reference the simple version far outweight thoses that are soely concerened with the conditional solution. This is indisputable, go to Google Shcolor and look, I did. And yes I am willing to list the sources to show it. Colincbn (talk) 00:18, 18 May 2010 (UTC)

Are you arguing that Martin does not want the article to endorse the simple POV? Or is your argument that it should, and rightfully so, because more sources that mention the MHP reference a simple solution than not? I think this is a point at which a mediator would be very helpful in clarifying policies around NPOV that are relevant here. Let's just say there's more to it than counting references. -- Rick Block (talk) 02:25, 18 May 2010 (UTC)

There is no new violation of NPOV going on here, beyond what's already still in the article. I presume it's customary to make claims of NPOV violation only AFTER they allegedly occur in an article. Then the burden would be on the claimant to demonstrate why his claim is valid. Seems a wholly unsupportable reason for a revert, that 'in my opinion this violates NPOV'. Kinda makes one editor subservient to another. This whole 'NPOV' debate is a ruse to keep the article from being changed by the consensus of editors. It's wholly abstract and unprovable until it occurs. So, let Martin, or whomever, make some edits, and let the chips fall where they may. There's no mediation going on, anyways. Good grief, is there still a mediator? Glkanter (talk) 02:36, 18 May 2010 (UTC)

Of course Rick is absolutely correct that the article should not endorse one POV to the derision of others. And that the layout can serve to endorse one over the others. However My point is that if worded properly the article can give the simple solution first without needlessly confusing anyone and still maintain a NPOV. In addition I feel that the popular, or simple, version is the more prevalent version and therefore should have the more prominent place. Now this does not in anyway mean I think we should cover up or discount the other solutions, I don't do math and would never claim one to be more right or anything like that. But which is right is irrelevant. As long as all legitimate solutions are represented in a manner consistent with WP policies who is right should never come into the argument.

Even the term used in the article now is the popular solution. I know you understand what the word popular means. If that solution is the more popular one then it can safely be made more prominent under the rules for balance and weight. Now, I understand that the word has connotations of meaning "non-academic" as well as "common". But the MHP is cited and used in many places that are non-academic. Besides the academic world does not give equal weight to the conditional solution so we should not either. It might get as much or more coverage in papers on probability, but those are certainly not the only papers that count. I argue that the MHP is at heart a psychology problem and therefore the way the problem is defined in psychology papers can safely be put in a more prominent place, as long as all solutions are represented in the article. Colincbn (talk) 02:55, 18 May 2010 (UTC)

I agree with Colin, in fact this has always been the point that I have been trying to make. The MHP is a simple mathematical puzzle that most people get wrong. This is why it is notable, that is why we are discussing it here, that is why this argument even exists. For some reason, the average human brain is somehow incapable of solving an elementary probability problem, even many well-above-average brains have had immense difficulty with the problem, long before Morgan raised the issue of host behaviour. I came here years ago in response to an RfC suggesting that a few editors were claiming ownership of the page and not allowing certain changes.

My initial thoughts were that the page failed to explain the basic, essential, problem well to the average reader. It is notoriously difficult and we need to do everything possible to help the reader understand. It soon became apparent that the reason that the problem was explained badly was due a few editors using a paper by Morgan et al to control the structure of the whole article, making it next to useless in helping the vast majority of readers understand the problem. Even if the Morgan paper had been accepted by everyone as a brilliant and insightful analysis of the problem, it would still have been better to keep it out of the way until the simple problem had been explained.

In fact, when I looked into Morgan's paper I found that it had many problem with it, philosophical, mathematical, and matters of accuracy and consistency. The whole story of what is wrong with the Morgan paper is given in great detail at my Morgan criticism page for all those interested. Some of this may be OR but some of what I say has is confirmed by reliable sources. The page has attracted some complimentary remarks and no serious criticism. Anyone interested is welcome to challenge any of my conclusions on the associated talk page.

So, my actual POV is that Morgan's approach represents a badly defined, somewhat perverse, version of the problem that is of interest only to those studying undergraduate level statistics (which is why it is prevalent in introductory statistics books). It deserves a mention here, but little more that a paragraph. Once you have got your head round the basic problem, the issue raised by Morgan is actually quite simple to understand. Unfortunately most people are not interested in it.

In the interests of progress, I am willing to put aside my POV about the Morgan paper, even though it looks to be shared by the majority of editors, and give the Morgan problem equal prominence in this article. Martin Hogbin (talk) 09:30, 18 May 2010 (UTC)

Why Does This Article Have 'Special Rules' Proposed?

Why are so many of you 'laying down the rules' for how to edit the MHP?

Each editor, until proven otherwise, is presumed to be operating in good faith. Does anyone know of any exceptions?

An edit that follows all Wikipedia rules should not be reverted solely because an editor assigns himself the duties of judge, jury and executioner.

There are any number of ways to respond to an edit that one suspects may violate NPOV. Reverting should be the last.

Two lines of text cannot take up the same space at the same time. Only one presentation of the article can exist at one time. That means someone is going to 'lose'. That doesn't mean the other guys cheated.

We've come a long way from 'host bias', disputed 'State of Knowledge', 'simple solutions are wrong' on these talk pages. At this point the 'unconditional' or 'omniconditional' problem statement have the same solution set as the symmetrical 'conditional' solution.

The article has not been updated to reflect the previous statement. The article is chock full of weasel words and caveats that don't belong.

Innocent readers keep reporting problems. Just like I did in October, 2008. Glkanter (talk) 16:17, 18 May 2010 (UTC)

Please provide examples of "chock full of weasel words and caveats". As I recollect, the last time you made a claim like this (I forget exactly what terminology you used, something like rife with pro-Morgan POV) I went through the entire article and there were a grand total of 4 references to Morgan, most of them in sections specifically talking about conditional approaches to the problem. If you don't want to list them here and would rather just make changes to the article go ahead, but per WP:BRD if someone reverts a change you make you should take that as an indication we need to talk about it (i.e. don't just revert back). -- Rick Block (talk) 17:23, 18 May 2010 (UTC)

Time to move on

Some years ago there was an RfC saying that a small number of editors had been claiming ownership of this page and preventing improvement. That is how I came here. Since that time there has been a steady stream of new editors all wanting change along the same lines, and a steady stream of readers who find themselves unconvinced by or unable to understand the article. The RfC expired without reaching a conclusion and Mediation also failed to do so but now it is the time to finally move on. There is a consensus for change here, along the lines that I have suggested and I suggest that the article is changed forthwith. I will make the changes if no one else does so.

Nothing is irreversible in WP but we can at least see how things look in a new format. Martin Hogbin (talk) 09:53, 18 May 2010 (UTC)

People can see what they look like, if you provide a full article suggestion (as rick suggested). There is no need for any modification on the current article needed for that. Furthermore:

consent doesn't exist simply because you claim it does.
changes in that regard should go through the mediation or wait until the mediation is officially determined.

There are however 2 things were we really should move on (because otherwise they are just smokescreens), that is:

Moving regarding de Morgan and stopping to use it as synonym for the conditional solution: There are enough other sources for the conditional approach, hence there is no need to constantly discuss de morgan as a thinly veiled proxy. I know you are willing to compromise here, so please do it amd move on without rehashing old false arguments pitentially distracting new readers.
MHP is at heart a psychological problem. Fine - please move on and write an extensive chapter on the psychological aspects using the various psychological papers, but do not use them to do the math part.

--Kmhkmh (talk) 10:44, 18 May 2010 (UTC)

Kmhkmh you have accepted my suggestion (which is essentially to move from the simple to the complex) before, I am not sure why you now object.

I have explained that I have no desire or intention to rewrite the article myself. There are plenty of editors waiting to improve this article if only the few that want to prevent this would allow them.

No one's consent is required to change the article, there is already a consensus to change it.
For whatever reason, mediation simply has not happened.

The paper by Morgan et al (which I call Morgan simply for brevity) was the first to make the point that the answer to the problem depends on the host's legal door choice. They were also the first to insist explicitly that the problem must be solved using conditional probability. This is what many here object to. Later sources have followed Morgan. If you know of an earlier source making exactly the same claims I will be happy to use that author's name to refer to the 'insistence that any solution must depend on the host's policy when choose a door to open if the player has initially chosen the car', otherwise I will continue to refer to Morgan. The use of just the term 'conditional' is singularly unhelpful in discussing this problem.
There is not and cannot be a distinction between the mathematical problem and the psychological one. The precise mathematics depends entirely on how the question is interpreted. Martin Hogbin (talk) 12:09, 18 May 2010 (UTC)

Well if there cannot be a distinction between math and psychological aspects, then you will to to stick to math sources for the math part - period.
I've not accepted your suggestion as in changing the article right now, but I said your suggestion should be moved to the mediation and in principle i consider it as acceptable. However at least Nijdam and Rick atill clearly oppose it. So don't claim consent where there is none. Though strictly speaking one can change an article at any time, it also follows from guidelines that in doubt larger or contested edits should seek a consent first. And you are very well aware of that.

--Kmhkmh (talk) 13:33, 18 May 2010 (UTC)

Actually I agree with Kmhkmh on this one. Both he and Rick have said they are OK with putting the simple solution first and with using the solution most used in psychology papers in a section that deals with the psychology of the MHP. That is the simple/popular/unconditional version. So how about this Martin, we both have tended to agree on structure; so if you put together a version of the article on your talk page and allow me to help edit it, to add the psychology bits and make sure it is neutral in its presentation of the different mathematical solutions, we can then bring it here, and to the meditation page, to see if we can get a real honest consensus to put it up. I know mediation has stalled, and never really got anywhere to begin with, but it is still technically open. And I would rather follow that path then simply make a change that might upset others simply because it will look like one editor acting unilaterally. We can take a bit of time for the sake of procedure, and that way no one can say later we did not "follow the rules" or anything like that. How would you feel about that? Colincbn (talk) 13:13, 18 May 2010 (UTC)

Sounds good to me. If the mediator officially bails out, then we have to live with that, but until then we should use the mediation. Maybe the mediator can starting with Martin's suggestion or its enhancement broker a deal than Martin, rick and Nijdam all can live with. In any case we should avoid starting a potential edit war on the article, which would be the likely result of unilateral changes right now. From my perspective the suggested approach is not the best , but at least acceptable, i.e. I would support it (+/- minor tweaks maybe) if it finally settles the issue once and for all. The real imported point is that all the relevant information is available to readers, the ordering of chapters and even a real or perceived minor POV doesn't really matter much in the big picture. So in that regard I think living with an article that most personally don't see as optimal but still as acceptable is worthwhile trade-off for reaching a stable article.--Kmhkmh (talk) 13:33, 18 May 2010 (UTC)

I'll note that the simple solution currently is first and has always been first. No one has ever prevented anyone from improving the simple solution. Fundamentally, Martin's proposal is only to put more distance between the simple solution and the conditional solution (and I don't know what Martin exactly means, but I mean a conditional solution of the symmetric problem like what I've repeatedly drafted, not Morgan's solution of the more general problem where the host's preference is treated as a variable). What I keep hearing, and what I object to, is an attempt to completely marginalize the conditional solution and have the article endorse the simple solution. This is what I'm saying would fail NPOV. -- Rick Block (talk) 14:28, 18 May 2010 (UTC)

The point that I raised above and that you should ask yourself, whether a slight POV or marginalization of the conditional solution (outside its own chapter) is not a worthwhile trade-off, if it results in article stability and that Martin finally leaves the article alone, i.e. refrains from further changes. Also at point everybody needs to ask himself, whether he's really interested to settle the edit conflict or whether he is only interested in pushing their notion of the optimal article or even worse secretly being happing with an neverending rather unproductive discussion.--Kmhkmh (talk) 14:59, 18 May 2010 (UTC)

I assure you it has never been my intention to marginalize the conditional solution, nor to promote one point of view over any other. I do admit that I was mistaken about some important aspects of this debate when I first came into it, but my main concern then is basically the same as now. while I would object to removing any information that currently exists in the article I strongly believe it should be rearranged to be more approachable to those without a background in math. My second issue is that there is a lack of coverage of the psychology of the problem given the number of papers published on the subject. The one about how pigeons are better at it than humans comes to mind. I also would strongly object to making any major change to the article without attempting to gain consensus for the specific changes first. Colincbn (talk) 15:47, 18 May 2010 (UTC)

Sorry folks, but it looks to me that we are back to square 1. The psychology of the MHP is all about why people think the answer is 1/2 rather than 2/3. We cannot possible start talking about that until we have convinced people that the answer is 2/3. We will never succeed in doing that whilst we continue to confuse readers with talk of incomplete solutions at the start of the article.

We seem to be in agreement then.--Kmhkmh (talk) 16:53, 18 May 2010 (UTC)

Maybe I have misunderstood the suggestion so I certainly have no objection to those who support it producing a development version for others to comment on. There is only one thing I want to see which the article start by giving a full and convincing simple explanation of why the answer is 2/3 and not 1/2. Martin Hogbin (talk) 16:24, 18 May 2010 (UTC)

Well depending how you read the problem that's not possible, i.e. what you want is only possible for a particular take on the problem. That particular interpretation can go first in its own chapter, without any references to the conditional interpretation in it , i.e. a combined treatment as Rick seems to insist on at all cost is imho not necessary. However what is not possible, is to exclude some short info about disambiguities and different interpretations in the lead, because doing so is not making the problem "simple" but is rather "simply misleading". Also the main paper for psychological aspects currently used in the article (K&W) does use conditional probabilities. So I'd like to see which psychological paper are supposed to be used here and for what aspects exactly.--Kmhkmh (talk) 16:51, 18 May 2010 (UTC)

I think having a statement in the lead of the simple solution explanation that points out there are more ways to look at the problem is perfectly fine. In fact I would say it is essential. Rick and Kmhkmh have both agreed to a simple solution section coming first. I think Martin should agree to allow a statement that points out that there is more than one way to approach the math in said section. I think this might be the solution no one likes but everyone can agree on that we have been looking for. I am more than willing to start a draft page in my user space and use it to write up a section dealing with the psychology, most likely I wont even have to mention much math at all, but it will have to wait until tomorrow as it is 2:00am where I am (Japan) and its time for me to go to bed.Colincbn (talk) 17:18, 18 May 2010 (UTC)

I have no objection in principle to a statement that refers to a number of possible interpretations and solutions to the problem, provided that it does not put the general reader off. Please no mention of conditional/unconditional, host behaviour, or incomplete/incorrect solutions. Something bland, just to preserve our mathematical decency, would be best. Maybe Seymann's comment, but not in quotes. I wanted to remove it earlier just because it was out of place. Martin Hogbin (talk) 17:34, 18 May 2010 (UTC)

Again that sounds good to me. But we need to make sure that rick, glkanter, nijdam and richard agree to that too. Also I'd suggest to move that to mediation and see whether the mediator is still interested and would push that point to get everybody to agree and make it happen.--Kmhkmh (talk) 17:50, 18 May 2010 (UTC)

It is easier to just ask them, the mediator is no longer active. What do you think people? Martin Hogbin (talk) 18:30, 18 May 2010 (UTC)

I've already suggested text and Martin (not sure about Glkanter) seems to object to it. So you don't have to go find it again, here's the text:

There are two main approaches to solving the Monty Hall problem based on a subtle difference in interpretation of the problem statement. Most popular sources present simple solutions based on the overall probability of winning the car by switching versus staying with the player's initial choice. The other main approach to solving the problem, used primarily in academic sources, is to treat it as a conditional probability problem.

Glkanter - are you OK with this?

Martin - If you think this could possibly "put a general reader off", please explain how. Our readers are not imbeciles. If they don't care what conditional probability is, presumably they wouldn't click the link and they wouldn't care to read that section of the article. If they only care about simple solutions presented by most popular sources they'll presumably stop reading after this section (will which come before the section describing the other approach). This wording lets them know what's coming, does not say either one is more "correct" than the other, but lets them know the basic difference. -- Rick Block (talk) 19:21, 18 May 2010 (UTC)

Rick, I said, ' Please no mention of conditional/unconditional, host behaviour, or incomplete/incorrect solutions'. You have mentiond 'conditional' but I should have added 'overall' to my list. Your wording is your POV. Many editors here do not accept that the simple solution only addresses the 'overall probability'. You must know this by now. No one is inclined to repeat two years worth of discussion at this stage.

This is how your wording will put the reader off:

I am a casual reader who want to know the answer to the MHP, maybe out of idle curiosity, maybe to win a bet who knows. The first thing I see is that there are two problems. Which do I want?
Now, is it the 'overall probability' that I want or something else?
Do I have to read through the whole article to get the answer to a simple question?

If we must have a disclaimer, please can we make it something more discreet like 'Seymann's statement. Kmhkmh, and Colin are OK with that. It still preserves our mathematical decency without stuffing it in the reader's face. Martin Hogbin (talk) 21:48, 18 May 2010 (UTC)

It doesn't say the simple solutions only address the overall probability - it says they're based on this (or are you even disputing this?). I can't see any problem with saying the other approach is based on conditional probability (because it is what these sources say). A perfectly accurate way to put it would be "There are two main approaches to solving the Monty Hall problem. Most popular solutions present solutions not based on conditional probability unlike many academic sources, which do." - but I assume you'd be apoplectic about this, so, in the spirit of compromise, how about:

There are two main approaches to solving the Monty Hall problem. Most popular sources present solutions based on simple probabilistic reasoning. The other main approach to solving the problem, used primarily in academic sources, is to treat it as a conditional probability problem.

Note I've dropped "subtle difference in interpretation of the problem statement" and moved "simple" from "solutions" to "simple probabilistic reasoning". I'd like to give the reader some clue as to what to expect. -- Rick Block (talk) 06:23, 19 May 2010 (UTC)

We have had a very long discussion about the simple solutions and on what basis that are, or are not, justified. The fact is that I and some others think they are justified and you and others think they are not. There is no way that this argument can be condensed into one sentence and there is certainly nothing simple about it. 'Simple' is just a low key way of saying 'not quite right'.

Not every undergraduate level conditional probability problem has a WP article on it. The only reason that the MHP has one is that the simple problem is notoriously difficult for most people to solve. A reader who is just about to try to understand one of the world's most most difficult brain teasers does not want their mind confused at the start by being told that ther ere two ways of solving the problem. We do not need to tell the reader what is coming, it is not a long article, the reader can see for them selves, those that are interested. You whole stance is still based on pushing the argument that the simple solutions are wrong, rather than helping the reader get to grips with the problem.

What is wrong with something along the lines of Seymann's comment, it is well-sourced, nobody disputes it, and it (intentionally vaguely) justifies treating the problem in more than one way. Martin Hogbin (talk) 09:30, 19 May 2010 (UTC)

I'm really bending over backwards to be accommodating here. We're going to have to label it eventually because it will have a section title. Your stance that even mentioning that there are two main ways of approaching the problem will be "confusing" to the reader strikes me as nothing more than an excuse for attempting to make the article endorse the "simple" POV - i.e. you don't want the article to be NPOV about this issue.

We all agree sources do not universally agree on how to approach this problem (right?). And, we all agree there are two "main" camps about this (right?). You're insisting we ignore this and start the article as if all sources agree the "simple" solutions are correct and complete, because otherwise the reader will be "confused". Ignore for the moment that we're talking about the MHP. Imagine ANY other topic where there is significant disagreement among sources (most of the ones I can think of off hand are too pejorative to even mention, so I won't - but an imperfect analogy is the existence of God). Now imagine starting an article about such a topic with what one side has to say, not just fully and completely but entirely convincingly, without even mentioning there's another side until after this exposition. Surely you agree that this would be POV, don't you?

No, not at all. That would exclude many good maths and physics text books. I have explained this many times. Martin Hogbin (talk) 16:37, 19 May 2010 (UTC)

My whole stance is NOT about pushing one POV over the other. It's about avoiding this. What you're doing is essentially denying there are different POVs. -- Rick Block (talk) 15:57, 19 May 2010 (UTC)

You seem utterly determined to get the term 'conditional' into the text as soon as possible. I fail to see what this achieves. How about, When dealing with questions of probability it should be noted that without a clear understanding of the precise intent of the questioner, there can be no single correct solution to any problem. This article starts with solutions of the type given in many popular sources. This is based on a quotation directly referring to exact question that we quote, it is from a reliable source, and it covers the fact that we start with one type of solution and move on to another without giving any confusing or potentially POV details. Martin Hogbin (talk) 16:37, 19 May 2010 (UTC)

Actually at least further up Martin somewhat agreed to mention disambiguities or 2 camp is the article lead. If he really agrees to that I think we can have the "simple solution" free of any reference to incompleteness or the conditional approach (I don't see this as optimal but it is acceptable). And as mentioned above I think you need as yourself, what you priorities are: Pushing for what you consider the optimal version of the article or pushing for a just acceptable but stable version and a resolved conflict. Picking your priorities either way is justified. However if you pick the former rather than the latter, you should state that clearly, because this endless discussion here and any mediation becomes entirely pointless. The gazillions justification by you or Martin why your respective version is better/not NPOV/whatever will do nothing to resolve this conflict, i.e. you both have to give significantly in to some degree. One possibility to do that might be, that Martin has to live with a clear reference to the disambiguities and the 2 camps in the lead and that you have to live with the simple solution section basically looking as envisioned by Martin.--Kmhkmh (talk) 16:38, 19 May 2010 (UTC)

[Edit conflict] How about my latest suggestion? Martin Hogbin (talk) 16:41, 19 May 2010 (UTC)

Kmhkmh - Here's my viewpoint. I AM giving significantly. I'm agreeing we start the article with a solution without mentioning (until much later) that many sources say this solution is not a solution at all, and also agreeing we then present a solution using conditional probability STILL not saying anything overtly critical of the simple solutions (I've agreed the criticisms can come in a later section, after the solutions are presented). As far as I can tell, Martin is completely unwilling to give up anything - he wants the article to explicitly endorse the view that the simple solution is correct and complete, and won't (and hasn't) budged at all. Identifying that there are two main approaches, and that one of them is based on conditional probability and (however we phrase it) that the other isn't is not "pro-Morgan POV". It seems to me Martin is so virulently opposed to the notion that conditional probability is necessary to the solution that he's completely missing the fact that presenting a solution using conditional probability does not inherently say the "simple" solution is wrong (have you read his "I hate Morgan page?" - he's really gone quite bonkers about this). Martin's contention that using the words "conditional probability" will confuse the reader is pure BS. There ARE two ways of solving the problem. Popular sources DO generally use one. Academic sources (in particular, most probability textbooks) DO generally use the other. Standing on our heads to avoid saying the academic sources use conditional probability and the popular sources don't because it might lessen the reader's conviction in the absolute truth of the popular solutions is essentially the definition of POV. I've given up as much as I can tolerate. It's now time for Martin to give up something. Saying that there are two kinds of solutions, and that one uses conditional probability and that the other is based on simple probabilistic reasoning seems like a trivial concession. -- Rick Block (talk) 21:29, 19 May 2010 (UTC)

Sorry though I mostly agree mostly with your view of the "best" or a good article, i haven't seen you giving in anything significantly at all. Your are only posting variations of the same thing and labelling them as "compromise". Martin has actually "compromised" significantly from his originally favoured version, though his compromise so far was only giving in to things, he was required to due to sources and WP guidelines anyhow, i.e. he's just given up on a version being unacceptable by WP standards to begin with. From my perspective it boils down to this. Martin tries have as much text as possible and as prominent as possible that does not mention caveats or problems with the simple solution, whereas you insist that problems with the simple solution are mentioned as often and prominently as possible. Both of you have only moved as much as WP standards would have forced you too anyhow (at least in my observation). Now if you want to resolve the editing conflict, you need move towards a prominence level of the caveats to the simple solution that you both can live with (and being with the boundaries of WP standards). Again my suggestion here would be that you trade the lead for the simple solution. You get the lead including references to the problems/caveats of the simple solution in the lead and you give up the "combined explanation" and the mentioning of caveats int the simple solution chapter itself. Again both of you need to give up on your respective perceived best/good and NPOV and move towards "still acceptable" and "just minor POV". If you are not willing to do that, because either of you finds such ompromise or a similar one as "too bad"/"not acceptable", then there is no way to resolve this editing conflict. If that's the case then at some point this has to be clearly stated or acknowledged, that there is an unresolveable editing conflict between you and Martin.--Kmhkmh (talk) 22:10, 19 May 2010 (UTC)

Rick, I have just made another suggestion above which states in neutral terms that there is more than one type of solution. Can you tel me specifically what you do not like about it. Martin Hogbin (talk) 23:05, 19 May 2010 (UTC)

@Kmhkmh: Seems like we're talking past each other since I think what you're suggesting I give up is pretty much exactly what I said I've given up. I'm definitely agreeing no caveats in the simple solution section itself. I'm not even saying any problems/caveats of the simple solution are mentioned in the lead in to the solutions ("simple probabilistic reasoning" is intended to be neutrally descriptive, not critical). I'm talking about something different from the drafts I've proposed, i.e. something only slightly different from Martin's outline (without seeing content I'm dubious about "aids to understanding" and rather than separate top level headings I still think these should go as separate parallel subsections in a single "Solution" section). Like I say - I'm compromising. Perhaps this is the point where a full draft is needed to avoid misunderstandings. -- Rick Block (talk) 23:46, 19 May 2010 (UTC)

More on the introduction to the simple solution

[continued from above] @Martin - What I specifically do not like about your suggestion is that it doesn't convey any information whatsoever. It doesn't say there are two main approaches. It doesn't say anything at all about how these approaches differ. It simply doesn't say anything. Reading this would make me think, huh? what's this doing here? As an editor, I'd be very tempted to simply delete it. It's particularly bad since I assume what you're then going to do in the "popular sources" section is present a solution without precisely defining the problem, unless you're going to invent your own problem in this section that is NOT what the popular sources you're referring to say the problem is. The popular sources nearly universally present the Parade version and don't say specifically what they think it means, so you'll be in WP:OR territory if you attempt to clarify on their behalf that the problem they're addressing is the "non-conditional" problem. It's issues like this that make it fairly important to be able to have a sense for what content you're thinking about for these sections. So, bottom line, what I don't like about your suggestion is that is doesn't say anything useful.

My comment is not intended to convey any information except to prevent an expert on the subject from thinking, 'These people are idiots, they are clearly not aware of the issues of conditionality raised by Moran et al', on a casual reading of the article, although this will all, in fact, be made crystal clear by the 'Conditional' section.

It probably is a good idea to leave the exact question unclear, mainly to avoid arguments about what solutions apply to exactly which problem statements. Martin Hogbin (talk) 09:08, 20 May 2010 (UTC)

What do you specifically not like about my suggestion? Can we go through it thought by thought?

There are two main approaches to solving the Monty Hall problem. OK so far, or is this offensive to you somehow?

It is your POV that there are only two main approaches to this problem, the proper, conditional approach, and the incomplete, inaccurate, limited, unconditional approach. There are many editors here who thing otherwise. That is another reason why it might be better to leave the exact problem a little vague at the start. I have no objection to the 'Academic' section starting with a recap and more detailed discussion of the simple solutions, complete with well-defined problems, ifthat helps

Most popular sources present solutions based on simple probabilistic reasoning. The idea is we're going to describe solutions that are presented by popular sources, and we're identifying the basic approach they use. If you find "simple probabilistic reasoning" offensive for some reason can you say why? How about if probabilistic is linked to probability, e.g. "simple probabilistic reasoning"? This is truly not meant to be pejorative, and if you're reading it this way is there any other description that you'd find acceptable? I think the goal should be to neither overstate or understate what these solutions say, so all of the following wouldn't be acceptable:

"based on sound probabilistic reasoning" - overstated
"based on probabilistic reasoning" - doesn't imply any contrast with conditional probability, which is what's coming
"based on the overall (or average, or unconditional) probability of winning by switching vs. staying" - you've already said you don't like this

How about "easily understood probabilistic reasoning" (essentially the same as "simple" - but since I don't really get what you object to about "simple" maybe you'll object to this as well).

On reflection maybe 'simple' would be the best. I could live with that.

The other main approach to solving the problem, used primarily in academic sources, is to treat it as a conditional probability problem. I have no idea what you don't like about this. Isn't it simply a succinct description of the sources that use the other approach and what this approach is?

What value to you imagine that using the term conditional probability will have at this stage? Most people will not understand exactly what it means (in fact I am not sure that anybody knows) and following the link to find out will be unhelpful and disruptive to the reader. Why not say something like, 'a more detailed treatment follows', especially if the 'Academic section' recaps the simple solutions.

I'm really NOT trying to convey any POV here. If you're reading this as conveying POV please tell me what I'm missing. -- Rick Block (talk) 05:25, 20 May 2010 (UTC)

Rick, that sounds good to me - maybe i missed/misunderstood your latest position. I'd suggest if in anyway possible to pick up the mediator suggestion for a live talk. If you and Martin can agree under the guidance of andreevan to iron out and fix the details you in principle seem to agree on now then i think the other editors would join and support that result (at least I would).--Kmhkmh (talk) 11:17, 20 May 2010 (UTC)

It would be good to have some other views at this stage. This is not simply an argument between Martin and Rick, many others have strongly held views on the subject. There is no point in Rick and I coming to a hard fought agreement if other editors are not going to accept it. If you think that Rick and I are arguing about pointless detail that is fine but please do not then argue about the compromise reached. Martin Hogbin (talk) 09:08, 20 May 2010 (UTC)

We need to start somewhere and you and Rick had the most exposed and contradicting views and you were wrangling the article for the longest time. so it is better if you find a way to agree first before getting the other editors onboard. Because if everybody just starts commenting before you and Rick agree we potentially get a lot of distracting chatter and might fall into the old pattern, ie. each side tries to muster support with editors and starts pushing for his personally favoured version again, i.e. back to square 1 as we had it so often before.--Kmhkmh (talk) 13:54, 20 May 2010 (UTC)

Here's the second sentence in the Popular solution section.

"Hence the car is then with chance 2/3 behind the remaining unopened door (Wheeler 1991; Schwager 1994). Switching doors thus wins the car with a probability of 2/3, so the player should switch (Wheeler 1991; Mack 1992; Schwager 1994; vos Savant 1996:8; Martin 2002). In order to convert this popular story into a mathematically rigorous solution, one has to argue why the probability that the car is behind door 1 does not change on opening door 2 or 3. This can be answered by an appeal to symmetry: under the complete assumptions made above, nothing is changed in the problem if we renumber the doors arbitrarily, and in particular, if we switch numbers 2 and 3. Therefore, the conditional probability that the car is behind door 1, given the player chose 1 and the host opened 2, is the same as the conditional probability that the car is behind door 1, given the player chose 1 and the host opened 3. The average of these two (equal) probabilities is 1/3, hence each of them separately is 1/3, too."

Weasel words, caveats, defensive, and the intro of 'conditional' too soon. Impossible to identify in any way as relating to the 'Simple solution'.Glkanter (talk) 18:41, 18 May 2010 (UTC)

This is in the "popular solution" section toward which I (and I think everyone here arguing to keep a "conditional solution" in the article) have maintained a more or less strictly hands off policy (because you think we're all evil incarnate). This is the doing of your fellow "simple solution" folks (Gill, if I remember correctly), i.e. it is the result of your previous "improvements". Why don't you try changing it and see what happens. -- Rick Block (talk) 19:45, 18 May 2010 (UTC)

You're hard to figure out, Rick. First you disagree with me that there are weasel words and caveats in the article. So I quote the article. Then you can tell me exactly which editor wrote the weasel words and caveats and when. How can that be? That's why I have to argue and disagree with you all the time. Glkanter (talk) 23:21, 18 May 2010 (UTC)

Easy. I thought you were talking about the rest of the article, rather than the one section that you have directly participated in editing. I look at every change made to the article (well, I intend to look at every change - sometimes I miss some). This one rang a slight bell. At the time I remember thinking how awful it was, but I'm not going to touch your precious simple solution (this section was added some time ago, and I was not in favor of adding it - I compromised). I consider this section of the article to be absolutely horrible, and not for the reason you're probably thinking, but because it's atrociously written. -- Rick Block (talk) 05:39, 19 May 2010 (UTC)

Gentlemen, would neither of you consent to a real-time mediation in some format? It doesn't need to be all parties - anyone who can make it. Nothing will be binding but maybe we can make progress and translate it on-wiki. Andrevan@ 06:11, 20 May 2010 (UTC)

Yes, I'm available. I would like to see an agenda before I participate. Thank you. Glkanter (talk) 06:44, 20 May 2010 (UTC)

As you will see, we are close to agreement so some mediation might help. What format do you propose. I would prefer Wiki based communication, with clear ground rules on who should comment where. Martin Hogbin (talk) 13:25, 20 May 2010 (UTC)

I'm specifically asking for a real-time conversation: IRC or Skype. Andrevan@ 15:33, 20 May 2010 (UTC)

If we can arrange a time that works for everybody, that'd be fine. -- Rick Block (talk) 16:09, 20 May 2010 (UTC)

I do not use these services. I am happy to set up a Martin Hogbin/Andrevan mediation page in my user space. Martin Hogbin (talk) 19:10, 20 May 2010 (UTC)

You can use irc via a normal browser (webchat) and the conversation can be logged so nothing gets lost.--Kmhkmh (talk) 01:27, 21 May 2010 (UTC)

You don't feel that something is lost via the wiki format? I can't make progress without something resembling a real life conversation, and real time is one important part of that. A phone call would be even better. Andrevan@ 04:01, 21 May 2010 (UTC)

No, I cannot see what is wrong with a wiki page. If we are both editing it is near simultaneous. Martin Hogbin (talk) 04:51, 21 May 2010 (UTC)

I have set up this page. What time would suit you? Martin Hogbin (talk) 04:57, 21 May 2010 (UTC)

See it as part of the compromise, i.e. use the medium others are willing/suggesting to use. I mean, if you can't even agree on at least trying to use a medium such as irc, it is really hard to imagine how you want to compromise on content issues for real. The discussion page approach has been used unsuccessfully for over a year now, i.e. there are very good reasons for trying a different route.--Kmhkmh (talk) 08:14, 21 May 2010 (UTC)

Sorry Kmhkmh, I cannot see any connection between compromising in a WP article and using IRC or Skype and I think it is improper for you to make such a connection. I also cannot see any problem using the medium that we are all clearly happy with which is a wiki. I am very willing to discuss anything with Andrevan in near real time on the page that I set up. Martin Hogbin (talk) 14:20, 21 May 2010 (UTC)

Sorry Martin, but I have to agree with Kmhkmh here. This seems like an analogous situation. You claim you're willing to participate in mediation. The mediator says we should use IRC or Skype. You prefer wiki, and are basically saying you won't participate unless you get your way. I mean, seriously, what conceivable difference does it make to you whether you're typing in a wiki edit window or an IRC client? How it comes across is as sheer stubbornness. -- Rick Block (talk) 20:00, 21 May 2010 (UTC)

This is beginning to look a little like a personal attack. This dispute is not about my character it about our differing opinions on the MHP. Martin Hogbin (talk) 21:58, 21 May 2010 (UTC)

No offense, but year long edit conflict between the same people over a somewhat minor things in the big picture is very very rarely due to the subject matter alone, but is often to a large degree due to the involved personalities as well (and in doubt their unwillingness for any real compromise). That holds for all involved of course. But again if somebody really wants to resolve an issue, he/she should be willing to talk "live" or in person. A blunt and general refusal to do so and stick to method that failed for over a year instead is imho a clear indicator for a lack of interest to find a compromise. It's a bit like politicians unwilling to meet and negotiate directly but sending each other public letters instead. One cannot help but wonder whether they really seek an actual compromise or just trying to turn the "publicity war" in their favour.--Kmhkmh (talk) 22:28, 21 May 2010 (UTC)

Nobody asked, but I'm an 'audit trail' guy myself. That's one of the great things about this tool we call Wikipedia that we've all agreed to work with to this point. Unless that audit trail can be assured, I see Martin's hesitance to change as reasonable. Glkanter (talk) 00:47, 22 May 2010 (UTC)

No offence, but it helps to read the actual conversation.s It was repeatedly pointed out, that you can log an irc discussions (in fact every participant can), i.e. it can be assured to have an "audit trail". That aside the goal of the live discussion is not final "back door deal", but to see whether Rick and Martin can come up with a common suggestion in a direct and live discussion with andrevan's help. If they manage to do that, they can post their common suggestion here to see whether the rest of the editors (at large) might agree to it.--Kmhkmh (talk) 01:30, 22 May 2010 (UTC)

In my opinion, if everyone agrees that we should have an IRC mediation except Martin, and Martin staunchly refuses to acknowledge the value of a real time mediation, then he is single-handedly holding up progress. There is no lack of audit trail on a real-time conversation and I've not heard any other objections raised except simple distaste. Andrevan@ 02:28, 22 May 2010 (UTC)

I would suggest that before anyone assigns the blame for 'single-handedly holding up progress', that person should reflect upon his own responsibilities to this mediation. Perhaps by not participating in any way whatsoever for over 30 days, and then only when prompted, maybe that person is already to be blamed for 'single-handedly holding up progress'. Glkanter (talk) 03:11, 22 May 2010 (UTC)

A mediator is not a miracle worker, i.e. he can only mediate if people are really willing to resolve the issue and a month ago imho they were mostly not.--Kmhkmh (talk) 03:33, 22 May 2010 (UTC)

@Andrevan, if you wish to exclude me from this mediation on the basis that I do not want to participated in off-wiki conversation that is up to you. I would see that as an abuse of your position of mediator here; there is an important point of principle at stake. I do not believe that any editor should be penalised for not wishing to engage in of-wiki discussion, that is clearly contrary to the the spirit of Wikipedia. I note that off-wiki discussion is permitted in the mediation policy but this is mainly for the benefit of editors who fear that their mediation discussions may be held against them at a later time. I have no such fears and am perfectly willing to have my comments remain on record. I would also ask you to note the following facts:

I am perfectly willing to talk to you in real time and I have set up a page in my user space for this purpose. We merely agree a time when we can both be on line (just as with any other medium) and start talking. Why not give this a try? If it fails the I will happily consider alternatives.
So far only one editor has actually agreed to off-wiki discussion with one implied agreement and one agreement subject to an agenda. To call my objection 'single-handedly holding up progress' is a gross exaggeration. Martin Hogbin (talk) 10:05, 22 May 2010 (UTC)
- On-wiki conversation is NOT real-time! If we edit at the same time, we will get edit conflicted. That's not a solution. Andrevan@ 03:14, 23 May 2010 (UTC)

In polite conversation between two people, both do not speak at the same time. I am willing to give it a go, are you? To save the others from all this irrelevance how about we discuss this further on the page that I have set up? Martin Hogbin (talk) 16:53, 23 May 2010 (UTC)

Sources and Wikipedia Policies

You guys crack me up with all this so-called 'horse trading'.

The rules are the rules. The article is poorly written, confuses innocent readers, and, imho, has a WP:Weighting problem with one source.

Nothing else matters. Glkanter (talk) 01:59, 20 May 2010 (UTC)

We have just had yet another visitor convinced that it is 50:50. That is the mistake which nearly everybody makes. Nobody cares which door the host opens. We must first convince people that the chances of winning by switching are 2/3. This article fails in its primary function of doing that. After that has been done we can talk about host behaviour and other variations.

Does anyone here thing that the recent IP editor to this article has read all about Morgan's solution? Of course not. He has given up in disgust, convinced that we are a bunch of idiots. Martin Hogbin (talk) 16:50, 23 May 2010 (UTC)

That is the result of incorrigible blinkered off-topic presentation of the problem. The central question being ignored, and, out of thin air, completely meaningless off-topic elements (alleged presentation of far-fetched aspects of the current constellation) control the lemma. Instead of treating them as what they are: malicious distortion of the central theme. The knock-on effect is obvious. Too bad. --Gerhardvalentin (talk) 17:53, 23 May 2010 (UTC)

This editor changed the "Popular solution" section, not the "Probabilistic solution" section, based on the (incorrect) reasoning that the following four possibilities are all equally likely:

1) The player initially picks the car and the host shows Goat A

2) The player initially picks the car and the host shows Goat B

3) The player initially picks Goat A and the host shows Goat B

4) The player initially picks Goat B and the host shows Goat A

I very highly doubt there is ANY "simple solution" that would convince this person, however the equivalent image (or the decision tree) in the "Probabilistic solution" clearly addresses this line of thinking showing that these possibilities (presented in "door centric" fashion, rather than "goat centric") are not equally likely, but instead have probabilities 1/6, 1/6, 1/3, and 1/3. How about replacing the image in the "Popular solution" section with vos Savant's table - i.e. this one:

Door 1	Door 2	Door 3	result if switching	result if staying
Car	Goat	Goat	Goat	Car
Goat	Car	Goat	Car	Goat
Goat	Goat	Car	Car	Goat

This table shows the same thing the image does, but without the complexity of distinguishing the goats. Although better, I suspect it's still subject to the same sort of misinterpretation, i.e. if the player picks door 1 and the host opens door 3 (like it says in the problem description) only the first two lines apply. In one case you win the car and in the other you win a goat - so the probability must be 50/50 (which is, of course, wrong). I think this particular confusion can only be addressed by clearly showing that the host opening a door when the player has initially picked the car cuts the probability in half. A table (from /Archive 15, showing expected cases in 300 samples of the show) that clearly shows this is:

Door 1	Door 2	Door 3	total cases	host opens Door 2		host opens Door 3
				cases	result if switching	cases	result if switching
Car	Goat	Goat	100	50	Goat	50	Goat
Goat	Car	Goat	100	0	N/A	100	Car
Goat	Goat	Car	100	100	Car	0	N/A

From this table it's clear that you win (unconditionally) 200 times out of 300 if you switch (same as vos Savant's table), but you also win 100 times out of 150 no matter which door the host opens. If your goal is to be convincing, I think you need to show the unconditional and conditional solutions are BOTH 2/3 chance of winning by switching. -- Rick Block (talk) 18:21, 23 May 2010 (UTC)

Yes Rick, it is clear to you, and to me, and to all the regular editors here, but it is not clear to many people who see the problem for the first time. This is the Monty Hall problem. For some reason most people do not believe the solution when they first see it.

To say, 'I very highly doubt there is ANY "simple solution" that would convince this person' is to give up. This person is not a one-off idiot, they are typical of the vast majority of the population; vos Savant's response tell us that. We have a duty to do all we can to convince readers of the correct answer before they lose interest in the article completely. Martin Hogbin (talk) 19:51, 23 May 2010 (UTC)

Martin - I'm suggesting a change here, not giving up. Specifically, what do you think about replacing the image that this user apparently found confusing with vos Savant's table? And, possibly separately, what do you think about the combined table above? -- Rick Block (talk) 21:00, 23 May 2010 (UTC)

Anyone have anything to say about this? If not, I'll replace the image with the table and see if anyone reverts. -- Rick Block (talk) 21:29, 24 May 2010 (UTC)

Until we have resolved the dispute about structure there is little point thinking about this. Martin Hogbin (talk) 22:06, 24 May 2010 (UTC)

There's already a section on popular (simple) solutions. Glkanter complained about it above and I've suggested he try to fix it, but he's done nothing. You're complaining here but are apparently even refusing to think about it until the dispute about the structure is resolved. It seems you and Glkanter are not as eager to make changes as you've been claiming. Like I said above, I think the current "popular solution" section is horrible. If neither of you are going to try to fix it, I will. -- Rick Block (talk) 02:57, 25 May 2010 (UTC)

As you well know Rick, being the prime participant, my edits to the article are nearly always reverted. Which is ironic as this most recently happened after you filed that RfC/U on me and 'charged' me with not editing the article enough and discussing things too much on the talk pages. So, I'd appreciate it if you would please refrain from discussing my frame of mind vis-a-vis editing this article. Glkanter (talk) 09:52, 25 May 2010 (UTC)

In fact, here's your most recent warning to me, just a week ago, that this will happen again when I edit the Popular section:

"If you don't want to list them here and would rather just make changes to the article go ahead, but per WP:BRD if someone reverts a change you make you should take that as an indication we need to talk about it (i.e. don't just revert back). -- Rick Block (talk) 17:23, 18 May 2010 (UTC)"

Or was this your way of suggesting to other like-minded editors that they do the same to my edits? Because I damn well know how editing and revert wars work. You've given me quite the education, thank you. Glkanter (talk) 10:08, 25 May 2010 (UTC)

I have just reverted yet another editor who thinks the answer is 50:50. Does anyone here still believe that the article is doing a good job of explaining the MHP to people? Martin Hogbin (talk) 08:48, 26 May 2010 (UTC)

Sorry Martin, think of Paul Erdoes! Nijdam (talk) 09:21, 26 May 2010 (UTC)

Yes, I do. There is no shame in getting the answer wrong. We all agree that the problem is one that most people get wrong at first sight, even famous mathematicians. That is why we must make every effort to explain the basic problem to the reader before we start on host legal door choice. It was the basic problem that fooled Paul Erdos, it was the basic problem that caused vos Savant to receive thousands of letters telling her she was wrong, it is the basic problem that we must address in this article first. Did you get my email by the way? Martin Hogbin (talk) 09:47, 26 May 2010 (UTC)

Information?

The article says that "A competing deeply rooted intuition at work in the Monty Hall problem is the belief that exposing information that is already known does not affect probabilities", and then goes on to say that sometimes this gives wrong answers. Well, the claim that exposing already known information $C$ does not affect probabilities is always trivially true, and ought to mean just that $P(A\,|\,B\cap C)=P(A\,|\,B)$ , where $B\subseteq C$ . Confusingly, that's not what is meant here, though. It is also not clear what is meant.

Apparently, the statement refers to the explanation "As the host opening a door to reveal a goat gives the player no new information about what is behind the door he has chosen, the probability of there being a car remains 1/3." in the "popular solution" section. But information that is not already known is exposed here: the player did not know that there was a goat behind the door that was opened. It is new information that affects probabilities, not already known information. -- Coffee2theorems (talk) 03:34, 24 May 2010 (UTC)

I agree that paragraph needs work. In addition the cited source seems to be about the 3 prisoner problem rather than MHP itself. Does anybody have the cited source at hand, so see what it says exactly?--Kmhkmh (talk) 03:45, 24 May 2010 (UTC)

I have a copy of Falk's paper. Falk quotes vos Savant's explanation involving the shell example that was published in Parade in December 1990:

The winning odds of 1/3 on the first choice can't go up to 1/2 just because the host opens a losing door. To illustrate this, let's say we play a shell game. You look away, and I put a pea under one of three shells. Then I ask you to put your finger on a shell. The odds that your choice contains a pea are 1/3, agreed? Then I simply lift up an empty shell from the remaining two. As I can (and will) do this regardless of what you've chosen [italics added], we've learned nothing to allow us to revise the odds on the shell under your finger.

Falk goes on to show that because vos Savant has not specified which of the two empty shells she would lift up if the pea is under the player's finger, it's possible she picks in a biased manner in this case. If the player knows the bias and it's an absolute bias, then if the preferred shell is the one that is lifted up the odds rise from 1/3 to 1/2.

Falk doesn't put it this way, but the problem with the argument (that because you already know one of the two doors must be a loser, knowing which one doesn't give you any information) is that knowing specifically which shell is lifted up (or specifically which door the host opens) is not the same as knowing that one of two shells (or two doors) must be a loser. Any suggestions for how to clarify this? -- Rick Block (talk) 04:20, 24 May 2010 (UTC)

That's one point from above where I disagree with you Rick. "...is that knowing specifically which shell is lifted up (or specifically which door the host opens) is not the same as knowing that one of two shells (or two doors) must be a loser." In the symmetrical problem there are various sources that say they are the same. Or, they leave out the 'obvious' part '...and this simple solution distributes equally over all contestant door selections and host reveal pairings'. There's nothing to clear up. Glkanter (talk) 05:04, 24 May 2010 (UTC)

Yes, you are quire right, Coffee2theorems "A competing deeply rooted intuition at work in the Monty Hall problem is the belief that exposing information that is already known does not affect probabilities", is incorrect and should not be in the article. If no new information of any kind is revealed then the probabilities are not changed, this is fundamental to the meaning of probability, but, as you correctly point out, information is revealed when the host opens a door. Martin Hogbin (talk) 09:18, 24 May 2010 (UTC)

What I'm suggesting we clarify is the point that Falk is making, which is that the (correct) intuition that exposing information that is already known is what makes the statements like "As the host opening a door to reveal a goat gives the player no new information about what is behind the door he has chosen, the probability of there being a car remains 1/3." seem like sound probabilistic reasoning when they really aren't. Again, knowing specifically which shell is lifted up (or specifically which door the host opens) is not the same as knowing that one of two shells (or two doors) must be a loser. The reason the probability the player's initial choice of door doesn't change when the host opens, say, door 3 even in the symmetric case is NOT that this does not provide any information to the player. It clearly does - which is what Coffee2theorems is saying. The player didn't know there was a goat behind door 3, and now does. This is what enables the player to revise her estimate of the chance of the car being behind door 3 to 0, and just as this information affects the chance of the car being behind door 3 it MAY affect the chance of the car being behind door 1 or door 2. Falk provides another example (from Shimojo and Ichikawa) based on the Three Prisoner's problem (not MHP) that doesn't even require host bias, but uses different initial probabilities for each prisoner. -- Rick Block (talk) 13:46, 24 May 2010 (UTC)

"As the host opening a door to reveal a goat gives the player no new information about what is behind the door he has chosen, the probability of there being a car remains 1/3." is perfectly good reasoning. I think this is where it all started. Martin Hogbin (talk) 22:24, 24 May 2010 (UTC)

Well not quite, since in the general case that is not true. It is only perfectly good reasoning in a particular context. In general case any new information can potentially affect all conditional probabilities.--Kmhkmh (talk) 22:52, 24 May 2010 (UTC)

It is true in all cases. If you want to argue the case, I suggest the arguments page. Martin Hogbin (talk) 22:55, 24 May 2010 (UTC)

No it is not and no offense, but i neither care for your private theories nor am I going to rehash the discussion of the whole last year.--Kmhkmh (talk) 22:59, 24 May 2010 (UTC)

Oh yes it is! Since you are not willing to discuss the subject or defend your claim using generally accepted theories of probability I guess we we may as well treat this disagreement as a pantomime. Martin Hogbin (talk) 08:35, 25 May 2010 (UTC)

If you want to discuss theories, use the usenet. I'm not interested in playing any "you need to argue with me or I'm right"-games with you. There was no claim that needed any defending, I just pointed out some textbook knowledge. Whether you want to believe it or not that's your choice.--Kmhkmh (talk) 10:02, 25 May 2010 (UTC)

You chose to challenge my statement. The talk pages are the correct place to discuss the subject matter of a WP article. You may choose argument by assertion; I do not. Martin Hogbin (talk) 11:30, 25 May 2010 (UTC)

It might help to stay focused on what Falk is saying, which is that the intuition that learning something you already know can't affect probabilities is what makes the "you already know one of the two doors hides a goat, so knowing which one can't change anything" argument so compelling (even though it's not correct unless you constrain the problem in other ways as well). -- Rick Block (talk) 23:27, 24 May 2010 (UTC)

Yes, I agree. I do not have a copy of the Falk paper, so I do not know exactly what is said. Martin Hogbin (talk) 11:15, 25 May 2010 (UTC)

Can you get a copy? It's available (for a fee) online, e.g. here or you should be able to find a copy at any university library. As per the abstract, the paper examines the beliefs people rely on to solve problems like the Three Prisoners problem and the Monty Hall problem. Falk identifies two primary beliefs at work in these problems: one is the equal probability assumption (which most people who get the answer wrong are firmly attached to), the other is the "no news" assumption (which we're talking about here) under which people (incorrectly - according to her) assume finding out that one of two doors (at least one of which is known to be a loser) is a loser cannot affect the probability of the player's initially chosen door (and most people who get the answer "right" are firmly attached to this). Her point is that neither of these are correct all the time. -- Rick Block (talk) 15:20, 25 May 2010 (UTC)

I did pay to get the Morgan paper and I begrudge every penny of it. I am not inclined to spend $31 to read the opinion of a psychologist on the meaning of probability. If someone could email me or post the relevant sections here that would be great. Martin Hogbin (talk) 16:15, 25 May 2010 (UTC)

If you don't want to pay for online access, then by all means go to a university library and find a copy. The summary I posted above is accurate. I can post some direct quotes if you'd like, but I'm not going to type in the entire 20+ page paper if you simply refuse to chase down sources on your own. The reason this particular paper is cited is because it is one of the standard psychological references about problems like the MHP - it is cited 57 times according to Google Scholar (Krauss and Wang, Mueser and Granberg, even Rosenhouse's book all cite it). BTW - she's not writing about her opinion of the meaning of probability, but rather about the psychological reasons why particular solutions appear to be true. She's listed as a "Prof E" (emeritus?) on the faculty page of the Hebrew University of Jerusalem with research interests in probabilistic and statistical reasoning, and solving puzzles, problems and paradoxes. She is a bona fide expert in the exact topic we're talking about here. -- Rick Block (talk) 22:13, 25 May 2010 (UTC)

I will see what I can find. I am not questioning Falk's credentials as a psychologist but you seem to be saying that Falk makes the statement that a probability can be changed even if no new relevant information is revealed. Is this what is said? Martin Hogbin (talk) 08:43, 26 May 2010 (UTC)

How to clarify the text is a good question. When you say that the intuition that "no change in information means no change in probabilities" causes problems, then you're right after a fashion. It causes problems because the intuition about what constitutes relevant information is not necessarily reliable, and you wouldn't be counting on it and thereby led astray if you didn't have the first (correct) intuition. Let's look at the notion of relevant information a bit more closely; you don't even need probabilities to see the problem here.

Clearly, any sensible notion of relevant information must at least include anything that would, under the rules of classical logic, allow you to deduce everything. For instance, if you picked the door number 1 (I'll assume this throughout for simplicity), and you were shown what is behind doors 2 and 3, then you would also know what is behind the door you have chosen. It wouldn't make any sense to insist that "no information" has been provided about what's behind door 1 in this case, simply because the the door remains closed, and you haven't actually seen what is behind it.

The same thing applies if you know that the host has joined the Cult of Even Numbers, and will choose to open door 2 whenever he can, because he would be committing dreadful sin if he were to slight an even number by preferring to open an odd-numbered door. Suppose that door 3 is opened. You know that there is no goat behind door 2, because if there were, your host would now be a very sinful man. You therefore know that there is a car behind door 2, and goats behind doors 1 and 3. In this situation you were provided with information about what's behind all the doors, even though only one was opened. The door the host chose was relevant information because of the extreme religious bias of the host.

In a probabilistic setting, the idea that "opening the door

D=2

or

D=3

to show a goat does not provide any information about whether the thing

X

behind door 1 is a car or a goat" makes sense, if you take it as the assumption that the mutual information

I(X;D)=0

, or equivalently that

P(X|D)=P(X)

, i.e. "knowing D does not tell you anything about X" (or "D and X are independent"). The assumption holds if and only if the host chooses uniformly at random among the possible choices. In any other case, the mutual information is nonzero, and the probabilities change in a way not consistent with the standard solution (like in the extreme case of the previous paragraph, where

P(D=2|X={\text{Car}})=1

, which is as far from 1/2 as you can get, and D = 2 gets preferential treatment). -- Coffee2theorems (talk) 11:47, 26 May 2010 (UTC)

After rereading my exchange with Martin above and putting this in the context of Coffee2theorems' original objection and in the context of the description of Falk's argument in Rosenhouse's book (p.137-139) as well, it seems to me that there's a language problem, because subtle changes in the formulation can change the problem completely (which anyhow is a core problem with MHP). There is a difference between

a)"If the host opening a door to reveal a goat gives the player no new information about what is behind the door he has chosen, the probability of there being a car remains 1/3."

and

b)"As the host opening a door to reveal a goat gives the player no new information about what is behind the door he has chosen, the probability of there being a car remains 1/3."

a) is basically Coffee2theorems correct argument and follows from the definition of conditional probabilities, i.e. it hold always. b) was Martin's argument which is in fact a rather different claim and is not true for all takes on MHP. Why is is that? Because b) contrary to a) states that we already know for sure that now new information is revealed. This is an additional assumption and precisely the one that the standard conditional solution dismisses. It is not always obvious when some (random) piece of new information does have bearing on the concerned problem and when not. Furthermore as Falk puts it, not only the perceived basic information matters, but also they way it was collected, as slight differences the collection procedure (or the way the information was formulated for/conveyed to us) can influence the way we model the problem. Or you could argue that small differences in data collection do present additional (new) information themselves.--Kmhkmh (talk) 10:40, 26 May 2010 (UTC)

The problem is that I do not (yet) have a copy of the Falk paper thus I cannot really argue about what it says. I would suggest that the offending sentence is removed until we can all agree on exactly what point Falk was making, whether this point is supported by other reliable sources, and whether the point is relevant to the article. Martin Hogbin (talk) 11:42, 26 May 2010 (UTC)

That's not necessary. Anybody with access to the paper may correct the formulation. That Falk is reputable and relevant source for the article is rather obvious, there isn't really anything to discuss there.--Kmhkmh (talk) 11:49, 26 May 2010 (UTC)

Can somebody explain what the issue is with the text in the article? It says:

A competing deeply rooted intuition at work in the Monty Hall problem is the belief that exposing information that is already known does not affect probabilities (Falk 1992:207). This intuition is the basis of solutions to the problem that assert the host's action of opening a door does not change the player's initial 1/3 chance of selecting the car. For the fully explicit problem this intuition leads to the correct numerical answer, 2/3 chance of winning the car by switching, but leads to the same solution for slightly modified problems where this answer is not correct (Falk 1992:207).

Is the issue that the first sentence is being taken to mean that Falk is suggesting exposing known information may affect probabilities? Although just because something is a belief doesn't mean it's not true, how about if we delete "the belief"? I think Coffee2theorems has this exactly right, i.e. the problem (vis-à-vis the MHP) is not that this intuition is incorrect, but that people's judgment about what constitutes "already known" information is not necessarily reliable. In the MHP, knowing there's at least one goat behind two closed doors is not the same as knowing there's a goat behind one specific door (and knowing a goat MAY be behind another). The latter implies the former, but not vice versa - i.e. these clearly do not constitute the same information. -- Rick Block (talk) 14:42, 26 May 2010 (UTC)

I see it basically as in your for first sentence. Though it doesn't have to be read that, it is at least easy to "misunderstand" the formulation that way. If this is due to literal repetition of Falk's original statement, I suggest that the WP author repeats Falk's argument in this own words avoiding that exact phrase.--Kmhkmh (talk) 16:13, 26 May 2010 (UTC)

Another thing that might need to be clarified here. Is Falk with her conclusions explicitly talking about the MHP or "just" about related problems as "3 prisoners" or "2 sons"?--Kmhkmh (talk) 16:19, 26 May 2010 (UTC)

Holding Up Progress

While you guys go over old ground, I was wondering if anybody has heard from the 'mediator'? Maybe it's time to request a different one? Glkanter (talk) 15:21, 26 May 2010 (UTC)

We certainly need something to move us on. Maybe another mediator could help. Martin Hogbin (talk) 17:48, 26 May 2010 (UTC)

There's Only One Formulation Of The MHP Still Standing

The host must reveal a goat, and he chooses amongst two goats uniformly at random. Selvin said this in 1975. Uninformed people neglect this fact.

The simple omniconditional solutions solve this problem whether one argues that the contestant must see the door opened or not, as this solution '...applies uniformly across any and all door selection and door revealed pairings'. Even Morgan admits this, finally. Everything else is clutter that needs to be kept out of the reader's way until necessary as per Wikipedia policy, or answers a different, irrelevant problem, and doesn't belong in the article. Glkanter (talk) 12:04, 27 May 2010 (UTC)

Exactly! Selvin clearly intended this to be a simple mathematical puzzle and that is how we should treat it here. Martin Hogbin (talk) 12:57, 27 May 2010 (UTC)

The original intent is only one part, the other and over time even more important one is the perception (in ltiterature). Also you are very well aware, that Selvin in his 2nd letter suggested a conditional solution as well.--Kmhkmh (talk) 13:04, 27 May 2010 (UTC)

The vast majority of sources do not mention any condition. Martin Hogbin (talk) 13:06, 27 May 2010 (UTC)

That is again a misrepresentation, as it has been pointed out to you several times now. If you keep repeating that we get nowhere.--Kmhkmh (talk) 13:12, 27 May 2010 (UTC)

The Meta Paradox of The Monty Hall Problem Paradox

Selvin poses the MHp in his first letter to The American Statistician. He solves it unconditionally at 2/3 vs 1/3 if you switch. This 'omniconditional' solution also satisfies any and all 'contestant door choice' and 'host goat door revealed' pairings. The problem is hailed as a great paradox.

vos Savant prints a letter inspired by Selvin in a general interest USA Sunday newspaper supplement. She solves it unconditionally at 2/3 vs 1/3 both when you made your choice, and when the switch is offered. Because Monty's actions don't impart usable knowledge to the contestant. It's a sleight of hand. Nothing happened.

All heck breaks out. Tens of thousands of letters, including over 1,000 from PhDs tell her she's wrong. And they are certain!

vos Savant soothes the savage beasts with logic and smarts. The unconditional solution carries the day. The problem is, again, hailed as a great paradox.

This group, "J. P. Morgan, N. R. Chaganty, and M. J. Doviak are Associate Professors and R. C. Dahiya is Professor, all in the Department of Mathematics and Statistics, Old Dominion University, Norfolk, Virginia" (284 The American Statistician, November 1991, Vol. 45, No. 4 (C 1991 American Statistical Association) develops the argument that the problem is only properly solved using a conditional problem statement. Their criticisms, etc. rest on this: That when faced with 2 goats, the host must decide which goat to reveal. This rests on the assumption (presumption, invention) that the contestant might somehow gain usable information as to the location of the car in this particular instance of the game by Monty's actions. It's left unstated whether Monty's actions would be shared with the contestant. And if they are shared, what method is used. But it's clear: in this instance of game play they claim, the subject contestant could be armed with more useful information that the average contestant.

The only problem is, well, there are two problems, actually. First, in Selvin's second letter to The American Statistician, he makes it quite clear that his solution relies on the host always offering the switch, and that the host chooses between two goat doors randomly. But Morgan does not mention Selvin in the paper. They may indeed, be ignorant of his contribution to the puzzle, even though his letters and Morgan's paper appear in the same professional journal. The second is that their 'assumption' is not consistent with the first words of the MHP problem statement: "Suppose you're on a game show...", as Hosts don't tell contestants where the car is hidden. Oh, and "Richard G. Seymann is Professor of Statistics and Business Administration, School of Business, Lynchburg College, Lynchburg, VA 24501" (1991 American Statistical Association The American Statistician, November 1991, Vol. 45, No. 4 287) wrote a paper that spoke only about Morgan's paper. It was included in the very same issue of the journal. It's weird. Is it a disclaimer, a clarifier? It's sure not an endorsement.

Others come out with papers supporting Morgans criticisms, including Gillman in 1992 and Grinstead and Snell 2006.

Others continue publishing unconditional papers. (It seems likely that if 3 Wikipedia editors plus Seymann find fault with the paper, so too would members of the Professional Mathematics Community. And as professionals, they don't make a big stink about it. They just ignore the paper and continue publishing articles that rely solely on the unconditional problem statement.)

So, has the Professional Mathematics Community decided that Morgan is right, and Selvin was a hack? I don't think so. Before, during and after Morgan's paper, respected, credentialed reliable Mathematics professionals continued to publish articles solving the MHP unconditionally. I don't know that any of these professionals in either camp have attacked or counter-attacked anyone else's paper. It looks to me, that in the Professional Mathematics Community nothing happened. No usable information was gained. Perhaps Morgan's paper, like Monty revealing a goat is just sleight of hand, imparting no usable knowledge? It's possible. Most published MHP articles say nothing of Morgan or conditionality.

Then, in May of 2010, two Wikipedia editors have a letter published in The American Statistician (only after a peer review by the journal) pointing out an error in one of Morgan's calculations. They derived a result of .693 rather than the correct .667. A very familiar number, indeed. Morgan thanks these editors, and further states (emphasis theirs): "Simply put, if the host must show a goat, the player should switch."

Which brings us, finally, to the Meta Paradox. The Wikipedia editors are arguing, essentially, over whether or not solving the unconditional problem is 'enough'.

Suppose you are given a story problem about a game show. The Professional Mathematics Community agrees heartily that this is a delightful paradox which can be 'proved' or 'solved' using an unconditional problem statement. Maybe not even requiring formal probability notation. Symbolic notation is often used. Then "J. P. Morgan, N. R. Chaganty, and M. J. Doviak are Associate Professors and R. C. Dahiya is Professor, all in the Department of Mathematics and Statistics, Old Dominion University, Norfolk, Virginia" come forth and say it must be solved conditionally, based on the arguments set forth in their paper, but which they ultimately temper, 19 years, when prompted by a letter from two Wikipedia editors pointing out a math error in their original paper. You are then offered to stay with the unconditional solution being complete, or you may switch to the conditional solution.

Many people are fooled by this paradox, and accept the switch. Because they don't realize that like Monty revealing the goat, no new usable information has been revealed by this paper. Nothing happened. Glkanter (talk) 18:27, 8 December 2009 (UTC) revision # 1 Glkanter (talk) 04:41, 28 May 2010 (UTC)

For a contrasting view, here's what Dr. Joseph G. Eisenhauer (at the time, an economics professor at Canisius College) has to say (from The Monty Hall Matrix):

When asked the probabilities of winning by switching and not switching, the vast majority of respondents answer that with two doors unopened and a prize behind one of them, the doors are equally attractive: the chance of winning is 1/2 in either case. On the other hand, it is sometimes argued that since one knows in advance that Monty will reveal a zonk, the revelation provides no relevant information to the contestant (see, for example, Nalebuff 1987). In this view, which Falk (1992) calls the "no news" argument, the probability that the prize is behind the chosen door is 1/3, just as it was a priori, whereas switching doors gives a 2/3 probability of winning.

The clash of these two perspectives led to something of a public uproar when columnist Marilyn vos Savant (1990a,b,1991) discussed the problem in a series of magazine articles, and asserted that the probabilities of winning are 2/3 for switching and 1/3 for not switching. Some 10,000 readers, including many irate teachers and college faculty, responded with letters, 90% of them vehemently disagreeing with vos Savant (and some personally denouncing her) in favour of the 50-50 odds (Tierney 1991). Adding to the confusion, vos Savant then gave a 'dubious analogy . . . [and] went on to defend her original claim with a false proof and also suggested a false simulation as a method of empirical verification (Morgan et al. 1991, p. 284). Consequently, what could and should have been a correct and enlightening answer to the problem was made unconvincing and misleading. Subsequent work by Gillman (1992) and Falk (1992) applied the correct Bayesian mathematics to derive the general solution, but several other authors continued to perpetuate the "no news" argument, which at best relies on an unstated assumption (see, for example, Engel and Ventoulias 1991; Gilovich et al. 1995).

This is a direct quote from a paper published in "Teaching Statistics" (a peer reviewed journal). -- Rick Block (talk) 05:50, 28 May 2010 (UTC)

I guess there should be something in the article for statistics students but the vast majority of our readers will not be studying statistics. The article should be principally about the simple probability puzzle that is the MHP and it should be written for the general public. Martin Hogbin (talk) 11:05, 28 May 2010 (UTC)

Effects of switching (all configurations)

Supposition: Symmetric random distribution of the three objects. Guest selects a door at random. There is only one car.
Thus the pair of the two unelected doors inevitably must contain at least ONE predetermined goat. Host opens one of them showing a goat. This event occurs every time.
In case the Host has TWO goats to select from he will open one door at random, never revealing any undue additional information whatsoever about the actual configuration.

Car behind door	Guest selects door	The non elected pair of two doors contains always at least 1 goat but in 2/3 of cases also the car	Loss by switching only in 3 of 9 cases: Only if (by chance) the original coice was the only car Thus: Loss only in one third of all cases	Prize gained by switching in 6 of 9 cases: Always if one of the two doors containing a goat was selected	Host opens a door showing a goat	Effect of switching:
1	1	Goat ⇔ Goat	Loss, no matter whether Host opens door 2 or door 3		2 or 3	Car door 1 was selected, switching hurts
1	2	Goat ⇔ Car		Prize	3	Goat door 2 was selected, switching to door 1 will win the prize
1	3	Goat ⇔ Car		Prize	2	Goat door 3 was selected, switching to door 1 will win the prize
2	1	Goat ⇔ Car		Prize	3	Goat door 1 was selected, switching to door 2 will win the prize
2	2	Goat ⇔ Goat	Loss, no matter whether Host opens door 1 or door 3		1 or 3	Car door 2 was selected, switching hurts
2	3	Goat ⇔ Car		Prize	1	Goat door 3 was selected, switching to door 2 will win the prize
3	1	Goat ⇔ Car		Prize	2	Goat door 1 was selected, switching to door 3 will win the prize
3	2	Goat ⇔ Car		Prize	1	Goat door 2 was selected, switching to door 3 will win the prize
3	3	Goat ⇔ Goat	Loss, no matter whether Host opens door 1 or door 2		1 or 2	Car door 3 was selected, switching hurts
Chance to win:	${\tfrac {1}{3}}$	$0$ ${\tfrac {2}{3}}$	Distribution of chances 1/3 : 0 : 2/3 is in effect from the start until the end of the game, according to the rules
Risk of loss:	${\tfrac {2}{3}}$	$1$ ${\tfrac {1}{3}}$	Distribution of risk 2/3 : 1 : 1/3 is in effect from the start until the end of the game, according to the rules

In that 1/3 of all cases that the Guest, by chance, has selected the only door with the car, switching was a loss.
That's just 3 of 9 options, so in only one third of the cases switching will lose the already selected car and hurts.

But in the remaining 2/3 of all cases, that the Guest had selected one of the two doors containing a goat, she will win the car by switching.
That is 6 of 9 options, i.e. in two thirds of the cases switching will win the car.

Without switching: The Guest will win only if her first choice had been the door with the car (probability 1/3).
By switching the Guest will always win the car when her first choice was one of the two rivets (probability 2/3).
By switching her chance of winning will double from 1/3 to 2/3.

(copy)

--Gerhardvalentin (talk) 22:19, 23 May 2010 (UTC)

This is basically an expanded version of vos Savant's table. Are you suggesting it's easier to understand? -- Rick Block (talk) 23:35, 23 May 2010 (UTC)

Rick: The paradox consists in the popular error (intuitively 1/2 instead of 2/3).
Besides this famous MHP-paradox also other scenarios – that significantly differ from the simple and fundamental "Ask Marilyn question" – have been discussed:
Was it eventually just a low-down, pretending and very tricky question? – Or not?
Does the host offer to switch only if the guest should, by chance, have chosen the only door hiding the car?
Or is the host eventually to deal closer with the respective actual current situation, giving away unexpected additional tricky hints about the respective actual current constellation?
Does he, under such condition, besides opening one door showing a goat, provide for unexpected additional "peep"-information regarding the respective actual current constellation?
Does he, for example, follow any specific door-preference, never opening a specific non-elected door unless he has no other choice, and by that showing clearly then: that under such "condition" his preferred door actually hides the car? Similar to opening both doors at once (Morgan et al.)?

– And, by opening his "preferred door", showing as well that both closed doors have equal chance of 1/2 each, then?

And if so, what is the rate of such deviant "telltale door-preference, very similar to opening even two doors"?
And who may know and can tell about that? The host himself? Or the guest? Or just the stage director, the producer or the lighting technician? Or someone out of the audience?

The mere "suspicion" of such a bias is never enough. In the absence of such a "known and quantified condition" any "conditional solution" is senseless and therefore useless, unnecessary and pure balderdash. Not part of the original MHP. Not part of the famous "nearly incredible" paradox of the pure "Ask Marilyn-question". Clear condition there: No tricky Host's bias, i.e. no "non uniform goat preference", and the guest may NOT peep behind closed doors.

Although such scenarios, deviantly telling additional information about the respective actual constellation never are provided for in the famous original MHP, they cannot alter the basic fact that two doors have double chance compared to one door. In all those preposterous scenarios, deviating from the original question, the host would remarkably be giving away only additional "conditional" information and closer "conditional" hints on the respective actual current constellation. Unable to change it at all. Never being able to change the actual constellation. Such freaky scenarios do not affect the fundamental paradox. Such "condition" is not part of the MHP. Such preposterous suspicion is quite another issue. But for students of probability theory such different scenarios occasionally are some welcome training ground to practice mathematical probability calculations, quite outside the MHP.

- And yes, I think it's easier to understand. Regards, --Gerhardvalentin (talk) 15:04, 1 June 2010 (UTC)

Error in Morgan paper confirmed

Some editors here may remember the discussion on the arguments page [1] in which I claimed that there was an error in the Morgan paper regarding probability of winning by switching given a noninformative prior distribution of q. That is to say that on the assumption that prior to a door being opened by the host the parameter q has a uniform distribution from 0 to 1. At the bottom of the first column on page 286 of their paper, Morgan give an answer of ln(2) which is about 0.693 whereas I claimed that the correct answer was 2/3. I calculated the correct probability of 2/3 for any distribution of q that was symmetrical about 1/2. Nijdam confirmed and completed my calculation and pointed out that the answer was 2/3 for any distribution of q that has an expectation value of 1/2. Glopk confirmed Nijdam's calculation.

Nijdam and I decided that we should write to 'The American Statistician' with this result and did so. After a long period of peer review, our letter has been published in the May 2010 issue as a letter to the editor, see [2]. This confirms that Morgan did indeed make an error in their calculation, in fact they have thanked us for correcting their mistake. It is interesting to note that the error was due to failing to 'use the information in the number of the door shown'.

I am not sure if there has been a case before where a discussion in Wikipedia has lead to a publication in a peer reviewed journal correcting a previous paper. Martin Hogbin (talk) 17:26, 26 May 2010 (UTC)

Congratulations to all involved! How might this peer-reviewed correction, in the same journal that Morgan was published in, alter Morgan's assertions? Do they stand by their orginal claim that the simple solutions are 'false'? Glkanter

Unfortunately for us the admitted error is only in the calculation of the probability of winning given a noninformative (uniform) prior distribution of q. They have also reconsidered some of what they say in the light of new information about Whitaker's letter, in particular they now say, '...had we adopted conditions implicit in the problem, the answer is 2/3, period'. Martin Hogbin (talk) 22:19, 26 May 2010 (UTC)

Does that acknowledgment allow the removal of some weasel words, and opaque caveats from the article? Glkanter (talk) 22:48, 26 May 2010 (UTC)

Well I think so, but others may not agree. Martin Hogbin (talk) 22:52, 26 May 2010 (UTC)

They also say this (emphasis theirs):

"Simply put, if the host must show a goat, the player should switch."

Now, I don't want to put words in anybody's mouth, but that does not sound like they're still saying you have to open a door revealing a goat in order to knowledgeably decide to switch. Or that, as they chastised vos Savant, simple solutions that say the identical thing as they say above, can still be, as they once pioneered the claim, 'false'. Still no mention of Selvin, though? The Earth is no longer flat, eh, Morgan? Glkanter (talk) 23:05, 26 May 2010 (UTC)

Kind of like the words in the original paper: "Hence we need not know, or make any assumption about, the host's strategy [meaning the probability of opening door 2 vs. door 3 in the case the player picks door 1] to state that the answer to the original question is yes. The player should switch, for she can do no worse and may well improve her chances." The issue has NEVER been about the yes or no answer to the question "should the player switch" - implying that it is, or that Morgan et al. are saying something fundamentally different than what their paper originally said is a complete mischaracterization. -- Rick Block (talk) 23:40, 26 May 2010 (UTC)

I stand by my post as written above, and reject your accusations. Glkanter (talk) 00:51, 27 May 2010 (UTC)

Well congratulations to Nijdam and Martin. Morgan et al.'s reply might actually open the possibility for an interesting side note in our article on MHP. Since they quoted a separate section of Craig's letter, I#m beginning to wonder whether there's a chance to get hold of the complete letter and possibly integrate parts of it into our article.--Kmhkmh (talk) 00:07, 27 May 2010 (UTC)

P.S. You want to consider to pass that info onto the WP sign post.--Kmhkmh (talk) 00:17, 27 May 2010 (UTC)

Wow, I have to say that is remarkable. This certainly should make some progress. I still think there are unresolved issues which a real-time mediation would help. But, I believe that those advocating giving equal weight to the Morgan paper now must seriously consider an "Academic interpretations" section. Andrevan@ 02:15, 27 May 2010 (UTC)

What? The POV Martin wants excluded is represented by dozens (if not hundreds) of sources. The basic conflict has essentially nothing to do with this single paper. The error cited here has absolutely nothing to do with the main point. -- Rick Block (talk) 03:59, 27 May 2010 (UTC)

I have been involved in these discussion for over a year and a half, and have almost always disagreed 100% with Rick Block's opinions and comments. This one sets a new standard. To deny that Morgan is the root of all evil here is pure nonsense. I don't know if he believes what he writes, or if he expects us to. Glkanter (talk) 04:26, 27 May 2010 (UTC)

I've referred to Gillman's paper numerous times. It says almost the exact same thing as the Morgan paper (i.e. criticizes vos Savant's solutions and says the "real" solution depends on the host's preference q and is 1/(1+q)), and as far as I can tell was published independently. It was demonstrably published nearly simultaneously - Morgan et al. was November 1991, Gillman was January 1992. What is pure nonsense is your claim that Morgan is "the root of all evil here". This paper is not in any sense a singularity. It is cited in the article because it is one of the basic references for the MHP (cited by any serious treatment of this problem). As Kmhkmh has said, nearly every introductory probability textbook presents a conditional solution to the MHP. Not all criticize vos Savant - but denying that conditional probability is at least a reasonable way to approach the problem is truly absurd. -- Rick Block (talk) 04:59, 27 May 2010 (UTC)

However this is not about an opinion of Rick but a fact. Morgan's error does not concern the (correct) main argument of his paper which is used in our article. Moreover this main argument has been put forward by many other publications and strictly Morgan is not needed. As laudable as Martin's effort in uncovering this error was, it was a moot point from the beginning as far as this article is concerned, since it was clear from the beginning that this error has no bearing for our article.--Kmhkmh (talk) 09:48, 27 May 2010 (UTC)

This is in Morgan's intro: "The solution and failed attempts at solution are rich in their lessons in thinking about conditional probability." Morgan's paper says all simple unconditional solutions are 'false'. And has accusations of vos Savant using a 'dubious analogy', and a 'false simulation', and then conclude the article patting themselves on the back for their 'correct resolution', and still they find time to joke about bewildered students asking '"How do you expect me to solve a problem that stumped scores of Ph.D.'s and confused the world's most intelligent person?" !" Bunch of hacks like I've never seen before.

After plastering the article with Morgan for years, now this is your argument, Rick: "...conditional probability is at least a reasonable way to approach the problem..." Oh, how the mighty have fallen. Glkanter (talk) 05:29, 27 May 2010 (UTC)

@Rick, I agree that this error has little to do with the main point of the article but that is simply because the Morgan paper has little to do with it either. The main point about the MHP is very simple, most people think the answer is 1/2 but in fact it is 2/3. Martin Hogbin (talk) 10:15, 27 May 2010 (UTC)

To Martin: EDIT CONFLICTS PREVENT NATURAL DISCUSSION. In a real discussion, people can't compose a response for 15 minutes only to find they had been "interrupted" 2 minutes in; by someone editing their previous response, no less.... If you have a wiki software which has a way around this, or even a traditional forum that allows concurrent posts without simultaneous editing of a document... fire away.

Andrevan, I do not wish to engage in off-wiki conversation, and writing in BOLD CAPITALS is not going to persuade me to do so. I have given full reasons why editors should not be required to engage in off-wiki conversations at Wikipedia_talk:Mediation_Committee/Policy as I believe that this principle should be incorporated into WP policy, for the benefit of others as well as myself. I will be happy to discuss the subject with you there. Martin Hogbin (talk) 08:25, 27 May 2010 (UTC)

Nobody claims you are required to live discussion. The point here was merely that a live discussion might help and you are not even willing to try without giving any reason other than personal distaste.--Kmhkmh (talk) 10:44, 27 May 2010 (UTC)

No one is denying that the conditional approach is reasonable. However, Morgan's error correction does confirm that the simple solution encompasses the conditional solution, and that in fact the simple solution isn't false even according to Morgan -- or do I misunderstand? Why isn't this enough reason to consider Morgan as part of a secondary "academic" section as proposed in Martin's compromise? The level of discourse required to properly discuss conditional probability exceeds the scope of the layman's definition of the problem. We can simply write in the explanation a sentence like, "The problem can also be described by conditional probability -- see #below." Andrevan@ 05:35, 27 May 2010 (UTC)

I don't quite follow you here. The correction of _Morgan shows by no means that the conditional solution is encompassed in the simple one. Not even from the numerical perspective (pick Q=q=1 as an example). As Nijdam has pointed out already depending on what prior distribution Q for the q you pick, you still get any value between 1/2 and 1 and not just 1/3. The essential argument of Morgan or the "conditional camp", that the simple solution is false or incomplete is not affected by Morgan's error, i.e. they still require a condition on the host's bevahiour (whether it is q=1/2 or the slightly generalized E(Q)=1/2) and without that condition 2/3 will be false.--Kmhkmh (talk) 10:39, 27 May 2010 (UTC)

The point about a solution using conditional probability is simply that the, somewhat contrived, formulation in which the host's legal door choice is not assumed to be uniform but the producer's car placement is assumed to be uniform at random can be used to demonstrate the pitfalls of conditional probability calculations. This is undoubtedly a valuable exercise for those studying conditional probability and it is the real point being made by the Morgan paper. On that basis, the conditional solution is worthy of mention somewhere in the article. Morgan also confirm that, whatever the host preference, if the host must show a goat, the player should switch, thus showing that the advice to switch applies to situations where the host might have a goat preference.

On the other hand, the vast majority of the population are not studying conditional probability yet vos Savant received thousands of letters telling her she was wrong. None of these considered the possibility that the host might have a non-uniform legal door preference but most of them were utterly convinced that the answer was 1/2. Selvin, in his second letter, specifically mentioned that the host chose randomly between goats, presumably to avoid the possibility that the answer might depend on the host's goat preference. None of the many sources that addressed the problem before the Morgan paper mention the fact that the host might have a non-uniform goat preference. Most of the sources, including academic ones, after the Morgan paper do not mention this either. There has been a regular stream of editors and readers visiting this page, most of whom have been claiming the answer is 1/2 and none of whom have mentioned the host's goat preference. The MHP is principally a mathematical puzzle, to be framed in such a way that conditional probability has nothing to do with it.

The MHP is notoriously difficult to solve and the first thing this article must do is to make sure that the reader is convinced that the answer is 2/3 and understands why this is so. Any distraction from this objective, such as mentioning conditional probability, saying the the solution given is false, incomplete, or does not answer the question, makes it even harder for the reader to understand and accept the correct solution. Most sources do not mention conditional probability and neither should we (except briefly in a later section).

So actually I am denying that the use of conditional probability is reasonable. It is an unnecessary complication only of interest to those who are studying the subject and those arrogant enough to believe that one of the world's toughest brain teasers is not quite hard enough for them. Martin Hogbin (talk) 09:21, 27 May 2010 (UTC)

Why the Morgan error is relevant to this article

The error in the Morgan paper was only in the section considering the probability of winning by switching given a noninformative prior distribution of q. At first sight, this may not be considered to be particularly relevant to this article.

Morgan introduce their calculation by referring to the disappointment felt by some students that there is no single answer for the probability of winning by switching, given that the the player has chosen door 1 and host has revealed a goat behind door 3. They then proceed to calculate this probability on the fairly reasonable basis that the host may have a preference but that this preference is equally likely to have any value of q from 0 to 1. In other words, rather than assume that the host will chose at random between goat doors, we assume that the host could have a preference but as we do not know what this is we take it to have a probability which is uniformly distributed between, always opening door 3 when the car is behind door 1 and never opening door 3 when the car is behind door 1. What Morgan then, incorrectly, show is that on this, not unreasonable, basis for dealing with the unknown host goat door policy, the probability of winning by switching is a number that that is not 2/3.

What Nijdam and I have shown is that, on the basis of Morgan's proposed uniform distribution of q from 0 to 1, the probability of winning by switch is the far more reasonable feeling (to me at least) value of 2/3. We have further shown that this answer also applies to any distrubution of host policy parameter q which 'averages' to 1/2.

My personal opinion is that it would be far simpler and no less rigorous simply to take q to be 1/2 by applying the principle of indifference at the start, but what has been shown is that, even using Morgan's basis for dealing with unknown host behaviour, the answer is still exactly 2/3. Martin Hogbin (talk) 09:51, 27 May 2010 (UTC)

I don't see how anything in of your argument changes what you see at first sight. You seem to try to make a logic connection, where there is none. The argument that instead of a fixed q=1/2 the result holds for any distribution Q with E(Q)=1/2, just means the condition for the host behaviour can be extended from exactly random (or symmetric) to random in average (or symmetric in average). So the condition to make the simple solution without any caveats has been generalized slightly, nevertheless it is still a condition. Note that various "variations" of the MHP use distributions for which E(Q)=1/2 is not true and that indeed the for the "majority" of of conceivable distribution Q E(Q)=1/2 is not true either. All that aside we use(d) q=1/2 in our article anyhow, the argument there was merely that this is a condition you have to require and nothing has changed there.--Kmhkmh (talk) 10:27, 27 May 2010 (UTC)

Yes, of course, there are variations with different answers. They should come in the variations section. Martin Hogbin (talk) 12:59, 27 May 2010 (UTC)

I believe that's what we have already and even that was already compromise for you.--Kmhkmh (talk) 13:35, 27 May 2010 (UTC)

It is not for me, it is for the considerable majority of editors who want change. Unfortunately, most of them have given up hope. Martin Hogbin (talk) 13:31, 29 May 2010 (UTC)

Controversy

The controversy is not the Morgan paper, but the different opinions on the problem itself and its solution.

Problem

The problem formulation states the knowledge of which door has been opened by the host. Yet some people won't take this into account, as they want to use the simple solution as a solution to the (their) problem. As a consequence they solve a different, simple version, of the problem.

This is not correct, there are many problem formulations. The most well known problem statement is that by Whitaker and that is rather vague about the door opened by the host. The actual words are, '...the host, who knows what's behind the doors, opens another door, say No. 3'. This is not the same as saying, 'the host opens door 3'. Door 3 is simply given as an example, just to make clear what is meant by 'another door'. If this question were asked to you in person, you, as a good statistician should inquire, 'Do you mean that the host opens either one of the two unchosen doors to reveal a goat, or are you referring to the specific case that you have seen door 3 opened?' Unfortunately we cannot ask this question of Whitaker thus there is no certainty as to exactly what the questioner intended. Martin Hogbin (talk) 11:15, 27 May 2010 (UTC)

Even if the formulation goes: the host opens a door with a goat and then offers the opportunity to switch, the player sees an opened door, and has to make her decision dependent on the door number, i.e. an answer for No. 2 and one for No. 3. So let's make it easy for the reader and mention, as in the formulation, that door No. 3 is opened. Nijdam (talk) 14:04, 27 May 2010 (UTC)

Actually we most likely can as your own letter publication at "The americian Statistician" shows (additional statements by Whittaker). Moreover does Nijdam not argue that there is no simple problem version with a simple solution, he states that below. The issue you here is, that the simple or unconditional version of is only one interpretation of an ambiguous problem and in fact to various publications it is the less likely one. Nobody in the conditional has an argument with a correctly stated simple version and its simple solution, the problem is that in your various suggestions you are not doing that, but your still pushing for providing the simple solution as "the" solution to an ambiguous problem ideally without any further comment and that is plain wrong.--Kmhkmh (talk) 11:22, 27 May 2010 (UTC)

I see nothing in the letter and reply that indicates that Whitaker intended to identify specific door numbers. Why would a person want to the answer to a question that referred only to specific door numbers. It is actually quite obvious that Whitaker just wanted to know what advantage there was in swapping if the host opened either of the two unchosen doors to always reveal a goat. Martin Hogbin (talk) 12:35, 27 May 2010 (UTC)

The door numbers are generic, i.e. whatever result you compute based on those door numbers, holds for any door number configuration. And you can always distinguish the doors, numbers or not. The question is rather why would you throw away additional information in your analysis, before you've checked whether it might matter or not?--Kmhkmh (talk) 13:31, 27 May 2010 (UTC)

Solution

Some people want the simple solution to be the solution of the (full) MHP. However it is not, and can not be taken as such.

Condition

As the player knows which door has been opened, this knowledge inherently forms a condition. Although it may be avoided to fully mention the term conditional probability, one can not avoid to take notice of this circumstance.

Hence we have people who

A: take the simple version to be the MHP, and correctly use the simple solution,
B: incorectly think the simple version is the same as the full version,
C: use the simple solution incorrectly as the solution of the (full) MHP,
D: correctly use some form of conditioning to solve the MHP.
Where do you stand? Nijdam (talk) 10:56, 27 May 2010 (UTC)

Option A is essentially what I advocated above. We start with Whitaker's statement which can be taken as a simple version (no door numbers) of the problem and then give the simple solution.

Later on we point out that, if we take Whitaker to be inquiring about specific door numbers, the problem is strictly (and rather pedantically in my opinion) speaking one of conditional probability. Martin Hogbin (talk) 12:25, 27 May 2010 (UTC)

If you choose for option A, you have to make clear in the article, that the player decides before the host has opened the door with the goat. Is that what you want? Nijdam (talk) 14:09, 27 May 2010 (UTC)

No, Whittaker's statement cannot be simply taken as the simple version.

It contains explicit exemplary door numbers.
Even without explicit door numbers, you still can distinguish the doors, hence door numbers do exist implicitly always (unless the problem would explicitly tell you to ignore them, which it doesn't)

Perhaps you can explain using my question below. Martin Hogbin (talk) 13:27, 27 May 2010 (UTC)

According to response to your own letter in The american statician there is an additional statement by Whitaker which seems to suggest, that he did not intend the simple solution alone.

There is no mention at all of door numbers in the Response, he simply makes clear that the host knows what is behind the doors and implies that he always reveals a goat. Martin Hogbin (talk) 13:12, 27 May 2010 (UTC)

He does no such thing. But I admit my first description was not correct either. Whitaker suggests 2 solutions depending on the host's behaviour. However his host behaviour is not exactly what Morgan was talking about, but rather whether the host only reveals goats or whether he may reveal cars at well.--Kmhkmh (talk) 14:23, 27 May 2010 (UTC)

What we can do is mention the disambiguity shortly in the lead and then go directly for the simple solution and not mentioning any caveats there.--Kmhkmh (talk) 13:00, 27 May 2010 (UTC)

The original question does have door numbers, and their "specificness" (?) has nothing to do with conditioning; they might just as well be doors A, B and C. When you ask what the conditional probability P(X | Y) is, you're asking "if I know that Y is true, what is the probability that X is true"? If you do not condition on Y, you are considering a situation where you do not know Y. Your state of knowledge determines the question you should be asking: the conditional probability question or the unconditional probability question. Just because the answers are the same under the natural assumptions does not mean that the questions are the same.

The unconditional interpretation assumes that you do not know which door the host has picked - maybe you close your eyes and the host says "I opened a door but am not telling you which, do you switch?" and then you say "yes", or maybe the host forces you to choose before he does, or maybe you assume that you must choose in advance, even though nobody tells you to. I think that such interpretations of the problem are rather contrived - the original statement does seem to say that you know which door the host opened, make your choice on the spot, and are free to choose either way. In that case the correct question is the conditional probability question, not the unconditional probability question. There's more choice in how you go about answering it (e.g. by noting that the answers must be the same and then answer the unconditional question instead), as long as you show that it does answer the right question. -- Coffee2theorems (talk) 14:18, 27 May 2010 (UTC)

completely agree.--Kmhkmh (talk) 14:25, 27 May 2010 (UTC)

I agree with this as well, however whether individual editors agree or not is largely irrelevant. What IS relevant is whether this is explicitly supported by reliable sources. And, indeed it is. -- Rick Block (talk) 14:42, 27 May 2010 (UTC)

Coffee2theorems, from whose state of knowledge do you think we should be answering this question? Martin Hogbin (talk) 21:50, 28 May 2010 (UTC)

The player's. It's the player who is in a decision-making situation (to switch or not to switch, that is the question), and needs a probability applicable to the situation he is in, so that he can base his decision on it. Besides, the player in the question is "you", so "you, the person solving the puzzle" and "the player" are one and the same. -- Coffee2theorems (talk) 02:45, 29 May 2010 (UTC)

I agree with that, especially as the question starts, 'Suppose you are a player....'. I am sure that you agree that we assume that the player knows what are generally taken to be the standard rules of the game, that the host always offers the swap and always opens an unchosen door to reveal a goat. It is also reasonable to assume that the player has no knowledge of where the car has been placed, and thus has to take this as uniform at random (or else the problem cannot be solved), and has no knowledge of how the host might choose which door to open when he has a choice, and thus must also take this to be uniform at random.

The result of the above natural assumptions are that the condition that a specific door is opened by the host can obviously have no effect on the probability that the player has originally chosen the car (although it obviously affects the probability that the car is behind the opened door). This fact may be shown by symmetry, or by means of a, rather pointless, conditional probability calculation. It may also be deduced from the fact that, if the player has originally chosen the car, the host choice of unchosen door is random and thus conveys no information. Do you disagree with any of this? Martin Hogbin (talk) 10:29, 29 May 2010 (UTC)

If I'm interpreting you correctly, then I agree with most of what you say, and with all the important parts. I don't agree that the conditional probability calculation is pointless, and your assertions that the principle of indifference must be used are stronger than I would make (I'd say just that the principle is reasonable and the standard way here).

I do not insist that the principle of indifference is applied, only that it is applied consistently. There are two relevant and similar cases where it might be applied, the original placement of the car, and the host's choice of goat door. Whatever perspective you consider these from, the information given in the question, the expected state of knowledge of a player, the likely mechanism in a historical or modern quiz show, the two should be treated in the same way. Actually, I do not even mind if they are treated differently so long as you come clean about it. If someone says, 'We are now going to consider the interesting case where the car is initially placed uniformly at random but the host may chose a goat door non-uniformly', that would be fine with me. What you cannot do is demand that the natural state of affairs is to make different assumptions in each case. Martin Hogbin (talk) 18:18, 29 May 2010 (UTC)

I think you're arguing for Nijdam's stance C though, not stance A. I think stance C is reasonable, as long as the word "incorrectly" there is replaced with "informally". Rick has claimed that by the sources, the article could say that MHP is conditional; if so, then stances A and B could just be ignored, if nobody argues for them. If your stance is C and his is D, then there is no problem, after all? It's stances A and B I'm arguing against here.

The stance C goes this way:

The MHP question is about P(switching wins | host has opened door 3), and because that is "obviously" (or "for reason X") equal to P(switching wins), one can therefore answer the MHP question by calculating P(switching wins). The probability P(switching wins) is 2/3, because [simple argument].

Isn't that what you just said? With stance A, you would instead argue that the MHP question is about P(switching wins) and not about P(switching wins | host has opened door 3), and that if these two actually were different, it would be the former one that is right and the latter that is wrong.

The unconditional solution could well be used as the informal explanation for the (conditional) MHP (stance C), and then be followed by a formal conditional solution (stance D). Both solutions are given in this article, which says that "Before presenting a formal solution to the Monty Hall Problem to my students, I find that it helps to give an intuitive explanation for the 1/3 - 2/3 solution." The "intuitive explanation" is the unconditional solution and the "formal solution" the conditional solution. The article also calls vos Savant's solution a "correct solution", and there is no criticism of the unconditional solution in it. Compatible stances. -- Coffee2theorems (talk) 17:14, 29 May 2010 (UTC)

The difference between A and C is, that for A you have a simple solution for a simple problem not requiring any particular knowledge and you lose that with C. Because in C you require an additional argument to turn the "informal/intuitive", "shaky", "incomplete" or "false" solution into a "formal", "form", "complete" or "correct" one. This basically what you can extract from the various sources (not always explicitly in a single one but at least if you combine them). However the fact that you use this additional argument needs to be mentioned somewhere and it requires more knowledge/understanding as A. Or in other words that additional argument in C is exactly the mentioning of a "caveat" that Martin doesn't want to have (in my understanding from this neverending discussion so far).--Kmhkmh (talk) 17:58, 29 May 2010 (UTC)

I agree with what you say above, except that a case can be made that Whitaker actually just wanted to know the answer to the unconditional problem, his words are not that clear and he may not have meant exactly what he said.

The problem is how to translate all this into a good WP article. My point is that we should fully explain the informal solution before adding any complications of any kind. The problem is notoriously difficult for most people the first time that they see it and we should not place any barriers to understanding in their way. This is the way your linked article seems to think, first get the basic paradox out of the way. After that I am happy to talk about subtleties and formalities. Martin Hogbin (talk) 18:18, 29 May 2010 (UTC)

Is the answer always 2/3?

Is there anyone who maintains that there is any reasonable unambiguous formulation of the problem to which the answer is not exactly 2/3? If so please give your unambiguous formulation below. Martin Hogbin (talk) 12:41, 27 May 2010 (UTC)

Yes. If you add "if Monty has the choice between to doors, he always reveals the left door". That's the q=1 scenario in Morgans's paper or what Rosenthal dubs "Monty Crawl".--Kmhkmh (talk) 13:25, 27 May 2010 (UTC)

I asked for an unambiguous formulation. You might use K&W's formulation as a starting point. Martin Hogbin (talk) 13:44, 27 May 2010 (UTC)

I answered you question for an unambiguous formulation. What i might start with you can leave to me, obviously I started with Whittaker.--Kmhkmh (talk) 13:55, 27 May 2010 (UTC)

You seem not to understand what is meant by unambiguous. Amongst other things Whitaker does not make clear is that the cars are placed at random, the host always offers the swap, the player chooses initially at random, shall I go on...?

Do you mean this?

There is a game show in which there are three doors. Behind one door is a car; behind the others, goats. The car and the goats were placed uniformly at random behind the doors before the show.

The player chooses a door uniformly at random and, after the player has chosen a door, the door remains closed for the time being. The game show host, Monty Hall, then has to open any one of the two remaining doors and ask the player to decide whether they want to stay with their original choice or to switch to the remaining door. Monty always opens door 2 when he has a choice.

Given only the above information and that the player originally chooses door 1 and the host opens door 3. What is the probability of the player winning the car if they switch to the remaining door? Martin Hogbin (talk) 15:35, 27 May 2010 (UTC)

Your point or question is what exactly now?--Kmhkmh (talk) 16:46, 27 May 2010 (UTC)

Exactly what I asked. Is that what you meant? Martin Hogbin (talk) 23:21, 27 May 2010 (UTC)

Ok I have no idea what you want here. I guess we'll have another smokescreen here (see below).--Kmhkmh (talk) 00:56, 28 May 2010 (UTC)

What you call a smokescreen I call mathematics. The point that I am making is that there are no reasonable interpretations of Whitaker's question that result in an answer of anything other than 2/3. Do you agree? Martin Hogbin (talk) 12:18, 28 May 2010 (UTC)

No, I don't and I guess this will lead to discussion about the nature of "reasonable" and whether an exact unambiguous needs to comprise. Strictly speaking from the mathematical perspective you achieve unambiguous only once you've defined the complete formal model (sample space, events of interest and probability measures). However the point of (applied) probability problems from the simple throwing of dice over MHP to whatever is, that coming up with a somewhat "reasonable" model is part of the solution. As far as Whitaker is concerned is see Monty Crawl as a reasonable or valid interpretation but not as the most likely one. To make this perfectly clear, why this thread looks like rhetorical excercise or a smokescreen to me and why I'm not interested to engage into an endless assessment, about what's reasonable and what's not. Because by all likelihood this will yield nothing and mean nothing for the article. Because we already know that various editors view the problem differently and that they assess the term "reasonable" differently and another rerun of such a discussion or related one is not yielding anything. The only the only way to move forward here is to concentrate on areas of compromise (still representing the sources sometwhat accurately) and come up with suggestions of which we honestly think they might be acceptable by the other side (while representing the sources accurately).--Kmhkmh (talk) 13:21, 28 May 2010 (UTC)

You are now just being perverse. Are you suggesting that Whitaker really wanted to know the probability of winning by switching on the basis that the host always opens door 2 when he has a choice, but somehow he forgot to tell us that crucial fact? Even Morgan now says, '...had we adopted the conditions implicit in the problem, the answer is 2/3, period'. By 'the problem' they are of course referring to Whitaker's statement.

As for compromise, I tried it, and you and Rick both backed out of your previous positions and tried to push to get things all your own way. Martin Hogbin (talk) 22:15, 28 May 2010 (UTC)

Is this formulation conditional?

There is a game show in which there are three doors. Behind one door is a car; behind the others, goats. The car and the goats were placed uniformly at random behind the doors before the show.

The player chooses a door uniformly at random and, after the player has chosen a door, the door remains closed for the time being. The game show host, Monty Hall, then has to open any one of the two remaining doors and ask the player to decide whether they want to stay with their original choice or to switch to the remaining door.

Given only the above information. What is the probability of the player winning the car if they switch to the remaining door?

Does anyone claim that this is a conditional problem? Martin Hogbin (talk) 13:27, 27 May 2010 (UTC)

Yes.--Kmhkmh (talk) 13:57, 27 May 2010 (UTC)

What is your original sample set and what is your conditioned set? Martin Hogbin (talk) 14:00, 27 May 2010 (UTC)

The sample set and condition is described in Monty_Hall_problem#Mathematical_formulation. For clarification I should add, that I assumed the player sees (or we know) which door the host opens. If your intention was to remove any knowledge regarding the door, then I wouldn't consider it conditional but i wouldn't consider it Whitaker MHP either (in that scenario the player always knows the specific door). Which begs the question is there any point to this? We all know and agree that you can have simple/unconditional version of MHP, the point is that's not the only version and by no means the obvious perception. Nor is is the predominant version in academic literature.--Kmhkmh (talk) 14:17, 27 May 2010 (UTC)

The question is quite clear, it says, 'Given only the above information'. You cannot make up information to suit yourself. Martin Hogbin (talk) 15:09, 27 May 2010 (UTC)

I think the was quite clear as well. Any part you didn't understand?--Kmhkmh (talk) 15:23, 27 May 2010 (UTC)

Perhaps you could explain why you say, 'I assumed the player sees (or we know) which door the host opens' when this information is not given in the question. Martin Hogbin (talk) 15:26, 27 May 2010 (UTC)

Martin - you're asking for opinions here rather than what sources say. You really should be arguing sources. Specifically, is this problem statement from any source? Which one? Are you claiming that most sources interpret the problem (however they state it) as if it were stated this way? Is there some source you would base this claim on, or is it simply your own opinion?

Kmhkmh and Rick, you both seem to use the same tactic. When you are losing an argument about probability you start talking about sources. When you are losing an argument about sources you start talking about probability. Can we stick to one thing at a time please. I was asking about my specific question. No sources have seen that. I have created a separate section for what the sources say. Martin Hogbin (talk) 15:08, 27 May 2010 (UTC)

We are not "losing an argument about probability" here. You got your answer already. The way you phrased the problem above it is unconditional. If you point was that my first "Yes" was an incorrect answer - yes it was (due to fast reading). However there is no (real) disagreement about that and never was.

As far as tactics are concerned, it might indeed be worthwhile to take a closer look. The tactic we actually do see at work here is a classical smokescreen. You start a thread or discussion on subject having no real relevance for the article itself and were you can be right and your opponents can be wrong(if they are dumb enough to fall for it as I did). Hence by association regarding the real issues 3rd readers might believe you are right as well and your opponents are wrong as well. A few concrete examples:

Coming up with an (unconditional) reformulation of MHP in which the door information is removed (what we've just seen and what I fell for)

You did not fall for anything. You eventually agreed that if no door numbers are specified in the problem then it is unconditional. This means that if we take it that Whitaker did not intend to specify door numbers in his question then it is unconditional. Martin Hogbin (talk) 12:29, 28 May 2010 (UTC)

Finding the error in Morgan's paper, you prove Morgan wrong on an issue, that doesn't really matter for the article. But association you are right and Morgan is wrong for the points that matter as well (looking at glkanter's reaction you see how it worked).

I have explained exactly why Morgan's error is significant in another section. Martin Hogbin (talk) 12:29, 28 May 2010 (UTC)

Constantly claiming that by far most sources only mention the unconditional solution. True enough if you google you probably get more hits the unconditional solution, so again a point where you can be right and your opponents can be wrong. But yet again a point without relevance for our article, since for WP sources have to to be ranked by reputability and domain (in addition many of those google hits wouldn't qualify as source for WP at all (even in the absence of domain knowledge)).

Who decides which sources are relevant? Martin Hogbin (talk) 12:29, 28 May 2010 (UTC)

That's the pattern that is at work here (and I've observed for more than a year now). All that might be fine for rhetorical games or to "win" arguments in a purely rhetorical sense, but it is useless for resolving an editing conflict nor does it help to resolve any real issues regarding the article's content.--Kmhkmh (talk) 16:16, 27 May 2010 (UTC)

I take it that by 'resolving an editing conflict' you mean agree with you. Martin Hogbin (talk) 23:28, 27 May 2010 (UTC)

No I don't, I do however expect that ir properly represents the sources and that the mathematical description is correct, i.e. we are not hiding the disambiguity from the reader or conceal to which exact interpretation of the problem a solution refers.--Kmhkmh (talk) 00:53, 28 May 2010 (UTC)

You have agreed above that the majority of sources do treat the problem unconditionally but you claim that the sources that disagree with your POV are not relevant. Many editors here disagree with that. Regarding mathematics, I am happy to discuss any mathematical issues with you or anyone else. Martin Hogbin (talk) 12:29, 28 May 2010 (UTC)

What the Sources say

On the flip side, even ignoring Morgan et al., treating the problem unconditionally is directly criticized by the following

Gillman: Marilyn's solution goes like this. The chance is 1/3 that the car is actually at #1, and in that case you lose when you switch. The chance is 2/3 that the car is either at #2 (in which case the host perforce opens #3) or at #3 (in which case he perforce opens #2)-and in these cases, the host's revelation of a goat shows you how to switch and win. This is an elegant proof, but it does not address the problem posed, in which the host has shown you a goat at #3.

Grinstead and Snell: This very simple analysis [as a preselected strategy, staying wins with probability 1/3 while switching wins with probability 2/3], though correct, does not quite solve the problem that Craig posed. Craig asked for the conditional probability that you win if you switch, given that you have chosen door 1 and that Monty has chosen door 3. To solve this problem, we set up the problem before getting this information and then compute the conditional probability given this information.

Lucas, Rosenhouse, and Schepler: This [the "high numbered Monty" variant - Monty opens the highest numbered door without revealing the car] shows that any proposed solution to the MHP failing to pay close attention to Monty’s selection procedure is incomplete.

Rosenthal Monty Hall, Monty Fall, Monty Crawl: This solution [what he calls "Shaky Solution" which basically says your original chance of selecting the car is 1/3 and this doesn't change since you knew the host would open a door revealing a goat] is actually correct, but I consider it "shaky" because it fails for slight variants of the problem.

Let's see. Three published papers and a textbook. Versus what, exactly? Are there any sources that directly support your opinion that the conditional approach over complicates the problem? -- Rick Block (talk) 14:30, 27 May 2010 (UTC)

Both the [first] two sources above refer only to Whitaker's question and choose to interpret it as giving specific door numbers. Are these sources to be regarded as expert in determining what an ordinary reader of a general interest magazine actually wanted to know? They are aimed at people studying probability and thus interpret the question in an academic way. They both look to be based on Morgan. Martin Hogbin (talk) 15:11, 27 May 2010 (UTC)

How could Gillman possibly be based on Morgan et al. given the respective publication dates (Jan 1992 and Nov 1991)? Moreover, what possible difference could it make if they ARE? Let's examine the possibilities:

1) They ARE based on Morgan et al. - then these are sources confirming what Morgan et al. have to say (specifically, the problem demands a conditional solution).

2) The ARE NOT based on Morgan et al. - then these are SITLL confirming sources, but in a much stronger sense since they're independent.

Either way, they're saying the problem demands a conditional solution. Are they experts in determining what an ordinary reader of a general interest magazine actually wanted to know? Why is this relevant? Wikipedia is an encyclopedia, not Parade magazine. What they are experts in is probability problems. Which actually is relevant. -- Rick Block (talk) 18:28, 27 May 2010 (UTC)

This [Rosenthal] is a fair description of the situation. This solution is actually correct [my italics this time] but it fails for slight variants of the problem. So Rosenthal is saying that the simple solution is correct for the standard version of the problem. Martin Hogbin (talk) 15:12, 27 May 2010 (UTC)

It is revealing that he says actually correct, and uses the term shaky. You better read on to section 4 and 5 of his paper.Nijdam (talk) 16:33, 27 May 2010 (UTC)

@Martin - He's clearly saying the solution produces the correct numeric answer (2/3 chance of winning by switching) but the logic behind the solution is shaky. -- Rick Block (talk) 02:36, 28 May 2010 (UTC)

I realize you're quoting someone else Rick, and he was 'speaking' conversationally in a instructional setting, but could you explain where 'shaky' logic fits in relative to 'valid' and 'invalid'? Glkanter (talk) 04:16, 28 May 2010 (UTC)

Typical flawed (BS) interpretations by Rick. Rosenthal's point, even as written above, in no way supports conditional, it's a 'variant', a different problem. Lucas is a 'variant', also. For the other two examples, it's arguable whether Whitaker cared about door 3, and Morgan's paper substantially ALTERED VOS SAVANTS'S COLUMN to make their case: "You pick door No. 1, and the host, who knows what's behind them, opens No. 3..." leaving out the key word, 'say', which may mean the door #s are nothing more than 'for descriptive purposes'. But, being the hacks they are, they falsified their paper. And they still haven't acknowledged Selvin. Glkanter (talk) 14:56, 27 May 2010 (UTC)

Rick,do you really want me to collect all the sources that treat the problem without mentioning conditional probability and list them here? Just Google the subject. Obviously, no sources tell us how to write this article, that is up to us. Martin Hogbin (talk) 15:14, 27 May 2010 (UTC)

If googling them is so easy for you, please humour us with a few examples of reputable literature explicitly stating that conditional solution is "overcomplicated" or an "academic distraction".--Kmhkmh (talk) 15:21, 27 May 2010 (UTC)

No sources tell us how to write this article. There are many that do not mention anything about conditional probability. Martin Hogbin (talk) 15:28, 27 May 2010 (UTC)

I suppose in plain English that means you have none. And that there are some reputable sources that use the unconditional solution only, is something we all agree on. However that was neither what Rick or me have asked you about.--Kmhkmh (talk) 16:21, 27 May 2010 (UTC)

Obviously there are no sources that say, 'If you are writing an encyclopedia, the conditional solution would not be the best one to start with because it is confusing or distracting'. The conditional sources are absolutely fine - for their target audience, which is probability students. They demonstrate the problems that can be caused when a distribution is assumed to be uniform but might not be, although, in fact, they are poor examples because Morgan are inconsistent with their assumptions (along with others who implicitly make the same mistake). This is no doubt a valuable lesson for those studying statistics. Martin Hogbin (talk) 13:43, 29 May 2010 (UTC)

Yet another draft of a compromise

Yet another draft. See User:Rick Block/Monty Hall problem (draft) (sections starting with "Sources of confusion" are unmodified from the current version of the article). The intent is to present a convincing simple solution and then an analysis based on conditional probability (with NO criticism of the simple solution). If anyone can read any POV into the solution section (in any direction) please suggest a way to fix it. -- Rick Block (talk) 19:23, 28 May 2010 (UTC)

I think the explanation "An even simpler solution is to reason that [snip]" is more confusing than vos Savant's tabular argument. It's not simpler, it's just shorter. How about saying e.g. "An even shorter solution is to reason that the switching strategy loses if and only if you initially pick the car, which happens with probability 1/3, so the switching strategy wins with probability 2/3." instead? This was paraphrased from this paper. -- Coffee2theorems (talk) 01:34, 29 May 2010 (UTC)

Good suggestion. This is mostly about form at this point - I'm trying to show the simple solutions and conditional solution don't have to be antagonistic toward each other. Unless there's a consensus in favor of the general approach fine tuning the explanations may be a waste of effort. -- Rick Block (talk) 02:07, 29 May 2010 (UTC)

Since this text was already in the article, I've added it (and the reference to Carlton). We'll see if anyone objects. -- Rick Block (talk) 03:11, 30 May 2010 (UTC)

@Martin - I've stated my objections to the structure you keep suggesting (see below). I'm going to quote your entire post from below:

Let me explain again my main concern, which has nothing to do with my POV. 95% of readers who come to this page will know little about probability and virtually nothing about conditional probability, and probably have no desire to learn about it either. They will want to know more about the MHP, maybe to settle a bet or argument or possibly because they have seen the problem elsewhere and do not believe the answer. The first thing that we need to do is to convince them that the probability of winning the car is 2/3 if you swap. So convinced are most people that the answer is 1/2 that any little thing that might make them think that there is some loophole or deficiency on the simple solution will cause them to lose confidence in it and continue with their erroneous belief that the answer is 1/2. For such people, whatever we write after that will be irrelevant.

Of course we will also get many other types of reader, including students of probability and experts on the subject. We need to show them that the subject is covered in depth, that we are aware of all sourced opinion and controversy on the subject and we need to present this neutrally. I have no objection to that being done after the simple solution Martin Hogbin (talk) 12:07, 29 May 2010 (UTC)

Can you please explain in what way the structure of this draft (section ordering) fails to meet this concern? Note in particular that the ENTIRE solution section makes no mention of the possibility that the host might choose between two goats in any way other than randomly. The conditional solution presented SUPPORTS the unconditional solution which BOTH unequivocally say the answer is 2/3 chance of winning by switching. You seem to be implying presenting a conditional solution that also says the answer is 2/3 will somehow lead people to think the answer is not 2/3 (??). I really don't understand how you can think this. Please explain. -- Rick Block (talk) 16:32, 29 May 2010 (UTC)

It just gets too complicated too quickly mentioning 'conditional probability', 'Bayes' theorem. Vos Savant's solution is fine but we nee some more simple solutions and discussion of why the answer is 2/3 not 1/2. This is the only thing that interests most people. Martin Hogbin (talk) 17:31, 29 May 2010 (UTC)

Can you be more specific, i.e. what additional simple solutions would you add? And would a forward reference to the "Why the probability is not 1/2" section (which we're going to have to talk about sometime) satisfy your second concern? -- Rick Block (talk) 19:22, 29 May 2010 (UTC)

Some questions regarding the compromise

Ok, I'm trying to summarize, where from my understanding an agreement was reached or seemed acceptable to the various parties and where there are still open problems

Agreed so far

Simple solution chapter goes first and contains no caveats
lead as it is

Still open

problem chapter
sources of confusion chapter
aids to understanding chapter
aside from structural issues in some cases agreements about the exact formulations at different locations might be needed

discussion of possible solution

Since we seem to have a constant turf war about sections where conditional and unconditional aspects mix (essentially in all 3 chapters above), I suggest to split these chapters and assign their content as subchapters or paragraphs within the simple solution chapter and the conditional solution chapters. So we would have something like that:

lead
simple solution (no caveats)
- subsections for problem,sources of confusions, aids for understanding
conditional solution
- subsections for problem,sources of confusions, aids for understanding

or essentially same but with slightly different chapter names:

lead
solution (no caveats)
- subsections for problem,sources of confusions, aids for understanding
mathematical analysis (conditional solution, caveats, the whole shebang)
- subsections for problem,sources of confusions, aids for understanding
psychological analysis

This way aside from the lead we have separated unconditional and conditional solutions completely and can describe each on its own according to the available sources and the only possible area of disagreements would be the lead i guess. Could everybody live with such a structure (that goes to Martin and Rick in particular).--Kmhkmh (talk) 23:41, 28 May 2010 (UTC)

Have you read my comments here? Or the draft linked above?

I don't mind your draft, but that doesn't matter for the mediation since Martin does. I'm trying to see whether there is a structure (and ultimately an article version), that you and Martin (and ultimately the rest) can live with. Personally I don't care that much for POV variations as long as the article as a whole covers and represents all important sources and sticks to an accurate description. For the latter it is in particular important that the readers after reading the (whole) article should have understood the subtle differences.--Kmhkmh (talk) 11:43, 29 May 2010 (UTC)

Without seeing content I'm not entirely sure, but my inclination is I would not be OK with either of these. I don't see how this is any different from what Martin has been suggesting. Both of these create a distinct structural POV, the second one reinforces this through the section titles. Rather than separate the simple and conditional solutions - as if they pertain to different problems - I think presenting both approaches in an integrated fashion is actually much more powerful. Some readers thinking of the conditional situation described in the problem statement MAY be convinced by a simple solution, but others will clearly find this extremely difficult and MAY be helped by an accessible conditional solution. Not only would this approach be scrupulously NPOV, but I think it better serves Martin's stated goal of convincing our readers. -- Rick Block (talk) 01:49, 29 May 2010 (UTC)

I'm not sure where exactly you see the POV here. In the order alone? Otherwise i see no problem if the leads mentions the ambiguity and refers to the various sections. The are reasonable arguments for and against an combined/separate explanation, but since this seems to be central issue in the conflict, I'd consider that as something that you (or we) could give to Martin, without compromising anything that really matters. Using Nijdam's list above the article needs to cover A and D, but it might do that in any order and separately or combined. In the big picture each of them is fine and I see no point in having a year long discussion which of the versions should be used, when either is fine.--Kmhkmh (talk) 11:43, 29 May 2010 (UTC)

Let me explain again my main concern, which has nothing to do with my POV. 95% of readers who come to this page will know little about probability and virtually nothing about conditional probability, and probably have no desire to learn about it either. They will want to know more about the MHP, maybe to settle a bet or argument or possibly because they have seen the problem elsewhere and do not believe the answer. The first thing that we need to do is to convince them that the probability of winning the car is 2/3 if you swap. So convinced are most people that the answer is 1/2 that any little thing that might make them think that there is some loophole or deficiency on the simple solution will cause them to lose confidence in it and continue with their erroneous belief that the answer is 1/2. For such people, whatever we write after that will be irrelevant.

Of course we will also get many other types of reader, including students of probability and experts on the subject. We need to show them that the subject is covered in depth, that we are aware of all sourced opinion and controversy on the subject and we need to present this neutrally. I have no objection to that being done after the simple solution Martin Hogbin (talk) 12:07, 29 May 2010 (UTC)

I understand your concern, but it is somewhat misplaced here, since we are writing an encyclopedia, where accuracy matters. First and foremost accurate and complete information matters and then we look for pedagogical best way to convey it. WP is for informing people and not preach them. If I polemically exaggerate your argument from the other side, I could essentially say, that you're essentially suggesting to lie to the (simple minded) reader for its own good. That's an unacceptable approach for an encyclopedia. But more importantly we are again repeating the pattern of the last year. We've had these arguments already, i.e. we know your concern and the conflicting concerns of the other editors. Why do we have to repeat this discussions over and over?--Kmhkmh (talk) 12:32, 29 May 2010 (UTC)

I too wonder why I have to keep repeating incontrovertible points over and over. Can you refute any of these points, which ignore my POV:

Most people get the MHP wrong and are very difficult to convince, I am not talking about the simple minded.
Virtually all mathematical or technical text books start with over-simplifications of a subject.
There is no need for any inaccuracy, we can explain the details later. Martin Hogbin (talk) 13:28, 29 May 2010 (UTC)

Nobody suggested most people would get it right. You referred to people (intentionally) ignoring the explanation to stick to their prior beliefs, those I called "simple minded". And again, we inform, we don't preach.

Many people stick to their beliefs regarding the MHP, they are not all simple minded. You appear to see WP purely as an intellectual exercise rather than something that will actually be of use to our readers. To show is not to inform. Martin Hogbin (talk) 15:22, 29 May 2010 (UTC)

Obviously this in an encyclopedia and not a text book. In any case the article lead would be an analogon to the abstract or foreword of a book and in them you do mention advanced or later material.

Yes, encyclopedias are generally intended to be more accessible to the general public than text books. The lead is in no way analogous to the foreword in a book. Martin Hogbin (talk) 15:22, 29 May 2010 (UTC)

There is also no need to suppress a short summary in the lead, making the reader of aspects other then the first chapter. The notion that single sentence in the lead (pointing to later details) turns a good article into a horrible one makes no sense to me at all. Also I really wonder how you ever want to reach a compromise with nijdam and rick, if even a complete separation without caveats is not good enough and single reference in the lead is such a big problem?

You are now just horse trading. Up until now no body has objected to the lead.

Lastly the actually incontrovertible points you are/were making have mostly little or no meaning for the article itself (see smokescreen discussion). The rest comes down to misrepresentations or questions of mere opinion. Anyhow if the suggestion above is helping neither you nor Rick to find a common ground, there's no reason in pursuing it any further. I'm not interested to participate in another round of an endless and somewhat pointless debate.--Kmhkmh (talk) 14:33, 29 May 2010 (UTC)

I do not see a discussion of how to make this a good and useful article for our readers as a pointless debate. WP is not intended to be a medium for people to show off their knowledge of undergraduate statistics it is intended to be something that helps people to learn and understand. Martin Hogbin (talk) 15:22, 29 May 2010 (UTC)

Either it is made clear the simple solution is a solution to a simplified problem, or the simple solution needs to mention the new situation with the opened door. Nijdam (talk) 16:16, 29 May 2010 (UTC)

Why? Martin Hogbin (talk) 16:26, 29 May 2010 (UTC)

Interpreting Whitaker

Here is Whitaker's question as it was printed in Parade:

Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?

Before I ask how it should be interpreted let me first ask if there is anyone who disagrees with Seymann's statement?

Without a clear understanding of the precise intent of the questioner, there can be no single correct solution to any problem. Martin Hogbin (talk) 14:28, 29 May 2010 (UTC)

Here you go again - next smokescreen.--Kmhkmh (talk) 14:35, 29 May 2010 (UTC)

You seem to argue purely by bluster and assertion. I have asked a perfectly reasonable question that is related to the improvement of this article. How about you answer it? Martin Hogbin (talk) 15:04, 29 May 2010 (UTC)

Any interpretation needs to account for the opened door No. 3. Nijdam (talk) 16:13, 29 May 2010 (UTC)

The simple solutions address door #3 being open. As well as door #1 and door #2. Glkanter (talk) 18:15, 29 May 2010 (UTC)

Do you agree with Seymann's remark? This is surely a fundamental principle of statistics. Martin Hogbin (talk) 16:23, 29 May 2010 (UTC)

I think I've already made clear how I interpret Whitaker, so I'll just comment on the Seymann statement. I do not know if I agree or disagree, but it is one POV that problems that have been posed with a set wording may have a single "correct" answer despite apparent ambiguity. See e.g. Jaynes's solution to the Bertrand paradox: he insisted that the problem has a single correct solution, even though the conventional wisdom is that it is ambiguous and has at least three potential interpretations. -- Coffee2theorems (talk) 18:05, 29 May 2010 (UTC)

An interesting paper but something of a red herring in this context. Janes' paper is about interpretation of seemingly ill-posed questions. Whitaker's question is indeed ill-posed if we take it literally, in other words to be answered as written. On that basis the natural symmetries of the problem would suggest applying the principle of indifference to the initial placing of the car, the player's initial choice of door, and the host's choice of goat door, the answer to that question being exactly 2/3 and the condition of which door the host opens therefore being unimportant. I have described it as a null condition. I would call it pedantic, to say the least, to insist that it is a conditional problem.

But the question was, in fact, a question from a presumably non-expert human who was hoping to learn something from the answer. The question clearly contains ambiguities that cannot be resolved by Janes' methods. For example no symmetry is going to tell us whether the host always offers the swap or must always reveal a goat. If I were forced to make a decision purely on what is said in the question then I would say that as we are only told that the host offers the swap and and reveals a goat we can only assume that this is what always happens. But this is just my judgment based strictly on the question wording.

Seymann's comment is much wider than that. It is quite possible that Whitaker actually wanted to know the answer to something other than the question he appeared to ask. In reality it is quite probable that he simply wanted to know whether it was better strategy to swap or not. I very much doubt he was asking about the possible significance of door numbers. Without Whitaker to tell us exactly what he wanted to know there can be no single correct answer to his question. That is Seymann's point. Do you agree with that? Martin Hogbin (talk) 20:38, 29 May 2010 (UTC)

The statement of Seymann's you quoted comes from a comment to the Morgan paper. More context: "The question of problem definition, undoubtedly a complication for those attempting to solve the three door game show problem, is not without its precedents. For example, in 1899 Joseph Bertrand (Weatherford 1982, p. 56) posed a problem that has come to be known as Bertrand's Paradox, and which may be stated as follows: [description omitted]. Without a clear understanding of the precise intent of the questioner, there can be no single correct solution to any problem." Now, clearly Jaynes didn't agree with Seymann's statement in the case of the Bertrand paradox, so it's not unheard of for someone to disagree with it. That's all I tried to say. I don't really know what stance to take on what is the "right" way to go about interpreting things in general. In the end, the right way on Wikipedia is to interpret things the ways the sources do. -- Coffee2theorems (talk) 23:51, 29 May 2010 (UTC)

If only it were that easy. The vast majority of sources give no description of the precise formulation that they are addressing but give a solution that is not conditional, essentially similar to vos Savant's. Several academic 'statistical' sources turn the problem into a conditional probability problem by taking Whitaker's words literally and adding their own assumptions. Many academic 'psychology' sources do not treat the problem conditionally. Martin Hogbin (talk) 22:55, 30 May 2010 (UTC)

Martin - We're all answered this innumerable times before, please see the archives if you've forgotten.

Everyone else - I strongly suggest we simply ignore this thread. -- Rick Block (talk) 16:48, 29 May 2010 (UTC)

I do not recollect any answers to this question, I am not sure that I have asked it before. You only have to say yes or no. I do sense a certain fear as to where the 'yes' answer will lead. Martin Hogbin (talk) 17:34, 29 May 2010 (UTC)

How Should New Information From A Peer-Reviewed Professional Journal

be incorporated into the article?

I guess there's a short-term (now) and a long-term (mediation) answer to this. Glkanter (talk) 15:21, 29 May 2010 (UTC)

The article currently includes no mention of the relevant point, i.e. the Bayesian probability computed using a uniform prior for the distribution of the host's preference between two goats. Logically, this could be added to the Variants section where this version of the problem (the host's preference is taken to be a variable) is discussed. If you're thinking of a specific change, why don't you say what it is (or, even, simply edit the article)? -- Rick Block (talk) 16:42, 29 May 2010 (UTC)

Rick, it is most unfair of you to criticise Glkanter for not editing the article. He an I are both trying to avoid edit warring, which is where our edits would undoubtedly lead. We have both made edits, only to find them immediately reverted by one of three editors. Martin Hogbin (talk) 17:37, 29 May 2010 (UTC)

If you make an edit and somebody reverts your edit it is NOT an edit war unless you make the same edit again (since they'll presumably revert again). Effectively any edit is a suggestion along the lines of "how about this?". If someone simply reverts your change it's a clear indication that they completely disagree and can't even see a way to edit your change into something they'd find acceptable (successive editing, rather than reverting, is actually how it is intended to work). If you want to push your point following a revert your next avenue is the talk page. Most experienced editors understand this. What I'm saying to Glkanter here is I have no clue what change he's suggesting (do you know?) and that he should be much more direct about what he's saying. The most direct way is to edit the article. This lets everyone know exactly what he's saying, in full context. Another direct way is to suggest a specific change on the talk page. I'm not criticizing here. I'm asking for clarification. -- Rick Block (talk) 18:03, 29 May 2010 (UTC)

Revised Problem section

I'd like to change the Problem section to what is contained at User:Rick Block/Monty Hall problem (draft). The built-in version diff tool doesn't make it very obvious what the diffs are (see [3]) so rather than simply make the change and have people puzzle out what the point is, here's a different view of the diffs.

Steve Selvin ~~wrote a letter to the American Statistician in 1975 describing~~ described a problem loosely based on the game show Let's Make a Deal in a letter to the American Statistician in 1975 (Selvin 1975a). In a subsequent letter he dubbed it the "Monty Hall problem" (Selvin 1975b). In one of its mathematical formulations (the so-called conditional version, see below), the problem is mathematically equivalent (Morgan et al., 1991) to the Three Prisoners Problem described in Martin Gardner's Mathematical Games column in Scientific American in 1959 (Gardner 1959a).

Selvin's Monty Hall problem was restated in its well-known form in a letter to Marilyn vos Savant's Ask Marilyn column in Parade:

[Parade quote]

There are certain ambiguities in this formulation of the problem: it is unclear whether or not the host would always open another door, always offer a choice to switch, or even whether he would ever open the door revealing the car Certain aspects of the host's behavior are not specified in this wording of the problem. For example it is not clear if the host considers the position of the prize in deciding whether to open a particular door or is required to open a door under all circumstances (Mueser and Granberg 1999). However, the common interpretation is to suppose that the host is constrained always to open a door revealing a goat and always to make the offer to switch, and that the initial choice of the player is correct with probability 1/3. It is common to suppose that the host opens one of the remaining two doors perfectly randomly (i.e., with equal probabilities) if the player initially picked the car The standard analysis is based on the additional assumptions that the car is initially equally likely to be behind each door and that the host must open a door showing a goat, must randomly choose which door to open if both hide goats, and must make the offer to switch (Barbeau 2000:87).

~~Without a clear understanding of the precise intent of the questioner, there can be no single correct solution to any problem (Seymann 1991).~~ ~~The following unambiguous formulation represents what, according to Krauss and Wang (2003:10), people generally assume the mathematically explicit question to be~~ According to Krauss and Wang (2003:10), even if these assumptions are not explicitly stated, people generally assume them to be the case. A fully unambiguous, mathematically explicit version of the standard problem is:

[K&W quote]

~~We also need to assume that winning a car is preferable to winning a goat for the contestant.~~

What is the point of all this you might ask? There are several points:

1) The equivalence to the Three Prisoners problem is misplaced - it belongs (and is) in the "History" section. Removing this has the added benefit of getting rid of the "so-called conditional version" malarkey as well.

2) The ambiguities cited to Mueser and Granberg are changed to be more literally what they say.

3) The common interpretation (cited to Barbeau) is changed to be more literally what he says.

4) The Seymann quote is deleted (it seems superfluous in this context - the entire paragraph is precisely defining the problem).

5) The Krauss and Wang point that the standard interpretation is what people assume is included in the same paragraph describing the standard interpretation, and their problem statement is presented not just as what people assume, but as the standard interpretation.

Does anyone find any of these changes to be objectionable? -- Rick Block (talk) 20:01, 29 May 2010 (UTC)

I am slightly puzzled that you want to make these seemingly minor changes in the middle of a heated discussion about the structure of the article. Martin Hogbin (talk) 20:50, 29 May 2010 (UTC)

The way out of a stalemate is to simply start DOING something. Maybe we can't agree on some things, but if the article is changed a little here and a little there it MIGHT end up acceptable to everyone. Nobody reverted the changes I recently made to the lead and to the "Popular solution" section, which I'm taking to mean nobody objects. Do you think these changes to the "Problem" section are incrementally better? -- Rick Block (talk) 23:32, 29 May 2010 (UTC)

Fine with me. Nijdam (talk) 12:35, 30 May 2010 (UTC)

Aids to understanding moved

I have moved the 'Aids to understanding' section to immediately follow the 'Popular solution' section. There are no other changes. This simple move solves 80% of my concerns with the article, although I cannot speak for any of the other 'simplists'.

This order follows that in most text books and encyclopedia articles where a simple treatment is given and fully discussed before a more complex treatment is introduced, even if the simple treatment is, strictly speaking, incorrect.

In this case there are several editors, including myself, who believe, for a variety of reasons, that the simple treatment is correct and that the conditional treatment is an academic sideshow, relevant only to those studying undergraduate statistics. Keeping the long text on the conditional solution and extensive mention of 'conditional probability' is therefore a considerable compromise for the 'simplists'.

Please can we keep this article in this format while we discuss it in some detail. Those that object, please explain exactly what your objection is. Martin Hogbin (talk) 09:15, 1 June 2010 (UTC)

Immediate reversion

After harassing me to edit the article rather that keep talking about it, Rick immediately reverts my change claiming that there is a consensus against it.

Rick, please tell me which editors demand that my change is reverted immediately. So far it is only you. Martin Hogbin (talk) 14:22, 1 June 2010 (UTC)

Also, some reasons would be nice. Can anyone tell me what is wrong with my change, which keeps all the original text but simply puts it in the normal order (simple then complex) for a technical article. 14:23, 1 June 2010 (UTC)

Martin - Unlike the (relatively small) changes I've been making which are attempts to make the article more to your liking, this is a big change you already know I do not agree with (and that Nijdam has already reverted once before, so you know he doesn't agree to it either). I've told you why repeatedly (POV issues).

I've copied this version to User:Martin Hogbin/Monty Hall problem (draft 2) so we can discuss it in detail. IMO, it fails NPOV - see specifically WP:NPOV#Article structure. I've linked to this section of WP:NPOV before, and even quoted it, but I'll quote it again:

It may also create an apparent hierarchy of fact: details in the main passage appear "true" and "undisputed", whereas other, segregated material is deemed "controversial", and therefore more likely to be false — an implication that may not be appropriate.

How this is relevant is the structure you're creating presents a "Popular solution" immediately following the "Problem" section, followed by several screens worth of "Aids to understanding", and only then a "Probabilistic solution" section. This structure makes it seem like the "Popular solution" and "Aids to understanding" are uncontroversial and are indeed the way the problem should be addressed, i.e. it endorses these solutions. However, there is another significant POV that is being ignored which is that these approaches fail to address the problem. From WP:NPOV:

The neutral point of view neither sympathizes with nor disparages its subject, nor does it endorse or oppose specific viewpoints. It is not a lack of viewpoint, but is rather an editorially neutral, point of view. [italics in the original]

This structure is not editorially neutral. -- Rick Block (talk) 14:58, 1 June 2010 (UTC)

Rick, there is absolutely nothing in my change that is not neutral. We still have the same wording in the 'Probabilistic solution' section which points out that some sources consider the simple solution to be incomplete. My order is exactly the same as that in Coulomb's law and Newton's laws and it is the perfectly normal order for a technical subject is which there is a simple solution or explanation that is not totally correct (except that in this case many editors dispute that there is anything wrong with the simple solutions) and a more complex but more general solution.

Even if the conditional solution were indisputably correct and the simple solution were agreed by everyone to be deficient, this order would be better. It helps the reader understand the extremely unintuitive central paradox of the MHP before showing them the details. It also defuses much of the argument that has been raging for years now. Martin Hogbin (talk) 15:08, 1 June 2010 (UTC)

Surely you must have a text book which says somewhere in the middle that one of the proofs or equations given at the start is not strictly correct or only applies in special circumstances. No one suggest that such books are 'pushing the simple POV'. Boris pointed out long ago that if a typical maths text book or article were to be written in the most rigorous way known to mathematicians it would be completely impenetrable and utterly useless. Martin Hogbin (talk) 15:13, 1 June 2010 (UTC)

I disagree strongly, Rick, and I've been involved with this article for quite some time. Your 'logic' is tenuous at best, non-existent is more likely. You have made yourself judge, jury and executioner on this. That's not in the spirit of Wikipedia consensus editing at all. Simply because the edit is not your 'preference' is not a valid reason for reverting. Glkanter (talk) 15:20, 1 June 2010 (UTC)

Like I said, the structure is not neutral - it creates an editorial endorsement of the simple solution. Martin knows there is not consensus for this change yet made it anyway and then reverted a revert. Like I explained above, any edit is fine. A revert of any edit is fine (although a rather strong response). Reverting a revert is NOT fine. We're already in mediation about this. We haven't reached any conclusion. This change is premature at best. -- Rick Block (talk) 15:44, 1 June 2010 (UTC)

Like I said, I disagree strongly, Rick, and I've been involved with this article for quite some time. Your 'logic' is tenuous at best, non-existent is more likely. You have made yourself judge, jury and executioner on this. That's not in the spirit of Wikipedia consensus editing at all. Simply because the edit is not your 'preference' is not a valid reason for reverting.

We can keep repeating ourselves here, if you like. I'm game. Glkanter (talk) 15:59, 1 June 2010 (UTC)

And it's funny how your changes to the actual text of the article are OK, Rick, even though we're in mediation, but Martin's re-ordering of paragraphs is not. Once again, despite this obvious inconsistency, you act as if you are the final arbiter of Wikipedia policy and protocol. I'll call that 'chutzpah', but 'arrogance' is more appropriate. Glkanter (talk) 16:03, 1 June 2010 (UTC)

Let me repeat. Any change is OK. Any revert is OK. Reverting a revert is not OK. Did anyone revert "my changes to the actual text"? Did I revert a revert? Did I reintroduce a change that had been previously reverted? Or, was I making changes specifically trying to address your concerns? I'm trying to cooperate here. You're making it extremely unpleasant and I would very much appreciate it if you'd stop harassing me. -- Rick Block (talk) 16:16, 1 June 2010 (UTC)

I wish you would stop, as well. Now your justification of your aggressive actions rests wholly on a 'revert is OK, but a revert of a revert is not' and nothing more.

So, you claim an edit during mediation is OK, a revert of an edit during mediation is OK, but a revert of a revert during mediation is not OK? Are you serious? That is quite an interpretation of Wikipedia policy. And such strident certainty!

Sadly, I've found over 18 months of arguing the MHP that your interpretations are usually flawed. You know, host bias, SoK, 'Morgan's is the prevailing POV, as they have not been directly challenged', 'disproving' the various published simple proofs by saying: 'but they don't work for this slightly different problem where the host might...', previous erroneous Wikipedia policy explanations, etc., etc. This is just another in a too-long list. Glkanter (talk) 16:36, 1 June 2010 (UTC)

I'm fully supporting Rick here. If anyone has behaved unpleasant during the ongoing discussion it's Glkanter.Nijdam (talk) 08:38, 2 June 2010 (UTC)

I think it would be best if we all concentrate on the content of the article. Martin Hogbin (talk) 08:44, 2 June 2010 (UTC)

Rick, the structure is just like most other technical subjects, as I have explained this several times above. There are crazy people who think that relativity is all wrong and Newton's laws are the absolute truth. The article on the subject starts by talking about Newton's laws as though they were perfectly correct. No one claims that the article is supporting the crazy anti-Einstein POV. Also, as I have said before, the actual text makes the situation perfectly clear. Martin Hogbin (talk) 16:14, 1 June 2010 (UTC)

In fact no one who has not been engaged in this argument for years would suspect that there is or even could be any differing POVs on this subject. It is explained simply then in detail. Martin Hogbin (talk) 16:17, 1 June 2010 (UTC)

Informal RfC

How about an informal RfC in which we ask all those who have been involved in this argument in the last year or two to give their opinion? Martin Hogbin (talk) 14:34, 1 June 2010 (UTC)

I'd like to see an RfC on Rick for his reversions of edits only because they offend his sensibilities. As an editor, I'm OK with your change. As you made not a single change to the text, obviously you couldn't have introduced any Wikipedia violations worthy of reversion without discussion and consensus. Rick has clearly failed to attempt to create this consensus before he reverted. He's done this before without cause, and *warned* that he would do it again without cause. His reign of terror on the MHP needs to be stopped, finally. Glkanter (talk) 15:05, 1 June 2010 (UTC)

Please can somebody explain...

...why we must have a disclaimer in the simple solution section warning the reader that it is all wrong. This does nothing to help the general reader and the expert reader will see later on that the Morgan POV is fully covered. I have moved Nijdam's comment to the start of the 'Probabiliistic solution' section and made some slight changes to make it neutral. Despite the fact that the majority of editors here consider the Morgan POV wrong, or at best contrived, it is fully covered and explained in the article. We do not need a disclaimer at the start to be non-POV. Martin Hogbin (talk) 09:06, 2 June 2010 (UTC)

Would it help to move the unambiguous K & W formulation to the start of the 'Probabilistic solution'. I leaves only Whitaker's vague question, which is capable of several interpretations, at the start of the simple question. This avoids having what some believe to be a clearly incorrect solution to a well-defined question. Martin Hogbin (talk) 10:04, 2 June 2010 (UTC)

Any reader should be aware of the restricted value of the popular solution. Especially the general reader, the expert already knows. Nijdam (talk) 11:08, 2 June 2010 (UTC)

Such information is given with full detail and prominence in later sections. Martin Hogbin (talk) 16:53, 2 June 2010 (UTC)

Do you agree any reader should know? Nijdam (talk) 17:55, 2 June 2010 (UTC)

Any reader who is interested should be able to easily find out from our article. We cannot force readers to know things that do not interest them. We should not discourage readers from studying and understanding the problem in more detail. Martin Hogbin (talk) 18:06, 2 June 2010 (UTC)

Regarding Martin's suggestion to move the K&W problem statement - do you mean just the problem statement itself or the entire "Certain aspects ..." paragraph? In either case, I would say no. The paragraph is there to clarify the standard assumptions that even the popular solutions are based on. The K&W problem statement is simply a "full text" version of what these assumptions say.

What would actually help (for me) would be for the outline to be changed slightly, by adding an encompassing "Solution" section that "Popular Solution" and "Probabilistic solution" would be subsections under and in this top level section explain what's coming (in completely NPOV terms), i.e. something like:

<lead>

Problem

as is

Solution

There are multiple approaches to solving the Monty Hall problem. Most popular sources present solutions based on simple probabilistic reasoning. A different approach to solving the problem, used primarily in academic sources, is to treat it as a conditional probability problem.

Popular solution

Aids to understanding (under "Popular solution", not same level header)

Probabilistic solution

Mathematical formulation

Sources of confusion

etc.

Anyone have any problems with this? -- Rick Block (talk) 15:17, 2 June 2010 (UTC)

I have no objection to reducing the heading level of 'Aids to understanding', and presumably the sub headings in this section.

I do have a strong objection the insistence of two editors in getting disclaimers into the Simple solution section. Martin Hogbin (talk) 16:51, 2 June 2010 (UTC)

I'm sorry, I can't tell whether you're agreeing or not. I'm suggesting reducing the heading level of both "Popular solution" and "Probabilistic solution" (to level 2 headers under a new level 1 "Solution") and further reducing the heading level of "Aids to understanding" (to a level 3 header). The lead-in under "Solution" I'm suggesting is not a disclaimer in the (level 2) simple solution section, but a lead-in to both the simple and conditional solution sections under the level 1 "Solution" header. -- Rick Block (talk) 18:02, 2 June 2010 (UTC)

I am OK with all the level changes (assuming the page still looks good) but I object to what you call the lead-in, Glkanter calls weasel words, and have called a disclaimer. We now have a good lead-in to the 'Probabilistic solution' which is accurate and neutral; it should remain there. Martin Hogbin (talk) 18:13, 2 June 2010 (UTC)

Please explain what you object to about this. It is flatly descriptive of what the two major sections contain, isn't it? There are no weasel words and it in no way suggests the simple solutions are wrong or incomplete (i.e. it is in no sense "a disclaimer"). The current (recently added) lead-in to the Probabilistic section is actually weasel worded and does not accurately reflect the prevalence of sources that present conditional solutions. As worded, it strongly implies there are only "some sources" that present conditional solutions and that all of these criticize the simple solutions. The actual situation is that many sources (for example, most introductory probability textbooks) present conditional solutions, and of these some (but by no means all) criticize simple solutions. IMO, the criticism here is misplaced, It definitely needs to be in the article somewhere, but implying that only a few sources present conditional solutions or that all sources that present conditional solutions are also criticizing simple solutions is not in the least accurate. -- Rick Block (talk) 18:39, 2 June 2010 (UTC)

What does it tell the reader? How does it help them? Surely it is better to brink up this point, as we now do, in the 'Probabilistic' section, when the whole issue of some sources saying others are wrong can be discussed properly. You seem determined to get the word 'conditional' into the text as soon as possible. Martin Hogbin (talk) 20:43, 2 June 2010 (UTC)

It tells the reader there are TWO typical approaches, not ONE. You seem to think the words "conditional probability" mean "the simple solution is wrong". Presenting a conditional solution is NOT the same as saying the simple solutions are wrong - this is the compromise I've been seeking for quite some time. All drafts I have proposed in the last several months, including the draft I proposed above (just before you moved "Aids to understanding"), have this characteristic. If you're reading criticism of the simple solution into them then you're reading them incorrectly. -- Rick Block (talk) 21:42, 2 June 2010 (UTC)

Maybe you should just have a "Solutions" section with an "Unconditional solution" (stance A) subsection and "Conditional solution" (stance D) subsection, and then summarize both at the beginning of the "Solutions" section. Equal time for both approaches, and the aids to understanding section later. At the beginning of the solutions section, you'd just say what the two possible interpretations are, what the corresponding answers are, and then explain the details in the two different subsections in a way that the reader can skip either one (let the reader choose!). In an encyclopedia, it is normal practice to state the final answers up front, and only later explain in detail why they are the answers. The approach where you lead the reader by the nose before revealing the final answers is for textbooks, not for reference works. Usually a lot of readers just want the answers, and may not be interested in the explanations at all (especially in this age of TL;DR). No answer can possibly be complete unless the reader understands the question that is being answered, and the reader shouldn't need to wade through long-winded explanations just to know what the precise questions being answered are.

The unconditional solution could be explained as answering the question "What proportion of all players who switch will win?", and the conditional solution as answering the question "What proportion of all players who see the host open door 3 and switch will win?". The first case also includes players who see the host open door 2, so it is not obvious that these answers must be the same, but they are. And that's all the reader needs to know before going on to read their subsection of choice, and there are no scary symbols ("undergraduate statistics") involved. The reader can then verify that the solutions to the different problems give the same numerical answer. If you also want to include stance C in the article, then you could have a third subsection ("Equivalence" subsection? or "Extension to the conditional case" subsubsection in the "Unconditional solution" subsection?) that would show how the unconditional solution can be used to solve the conditional problem by using a symmetry argument or a "no information" (independence) argument. That would cover all the bases. -- Coffee2theorems (talk) 00:59, 3 June 2010 (UTC)

The simple solutions address the 'door 3 is opened' scenario. And every other contestant door choice and host door opening pairing. Just look at the 3 line table at the start of the Popular section. And the formal probability solution of 'conditional' *could* be in the same solution section as the simple solutions. Except that there's Morgan originally saying the simple solutions are false, though they later say in response to the letter correcting their calculation (emphasis theirs), "Simply put, if the host must show a goat, the player should switch". Which sounds an awful lot like many of the simple solutions. And a bunch of editors are confusing the textbook style of introducing conditional probability to their students with being a 'criticism' of the simple solutions. Glkanter (talk) 01:40, 3 June 2010 (UTC)

What Coffee2theorems is saying is nearly exactly what I've been saying for some time (months).

@Glkanter - you never replied to my suggested change to the Probabilistic section, see #Suggested change to the Probabilistic solution section (just before Martin moved the "Aids to understanding" section). The draft is still at User:Rick Block/Monty Hall problem (draft). Again, the Probabilistic solution section in this draft says NOTHING about Morgan et al and in no way criticizes the simple solution - it's nearly a complete (text) rewrite of the existing Probabilistic solution section. To be clear I'm not agreeing Morgan's (and Gillman's, and Grinstead and Snell's, and Lucas, Rosenhouse, and Schepler's, and Rosenthal's, and Falk's) criticism should be banished from the article - but I am willing to agree the initial presentation of a conditional solution doesn't have to include this criticism. -- Rick Block (talk) 03:53, 3 June 2010 (UTC)

Rick, I read in detail a recent version you posted where the deletions were clearly shown alongside the new text. I think I said to myself, this is alright. But, as we have seen, other editors are not attempting to play the same reindeer games as you, and Martin and I. While you and I don't appreciate each other's style, we both seem to play, fairly most of the time, when it comes to editing the article. Mainly by exercising restraint. So, it is of little utility for you, Martin, and myself to make and debate proposals, only to find other editors going their own way, at cross purposes to your various proposed attempts at compromise.

You've read my posts for a long time now. You know I am black and white on issues. But most of the other editors are not as definitive as me. So, I can't tell how many editors still believe Morgan's 'all simple solutions are false', or how many think Morgan backed away from that with their later response to Martin & Nijdam (emphasis theirs), "Simply put, if the host must show a goat, the player should switch" I guess people avoid these direct question because it's me asking them, or because the answers undercut their agenda. So, this drags out, allegedly mediated, with no end in sight. Glkanter (talk) 04:59, 3 June 2010 (UTC)

Glkanter, you forgot to point out that Morgan do not just say that the player should swap but say that the odds of winning if she does so are exactly 2/3. In their words, "...had we adopted conditions implicit in the problem, the answer is 2/3, period". Martin Hogbin (talk) 08:34, 3 June 2010 (UTC)

Coffee2theorems, what you are suggesting completely misses the point of this article in my opinion. The only reason that the MHP is notable and that we have this article at all is that most people think the answer (probability of winning by switching) is 1/2 when it is actually 2/3. This is one of the most tenacious and unintuitive simple mathematical problems known. Most people get the answer wrong and strongly resist any reasoning the gives them the correct answer. The first duty of this article, therefore, is to tackle the simple mathematical puzzle and convince readers of the correct answer.

It is possible, with some contrivance, to turn the MHP into an undergraduate level conditional probability problem, a valuable and instructive problem, but no more notable than most of the other problems that might be found in a probability text book. Our arguments here about the conditional nature of the problem are of no interest whatever to almost everyone, and building the article around a so called neutral position helps no one. The subject should be presented to the reader in the same way as most other technical subjects, a complete simple treatment first followed by a more detailed treatment for those interested.

So let me make my position absolutely clear. The conditional treatment of the MHP (as typified by the paper by Morgan et al) does nothing but obfuscate a simple and highly unintuitive simple mathematical puzzle. For those that have not read it my complete criticism of Morgan's paper can be hound here [4]. It is, of course, an interesting problem for those studying conditional probability but it is of no interest to anybody else and thus should only form a minor part of this article. My suggestions have been aimed at reaching a compromise so that we can end this argument. I would really like to see the 'conditional' section greatly reduced Martin Hogbin (talk) 08:34, 3 June 2010 (UTC)

And, let me make my position absolutely clear. What you're suggesting should be the "main point" of the article is nothing more than your own opinion, completely unsupported by any Wikipedia content policies or guidelines. The main point of the article, by fundamental Wikipedia policies, is to present facts - not to convince the reader that the answer presented is correct.

WP:NOT: "Wikipedia is an encyclopedic reference, not a textbook. The purpose of Wikipedia is to present facts, not to teach subject matter."

WP:NPOV: "All Wikipedia articles and other encyclopedic content must be written from a neutral point of view, representing fairly, proportionately, and as far as possible without bias, all significant views that have been published by reliable sources. This is non-negotiable and expected of all articles and all editors."

Your absolute refusal to present any solution based on conditional probability as a mainstream approach to solving the problem is inconsistent with the bulk of the technical references. Your notion that any conditional solution is equivalent to the Morgan et al. paper, or is fundamentally based on this paper, is simply wrong and merely reflects your own hatred of this paper. Conditional probability is the EXACT tool used to analyze problems like the MHP. There are certainly other ways to get to the correct answer, but conditional probability is the direct way. For the article to try to deemphasize this approach or treat it as an academic contrivance is not only willful stupidity but a direct violation of core Wikipedia content policies. -- Rick Block (talk) 15:18, 3 June 2010 (UTC)

And except where you cite WP policy, Rick, everything you wrote above is your personal point of view. But here's a fact, nobody would care about the MHP's glorious paradox if the formal conditional probability solution were the focus. The formal conditional probability solution isn't required to understand the paradox or the simple solutions (for the WP article, it is required), nor has it been widely acclaimed as 'the direct way'. Glkanter (talk) 15:28, 3 June 2010 (UTC)

Isn't the purpose of an encyclopedia primarily to inform, not to persuade? If these two goals are in conflict, it should be the former goal that takes precedence. A reader who stops reading before any (informal) proofs are given should still be left with a clear understanding of the possible interpretations of the question and the corresponding answers. An encyclopedia is a reference work, and should give the final answers up front, before any proofs.

You say that the conditional interpretation is contrived. I think the opposite: the unconditional interpretation is contrived. The conditional answer is of interest to people who interpret the question conditionally, and the unconditional one to people who interpret it unconditionally.

If people who interpret MHP unconditionally (stance A, not stance C) really exist, then both interpretations and answers should be given up front. If they don't exist (being stance C people instead), then the article should say that MHP is a conditional problem, and can be answered either by directly using conditional probabilities, or by the scenery route of first considering the unconditional problem and then extending it into the conditional case. Either way makes the presentation clear. Trying not to choose between these, intentionally leaving the article text ambiguous so that it may be read any which way, is going to leave the reader even more confused and frustrated than they originally were. -- Coffee2theorems (talk) 15:33, 3 June 2010 (UTC)

I agree completely. Unfortunately this seems to turn into another rerun of the former discussions. Those exact points about clarifying that simple solution addresses the unconditional problem (stance A) or that it serves as a heuristic or motivation to solve the conditional problem (stance C), that could be extended to a complete solution by various means, were raised over year ago already. Apparently (some) people weren't willing to listen back then, so I doubt they will now.--Kmhkmh (talk) 15:47, 3 June 2010 (UTC)

There is a difference between using the formal conditional probability proof and solving for the condition where door 1 is selected and door 3 is open. The simple solution in the Popular section does exactly that.

You're arguing about technique. Nothing more. Glkanter (talk) 15:40, 3 June 2010 (UTC)

No, I am not arguing about technique. I am arguing about interpretation. It is an entirely different matter. If it helps, what I said would still hold even if the article were to omit all proofs (and therefore all technique) entirely. -- Coffee2theorems (talk) 16:00, 3 June 2010 (UTC)