Talk:Great complex icosidodecahedron

Complex vs vs compound vs "generalized polyhedron"

This terminology is confusing and needs clarity. There are complex polytopes that exists with Complex numbers (not this!). This usage seems closer to the meaning of simplicial complex which are open collections of triangular faces. There are polyhedron compounds which are usually made of disjointed sets of faces/vertices/edges (not this!). But it can still meet the general definition of compound, even if fully connected.

So a generalized polyhedron apparently allows coinciding vertices, and edges, like the great disnub dirhombidodecahedron, which is apparently the ONLY uniform polyhedron with this property! Since this wasn't listed, there must be some missing component. My understanding is that is counted because it can be seen as a topological polyhedron, with overlapping edges counted twice in topological space.

There's definitely not a singular vertex figure for this object. The vertex figure itself looks like a pentagram/pentagon compound, and there's multiple possible paths, from (5.5.5.5.5.5/2.5/2.5/2.5/2.5/2) to (5.5/2.5.5/2.5.5/2.5.5/2.5.5/2) and who knows how many other paths. So my guess is a single vertex figure can't propagate the whole figure, but some mixture of forms that look the same. So anyway, I can't help any more, and the Mathworld link I added is next to useless.

This object seems a useful example for a larger class of polyhedra, but I've never seen such a list. It might include a good number of degenerate uniform polyhedra from Coxeter's paper. Tom Ruen (talk) 07:12, 25 January 2010 (UTC)[reply]

I linked to Klitzing's site, description: [1] 75.146.178.58 (talk) 09:12, 25 January 2010 (UTC)[reply]

Klitzing says "Looks like a compound of the great icosahedron (gike) and the small stellated dodecahedron (sissid), and indeed edges coincide by pairs, but vertices are identical. Note that without edge-doubling this would be a tetradic figure (type C)." SO 60 edges (2 sets of 30 overlapping), and 12 vertices - confusing business! Tom Ruen (talk) 09:47, 25 January 2010 (UTC)[reply]

Vertex figure is:

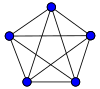
It's the union of the verfs of two polyhedra. (Label pentagram edges as 3, and pentagon edges as 5/2 Tom Ruen (talk) 21:41, 25 January 2010 (UTC)[reply]

These generate forms are listed in Coxeter's 1954 paper, copied at[2] (Table 6, degenerate cases) This polyhedron is both the third and fifth vertex figures listed. Tom Ruen (talk) 22:17, 25 January 2010 (UTC)[reply]

I linked the two CORRECT vertex figures (TWO of them) from Coxeter's paper. Tom Ruen (talk) 02:23, 26 January 2010 (UTC)[reply]

.