Portal talk:Mathematics/Archive2020

Duplicate "Did you know"

Number 34 and Number 43 in “Did you know” of Mathematics Portal are the same. — Preceding unsigned comment added by AshrithSagar (talk • contribs) 08:22, 5 June 2020 (UTC)

I have replaced #43. - dcljr (talk) 09:42, 7 June 2020 (UTC)

WP:RECOG discussion

dcljr, what do you think about automating the "Selected article" section using {{Transclude list item excerpts as random slideshow}}? This can be done after JL-Bot populates the section #Recognized content above. For an example of how it works, see Portal:Sports and its list of articles populated by the bot. —⁠andrybak (talk) 18:14, 8 June 2020 (UTC)

Have not had a chance to look into this. Hang on… - dcljr (talk) 07:22, 10 June 2020 (UTC)

Dcljr, JL-Bot has updated the section above. 48 featured and good articles in total. Perhaps, more templates and categories could be added to the current list, which I made from Wikipedia:WikiProject_Council/Directory/Science#Mathematics. —⁠andrybak (talk) 16:38, 18 June 2020 (UTC)

The bot output has been moved to Portal:Mathematics/Recognized content. —⁠andrybak (talk) 15:12, 5 November 2020 (UTC)

Here's a demo of how this would look like:

• 

  

  A perspective projection of a dodecahedral tessellation in H³. Note the recursive structure: each pentagon contains smaller pentagons, which contain smaller pentagons. This is an example of a subdivision rule arising from a finite universe (i.e. a closed 3-manifold).

  
  
  In mathematics, a finite subdivision rule is a recursive way of dividing a polygon or other two-dimensional shape into smaller and smaller pieces. Subdivision rules in a sense are generalizations of regular geometric fractals. Instead of repeating exactly the same design over and over, they have slight variations in each stage, allowing a richer structure while maintaining the elegant style of fractals. Subdivision rules have been used in architecture, biology, and computer science, as well as in the study of hyperbolic manifolds. Substitution tilings are a well-studied type of subdivision rule. (Full article...)
• 

  

  
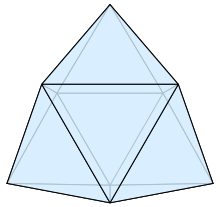
  The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron, composite polyhedron, and Johnson solid.
  
  The edges and vertices of the triaugmented triangular prism form a maximal planar graph with 9 vertices and 21 edges, called the Fritsch graph. It was used by Rudolf and Gerda Fritsch to show that Alfred Kempe's attempted proof of the four color theorem was incorrect. The Fritsch graph is one of only six graphs in which every neighborhood is a 4- or 5-vertex cycle. (Full article...)
• 

  

  A spiral staircase in the Cathedral of St. John the Divine. Several helical curves in the staircase project to hyperbolic spirals in its photograph.

  
  
  A hyperbolic spiral is a type of spiral with a pitch angle that increases with distance from its center, unlike the constant angles of logarithmic spirals or decreasing angles of Archimedean spirals. As this curve widens, it approaches an asymptotic line. It can be found in the view up a spiral staircase and the starting arrangement of certain footraces, and is used to model spiral galaxies and architectural volutes.
  
  As a plane curve, a hyperbolic spiral can be described in polar coordinates $(r,\varphi )$ by the equation
  $$r={\frac {a}{\varphi }},$$
  for an arbitrary choice of the scale factor $a.$ (Full article...)
• 
  The number π (/paɪ/; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.
  
  The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as ${\tfrac {22}{7}}$ are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
• 
  Donkey Kong Jr. Math is an edutainment platform video game developed and published by Nintendo for the Nintendo Entertainment System. It is a spin-off of the 1982 arcade game Donkey Kong Jr. In the game, players control Donkey Kong Jr. as he solves math problems set up by his father Donkey Kong. It was released in Japan in 1983 for the Family Computer, and in North America and the PAL region in 1986.
  
  It is the only game in the Education Series of NES games in North America, owing to the game's lack of success. It was made available in various forms, including in the 2002 GameCube video game Animal Crossing and on the Virtual Console services for Wii and Wii U in 2007 and 2014 respectively, and in 2024 for the Nintendo Switch Online service. Donkey Kong Jr. Math was a critical and commercial failure. It has received criticism from several publications including IGN staff, who called it one of the worst Virtual Console games. (Full article...)
• 
  69 (sixty-nine; LXIX) is the natural number following 68 and preceding 70. An odd number and a composite number, 69 is divisible by 1, 3, 23 and 69.
  
  The number and its pictograph give its name to the sexual position of the same name. The association of the number with this sex position has resulted in it being associated in meme culture with sex. People knowledgeable of the meme may respond "nice" in response to the appearance of the number, whether intentionally an innuendo or not. (Full article...)
• 
  
  

  

  Kaspersky in 2018

  
  Yevgeny Valentinovich Kaspersky (Russian: Евгений Валентинович Касперский; born 4 October 1965) is a Russian cybersecurity expert and the CEO of Kaspersky Lab, an IT security company with 4,000 employees. He co-founded Kaspersky Lab in 1997 and helped identify instances of government-sponsored cyberwarfare as the head of research. He has been an advocate for an international treaty prohibiting cyberwarfare.
  
  Kaspersky graduated from The Technical Faculty of the KGB Higher School in 1987 with a degree in mathematical engineering and computer technology. His interest in IT security began when his work computer was infected with the Cascade virus in 1989 and he developed a program to remove it. Kaspersky helped grow Kaspersky Lab through security research and salesmanship. He became the CEO in 2007 and remains so as of 2024. (Full article...)
• 

  

  A three-page book embedding of the complete graph K₅. Because it is not a planar graph, it is not possible to embed this graph without crossings on fewer pages, so its book thickness is three.

  
  In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.
  
  Every graph with n vertices has book thickness at most $\lceil n/2\rceil$, and this formula gives the exact book thickness for complete graphs. The graphs with book thickness one are the outerplanar graphs. The graphs with book thickness at most two are the subhamiltonian graphs, which are always planar; more generally, every planar graph has book thickness at most four. It is NP-hard to determine the exact book thickness of a given graph, with or without knowing a fixed vertex ordering along the spine of the book. Testing the existence of a three-page book embedding of a graph, given a fixed ordering of the vertices along the spine of the embedding, has unknown computational complexity: it is neither known to be solvable in polynomial time nor known to be NP-hard. (Full article...)
• 
  The IEEE Symposium on Security and Privacy (IEEE S&P, IEEE SSP), also known as the Oakland Conference, is an annual conference focusing on topics related to computer security and privacy. The conference was founded in 1980 by Stan Ames and George Davida and is considered to be among the top conferences in the field. The conference has a single track, meaning that all presentations and sessions are held sequentially in one venue. The conference also follows a double-blind review process, where both the authors' and reviewers' identities are concealed from each other to ensure impartiality and fairness during peer review process.
  
  The conference started as a small workshop where researchers exchanged ideas on computer security and privacy, with an early emphasis on theoretical research. During these initial years, there was a divide between cryptographers and system security researchers, with cryptographers often leaving sessions focused on systems security. This issue was eventually addressed by combining cryptography and system security discussions in the same sessions. In 2011, the conference moved to San Francisco due to venue size concerns. (Full article...)
• 
  
  

  

  Visualization of the binary search algorithm where 7 is the target value

  
  In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
  
  Binary search runs in logarithmic time in the worst case, making $O(\log n)$ comparisons, where $n$ is the number of elements in the array. Binary search is faster than linear search except for small arrays. However, the array must be sorted first to be able to apply binary search. There are specialized data structures designed for fast searching, such as hash tables, that can be searched more efficiently than binary search. However, binary search can be used to solve a wider range of problems, such as finding the next-smallest or next-largest element in the array relative to the target even if it is absent from the array. (Full article...)
• 

  

  An m × n matrix: the m rows are horizontal and the n columns are vertical. Each element of a matrix is often denoted by a variable with two subscripts. For example, a_2,1 represents the element at the second row and first column of the matrix.

  
  
  In mathematics, a matrix (pl.: matrices) is a rectangular array or table of numbers, symbols, or expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object.
  
  For example,
  $${\begin{bmatrix}1&9&-13\\20&5&-6\end{bmatrix}}$$
  is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a "$2\times 3$ matrix", or a matrix of dimension $2\times 3$. (Full article...)
• 

  

  The first five points in a farthest-first traversal of a planar point set. The first point is chosen arbitrarily and each successive point is as far as possible from all previously chosen points.

  
  In computational geometry, the farthest-first traversal of a compact metric space is a sequence of points in the space, where the first point is selected arbitrarily and each successive point is as far as possible from the set of previously-selected points. The same concept can also be applied to a finite set of geometric points, by restricting the selected points to belong to the set or equivalently by considering the finite metric space generated by these points. For a finite metric space or finite set of geometric points, the resulting sequence forms a permutation of the points, also known as the greedy permutation.
  
  Every prefix of a farthest-first traversal provides a set of points that is widely spaced and close to all remaining points. More precisely, no other set of equally many points can be spaced more than twice as widely, and no other set of equally many points can be less than half as far to its farthest remaining point. In part because of these properties, farthest-point traversals have many applications, including the approximation of the traveling salesman problem and the metric k-center problem. They may be constructed in polynomial time, or (for low-dimensional Euclidean spaces) approximated in near-linear time. (Full article...)
• 

  

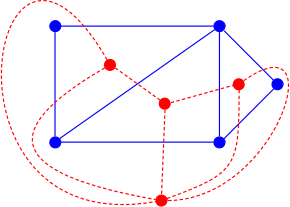
  The red graph is the dual graph of the blue graph, and vice versa.

  
  In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs (graphs that are already embedded in the plane) rather than planar graphs (graphs that may be embedded but for which the embedding is not yet known). For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
  
  Historically, the first form of graph duality to be recognized was the association of the Platonic solids into pairs of dual polyhedra. Graph duality is a topological generalization of the geometric concepts of dual polyhedra and dual tessellations, and is in turn generalized combinatorially by the concept of a dual matroid. Variations of planar graph duality include a version of duality for directed graphs, and duality for graphs embedded onto non-planar two-dimensional surfaces. (Full article...)
• 

  

  A depiction of how site isolation separated different websites into different processes

  
  Site isolation is a web browser security feature that groups websites into sandboxed processes by their associated origins. This technique enables the process sandbox to block cross-origin bypasses that would otherwise be exposed by exploitable vulnerabilities in the sandboxed process.
  
  The feature was first proposed publicly by Charles Reis and others, although Microsoft was independently working on implementation in the Gazelle research browser at the same time. The approach initially failed to gain traction due to the large engineering effort required to implement it in a fully featured browser, and concerns around the real-world performance impact of potentially unbounded process use. (Full article...)
• 

  

  Pell's equation for n = 2 and six of its integer solutions

  
  Pell's equation, also called the Pell–Fermat equation, is any Diophantine equation of the form $x^{2}-ny^{2}=1,$ where n is a given positive nonsquare integer, and integer solutions are sought for x and y. In Cartesian coordinates, the equation is represented by a hyperbola; solutions occur wherever the curve passes through a point whose x and y coordinates are both integers, such as the trivial solution with x = 1 and y = 0. Joseph Louis Lagrange proved that, as long as n is not a perfect square, Pell's equation has infinitely many distinct integer solutions. These solutions may be used to accurately approximate the square root of n by rational numbers of the form x/y.
  
  This equation was first studied extensively in India starting with Brahmagupta, who found an integer solution to $92x^{2}+1=y^{2}$ in his Brāhmasphuṭasiddhānta circa 628. Bhaskara II in the 12th century and Narayana Pandit in the 14th century both found general solutions to Pell's equation and other quadratic indeterminate equations. Bhaskara II is generally credited with developing the chakravala method, building on the work of Jayadeva and Brahmagupta. Solutions to specific examples of Pell's equation, such as the Pell numbers arising from the equation with n = 2, had been known for much longer, since the time of Pythagoras in Greece and a similar date in India. William Brouncker was the first European to solve Pell's equation. The name of Pell's equation arose from Leonhard Euler mistakenly attributing Brouncker's solution of the equation to John Pell. (Full article...)

—⁠andrybak (talk) 15:14, 5 November 2020 (UTC)

Unfinished selected pictures

dcljr, please see the added captions:

1. Special:Diff/987171957
2. Special:Diff/987172036
3. Special:Diff/987172086
4. Special:Diff/987172114

If that's enough, I'll remove the disclaimer and add these pictures to the rotation on the portal's page. —⁠andrybak (talk) 13:29, 5 November 2020 (UTC)

I did it, thanks. (I still plan to do additional copyediting/expansion of the description text for each, but what's currently there will do for now.) - dcljr (talk) 02:16, 6 November 2020 (UTC)