Science desk
< May 6	<< Apr \| May \| Jun >>	May 8 >

Welcome to the Wikipedia Science Reference Desk Archives
The page you are currently viewing is a transcluded archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

May 7

Why is there a "do not freeze" instruction on baking dough products?

I am referring to this item: [1]. Purchased them quite a while ago; threw 'em in the freezer; forgot all about them. I ran across them the other day; decided to make them, finally, after all. As I was starting to prepare them, I noticed on the package that it says: do not freeze (or microwave) uncooked dough (or words to that effect). Why is that? What's the problem ... or potential problem? I am only "worried" about the "do not freeze" directive; not the "do not microwave" directive. Thank you. 32.209.55.38 (talk) 03:55, 7 May 2020 (UTC)[reply]

Lots of google hits for this and other rising dough products that come in packages that you "burst" open. The idea is that freezing could lead to it bursting open. If it doesn't, and you fully defrost later, nobody seems to report any patterns of problems with the resulting baked item. DMacks (talk) 04:19, 7 May 2020 (UTC)[reply]

It could also impact the texture and taste, since freezing of course causes ice crystals and condensation to form. This can "unmix" fat-soluble and water-soluble components of the dough colloid. The same thing can happen when refrigerating/freezing other things like chocolate (see chocolate bloom). None of this will make you sick; it can just make the product less appealing. --47.146.63.87 (talk) 18:57, 7 May 2020 (UTC)[reply]

Thanks, all. Joseph A. Spadaro (talk) 17:17, 9 May 2020 (UTC)[reply]

Starlink launch/visibility

When the previous Starlink satellites were launched, it takes several days for them to be visible on the east coast of the US. Previous launches were in the daytime at Cape Canaveral but the next one is scheduled for the middle of the night. I think this should change the number of days until the satellites are visible on the east coast of the US, but I don't know how it is affected. With the next launch, how long should it be until they are visible on the east coast of the US? Bubba73 ^{You talkin' to me?} 06:25, 7 May 2020 (UTC)[reply]

I think we'll need to wait post launch, after NORAD starts publishing the orbital elements. Then sites like n2yo.com can track the satellites. By quick visual estimation, an individual Starlink flies over the same spot every 30 hours or so (2000 km longitudinal difference per 90 minute orbit on a 40,000 km circumference ball). This is not accurate enough to figure out overhead passes at times when the angle to the Sun is such that it is dark but the satellite is still in sunlight, making it eyeballable. I haven't seen targeted orbital elements being published pre-launch. Day vs. night launch is not important for eyeball observation as the things orbit the Earth once every 90 minutes. 85.76.71.1 (talk) 15:12, 7 May 2020 (UTC)[reply]

Thanks. My point about the day/night launch is that when they were launching in the middle of the day, it was taking at least 5 days or so for them to become visible here, which is about 1 to 1.5 hours after sunset or before sunrise. I thought that launching roughly 1/2 day later might affect that. Bubba73 ^{You talkin' to me?} 18:59, 7 May 2020 (UTC)[reply]

Bear in mind that successive launches do not necessarily put their satellite "batches" into the same orbits (so as to maximise coverage), and that such a satellite's visibility varies with the time of year, because you can only see it when you are in darkness but it is in sunlight, a circumstance greatly affected by the season at your location. {The poster formerly known as 87.81.230.195} 2.219.81.243 (talk) 21:45, 7 May 2020 (UTC)[reply]

Custom Coronavirus Graphs

Is there a website where I can select custom coronavirus graphs? Two things I would like to do right now would be (1) to plot daily new cases or daily new death for USA and for USA excluding New York and (2) plot deaths with and without probable deaths includes. I'd also like to plot these rates for different countries but corrected for population. Thanks in advance! — Preceding unsigned comment added by 173.72.208.160 (talk) 13:56, 7 May 2020 (UTC)[reply]

A daily updated graph with total COVID-19 confirmed cases and deaths per million people for the United States (including New York), based on data from the ECDC, can be found at Our World in Data. Data for the US and New York, based on info provided by State officials, is found in our articles COVID-19 pandemic in the United States, COVID-19 pandemic in New York (state) and COVID-19 pandemic in New York City. There are various online graphing websites (e.g. here, one of many). You will have to do the subtractions yourself. --Lambiam 17:59, 7 May 2020 (UTC)[reply]

Wrong explanation and opposite effect for the tides

I've read before (sorry, can't find the article) that the moon and sun do not attract the water, but wikipedia says otherwise here. I read that the moon and sun actually attract the earth, that is not solid, the earth elongates, so the water flows down in the other direction, making the tides.

I just checked the tide and moon positions for my city and it's consistent with what I read. I'm in Quebec City, the full moon was on the horizon around 6am (May 7th 2020), and it was a high tide, and at 2pm the moon will be at nadir (down) and the sun up, making a low tide (I checked the moon position with the SkyMap app and the tides here: www.tide-forecast.com/locations/Quebec-City-Quebec/tides/latest). I googled a bit and it seems that most webpages are consistent with wikipedia, but it's not what I just observed when looking at the actual data.

Someone care to tell me if I'm disastrously wrong, or if they're teaching wrong everywhere? Thanks! Ccvieira (talk) 15:56, 7 May 2020 (UTC)[reply]

Everything that has mass exerts an attractive force on everything else that has mass. That includes the Earth, the Moon, and the water in the oceans. If you look at a tide table, you will see that there are two high tides per day. Every day, these high tides occur slightly over half an hour later than the day before. Every day, the Moon also rises slightly over half an hour later than the day before. If there were no land masses and friction was negligible, the tides and the Moon would be perfectly in sync, and almost the same tide table would apply along a circle of constant longitude. But because of non-negligible effects, such as that the water of the bulges in the oceans needs time to flow around the obstructing continents, the tides for a given spot are out of phase with the moon, with different phase offsets for different spots. This youtube video explains the tidal forces. Unfortunately, even the simplest correct explanation is somewhat complicated. --Lambiam 16:54, 7 May 2020 (UTC)[reply]

Regarding the moon rising half an hour later each day, I once read it's actually 18 minutes. But there might be a ellipsoid-type of sine wave so that it's actually 18 +/- some minutes depending. 67.175.224.138 (talk) 15:39, 8 May 2020 (UTC).[reply]

It is closer to 49 minutes. In one lunar month of 29.5 days, the combined delays need to add up to 24 hours on average, since at the beginning of a lunar month (New Moon) the Moon rises and sets with the Sun. So divide 24h = 24×60 minutes by 29.5. --Lambiam 22:20, 8 May 2020 (UTC)[reply]

Also, the (solid part of) Earth does not elongate – at least, not to an extent that is significant in this context. --Lambiam 17:02, 7 May 2020 (UTC)[reply]

Here is a VERY simple one-line explanation from the Royal Observatory, Greenwich. Alansplodge (talk) 18:21, 7 May 2020 (UTC)[reply]

The reason for two bulges, however, is not readily apparent unless you think about it geometrically. Gravity follows an inverse square law with relation to distance, which means (for our purposes) that gravity is weaker farther from the mass concentration in question. The side of the earth closest to the moon feels the greatest force of attraction from the gravity, so it gets pulled closest to the moon, while the side of the earth opposite from the moon feels the weakest force of gravity, so in essence, so it gets pulled least towards the moon. If it gets pulled least, it would be left furthest back, generating the opposite-side-bulge in the oceans. --Jayron 32 18:44, 7 May 2020 (UTC)[reply]

I think what OP is saying is that the water sphere is elongated at 90° angles from the rigid earth sphere because the water collects in the depressions caused by the elongation of the rigid earth. However it makes more sense to me that the geoid, aka plane of equal grav. potential, is also distorted, which wouldn't make water pool in the depressions because the depressions would be areas of equal GP as the elongations on the Sun-Earth-Moon axis. In fact, as far as I understand, since the rigid earth deforms less readily than water (a few centimeters in amplitude), not only does the water sphere get elongated on the same axis as the rigid earth (because the same tidal forces apply to water), but it will actually end up compensating by pooling in the high GP area along the tidal axis, while having lower levels in the "depressions" at 90° angles. (Yes, water is attracted by gravity!)

There are however many confounding factors in the ways water tides manifest on Earth's coastlines. It takes time for Earth to deform and it also takes time for masses of water to travel along Earth. I think there's supposed to be a 1-2 hour lag in open ocean, but for narrow bays and long inlets like St. Lawrence River where Quebec City is located such lags will likely be longer. I think it's not impossible that some places, including QC, might be even 6 hours out of phase from the astronomical tide, which would give off the impression to those watching the local tide chart that water elongates at right angles from where Earth elongates. 93.136.11.212 (talk) 22:53, 7 May 2020 (UTC)[reply]

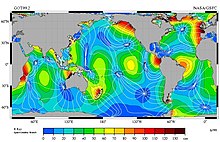
Tidal forces from the Moon try to create two tidal bulges in the oceans, travelling around the Earth every 25 hours, as explained very well by Jayron32. However, that doesn't happen. The reason is that there are continents in the way. So what happens in reality is that we have a forced, damped oscillator. It can be described as a standing wave for each frequency. Frequencies are for example once per 12.5 hours (caused by the Moon), once per 12 hours (by the Sun) and various beatings and harmonics. Keep in mind that every standing wave is a superposition of travelling waves and every travelling wave is a superposition of standing waves, so we are free to describe it as a standing wave. Now we can find a set of complex functions

\Psi _{\nu }(\theta ,\phi )

of latitude and longitude, one for each frequency ν and following in a hard to predict way from the topography, such that the tide T at a given spot (θ, φ) and time t can be found as

T(\theta ,\phi ,t)=Re\left(\Sigma _{\nu }\Psi _{\nu }(\theta ,\phi )\cdot e^{2\pi it\nu }\right)

So the phase of the tide is hard to predict from just the position of the Moon in the sky, as it depends on local topography. In case of Québec, you may notice that in Rimouski, a few hundred kilometres downstream on the Saint-Laurent estuary, the tides are about 4:15 hours ahead of those in Québec city, even though the Moon rises and sets at almost the same time. PiusImpavidus (talk) 08:50, 8 May 2020 (UTC)[reply]

Sorry, forgot a factor

i

and mixed up period and frequency. I was a bit in a hurry this morning. Attentive readers might have guessed we need a complex exponential there. Fixed now. PiusImpavidus (talk) 17:45, 8 May 2020 (UTC)[reply]

Thanks for writing this. I expected it was something complicated, I didn't know it was a standing wave. --93.136.11.212 (93.136.2.211 (talk) 00:31, 10 May 2020 (UTC))[reply]

Ccvieira may also wish to read Land tide or Earth tide. They involve significantly larger displacements than most people realize -- on the order of 55 centimetres (22 in) at the Equator -- but these do not dive the ocean tides. -- ToE 13:08, 8 May 2020 (UTC)[reply]

Good illustration you added there. Referring to my formula above, this map shows the value of

\Psi _{\nu }(\theta ,\phi )

for ν=1/12.5 per hour, with the colour showing the absolute value of Ψ and the lines connecting points where Ψ has the same argument. PiusImpavidus (talk) 17:45, 8 May 2020 (UTC)[reply]

Good info at What Physics Teachers Get Wrong About Tides!. Johnuniq (talk) 06:42, 11 May 2020 (UTC)[reply]

The OP read correctly that the Moon and Sun do not attract water, strictly speaking. On an Earth covered by a world-wide ocean, if the elliptical tide generating force is split into its vertical and horizontal components (to Earth's surface), only the horizontal component is called the tractive force because only it can move water. The vertical component on the Earth-Moon line is about one ten millionth of Earth's gravity so has little effect on water, but the horizontal component is unopposed by gravity so it easily moves water. Its greatest effect is at 45° from the zenith (sub-lunar point) pushing the water toward that point, and at 135° pushing that water toward the nadir (anti-podal point to the Moon). When the extra water in the bulges reaches equilibrium between vertical gravity and horizontal force the difference between the height of the water at the peaks and the equatorial valley on the prolate ellipsoid is about 55 cm. See [2] §4 and [3]. — Joe Kress (talk) 23:50, 12 May 2020 (UTC)[reply]

Nuclear fusion chain reaction

What causes the chain reaction in nuclear fusion? Fission relies on the release of high speed neutrons which collide with other atoms which makes them split which releases more neutrons, etc. What is the equivalent process in fusion? Why should a group a hydrogen atoms fuse just because two of them did to start? --Puzzledvegetable^{Is it teatime already?} 20:48, 7 May 2020 (UTC)[reply]

See Proton–proton chain reaction. In short, it isn't really a chain reaction. The protons fuse when they have a high enough kinetic energy to overcome electrostatic repulsion. That happens by being at very high temperature (basically a measure of kinetic energy). In so far as fusion itself releases energy that causes heat, it can be self-sustaining, but it isn't a chain reaction in the same sense as fission, which releases neutrons that directly cause neighboring atoms to split. --OuroborosCobra (talk) 21:09, 7 May 2020 (UTC)[reply]

So it’s not that each reaction causes the other ones, it’s just that the conditions that caused one of the reactions, will cause the rest of them, in time. Correct? --Puzzledvegetable^{Is it teatime already?} 01:49, 8 May 2020 (UTC)[reply]

Schematically, high temperature → nuclear fusion reactions → heat → high temperature → ... . Inasmuch as the condition causes the condition, it does so indirectly. Expressed in words, I'd formulate it the other way around: The reactions caused by the condition help to sustain that condition. You need to reach a certain threshold and excellent containment before fusion will be a self-sustaining process. --Lambiam 10:34, 8 May 2020 (UTC)[reply]

Kinetically, the proton-proton fusion reaction is basically identical to an exothermic, self-sustaining reaction, i.e. it is functionally equivalent to simple combustion. Any process which is exothermic enough to overcome its own activation energy will be self-sustaining (with some other considerations, but let's keep it simple). That is to say, considering a diagram like this: [4] if the Ea value is significantly lower than the ΔG value, the reaction is self-sustaining. From that point of view, proton fusion is perfectly describable using basic principles of kinetics and thermodynamics one learns in an introductory university-level chemistry course. The mechanistic aspects are different, but the kinetic modeling here really resembles simple combustion. --Jayron 32 15:22, 8 May 2020 (UTC)[reply]

Indeed, and even then, there are competing forces that allow for it to be a longterm, sustained process, instead of an instant "boom." In overly simplistic terms, the energy released by nuclear fusion in a star creates an outward pressure and expansion, which itself runs against further nuclear fusion happening. This is countered by the huge mass of the star, which results in gravity pulling material (fuel) back together, which also generates heat towards continued fusion. When these forces reach an equilibrium, you have a star, which can sustain a fusion reaction for billions of years. This balance can, of course, be spectacularly broken. --OuroborosCobra (talk) 19:25, 8 May 2020 (UTC)[reply]

Nuclear fusion elaboration: when free protons get close enough the nuclear force attracting them to each other overpowers their electromagnetic repulsion. This will happen to any two protons if you squeeze them closely enough. The hard part is getting them close enough, which requires doing work against that repulsion. Stars accomplish this by simply being enormously massive, enough that the force of their gravitational collapse produces sufficient pressures in their cores; since a gas gets hotter as it's compressed, the protons in the core get to such high temperatures—and therefore energies—to overcome that electromagnetic repulsion. It's not a "chain reaction" in the sense it's used when referring to fission, where a reaction product triggers further reactions in other matter. It appears to me it got the name because in stars, the conditions happen to be right to also produce a "chain" of further fusion reactions that ultimately produces helium-4. This is basically the inverse of a decay chain, where fission of large nuclei produces less-massive products, also through a series of reactions. --47.146.63.87 (talk) 00:16, 9 May 2020 (UTC)[reply]

Annoyed Superman question...

I'm quite familiar with the fact that Superman would be unable to carry an iceberg since the iceberg would fall apart, but another question sprung to mind from one of the old comics. If Superman is annoyed at something and flings it upwards with enough force to reach space (use the NASA definition of where space starts) is there *anything* that could survive to reach space. The amount of force that would have to be exerted over only 3 feet (from the height of his waist to the height of his head) in order to get enough velocity to reach space would be enormous. Let's assume the thing must likely to survive in any way would be a two inch wide and two inch wide point up cone made of Osmium(small enough to fit in one hand and for the hand to stay underneath). Does it simply deform and flow off of his hand as he exerts force and also, what happens as that cone as it travels through the atmosphere? If something else would be better than the osmium cone, please let me know. Also, would the answer be different for enough force to reach geosynchronous orbit.Naraht (talk) 21:40, 7 May 2020 (UTC)[reply]

A fictional character can do anything its writers want. ←Baseball Bugs ^{What's up, Doc?} carrots→ 22:22, 7 May 2020 (UTC)[reply]

Operation Plumbbob is probably as close to an experiment of this as you're gonna find. 93.136.11.212 (talk) 22:33, 7 May 2020 (UTC)[reply]

See: Project HARP. See also: suspension of disbelief. 2606:A000:1126:28D:CD3D:D2B2:F9A0:8975 (talk) 22:47, 7 May 2020 (UTC)[reply]

If Superman has his knees bent at the beginning of the throw and is standing up with his arm fully extended at the moment of release, he can possibly traverse a distance of 2 metres with his hand. Let us suspend our suspension of disbelief for a moment, Neil deGrasse Tyson-style. The atmospheric friction is non-negligible, so the initial speed on release needed to reach outer space is much higher than if the irksome object is flung in a vacuum. The latter can be calculated relatively easily. Using the Kármán line at 100 km as the boundary to be reached, and taking for simplicity a uniform gravitational field (for such near boundaries we can neglect the inverse-square law for a rough-and-ready approximation), that speed equals

v_{\mathrm {vac} }={\sqrt {2g_{0}h_{\mathrm {K} }}}

, where

g_{0}=9.80665~\mathrm {ms^{{-}2}}

(the standard acceleration due to gravity), and

h_{\mathrm {K} }=10^{5}~\mathrm {m}

(the Kármán line). Plugging in these values results in

v_{\mathrm {vac} }\approx 1400~\mathrm {ms^{{-}1}}

, roughly Mach 4. To overcome atmospheric friction, the speed will need to be much higher; at such speeds the heating will be such that the thrown object has evaporated before reaching space. Returning again to an airless Earth, to reach speed

v

within a distance

d

, the required acceleration

a={\tfrac {1}{2}}v^{2}d^{{-}1}

. Using the vacuum lower bound, so that

v\geq v_{\mathrm {vac} }\approx 1400~\mathrm {ms^{{-}1}}

and

d=2~\mathrm {m}

, we obtain

a>490,000~\mathrm {ms^{{-}2}}

, or 50,000 g. --Lambiam 10:18, 8 May 2020 (UTC)[reply]

I don't get your question. Your question makes it seem that it's all about the initial force, like hitting a baseball with a bat that can circle the Earth's perimeter. Why is Superman's initial velocity or force relevant? Can't he just fly 5 mph then gradually accelerate? And if this is about miles above ground, then keep in mind Earth's gravity gets weaker as you get farther, so is there something I'm missing? Anyways, I have been watching some physics-videos on how Pokemon stuff is false. 1 such video talked about a pokemon that can punch something over the "horizon." And they used the horizon proportional to his height. Video concluded such a force would not be possible to punch someone without breaking that someone. Another video was of a fire pokemon's fire that can melt an entire glacier/iceberg, and concluded it would have to be more powerful than the sun to do that in an hour. 67.175.224.138 (talk) 15:47, 8 May 2020 (UTC).[reply]

"Can't he just fly 5 mph then gradually accelerate?": No, because the question is about him throwing something into space. --76.71.5.208 (talk) 19:25, 8 May 2020 (UTC)[reply]

Okay, that's never happened before (on Earth's ground). There's clips of Superman flying to the ionosphere, then throwing something away, but never seen him throwing something from Earth's ground. 67.175.224.138 (talk) 20:14, 8 May 2020 (UTC).[reply]

Thanks Lambian, I'm pretty sure you understand what I meant. If I'm understanding your statements correctly, the object would have to accelerate at 50,000g for those 2 meters in the case of no atmosphere, and of course even faster with an atmosphere and that *any* object that Superman could put on his hand would evaporate under these conditions due to atmospheric friction. Is that correct?Naraht (talk) 21:27, 8 May 2020 (UTC)[reply]

Yes, but with the evaporation due not to the initial acceleration but to the speed and resulting aerodynamic heating. I have not tried to estimate the initial speed needed to overcome air friction and reach outer space from the surface of an atmospheric Earth (assuming an indestructible object), and I don't know how to calculate the aerodynamic heating. --Lambiam 22:03, 8 May 2020 (UTC)[reply]

Funny thing: something like this actually has happened in real life: Operation Plumbbob § Missing steel bore cap. An underground nuclear test accidentally "shot" a steel plate into the atmosphere. It's estimated that this was with enough force to reach space, but unfortunately as this was unintended nothing was set up to observe what happened. As discussed, some think the plate vaporized due to heating before reaching space. --47.146.63.87 (talk) 00:26, 9 May 2020 (UTC)[reply]

Ah, I see someone mentioned this above. My eyes went right past it until just now. --47.146.63.87 (talk) 06:02, 9 May 2020 (UTC)[reply]

Is there a graph about the possibility of life at different masses of the up and down quarks?

I remember seeing on wikipedia an image of a yellow-tinted graph that showed the mass of the up and down quarks on its axes, and showed what set of masses would allow life. Does anyone have a link to it? 82.17.164.224 (talk) 21:55, 7 May 2020 (UTC)[reply]

Perhaps File:Fine-tuned universe - the parameter space of the masses of the up and down quark.png – not currently used on the English Wikipedia, having recently been removed in this edit. --Lambiam 08:41, 8 May 2020 (UTC)[reply]

Thanks 82.17.164.224 (talk) 08:52, 8 May 2020 (UTC)[reply]