Disclaimer

Could we have a section with lower standards for verifiability and rigour with some kind of disclaimer? I suggest that we could, it is not uncommon in mathematical articles and text books for there to be a note to the effect that for the benefit of clarity some of the more complex or technical issues have been ignored.Martin Hogbin (talk) 10:33, 7 September 2008 (UTC)[reply]

Another solution - one that doesn't need a separate 'sources of confusion' section

I do not understand point 2 in the above solution.Martin Hogbin (talk) 21:43, 10 September 2008 (UTC)[reply]

I got to this page by accident - and I can't help but wonder why you posted the above comment here instead of the page you are referring to.

I suspect you don't understand point 2 only in the sense that it seems obvious. It is there because it is answer to the question: Why is it that the host opening a door at random to show a goat by chance changes the probability of the contestants initial choice from 1/3 to 1/2 and opening a door he knows hides a goat does not?

My argument is that since the host opens a door he knows hides a goat in every play of the game, if it were to alter the aforementioned probability it would do it every game - meaning the original choice really wasn't a 1/3 chance. Yet we know for certain it is 1/3. Doesn't it make sense to you that if the contestant's chance of picking the car was 1/2 in every play of the game then he'd pick it 1 time out 2 and not 1 time out of 3 overall?Millbast5 (talk) 22:39, 2 October 2008 (UTC)[reply]

New Source of Confusion

I think this is on the right track. The difference between, 'must open a goat door' and 'opens a goat door by chance' is crucial and to most people it is not immediately obvious that there is a difference.Martin Hogbin (talk) 17:27, 3 October 2008 (UTC)[reply]

I think people do understand the difference, but its slippery and they don't think about it much of the time. If you presented it like this: When the host opens a door at random he reveals a goat 2/3 of the time and the car 1/3 of the time but when chooses to open a door he knows hides a goat he reveals a goat 3/3 of the time. I think few people would disagree or even have any qualms about accepting it. That still doesn't mean that every time they think of the host opening door at random to reveal a goat they are going to realize that 'opening the door at random' is the meaningful part and revealing the goat is merely incidental. —Preceding unsigned comment added by Millbast5 (talk • contribs) 02:14, 4 October 2008 (UTC)[reply]

Cases where the chances of getting a car on switching are 0.5.

I think it may be constructive to think of examples of cases where the chances of the player getting a car would be 0.5 if he switched. I will list some below. It is not always obvious why these situations give answers different from the standard conditions and I think that may be a cause of confusion.

Host opens door at start

If the host opens a door revealing a goat at the start (it does not matter whether he does this intentionally or by chance) the problem is then very simple, we have one car and one goat and the player chooses at random between them.

This version is superficially the same as the standard problem and may be what most people have in their minds when they think about the standard problem.Martin Hogbin (talk) 11:11, 4 October 2008 (UTC)[reply]

Host chooses randomly

In this version the host chooses randomly which door to open. If he happens to choose a car the games is re-run from the start until he chooses a goat. In this version the player has a 0.5 chance of winning the car, whether he swaps or not.

It is easy to assume that this game has the same result as the standard game.Martin Hogbin (talk) 12:00, 4 October 2008 (UTC)[reply]

Host opens absolutely preferred door

In this version the host has a preferred door which he opens unless the car is placed behind it. If he opens this door rather than the non-preferred door the player has a 0.5 chance of winning.

This version differs from the standard version only because of the constraint that the host opens one of two goat doors (in the case where the player initially selected the car) with equal probability. It is used in the Morgan et al. paper to demonstrate why the problem must be approached as a conditional probability problem - rather than add the constraint they solve the problem without this constraint treating the host's preference for one door over another as a variable p. -- Rick Block (talk) 17:59, 27 October 2008 (UTC)[reply]

Host opens doors using any combination of random and intentional that reveals goats and cars in a two to one ratio

Random openings reveal goats and cars in a 2 to 1 ratio but if he intentionally reveals them in that same ratio the same probabilities result, which for the cases he reveals a goat the probability of the initial pick is 0.5. Thus he can mix random and intentional openings in any way he wants and reveal the same distribution of goats and cars. The revealed cars would be dealt with the same way mentioned in the Random openings.Millbast5 (talk) 07:47, 28 October 2008 (UTC)[reply]

Monty's Action Doesn't Change the Probabilities

This explanation is not particularly clear to me. One problem is that everybody has their own pet explanation which they like and which is crystal clear to them but not necessarily to everyone else. Maybe we need several explanations. Martin Hogbin (talk) 17:55, 26 October 2008 (UTC)[reply]

Generally I would say the shorter the better. Martin Hogbin (talk) 18:03, 26 October 2008 (UTC)[reply]

Well, obviously, I'm curious. Where does my solution require more clarity? And what is the goal of a potential new Solutions paragraph? Is it to be perfect? Or is being a lot better than the existing Solution going to be good enough? As I pointed out on the Monty Hall Problem Discussion page, the very first sentance in that Solution paragraph is erroneous. It pretty much goes downhill from there.

Glkanter (talk) 18:36, 26 October 2008 (UTC)[reply]

I really wanted to post this on the Monty Hall Discussion page, but I'm honoring Martin's request to discuss the issue here.

Martin has a one sentence proof: In the 2/3 of the instances where the contestant chooses a goat, Monty reveals the other goat, leaving the car. Anything else said is either a re-statement of the premises, or a statement of Probability Theory. Which is why the diagrams included are overly complex. We don't care which goat, and we don't care which door. Showing fractions such as 1/6, while accurate, are not friendly to readers, and are not part of the proof.

Using diagrams to convince those that don't 'get it'?. OK, that will help some people. But would you use diagrams to solve a 'Deal or No Deal' type problem? Probably not. Would you use diagrams to demonstrate the 'Assume a 1,000,000 doors proof? Certainly not. The diagrams are an aide, they are not the proof itself.

As for the cautionary statements at the top of the discussion page about the results being proven by experiment, which is stated twice? Shows a lack of confidence in the proofs provided. Someone really did the experiment? They went on a Hollywood sound stage, bought 2 goats and a car...? No, they did something similar. How many times was it done? How many times is enough to prove this? The caution, if there should even be one, should direct the user to disprove the proofs provided.

As for simulations? They may convince some people, but they are not a proof.

And lastly, being opposite the majority of editors with these comments? Mathematics, as I stated earlier is not a popularity contest. I've demonstrated that about 90% of the Solution is chaff that does not aid the understanding of the puzzle solution. I'm in the minority regarding a valid mathematical proof? Absurd. But that's human nature. I imagine these discussions get pretty heated on Wikipedia when the topic is politics, etc. Just look at what happens when we're discussing the simple statement: "In the 2/3 of the instances where the contestant chooses a goat, Monty reveals the other goat, leaving the car.". Glkanter (talk) 13:56, 27 October 2008 (UTC)[reply]

And the figure at the top of the problem page? Showing an open door plus two identical remaining doors? How does this (incomplete) snapshot of the middle of the game help understanding of the solution? It doesn't. It misleadingly re-inforces the notion that the end probability is 50% - 50%. Glkanter (talk) 14:10, 27 October 2008 (UTC)[reply]

Now, if you want a figure that acurately represents the puzzle, and it's solution, look in the 'Combining Doors' section. There you see 2 doors grouped, with a 2/3 value assigned. If more than one proof can be provided in the Solution paragraph, this one might be a candidate.

But only after removing this paragraph: "The game assumptions play a role here—switching is equivalent to taking the combined contents if and only if the game host knows what is behind the doors, must open a door with a goat, and chooses between two losing doors randomly with equal probabilities." Stating that the assumptions are important is unnecessary, and therefore is a distraction. Further, Monty choosing goat doors randomly is not a premise of the puzzle, and is not important. Glkanter (talk) 14:27, 27 October 2008 (UTC)[reply]

Rick's objections, based on Morgan et al.

If we assume the question is asking about the probability of winning by switching after the host has opened a door (which the usual problem statement seems to imply), Martin's one sentence explanation and the Monty's action doesn't change the probabilities explanation (and similar "simple" explanations) can be paraphrased as follows:

The player has a 1/3 chance of initially picking the car. When the host opens a door this probability does not change, so the remaining door must have a 2/3 probability.

The problem is the phrase "when the host opens a door this probability does not change". Given the fully unambiguous version of the problem statement, specifically including the constraint that the host choose between two goat doors with equal probability (in the case the player has initially selected the car), this statement is in fact true but it is certainly not given by the problem statement. These solutions are simple, and intuitively appealing, but incomplete unless there's some reasoning added to back up the claim that the host hasn't affected the probability. PUTTING THE CLAIM IN ALL CAPS is not sufficient. Saying it over and over again is not sufficient. Saying anyone who asks for reasoning doesn't understand probability is not sufficient.

The simple case analysis solutions, like the one vos Savant presented in Parade magazine and like the one currently at the beginning of the Solution section of the article are actually valid, but address the probability of winning by switching evaluated before the host has opened a door (with knowledge that the host will indeed open a door). The clue that this is true is that they don't make any mention of which door the host opens. For casual readers this may be sufficient, but IMO for an encyclopedia article on this problem (which is the topic of dozens of papers in Mathematics journals) not answering the question that's actually asked seems woefully insufficient.

I think this leaves us with addressing the actual question, which requires working out why the constraints on the host make it so that opening a door doesn't change the initial probability. The initial figure in the article actually shows this. The probabilities of the player's initial pick are (1/6-car + 1/3-goat) in the case the host has opened Door 2 and the same in the case the host has opened Door 3. Note that the 1/6 is because in the case the player initially selected the car the host is constrained to open Door 2 and Door 3 with equal probability. Regardless of which door the host opens, the conditional probability of the initially chosen door being the car is 1/6 out of 1/2, which is 1/3 and the other remaining door is 1/3 out of 1/2 which is 2/3. -- Rick Block (talk) 18:35, 27 October 2008 (UTC)[reply]

My main point is this. What makes the probability calculation of Monty Hall problem especially notable and therefore worthy of an article in WP is the fact that, even when unambiguously presented, most people get the answer wrong. We do not have detailed statistical analyses of all other TV game shows. I therefore suggest that it would be quite in order, in fact desirable, to gloss over any statistical subtleties on order to make the basic solution clearer and more convincing.

It is not unknown in 'serious' mathematical proofs to initially answer a different question from the one asked and then to describe how the question answered relates to the one actually posed. This may form the first stage of solving the real question.

Now to the conditional/unconditional issue. I think the relevance of this is greatly exaggerated. It a situation in which no information is given on how a choice is made, it is normal, indeed mandatory, to assume that the choice is random. If I tell you that I am going to toss a coin and ask you what the chances are that it will come up heads you would say 1/2. Now it could be that I have practised deliberately manipulating the toss to come up heads and that the real probability is 3/4 but if you are not told this you are correct to assume a 1/2 probability. We are told nothing about the way Monty chooses which door to open therefore it is quite correct to take it that he does this randomly.

The above having been said, I think that the basic solution should be to as simple as possible with the primary aim of convincing people. It should the be followed by a 'Sources of confusion' section purely about the basic problem. We both agree that a more detailed analysis should follow. I will make my criticism of the basic solution given in another section below.

Perhaps you could also clear one thing up for me. In the standard version of the problem we agree that it is intuitivley true and indeed a fact the Monty's actions do not change the odds that the player has chosen the car but you go on to say that this is not easy to prove. Could you explain why please? Martin Hogbin (talk) 20:04, 27 October 2008 (UTC)[reply]

Re the very last point, see below. -- Rick Block (talk) 02:16, 28 October 2008 (UTC)[reply]

I'm glad we're focussing on the Monty Hall Problem, and not a variant. My experience has been that a proof is posited. Then it is given scrutiny, that is, is each statement of the proof true and valid? Does the proof reach the proper conclusion? If the answers are yes, then it's a valid proof. And needs no further support. No such thing as 'yes, sort of, but does not meet rigorous enough scrutiny'. For clarity, one could include a given Probabilty law, for example, one might include 'The probability must equal 100%.' Unimportant issues should be avoided in a proof. Which goat is unimportant. Which door is unimportant. That's why the proofs don't address them. They could be a goat and a pig, and as long as Monty has to reveal a farm animal, it's not important which one he shows. I don't see what the discussion of 'conditional' has to do with all this.

"When the host opens the door the odds don't change" is a correct and valid statement. The hosts action, as per the premisies, does not consider the contestant's door. This is because the probability statement at that point in time is 1/3 + 2/3 = 100%. The "+" is critical. Monty's action, since it is not distributed over all 3 doors, only affects the right side of the equation. So, since the probability must always = 100%, we can validly state "Monty's action doesn't affect the odds. They remain 100% - 1/3 = 2/3". (BTW, the only way Monty's action could affect the contestant's door's odds would be if he revealed the car. Then all heck would break loose. Then we have enough knowledge that the formula becomes 0 + 1/1 = 100%. But that's a different puzzle.)

The host's action can affect the probability without revealing the car. In the problem as given, they happen not to but basing a "proof" on this claim is faulty. The counterexample (and one counterexample is enough to destroy a proof) is the variant where the host always opens the leftmost door that is available. 1/3 + 2/3 = 100% in this variant, just like the regular version (and, BTW, in many versions whether the host has a preference for one door over the other is not specified in which case this "peculiar" variant is not excluded by the problem statement). The host "does not consider the contestant's door" (whatever this means). Before the host opens a door the player has a 2/3 chance of winning by switching (1/3 + 2/3 = 100%). After the host opens a door the chances are either 50% (in the 2/3 of the time the host opens the leftmost door) or 100% (in the 1/3 of the time the host opens the rightmost door). The corresponding equation is now 2/3(50% + 50%) + 1/3(0 + 100%) (where the leftmost term is the situation if the host has opened the leftmost door and the rightmost term is the situation if the host has opened the rightmost door) which of course totals to 100%. The claim that when the host opens the door the odds don't change is not made true because the host "does not consider the contestant's door", or because the host is acting only on the unchosen doors, or because we already know one of the unchosen doors must be a goat (all of which are true in this variant, in which the odds DO change), but because the host is constrained to make a random choice between two goat doors (if this comes up). We could say

The player has a 1/3 chance of initially picking the car. Because the host is constrained to make a random choice between two goat doors (which comes up if the player initially selects the car), when the host opens a door this probability does not change. So the remaining door must have a 2/3 probability.

but I'd be willing to bet the average (probably even an exceptional) reader would find this to be a fairly curious statement. -- Rick Block (talk) 02:16, 28 October 2008 (UTC)[reply]

But Martin's proof is more elegent. 2/3 of the time the contestant chooses a goat. (True? Valid?) 100% of those times, Monty reveals the second goat. (True?, Valid?). Therefore, when there is 1 door remaining there is a 2/3 chance it is a car.

Bear with me here. Rerun these same statements with the "host opens leftmost door if possible" variant. 2/3 of the time the contestant chooses a goat. True. Valid. Check. 100% of those times, Monty reveals the second goat. True. Valid. Check. Therefore, when there is 1 door remaining there is a 2/3 chance it is a car. Not true. Not valid. "Therefore" is therefore incorrect. There needs to be something more. If I have a proof of X, and each and every step can be used to prove Y, but X is true and Y is not there's something wrong with the proof. -- Rick Block (talk) 02:16, 28 October 2008 (UTC)[reply]

Mr. Block has not disproven Martin's proof. He's engaging in something other than 'classic probability theory' analysis. THEREFORE there's really nothing more for me to contribute here. Glkanter (talk) 02:40, 28 October 2008 (UTC)[reply]

Where am I engaging in something other than classic probability theory? We're evaluating the probability of winning by switching knowing which door the host has opened. The "host opens leftmost door if possible" variant has the awkward property that this probability differs depending on whether the host opens the leftmost or rightmost door (and also differs depending on whether we evaluate it before or after the host opens a door). Classic probability theory is entirely sufficient to cover this. It's the same as having a population of, say 50 each, exclusively blue-eyed blondes and brown-eyed brunettes. The probability of a single person in this population having blue eyes is 50%. If we then divide this population into two groups by hair color and after they've been divided pick one person and ask what is the probability of ending up with a blue-eyed person, we wouldn't say 50%. We'd say 0% if the person was from the brown haired group, but 100% if the person was from the blonde haired group. If we do this repeatedly we'll end up with a blue-eyed person 50% of the time, but any given time we do it we know with certainty (based on what group the person was selected from) whether we have a blue-eyed person or not. If we randomly place the original 100 people into two groups we end up with a 50% chance of selecting someone with blue eyes from either group. The analogy to Martin's proof is that it ignores how we've placed the people into groups (which our problem statement says must be random) and instead says that it's simply impossible to create subgroups with different distributions than what we started with. -- Rick Block (talk) 04:52, 28 October 2008 (UTC)[reply]

Specifically? Since we agree the statement 100% of those times, Monty reveals the second goat is true and valid, the conclusion is true and valid. We've accounted for all the goats, all that can possibly remain is a car. You claim the conclusion, however, is not true. But, it is true. In fact, you've previously agreed that switching results in 2 times the liklihood of selecting a car. Which is the conclusion Martin draws. According to you, then, the statement can be both true and false at the same time. That's not a possibilty in 'classic probability theory'. THEREFORE, you're either engaging in something other than 'classic probability theory' or you don't know what you're talking about. I don't think these choices are mutually exclusive either.

Glkanter (talk) 08:59, 28 October 2008 (UTC)[reply]

During Watergate, Deep Throat told Woodward and Bernstein to 'Follow the money'. In this puzzle, the advice is 'Follow the car'.

""Host opens leftmost door if possible" variant?" It's all about the car.

"50 each, exclusively blue-eyed blondes and brown-eyed brunettes"? It's all about the car.

2/3 of the time Monty leaves a car by revealing a goat. And Martin proved it in no more than 2 statements of probability.

Glkanter (talk) 09:20, 28 October 2008 (UTC)[reply]

Martin and others have met the burden of proof. Bringing up all that other stuff IS NOT SUFFICIENT to disprove the proofs. Glkanter (talk) 20:19, 27 October 2008 (UTC)[reply]

The question that is being solved is 'Does the contestant better his/her chances of selecting the car by switching?' Martin's solution, and the others, answers that question, and that question only. The only thing that matters is that there is an unopened door on the stage. Not 'which door, nor which goat, nor why that goat?'. Any insistance that these matter, imho, is misguided. Glkanter (talk) 20:33, 27 October 2008 (UTC)[reply]

Thanks, Glkanter for your support of my proposed solution but do I agree with Rick that certain possible host actions or strategies would invalidate it. My point is that we should initially ignore that fact (for reasons I have given above and will expand upon is a section below) in the interests of clarity of the basic explanation. Martin Hogbin (talk) 09:27, 28 October 2008 (UTC)[reply]

I am stunned by your response. Using freshman year college level probability analysis, I and others have demonstrated various proofs of the solution. Mr. Block's most recent 'dis-proval' relies on a statement being both true and not true at the same time. Balderdash. BTW, all it takes is a single valid proof to prove the arguement, and Martin, your own proof does that.

Contestant takes a goat, monty reveals a goat, door hides a car.

Contestant takes the car, monty shows a goat, door hides a goat. Nothing else can take place. There are no other variables.

Now, we're discussing 'host actions' and 'strategies' that alter the above? There are no other host actions. There are no other strategies. The contestant chooses randomly. Monty acts benevolently, by showing a goat, all the time.

Honestly? As an outsider reading all this, and what came before me? It's like you all drank the kool aid.

Of course this will continue to come up, as Millbast5 says below. Because the page could, and should be elegantly simple in its explanation. And it's not.

Millbast5 asks the right question below. What's the point? You guys need to re-think your entire approach to the page, FA or not. Until you agree that all that other stuff does not support or contradict the solution, and that it doesn't belong anywhere near the Solutions, or 'Aids to Understanding', readers like myself will innocently try to help. And then fall into this nexis of futility you have created.

Glkanter (talk) 12:44, 28 October 2008 (UTC)[reply]

Apparently, this user/editor community relies on the knowledge and skills of someone(s) (Morgan perhaps?) for their understanding of how to solve this problem. Whoever it is, you might want to re-evaluate his/her/thier level of expertice.

Here's the line I deleted from the existing Monty Hall Problem page. It was the very first sentance under the heading "Solution".

"The overall probability of winning by switching is determined by the location of the car. "

This is contrary to the most basic principal of probability. Yet it had been vetted by this community, and was determined to be the most important statement to make in the understanding of the solution. To me, this calls into question the level of knowledge of the topic of the individual who provided it, and the collective body that originally approved it, and subsequently let it remain there.

Glkanter (talk) 14:23, 28 October 2008 (UTC)[reply]

I'm growing weary of your insults and would appreciate it if you'd stop. What you seem to be missing is that there are two different questions which can have different answers. If we assume all players initially choose Door 1, there are three different populations of players. All players. Only those players who see the host open Door 2. And only those players who see the host open Door 3. We all agree 2/3 of all players who switch will win (on average) by doing so. What I'm saying is that this does not necessarily mean that 2/3 of both the "Door 2" and "Door 3" populations also win by switching. The usual form of the MH problem is not asking about the population of all players, it's asking about the players in the other two groups (the usual phrasing asks specifically about the Door 3 group). The reason we include the constraint on the host that he choose between two goats with equal probability (when he has a choice) is because this turns out to make the Door 3 group and the Door 2 group have the same probability of winning by switching, and if these are the same they each must be the same as the probability for all players. Without this constraint we can create situations where the Door 2 group and Door 3 group have different probabilities, even though the probability for all players remains 2/3. Martin's proof shows the probability for all players is 2/3. Saying that this means the probability for the Door 3 group is therefore 2/3 is incorrect. -- Rick Block (talk) 14:47, 28 October 2008 (UTC)[reply]

I didn't come here looking for a fight, ok? We seem to be using two different rule books to prove or dis-prove a theory. I'm not familiar with the one you're using. It contradicts the one I know. And the more you post, the greater the disparity becomes.

Glkanter (talk) 15:16, 28 October 2008 (UTC)[reply]

We also seem to be discussing two different Monty Hall Problem definitions. You state above, "The usual form of the MH problem is not asking about the population of all players, it's asking about the players in the other two groups (the usual phrasing asks specifically about the Door 3 group)." The Monty Hall Problem that I am familiar with does ask about the population of all players. In my opinion, that's what Probability Theory is all about.

Glkanter (talk) 15:21, 28 October 2008 (UTC)[reply]

The usual phrasing includes words like "imagine you've picked Door 1 and the host opens Door 3, and then asks would you like to switch to Door 2?". There's certainly an argument that this is an overly literal interpretation, but this question seems to relate to the Door 3 group rather than the "all players" group. In more general terms, it's clearly asking the player to decide after the host has opened a door with knowledge of what door the host has opened. Answering the question for the "all players" group is effectively answering the question before the host has opened a door which would be more consistent with wording like "imagine you've picked Door 1 and the host says 'I'm going to open a door revealing a goat - would you like switch to whatever door I don't open?'" The difference is fairly subtle, but very real. Morgan is a statistics professor at Virginia Tech. His paper I keep referring to was published in response to the nationwide furor about the MH problem following its publication in Parade Magazine in 1990. I believe it was the first authoritative examination of the MH problem (published in a peer reviewed mathematics journal). The solution vos Savant published in Parade answered the question about "all players", but the version of the problem she published included the typical "imagine ..." phrasing and didn't specify that the host is constrained to pick between two goats with equal probability. Bayesian treatments of the problem always assume the "equal goat" constraint - if they don't the answer isn't 2/3. It's not just splitting hairs. -- Rick Block (talk) 16:49, 28 October 2008 (UTC)[reply]

This is from the 'Problem' section of the Monty Hall Problem page. It appears immediately before ths 'Solutions' heading:

Hence a more exact statement of the problem is as follows:

Suppose you're on a game show and you're given the choice of three doors. Behind one door is a car; behind the others, goats. The car and the goats were placed randomly behind the doors before the show. The rules of the game show are as follows: After you have chosen a door, the door remains closed for the time being. The game show host, Monty Hall, who knows what is behind the doors, now has to open one of the two remaining doors, and the door he opens must have a goat behind it. If both remaining doors have goats behind them, he chooses one randomly. After Monty Hall opens a door with a goat, he will ask you to decide whether you want to stay with your first choice or to switch to the last remaining door. Imagine that you chose Door 1 and the host opens Door 3, which has a goat. He then asks you "Do you want to switch to Door Number 2?" Is it to your advantage to change your choice? (Krauss and Wang 2003:10)''

Note that the player may initially choose any of the three doors (not just Door 1), that the host opens a different door revealing a goat (not necessarily Door 3), and that he gives the player a second choice between the two remaining unopened doors."

So, that's the problem statement. It seems clear that we are, of course, talking about all possibilities.

Glkanter (talk) 17:14, 28 October 2008 (UTC)[reply]

It seems clear to me that we are talking about the situation after the host has opened a door with knowledge of which door the host has opened, and although we might dearly want it not to be true the doors are distinguishable. This problem isn't quite the same as the "balls and urn" version Millbast5 has proposed (rather than doors and goats and cars, we talk about three identical balls one which has the word "car" written on it - you pick one without looking at it, the host looks in the urn and withdraws one that doesn't say "car" on it and shows it to you - do you want to switch yours for the remaining one in the urn?). In the balls and urn version, the host has no choice but to pick one of the losing balls randomly (since they're indistinguishable). In the MH problem, the doors are inherently distinguishable so we don't have the luxury of treating them as if they aren't. Martin's proof is just fine for the balls and urn problem, it just isn't quite right for the MH problem. An urn problem exactly equivalent to the MH problem would be to start with three balls, one that says "loser 1", one that says "loser 2" and one that says "car". Same mechanics. Across all players the answer is identical (2/3 chance of winning by switching), but we can now ask what the chances of winning are if the host shows you a ball that says "loser 2". And the answer, just as in the MH problem, is that it depends on how the host picks between the two losing balls (if given the choice). If the host picks randomly, the answer is 2/3. If not (for example if the always picks "loser 2" if given the choice), it can be anywhere between 1/2 and 1 even though across all players the answer is still 2/3.

Want to or not, the phrasing of the MH problem puts us in the position of answering the harder conditional question, not the "all players" question. The solution needs to address the actual problem, not what we'd like the problem to be. -- Rick Block (talk) 18:49, 28 October 2008 (UTC)[reply]

Now it's 'balls and urns'. It's always something other than validating a solution to the Monty Hall Problem. I've re-read the Monty Hall Problem discussion page. It always goes like this. Then the new guy, who invariably points out the same things that I've been saying, gets fed up and leaves.

So, I'll ask again. Does Mr. Block have a supervisor that can be spoken to, or is his the final word?

Glkanter (talk) 20:00, 28 October 2008 (UTC)[reply]

Why are we still talking about this?

Are we back to this again - I thought we settled this issue a couple a weeks ago when I calculated that, regardless of the value of Morgan's et al.'s p, the overall probability of winning by switching is 2/3. IIRC, Rick said then that Morgan et al. had proved the same thing. Does this not mean that the value of p is irrelevant if you are interested in determining the overall probability of winning by switching? Moreover, if the host has a preference and the contestant knows the exact value of p for the pair of doors in question, he can do nothing with that information to change the outcome. All that happens is that he knows after the host opens a door his 2/3 overall probability of winning by switching will become 1/(1+p) for one door and 1/(1+(1-p)) for the other. And moments later it will become either 1 or 0, depending on whats behind the door he settles on. [The minimum value is 1/(1+1) = 1/2 so it never less than the value by not switching, hence my statement that the contestant cannot capitalize on his knowledge.]

I believe that if we agree that the primary goal of this page is to convincingly establish the overall probabilities of winning by the switch and non-switch strategies then we should thank Morgan et al. for showing their door preferential 'p' plays no role in determining those values and refrain from mentioning it again.

Let me back up. Does anyone or everyone agree that the primary goal of this page is to convincingly establish the overall probabilities of winning by the switch and non-switch strategies? If not, what do you see as the primary goal? Or if you think I'm just somewhat off target and there is a better way to describe the goal, what is that?

I'm not trying to split hairs here - this issue keeps coming up and taking over any discussion we have about solutions or sources of confusion.

Rick? Martin? Glkantar? Anyone else?Millbast5 (talk) 11:11, 28 October 2008 (UTC)[reply]

The "overall" probability of winning by switching is 2/3, regardless of Morgan et al..s p. That's not the issue. The issue is that the standard form of the problem doesn't ask about the overall probability, it asks about the conditional probability given knowledge of which door the host opens. That's why the problem statement has to say the host chooses between two goat doors randomly. This constraint is crucial toward making the probability 2/3 (it's used in the Bayesian analysis, and must be provided as a given or the probability cannot be shown to be 2/3).

The goal of any article at Wikipedia is to meet the featured article criteria. Germane to this discussion are 1(b) and 1(c). Wikipedia is not Parade Magazine (which has a distinctly non-technical audience), but neither is it a mathematics journal. Perhaps the best comparison is Encyclopedia Britannica - scholarly, but not unapproachable by an educated adult and firmly based on reliable published sources. There are very few featured articles here about individual problems in mathematics (see list at WP:FA#Mathematics), but the goal is to be comprehensive - and, directly answering your question I don't think the primary goal is to be convincing (although I think a clear and accessible article should naturally be convincing as well). The guideline at Wikipedia:Make technical articles accessible suggests putting more accessible aspects of a topic earlier, which is exactly the current structure of the existing Solution section. It contains a short, but valid, case analysis meant to be accessible to nearly anyone which also functions as a lead-in to a more detailed analysis responsive to the question that is actually posed (the conditional probability question).

The suggestion on this page seems to be that the existing solution section is simply too difficult to understand, so we should dumb it down so our more doltish readers don't get confused. I say absolutely not. It can certainly be improved, but I think trying to avoid addressing the fact that the MH problem is fundamentally about conditional probability is not the right approach. -- Rick Block (talk) 14:11, 28 October 2008 (UTC)[reply]

I agree with Millbast5 that the issue of host behaviour is a complete distraction from the essential Monty Hall problem. (See my thoughts in the section below.) In the 'standard' case the conditional and unconditional probabilities are exactly the same. Martin Hogbin (talk) 19:12, 28 October 2008 (UTC)[reply]

Per my discussion with Glkanter above I don't really agree with this. We might want the MH problem to have used indistinguishable balls and be a more "pure" probability problem (and perhaps this is its essence), but the fact is it uses distinguishable doors and therefore distinctly ventures into conditional probability territory. I'm fine with a solution that starts by treating it in some sense as a "pure" probability problem, but the solution should be accurate and we should proceed to a solution for the actual problem rather than one we might prefer it to be. -- Rick Block (talk) 20:08, 28 October 2008 (UTC)[reply]

Why not go that way then? We could start with a very simple solution to the basic problem then progress through the basic solution to the more complicated one. I will restate this is a new section below. Martin Hogbin (talk) 22:41, 28 October 2008 (UTC)[reply]

I understand why you suggest a basic and a complicated solution. My disagreement with that approach is that it gives merit to the 'condition probability' theory of solving the Monty Hall Problem. It is meritless and should not be included in a 'Solutions' heading.

Glkanter (talk) 23:11, 28 October 2008 (UTC)[reply]

That is a battle you are not going to win. Leave the fancy stuff for those who want it and let us just add a clear solution. Martin Hogbin (talk) 23:59, 28 October 2008 (UTC)[reply]

Rick,"The issue is that the standard form of the problem doesn't ask about the overall probability, it asks about the conditional probability given knowledge of which door the host opens."

Rick, I do thank you for that clear statement but I totally disagree with it and so do most of the published solutions to the Monty Hall problem. Naturally, they do not bother to state this disagreement but they always solve for the overall probability of winning by switching. The problem in this form is not isomorphic {isomorphic meaning, mathematically the same) to The Three Prisoner Problem or Bertrand's Box Problem, contrary to what the article states. This isomorphism is stated in many published articles as well.

What you are saying is that here at Wikipedia the Monty Hall Problem does not mean the same problem that name refers to in the bulk of the published literature - many of which appear in the article's list of references. Is that not in direct violation of Wikipedia standards for featured or any other articles? Doesn't that mean that our editors failed in their their duty to keep our article consistent with the established interpretation of the problem? Should we not rectify this as quickly as possible?

Obviously, I should read the Wikipedia guidelines so I'm not guessing about what they say. I will rectify that as soon as I can figure out how to find them - and I will apologize to Rick and others if I find I was in error.Millbast5 (talk) 22:06, 28 October 2008 (UTC)[reply]

Doesn't Wikipedia have some sort of 'escalation' procedure to break log jams? Think about it. For some period of time, you guys know better than I, various people have contributed to the Monty Hall Problem Discussion page and said the same thing. It then seems that a single admin/editor, who I believe does not understand the topic, puts a kibosh on any meaningful change.

This hijacking of the Monty Hall Problem has gone on long enough. The existence of this secondary discussion page is proof of that. Everywhere I look, the same gibberish appears. The page itself, the discussion page, and now these two pages Martin put together. Well meaning contributors come and go, but the gibberish continues unabated.

Stop the madness!

Glkanter (talk) 22:21, 28 October 2008 (UTC)[reply]

GlkanterI do not think that Rick is stopping any changes, he is just stating his own position, I was the one who suggested doing some preliminary work on a separate page to avoid ruining the article while we all argue. I am going to make a suggestion below as to how we might proceed. Martin Hogbin (talk) 22:41, 28 October 2008 (UTC)[reply]

I'm actually finding this kind of amusing. In the archives of the talk page, starting at Talk:Monty Hall problem/Archive 6#Rigorous solution there was an extended, heated discussion about the same topic we're talking about now. At the time, the article looked like this and the solution section did not mention conditional probability. I was initially one of the folks who argued against including a conditional analysis on the grounds that the anonymous user who was bringing this up was trying to make the problem into something that it's not (and, frankly, didn't initially understand wtf his problem was). Over several weeks the argument raged (with many more people involved than have weighed in here). The anonymous user stood his ground (at times pushing the edge of civility, which was definitely not helpful to his cause). He ultimately convinced me and several others that he had a very valid point. After tens of thousands of words, including an entire draft page with a new version of the article, and several editors giving up in frustration and a featured article review, we finally ended up with an uneasy compromise reflected in the current version of the article. I suspect the lack of participation here is largely due to this prior experience which, looking at the timestamps, really wasn't all that long ago (this past February).

To Millbast5 - you're perhaps looking for Wikipedia:Neutral point of view, although it's rarely referenced with regard to mathematics articles. I think I have all the references from the article (and more) and I'm not sure I agree most of the published literature treats MH as an unconditional probability problem. Certainly most of the popular literature (Parade Magazine, etc.) does, but I think most of the academic literature is written with the same understanding initially put forth by Morgan. Indeed, the whole "host must choose between two goat doors with equal probability" addendum to the problem statement is motivated by this understanding (although this is perhaps sometimes added to support the Bayesian treatment it also conveniently makes the conditional and unconditional answers the same). IMO, treating the problem as an unconditional problem is just sloppy math (yeah, converts are the worst). -- Rick Block (talk) 01:30, 29 October 2008 (UTC)[reply]

Host behaviour

I know this has been discussed at length several times before but I want to add my take on this subject in support of my proposal. The following behaviours would affect the probability that the player has initially chosen a goat.

Monty does not always offer the swap

This makes the most difference to the game. If Monty only offers the swap when the player has picked a goat then the (conditional) chances of the player having a goat (and winning the car on swapping) is 1. If Monty only offers the swap when the player has picked a car, the chances of them having a goat (and winning the car on swapping) is 0. This host behaviour has such a dramatic effect that, if we believe it to be the case, there is no point doing any probability calculations; the chances of gaining by swapping are entirely under the host's control.

In the 'Parade' version of the problem it states, 'He then says to you, "Do you want to pick door No. 2?" '. This is s simple declarative statement'. It does not say 'sometimes says' or 'might say' so we must take it to mean 'always says'. In other words, in the most famous statement of the problem, he always offers the swap Martin Hogbin (talk) 12:28, 29 October 2008 (UTC)[reply]

We can therefore discount the possibility that the swap is not always offered in any probability calculation.

I don't agree with this interpretation of the 'Parade' version and I remember when it appeared various readers had different takes on it. The majority interpreted just the way you say. It doesn't matter a whole lot because we are going to stipulate that interpretation for the main body of the article. More to the point, that condition is stipulated, implicitly if not explicitly, in virtually every published article about or referencing the MHP (Monty Hall Problem).Millbast5 (talk) 21:43, 29 October 2008 (UTC)[reply]

I do not understand what there is to interpret, 'He then says to you, "Do you want to pick door No. 2?" '. Surely ther is only one way that can be interpreted. Martin Hogbin (talk) 23:08, 29 October 2008 (UTC)[reply]

It doesn't say that offering a chance to switch happens without fail so it is open to the interpretation that it happens some of the time but not necessarily all the time - that's my opinion. If I were stating the problem I'd say the host did it invariably if I wanted to convey that information. Also, I liked it being variable because the problem then becomes interesting to solve - prescribe the host behavior and its too simple to be a challenge. Like I said, most people interpreted it the way you did but some people did believe it was open to my interpretation - and then they said that it was impossible to solve if you didn't assume it meant the host always did it. It isn't impossible but its definitely challenging. BTW, I had no doubt that the person who asked the question intended it to be interpreted the way most people did.

Suppose the game show happens to be set on the floor of the Roman Coliseum and two of the doors conceal hungry lions while the third leads to a tunnel out of the Coliseum. With the crowd howling for your blood, the host asks you to pick a door, which you do. He then opens a small window in one of the other doors and a lion sticks its head out. At that point he asks you if you'd like to switch to the third door. Would you blythly switch figuring you were doubling your chances or would you consider the possibility that the only reason you were being given the opportunity to switch is that you'd selected the door to the tunnel? Exact same problem - just a slight change in the setting and prizes. Still think only one interpretation is possible? (I sent this to scenario to "Ask Marilyn" when she insisted only your interpretation was possible... she didn't choose to print my letter. Marilyn is not a good sport when she is caught out.)Millbast5 (talk) 09:19, 30 October 2008 (UTC)[reply]

We are talking about the question as stated in Parade. It is not normal in the statement of a probability problem to put 'always' or 'without fail' on front of every statement. This is assumed to be the case unless there is a statement to the contrary. Martin Hogbin (talk) 22:51, 30 October 2008 (UTC)[reply]

I was speaking about the Parade version. Contrary to what you say, it is quite normal in the statement of probability problems to state everything relevant - even Miss vos Savant eventually agreed that she was making assumptions about the host always opening a door and always revealing a goat. At first she took your view but with a spate of other articles disagreeing with her about it, she did back down. If another mathematician stated the problem exactly as it appeared in Parade it would not even cross my mind that he meant the solvers were supposed to make any assumptions other than that he meant precisely what he stated. Of course, in that case it wouldn't be appearing as a Sunday supplement problem.Millbast5 (talk) 08:16, 1 November 2008 (UTC)[reply]

Monty does not alway pick a goat door

There has never been a televised case where Monty has opened a door to reveal a car; if he did so it would ruin the show. The only other possibility would be that Monty chose a door randomly but if this revealed a car the show was re-run. Doing things this way would waste the TV company a lot of money. If they wanted only shows where Monty always revealed a goat they would ensure that he always did this first time. We can therefore discount this possibility in any probability calculation.

Though this problem is called the Monty Hall Problem it has nothing to do with the real Monty Hall TV program. Or any TV program. Its just a puzzle phrased in a recognizable manner, so we can't decide it based on our guesses at what TV executives may or may not do. The best argument against car revelations is that the puzzle gives no hint of it happening. For us the only thing is that it is not allowed for in published interpretations of the puzzle.Millbast5 (talk) 12:54, 30 October 2008 (UTC)[reply]

I am not sure that I agree yours is the best argument but it is certainly another argument for taking it that Monty always opend a goat door. I do agree with you that all published statements of the puzzle give no indication that a car might be revealed and also no indication of what would happen if it were. This latter point also indicates that we can take it that Monty never reveals a car.

Martin Hogbin (talk) 22:57, 30 October 2008 (UTC)[reply]

Monty does not pick a random goat door

We (that is the player, the audience, or the public in general) have no information telling us what method Monty might have used to select a door. We therefore can, indeed we must, take it to be random. We can therefore discount this possibility in any probability calculation.

I don't think you are saying that this should not be discussed at all in the article because that would rule out discussing the 'academic' version. I kind of like including that someplace because then we can bring out Morgan et al.'s result that every possible door preference leads to the same (overall) probability of winning by switching. Implicit in that is the fact that if the host has a preference and the contestant knows exactly what it is, the latter cannot use it to his advantage. I also like to bring out that the probability is 2/3 before the host opens the door, then it transitions to either 1/(1+p) or 1/(1+(1-p)) briefly before it comes to rest at either 1 or 0.Millbast5 (talk) 22:11, 29 October 2008 (UTC)[reply]

I do not want to rule out the academic version but put it on a proper footing. It is not that there are assumptions in the 'basic' version but there are extension in the 'academic' version.Martin Hogbin (talk) 23:11, 29 October 2008 (UTC)[reply]

I have no idea what you mean by "extension in the academic version." I'm not sure my bafflement is of any significance unless you were trying to disagree or amend or extend what I said.Millbast5 (talk) 12:22, 30 October 2008 (UTC)[reply]

What I mean is that, for various reasons, academics have chosen to extend the statement of the problem to include cases that should be excluded by any sensible interpretation (such as that Monty does not always open a goat door). Martin Hogbin (talk) 23:01, 30 October 2008 (UTC)[reply]

Now I am not going to insist that everything above is absolutely correct, and I accept that it is my OR, but I think it does make a good case for ignoring host behaviour in the basic solution. Martin Hogbin (talk) 19:08, 28 October 2008 (UTC)[reply]

Except for the part about me not agreeing, I think what I said above applies to all of these conditions. At times there are discussions of possible other interpretations. Millbast5 (talk) 21:47, 29 October 2008 (UTC)[reply]

A way forwards?

How about leaving the article essentially as it is but adding a simple and convincing solution at the beginning? There are at least three editors who strongly believe that the current article is too complicated, is not convincing, and does not address the real issues of the Monty Hall problem. I will start something on something on the project page here and perhaps we can all work together to knock it into shape. Martin Hogbin (talk) 22:52, 28 October 2008 (UTC)[reply]

I have now started something for us to work on it is under "Martin's solutions - Proposed basic solution to go at the start of the existing article". Martin Hogbin (talk) 23:08, 28 October 2008 (UTC)[reply]

I would change the words 'the door he opens must have a goat behind it' to 'the door he opens will always reveal a goat'.

I would eliminate entirely the sentance 'Imagine that you chose Door 1 and the host opens Door 3, which has a goat.' and then substitute for '"Do you want to switch to Door Number 2?"' with 'Do you want to switch doors?' This is consistant with the proposed solutions, which posit that the doors are all the same.

Glkanter (talk) 23:35, 28 October 2008 (UTC)[reply]

The idea is to discuss changes to the proposed article here and edit the article page, so I have moved your comments here. You cannot change the wording because it is a quotation. You could rewrite the whole statement but the quotation is from a good source. Martin Hogbin (talk) 23:48, 28 October 2008 (UTC)[reply]

I'm responding quickly so you guys don't interpret my silence to mean I concur with this plan. Now that I understand Rick's position that our version of the Monty Hall Problem is not about the overall probability of winning with the switch strategy and is about the conditional probability of winning given the particular door the host opens, I believe the whole article is tilted. To start, with that means that the article is not about the Monty Hall Problem that is generally referred to by that name in the published literature - in violation of Featured Article guidelines 1b, 1c and 1d.

I am not sure that I understand you here. Are you saying that the concentration on possible host behaviour and its effect on the probabilities is a bad thing? If so, I agree.

Yes, that is correct. And the worst effect is that we cannot have anything in the article that is outside this perspective. Look at the evolution of the discussions regarding your (Martin's) very concise solution or Glkantar's - Rick mired them both down with his insistance on relating them to the hosts behavior.Millbast5 (talk) 13:08, 29 October 2008 (UTC)[reply]

I have no idea whether his view was widely shared at the time the current version of the article was created. Its hard to believe that it was because its such a complete violation of the guidelines.

I would not put it as strongly as this, to me the article sticks too rigidly to some WP policies to the detriment of others.

I am currently reading the article by Krauss and Wang(2003) from which our 'standard' statement of the problem is taken. That particular statement of the problem does ask about a specific door and uses specific doors all through the problem statement with nothing to indicate the specific doors are merely a device for posing the problem. The problem statement also specifies that the host chooses at random between two goat doors, when he is faced with choosing. While random choosing means the result is not dependent on the particular door the host opens the question is asked, as Rick says, about a particular door.

In essence, this is saying that our version of the problem is the Morgan et al. variant with the value of p set to 1/2 for every pair of doors. Mathematically, there is nothing wrong with that but what it means for us is that any simple, comprehensible solution or restatement of the problem will be dismissed for being outside the problem paradigm - Rick's vision of it. Indeed, we've seen exactly that happen with every significant suggestion we've come up with.

So far in the Krauss article it has talked about the effect of identifying specific doors in the problem statement and said their experiments have shown that the more specific doors that are mentioned the more difficulty people had understanding the problem and its solution. Naturally, this has me wondering if the problem statement we elected to use was one they gave as the worst possible way to state the problem.

I imagine its quite clear to Rick at this point that I am the enemy and I understand what he's doing. He's probably well intentioned and believes the article is better for his participation but I can't see him ever willingly relinguishing what control he has over the article nor going along with suggestions that change the basic tenor of the article. Yes, he'll act like he's being a paragon of openness and cooperation but in the end he'll dig in his heels and kill, if he can, any suggestion that is not in line with his views. Actually, I was probably recognized as the enemy when I ripped the "Sources of Confusion" to shreds - because I'm sure it was one of his contributions and he is rather proud of it. In a way he should be proud of it - it is easily the worst part of the whole article and it takes a certain amount of talent to create such a mess and get others to go along with letting it see the light of day. Or maybe persistence is enough.

Frankly, I think I've just talked myself into chucking the whole thing - it would probably take a year to root Rick out control and its not worth it to me. I'm rather fond of the Monty Hall Problem and Wikipedia but one has to admit that very little hangs in the balance here especially from a mathematical point of view. At least I'm going to get a minor mathematics article for my time spent here.Millbast5 (talk) 03:32, 29 October 2008 (UTC)[reply]

I think you are being unfair to Rick, he has at least been kind enough to state some of the opposing viewpoints on this talk page. I suspect we will see much stronger opposition to change when we start editing the real article.

I pretty much agree what I take your view to be: that the issues that make the conditional and unconditional probabilities different are not relevant to the MH problem as it is generally understood and that the doors should be treated as indistinguishable.

Although I strongly support giving a clear solution to the 'basic' MH problem it is a fact that there has been much study of what I am calling the 'academic' version. I therefore think it is correct that that version should be represented in the article. The two types of problem could each be preceded with a short introduction giving the rationale for treating the problem in that particular way. Martin Hogbin (talk) 10:13, 29 October 2008 (UTC)[reply]

I don't have any objection to the 'academic' version being represented in the article - even though I'm not sure just what the academic version is. I'm guessing it the version that considers the host choice of doors when he has a choice. If that is allowed to be the principal version we wind up with the tail wagging the dog - the state we are in right now.

One thing that occurred to me just recently was that the 'standard' problem statement we have adopted, as awful as it is, does state that the host chooses randomly between two goat doors. With that condition in force, the conditional probability is always equal to the overall probability - that follows from Morgan et al. door preference, p, always having the value 1/2 (random choice between two alternatives) as a direct computation, it does not require a proof. In other words with our standard statement in force throughout the article, except when indicated otherwise, we do not ever have to bring up the host choice question or conditional probability and we are free to use 'overall probability' as our goal and our guiding principle. We can even refer to it as 'the probability' instead of 'the overall probability'!Millbast5 (talk) 13:08, 29 October 2008 (UTC)[reply]

I don't think of anyone here (or much of anywhere) as the enemy and really (seriously) have no particular ax to grind. I don't know if you read my post above yet, but the last time this issue came up I was initially on your side, thought about it (a lot), and ended up supporting changing the "basic tenor of the article". BTW - Krauss and Wang's statement of the problem matches others I've seen in the academic literature. The popular literature is full of simplistic explanations (if you're looking for one, vos Savant's Parade explanation is as good as any). My hands are indeed all over this article. Many of the references are references I found, many of the words are words I wrote. I am not particularly proud of the "sources of confusion section" (which I did indeed write - learning how to use the history feature?), although I do think it's much better now than it was in this version.

Nope, I haven't tried the history feature yet. After your second set of responses it dawned on me that you were as aware of the details of Morgan et al. as was the author of the 'confusion' so it seemed highly likely the two of you were one.

You clearly don't want me here, so I'll go away. If you'd like me to comment on anything I'll be happy to. My talk page is linked from my sig. -- Rick Block (talk) 04:13, 29 October 2008 (UTC)[reply]

Rick, I for one, am grateful for your contributions here. You are putting the case for what I might call the 'academic' version of the problem clearly and politely, which is very helpful to me at least. At your suggestion, I have read through much of the history of the article and seen the fierce debates where the other side of this discussion was very forcefully put. I suspect we will get a much rougher ride when we move this discussion back to the real article talk page, and I think it is now time to do this.

Do you know if we can find the vos Savant solution online? Martin Hogbin (talk) 10:13, 29 October 2008 (UTC)[reply]

So what do we do now? Repeat on the official discussion page everything we posted either here or on the official discussion page? BTW, is there consensus with Millbast5 that there is no need to solve the puzzle using anything other than the standard proofs?

Glkanter (talk) —Preceding undated comment was added at 13:30, 29 October 2008 (UTC).[reply]

I think we should work on the proposed solution on my user page until we think that it is good enough to cut and paste into the main page. Some thought should be given to how it integrates with the material already there. What I will do us put our proposed solution in front of the copy of the current solution so we can work on the whole start of the article. Martin Hogbin (talk) 21:14, 29 October 2008 (UTC)[reply]

We may as well face the 800 pound gorilla in the room. I estimate that more than 50% of the content of the article relates to 'conditional probability, et al'. If that is to continue, then I'm not ready yet to work on any new page.

Glkanter (talk) 21:20, 29 October 2008 (UTC)[reply]

I have added a section to my page called 'Proposed new Problem and Solution for the article' I suggest that you edit that as if it were in the main article. Of course no one can stop you editing the main article itself but if you try to make major changes in one go the you will face enormous opposition. My plan is to produce something that is acceptable to both sides, paste it into the main article and then all work on it.Martin Hogbin (talk) 21:40, 29 October 2008 (UTC)[reply]

I agree with Glkantar. I will find it hard to work on any new material until I'm convinced that what ever we come up will not be summarily dismissed. I think that means Rick has to be in favor of it - clearly he is a very good advocate for what he believes in and that will be needed. Assuming that hurdle can be cleared, I would say we need to start with an outline or overall description so we are all pretty much on the same page. I think Rick needs to bless the outline first if not be an active participant in creating it. Maybe the first thing is a very compact 'mission statement'.Millbast5 (talk) 22:36, 29 October 2008 (UTC)[reply]

All you can do is edit the article then. Rick does not have any special powers to control what is in the article and I am sure that he does not claim any. Martin Hogbin (talk) 23:15, 29 October 2008 (UTC)[reply]

As far as 'host behaviour and asumptions'...yes, the Parade version was not specific. The 'Monty Hall Problem', however is. Is it not 'universally' recognized as a paradox? That the contestant's best action, switching, runs counter to your first impression? That tells me that the whole point of the puzzle is to show the 2/3 vs 1/2 dichotomy. Host's behaviour? If he does anything other than show a goat every time, it's not the 'Monty Hall Problem'. And I'll repeat myself here. The puzzle, and it's proofs, don't care which goat, or which door. So any discussion of this off-shoot, other than to briefly explain it away, is not constructive. Including this entire paragraph I felt compelled to post. Glkanter (talk) 13:47, 30 October 2008 (UTC)[reply]

Apart from a few minor quibbles, I agree with you. Martin Hogbin (talk) 23:05, 30 October 2008 (UTC)[reply]

Plan not working

It seems that my plan to develop an alternative starting section to the article on this page is not working. We all agree that the 'basic' problem is what counts but we seem to be arguing over minor differences. Perhaps we should now all move to the main article and talk page and start editing.Martin Hogbin (talk) 23:14, 30 October 2008 (UTC)[reply]

Minor quibbles, eh? That's pretty good! It seems to me that the last 3 or 4 opinions have agreed on a desire for a few short and sweet approaches to the Solution. No variants, no host behaviour, no conditional probability. Now that's something I can get behind.

So, how does one begin editting?

Glkanter (talk) 23:45, 30 October 2008 (UTC)[reply]

Just do it. Martin Hogbin (talk) 09:26, 31 October 2008 (UTC)[reply]

Can I delete this from the Solution heading?

According to the problem statement above, a car and two goats are arranged behind three doors and then the player initially picks a door. Assuming the player's initial pick is Door 1 (the same analysis applies for any other door the player picks):

The player originally picked the door hiding the car. The game host must open one of the two remaining doors randomly.
The car is behind Door 2 and the host must open Door 3.
The car is behind Door 3 and the host must open Door 2.

Players who choose to switch win if the car is behind either of the two unchosen doors rather than the one that was originally picked. In two cases with 1/3 probability switching wins, so the overall probability of winning by switching is 2/3 as shown in the diagram below. In other words, there is a 2/3 chance of being wrong initially, and thus a 2/3 chance of being right when changing to the other door.

Car hidden behind Door 1		Car hidden behind Door 2	Car hidden behind Door 3
Player initially picks Door 1

Host opens either goat door		Host must open Door 3	Host must open Door 2

Switching loses with probability 1/6	Switching loses with probability 1/6	Switching wins with probability 1/3	Switching wins with probability 1/3
Switching loses with probability 1/3		Switching wins with probability 2/3

The reasoning above applies to all players at the start of the game without regard to which door the host opens, specifically before the host opens a particular door and gives the player the option to switch doors (Morgan et al. 1991). This means if a large number of players randomly choose whether to stay or switch, then approximately 1/3 of those choosing to stay with the initial selection and 2/3 of those choosing to switch would win the car. This result has been verified experimentally using computer and other simulation techniques (see Simulation below).

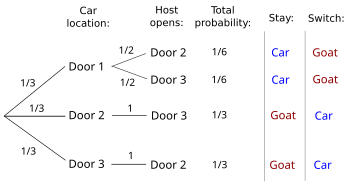
A subtly different question is which strategy is best for an individual player after being shown a particular open door. Answering this question requires determining the conditional probability of winning by switching, given which door the host opens. This probability may differ from the overall probability of winning depending on the exact formulation of the problem (see Sources of confusion, below).

Referring to the figure above or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138) and considering only the cases where the host opens Door 2, switching loses in a 1/6 case where the player initially picked the car and otherwise wins in a 1/3 case. Similarly if the host opens Door 3 switching wins twice as often as staying, so the conditional probability of winning by switching given either door the host opens is 2/3 — the same as the overall probability. A formal proof of this fact using Bayes' theorem is presented below (see Bayesian analysis). —Preceding unsigned comment added by Glkanter (talk • contribs) 14:44, 31 October 2008 (UTC)[reply]

You can do what ever you like, there is no point asking here. This was what my plan was all about. If you delete a large section without replacing it with something than it will probably be reverted, with some justification and it will leave a large hole in the article. My plan was to develop a replacement, or addition to the section above, then past it in to the article. That way it has more chance of being accepted. Martin Hogbin (talk) 18:11, 31 October 2008 (UTC)[reply]

Lets slow down a little bit and consider a different approach

I've been going over the Krauss & Wang article listed in our references and from which we copied the standard statement of the problem. (This particular article has a direct link in our list of references so its easy to check out yourself.) Indeed, as I rather jokingly suggested before, the problem statement we chose is the one that resulted in the worst performance by their experimental subjects. They didn't test them on versions of the problem statement with no doors identified (e.g. contestant chooses Door 1 initially). They did however test them on version where only the contestants choice of doors was identified - the door Monty opened to show a goat was not identified. That one change is the problem statement resulted in almost doubling the percentage of testees who favored switching over not switching (21% vs 38%) - in one experiment. In another experiment they changed things somewhat so there is no direct comparison but the closest comparison had only a minor effect - still positive, however.

But they did make more changes than just identifying one door in both experiments and those resulted in 59% and 50% of the testees electing to switch. Those three other changes are:

1) reminding subjects that car can be behind any door after posing the question

2) asking them to write down how many cases out 3 would they win by switching and the same for not switching

3) Asking them to consider the problem from Monty Hall's perspective - which necessitated some alterations to the questions asked to stay consistent with MH's perspective.

After the subjects in experiment 1 had completed their testing they gave them each one of three different explanations of the Monty Hall problem then tested them on their ability to solve and justify their answer to a different puzzle. One of the explanations resulted in 82% correct justifications - considerable higher than the other two. The same subjects were tested 10 weeks later on three other puzzles of similar complexity and those exposed to the best of the three explanations also scored higher on all of those puzzles.

To me it makes all the sense in the world to base our problem statement and solution (explanation) on results like these. Wouldn't it make our case to implement changes much stronger if we could give reference to experiments done to find the most effective problem statements and solutions?Millbast5 (talk) 01:53, 1 November 2008 (UTC)[reply]

You now seem to be moving in the direction of the more academic. I think that the point you make would be better made on the real article talk page, where you will have much wider participation in the discussion. The point of my pages was to produce an alternative, simple, intuitive, and convincing solution to the 'basic' problem. This could be developed to a sufficiently high quality that it could be added to the main article without spoiling it. I have no objection to your putting new suggestions to improve the article here but, to some degree, that will be a wast of your time as you may have to go through the same discussion again with other editors on the article talk page.Martin Hogbin (talk) 10:13, 1 November 2008 (UTC)[reply]

Now I'm confused.

"This could be developed to a sufficiently high quality that it could be added to the main article without spoiling it."

You mean make the article even longer? Ugh!

Not necessarily, we could replace some of the existing article with a new bit.Martin Hogbin (talk) 23:07, 1 November 2008 (UTC)[reply]

"...as you may have to go through the same discussion again with other editors on the article talk page."

Isn't this true for whatever we develop here?

Glkanter (talk) 11:47, 1 November 2008 (UTC)[reply]

To some degree. But, if we are not going to work together to produce a good quality new section for the article here, this page serves no purpose. I suggest we all transfer to the real article. Martin Hogbin (talk) 23:07, 1 November 2008 (UTC)[reply]

I'm not thinking in terms of our adding to the article as it stands... that idea appeals to me about as much as it does to Glkanter. I'm sure it would be helped some by adding "an alternative, simple, intuitive, and convincing solution to the 'basic' problem" but if we succeeded in producing that, it would help a lot more if it replaced much of the current article. I agree with some quote Glkanter made a while back "what doesn't help, hinders" - to further paraphrase it.

I don't see it as a valid criticism that the source I referred to is of academic origin. We should have no bias against any source that is in line with our aims. It is concerned only with the basic problem and not what you call 'academic extensions'.

If you read the article you will find that it refers to the published work of others which is aimed increasing the puzzle solvers likelihood of adopting the switch strategy. Only one of those was readily accessible and it mainly explored the effect of bribing the contestant to switch - which I didn't think would be profitable for us. One of the others might yield something we find even more suitable. I don't have any commitment to the article I referenced but I see it as a worthwhile starting point. Besides, we could use their results without lifting their exact formulations - to evaluate formulations found elsewhere.Millbast5 (talk) 23:14, 1 November 2008 (UTC)[reply]

I have lost the plot.

I proposed an approach for changing the main Monty Hall problem article to address the complaints that we all seem to have. But I have rather lost the plot on where we all stand regarding this. Perhaps you could all answer the questions below just so we all know where we stand.

Who agrees that the current MH article would benefit from a greater concentration on the basic MH problem, with a simple, intuitive, and convincing solution? By basic problem, I mean what most people take the problem to be (Monty always offers the swap, he always opens a goat door, and he chooses randomly when he has a choice).

My plan was to develop a replacement section here, then paste it into the main article (maybe removing some of what is there now). Who agrees with that?

If you do not agree with the above plan, in what way would you like to move forwards?

Thanks all.Martin Hogbin (talk) 11:50, 2 November 2008 (UTC)[reply]

I'm on board! And, I want to take it further. Get rid of Sources of Confusion, Variants, and Bayesian Analaysis, for a start.

Glkanter (talk) 14:56, 2 November 2008 (UTC)[reply]

Firstly , could you answer the second question above. Do you agree with developing a dummy section here then moving it to the real article?

Secondly your aim is too ambitious. I agree that sources of confusion currently adds more confusion but ther mill be much pressure to keep the variants (what I have called the 'academic' problem). Personally I have no problem with keeping them but they should be introduced as variants of the real problem not as a more correct version of the problem. Many people like Bayesian analysis and you will not be able to get rid of that. We need to be realistic in our aims. Martin Hogbin (talk) 16:10, 2 November 2008 (UTC)[reply]

Yes, I support the idea of developing the improvements here. I presume that 'edit wars' conducted directly on articles get ugly. Too ambitous? Well, I'm choosing to be forthright in what I hope we accomplish. I'm for change we can believe in.

Glkanter (talk) 17:00, 2 November 2008 (UTC)[reply]

I'm in favor of developing it here, as well.

I will hold fast to the idea of using problem statements and solutions from other sources - which, as I understand it, is the preferred methodology for Wikipedia articles. I also like the idea of having multiple solutions of the basic problem, because that increases the chances a reader will find one that makes sense to him.

I don't think the Bayesian analysis is very useful - very few of the people who can follow it all are in need of it. I'd be surprised if it ever played a role in convincing anyone. However, it may be expedient to keep it just to keep the resistance to change from becoming too strong. One alternative would be to find another source for it that we can refer to - I remember some currently referenced source having it in an appendix. If we could replace it that way, it shouldn't create too much resistance because currently it is OR.

I think the variants - in their place, as Martin says - are fine. In fact, I'd like to add one - the general form for all frequencies which the host can use to offer the switch option. Two or three specific frequency variant cases already appear so it would not be something really new. Guess this isn't the time to bring that up.

Sources of Confusion is probably not the best title but a section which summarizes the work that's been done investigating why basic MHP confounds so many people is probably worth while. That is what the current "SoC" attempted do but its a difficult task and one has to be extremely careful to summarize accurately. And stick to basic MHP.Millbast5 (talk) 02:49, 3 November 2008 (UTC)[reply]

Problem statement from Krauss and Wang has been added to the 'draft' page

I did my best to duplicate it - couldn't copy and paste it. We may want to make some alterations... check it out!Millbast5 (talk) 01:48, 6 November 2008 (UTC)[reply]