Purpose of page

This page is for editors to develop clear and convincing explanations of the basic Monty Hall problem. Specifically it is intended to develop solutions that show that the chances of a player who switches getting a car is 2/3. To some degree (but as little as possible) this page is for explanations where rigour and verifiability are sacrificed in favour of clarity and the ability to convince.

I don't believe any rigour or verifiability are sacrificed by the solutions we've been discussing. Maybe we can delete that sentence above?

Glkanter (talk) 13:55, 31 October 2008 (UTC)

I propose that if any solutions presented here reach a stage where they are considered valuable and appropriate additions to the main article, which is a featured article, they are transferred there into a new section there.

Please feel free to add your pet solution here and to comment on or edit existing ones.

Important Issues

Solutions presented here are likely to involve a degree of original research, which is strongly discouraged in WP. I suggest that it may help to allow such solutions here, with the intention of addressing the problem of OR later.

The main article discusses the distinction between the unconditional (in which the player decides at the outset whether to swap or not) and the conditional (in which the player decides what to do after a door has been opened) statements of the problem. As it turns out, the chances of getting a car are the same in both cases for the normal statement of the problem, but this is not always the case. In my opinion discussion of this difference at the outset confuses the main issue thus I suggest that solutions presented here find ways (within the WP guidelines) of circumventing this issue.

I think it's fine to present an "intuitive" solution that ignores this issue, but it is at the heart of many mathematical criticisms of popular solutions (some of which go so far as to call these "false solutions") so I think it must be addressed in the main Solution section. The current version of the article attempts to do this. It could certainly be done better, but not including a solution based on what has been published in refereed mathematical journals in the interest of not confusing the main issue seems like not the best idea. -- Rick Block (talk) 14:08, 27 October 2008 (UTC)

I do not know if it is generally considered appropriate, but maybe a disclaimer stating that the normal standards of WP have been suspended for a particular section could be considered.

Disclaimer, no, but it would be possible to preface one of the popularly presented solutions (e.g. vos Savant's as published in Parade) with something like "A popularly presented solution is ...". I've suggested this before and at the time there was a fairly strong sentiment against including something like this. -- Rick Block (talk) 14:08, 27 October 2008 (UTC)

Statements of the problem

The following may be taken as standard statement of the conditional problem:

Suppose you're on a game show and you're given the choice of three doors. Behind one door is a car; behind the others, goats. The car and the goats were placed randomly behind the doors before the show. The rules of the game show are as follows: After you have chosen a door, the door remains closed for the time being. The game show host, Monty Hall, who knows what is behind the doors, now has to open one of the two remaining doors, and the door he opens must have a goat behind it. If both remaining doors have goats behind them, he chooses one randomly. After Monty Hall opens a door with a goat, he will ask you to decide whether you want to stay with your first choice or to switch to the last remaining door. Imagine that you chose Door 1 and the host opens Door 3, which has a goat. He then asks you "Do you want to switch to Door Number 2?" Is it to your advantage to change your choice? (Krauss and Wang 2003:10)

Krauss and Wang (2003:10) conjecture that people make the standard assumptions even if they are not explicitly stated.

This is a statement of the unconditional problem (is this from Morgan et al.?):

'You will be offered the choice of three doors, and after you choose the host will open a different door, revealing a goat. What is the probability that you win if your strategy is to switch?'.

Perhaps rather than calling these "conditional" and "unconditional" we should call these something else. I think the basic distinction is whether we're evaluating the probability before (unconditional) or after (conditional) the host has opened a door. As far as I know, all "standard" versions of the problem have the player deciding whether to switch after the host has opened a door, which I think strongly argues for evaluating the probability at this point (even though doing this makes the solution harder to understand). I believe this is the central issue that led to the creation of this page and has been the topic of numerous lengthy discussions at talk:Monty Hall problem. -- Rick Block (talk) 14:22, 27 October 2008 (UTC)

Proposed new Problem and Solution for the article

Problem

Steve Selvin wrote a letter to the American Statistician in 1975 describing a problem loosely based on the game show Let's Make a Deal (Selvin 1975a). In a subsequent letter he dubbed it the "Monty Hall problem" (Selvin 1975b). The problem is mathematically equivalent (Morgan et al., 1991) to the Three Prisoners Problem described in Martin Gardner's Mathematical Games column in Scientific American in 1959 (Gardner 1959a).

Selvin's Monty Hall problem was restated in its well-known form in a letter to Marilyn vos Savant's Ask Marilyn column in Parade:

Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice? (Whitaker 1990)

Some consider that there are certain ambiguities in this formulation of the problem: it is unclear whether or not the host would always open another door, always offer a choice to switch, or even whether he would ever open the door revealing the car (Mueser and Granberg 1999). The standard analysis of the problem assumes that the host is indeed constrained always to open a door revealing a goat, always to make the offer to switch, and to open one of the remaining two doors randomly if the player initially picked the car (Barbeau 2000:87). Hence a more exact statement of the problem is as follows:

Suppose you're on a game show and you're given the choice of three doors. Behind one door is a car; behind the others, goats. The car and the goats were placed randomly behind the doors before the show. The rules of the game show are as follows: After you have chosen a door, the door remains closed for the time being. The game show host, Monty Hall, who knows what is behind the doors, now has to open one of the two remaining doors, and the door he opens must have a goat behind it. If both remaining doors have goats behind them, he chooses one randomly. After Monty Hall opens a door with a goat, he will ask you to decide whether you want to stay with your first choice or to switch to the last remaining door. Imagine that you chose Door 1 and the host opens Door 3, which has a goat. He then asks you "Do you want to switch to Door Number 2?" Is it to your advantage to change your choice? (Krauss and Wang 2003:10)

Note that the player may initially choose any of the three doors (not just Door 1), that the host opens a different door revealing a goat (not necessarily Door 3), and that he gives the player a second choice between the two remaining unopened doors.

Simple Solution

Compare the fate of players who swap with those who do not

You choose a door
You choose a door with a goat		You choose a door with a goat		You choose a door with a car
You Stick	You Change	You Stick	You Change	You Stick	You change
You get a goat	You get a car	You get a goat	You get car	You get a car	You get a goat

A player initially has a probability of 2/3 of picking a goat to start with.

If the player initially picks a goat and takes the swap he will always get the car. (That is because he has picked one goat and Monty has revealed the other.)

The fact the Monty has opened a door does not provide any new information as to the likelihood that the player has initially chosen a goat, this remains at 2/3(Devlin 2003).

Therefore he has a 2/3 chance of getting the car if he swaps.

To summarise:

The player has a 2/3 chance of picking a goat initially.

If he initially picks a goat and takes the swap he will always get the car. (That is because he has picked one goat and Monty has revealed the other.)

Therefore he has a 2/3 chance of getting the car if he swaps.

Alternative solution

Combining doors

Instead of one door being opened and shown to be a losing door, an equivalent action is to combine the two unchosen doors into one since the player cannot, and will not, choose the opened door (Adams 1990; Devlin 2003; Williams 2004; Stibel et al., 2008). The player therefore has the choice of either sticking with the original choice of door with a 1/3 chance of winning the car, or choosing the sum of the contents of the two other doors with a 2/3 chance as shown.

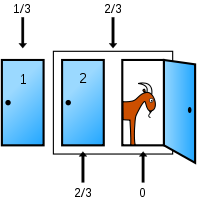
The only difference between trading for both doors and the trade that is actually offered is whether the host opens one of the two doors. Opening one shows which of these doors the car must be behind if it is behind either. At least one of the two unpicked doors contains a goat, and the host is equally likely to open either of these doors so opening one gives the player no additional information; opening one does not change the 2/3 probability that the car is behind one of them (Devlin 2003).

----End of section to be pasted into the main article-----

L2 variant

The 'Problem' in the Monty Hall Problem has to do with the way people intuitively assess probabilities. Given the problem as described above, it is easy to see that the initial odds of picking the car are 1 in 3. There are only three possible spots the car can be - i.e. three possible permutations of the car and goats - and whichever door the contestant chooses (in this example, she chooses door #1). there is only one chance out of three that she will pick the one with the car.

Car hidden behind Door 1	Car hidden behind Door 2	Car hidden behind Door 3

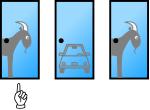
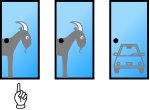
At this point, Monty Hall opens one door to reveal a goat, and most people will intuitively re-evaluate the odds, noting that there is now only one goat and one car remaining, giving odds of 1 in 2 that the car is behind a given door. This intuition is incorrect, however; it assumes that the positioning of the remaining goat and car are a statistically independent event, when in fact that postioning is conditioned on the contestant's original choice. In fact, if Monty Hall did not open a door to reveal a goat, then switching would make no difference; the odds would remain set at 1 in 3 of selecting the car, regardless. But he does open a door (always a door that reveals a goat) and that act excludes two of the six possible outcomes - the two in which a contestant could switch from one door with a goat to the other door with a goat.

I would remove the 'L2 Variant' entirely. I've previously stated my reasoning. The same goes for most of the stuff that follows this.

Glkanter (talk) 23:35, 28 October 2008 (UTC)

Choice 1
Car hidden behind Door 1		Car hidden behind Door 2		Car hidden behind Door 3

Choice 2
Change = goat	Change = goat	Change = car	Change = goat	Change = goat	Change = car
			Not Possible	Not Possible
Switch always yields a goat		Switch always yields a car		Switch always yields a car

In effect, a contestant who first chooses the door with the car can only switch to a goat, and a contestant who first chooses a door with a goat can only switch to the car, and since there is a 2 in 3 chance of choosing a goat in the first place, there is a 2 in 3 change that switching will give the door with the car.

This result has been verified experimentally using computer and other simulation techniques (see Simulation below). A formal proof of this fact using Bayes' theorem is presented below (see Bayesian analysis).

Another solution - one that doesn't need a separate 'sources of confusion' section

I believe the problem is greatly simplified if you consider a large number of plays of the game instead of focusing on a single play.

1. Over a large number of plays of the game, the original choice of the contestant is the door with car behind it 1/3 of the time. Nothing that happens or can possibly happen will change that.

2. Someone who knows what is behind the doors can open an unchosen door with a goat behind it every play of the game. So if that changed the odds of car being behind the contestants' original choice of doors then it would change it every time, contradicting the fact that over a large number of trials the chances are 1 out of 3. Hence, it never changes the odds of the original choice.

3. The car is behind the door shown to have a goat behind it with probability 0.

4. 1 - 1/3 - 0 = 2/3 of the time the car is behind the door which was not the contestants' original choice and not opened to show a goat - that is to say. the door to which the switch strategy leads the contestant every time.

5. You can do things that change the odds of the car being behind the chosen door in particular instances - for example if you open both other doors then the chances are either 0 or 1 in that instance. The first value occurs when opening the other two doors shows a car which is 2/3 of the time, and probability 1 occurs when opening the other two doors showed two goats which happens 1/3 of the time - for an overall probability of 2/3 * 0 + 1/3 * 1 = 1/3.

6. If you open one other door at random then you have possibilities 0 and 1/2 depending on whether the car was behind it or not. This does not contradict the long term probability being 1/3 because 1/3 or the time the randomly opened door has a car behind it and 2/3 of the time a goat - combining the probabilities one gets: 1/3 * 0 + 2/3 * 1/2 = 0 + 1/3 = 1/3.

7. The contestant cannot tell the difference between a door which is known to have a goat behind it being opened and a door being opened at random and, by happenstance, has a goat behind it. Thus he has to have some information aside from just seeing what happens as the game unfolds. Observing prior plays of the game or being told how the game is played can provide him with the information. Millbast5 (talk) 21:31, 8 September 2008 (UTC)

Your point 7 is debatable. If the door the host opens is random then there will be cased when the host opens a door with a car. It is not clear what then happens. Martin Hogbin (talk) 14:42, 28 September 2008 (UTC)

I don't think it belongs here because I was harking back to the original statement of the problem. We have agreed at this point that the problem were concerned with is the standard which does not involve random door openings by the host. I was beating a dead horse, so to speak.

My item 6 mentions random openings but only to contrast the difference it makes when you have an event with two possible outcomes, like a random door opening, compared to an event that has only one possible outcome, like opening a door known to hide a goat. Item 5 shows that one does not need to have a random event to alter the probabilities in a particular instance - the crucial thing is the the event has two (or more) possible outcomes.

The actual computation of the probability of winning via the switch strategy is complete with item 4 - and it would probably be better to have items 5 and 6 not appear as though they were continuations of the computation.

The crux of the argument is item 2 because the intuitive reaction is that opening a door known to conceal a goat alters the probability of the originally chosen door in exactly the same way that opening a door at random and thereby revealing a goat does. Hopefully, it will be clear to everyone that an event with a single possible outcome that changed the probability at each instance would have to alter the overall probability.

Note that the fact that opening a door known to reveal a goat not changing the probability of a winning initial choice is not saying that the event conveys no information. Before it was opened we knew there was an unchosen door that concealed a goat and afterward we knew, in addition, which door it was.Millbast5 (talk) 04:56, 29 September 2008 (UTC)

A more compact statement of the solution.

It has no new ideas but I believe when we are trying to convince someone, that compactness is important - essentially they are looking for reasons to reject any argument. Of course, if they could point to a flaw they would but the more lengthy or complicated an argument is the easier it is to reject for that reason. Typically, they have a simple argument for their belief that the two strategies are equally good and they might actually contemplate another argument that is about equally simple in appearance.

Personally I don't like pictures where they aren't needed and I wouldn't think three doors that conceal two goats and a car taxes anyone's ability to imagine. I'm probably in the minority on this point so I'm not going to push the elimination of solutions with pictures but I think its a mistake not include at least one with none. I would put the solution with pictures after the picture-less one because because the pictures stand out visually so the reader couldn't miss it if that is what he wants to see. On the other hand a very compact argument could easily be overlooked in a secondary position.

Here is my latest offering:

At the point of the game where the host has opened a door he knows hides a goat, the car is behind one of the two closed doors - the one the contestant picked or the one he can switch to. When the contestant made his pick he got 1 car for every two goats on average and, unless someone behind the scenes is moving cars and goats around, he still has the same car or goat he started with. Whenever he has a goat the 'switch' door hides the car, so it hides the car 2 times out of 3, on average. Indeed, the switch strategy wins twice as often as not switching.Millbast5 (talk) 23:18, 2 October 2008 (UTC)

Comment We don't seem to doing much discussing in here. I have no idea whether any of my suggestions strike a chord with anyone else or not - and there hasn't been any more said about other suggestions. If I'm flogging a dead horse here I would like to know it.

Response Thanks for your contribution - you are very welcome here. I agree that it is a pity that more editors from the main article to not post and discuss their ideas here, including those frightened away by rather protective policy being adopted by the current editors. Note that there is a talk page for this page. I will move this there when you have read it. The talk page will also have my comments on your contribution

Here is a suggestion for the Source of Confusion Section, which at present does very little to lessen the confusion a person might have, in my opinion. Maybe this will stir up some discussion.

Monty's Action Doesn't Change the Probabilities

Premise 1: The original odds of choosing a car is 1/3. The probability therefore is 1/3 + 1/3 + 1/3= 100%.

Premise 2: We KNOW Monty is going to show a goat.

Premise 3: It makes NO DIFFERENCE to the contestant which door Monty reveals.

Contestant picks a door.

Now the probability is 1/3 (contestant's door) + 2/3 (2 doors remaining)= 100%.

Monty reveals a goat.

Here's the point: Monty's action did not change our knowledge about the door that the contestant selected, so no change of probability there. Nor does he give us any useful knowledge about the remaining doors. We knew he was going to show a goat, and we didn't care which door he showed. These are premises 2 & 3 above. No change of probability there, either.

[I could skip the remainder of the paragraph beginning with 'Nor does he give us any useful knowledge about the remaining doors...' and instead say, 'Since the contestant's probability of 1/3 didn't change, the remaining door's probability has to remain at 2/3, in order for the overall probability to remain at 100%.']

So, the probabilty remains 1/3 (contestant's door) + 2/3 (1 remaining door) = 100%.

Contestant now may switch.

Conclusion, you're twice as likely to get a car if you switch.

Which is why the actual game show was different. Monty didn't always show a goat, and he offered cash bribes.

Glkanter (talk) 17:41, 26 October 2008 (UTC)

Its good to have you on board Glkantar and I'm particularly glad to have you because your ideas on several issues are in agreement with mine. Maybe by working together we can arrive at some changes that Rick and Martin - the two editors/contributors who are currently active in these discussions - agree are beneficial to the article. (I haven't been active on here the last ten days because I've been attending to some family matters that came to a head recently.)

Of course your solution arrives at the right answer and it contains no errors but people who do not believe the solution is correct, and there are many, will not be ready to concede that the host exposing a goat gives no information about the probability with which the originally chosen door hides the car. They know that if the host opened the same door at random and revealed the goat it would change the probability - and they are not wrong about that. Their mistake is in equating opening a door at random to reveal a goat with opening a door known to hide a goat but they do just that and are quite certain it is not a mistake. It is a rather subtle distinction, which I have been trying to make in a clear and understandable manner in several of my suggestions. If I'm not mistaken you said somewhere that you came to this site to clear up this very issue in your own mind, so I would think you'd appreciate their state of mind.

If you read the solution I proposed just a few lines above under the heading "here is my latest offering" you will see that I didn't talk about probabilities, which may or may not change - in their view - but what was behind the contestant's chosen door, which they will admit does not change whether the host opens the door at random or purposefully to reveal a goat. I don't imagine it will convince all the disbelievers but for some I think it will finally click that the change in probabilities that happens when the host randomly reveals a goat simply doesn't play a role in solving this puzzle. By not mentioning probabilities explicitly there is no trigger for them to reject the solution and jump to the solution that they are comfortable believing in. Needless to say, the underlying logic of my solution is the same as in your solution.

I would make one change to "here is my latest offering" - in the penultimate sentence I would change "Whenever he has a goat" to "Whenever he initially picked a goat" because the latter is an event that is more strongly believed to happen 2 times out of 3. In fact, I will do that eventually.

About your solution specifically. Stylistically - the capitalized words are counter productive because they carry an implication that the reader can't understand simple English without help.

In Premise 1, what does 1/3 + 1/3 + 1/3 represent? You only explained one 1/3. Why do you say 'therefore' in the 2nd sentence when the equation is true on its own? Stylistically, jumping back and forth between fractions and percentages in one equation is jarring.

I don't understand why Premise 3 is there. Of course it makes no difference to the contestant but why elevate that to a premise - you don't use it in making an argument, you merely repeat it later on.

"Here's the point:" is talking down to the reader again. As I discuss above the bald statement that Monty's action does not change probabilities will convince few people as that is precisely what they are uncertain about - and your opinion won't carry a lot of weight with them.

The statement "Nor does he give any useful knowledge about the remaining doors." is not used in making your argument so it is merely a comment or opinion. However it is there to disagree with and I disagree with it. Suppose you were a contestant on a game show that followed the rules we've agreed apply to this problem. Imagine beforehand you were chatting with Monty and gave him your opinion on this matter. You pick door 1 and Monty says to you, "I won't waste your time by giving you useless information, would you like to switch to one of the other doors?" You protest that the rules say he has to open a door to reveal a goat. "Okay, I will but since it conveys no information to you, I will blindfold you." He does that then asks "Do you want to switch to door 3 or to door 2?" You say, "The rules say you have to allow me to switch to the unopened door." He responds, "I'm allowing you to do that now - which door do you want to switch to?." You: "I want to switch to the unopened door." Monty: "Go right ahead... which door do you want to switch to?" You: "I don't know which door is the unopened one." Monty: "Is that information you would have if you'd watched me open the door?"

Granted the amount of information Monty gave when he opened the door is minute - it can be stored in 1 binary digit - but it is information. Before he did it you knew he was going to open a door and it didn't matter which door he opened but after he did it you knew a specific door which hid a goat and you didn't know that before. As the problem is presented that new information is obvious to all - the contestant, Monty and the problem solver - so it could be used implicitly to designate a certain door. Nevertheless, it is used and my little scenario just brings that into sharper focus. (Game shows seem to like contestants pushing buttons so maybe it would have been more graphic if I'd had the contestant required to push the button associated with the door he wants to switch to.)Millbast5 (talk) 22:28, 27 October 2008 (UTC)

Thank you for your encouragement. The explanation I provided was indeed intended to highlight certain parts of my arguement. Certainly it would be cleaned up if it was selected for inclusion as a Solution.

Personally, as you can tell, I favor the probability statements approach. As far as I know, it's the only method that allows for proving each statement in order to prove the conclusion. Diagrams also work, I guess, as long as the permutations are managable. Whatever leads the reader to understand the solution.

My concerns are that something other than a 'classic probability theory' threshhold is being required here. I don't understand what that's all about, and therefore I reject it. I've referred to Martin's solution as 'elegent'. Another way of saying that is that it is of 'high quality'. The book 'Zen and the Art of Motorcycle Maintenance' is all about the issue of quality. I'll grossly paraphrase here, 'What doesn't add value, subtracts value'. The current page, even with the deletion I made, is not of 'high quality'. I've given my reasons for saying this many times in the last few days.

Hence, my confusion with the conversations of the last few days. Is there a standard other than 'classic probability theory' required? By whom? More importantly, for who's benefit? The page is confusing, starting with the first figure at the top of the page (does it add value to understanding the solution? I don't think so. Therefore I conclude it gives the page 'less quality').

Hopefully the page will be improved. That's why we're having this discussion, right?

Glkanter (talk) 23:03, 27 October 2008 (UTC)

New Source of Confusion

(I realize this is written mostly in the first person, which is not ideal, but that isn't too hard to rectify if people agree it is an improvement from a conceptual standpoint.)

How does our intuition mislead us in this puzzle? It mainly does it when we consider the effect of the host opening a door he knows hides a goat. For one thing, the contestant is looking at two closed doors and either one might hide the car so our intuition tells us its an even money guess. The other thing is that he knows if the host had opened the very same door at random the outcome has to be the same and also reasons, correctly, in the random case it is even money which door hides the car. Its almost impossible not to conclude that when the host opens a door he knows hides a goat that it is an 50-50 proposition to switch or not.

Lets go through the play of the game in a manner which shows how this intuition goes awry.

We'll describe it slightly differently so its easier to talk about - there are two players simultaneously, N and S. They have to agree on the same initial choice of doors but after the host has opened a door then S has to switch to the remaining door and N has to stick with the initial choice. Of course, N represents the player choosing a non-switch strategy and S represents the player using the switch strategy. Also we'll talk about the aggregate results of 99 plays of the game, so we can convert probabilities to number of occurences. For example, the initial choice is right 1/3 of the time so we translate that to being right 33 of the 99 tries.

For the moment we consider the host opening a door at random from among the two doors the contestants didn't pick initially. Thats easy to analyze - the host opens a door to reveal a goat in 66 games and the car in 33 games. N gets the 33 cars where the initial pick was right and S gets the remaining 33 cars.

Consider the 66 cases where the host revealed a goat. It can't matter why he opened that door because the play of the game is rigid so the end result is exactly the same - N/S intially pick same door, host opens same door, forcing S to switch the same door. Those 66 games are exactly the 66 which N or S wins and each wins 33 times. Our intuition is right on track - regardless of why the host picks the door the outcome is the same and switching and not switching are equally good, each winning half the time.

Now consider the 33 games where the host's randomly opened door revealed the car. The real rule is that he has to open a door that hides a goat, so a 'do-over' is necessary. N/S still have the same initial choice so the host can't change to that door - the only door possible is the one that S was forced to take in the random play. Indeed that reveals the goat he is required to show and S is now forced to switch to the door the host opened in the random play - the door that concealed the car. It hardly seems fair, S is forced to take all 33 cars the host exposed and he still has the 33 that he got when the host's randomly opened door revealed a goat. Poor N still has his 33 cars but no more.

Clearly what happens is: the host opening a random door to reveal a goat having the same result as his opening the door because it hides a goat, we turn around in our mind to mean: the host opening a door because it has a goat behind it has the same outcome as opening a door at random to reveal a goat. That is not true at all because the host cannot open 99 doors at random and get 99 goats - he has to reveal the car 33 times. In a single play of the game it makes sense to talk about opening a door at random to reveal a goat but over the long haul it is nonsense - saying something is random and yet has the same result every time is a contradiction in terms. Opening the door at random means he gets what he gets and that is a goat only 2 times out of 3 tries.

One could say that our intuition is right 2/3 of the time but in the stated game the host reveals a goat every time so the contestant has no idea whether he is in that 2/3 or in the other 1/3 - and in that other 1/3 our intuition is disastrously wrong. Its probably more accurate to say we don't think about that other 1/3 even being there because its so well hidden. Millbast5 (talk) 05:45, 3 October 2008 (UTC)

Yet another approach to presenting a solution

Here is an interesting idea - why not use our "deeply rooted intuitions" to solve the problem. There is a good deal of talk on the page about the deeply rooted intuitions leading to erroneous conclusions about this game but it turns out it is quite easy to use those same intuitions to come to the correct solution.

Basic Intuition: A random event is one with a number, larger than 1, of outcomes and each of the outcomes occurs with the same frequency but not in a predictable order. If there are 2, 3 or 10 outcomes the frequencies are, respectively, 1 in 2, 1 in 3 or 1 in 10.

Note: In the case of interest there are 3 outcomes: a goat, a different goat, or a car. For convenience we lump the two goats together and combine their frequency of occurrence into 2 times out of 3.

Intuition 1. The contestant is essentially picking at random so he/she picks the door concealing the car 1 time in 3 and picks a door concealing a goat 2 times in 3.

Intuition 2. If the host opens a door at random he also picks the door concealing the car 1 time in 3 and picks a door concealing a goat 2 times in 3.

Intuition 3. When the host opens a door at random and reveals a goat then the switch and non-switch strategy each wins(picks the door concealing the car) with equal frequency - and each wins with frequency 1 in 2. (Note, these are relative frequencies in that they relate only to cases when the host randomly reveals a goat. Overall the winning frequency for each is 1 out 3.)

First we analyze a game which is the same as the standard game except that the host opens a door at random after the contestant his made his pick. This affords some practice and this game has elements that people who dispute the accuracy of the solutions to the standard game, use in their reasoning. It is also hoped that they might believe an argument that uses the same intuitions they use in their arguments. Also the similarity of the two games might allow the standard game to carry over arguments from the 'random' game and get to a speedy conclusion.

There are two events in each play of the game - the contestant picking a door and the host subsequently picking a door to open. We do not proceed to the final event where the contestant chooses between keeping his original pick and switching to the remaining door because its not necessary for the purpose of deciding which choice would be better. Each of the two events has two outcomes, but the combination in which the contestant picks the door concealing the car and the host opens the door concealing the car cannot happen since there is only 1 car and the host is prohibited from opening the door the contestant picked. That leaves three possibilities:

A. Contestant picks the door concealing the car; host opens a door to reveal a goat; remaining door, the 'switch-to' door, conceals a goat. B. Contestant picks a door concealing a goat; host opens a door to reveal a goat; remaining door, the 'switch-to' door, conceals the car. C. Contestant picks a door concealing a goat; host open a door to reveal the car; remaining door, the 'switch-to' door, conceals a goat.

Intuition 1 says A happens 1 time in 3 because whenever the contestant picks the door concealing a car there are only two goats for the host to pick between and so A constitutes all cases in which the contestant picks the car. Intuition 3 says B happens with same frequency as A, so 1 time in 3. A and B are the only sequences in which the host opens a door at random to reveal a goat so the rest of Intuition 3 is right on - each strategy wins half of them. By Intuition 1, B and C together must occur 2 times in 3 because together they constitute all cases where the contestant picks a door concealing a goat. Since B happens 1 time in 3, C must happen 1 time in 3. That agrees with the part of Intuition 2 that says the host reveals the car 1 time in 3. Since each of A, B and C happens 1 time in 3, together they happen 3 times in 3 which is always a good sign as it means we didn't overlook a possibility.

This game does result in the switch and not switch strategies winning equally often so in that regard it matches the result that those who dispute the purported solutions of the standard game, claim to be the right result.

Now consider the standard game, in which the host always opens a door to reveal a goat. In this case the host opening the door is not a random event because there is only a single outcome. We could come to the same conclusion by using Intuition 2 - if it were random then the host would reveal the car 1 time in 3 tries and since he does not, the event cannot be random. Intuition 3 is rendered useless because the host isn't picking at random.

No new event or outcome occurs in this game so A, B, and C cover all of the possibilities for this game as well. Their frequencies of occurrence might well change, however.

A still happens 1 time in 3 by Intuition 1, the same as above. C happens 0 times in 3 because any occurrence would violate the condition of the game that the host always opens a door to reveal a goat. As above, by Intuition 1, B and C together happen 2 times in 3 as together they constitute all cases where the contestant picks a

door concealing a goat. But in this game C happens 0 times in 3, so B happens 2 times in 3. Again A, B, C combined happen 3 times in 3 - still a good sign.

As with other purported solutions switching wins 2 times out of 3 and not-switching 1 out of 3.

As hoped the argument for A's frequency carried over intact and the general form of the argument for B's frequency carried over with only a change in the numeric value of C's frequency. The computation for C is dramatically different but extremely straightforward and unlikely to be a source of dispute.

So much for the idea that our deeply rooted intuitions lead us astray.

Remarks on random events

It is certainly not true that the possible outcomes of random events are always equally likely. For example, the up faces of two randomly throw dice sum to the numbers 2 through 12 but they are not remotely equally likely - 7 comes up six times as often as either 2 or 12. In poker there are huge variations in the frequency of different hand types. Those examples however are built up from random events that are equally likely. In dice, each one of the thrown dice randomly shows up a number 1 through 6 which are equally likely. In poker and most other card games the probability of getting any individual card is the same for all cards. The scientific investigation of probability began with realizing that some equally likely random event underlay many events and it was very useful as the means of calculating the probability of the composite events. Lumping the two different goats together is an example of making a composite event.

In any case our intuition is that each outcome of a random event is equally likely - until proven otherwise. As we've seen with the standard game convincing someone that the outcomes of certain random events are not equally likely can be very difficult at times. Its a powerful and extremely useful intuition so it makes sense not to give it up lightly.Millbast5 (talk) 19:32, 5 October 2008 (UTC)

A question for Martin

I just reread the intro to this page and noticed that it said the page was for discussing possible solutions. Does that mean that my suggestions for the "Sources of Confusion" are out of place here? In general, I'm not sure what goes here and what should go on the the general discussion page.

I am not sure that I know either but the concept was that what you would want to show in the real article should go on the this page, so that would include your proposed 'Sources of confusion' and people could discuss it on the talk page (which is where this discussion should be).

I have an operational question or two and maybe you can point me to the things I need to read. For instance, I'd like to know how to isolate the recent edits to the main article. The same is true for the discussion page and probably soon for this page, too. Also, I can't figure out what 'watch' does - I click on it but nothing seems to come of it.Millbast5 (talk) 22:28, 27 October 2008 (UTC)

I am not sure what you mean by isolate recent edits. If you click watch it adds the page to your watchlist, which is the list of pages you are interested in. If you click 'my watchlist' at the top right of a page it will take you to your watchlist. Martin Hogbin (talk) 22:39, 27 October 2008 (UTC)

Isolate edits means to find the recent changes to a page... with these huge pages its very hard to find replies or new things people add... I even forget where I typed things. In software we have filecompare or diff(Unix) to locate changes/differences. It might help if we had something that jumped down the page finding all entries by one contributor as it went along. Thx for the info about watchlist... for the first time mine has something in it but before it never did. I think that's going to help me keep up with things.Millbast5 (talk) 07:04, 28 October 2008 (UTC)

The history of all edits to every page is maintained. Click the "history" tab at the top of the page. From the history page you can view any individual edit that has ever been made to a page as well as a diff between any two versions in the history as well. -- Rick Block (talk) 13:01, 28 October 2008 (UTC)

Problem statement with high rates of success in experiments

In our reference Krauss and Wang(2003) the following statement of the problem had the highest rate of contestants electing to switch (59% in one experiment & 50% in another) which is 2 to 3 times as many as switched with a problem statement similar to our current statement. In addition it had far and away the highest rate of people who gave correct reasons for why they decided to switch. The key elements of the differences are: not having the host opening a specific door to reveal the goat; changing the perspective to that of the host instead of the contestant; guiding their analysis by asking them to count cases; and, emphasizing that the car can be behind any door. K&W tested intermediate variants which their article lists along with their results. Each person tested only saw one version of the problem statement and the numbers that were exposed to each in each test was about 33 people.

I could not quote the text of the problem statement - it seems to be an embedded picture - so I've duplicated it as best I could. The only change I purposefully made was adding the note about the random placement of the prizes behind doors and random choice between goats by the host. We've agreed that we want that information to be added and making it a footnote seemed the least disruptive to their statement.

___________________________________________________________________________________________

A contestant on a game show is allowed to choose one of three closed doors. Behind one door is the first prize, a new car; behind each of the other doors is a goat*. After the contestant has chosen a door, the door remains closed for the time being. According to the rules of the game, the game show host, Monty Hall, who knows what is behind the doors, now has to open one of the two unchosen doors and reveal a goat*. After Monty Hall shows a goat to the contestant, he asks the contestant to decide whether she or he wants to stay with the first choice or to switch to the last remaining door.

Task: Imagine you are Monty Hall, the host of this game show, and you know which door the car is behind.

The contestant chooses a door, say, number 1.

              X  Monty Hall
    
    door 1      door 2      door 3
     ____        ____        ____ 
    |    |      |    |      |    |
    |    |      |    |      |    |
    |   -|      |   -|      |   -|
    |    |      |    |      |    |
    |____|      |____|      |____|
      /\
      || 
      ||
          X  Contestant

In accordance with the rules of the game, you then open another door and show the contestant a goat. Now you ask him/her whether he/she wants to stay with the first choice (door 1) or to switch to the last remaining door.

The car may be behind any of the three doors.

In how many of the these three possible arrangements would the contestant win the car after you open a "goat door",

- if she/he stays with the first choice (door 1)? in ____ out of 3 cases

- if she/he switches to the last remaining door? in ____ out of 3 cases

What should the contestant therefore do? ____ stay ____ switch

Note: The car and goats are placed randomly behind the doors. If the host has to choose between two goats when revealing one of them, he chooses at random.

__________________________________________________________________________________________

Millbast5 (talk) 01:27, 6 November 2008 (UTC)