User:Double sharp/Polychora

This page is just a reference for the full list of uniform polychora. It's not defendable content for Wikipedia, but since Tomruen has his own (User:Tomruen/list of uniform polychora), here's mine (this one has the full names as well!) All information is based on Jonathan Bowers' polychoron website. Only categories 16 and 23 are not given there. So I invite you to click there if you want to see actually comprehensible information and great writing instead of incomprehensible tables filled with Greek names. :-Þ

AFAIK, only Bowers' pages also give correct full names, but he abbreviates the Greek prefixes (e.g. "hexacosi-" becomes "600" on his website). I have tried to solve problems caused by vowel collision (e.g. for hinnit, the "16intercepted tesseract", where I changed "hexadecaintercepted" to "hexadekintercepted") using strategies by Bowers, Johnson, Klitzing, etc.

Here, the polychora have been split into different pages corresponding to Bowers' categories, unlike Tomruen's subpage where they are all on one page. This is done here simply to make things easier and faster to read.

Some might remember having seen something very much like this before I changed username. That's been deleted: most of it was wrong (WikiChoron seems to have messed up some of the names: maybe they didn't have the full names and just extrapolated them from the Bowers acronyms?). Everything should be correct now (though if you want to be sure, go to Bowers' website. It's prettier and more comprehensible.)

Updates:

2012

20 July – Created this main page, and added categories 1, 2, 3, 4, and 5.
21 July – added categories 6 and 7.
22 July – added categories 8, 9, and 10.
23 July – added categories 11, 12, and 13.
28 July – added category 14.
29 July – added categories 17 and 18. Also made a minor correction to category 7.
30 July – added categories 19, 20, 21, and part of 22.
31 July – completed category 22. Also added categories 26 and 27.
4 August – added categories A and B.
5 August – Tomruen and I add links to the articles for those uniform polychora that have articles.
8 August – added categories 24 and 28.
9 August – added conversion from linear abbreviation. Tamfang adds Schläfli symbols to category 1 and I add Coxeter-Dynkin diagrams to categories 1, 2, and 3. However, so many of the nonconvex uniform polychora are non-Wythoffian that such a column would have nothing but blanks in some categories, and would be almost empty in many more.

2013

23 March – added category 29.

2014

4 May – added links to the scaliforms. Also added categories 15, S1, S2, S3, S4, S5, S6, and S7.

Coming Soon: categories 16, 23 and 25. Also, Coxeter-Dynkin diagrams for the Wythoffian ones, cells, and regiments. (done: Categories 1–5 and 7)

Conversion from linear abbreviation (the 4D TOCID symbol):

5 – penta/pentagon
T – tesseract/truncated
16 – hexadeca
24 – icositetra
HI – hecatonicosa
X – hexacosi
F – faceted/fissary
G – great
& – grand
S - small/stellated
h – hemi/hexis
8 – octa/octagonal
dt – ditrigonal
Q – quasi
R – rectified/rhombated
f – faceto
P – penta/prismato/prismattic
N – intercepted
d – dis
r – retro
A – anti
v – verted
i – inverted
p – pental/pentis
L – polar
n – intercepted/spino
O – omni/octis
m – circum
t – tris (previously called triakis)/toroidal
W – spheno
10 – deca
48 – tetracontocta
C – cubi
o – omni
K – skew
+ – tetris
720 – heptacosicosa
5/2 – pentagram
4 – tetra
d4 – ditetrahedral/ditetragonal
M – medial
Di – double
dT – ditrigonal
I – icosi
D – dodeca
$ – snub
s – swirl
240 – diacositetraconta
480 – tetracosioctaconta
360 – triacosihexaconta
c – capped
b – based
tT – tritrigonal
B – blendic
k – deca
7 – heptis
DP – duoprism
3 – trigonal
dp – dipesic
tp – tripesic
8/3 – octagrammic
diortho – diortho(?)
- (hyphen) – (nothing)

Conversion from linear Coxeter-Dynkin diagram notation is given at http://www.polytope.net/hedrondude/glossary.htm. I use this because it's the fastest way to type Coxeter-Dynkin diagrams. (If only you could parse them into {{CDD}}!)

Listing

Category A: Duoprisms
Category B: Antiduoprisms
Category 1: Regulars (Polychora 1 – 17)
Category 2: Truncates (Polychora 18 – 38)
Category 3: Triangular Rectates (Polychora 39 – 59)
Category 4: Ico Regiment (Polychora 60 – 72)
Category 5: Pentagonal Rectates (Polychora 73 – 132)
Category 6: Sphenoverts (Polychora 133 – 297)
Category 7: Bitruncates (Polychora 298 – 306)
Category 8: Grombates (Polychora 307 – 329)
Category 9: Omnitruncates (Polychora 330 – 351)
Category 10: Prismatorhombates (Polychora 352 – 441)
Category 11: Antipodiumverts (Polychora 442 – 481)
Category 12: Podiumverts (Polychora 482 – 551)
Category 13: Spic and Giddic Regiments (Polychora 512 – 551)
Category 14: Skewverts (Polychora 552 – 611)
Category 15: Afdec Regiment (Polychora 612 – 664)
Category 16: Affixthi Regiment (Polychora 665 – 763) – affixthi =
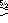
Category 17: Sishi Regiment (Polychora 764 – 777)
Category 18: Ditetrahedrals (Polychora 778 – 888)
Category 19: Prisms (Polychora 889 – 962)
Category 20: Miscellaneous (Polychora 963 – 984, 1846 – 1849)
Category 21: Padohi Regiment (Polychora 985 – 1065)
Category 22: Gidipthi Regiment (Polychora 1066 – 1146)
Category 23: Rissidtixhi Regiment (Polychora 1147 – 1303) – rissidtixhi =
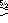
Category 24: Stut Phiddix Regiment (Polychora 1304 – 1382)
Category 25: Getit Xethi Regiment (Polychora 1383 – 1461) – getit xethi = (intended as a two-loop graph)
Category 26: Blends (Polychora 1462 – 1473)
Category 27: Sidtaps and Gidtaps (Polychora 1474 – 1491)
Category 28: Idcossids (Polychora 1492 – 1668)
Category 29: Dircospids (Polychora 1669 – 1845)

User:Double sharp/Polychora

Listing

Scaliform polychora

See also