Talk:Hypercube/Archive 1

Archive 1

redirect to tesseract

Resolved

I changed the redirect from measure polytope to Tesseract. I agree a hypercube can imply HIGHER polytopes than a tesseract, but 99% of the time I expect people MEAN a 4-polytope, so I judge it better to link to tesseract specifically and let readers go to the more general (family) secondly from there. Tom Ruen 06:21, 14 October 2006 (UTC)

Since my redirect was reversed, I removed the redirect and put two links in here.

I still disagree - I NEVER mean "n-dimensional hypercubes" and say hypercube since that is ambiguous what I mean. I'd say n-cube or n-hypercube or n-measure polytope. If there's no dimension offer I assert 4 is implied. Tom Ruen 09:47, 12 November 2006 (UTC)

I disagree. I ALWAYS mean the general case when I say "hypercube", and would specify 4-dimensional if that's what I mean. I don't think 4d is the default, and I think hypercube should be the preferred name for what is now measure polytope. I see tesseract as a special case, that should be prominently linked from the hypercube page but not redirected from it. And according to WP:D disambiguation pages (such as the current state of this page) are for when there are several links to disambiguate, but here there are only two. —David Eppstein 18:18, 15 November 2006 (UTC)

Later: I made this a little more texty and added a link to hypercube graph. So now it looks a little more plausible as a dab page. I'd still prefer this to be the main name for measure polytope, though, and am still not convinced having a separate dab page is necessary since the tesseract and hypercube graph articles are linked from that page anyway. —David Eppstein 18:29, 15 November 2006 (UTC)

I agree with David Eppstein. The mathematical community does not mean 4-dimensional when it says "hypercube". I do believe the name "hypercube" has been used, e.g. in science fiction, for the 4-cube, and it would be good to give that as a secondary meaning with a link to tesseract.

Here's a suggestion: Keep "hypercube" as a disambiguation page, since there are several meanings, such as the graph. Create hypercube (geometry) to move measure polytope to. Put into measure polytope a short definition as a unit hypercube (named by Coxeter, not common). I throw these ideas out for reactions. Let's hear! Zaslav 01:41, 16 November 2006 (UTC)

Hypercube, Hypercube graph, n-cube, and measure polytope are too closely related to be considered disambiguous. While the A_(disambiguation) article could be referring to a number of different completely unrelated concepts from many different fields. Same with the error page, it has a separate disambiguous page, however, hypercube only has one unrelated concept mainly the movie. The hypercube article will now contain what was once the measure polytope page, have a single disambiguous link to the movie at the top, and the article will refer to an n-cube when referring to a specific dimension, measure polytope should only be used when applied to hypercubes of unit length (side length, wrong terminology) one. --ANONYMOUS COWARD0xC0DE 00:23, 25 December 2006 (UTC)

Good! That's what I meant all along, really, really! (Also, the principal meaning of "hypercube" is obviously the geometrical one.) Thanks to whoever carried out the merge/move. Zaslav 06:40, 30 January 2007 (UTC)

Every geometry textbook I've looked at uses the term hypercube to mean tesseract specifically, and it is clearly and patently illogical and nonsensical to use it to name figures with fewer than four dimensions. What "David Eppstein" "always [means]" by hypercube is utterly irrelevant. —Preceding unsigned comment added by 24.183.105.240 (talk) 12:53, 8 December 2007 (UTC)

I hesitate to pull rank, but given that some of my professional research papers concern hypercubes I think it is relevant. —David Eppstein (talk) 17:14, 8 December 2007 (UTC)

I'm curious what text books you have? Sommerville calls a tesseract a hexahedral 8-cell. Coxeter says tesseract. Coxeter does use hypercube in a table of regular polytopes {p,q,r}, but that implies which hypercube. He also says regular simplex in the context of 4-d figures, which would otherwise be ambiguous.

I might support calling this article the Hypercube family since it's not a single object all. Others support n-cube which parametrizes the family member. I agree saying a cube is a hypercube sounds silly. I also tend to think 4-cube/tesseract when someone says hypercube, but again, it's a family. People call me by my family name, and I can understand, but its still ambiguous. Tom Ruen (talk) 20:45, 8 December 2007 (UTC)

Re the silliness of low-dimensional hypercubes: Google scholar has 30 hits for one-dimensional hypercube, 112 hits for two-dimensional hypercube, and 277 hits for three-dimensional hypercube. —David Eppstein (talk) 21:33, 8 December 2007 (UTC)

The fewer dimensions meant, of course, the sillier it is to use the term hypercube, and you'll have noted that, correspondingly, according to your little (and inconsequential, I'm afraid) survey, the fewer dimensions the fewer "hits". —Preceding unsigned comment added by 24.183.105.240 (talk) 07:49, 11 January 2008 (UTC)

Re: "I also tend to think 4-cube/tesseract when someone says hypercube, but again, it's a family.":

Logically the term hypercube can mean an n-dimensional figure (with "family traits") such that n > 3, although it is commonly used to mean tesseract in particular. It cannot logically mean one such that n <= 3. —Preceding unsigned comment added by 24.183.105.240 (talk) 08:01, 11 January 2008 (UTC)

Merge Hypercube<--Hypercube graph

Resolved

To me it just seems that hypercube graph could be a section within Hypercube. Any dissenting view points? --ANONYMOUS COWARD0xC0DE 00:36, 10 January 2007 (UTC)

I don't see why a single merged article would improve the current situation, and I think the significant differences between hypercubes and hypercube graphs could make a merged article quite confusing. Hypercube graph lies in Category:Graphs, which may not be as relevant for hypercubes as geometric objects. There is also some important graph theory I hope to add but haven't yet concerning median graphs (retracts of hypercubes) and partial cubes (isometric subgraphs of hypercubes). A hypercube has faces of many dimensions while a hypercube graph has only vertices and edges. A hypercube is topologically equivalent to a ball while a hypercube graph has a large homology group. A hypercube has high dimension while the hypercube graph article talks about two-dimensional unit distance representations. We don't merge complete graph and simplex; why is this any different? —David Eppstein 07:41, 10 January 2007 (UTC)

Ok. I withdraw my request. --ANONYMOUS COWARD0xC0DE 04:51, 12 January 2007 (UTC)

"Measure polytope"

I changed the wording about and usage of this term, because a reading of Coxeter (1973) shows that he did not mean it to refer only to a unit hypercube. He meant it to be any "hyper-cube" (his spelling). Also, it seems clear to me, from his language, that he invented the name. Zaslav 17:41, 8 February 2007 (UTC)

n cube rotation

Can we get rid of this section? Maybe note that rotation involves 2 axes, so an N cube has N*(N-1)/2 axes of rotation (if we are counting only "square" rotations). —The preceding unsigned comment was added by Paul Murray (talk • contribs) 04:09, 30 April 2007 (UTC).

It's badly written in a way that makes it sound like OR, but actually the symmetries of hypercubes are well known, and their symmetry group is the same as the signed permutations. Probably this should be completely rewritten. I don't know why you would only consider square rotations, though. —David Eppstein 04:29, 30 April 2007 (UTC)

It states "a 2-dimensional hypercube can only be rotated by vertex" In a 2 dimensional plane, a square can only be rotated by its center or its edge. If you rotate it by its vertex, it will lift of the plane, directly contradicting what a 2d object is. —Preceding unsigned comment added by 71.99.30.19 (talk) 02:52, 1 February 2008 (UTC)

There is no reason why it can't rotate by the vertex (think of a square hanging on a wall, hinged on one corner: it can spin around without leaving the wall's surface).

Anyway, that's besides the point. I tried to rewrite the section so that it makes more sense, but then I realized that the material belongs more in rotation than here, so I'm thinking to delete this section altogether. Any objections?—Tetracube (talk) 19:58, 29 September 2008 (UTC)

Significance

Could somebody explain what the significance of the Hypercube is? Why are we looking at it? What does it represent? ThePeg 18:49, 30 April 2007 (UTC)

I don't know but now I understand you make a "sweeping of the things" to make dimensions. Crikey I get it!!! WinterSpw 05:37, 24 May 2007 (UTC)

If you are going to require that mathematical concepts "represent" things or have concrete analogs, you are going to have to start discussions on a lot of pages. Much of the time, mathematical matters are allowed to exists in and of themselves, as "knowledge for knowledge's sake." Krychek 16:29, 8 June 2007 (UTC)

There are two important sets that hypercubes (or rather their vertices) can be be thought of as representing, though:

1. the set of all binary strings of a fixed length (the length of the string = the dimension of the hypercube)
2. the powerset of a finite set (the size of the set = the dimension of the hypercube).

In addition, the hypercube forms a fundamental building block for d-dimensional Euclidean space and forms the unit of measurement for volume in that space. It is much more than simply a shape that can be defined to exist in and of itself. —David Eppstein 23:48, 9 June 2007 (UTC)

Furthermore, understanding the properties of hyper-dimensional objects is crucial for work in modern M-Theory which states that 7 of the 11 dimensions in our universe are curled up. —Preceding unsigned comment added by 71.99.30.19 (talk) 02:48, 1 February 2008 (UTC)

Is there any practical application of this concept in the physical world? I am an extreme layman, at least in this subject, and would like to know what use this has outside of pure mathematics(and the extensions of the mathematical usage). I find what little I understand of it fascinating and would like to see a layman's explanation as well as the preceding in the article, or at least a link to somewhere that has one.--98.148.26.113 (talk) 03:16, 20 August 2009 (UTC)

Fatal inconsistency!

We say that a hypercube is convex, but immediately proceed to describe it as a union of line segments. A few lines later we revert to describing each hypercube as the result of sweeping its predecessor in a direction orthogonal to itself. Do we wish hypercube to denote the n-simplex or its 1-skeleton? Or do we wish to retain the flexibility to use it in both ways? Whichever choice is made, the current lack of rigor scarcely supports aspirations to an encyclopedic treatment of the topic.----PaulTanenbaum 21:27, 17 August 2007 (UTC)

I don't understand this criticism enough to answer anything in a helpful way. I see nothing so dramatic. What does a simplex has to do with this? With all polytopes there's interpretations of interior vs surface. Feel free to improve it or make suggestions. Tom Ruen 22:34, 17 August 2007 (UTC)

Tom, here's the problem. The 1-skeleton (i.e. the union of line segments) is not convex for any n > 1, in other words for the square or beyond. But I'm happy to say that David Eppstein has fixed things up nicely.

---

PaulTanenbaum 13:21, 18 August 2007 (UTC)

Cellular Automaton

The recurrence relation that generates the number of elements in an n dimensionalc cube struck me as similar to the cellular automaton of Wolfram. It is a repetitive iterative process based on a very simple rule, albeit not producing black or white squares, but still very similar. Is this not worth a mention? In addition I believe Wolfram has suggested automata could be doing something fundamental in physics. It might be worth finding out if he has reported automata could have some connection with dimensions/hypercube. --- Plexos | Talk 05:16, 27 October 2007 (UTC)

Recurrence relations and cellular automata are two quite different things, and neither one was invented by Wolfram. The recurrence relation is easy to explain directly, by the way: if you view an n-cube as the Cartesian product of an interval and an (n−1)-cube, each m-dimensional face of the n-cube is either the product of an m-dimensional face of the (n−1)-cube with an endpoint of the interval (there are 2E_m,n−1 of these) or the product of an (m−1)-dimensional face of the (n−1)-cube with the whole interval (thera are E_m−1,n−1 of these). Add these two sets of faces and you get the recurrence. But I'd hesitate to put an explanation like that into the article without a proper citation for fear of violating the prohibition against original research. For the same reason, you should probably avoid putting things in because they "strike you as similar" and wait until you can find a reliable source for them. —David Eppstein 05:23, 27 October 2007 (UTC)

All $E_{m,n}$ for all hypercubes can be generated from the linear recurrence relation of the form e = 2a + b, there's nothing more to it. This is Occam's razor at it's sharpest and you might say that the relation "is" the hypercubes. Can the cartesian product system derive this relation or a simpler one for all m and n? If it can then I would be interested to see the maths. You only mention faces (cases $E_{n-1,n}$) above but what about others like lines and points for a cube? As for original research, Jimmy Wales is wrong about this, what better place than Wikipedia with all it's credibility, software tools, discussion system, history control, etc on tap for creators. In addition the increased presence of such experts would raise standards throughout. --- Plexos | Talk 17:49, 27 October 2007 (UTC)

The objects counted by $E_{n-1,n}$ are "facets". "Faces" are elements of any dimension. As for whether Wales is right or wrong: if you disagree with him you're welcome to start your own encyclopedia but we have to play by the rules here. —David Eppstein 18:14, 27 October 2007 (UTC)

I had a look at the NOR page and it has a point, you can't have all sorts of cranks posting wrong information. It's a pity genuine creators go down with the ship though. They could allow special original research pages like say Original Research:Hypercube, though with their own ruleset and moderators. --- Plexos | Talk 07:48, 30 October 2007 (UTC)

Visualization

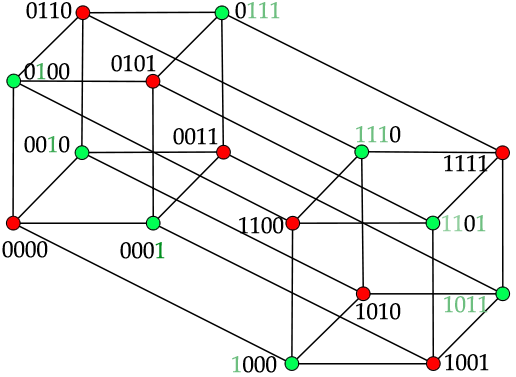
It's possible to see a 3-cube on a 2D image.

Is it possible to see a 4-cube if we made a 3D model of it? —Preceding unsigned comment added by 125.238.140.173 (talk) 23:18, 20 November 2007 (UTC)

What do you mean by "possible", "see", and "model"? It's certainly possible to make 2d drawings and 3d objects that help visualize some aspects of 4-cubes; there are several in tesseract. —David Eppstein (talk) 23:32, 20 November 2007 (UTC)

Certainly, by projecting a 4-cube into 3-space, we can apply dimensional analogy to obtain an intuitive idea of what it is like in its native space (just as we have an intuitive grasp of 3D objects which we have only ever seen as 2D projections onto our retina). But obviously this isn't quite the same thing as actually seeing a 4-cube, since to do so would require a 3D retina (3D array of retinal cells), which we don't have. (And even if we did have, it would not help, since we are confined to 3D and there is no way light can reach any cells in the retina except the ones on the boundary, thus rendering it useless.)—Tetracube (talk) 20:04, 29 September 2008 (UTC)

The picture of the tesseract projection in the article is actually of a transparent tesseract (otherwise it would look just like a regular transparent 3d cube). I think it would be better to either change the second picture to a simple transparent cube and leave the first one unchanged, or change only the first picture to a transparent cube. Chronometrier (talk) 23:05, 11 January 2008 (UTC)

The Values of n

All the given examples talk of n-cubes in which the value of n is an integer, I think it should be mentioned whether or not it is always the case. Knowing how pure mathematics work, I see no reason why hypercubes would only be integer-cubes and never (-3)-cubes, 1,5-cubes, pi-cubes or i-cubes, so it would be more complete if it were mentioned no?. 24.200.59.201 03:26, 1 December 2007 (UTC)

I think you mean whole numbers (o-oo), not integers. This does not happen simply because n tells us how many lines can be put in at a right angle at a corner. Look at a 3n cube. At each corner there are 3 right angles. So, how can you have 1/2 of a line? Any length of line is one whole line. Same thing with negative values. How can you have -3 lines? —Preceding unsigned comment added by 71.99.30.19 (talk) 02:39, 1 February 2008 (UTC)

The formulas of hypercubes elements

It is said that the number of vertices of a n-cube is 2^n and the number of "(n-1)-cubes sides" is 2n, but maybe some formulas for other elements could also be given: the number of edges, I calculate, is n2^(n-1) and the number of faces is 2^(n-2) times the summation of "a" from 1 to (n-1)[or the (n-1)th triangle number] and all elements are probably so calculable. I simply do not want to waste my time on calculating all of them myself if the formulas are already known (which they probably are) or, worse, if there is some mean of calculating any number of m-dimentional elements in a n-cube with a single formula. 24.200.59.201 03:26, 1 December 2007 (UTC)

The formula is given as a combination:

The number of m-dimensional hypercubes (just referred to as m-cube from here on) on the boundary of an n-cube is

$E_{m,n}=2^{n-m}{n \choose m}$,     where ${n \choose m}={\frac {n!}{m!\,(n-m)!}}$ and n! denotes the factorial of n.

Tom Ruen 03:53, 1 December 2007 (UTC)

Oh, and that is what is written in the article, I had misunderstood what it meant. thanks. 24.200.59.201 (talk) 23:39, 5 December 2007 (UTC)

Maple program

The following text was removed from Hepteract. Tom Ruen 19:07, 2 December 2007 (UTC)

for i from 0 to 13 do seq(binomial(i, j)*2^(i-j), j = 0 .. i-1) od;##

                                  2
                                 4, 4([[square]])
                               8, 12, 6  ([[Cube]])
                            16, 32, 24, 8 ([[Tesseract]])
                          32, 80, 80, 40, 10 ([[Penteract]])
                      64, 192, 240, 160, 60, 12 ([[Hexeract ]])
                   128, 448, 672, 560, 280, 84, 14 ([[Hepteract]])
              256, 1024, 1792, 1792, 1120, 448, 112, 16  ([[Octeract]])
           512, 2304, 4608, 5376, 4032, 2016, 672, 144, 18
      1024, 5120, 11520, 15360, 13440, 8064, 3360, 960, 180, 20
 2048, 11264, 28160, 42240, 42240, 29568, 14784, 5280, 1320, 220, 22
4096, 24576, 67584, 112640, 126720, 101376, 59136, 25344, 7920,1760, 264,  24
8192, 53248, 159744, 292864, 366080, 329472, 219648, 109824, 41184, 11440, 2288, 312, 26

Other:http://www.research.att.com/~njas/sequences/A038207

Hypercube names

George Olshevsky calls a 10-cube, a dekeract [1], but only case I know. Tom Ruen (talk) 01:59, 15 December 2007 (UTC)

George Olshevsky can continue calling it that on his web site. We should use more reliable sources here. —David Eppstein (talk) 02:14, 15 December 2007 (UTC)

you could continue the pattern. a 5-cube could be a penteract, sexeract (lol), septeract, octeract, noveract, ect. —Preceding unsigned comment added by 71.99.30.19 (talk) 02:43, 1 February 2008 (UTC)

It's not septeract; it's a hepteract. Weatherlover819 (talk) 03:44, 15 March 2008 (UTC)

Consideration

I think the Cartan's triangle is the appropriate arithmetic triangle for hypercubes. I think the Cartan's triangle (sandbox) should have its own article. I have written a sandbox, so put this into consideration. Weatherlover819 (talk) 03:44, 15 March 2008 (UTC)

Dimension -1

The article and the table should be modified to include the empty (-1)-polytope, and a column in the table for the (-1)face of each n-cube, though this view will have dissenters. Since this debate has already raged in the Simplex article, my suggestion would be continue it there rather than fracture it.SLWoolf (talk) 04:34, 28 October 2008 (UTC)

Hmmmm... Given this element relation, what does it mean when m=-1?

The number of m-dimensional hypercubes (just referred to as m-cube from here on) on the boundary of an n-cube is

$E_{m,n}=2^{n-m}{n \choose m}$,     where ${n \choose m}={\frac {n!}{m!\,(n-m)!}}$ and n! denotes the factorial of n.

$E_{-1,n}=2^{n+1}{n \choose -1}$ ??? (I would say this isn't defined!)

Tom Ruen (talk) 18:17, 28 October 2008 (UTC)

Why must the null polytope be included in every table and every article that mentions polytopes? I think it is sufficient to add a note that sometimes the empty set is regarded as a (-1)-dimensional null polytope, and perhaps enumerate a few cases where this may be useful (in the relevant article). There are some cases for which this notion is not of much use, or as Tom Ruen pointed out, outright problematic, so why insist on including it everywhere?—Tetracube (talk) 19:40, 28 October 2008 (UTC)

Deleted rotation section

I deleted the following text (in a section labeled "n-cube rotation") because nothing in it is about hypercubes:

In general, rotation is a planar phenomenon requiring two dimensions to operate. Any additional dimensions in the space that the rotating object is embedded in manifests itself as a stationary set.

No rotation is possible in 1 dimension. An object in 1 dimension cannot rotate without leaving that 1-dimensional space.

In 2 dimensions, both dimensions are used for rotation, leaving a 0-dimensional stationary point. Hence, an object in 2 dimensions rotate about a point. The rotational axis commonly associated with 2-dimensional rotation actually lies outside of the 2-dimensional space itself, and thus is merely an artifact of anthropocentric bias toward 3-dimensional space. Hence, rotation in 2 dimensions is more properly understood as rotation about a center of rotation. Rotations in 2 dimensions are uniquely identified by the center of rotation and the rate of rotation.

In 3 dimensions, objects rotate about an axis, a stationary line, since there is one dimension "left over" as the other two participate in the rotation. The rotational axis is peculiar to odd-numbered dimensions. Rotations in 3 dimensions are uniquely identified by the axis of rotation and the rate of rotation.

Rotation in 4 dimensions are of two kinds: plane rotations and composite rotations. A plane rotation has a stationary plane which an object may rotate "around". This is because two dimensions participate in the rotation while the other two are stationary. Objects in 4 dimensions can also rotate independently in these two leftover dimensions, resulting in a composite rotation composed of two plane rotations at two independent rates of rotation. These composite rotations have a stationary point, just as in 2 dimensions. Hence, rotation in 4 dimensions are identified by a center of rotation, and two rates of rotation (planar rotation being a special case where one of the rates is zero).

In 5 dimensions, rotations have either a rotational axis or a rotational 3-space. With the former, there are two independent rates of rotation, just as in 4 dimensions. With the latter, there is 1 rate of rotation (2 dimensions participating in the rotation, and 3 dimensions forming the stationary 3-space).

In general, in n dimensions, if n is odd then rotations have an axis, and there are (n-1)/2 possible simultaneous plane rotations around that axis. If n is even, then rotations have stationary points (rotational centers), with n/2 possible simultaneous plane rotations. Each possible plane rotation has its own rate of rotation.

—David Eppstein (talk) 22:37, 25 January 2010 (UTC)

Fair enough, it's vaguely related but it's already covered elsewhere, and I thought when looking at it that it needs a re-write anyway.

Perhaps more appropriate would be something on the symmetry groups of the n-cube. I've not done group theory for a long time so don't feel confident adding anything myself, but a short section listing the groups with links to more general results would be useful. --JohnBlackburne^words_deeds 22:44, 25 January 2010 (UTC)

I agree that something about the symmetry groups of the n-cube would be appropriate. There's a link in the see-also section for hyperoctahedral group but we could include more in the article itself. —David Eppstein (talk) 22:54, 25 January 2010 (UTC)

Rendering of 3-cube appears wrong

3-Cube should have 8 (2^3) vertices however the rendering only possesses 7. This is a fatal error. 130.56.95.48 (talk) 00:23, 22 March 2011 (UTC)

Are you acquainted with opacity? —Tamfang (talk) 05:43, 22 March 2011 (UTC)

He has a bit of a point in that the 3-d figure is opaque whereas the 4d one is transparent. Perhaps a transparent cube should be there to make them comparable. Dmcq (talk) 18:43, 22 March 2011 (UTC)

How about this one ? It's also more like the tesseract in colour and style.--JohnBlackburne^words_deeds 19:22, 22 March 2011 (UTC)

Seems good thanks Dmcq (talk) 19:29, 22 March 2011 (UTC)

I believe he is referring to the orthographic projection of the 3-Cube.130.56.91.216 (talk) 09:09, 5 April 2011 (UTC)

Who is 'he' please? Do you believe there is a problem that has not been dealt with? Dmcq (talk) 09:18, 5 April 2011 (UTC)

Number of Vertices in the 3-Cube

The 3-Cube has 8 vertices, but the image accompanying it only has 7. Where is the 8th vertex? 68.116.170.64 (talk) 16:42, 12 April 2009 (UTC)

It is obscured from view by the front face of the cube.—Tetracube (talk) 16:29, 13 April 2009 (UTC)

The central orange vertex in the image is doubled (see Penteract and Hepteract for such notes). 3.14159265358pi (talk) 23:30, 29 November 2011 (UTC)

Visualization question

And this may be off topic, I apologize.

A human observer can watch a point (1D) sweep out a line (2D) while the observer moves in time (4D). Is it possible to watch a point sweep out a line while the observer moves in depth (3D)? Obviously we can't observe the progression through dimensions higher than 4D, but are we limited to progressions that include 4D only?

Also, apologies if I'm totally misunderstanding how the levels of dimensions work.12.53.10.226 (talk) 07:17, 10 April 2011 (UTC)

The hypercube described in this article is of four spatial dimensions. One can also consider time as a space time dimension as one way of trying to imagine a four dimensional object. In the real world time is not a spatial dimension but something a little different as described in Minkowski space-time but that's no great problem for imagination purposes.

In the four dimensions a line or point or whatever simply is just like a line in our three dimensional space simply is without moving. The moving bit in the imagining is taking slices out of the four dimensional space and looking at the three dimensional slices. Personally I do not do that at all as I feel it is like just seeing a square as two moving dots rather than all together and I think you are better off just imagining the four dimensions directly all at once perhaps starting off by using different colours for the slices or making things fuzzier as they are farther away in the fourth dimension. With this you will notice the less fuzzy bits should obscure the more fuzzy ones exactly like you only see the near side of a cube. Dmcq (talk) 11:14, 10 April 2011 (UTC)

Why do 11-cube & 12-cube redirect to the article?!

Why do 11-cube & 12-cube redirect to the article?! Who came up with that stupid idea, anyway?! --99.68.220.64 (talk) 00:17, 10 December 2011 (UTC)

Because there is nothing special about the 11-cube or the 12-cube that distinguishes them from cubes of other dimensions enough to justify having separate articles for them? —David Eppstein (talk) 01:51, 10 December 2011 (UTC)

Whatevcer impelled you to look up 11-cube in the first place? It hardly sounds to me like something one would think of looking for. In fact why on earth do we have articles on 10-cube 9-cube 8-cube 7-cube and 6-cube? They're not exactly notable for anything are they. Everything that is there about the lot of them could be put into one article and remove most of the pictures without losing anything in the least worthwhile that I can think of. Dmcq (talk) 11:31, 10 December 2011 (UTC)

It's not just cubes but dozens of regular and semiregular solids. To me it falls under the category of stuff that would be more trouble to remove than it was to add it in the first place. In other words go ahead an replace 10-cube with a redirect but I predict a) it will be immediately reverted and b) you will be flamed for your trouble.--RDBury (talk) 18:56, 10 December 2011 (UTC)

So due to that, I suggest you are to read the Redirect:11-cube page for a bedtime story to your children (if you have any) tonight! So HA!!! --3.14159265358pi (talk) 22:36, 12 December 2011 (UTC)

Well I've found one thing the 10-cube is notable for. It is referenced from WP:NTHINGS about things not to write about as 'That you can prove that three 9-cubes can be fused together to form a 10-cube'. Which I think exemplifies my attitude to it. Except you can't fuse three 9-cubes to form it you need 20 of them, oops eek aargh, I need my tinfoil hat to defend myself! ;-) Dmcq (talk) 11:50, 14 December 2011 (UTC)

Check who added that entry, and a ridiculous number of others. --Redrose64 (talk) 18:59, 14 December 2011 (UTC)

At least there are orthogonal projection vertex-edge graphs of the 11-cube and 12-cube here at Hypercube#Graphs! Tom Ruen (talk) 04:07, 16 December 2011 (UTC)

Waste of bandwidth is my opinion. Dmcq (talk)

Bah humbug! :) I think it's interesting that the n=2^k dimensional n-cubes apparently create petrie polygon projections that have no overlapping vertices, while apparently the n=prime number dimensions produce graphs that only have overlaps at the center. I'm sure someone could explain this fact, but I have no sources on it. Tom Ruen (talk) 20:34, 16 December 2011 (UTC)

Link on the word Compact in first paragraph

The word Compact links to the Compact space page, but shouldn't it link to Compactness measure of a shape instead? As the latter page says, "The meaning of "compact" here is not related to the topological notion of compact space." ssl 02:19, 12 November 2012 (UTC) — Preceding unsigned comment added by Sslandy (talk • contribs)

Hm, it's true that the hypercube itself is not a space ... —Tamfang (talk) 07:03, 12 November 2012 (UTC)

Integration used as a term for Constructing hypercubes

The term "integration" accurately describes the creation of a hypercube of one dimension higher than the original hypercube, wheareas the term "move" does not.

When a line is integrated, area is 'swept out', and similarly, when a plane is integrated, volume is swept out. Similarly, when a line segment of length x is extended into the second dimension (the y direction), the area swept out by the resulting rectangle can be represented by $\int _{0}^{y}x\,dy=xy$, where x is the length of the rectangle and y is the width. Of course, for the purpose of hypercubes, x = y = z = w =...) This can be easily proved using a graphing calculator to integrate the function f(x)= 1 from 0 to 1; the result will be 1, which represents one square unit.

An integral is a sum, so, for example, the integral of a square would be a sum of squares. This can be imagined as several congruent squares being stacked on top of one another so that the total height of the stack is equal to the length and width of each of the squares. So, when a square with area xy is integrated from zero to z, the resulting cube is the sum of various squares of area xy and height dz, or a small change in z. This gives the integral$\int _{0}^{z}xy\,dz=xyz$, where in this case x,y,z = 1, and xyz represents the volume of the resulting cube.

The current word being used to describe the creation of a hypercube of a higher dimension in this article is move. This term is incorrect both literally and mathematically. For example, if line segment AB is integrated to form square ABCD, line segment AB did not move; it is in the same place that it started and still exists as an edge of the newly formed square.

Please consider the validity of my arguments before continuing to undo my edits! If you would like to debate the use of the term, feel free to post to my talk page, as I am more than happy to discuss this. I have spent time and effort both discussing the use of the term with others and ensuring that the mathematics behind it are sound, and it is frustrating to have my edits undone simply because somebody else disagrees. If you're going to undo any more of my edit, please at least discuss your concerns on this topic with me.

Anion24 (talk) 22:01, 22 March 2013 (UTC)

This page is where we discuss how to write and improve this article. A strong personal belief that something should happen is not relevant -- we go by what independent reliable sources say on the subject. Are there scholarly papers or books that use this terminology? If not then however compelling your arguments for what words ought to be used, we cannot accept them in favour of the words that actually are used. I see that you have inserted this non-standard terminology yet again. This is now Wikipedia:Edit warring and unless you revert your changes pending a consensus here on the talk page, this are likely to be reported at Wikipedia:Administrators' noticeboard/Edit warring. Deltahedron (talk) 22:20, 22 March 2013 (UTC)

I do not see how valid, mathematically correct integrals convey any strong personal belief. The page previously gave no explanation for the formation of hypercubes, it just said "if you move this point, a line segment is formed." Even if my arguments were incorrect, at least they would still be an attempt to explain something. But they are correct, and offer a mathematically sound explanation.

About the 'edit war': Perhaps the fact that I previously used the term integration without actually including the integrals was incorrect and misleading, but I have added them, and now it is apparent that the term integrate is no longer non-standard, for it literally applies directly to the intergrals listed.

"If not then however compelling your arguments for what words ought to be used, we cannot accept them in favour of the words that actually are used."

Move isn't a term that is actually used! What is actually happening in the shown figure might be very hard to find a word for, but move isn't the right one, as I've already mentioned, so there is no valid reason to favor it over any other word, be it "integral," "fractal", "rocket", or "cupcake", the latter three of which make about as much sense as the word "move", seeing that nothing at all is actually moving. None of the users who have previously undone my changes have undone them again since I posted my argument to this talk page and included the actual integrals on the article page, and if someone who disagrees with my facts undoes my changes again without reading my post to this talk page, I'll probably just give up. If someone can't be bothered to explain why they're deleting my posts before deleting them, that is just a simple etiquette issue, which is not my problem, and they aren't worth my time, and I doubt that they're worth yours; you must have spent almost as much time on this issue that I have.

I understand that it is your job to resolve disputes, and respect that you are doing your job by addressing your concerns with my contributions. But the 'edit war' is over; if nobody has a problem with the current Construction section of the Hypercube page, which includes the term integration as well as integrals for the example that was posted by another user, then nobody will remove it, and if someone does have a problem with it, they'll delete it and you won't hear any more about it from me. Like I said before, using the word integrate without demonstrating the fact that something is actually being integrated was a poorly-thought out decision, but I have since added support for the term.

Anion24 (talk) 23:07, 22 March 2013 (UTC)

Please see our guidelines on neologisms and original research. In a nutshell, if you want to make a change to mathematical terminology, this is not the place. At Wikipedia, we reflect the mainstream of mathematical knowledge rather than guiding it. If you want to use the word "integrate" in this non-calculus-related way, you need to dig up sufficiently many published reliable sources to convince us that it is already standard terminology used by others and not just you. —David Eppstein (talk) 00:54, 23 March 2013 (UTC)

Thank you for at least explaining why you felt that it was necessary to remove my edits. First of all, none of my edits regarding the concept of integration are based off of original research; only the posts about 'sets' under the Elements section were, which I have since submitted to a database to be evaluated and hopefully published and eventually posted here with a citation. The words 'set', 'anterior set', 'integrated set' and 'derivative hypercube' are all neologisms and it was wrong for me to post them to Wikipedia, but those terms are not related to the current issue at hand.

"If you want to use the word "integrate" in this non-calculus-related way, you need to..."

How is using the word 'integrate' being used here in a non-calculus way? Did you read latest revision to the article at all, or simply see that I had edited the article, assumed that it was unverified original research, and delete it? The word integrate is EXPLICITLY being used to describe functions being integrated, which is certainly a calculus-related use for the term.

You seem to be under the impression that I am trying to alter or revise a mathematical term or concept. I'm not, I'm only using established facts in calculus to explain part of this article, seeing that nobody had previously done so on Wikipedia. I am not the first person to propose this, explain it, or prove it, and it is astounding to see that I am the first person to attempt to publish it.

Now that we have established that I'm using the word integration to refer to actual integrals and that I'm not changing any existing terminology nor incorrectly using any existing terminology nor creating a new meaning for any existing term, what must I do to have this small piece of mathematical knowledge added to Wikipedia?

Anion24 (talk) 01:31, 23 March 2013 (UTC)

I said it before but you didn't listen. What you need to do is find published reliable sources (by other people than you) convincing us that your take on this subject is mainstream enough to go into the article. —David Eppstein (talk) 03:09, 23 March 2013 (UTC)

Apparently no such sources exist. I will have to work with a professor at my university to write and submit a scholarly article on this topic, and I have no way of knowing how long this process will take. I will post the link of that source here and wait for your approval before proceeding to further edit this page, and until then, I believe that the issue at hand has been resolved.

Anion24 (talk) 04:09, 23 March 2013 (UTC)

External links modified

Hello fellow Wikipedians,

I have just added archive links to one external link on Hypercube. Please take a moment to review my edit. You may add {{cbignore}} after the link to keep me from modifying it, if I keep adding bad data, but formatting bugs should be reported instead. Alternatively, you can add {{nobots|deny=InternetArchiveBot}} to keep me off the page altogether, but should be used as a last resort. I made the following changes:

• Attempted to fix sourcing for //www.jpbowen.com/publications/ndcubes.html

When you have finished reviewing my changes, please set the checked parameter below to true or failed to let others know (documentation at {{Sourcecheck}}).

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

• If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
• If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—^{cyberbot II}_{Talk to my owner:Online} 06:33, 30 March 2016 (UTC)

This table looks better with 4 columns when the page is enlarged than the 5 columns in the article. Can I change it?

Petrie polygon Orthographic projections

Line segment	Square	Cube	tesseract
5-cube	6-cube	7-cube	8-cube
9-cube	10-cube	11-cube	12-cube
13-cube	14-cube	15-cube

If you agree, just cut and paste it, in place of the 5 column version in the article. — Preceding unsigned comment added by 201.124.223.123 (talk) 10:17, 27 August 2018 (UTC)

Beautiful, but very poorly explained

The pictures in the article of a projection of the n-dimensional cube for n up to 16 are extremely beautiful. But they are left completely unexplained.

A mysterious link to another Wikipedia article is no excuse for a complete lack of explanation.

This typifies the worst of Wikipedia. I hope someone knowledgeable will take the trouble to explain how these projections are defined. 2601:200:C000:1A0:3192:F460:5650:3286 (talk) 00:57, 16 August 2021 (UTC)

Most of the volume is near the corners

I've see a few places where it has said most of the volume of a n-cube is near the corners. This is by comparison to a n-ball. It might be worth putting in though I had a look and it is more nuanced than that. You might like thislittle proof that most of the volume is not at the corners, though it's not published so you can't put it in!

Consider an n-cube of side 2. Then each corner is an n-cube of side 1 with the centre of the original n-cube at the opposide corner. Then how big an n-cube round the corner would be needed to have proportion P say 9/10 of the whole n-cube? That would have to be of side nth root of P. As n grows P^1/n tends to 1 so practically none of the volume of an n-cube is in its corners! For instance for n-cube shaped corners of a tesseract to contain 9/10 of the total volume they would have to take (9/10)^(1/4)=0.974 of each side and just leav 0.026 wide strips round the centre. Considering the volume isn't in an n-ball round the centre either it seems to just be slipping away in the cracks ;-) NadVolum (talk) 20:57, 16 October 2021 (UTC)

Adding a Parallel projection

I noticed that we have a perspective projection of an n-cube, so I was thinking of adding a parallel (graphical) projection of a 4-cube shown below:

It may be nice to add it under the perspective projection image to help readers have a better visual and mathematical aid of the structure. If no one opposes this I may add it.

Mike1291 22:46, 22 November 2021 (UTC)

15 Jan 2022, Lem Dear Mike (and others?), I am not a polytopist, but have a question. In 4-D, are projections (i.e. 'images' in 3-D ever discussed; the algebra, if not a supposed visualization. (That would be similar to the 2-D projections we can draw of 3-D objects.) If so, has the following version of an all-integer 'Laplace four Square' Equation come up? & For edge E, and the four projections A, B, C, and D: 3*E^2 = A^2 + B^2 + C^2 + D^2. I've obtained several, and used these to construct equations for those five variables using four parameters. Each contains the same square root of the sum of six pairwise products or the four parameters. & For N dimensions, this generalizes to: (N-1)*E^2 = A1^2 + A2^2 + A3^2 + ,,, +[Asub(N-1)]^2 + [Asub(N)]^2. N = n parameters are needed. The n parametric equations each contain n-1 simple terms, plus the SQRT containing nC2 pairwise products. I could add more details if any of this rings a bell for any polytopist out there. Lemchastain (talk) 04:49, 16 January 2022 (UTC)

No idea re the integer equations, but we would need a source to add it to the article.

Incidentally, I undid the addition of the image above, with the edit summary: "This article is already overloaded with images, including at least two parallel projections. Also, I'm unconvinced that this is a correct parallel projection: what is the projection vector and how does it produce that particular combination of edge lengths and angles?" —David Eppstein (talk) 05:39, 16 January 2022 (UTC)

Tesseract

Why is this article different from that of the Tesseract? It feels like roughly the same thing, at least close enough to be merged. Language Boi (talk) 20:33, 22 December 2023 (UTC)

That one is only about four-dimensional things. This one is about the generalization to any number of dimensions. Four dimensions is still low enough that the regular polytopes there are special — in five or more dimensions there are always exactly three regular polytopes (the hypercube being one of them) but just as three dimensions has the five Platonic solids, four dimensions has six regular polytopes. So I think that as part of this set it has enough independent notability as a mathematical topic to justify a separate article from the general hypercube article. And certainly the same is true for the section on cultural uses. —David Eppstein (talk) 20:37, 22 December 2023 (UTC)

Ah, I see. That should probably be clarified at the top of the article though--because I would probably use the two words interchangeably. Whether that's correct or not I don't know, but I know it's common. Language Boi (talk) 21:21, 23 December 2023 (UTC)

You mean like the clarification that already exists in the hatnote at the top of the article? Or the one already in the caption of the figure at the top of the article? —David Eppstein (talk) 22:39, 23 December 2023 (UTC)