Talk:Hill sphere
| This is the talk page for discussing improvements to the Hill sphere article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| This article is rated C-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
Diagram request
[edit]| It is requested that an orbital mechanics diagram or diagrams be included in this article to improve its quality. Specific illustrations, plots or diagrams can be requested at the Graphic Lab. For more information, refer to discussion on this page and/or the listing at Wikipedia:Requested images. |
| It is requested that an astronomy diagram or diagrams be included in this article to improve its quality. Specific illustrations, plots or diagrams can be requested at the Graphic Lab. For more information, refer to discussion on this page and/or the listing at Wikipedia:Requested images. |
I added the image from Lagrangian points article to here aswell, because the plot shows the Hill spheres also. Not sure if a specific diagram would be better. --Petteri Aimonen (talk) 12:06, 29 September 2009 (UTC)
- The diagram is marginally acceptable, as a vaguely schematic representation, although my experience with astronomy students (who MIGHT be a bit more questioning and/or perceptive than the average reader of this article would have them confused or challenging the diagram for showing presumptively spherical shapes while the article rightly mentions the real shape is somewhat conical.
- I find some of the challenges of the article pathetically ignorant, like citation needed for 0.01 AU.
- Comments based on 34 years as Professor of Astronomy, 3 years working on Apollo, much of it on orbits 2603:7000:6A00:32DA:E8ED:D59E:66A1:3B17 (talk) 11:16, 26 September 2023 (UTC)
- You might read WP:VERIFY to see why statements made in Wikipedia should be referenced properly.
- The article states that the "Hill sphere for Earth thus extends out to about 1.5 million km (0.01 AU)"; that statement is tagged {{citation needed}}. Why is that tag pathetic? Where did the information come from? If you are the expert you claim, you should have no problem providing a reliable source to back up the statement; when you have, add it to the article, or give its details here and I'll do it. Bazza (talk) 11:25, 26 September 2023 (UTC)
- What about this: The citation needed that is associated with the statement that a sphere is defined by it's radius:
- "The Hill radius or sphere (the latter defined by the former radius[citation needed])" Dllahr (talk) 11:06, 16 March 2024 (UTC)
Roche lobe
[edit]Most of the sources I can find seem to indicate that the roche lobe and the hill sphere are really the same thing. (the latter being a spherical approximation of the former?). They both have similar definitions and represent the same concept as far as my understanding goes. However the article seems to say that the two must not be confused. Is anyone able to clarify this? 69.157.226.139 16:55, 18 April 2007 (UTC)
- Mathematically, the concepts are related because they're both about gravitational zones of influence. However, in use, those are very different concepts. A Roche lobe is related to binary stars. It's the (pear-shaped) volume that a stellar object (typically a swelling red giant) can occupy before some matter falls down to its binary companion (typically a compact star, such as a white dwarf or a neutron star). In contact binaries, the Roche lobe is actually filled with stellar matter.
On the other hand, the Hill sphere of a planet (or a moon) is an abstract sphere in the planetary system, within which a satellite can safely orbit. 2A01:E34:EF75:CCE0:223:12FF:FE57:5ADD (talk) —Preceding undated comment added 14:02, 28 December 2015 (UTC)
- One needs to think of the restricted three-body problem and everything becomes clear. The Roche lobe is physically defined by a zero-velocity surface, which contains the Lagrange point L1. Therefore, any body of negligible mass (compared to the two massive bodies) orbiting the secondary (i.e., the smaller mass) cannot cross this surface. The Roche lobe properly identifies (in physical terms) the region of space dominated by the secondary's gravity. There is no spherical symmetry in the problem (hence any concept of a sphere, such as the Hill sphere, is an artifact which cannot exist in the physical world). There is though a cylindrical symmetry about the line connecting the two massive bodies: the Roche lobe is symmetric around this line, i.e., it is a solid of revolution. The Hill radius is taken as the distance of the L1 point from the secondary, because beyond this distance a satellite cannot be bound to the secondary (and it does not matter if the secondary is a black hole, a star, a planet, or an asteroid). But the L1 point is also the farthest point of the Roche lobe from the secondary. Therefore, the Hill sphere fully contains the Roche lobe and its volume can be quite larger than the volume of the Roche lobe (which depends on the secondary-to-primary mass ratio and it's all but straightforward to compute!). For example, if the Sun is the primary and Jupiter the secondary, the volume of the Roche lobe is about 0.34 times the volume of the Hill sphere (Eggleton 1983, The Astrophysical Journal, 268, 368)! However, given the complicated nature of the Roche lobe (as a volume), it is often useful to think in terms of the Hill sphere. One should also add that there is a local approximation of the three-body problem (the Hill approximation) in which there is spherical symmetry around the secondary. In this case there is no Roche lobe, but only the Hill sphere. Therefore, the whole concept of the Hill sphere arises from an approximation of the three-body problem. --Messier8 (talk) 22:08, 6 May 2016 (UTC)
Hill sphere of moon
[edit]Does anyone know if the Moon can support a stable orbit? A quick calculation gives it a Hill sphere of ~60,000 km with respect to Earth, and ~350,000 km with respect to the Sun, however it's not really a 3-body but a 4-body problem in this case. Deuar 21:53, 9 June 2006 (UTC)
- As long as the Hill sphere for the Moon considered in terms of its orbit about Earth lies entirely well inside the Earth's Hill sphere (about Sun), I would suppose the Sun's influence on orbits about the Moon can be ignored, getting you back to a 3-body situation. Your numbers together with those in the article would seem to say this is indeed the case, with ample margin - so no problem :-) -- Eddy 84.215.214.94 (talk) — Preceding undated comment added 14:16, 6 October 2014 (UTC)
Comments, verification
[edit]Article states "It is also called the Roche sphere because the French astronomer Édouard Roche independently described it." My information points to Roche describing it mathematically and the concept merely being borrowed intellectually for the specific purposes intended by Hill, in which event it may indeed be called a Hill sphere or a Roche sphere, but it was not "independently described" by Roche - it was more a "child" of his work. Please let's discuss!
24.215.19.163 11:22, 18 December 2006 (UTC)
- Yeah, Roche Sphere redirects to Hill Sphere, but then Hill Sphere says:
- It is sometimes confused with other models of gravitational influence, such as the Laplace sphere or being called the Roche sphere, the latter causing confusion with the Roche limit. It was defined by the American astronomer George William Hill, based on the work of the French astronomer Édouard Roche.[not verified in body]
- So
- is Roche Sphere the same as Hill Sphere? If so, the intro should say so.
- Or, maybe, there is no Roche Sphere concept, but people keep confusing it with Roche Limit and Roche Lobe? If so, please say so.
- Or, maybe there is a Roche Sphere concept, different from Hill Sphere, but that article got lost in the confusion? Not sure if such a thing can be retrieved.
- Here's some more info: astronomy.stackexchange
- --OsamaBinLogin (talk) 21:54, 4 August 2024 (UTC)
Hill sphere and Distance a (part 1)
[edit]In using the Semi-Major Axis in the formula, a literal interpretation would mean distance to the barycenter (shared by the two bodies), not the distance between the actual bodies themselves. Does the author mean the distance to the barycenter (which could be many km outside the larger body)? Or, does the author mean the distance between the two bodies (center to center)? I assume that it is the latter (since the barycenter is the result of the shared orbits). Tesseract501 10:48, 24 February 2007 (UTC)
- Well I'm not the author, but I would surmise that the shortest distance between the large and smaller body is most critical. The moment of closest approach is the time when the third orbiting body is most perturbed. Of course since the large body in question is usually the Sun, the difference is insignificant anyway. Especially since we have a ≈ in the formula, indicating that the true practical distance at which bodies orbiting the smaller mass may begin to be lost differs by many percent with respect to the value obtained from the formula. So, the details of whether it's distance to the barycenter or what is lost anyway in general slop and uncertainty. Deuar 14:58, 26 February 2007 (UTC)
- The relevance of the semi-major axis is just that it's what Kepler's law cubes to get an answer proportional to the square of orbital period. When you do the derivation of the standard two-body bound orbit in an inverse square central force system, you get an ellipse whose (semi-) major axis turns out to be the decisive geometric parameter (regardless of minor axis) for period and total energy. The derivation section seems to think the periods of orbits matter; these are obtained from √(m/a3) with the semi-major axis as a. However, note that the article starts with a formula in a.(1−e); this is, in fact, the distance of closest approach between primary and secondary. The article might be improved by mentioning that – if you can find a suitable reference to cite for it ! -- Eddy. 84.215.40.194 (talk) 14:42, 6 October 2014 (UTC)
Hill sphere and Distance a (part 2)
[edit]Another queston: The formula in this article indicates the value for "a" as the Semi-major Axis. I've seen other sites use the distance of closest approach (Periapsis) in the assumption that the Hill Sphere size changes based on the distance of the two objects. Which is correct? The formula on this page incorporates the eccentricity of the orbit. Does that support using the SMA? What if the eccentricity is high and the smaller, comet-like object is much closer at Periapsis than at Apapsis? If the Hill Sphere does, in fact, shrink at Periapsis, using the SMA in the formula may show a Hill Sphere that is too large to accommodate stable orbits at closest approach. Tesseract501 10:52, 24 February 2007 (UTC)
- The formula with the eccentricity is the correct one. Since the loss process involves an acumulation of small kicks at each orbit, it is useless to talk about the Hill sphere changing with location in the orbit. If the body is too far out at any time at all, it will eventually be lost after making enough orbits. This is why the moment when perturbations are strongest (perihelion) is the relevant time at which to calculate the Hill radius. Deuar 14:58, 26 February 2007 (UTC)
- Semi-major axis scaled by 1−e, as used in this page's formula, is the radius of closest approach, as mentioned in the other article you refer to; so this page is just saying the same thing as the other, phrased differently. -- Eddy. 84.215.40.194 (talk) 14:50, 6 October 2014 (UTC)
Hill sphere and Distance a (part 3)
[edit]One last question, regarding the reference to the moon having to be LESS THAN 7 months within the Hill Sphere. That sentence seems to pop out with no explanation as to what or why (then again, it may be ignorance). Does the sentence tie in to the use of SMA (instead of using the distance of closest approach)? To me the sentence implies a safety period for a stable orbit that is temporarily outside of the Hill Sphere? If necessary, may someone clarify the meaning of the 7-month statement? Tesseract501 10:58, 24 February 2007 (UTC)
- This seems to be just someone's way to phrase the fact that all stable orbits around the Earth must have an orbital period of 7 months or less. It does not refer to orbits around any other object. Should be rephrased since it's evidently causing confusion. Deuar 14:58, 26 February 2007 (UTC)
- Finally getting back to you. Thanks for all the feedback. You (Deuar) are one of the most helpful folks in Wikipedia-space ... in my fuzzy opinion at least. Your input on talk pages is consistently clear, respectuful, and to the point. I fail that test, especially the last part. I had great fun with the Hill Sphere logic, after I got my head around it. That, along with the logic for orbital mechanics, L-points, and a bunch of other suprise rules that crepted (or screamed) up ... I've designed (in data tables that is) a funny little system made up of three planets (well four, since one is its own sub-binary), and a mass of shared and unshared satellites. 32 co-orbiting bodies together (not to mention the system being part of a tri-star binary system as well. The whole thing in a highly improbable, but with equal parts of imaginative and insanity. All the 32 bodies ultimately share the same principle barycenter. So, its like rush-hour traffic, along 3 axes. In theory at least, the whole dance should hold together. I guess I have too much time on my hands! Wish I could put it in software and see it in action. I did it all in boring data-tables. Tesseract501 (talk) 02:02, 9 March 2009 (UTC)
I too found this remark confusing as it seems to come out of nowhere with no explanation. I've tagged it "vague" for now but would appreciate an explanation or removal for clarity. MikeEagling (talk) 10:55, 28 March 2010 (UTC)
Derivation
[edit]In the section on derivation, the derived formula has a "3" missing, when compared with the formula quoted at the start of the article (and in many other sources). I can't see how the derivation argument can be modified to produce the "3", so am doubting the validity of the derivation. There at least needs to be some explanation of why the "3" is missing.
87.127.140.166 (talk) 18:50, 14 April 2010 (UTC)
- Indeed, I noticed the same lack. The discrepancy is surely due to the crudeness of the rule of thumb that asks for equal angular speeds to mean equal tendencies to effect the body. This rule of thumb could also do with some justification. The primary's tidal influence on an orbit about the secondary tends to lengthen it along the primary-secondary axis and shrink it perpendicular to this, I would suppose; if the period of the orbit about the secondary is much shorter than the secondary's period of orbit around the primary, variation in the primary-secondary direction shall cause this influence to average itself away; but, as the two periods get close to equal, the potential for a resonance arises. Even when the orbit's period is a bit shorter than that of primary about secondary, the beginnings of such a resonance could make the orbit unstable; but I cannot immediately think of a reason why the critical ratio of periods would be √3 (leading to a factor of 3 on mass or its cube root for radii). Some relevant literature is needed ! It also strikes me that the tidal effects themselves are also m/r3, just like the squared angular speeds; in particular, they have different sign radially (tension) as compared to (compression) tangentially and axially; IIRC, the directions also have different strengths, which might be relevant to where our factor of three comes from. The derivation section would be greatly improved by adding at least some justification for the existing "rough equality of periods" formula (e.g. "tidal resonances make an orbits about the secondary unstable if its period is close to that of the secondary about the primary"), preferably with at least some attempt at a rationale for the √3 ratio of periods. Alternatively, the "derivation" could be so phrased as to make clear that it's only attempting to get the power law for relevant masses and radii. -- Eddy 84.215.214.94 (talk) 14:06, 6 October 2014 (UTC)
SoI (astrodynamics)
[edit]On the Talk:Sphere of influence (astrodynamics) page back in April of 2009, an editor raised the question about the similarity between the Hill sphere and the SoI (astrodynamics) pages. Are these candidates for a merge?
— Paine (Ellsworth's Climax) 17:00, 19 June 2010 (UTC)
No. After looking more closely at the two articles, I see differences between the Hill sphere and the SoI, so I no longer see the need to merge the two articles. There does seem to be an anomaly, though. (more to come)
— Paine (Ellsworth's Climax) 22:52, 25 June 2010 (UTC)
The Hill sphere for Earth, as given in this article, has radius of 1.5 million km, which is about 932,000 miles. This article also states that it appears that stable satellite orbits exist only inside 1/2 to 1/3 of the Hill radius. The other article on the SoI gives a radius value of 925,000 km, which is about 575,000 miles, or about 62% of the radius of the Hill sphere. So:
- Hill radius = 1,500,000 km or 932,000 miles
- SoI radius = 925,000 km or 575,000 miles
Now comes the truly interesting part. Editors please note the derivation from the SoI article:
- The general equation describing the radius of the sphere of a planet:
- where
- is the semimajor axis of the planet's orbit relative to the largest body in the system, usually the Sun
- and are the masses of the planet and Sun, respectively.
And now, please note the derivation from this, the Hill sphere article:
Now, I'm no math wizard, yet it seems to me that these formulas tell us that the SoI radius is greater than the Hill radius for any given mass relationship. Am I missing something? Isn't the SoI supposed to be smaller than the Hill sphere?
— Paine (Ellsworth's Climax) 04:52, 5 July 2010 (UTC)
- Read the derivation again. The article derives the Hill Sphere as approximately
- The Sphere of Influence (aka the Laplace Sphere) on the other hand does not have that factor of 1/3:
- This means that a smaller body must be less than 1/243 of the mass of the central body for the Hill Sphere to be larger than the Laplace Sphere. As the Moon is about 1/81 of the mass of the Earth, this means that the Moon's Sphere of Influence is larger than is its Hill Sphere. 2601:2C4:C400:5730:3DE7:8347:70A3:8FCD (talk) 15:03, 19 November 2023 (UTC)
Guys the reason why the two are so similar is because they're identical. The SOI is just another name for the Hill Sphere or even the Laplace Sphere. And the article actually derives the Laplace Sphere NOT the Hill Sphere, which is a 0.4 power of the ratio of the masses, not the 1/3 power referenced. I just need to track down an actual proper reference before I can do a proper edit.
—Qraal (talk) 11:41, 2 September 2010 (UTC)
- They are not identical. Note the power of 2/5 versus the power of 1/3. 2601:2C4:C400:5730:3DE7:8347:70A3:8FCD (talk) 15:04, 19 November 2023 (UTC)
Why isn't Roche mentioned in the first para?
[edit]For Pete's sake! A common alternate name is usually incorporated into the first paragraph, in brackets, along the lines of (also known as a Roche Sphere). What's going on here? The first mention of Roche isn't until the middle of para 2. It feels as if a particularly pedantic editor has been at work. Blitterbug (talk) 07:41, 2 April 2011 (UTC)
- Perhaps it's because the necessary parenthesis "not to be confused with the Roche limit" seems too 'heavy' for the lede. —Tamfang (talk) 00:28, 3 April 2011 (UTC)
Tidal forces
[edit]Why "tidal forces" are mentioned in the 2nd paragraph? May be I'm wrong, but IMHO tidal forces don't influence at all the described process. These are pure, simple gravitational forces, that rule the process, as long as we consider "a[ny] third object", regardless of its size.
Oh.... it seems that I've realized. The article considers tidal forces influencing not the third object alone, but the system "second object - third object". That's correct. — Preceding unsigned comment added by 213.87.192.62 (talk) 13:13, 12 September 2011 (UTC)
Further Examples confusion
[edit]"An astronaut could not orbit the Space Shuttle (with mass of 104 tonnes), where the orbit is 300 km above the Earth, since the Hill sphere of the shuttle is only 120 cm in radius, much smaller than the shuttle itself. In fact, in any low Earth orbit, a spherical body must be 800 times denser than lead in order to fit inside its own Hill sphere, or else it will be incapable of supporting an orbit. A spherical geostationary satellite would need to be more than 5 times denser than lead to support satellites of its own; such a satellite would be 2.5 times denser than osmium, the densest naturally-occurring material on Earth. Only at twice the geostationary distance could a lead sphere possibly support its own satellite; since the moon is more than three times further than the 3-fold geostationary distance necessary, lunar orbits are possible."
The space shuttle example makes sense: (radius of earth + 300 km) * ((104000 kg)/(3 * mass of earth))^(1/3) = 1.2 meters (paste the LHS into google to evaluate). But I don't buy the latter examples, perhaps I'm doing something wrong? e.g. a 10cm radius sphere merely twice as dense as lead in LEO: (radius of earth + 300 km) * ((4/3 * pi * (10 cm)^3 * 22 g/cm^3)/(3 * mass of earth))^(1/3) = 11.5 cm, outside its own radius. Or a lead sphere in GEO, with an Hill sphere around 50cm radius.
I don't understand the original page as written. Is the author referring to "a spherical body of the same mass as a space shuttle" throughout, or is the mass that is being used at the geostationary orbit that of the space station? PhysicistQuery (talk) 22:27, 30 November 2016 (UTC)
Solar Hill sphere?
[edit]- I am wondering what size is the solar hill sphere to the Milky Way? Reddwarf2956 (talk) 15:37, 22 April 2012 (UTC)
- The page for astronomical unit lists it as 230,000 AU. Nikki (talk) 23:27, 5 June 2012 (UTC)
I calculated it myself as ~266,000 AU using 26,000 ly as the Solar mean orbital radius and 237.5 Ma (mean value of 225-250 Ma) as the Solar orbital period:
- c = 299,792,458 m/s
- G = 6.67384 × 10−11 m3/kg/s2
- 1 d = 86,400 s
- 1 a = 365.25 d
- 1 ly = c(1 a)
- m⊙ = 1.98892 × 1030 kg
- rμ⊙ = 26,000 ly
- P⊙ = ½(225 + 250) Ma ≈ 238 Ma
- vμ⊙ = 2πrμ⊙/P⊙ = √(GM2/(rμ⊙[M + m⊙])) ≈ 206 km/s
- M = 2π(2πrμ⊙3 + √(Gm⊙P⊙2rμ⊙3 + π2rμ⊙6))/(GP⊙2) ≈ 7.88 × 1010 m⊙
- rH⊙ = rμ⊙∛(m⊙/(3M)) ≈ 3.978 × 1016 m ≈ 265,900 AU ≈ 4.205 ly
This is very close to the orbit of Proxima Centauri (Alpha Centauri C at 4.243 ly from Sol) around Alpha Centauri AB (at 4.366 ly from Sol). More likely the practical Hill radius for Sol corresponds the maximum extent of the Oort Cloud (at ~100,000 AU or ~1.58 ly).
Using instead an instantaneous orbital speed of 251 km/s and a corresponding orbital radius of 27,000 ly yields a central mass equivalent of 1.21 × 1011 m⊙ and a more reasonable Solar Hill radius of ~3.78 ly (~239,000 AU), which is likely the rounded value given on the astronomical unit page.
Nikki (talk) 02:00, 6 June 2012 (UTC)
- Should the comments in this section be brought to the main page? Reddwarf2956 (talk) 15:56, 17 August 2012 (UTC)
- Yes, they should be. The article is misleading because it right away mentions the Sun's Hill sphere, but doesn't tell us how big it is. Instead it footnotes to a Russian article from 1964 which is clearly wrong, since it gives a size of 230,000 AU, an impossible number, since it would mean that an object that far away (which would bump into the Alpha Centauri system, which has twice the Sun's mass) is still bound to the Sun. 47.20.120.205 (talk) 15:16, 29 December 2014 (UTC)captcrisis
- The Russian article is not "clearly wrong". Hill spheres are described here as approximations, and needn't take into account other bodies like Alpha Centauri. Furthermore, other stars don't stay nearby long compared to the orbital period of a comet that far away from us. It is correct that the influence of passing starts means that the orbits of distant comets are more unstable over the long term. But these more detailed analyses are not appropriate for this page. ★NealMcB★ (talk) 17:49, 20 October 2019 (UTC)
- Yes, it is indeed "clearly wrong". Hill spheres are *defined* according to the effect of other bodies, and how far or near they are, and how massive. For example, the article points out that an object in Low Earth Orbit would need to be denser than lead in order to fit inside its own Hill sphere. That's because of the much greater mass of the nearby Earth. The Sun's Hill sphere depends on the stars around it. If there were no stars within 100 light years, it would be a lot bigger than it is. 68.196.7.190 (talk) 20:05, 20 July 2024 (UTC)captcrisis
- The Russian article is not "clearly wrong". Hill spheres are described here as approximations, and needn't take into account other bodies like Alpha Centauri. Furthermore, other stars don't stay nearby long compared to the orbital period of a comet that far away from us. It is correct that the influence of passing starts means that the orbits of distant comets are more unstable over the long term. But these more detailed analyses are not appropriate for this page. ★NealMcB★ (talk) 17:49, 20 October 2019 (UTC)
Wouldn't the Alpha Centauri system's Hill sphere interact and shape that side of the Solar Hill sphere? Could the proximity of the Solar and Alpha Centauri systems be a grand binary galactic formation (sorry I don't know what to call it,) creating an even larger Hill sphere? --CrownPaisley (talk) 14:00, 16 April 2016 (UTC)
Derivation
[edit]The "derivation" section isn't very satisfying and I suggest removing it, since it doesn't even result in the right answer. (Misses by a factor of 3). It also seems conceptually challenged, since the orbital speed is sqrt(GM/a), not sqrt(GM/a^3).
I'd rewrite this myself, but it looks like a rigorous derivation is pretty complicated. Anyhow, suggest removing this unless it can be corrected. — Preceding unsigned comment added by 138.110.75.55 (talk) 18:21, 24 January 2013 (UTC)
- See also: previous Derivation section of this Talk page (in which I hand-wave some justifications that might improve the Derivation section, if you can find a reference) and the discussion of the SoI radius (with a 0.4 power instead of a 1/3 power), where someone seems to be claiming there's more to be said here. -- Eddy. 84.215.40.194 (talk) 15:24, 6 October 2014 (UTC)
Sphere of influence
[edit]What is the difference with Sphere of influence (astrodynamics) ?--Io Herodotus (talk) 20:09, 24 August 2014 (UTC)
- We need a source asserting this, but my understanding is that one term is most properly used when asking if an apparently-orbiting body (e.g. a spacecraft) is truly "captured" into a stable orbit; the other term is used most properly when asking where to "patch" together trajectory segments in a "patched conic" trajectory approximation. If someone can find a source that says that, including it in both articles would greatly improve each! (sdsds - talk) 01:34, 25 August 2014 (UTC)
- This conversation started a long time ago, see above "SoI (astrodynamics)"; and nobody gave a clear answer.--Io Herodotus (talk) 12:22, 28 August 2014 (UTC)
- Yes, orbits within the Hill sphere are guaranteed to at least be quasi-stable for an orbit or two. If they're only within the sphere of influence, they're not guaranteed to be, and in fact are not usually going to be stable relative to the primary body, although some may be if there's a resonance or something.GliderMaven (talk) 16:54, 28 August 2014 (UTC)
- The Hill sphere is larger than the sphere of influence.--Io Herodotus (talk) 19:47, 28 August 2014 (UTC)
- Yes, orbits within the Hill sphere are guaranteed to at least be quasi-stable for an orbit or two. If they're only within the sphere of influence, they're not guaranteed to be, and in fact are not usually going to be stable relative to the primary body, although some may be if there's a resonance or something.GliderMaven (talk) 16:54, 28 August 2014 (UTC)
- I found a qualitative explanation about how the two are different that I think is quite clear and concise on StackExchange. I also found a print reference about the two in Google Books:
- "Let denote the distance between and ; let and denote the masses of and . Then the Hill Sphere of in presence of is an approximation to the gravitational sphere of influence of in the face of perturbation from . Its radius is about "[1]
- The Hill sphere is larger than the Sphere of Influence as long as the larger body is more than 243 times the mass of the smaller body. WolframAlpha solution for Hill sphere < SOI. For eccentricity I used , since WA really wanted the variable e to be the constant . Note the first solution has an imaginary component, and so is meaningless. TruthusFactus (talk) 06:51, 17 August 2019 (UTC)
- I found a qualitative explanation about how the two are different that I think is quite clear and concise on StackExchange. I also found a print reference about the two in Google Books:
References
- ^ Deza, Michael Marie; Deza, Elena (May 28, 2009). Encyclopedia of Distances. Springer Science & Business Media. p. 460. ISBN 978-3-642-00234-2.
3rd paragraph of OP is confusing
[edit]"In the example to the right, the Hill sphere (of the Earth?) extends between the (Earth's) Lagrangian points L1 and L2, which lie along the line of centers of the two bodies. The region of influence of the second body is shortest in that direction, and so it acts as the limiting factor for the size of the Hill sphere. (tautology?) Beyond that distance, a third object in orbit around the second (e.g. Jupiter) (What?! Jupiter in orbit around the Earth?!) would spend at least part of its orbit outside the (Earth's?) Hill sphere, and would be progressively perturbed by the tidal forces of the central body (e.g. the Sun), (the Sun isn't just an example of something that the Earth might orbit!) eventually ending up orbiting the latter." ..Clear as mud, right? So are we talking about 2 imaginary bodies, perhaps with a 3rd thrown in, or are we discussing the actual Sun and Earth? And what's up with Jupiter?! Please make this clearer. Thanks. nagualdesign 19:03, 9 September 2014 (UTC)
- The paragraph you're criticising doesn't suggest the secondary body is the Earth; you jumped to that conclusion for yourself (possibly thanks to an earlier paragraph mentioning Earth as an example); without it, you'd have saved yourself most of your confusion. It's describing a general system and only makes (parenthetical) reference to one example; it could, perhaps, make it clearer that this has the Sun in the centre, Jupiter as the secondary body (on the right of the diagram, with its Lagrange points marked), while considering stability of orbits about Jupiter (e.g. by its moons). Aside from that, your comment suggesting a tautology relates to an attempt to give the reader a rough outline of how L1 and L2 provide a bound on the Hill sphere. It's possible the whole paragraph could be significantly improved by developing a better diagram, specific to this page (if you look above, you'll see the present diagram is borrowed off the page on Lagrange points as a temporary measure by someone advocating an improvement on this), for it to refer to. -- Eddy. 84.215.40.194 (talk) 15:41, 6 October 2014 (UTC)
I too was confused by paragraph 3 and went to this talk page for help. In this discussion Nagualdesign was questioning whether the body between L1 and L2 was the earth, Eddy states that it is not the earth. But now (August 10, 2018) the paragraph reads "In the example to the right, Earth's Hill sphere extends between the Lagragian points L1 and L2.." implying that it is the Earth. I am not a scientist, so I do not know which is correct, but I do think the paragraph is confusing. Thank you. DavidRBarker (talk) 19:32, 10 August 2018 (UTC)
The current version of this paragraph is somewhat clearer, but I still have trouble understanding the "extends between the Lagrangian points L1 and L2" part. If we let:
r denote the radius of the smaller body's Hill sphere.
d1 be the distance between the smaller body and L1
d2 be the distance between the smaller body and L2 (with d1 and d2 approximately but not exactly equal, I understand d2 is the greater?)
then I can't tell if the article is saying:
r < min(d1, d2)
r <= min(d1, d2)
r < max(d1, d2)
r <= max(d1, d2)
d1 < r < d2
d1 <= r <= d2
or something else? AstridRedfern (talk) 19:26, 27 December 2019 (UTC)
Calculations
[edit]Are the calculations correct? The article states
"In fact, in any low Earth orbit, a spherical body must be 800 times denser than lead in order to fit inside its own Hill sphere, or else it will be incapable of supporting an orbit. A spherical geostationary satellite would need to be more than five times denser than lead to support satellites of its own; such a satellite would be 2.5 times denser than osmium, the densest naturally-occurring material on Earth. Only at twice the geostationary distance could a lead sphere possibly support its own satellite; since the Moon is at more than ten times the geostationary distance, lunar orbits are possible."
From the equation given in the article:
3 r^3/a^3 = m / M
where r is the Hill radius, a is the distance from the center of mass of the large object, m is the mass of the small object, and M is the mass of the large object. Noting that density, ρ = m/V and that for a sphere, ρ = 3m / (4π r^3), => m = 4/3 π r^3 * ρ we have
3 r^3 / a^3 = 4/3 π r^3 ρ / M
a = (9 M / (4 π ρ) )^1/3
Solving for osmium, with a density of 22588 kg/m^3, you get 5751 km, less that the radius of the Earth (which means an Osmium sphere at the Earth's surface should exert a Hill sphere beyond its radius and that you'd have to solve the Gaussian sub-volume of the Earth to get an accurate number for when the Hill sphere of the osmium sphere developed its own Hill sphere). The article states a geostationary orbit (35,786 km from the surface or 42,157 from the center) would need an object with 2.5 times the density of osmium. Did I screw up the calculation or is this section wrong?--Burzum (talk) 23:05, 16 November 2014 (UTC)
Additionally, the second derivation is different from the first by a factor of 3. For the calculations above this has no real significance except to reduce the Hill sphere by a factor of 1.44. But the article doesn't even discuss this discrepancy.--Burzum (talk) 23:12, 16 November 2014 (UTC)
Circular citations
[edit]I find it odd that this article references a blog post at all, but even more strange is that the blog post also links back to this Wikipedia page!
Wouldn't a site that cites Wikipedia not be scholarly enough for Wikipedia to cite? -- עבד יהוה talk 00:06, 14 August 2017 (UTC)
explanation needed
[edit]Someone has to tell what the red and blue triangles are in the picture. I don't even know [anon]
- The caption used at Lagrangian_point#Mathematical_details includes "The arrows indicate the gradients of the potential around the five Lagrange points—downhill toward them (red) or away from them (blue). " - Rod57 (talk) 23:12, 12 February 2018 (UTC)
Request: solar & stellar Hill spheres
[edit]I would appreciate discussion in the article of the solar Hill sphere and the Hill spheres of nearby stars such as alpha Centauri A, Barnard's star, etc. How large are they? Do they interact? Can objects from one sphere migrate into another sphere? Can stellar wind play a part in pushing an object from one sphere into another?
Thank you, ELSRG (talk) 01:26, 19 January 2018 (UTC)
The figure showing the Lagrnge points is not labeled and has the wrong scale for Earth as the secondary body
[edit]The scale in the figure showing the Lagrange points is exaggerated by using a small mass ratio between the primary and secondary bodies. The actual distance to the Sun-Earth L1 and L2 Lagrange points is about 0.01 AU which would make it hard to see the hill sphere on the scale of a diagram that also shows the Sun and the L3, L4 and L5 points.
The reference later in the same paragraph to "a third object in orbit around the second (e.g. a satellite of Jupiter)" instead of the Moon which is a satellite of Earth is confusing and makes the paragraph unreadable.
A discussion of the Artemis and WIND spacecraft orbits which move in and out of the Moon's Hill sphere would make better examples especially since the Earth Moon Lagrange points are about 1/6 of the distance from the Earth to the moon which means there is no need to use an exaggerated figure. — Preceding unsigned comment added by Annette Maon (talk • contribs) 17:30, 29 July 2018 (UTC)
Confusion Attempting to Reconcile Paragraphs 1, 3 and the Lagrangian Plot
[edit]I came to this page to understand more about the concept of a Hill sphere, but became confused about what I think is a pretty simple concept. I believe there are a handful of interrelated mismatches and "disclarities" between paragraphs 1 and 3, the contour plot, and its caption.
Are Hill Spheres Actually Spherical?
[edit]In paragraph 1, the first two sentences read
- The Hill sphere of an astronomical body is the region in which it dominates the attraction of satellites. The outer shell of that region constitutes a zero-velocity surface.
Clicking on the zero-velocity surface link shows a Jacobi constant, zero velocity surface, which looks a lot like an alternate visualization of the contour plot, but is a complex surface that is definitely not a sphere, although it contains some parts that look (incompletely) spherical. This is confusing. Is it right to call the latter a "Hill surface?"
-
A contour plot of the effective potential of a two-body system due to gravity and inertia at one point in time. The Hill spheres are the circular regions surrounding the two large masses.
-
Jacobi Constant, Zero Velocity Surface and Curve
The Earth's Hill Sphere Doesn't Appear in the Diagram
[edit]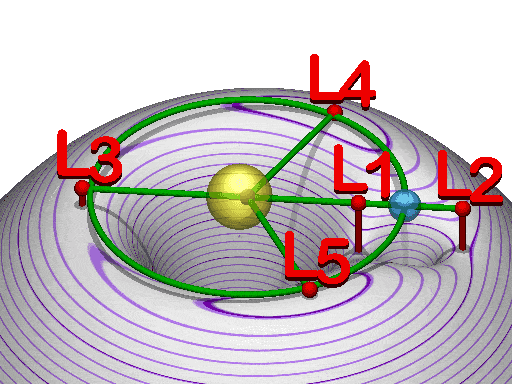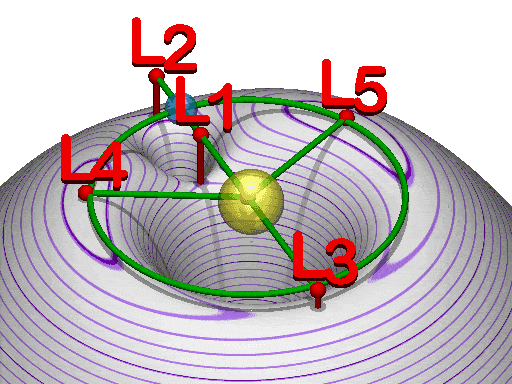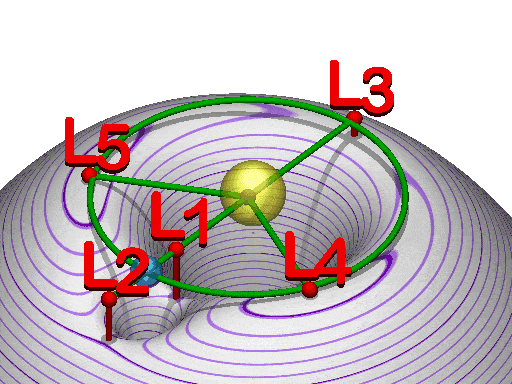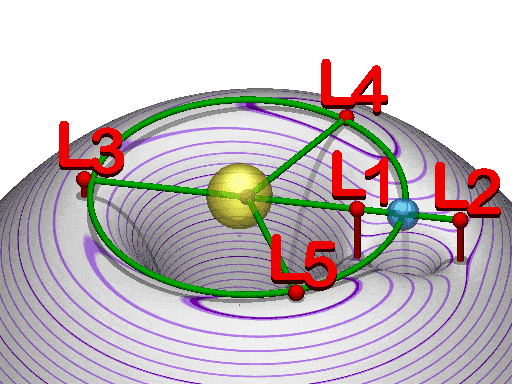
In paragraph 3, the statement
- In the example to the right, Earth's Hill sphere extends between the Lagrangian points L1 and L2, which lie along the line of centers of the two bodies.
is difficult to correlate with the diagram. There is no circle passing through both L1 and L2, but that's what I expect from the text. Additionally, when I look at the animation to the right (which I found on the Lagrangian page where the contour plot originated), that's what I expect too. Instead, the contour plot has an orange circle that passes through L2 and encompasses L1, L3, L4 and L5 inside it, with parts of the circle clipped out of the diagram. I thought at first maybe it was supposed to be a Hill sphere for the entire system, but... I don't know what it is. I went to the Lagrangian point page where Petteri Aimonen got the image, but it doesn't say there either.
Contour Plot Caption Is Too Busy, Caption Confusing and Incomplete
[edit]The caption for the contour plot says,
- The Hill spheres are the circular regions surrounding the two large masses.
There are a lot of circles in this diagram, and I don't know if any of them are actually Hill spheres, and if so, which ones. None of the colored circles are; the blue one is Earth's orbit around the sun, the red one the moon's orbit around the earth and the orange one is... what? There are multiple white ones but those are gravitational(?) effective equipotential bands. It can't be the innermost ones, since the Earth is outside the five innermost ones of the Sun, and the moon is outside the innermost one of the Earth. And based on the first line in the article, I believe I'm looking for a bounding sphere, or circle in this case, for each mass that encompasses all the volume/area of the mass' orbital capture distance. Maybe the outermost circles? But in the case of the Sun, they are mostly outside the diagram, and in the case of the Earth, there is no circle through L1 and L2. Maybe the orange circle represents the Hill sphere for the combined two body system, but the caption says circular regions are, plural, and again part of the circle is clipped, so it doesn't seem like it is the focus of the diagram.
Also, I was able to deduce the meaning of the red and blue triangles based on what I already knew about Lagrangian points, but I was surprised neither they nor the Lagrangian points were called out in the caption.
Suggestions
[edit]- I came away from the article not knowing if a Hill sphere is actually a sphere. Between Para 1 sentences 1 & 2, and the similarity between zero-velocity surface and the contour diagram, I don't even know if they are closed surfaces. I think this should be clarified in the first two sentences: whether a Hill sphere is actually a sphere, something quasi-spherical like an ellipsoid or an oblate spheroid, or something else, and whether it is open or closed. Based on other reading, I believe it is a sphere, because it is an approximation model, so it is a sphere by definition.
- The contour plot should either be replaced by a specific diagram or modified to more clearly show the Hill spheres. What I expect to see is something like this:
- An circle around Earth, passing through L1 and L2, representing its Hill sphere
- An circle around the Sun, passing through L1 and L3 (is this right?) representing its Hill sphere
- An circle around the three bodies representing the Hill sphere for the three-body system as a whole
- However, I don't know if all that that is correct, or if the last one is even meaningful.
- In any case the items in the diagram should be explained in the caption.
TruthusFactus (talk) 23:45, 16 August 2019 (UTC)
Problems in the lead
[edit]Moving out of the lead a long comment, written by somebody else in July 2023:
the lead:
- repeatedly introduces concepts not developed and cited in the main body, in violation of WP:INTRO
- introduces what appear to be original Jacobi integral interpretations unsupported by citations, in violation of WP:OR
- jumps too quickly to the complex (i.e., to 3-body, Lagrange-requiring) case, before defining basic concepts from reliable secondary and tertiary sources, required if wikilinks for "gravity well" and related concepts continue to direct here

















![{\displaystyle d(m,M){\sqrt[{3}]{\frac {S_{m}}{3S_{M}}}}.}](https://wikimedia.riteme.site/api/rest_v1/media/math/render/svg/64be49832ec3fc3e797b0b1e3f894c9fbf71c0f3)



