Talk:Coriolis force/Archive 7

Archive 1

←

Archive 5

Archive 6

Archive 7

Expect that this point is made above but I am too lazy to read all the way through it.

So I am making the point briefly in its own section. I am not at all happy to accept that either the Coriolis force or the centrifugal force is a non-force. I write as an engineer who must consider real forces, such as those which might result in the bursting of a rotating machine, or which might stress the casing of a centrifugal pump, but who may happily and safely ignore anything which does not exist, or which may exist in only a metaphysical sense. If a force is of significance in a practical case, then it must be defined in such a way that its reality is properly acknowledged. It makes no sense to me to define a force, and then say it is a non-force, or, as in the preceding section, to speak of a force when the observed motion depends precisely on the absence of any such force, and is properly described strictly in accordance with Newton's first law (unaccelerated motion in a straight line relative to an inertial frame).

Here is a better approach to the C force which acknowledges it in cases where it exists, and excludes it where it does not: The Coriolis force is the force required to constrain a moving mass to move in a straight line relative to a rotating frame of reference. For example, if a body is constrained to move radially on a rotating turntable, a lateral (tangential) force must be applied. Convention might require that we say that the C force is actually the reaction to the force so defined - others others can argue about that. If a moving body is not so constrained (as in the case of clouds moving in a cyclone), it is obvious and pleonastic to say that no lateral force exists (the motion is unconstrained). The observed lateral acceleration must then be explained without recourse to a force which simultaneously exists and does not exist. Such an explanation can be given by deducing that the observed motion (i.e. acceleration without a force) is observed with respect to a rotating frame, and then applying Newton's first law.

Similarly we can define a real centripetal force as a force required to constrain a mass to move in a circular path, and the centrifugal force is then the reaction to the centripetal force. Such a reaction is experienced by our bodies while in a cornering car. 1 Oct 2015

I have returned to this after having read some more of the contributions above, but still find I have not sufficient energy to give the entire discussion proper critical consideration. I will add two further points however. (1) Many internet sources discuss the "Coriolis Effect" (this is also the title of the present article), which avoids the problem of a force which does not exist, and merely seeks to explain the movement of, for example weather features, in terms of the rotation of the earth. This is commendable, and raises no objections. (2) The question of whether the Coriolis "force" exists is entirely a matter of giving precedence to either a rotating frame, or an inertial frame. In the first case it is a real force (from that point of view), in the 2nd case it does not exist (from that point of view). Thus it appears that those who write of it as a non-force are making an implicit and unstated assumption about their preferred frame of reference. However, the choice of the point of view that gives the C force reality must be seen as unsatisfactory, since there is no way of measuring such a force, and its existence must remain mystifying and metaphysical. Better to say plainly that it does not exist (and therefore need not be discussed) unless, that is, it is defined in the way I have suggested above (constrained radial motion on a rotating system). g4oep

You are probably wrong but I am too lazy to read all that you have written. Martin Hogbin (talk)

@77.96.58.212: Regardless of your personal anecdotes and opinions, the current article sticks pretty close to reliable sources. Either indicate where you feel reliable sources are being represented improperly or poorly, or provide other reliable source not currently represented in the article. Otherwise, whether correctly or incorrectly, you're likely to be ignored for pushing fringe viewpoints. --FyzixFighter (talk) 06:52, 3 November 2015 (UTC)

lol.. i would expect that the view that something that does not exist need not be discussed would warrant a more serious comment. Would you like to take it as a challenge  ? where is my 'anecdote'. Have you a comment on my suggestion that the C force should be more satisfactorily defined as a real force which can be measured using conventional force-measuring equipment, and that a non-force definition or usage of it is objectionable as mystification ? g4oep — Preceding unsigned comment added by 77.96.58.212 (talk) 09:10, 3 November 2015 (UTC)

The article already says, 'The Coriolis effect exists only when one uses a rotating reference frame. In the rotating frame it behaves exactly like a real force (that is to say, it causes acceleration and has real effects). However, the Coriolis force is a consequence of inertia,[12] and is not attributable to an identifiable originating body, as is the case for electromagnetic or nuclear forces, for example'. If you do not understand what this means you can ask on my talk page. Martin Hogbin (talk) 17:38, 3 November 2015 (UTC)

Ok- I can see that the alternative definition I am referring to is unfamiliar to some. I have added a short paragraph which supports the definition with a diagram. The text I have added is almost verbatim from the sources I refer to. Someone deleted this without giving a reason, but it seems to me that the references are impeccable, and that what I have written is an established alternative definition of the C force & acceleration. Please do not delete it again without good reason. g4oep — Preceding unsigned comment added by Andrewg4oep (talk • contribs) 14:14, 8 November 2015 (UTC)

Actually, IMO, your alternative definition is the same mentioned in the article. I don't have access at the moment to the first source, but I do for the second source. I have a few concerns from what I have been able to access. First, at least with respect to the second source, I think you are misreading the source. I think that might also be true for the first source. Could provide the verbatim text that you are trying to paraphrase so other editors can also assess. Second, I doubt that statements like "Note that the accelerations are relative to a fixed, non-rotating reference frame" or "The Coriolis force, thus defined, has an origin (the rotating arm) and is in no sense a pseudo-force" are actually supported by the cited references (again, I didn't see it in the one I was able to access), and therefore represent WP:OR. Third, I would argue that the source I can see is poorly worded in parts and perpetuates a common misconception with respect to the centrifugal force (a misconception identified by a few other sources and seen when compared to the larger body of reliable sources).

More particularly, because you are describing the motion along the rotating arm, you are necessarily in a rotating system. Leibniz made the same implicit assumption when he first described the centrifugal force (for example, see Aiton, The celestial mechanics of Leibniz in the light of Newtonian criticism, who noted "Leibniz's study of the motion along the radius vector was essentially a study of motion relative to a rotating frame of reference.") Section 1.3.3 in your second source is unfortunately vague on whether it is in a rotating frame or not, but IMO it appears to be Leibniz-like and therefore not a stationary frame. On the other hand, section 1.3.4 in the same source is explicit in showing that the Coriolis force arises only when we are relating the acceleration in a non-moving coordinate system to acceleration and motion in the moving coordinate system.

You were bold, but others have reverted you. Now, per the suggestions of WP:BRD, we should discuss before reinserting. Again, providing the verbatim text you are paraphrasing would be helpful to the discussion. As an aside, I you can sign your posts on the talk page using ~~~~, and your attempt at getting the header for the subsection still wasn't correct - see MOS:HEADINGS for the correct method --FyzixFighter (talk) 15:09, 8 November 2015 (UTC)

Yes - I have gone beyond my sources with some very minor comments and added emphases. But I feel that the extent to which I have done so does not exceed other extrapolations in the article. To me it seems very clear that this is truly an alternative definition which is commonly used among engineers, and which therefore deserves inclusion. The C force is here defined as the force which is required to constrain a moving body in a straight-line path relative to a rotating frame; the force is not a pseudo force. It does not conform to this definition: "The force F does not arise from any physical interaction between two objects, but rather from the acceleration a of the non-inertial reference frame itself. " (taken from the wikki entry on pseudo-force). The force I am talking about is applied to the radially moving element by the rotating arm. As I have written, this force could cause the rotating arm to fail mechanically, and it is for this reason that engineers take an interest in it. The situation is quite distinct from that which occurs when a weather formation is seen to be moving in a curved path when viewed from the surface of the earth. In this latter case the curved path appears to need a force for its explanation, but no such force exists; the curved path would appear straight when viewed from an inertial frame. According to the engineers, if the clouds were constrained to move in a straight path relative to the surface of the earth, THEN a coriolis force would be required, but in fact no such force acts on the clouds; they are unconstrained and move strictly according to Newton's first law. They are NOT seen to move in a straight line relative to the surface of the earth. The two situations under consideration are quite distinct. One requires a real force which can be measured and which might cause a mechanism to fail when set in motion, the other requires no force at all, or at best a pseudo-force or notional force which exists only in the imagination and which is therefore of no interest to an engineer. Andrewg4oep (talk) —Preceding undated comment added 16:01, 8 November 2015 (UTC)

Andrewg4oep, I agree with FyzixFighter. You seem to be trying to add your own interpretation of Coriolis force and pseudo-force (in my opinion better called an inertial force because it can be very real) to this article based on an combination of two sources. Please do as FyzixFighter suggests and give us the verbatim text from both the sources that you think support your assertions so that we can discuss this further. Martin Hogbin (talk) 16:46, 8 November 2015 (UTC)

@Andrewg4oep - I think we need to be careful to distinguish between accelerations and forces. Only in simple cases is there a one-to-one correspondence between the individual forces and the terms within the expression for acceleration for a given coordinate system. For example, the second source, Smith's "Mechanical Engineer's Reference Book, only talks about accelerations on page 1/7. In the example on that page, the four parts of the total acceleration are the terms when writing out the acceleration in polar coordinates (${\ddot {\vec {r}}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {r}}+(2{\dot {r}}{\dot {\theta }}+r{\ddot {\theta }}){\hat {\theta }}$). And here is where we get into an apparent confusion in the literature. Smith calls the $2{\dot {r}}{\dot {\theta }}$ term of the acceleration the "Coriolis acceleration", and I have seen others use similar terminology - I've also seen people call it a "Coriolis term", which is my preference. The term "Coriolis acceleration" is also used in sources to refer to the apparently anomalous acceleration perpendicular to an object's velocity when describing motion in a rotating frame, which we attribute to the Coriolis inertial force. The confusion arises because the "direction" of this Coriolis term is actually opposite that of the Coriolis force (the inertial force) acting on the block in the frame tied to the rotating link. While there appears to be disagreement in the literature what "Coriolis acceleration" should refer to, I have yet to see a reliable source that talks about a Coriolis force/effect outside of a rotating frame.

Back to the block on link example, if we assume this is a simple example, then the only forces on the block are a contact force from the link in the theta-hat direction and any frictional force between the block and link in the r-hat direction. However, I would still not call the theta-hat contact force a Coriolis force since, in Newton's 2nd law, it is the force paired with both the Coriolis term and the angular acceleration term - also note that Smith does not call anything a Coriolis force. More generally, there is no requirement that the force that generates the "Coriolis term" acceleration be a single force, it could be very easily a sum of forces, hence why I don't think it is wise to call anything a Coriolis force in this context. --FyzixFighter (talk) 20:05, 8 November 2015 (UTC)

Atmospheric slippage?

As a disclaimer, I am not an expert on this nor anything close to it. However, when considering the example of the coriolis affect causing drift of a bullet fired over a large distance, it seems intuitive that the only reason this drift occurs is because the bullet is no longer "fixed" to the earth and does not gain the angular momentum of the lower latitude when it travels there. For example, assume that you shoot the bullet at a latitude with a rotation of 1000 mph and it impacts at a latitude of 1001 mph. Theoretically, if there was no atmospheric slippage (in a fluid dynamics sense of the word slippage) then the atmosphere would simply "push" the bullet sideways at the same speed it is rotating and therefore the bullet would gain the additional 1 mph in angular momentum and would not seem to drift. So, in a sense, the coriolis effect in the sense of the atmosphere seems to be due to this atmospheric slippage, at least from the way I am understanding it, which could very well be flawed. Can someone who understands this better clarify this point in the article? If I don't get any responses I'll try to do some research on this when I have some "free time" but that might not be for a few weeks/months. Thanks! (PS - I was thinking about this after considering how oars suffer slippage through water in a rowboat or racing shell.) Ahp378 (talk) 03:33, 27 December 2015 (UTC)

Hello @Ahp378: There is a Coriolis effect on a moving bullet. Think of a projectile fired north from the equator with the speed and firing angle necessary to reach, for example, the Tropic of Cancer. the difference in latitude 23.437° in the example implies a cos(23.437)=8.3% smaller radius, so at impact, (disregarding friction up to that point) and due to Newton's first law, the bullet is moving 8.3% faster towards the right than Both the ground and the atmosphere. So the atmosphere may indeed reduce slightly the Coriolis effect, how much would depend on the aerodynamics of the projectile, my intuitive feeling is that in a projectile capable of reaching such a long distance the effect of that side air drag would be almost negligible with respect to Coriolis (and orders of magnitude less than the front air drag). The reduction should probably be similar to the drag that the projectile would experience if you could throw it sideways (and it stayed that way) towards the East at a speed equal to the difference of the surface speeds at the equator and the tropic as measured from an inertial frame of reference, approximately 465*(1-cos(23.437)) = 38.36 m/s (138 km/h)

Another way of understanding this with a practical example that you can actually try, is to see what happens when you are swinging a whistle in circles on a cord and you let it wrap around your finger. You will see how the angular velocity of the whistle increases as the radius of rotation gets smaller. Even if you blow against the whistle as it rotates to account for the atmospheric slippage of our example you would notice very little difference, the angular velocity of rotation would still increase. In our previous example the projectile would be the whistle and gravity the cord that shortens the radius of rotation when moving north from the equator. I hope that helps explain your question. Regards.--Crystallizedcarbon (talk) 10:06, 28 December 2015 (UTC)

Hi @Crystallizedcarbon:, thanks for your write-up. I think I understand what you're saying, that one would essentially consider friction negligible, and so the "base state" of the coriolis force is frictionless and you then add in any applicable friction, as opposed to the other way around, starting out at a base state of perfect friction and then considering the amount subtracted to be the coriolis force. I guess another way to phrase my line of thinking is this: in the example of the sphere rolling in a straight line along a rotating circle, what would happen if you replaced the sphere with a cylinder? Or as another example, if instead of a bullet flying through the air, you simply drive your car south on a road - you wouldn't drift sideways. I'm just trying to think if there's some way to clarify in this article that the coriolis force is essentially created by a lack of friction, since that was not quite clear to me when I was reading it. Thanks! Ahp378 (talk) 01:01, 5 January 2016 (UTC)

Misconception by omission

I have read the article and the discussion of the article on this Talk Page. From all of this, it is clear that the article does not do justice to what has been discussed at length on this Talk Page.

In the Introduction to the article, “the Coriolis effect is [defined as] the apparent deflection of moving objects when the motion is described relative to a rotating reference frame”. This statement is not qualified by exceptions or limitations. This is correct. It applies to ALL motion observed from a rotating frame of reference, which includes all the examples given in the article (of missiles launched across rotating turntables or spinning bowls of water, and of trains speeding east- or westwards along, especially, the equator). But it also includes EVERYTHING ELSE observed from our rotating and orbiting earth. While several types of motion seen on earth (such as the winds, the circulation of the oceans, the trajectory of missiles fired from cannons resting on the earth, and the apparent difference in weight of aircraft flying eastward or westward along a lines of latitude, especially the equator) are universally accepted as genuine instances the Coriolis Effect, the definition of the Coriolis Effect is not limited to these examples. Yet the article is written as if these are indeed the only examples of the Coriolis Effect. This is misleading and confusing, in addition to being dishonest.

The definition of the Coriolis Effect makes no distinction between these examples and, for instance, the apparent movement of the “fixed” stars, the planets, various asteroids and meteorites and even the artificial satellites (including the geostationary satellites) as seen from our rotating and orbiting earth. The only difference between these last named movements, and the ones mentioned in the article, is that in the former, invoking Coriolis Forces to calculate their motion as seen from our rotating frame of reference is unnecessarily clumsy. It is far simpler to understand these motions as if observed from an inertial frame of reference, away from the earth, and then applying the Newtonian Laws of Motion to them. This does not invalidate the fact that the complex movement of the planets in the sky, as observed from our orbiting earth, are instances of the Coriolis Effect. The same applies to the apparent spinning of the “fixed” stars round an axis that passes through the Earth’s north and south poles. It is simply not convenient, or helpful, to calculate the apparent Coriolis Forces that would account for these puzzling movements. And therefore these movements are never referred to as instances of Coriolis Effects in any physics or astronomy textbooks. A student is considered better off thoroughly understanding Newton’s Laws of mechanics than getting embroiled in Coriolis Forces, which are, in any case, “fictitious” forces, which do not further the student’s understanding of the universe. The important point remains, nevertheless, that the motion of the planets during the course of the year, and those of the fixed stars during the course of the night ARE instances of the Coriolis Effect. There is no reason why this cannot be explained in the article. I do not believe that students, or Wikipedia’s wider readership, need to have this information withheld from them. In fact doing so simply adds confusion, and puzzlement.

From a historical point of view, it was these very Coriolis Effects that confused the pre-Copernicus astronomers. These effects are very real, but mathematically enormously confusing, until Copernicus, Galileo and Newton (among others) suggested metaphorically stepping off our rotating frame of reference, and calculating these movements from an inertial frame of reference. This last sentence would adequately and simply put the Coriolis Effect, as it applies to astronomy, in the correct perspective (as agreed to by most if not all the contributors to this Talk Page).

I think that not acknowledging the spinning of the fixed stars round Polaris (in the northern hemisphere) as an instance of the Coriolis Effect, is equivalent to describing Evolution by Natural Selection, but pointedly ignoring Human origins by these means. It is not necessary to actively deny the Human relatedness to the apes, to instill, propagate or support a misconception about Human origins. The same applies to the discussion of the Coriolis Effect.

I hope this helps. Cruithne9 (talk) 11:37, 14 January 2016 (UTC)

I agree with what you say although I did not think that the article was quite as bad as you seem to be suggesting. Do you have any specific suggestions for improvements? Martin Hogbin (talk) 12:30, 14 January 2016 (UTC)

(edit conflict)

Yes, our article says:

The vector formula for the magnitude and direction of the Coriolis acceleration is

${\boldsymbol {a}}_{C}=-2\,{\boldsymbol {\Omega \times v}}$

where (here and below) ${\boldsymbol {a}}_{C}$ is the acceleration of the particle in the rotating system, ${\boldsymbol {v}}\,$ is the velocity of the particle with respect to the rotating system, and Ω is the angular velocity vector which has magnitude equal to the rotation rate ω and is directed along the axis of rotation of the rotating reference frame, and the × symbol represents the cross product operator.

So looking at the relevant vectors, indeed a star's apparent tangential ${\boldsymbol {v}}\,$ (caused by the rotation), trivially produces a constant magnitude Corriolis acceleration toward the poles, resulting in pure circular motion. I don't see any objection saying something about this in the article. - DVdm (talk) 12:49, 14 January 2016 (UTC)

From our point of view here on Earth, fixed stars rotate on the night sky

To an observer on the rotating Earth, both satellites appear stationary in the sky at their respective locations.

A thought I have had on this subject, although I am not convinced it is necessarily the best suggestion possible, is the creation of a new heading: Other instances of the Coriolis Effect. Here the various illustrations that appear on this page, like the stars circling Polaris, and the diagram of geostationary satellite, could be used together with a few words of explanation, along the lines indicated above, noting that these are other instances of the Coriolis Effect, but that, while it is possible to calculate the Coriolis Forces that would apply to these cases, the math is clumsy and not useful. It is better to follow Copernicus, Galileo and Newton's suggestion to metaphorically step off our rotating frame of reference, and calculate these movements from an inertial frame of reference.

Cruithne and Earth seem to follow each other because of a 1:1 orbital resonance.

Cruithne appears to make a bean-shaped orbit from the perspective of Earth.

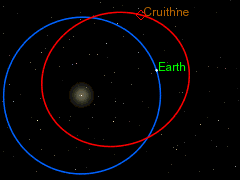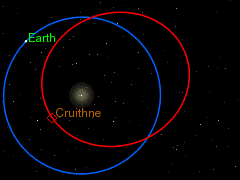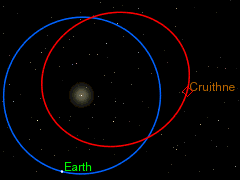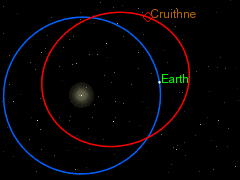
I also like the curious orbit of 3753 Cruithne as seen from our orbiting frame of reference round the sun, as a particularly spectacular instance of the Coriolis Effect. But because astronomers have little use for Coriolis "forces" in their calculations of the orbits of objects in our solar system, most of them seem to be unaware of the term "Coriolis Effect", even though the diagram on the right shows that they are acutely aware of the phenomenon (despite not having a name for it). Cruithne9 (talk) 13:39, 14 January 2016 (UTC)

I added three simple examples to the Centrifugal force article. One of them Centrifugal_force#An_equatorial_railway might be useful here. Martin Hogbin (talk) 13:55, 14 January 2016 (UTC)

Two quick thoughts. First, the geostationary satellites are not a good example for the Coriolis effect/force. If they are stationary, ie their velocity is zero, in the earth's rotating frame, then the Coriolis force is also zero. Second, the example of the 3753 Cruithne looks to me like an example, albeit slightly extreme example, of the stability of the L4/5 Lagrangian point. I would rather include mentioning the stability L4 and L5 points in the context of the Coriolis effect/force, with the appropriate references of course, than focus on a single asteroid. A quick google search of "Lagrangian point" and "Coriolis" would probably show more results then "Cruithne" and "Coriolis". --FyzixFighter (talk) 00:50, 15 January 2016 (UTC)

@Cruithne9: Also, how does the proposed Other instances of the Coriolis Effect section differ from the existing Coriolis effects in other areas section? Perhaps the heading could be reworded and the section moved within the article, but IMO the existing section is where such examples of the Coriolis effect in astronomy would fit so there is no need to add a new heading. --FyzixFighter (talk) 07:40, 17 January 2016 (UTC)

@FyzixFighter: Sorry, I had not noticed that heading - only its contents. You are quite right that the astronomical examples of the Coriolis effect should be slotted into there.

I will not be able to write this subsection, because I do not have suitable references to hand; but also because I am sure I will get into trouble! For instance, in the Introduction the Coriolis Effect is defined as the apparent deflection of moving objects when the motion is described relative to a rotating reference frame. Then there is the Coriolis Force which is the fictitious force an observer on a rotating frame of reference needs to postulate to account for the curved trajectories of objects moving across his/her field of view. Obviously, when an object co-rotates with the rotating frame of reference, the observer records a zero Coriolis Force; but to my mind that does not mean that there is no Coriolis Effect. Consider the following example: An object moves in a straight line at uniform speed across a rotating turntable, from one rim to the other. It does not cross the center point of the turntable. The velocity of the object is adjusted so that it crosses the rim (onto the turntable) at the same point as where it leaves the turntable a short while later. The track of the object on the turntable forms a loop. At the point on the loop nearest the center of the turntable, the object is, for an instant, stationary with respect to the turntable – its velocity is exactly the same as the angular velocity at that point on the turntable. Thus, for that instant in time, v is zero, and the Coriolis Force is zero. So, for a moment the Coriolis Effect is suspended, which sound very much like the contention that when a missile is shot vertically upwards and its velocity slows to zero at the apex of its flight, the force of gravity acting on it is zero.

A similar argument can be mounted against the geostationary satellite not being an example of the the Coriolis Effect, because its motion relative to the rotating earth is zero, so there must be a zero Coriolis Force at play here. But change its orbital path slightly, and immediately the Coriolis Forces come into play again, either as the "Eötvös effect", if it continues orbiting in the plane of the equator, or as a curved trajectory if it starts crossing lines of latitude.

Someone who can authoritatively deal with these contradictions will have to write the proposed subsection on the "Astronomical examples of the Coriolis Effect", or whatever heading is deemed appropriate. Cruithne9 (talk) 09:06, 17 January 2016 (UTC)

What is the objection to Centrifugal_force#An_equatorial_railway? It is a well know undergraduate problem showing how the same situation can be analysed in two different frames; on rotating and one not. Martin Hogbin (talk) 12:51, 17 January 2016 (UTC)

@Martin: Don't we already have the equatorial railway example in the Coriolis effect#Eötvös effect section? What would you add to it or how would the example you propose be different? --FyzixFighter (talk) 17:20, 17 January 2016 (UTC)

Yes we do. I forgot that. Martin Hogbin (talk) 17:57, 17 January 2016 (UTC)

@Cruithne9: Let me counter by going to the other extreme - do we talk about a Coriolis effect when talking about a person sitting still on the surface of the earth? It's technically geosynchronous motion. Maybe it does make sense for geosynchronous satellites, but I would feel more comfortable if we had a source that connected the two ideas together. On a related note, I might try rearranging the sections a bit and adding something on Lagrangian points and the Coriolis force/effect (I know I have sources for a section on that). --FyzixFighter (talk) 17:20, 17 January 2016 (UTC)

I did think about the person sitting on the surface of the surface of the earth as posing the same coriolis problem as the geostationary satellite. Anything observed from a rotating frame of reference will appear to be moving or not moving differently if viewed from an inertial frame of reference. This could be pointed out in the new section. I'll give another example: User:DVdm, above has pointed out that the stars circling Polaris have Coriolis Forces acting on them, and are therefore a good example of the Coriolis Effect. But that raises the question about Polaris itself. Why should it be the single exception simply because its velocity is zero when viewed from our rotating frame of reference? The new section would be incomplete if these seemingly contradictory instances were not explained or discussed.

Maybe all that is necessary, if no sources can be found for these conundrums, to mention that the "Coriolis Effect" is riddled with conventions. Then at least the reader is informed about the Coriolis Effect's real scope.

I like your idea about including a discussion about the Lagrangian points. They definitely deserve a mention in the new section. The article would be incomplete if they were not described. Cruithne9 (talk) 04:52, 18 January 2016 (UTC)

You seem to be straying off the main subject, which is the Coriolis force. The thrust of your original post was that the article was not clear enough about what the Coriolis force is. The fact that the same thing may have a different motion when viewed from a different frame of reference is, of course, true but not the main point of this article which about one particular aspect of rotating frames.

By the way, there are no real conundrums and or conventions necessary for special cases. The Coriolis force is clearly defined as the force acting on an object when considered in a rotating frame. The physics is quite clear and there are no exceptions that need special conventions. Martin Hogbin (talk) 11:23, 18 January 2016 (UTC)

Thanks @Martin Hogbin. Actually my original plea was to separate the Coriolis Force from the Coriolis Effect (the discrepancy between what is seen from a rotating frame of reference and that seen from an inertial reference frame). But I realize that the convention states that there is only an Effect if the Force is not zero. The article should state that unambiguously with a reason. (The reason is probably that most people accept that a tree remains where it is because there are no forces, Coriolis or otherwise, acting on it - wind and storms excepted). That then suggests that trees which co-rotate with the earth, are unaffected by the Coriolis Effect. But this then leads to a variety of conundrums which include making Polaris an exception to all the other stars, as seen from our rotating frame of reference, as well as making the geostationary satellites exceptions to all the other satellites that orbit the earth. It also then means that a ball moving in a straight line at uniform speed across a rotating turntable, crossing the rim on to the turntable at the same point from which it leaves it, without going through the turntable's center, suddenly, for an instant, not subject to the Coriolis Effect, even though it is one smooth continuous movement. I have absolutely no objection to this, but the convention and its curious consequences must be acknowledged. Science, and physics in particular, 'abhor' such arbitrary exceptions. (In the physics of gravitation, even a mote of dust exerts a gravitational force, even though it is negligible in almost every practical application, and can consequently be ignored.) The only place in the article where zero velocity on the earth's surface is treated as a point in a continuum of values is when the "Eötvös effect" is described.

Of course the tree is subject to a Coriolis Force, but because it is anchored to the rotating frame of reference, it does not move; whereas the air around it is affected by Coriolis Forces, and moves accordingly. If we replace the tree with a Foucault pendulum it immediately becomes apparent that there is a Coriolis Force acting on that anchored spot. Cruithne9 (talk) 16:33, 18 January 2016 (UTC)

I would certainly support moving this article to "Coriolis force".

Polaris and Geostationary satellites are exceptions in the rotating refernce frame of the Earth because both happen to be stationary in that frame. There are no exceptions in the physics. In a frame rotating about a different axis there could be a Coriolis force on both. I think it is important, as you said, to make clear that the Coriolis force on an object depends entirely on what reference frame you use. Because the Earth's rotating frame is particularly convenient for some purposes, like meteoroloigy, it is often incorrectly thought that the Coriolis force has something to do with the physical rotation of the Earth. Martin Hogbin (talk) 14:58, 19 January 2016 (UTC)

Hi @Martin Hogbin:. I think this would be a brilliant idea. In the article under the new name, it could be explained that in addition to objects that do not move relative to the rotating frame of reference having no Coriolis Force acting on them, objects whose trajectories are along great circles on the rotating earth also have no Coriolis Force acting on them, because they would be moving in straight lines as seen from our (earth-bound) rotating frame of reference. In effect this means that stars on the celestial equator, and satellites orbiting the earth in the plane of the equator, though moving, have no Coriolis Force acting on them. It could be mentioned that as one considers stars closer and closer to Polaris the Coriolis Force acting on them approaches zero, becoming zero at the celestial pole. Similarly stars close to the celestial equator also have Coriolis Forces acting on them that approach zero the closer they are to the celestial equator. I think an explanation of this sort would remove the temptation to think of these instances as "exceptions", but rather as points in a continuum of values, which, in this case does not have negative values (or are they theoretically possible, for certain types of motion seen from earth?) Cruithne9 (talk) 05:22, 21 January 2016 (UTC)

This will not be easy, I think the subject has been discussed before.

The reason I would like to make the move is that the Coriolis force is a very well defined concept of general applicability. The effect is rather less well defined.

For example, this article starts with a sentence saying, 'In physics, the Coriolis effect is the apparent deflection of moving objects when the motion is described relative to a rotating reference frame'. Problems that I see with this are:

It is inherrently vage because it suggests no way of putting numbers to the 'effect'.

There may not actually be a deflection, if the object is constrained, for example.

If there is a deflection, it is real deflection, not an apparent one when measured in the moving frame

As soon as the article starts to make any serious inroads into the subject it moves on to talk about the Coriolis force. Martin Hogbin (talk) 10:32, 21 January 2016 (UTC)

Proposed move to 'Coriolis Force'.

I propose moving this article to 'Coriolis force'. Martin Hogbin (talk) 17:15, 21 January 2016 (UTC)

• Support per Google Scholar "coriolis force" (53,700) vs Google Scholar "coriolis effect" (15,000) and Google Books "coriolis force" (91.700) vs Google Books "coriolis effect" (35.400). - DVdm (talk) 19:06, 21 January 2016 (UTC)
• Support (as proposer above). The term 'Coriolis force' is much more clearly defined than 'Coriolis effect'. 'Coriolis effect' seems to refer only to effects caused by the Earth's rotation. These are definitions from the first few Google links: 'The Coriolis effect causes a deflection in global wind patterns', 'Offers a fairly simple explanation of why objects curve on the Earth when they should move straight', 'Learn about the Coriolis effect, which appears to deflect items moving on or above the earth's surface based on the rotation of the earth. Martin Hogbin (talk) 16:07, 22 January 2016 (UTC)
• Support - while the term "Coriolis effect" is more probably more common in meteorological literature, where as pointed out above it is almost exclusive in the context of earth's rotation. However in the more general physics literature, "Coriolis force" is more common. I favor going with the broader and more general article title. --FyzixFighter (talk) 15:08, 23 January 2016 (UTC)
• Support I strongly support this proposal as it will eliminate a considerable amount of confusion on this topic. But may I put in a request that the new article is not confined to a discussion of objects moving across the surface of the earth, or turn tables in a laboratory, but that due consideration is also given to the apparent motion of the "fixed stars", and orbiting earth satellites (which in the present article are only discussed in terms of the curvature of great circles on Mercator Projection maps - nothing to do with Coriolis forces or even "effects"). The earth's orbit around the sun is also a rotating frame of reference and therefore a source of Coriolis Forces. Cruithne9 (talk) 07:12, 24 January 2016 (UTC)

No problem, provided anything you like to add is properly sourced. Only if the established literature refers to Coriolis force in a particular context, we can mention that context here. Otherwise we cannot have it, even if it stares us in the face, so to speak. In other words, be well aware of wp:original research, and specially WP:SYNTHESIS. DVdm (talk) 09:55, 24 January 2016 (UTC)

In that case, it might be worth mentioning that effect X which appears to be a genuine instance of a Coriolis Force acting on an object Y, is nowhere, in the astronomical or physical science literature, referred to as such. This information about the Coriolis Force is worth knowing and being informed about. Cruithne9 (talk) 10:16, 24 January 2016 (UTC)

Perhaps, but, again for the same reason we can only mention that "something is not mentioned in the literature", provided that this is mentioned in the literature itself. - DVdm (talk) 10:23, 24 January 2016 (UTC)

I was going to add that the problem could be stated in the positive: that Coriolis Forces are calculated and used almost exclusively in the following contexts..... In all other cases it is generally considered simpler and more convenient to use an inertial frame of reference, even though the observations are being made from a rotational frame of reference. But I suppose this too would have had to have been said before in an authoritative text book or review article. Pity, but understandable. Cruithne9 (talk) 10:36, 24 January 2016 (UTC)

Consensus to move

Anyone know how to do this? I tried but could not because of the existing (redirected to here) article at Coriolis force. Martin Hogbin (talk) 17:33, 24 January 2016 (UTC)

The redirected page must be deleted first. See WP:RM#TR. I made the request. When the redirected page is gone, the move can be done. - DVdm (talk) 18:15, 24 January 2016 (UTC)

 Done Thirteen subpages, mostly archived talk pages, have also been moved. --Malcolmxl5 (talk) 19:03, 24 January 2016 (UTC)

I see that you also created Coriolis effect and redirect to here. Thanks! - DVdm (talk) 20:21, 24 January 2016 (UTC)

Thanks Malcolmxl5 and DVdm. I have changed the first sentence of the lead to match the new title. Martin Hogbin (talk) 21:23, 24 January 2016 (UTC)

I have changed the article now to reflect the new title so generally now we use 'force' rather than 'effect' although 'effect' is stll appropriate in some cases. Martin Hogbin (talk) 21:38, 24 January 2016 (UTC)

What now?

The move to Coriolis force is now complete. What changes, if any, do we now want to make? Martin Hogbin (talk) 11:50, 25 January 2016 (UTC)

Whatever that was discussed above, but properly backed by sources, without wp:ORing or wp:SYNTHing . - DVdm (talk) 13:13, 25 January 2016 (UTC)

Cruithne9, I am finding it hard to understand the point that you are making above. Could you give an example of the text that you would like to add to the article. Martin Hogbin (talk) 17:08, 25 January 2016 (UTC)

Thank you for inviting me to comment. I stated my original problem with the article at the beginning of the Misconception by omission section. I am concerned that the text deals with events only on the surface of the earth, and with high school laboratory examples of rotating turn tables and spinning bowls of water. There is no mention of motion beyond the earth’s surface observed from our rotating frame of reference either in the form of the rotating earth or the orbiting earth. In the course of the ensuing discussion Martin Hogbin stated: “The fact that the same thing may have a different motion when viewed from a different frame of reference is, of course, true but not the main point of this article which about one particular aspect of rotating frames.” My point is that a general article entitled “Coriolis Force” cannot confine itself to “one particular aspect of rotating frames”. This is equivalent to an article entitled "Gravity", only describing the physics of gravity on earth. The apparent spinning of the stars round Polaris when seen from our rotating frame of reference on earth is not mentioned in the article even though DVdm states this to be a simple application of Coriolis Forces. The apparently curved trajectories of the artificial satellites across the earth’s surface is described inaccurately and totally inappropriately as being examples of great circles drawn on Mercator projections of the earth. (In fact they do not trace great circles across the earth’s surface, but tracks that are influenced by the earth’s rotation, i.e. Coriolis Forces. The Mercator projection is a red herring in this context.)

Cruithne and Earth seem to follow each other because of a 1:1 orbital resonance.

Cruithne appears to make a bean-shaped orbit from the perspective of Earth.

Obviously the Coriolis Forces acting on objects that are co-rotating with the earth, or are opposite the poles, are zero. This is not the same as saying that saying there are "no Coriolis Forces acting on these objects", which leads one to suspect that Polaris and the geostationary satellites are exceptions to the rules of the Coriolis Effect. But Martin Hogbin makes it quite clear (and I agree) that “The Coriolis force is clearly defined as the force acting on an object when considered in a rotating frame. The physics is quite clear and there are no exceptions (my italics) that need special conventions.” In other words, zero force is just part of a continuum of values (from positive through to negative) that can be obtained for Coriolis Forces acting on different objects – or, state differently: the closer a fixed star is to Polaris the smaller the Coriolis force acting on it (as seen from earth), until the value becomes zero at the celestial poles. Similarly, the closer a star is to the celestial equator the more the Coriolis Force acting on it approaches zero (stars and artificial satellites in the plane of the equator seem to travel in straight lines along a great circle). As one crosses the equator the sign of the Force changes and stars start rotating clockwise, whereas, in the northern hemisphere, they turn counter-clockwise. It is this sort of explanation that turns the article from an exercise in pure math, into an informative encyclopedic entry.

The earth orbiting the sun is another rotating frame of reference from which the objects moving in the solar system can be viewed, and this too causes Coriolis forces. But as DVdm points out this “is not a problem, provided anything you like to add is properly sourced…. Otherwise we cannot have it, even if it stares us in the face, so to speak. In other words, be well aware of wp:original research, and specially WP:SYNTHESIS.” But it is clear from the diagram on the right, taken from the 3753 Cruithne article, that the authors of that article and the diagram are very obviously thinking in Coriolis terms, though without using the word “Coriolis”. The whole point about the discussion of Cruithne’s bean-shaped orbit and it being dubbed (incorrectly) earth’s “second moon” is that it is an exercise in pure, unashamed Coriolis physics. That is reason and justification enough to include it into the Coriolis article. It is a very simple, uncomplicated application of the general principle, which has no exceptions referred to by Martin Hogbin. It is not original research, or an original idea, and therefore not subject to a very narrow interpretation of wp:original research, and WP:SYNTHESIS. Cruithne9 (talk) 06:58, 27 January 2016 (UTC)

Re "But it is clear from the diagram... ...though without using the word “Coriolis”": well, that is precisely what wp:OR and wp:SYNTH are about. We really cannot take that. - DVdm (talk) 12:29, 27 January 2016 (UTC)

I agree with DVdm on this - you have to understand that there have been a number of proponents of fringe science on this and related pages, and a close reading of WP:OR and WP:SYNTH is the quickest way to keep those editors in check without the talk page discussions devolving into long-winded physics lessons. Some of your comments above actually, imo, show why this is necessary. Stars that lie on the celestial equator do experience a non-zero Coriolis force. They have a non-zero velocity in the earth's frame and that velocity is not parallel to the axis of rotation of the frame, therefore the Coriolis force is non-zero. And there ends the physics lesson - maybe I'm wrong though and maybe I'm missing something in the math or mechanics, but the best way to rebut that reason for excluding that type of example is to provide a reliable source. The example of 3753 Cruithne is different matter, complicated by the fact that the kidney bean shaped orbit also drifts around the earth's orbit - it's not just stuck at the L4/5 points. I think that the better example, which is relevant to this page, addresses your concern, and can be properly sourced, is the stability of Lagrangian points. Perhaps take a broader view than just that particular asteroid and look at the more general case and see what you can write up. --FyzixFighter (talk) 13:09, 27 January 2016 (UTC)

Yes, for example from this

References

More to pick from Google Books. - DVdm (talk) 13:36, 27 January 2016 (UTC)

Cruithne9, I cannot understand what it is that you wnat to change in this article. Could you propose a change of wording for discusion.

I think we all agree that in a reference frame rotating with the Earth round the sun, Cruinthe, along with all other objects will, in general, be subject to the centrifugal and Coriolis forces. The orbit of Cruinth could be analysed in such a frame, as could the orbits of all the planets but I do not know of any advantage, except as an academic exercise, in doing so. I do not think that your two animations are particularly instructive regarding the Coriolis force.

I, for one, do not understand what your point is. By all means make a change to the article to show what you want. It is likely that it will quickly be reverted but then at least we would know what your point is. Martin Hogbin (talk) 15:34, 27 January 2016 (UTC)

I was too hasty with my example of the stars on the celestial equator - I realized my mistake after I had recorded it on this page. I withdraw from this discussion and any attempt to edit the article. I do not have the resources at my disposal to contribute anything meaningful to either. I thank you all for your patience in trying to discuss this fascinating topic with me. Cruithne9 (talk) 18:51, 27 January 2016 (UTC)

British English

The English used in this article was mixed Brit US. I have changed it all to British as that is how it started out. SeeWP:Engvar. Martin Hogbin (talk) 20:25, 29 January 2016 (UTC)

Lowercase Phi

Hi readers. Can someone explain why phi appears in two different cases in this section? As a non-scientist, I had to look up the Greek alphabet to refresh myself on the difference between upper- and lowercase phi. As a shameless editorializer, I think this section intentionally alienates non-specialized readers and attempts to subjugate the non-elite to a technocentric, fascistic point of view of the role science plays in everyday life. It reaffirms that, if you can't understand a difficult concept in the terms prescribed by post-secondary education at elite universities, you don't deserve to learn about it. I think the people who contributed to this portion of the article are capital-B bad humans for that reason. Just my two cents. But someone change the case of the Greek letters though seriously. — Preceding unsigned comment added by 2602:306:CCA6:67E0:993D:7412:9FA8:E4CF (talk) 03:48, 6 March 2016 (UTC)

Please put new talk page messages at the bottom of talk pages and sign your messages with four tildes (~~~~). Thanks.

I don't see any uppercase $\Phi$ or Φ in the article, only $\varphi$ in the equations and the corresponding φ in the text. - DVdm (talk) 09:46, 6 March 2016 (UTC)

External links modified

Hello fellow Wikipedians,

I have just modified one external link on Coriolis force. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:

• Corrected formatting/usage for http://met.no/english/topics/nomek_2005/coriolis.pdf

When you have finished reviewing my changes, please set the checked parameter below to true or failed to let others know (documentation at {{Sourcecheck}}).

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

• If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
• If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—^{cyberbot II}_{Talk to my owner:Online} 00:51, 1 April 2016 (UTC)

Trimming the examples

Currently, we have a number of examples in this article. In fact, some IMO would cross the line into textbook-like example problems (the editor who added these in often was criticized by others, myself included, for crossing the textbook line). The example sections we have are:

• Cannon on turntable
• Tossed ball on a rotating carousel
• Bounced ball

I'd like to trim it down to a single simple case, but would like to hear others' thoughts. If we were to trim it to one example, which should it be? --FyzixFighter (talk) 22:20, 9 September 2016 (UTC)

Comment - I don´t have a set stance in this matter, I see the problem as a trade-off, in my personal opinion, I think that having three examples is not too much of a problem in this case. The subject of the article is not an easy concept to grasp for most readers, so having more than one example (like the second and third) might help readers not familiar with Coriolis in gaining an intuitive understanding. --Crystallizedcarbon (talk) 16:55, 10 September 2016 (UTC)

Clarifications regarding Coriolis force

First of all, at least in Newtonian physics, all forces arise from corrections to velocity; a force serves one function only, that is, to describe any discrepancy or 'acceleration' that deviates from linear motion. It doesn't matter whether a force is labeled 'real', 'fictitious', 'geometric', or 'physical', as long as the accelerations are consistent from description to description. There are ways to not 'feel' a physical force, such as when falling in orbit (although the experience may feel unnatural because we're so used to having the Earth 'below' us preventing any acceleration). One may argue that 'fictitious' forces arise to compensate for non-inertial/non-linear motion of an observer's frame; but there is no special accelerating or non-accelerating frame, just as there is no special moving or at-rest frame. An observer in a rotating frame may well argue that a 'non-rotating' frame is a special case in which the centrifugal force becomes zero due to the relative rotation, from his or her perspective, of the 'non-rotating' frame.

Second, it is clear from the math that the Coriolis term is distinct from the centripetal/centrifugal term. Therefore, Coriolis force describes a very specific type of acceleration, namely, one that arises when a target is in motion even when observed in a frame that is rotating at an angular velocity Ω. This is why the circumpolar motion of the stars, as viewed from a fixed location and orientation on the surface of the Earth, is typically not explained using Coriolis acceleration, because it is typically already taken into account by the centripetal/centrifugal acceleration. There is typically zero velocity in the rotating frame of the stars that is set up, so the math would reflect that the Coriolis term is zero, unlike the centripetal/centrifugal term. Viewed from a fixed orientation and location on Earth, the stars are moving under centripetal acceleration with no velocity in the rotating frame. Viewed from a frame co-rotating with the stars, however, the 'stationary' stars will have a velocity as seen from Earth and thus generate a Coriolis term that is twice as large as an opposing centripetal/centrifugal acceleartion. After summing, everything comes out the same in terms of acceleration, even though the attribution may go to different 'forces'. From our point of view, the motion of 3753 Cruithne seems to require non-inertial explanations, but whether they invovle Coriolis acceleration specifically, although likely, should be calculated, specifying the frames being used, and not just assumed.

Third, there may be a point of confusion when applying any velocity that moves tangentially or circumferentially in the plane of rotation, as opposed to radially. Sometimes Ω is pegged to another value (eg the rotation of the Earth), and any discrepancy between it and any circumferential velocity is factored into the v in the 2Ω(cross)v Coriolis term (v=0 in the typical treatment of circumpolar stars). Sometimes Ω is derived from the tangential velocity directly, and any change to it updates the Ω in the Ω(cross)Ω(cross)r centripetal/centrifugal term as well as the Ω in the 2Ω(cross)v Coriolis term, but you'd also have to transform v into its value as observed under the updated Ω, not the original Ω. Otherwise, things won't be applied correctly per equation and cancel out to give the same result regardless of your approach. This is also why the Eötvös effect is sometimes considered Coriolis but other times centripetal/centrifugal. For those of you more familiar with the coordinate transformation derivation from, say, x and y into r and θ, that would match the second approach above, which may be easier to remember, since any circumferential velocity goes into the centripetal/centrifugal term, whereas only radial velocity contributes to the Coriolis term. I think FyzixFighter gave the nice formula ${\ddot {\vec {r}}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {r}}+(2{\dot {r}}{\dot {\theta }}+r{\ddot {\theta }}){\hat {\theta }}$ previously.

Hopefully, this clarifies things a little bit for anyone who's become more confused after reading the earlier Talk page discussions or is interested in improving the article further.

204.89.11.242 (talk) 02:02, 13 October 2016 (UTC)

Simple Coriolis force

There's a very simple and very observable display. We have all seen it, whether we have paid attention to it or not. Watch the water in the bathtub while it drains. In the Northern hemisphere, it will "whirlpool" (spin) counter-clockwise. In the Southern Hemisphere, this will be clockwise. — Preceding unsigned comment added by 50.141.41.219 (talk) 03:50, 1 April 2017 (UTC)

You can read the article to find out how and why it doesn't. - DVdm (talk) 09:39, 1 April 2017 (UTC)

Lead

I am not crazy about the last sentence of the lead. I dislike this type of "explanation" because it gives rise to a number of misconceptions, most importantly that the Coriolis force is only present or is stronger when an object moves north-south (and is nonexistent or weaker when it moves east-west), when in fact the horizontal component is the same magnitude regardless of the direction of motion, and the vertical component (generally unimportant for geophysical dynamics) is largest for east-west motion. If an "intuitive" explanation is called for, I would be in favor of an example at the pole rather than the equator, basically explaining in words what is shown in the animated graphic alongside the lead. My deletion of the sentence was reverted, so here I am. Rracecarr (talk) 18:37, 1 April 2017 (UTC)

How about something along these lines (still risks implying that only north-south motions are susceptible): A frictionless hockey puck shot from the North Pole over the frozen Arctic Ocean toward a distant goal takes some time to travel the distance. During that period, the Earth rotates, moving the goal to the east. The shooter observes that the puck misses to the west, and attributes that curvature to the Coriolis force.Rracecarr (talk) 18:52, 1 April 2017 (UTC)

I think that the content that you deleted (and that I restored) was properly sourced and okay, and I don't think that it gives rise to misconceptions. Your alternative is valid too. There is just a difference in the initial conditions: in the non-rotating inertial frame, the equator object has an initial velocity that is larger than the ground velocity at higher altitudes, whereas the pole object has an initial velocity that is smaller (zero, actually) than the ground velocity at lower altitudes, resulting in deflection to the right on the northern hemisphere (—or to the left on the southern hemisphere—) in both cases. I see no reason to remove the properly documented current example, but of course, feel free to add your example, provided you can stick a proper source to it. Should be easy to find. - DVdm (talk) 19:20, 1 April 2017 (UTC)

External links modified

Hello fellow Wikipedians,

I have just modified 2 external links on Coriolis force. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:

• Added archive https://web.archive.org/web/20051120121513/http://www-paoc.mit.edu/labweb/lab5/gfd_v.htm to http://www-paoc.mit.edu/labweb/lab5/gfd_v.htm
• Added archive https://web.archive.org/web/20060321094211/http://www.mensch.org/physlets/inosc.html to http://mensch.org/physlets/inosc.html

When you have finished reviewing my changes, you may follow the instructions on the template below to fix any issues with the URLs.

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

• If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
• If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—InternetArchiveBot (Report bug) 04:46, 13 August 2017 (UTC)

In physics

User A Simple Name (talk · contribs) seems not to like the "In phycis" qualifier of the openining sentence: [1] [2]. I have reverted twice ([3], [4]) because this clearly is a physics related article. Comments welcome. - DVdm (talk) 09:18, 10 September 2017 (UTC)

"In physics" adds absolutely nothing as a modifier. It is extraneous verbiage. The definition stands on its own, apart from the fact it has relevance to physics. It also has relevance to Earth Science and Meteorology. It needs to be eliminated." A Simple Name (talk) 14:59, 10 September 2017 (UTC)

And again, the animation is not in proper context with their text

The trajectory is:

- in the inertial reference frame a curve, because of conservation of the angular momentum

the lower part of the animation,with the resting disc in the inertia reference frame of the observer.

- in its own noninertial rotating reference frame of the cannon ball it is a straight line

the upper part of the animation, where the disc is rotating in the own reference frame of the canonball

- in any other rotating reference frame it is curve

A suitable observer is always in his own inertial reference frame, if he is not accelerated. This is the reference frame of observation and description. — Preceding unsigned comment added by 2a02:8071:3e90:6200:d9bd:ecc7:25c8:c8f2 (talk • contribs) 10:12, 3 October 2017 (UTC)

I think you are misreading or misunderstanding the caption and text accompanying the animation. The top part is the system as seen from an inertial frame - imagine the rotating disc is vertical and the ball is being dropped from the center and falls straight down. The lower part is the system as seen from a frame attached to the rotating disc. I'm not saying that the image is perfect and cannot be improved (changing the perspective from the upper to lower part seems to confuse a lot of people), but your interpretation that the animation is incorrect seems to be based on a faulty reading of the caption. --FyzixFighter (talk) 13:18, 3 October 2017 (UTC)

Also, this is probably one of the worst external links on the subject. It's an unpublished, personal essay written by a known fringe science advocate that was actually banned from editing Wikipedia because of his behavior. --FyzixFighter (talk) 18:30, 3 October 2017 (UTC)

The correct equations of motion

the correct Coriolis motion equations proved by my simulation. I suggest that the article be completely rethought.

Trajectory of the equations of motion in the inertial frame of reference. applied at "Hurican", Isabel of 16. Sep. 2003

Trajectory of the equations of motion in the inertial frame of reference. applied at "Hurican", Isabel of 16. Sep. 2003

Petre Pascu (talk) 17:34, 17 October 2017 (UTC)

External links modified (January 2018)

Hello fellow Wikipedians,

I have just modified 2 external links on Coriolis force. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:

• Added archive https://web.archive.org/web/20131011124201/http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/ferrel-nashville56.pdf to http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/ferrel-nashville56.pdf
• Added archive https://web.archive.org/web/20070304082822/http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/Coriolis-1831.pdf to http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/Coriolis-1831.pdf

When you have finished reviewing my changes, you may follow the instructions on the template below to fix any issues with the URLs.

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

• If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
• If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—InternetArchiveBot (Report bug) 12:56, 21 January 2018 (UTC)

Improving the "Intuitive explanation" subection

Hi all,

The current version of the "Intuitive explanation" section is opaque and also has physical errors. "bending in the opposite direction to our actual motion" implies that motion is reversed, which is incorrect. The subsequent sentences are not comprehensible to me, and I am a professor of atmospheric physics (note: not appealing to my authority here, just noting this for context).

I believe an "intuitive explanation" should explain the effect using basic physical concepts and in the context specifically of motion on the Earth -- North/South/East/West -- since this is what a layperson would think about (why are objects turned by the Coriolis force?). The current form does not do this.

I propose text I modified in an archived version of the page: https://wiki.riteme.site/w/index.php?title=Coriolis_force&oldid=849413767

A suitable source for this text is this introductory book on atmospheric science: Holton, J.R. and Hakim, G.J., 2012. An introduction to dynamic meteorology (Vol. 88). Academic press. (Note that the current text does not contain any sources.)

Thoughts? Thanks. Drchavas (talk) 21:59, 8 July 2018 (UTC)

Note to others, see also at my User_talk:DVdm#Coriolis_Force_"Intuitive_explanation".

Indeed, comments and thoughts welcome, and a source for current would be nice. But let's keep it really intuitive—or otherwise change the section title . - DVdm (talk) 22:25, 8 July 2018 (UTC)

Hmm no feedback on this thusfar.

Yeah I suppose the question is what is meant by "intuitive"? The reason I am trying to update this section is because no truly simple intuitive explanation exists, and the ones that try to create one are just gobbledigook about things rotating "underneath" you. In the end the effect occurs because of angular momentum conservation and changes in the centrifugal force -- this is the simplest physical explanation. To me "intuitive" means explain these two effects in simple and accessible terms (e.g. using common examples such as the figure skater).

But you're right that maybe "intuitive" implies something even simpler -- how about we update the section title to "Simple physical explanation"?

I have already addressed the source issue, that's not a problem.

Drchavas (talk) 11:41, 17 July 2018 (UTC)

Personally, I'm not a fan of a simple physical explanation that relies on an understanding of the centrifugal force, which is, like the Coriolis force, an artifact of the rotating reference frame. I'd be more comfortable starting at explanations given in reliable sources. --FyzixFighter (talk) 19:28, 17 July 2018 (UTC)

Thanks for the input. The centrifugal force is tangible to the layperson (e.g. a merry-go-round), similar to the figure skater for angular momentum. I guess I'm not sure what "explanations given in reliable sources" means -- do you have an example of what you're looking for?

The physical explanation based on angular momentum and centrifugal force is taken directly from the mathematical derivation of the Coriolis force as outlined in e.g. Holton and Hakim (2012). I'm not sure what source is more reliable than the math itself. Here I am simply trying to translate that math into essential concepts and words. Drchavas (talk) 20:39, 17 July 2018 (UTC)

I'm all for making the explanation as simple as possible, but not more so, especially at the cost of introducing incorrect concepts. From the perspective of the figure skater, angular momentum is not conserved which is why these fictitious forces, both the coriolis and centrifugal forces have to be introduced (from the skater's perspective the coriolis force provides the angular acceleration, the centrifugal force is what he is working against when he pulls his arms in). To me an explanation that talks about angular momentum and centrifugal force seems to not be sure which perspective it is in - the skater's or an outside observer. What page/section is the explanation in Holton and Hakim located. One of my concerns is that some errors have been introduced in translating the math from Holton and Hakim into essential concepts and words. Can you provide the text in Holton and Hakim from which you are basing the intuitive explanation? --FyzixFighter (talk) 03:06, 18 July 2018 (UTC)

Sorry for the long delay, we just had a baby. Holton and Hakim is in my office, which I won't have access to for a few weeks unfortunately. For now here is an alternative source for the derivation: http://www.geo.cornell.edu/geology/faculty/Cook/Coriolis_force.doc . It explicitly shows how the two dominant terms of the Coriolis Force reduce to

F_c = f*v \hat(i) - f*u \hat(j)

where f = 2*omeg*sin(phi),

and these terms correspond physically to conservation of angular momentum (north-south motion) and excess centrifugal force (east-west motion). This equation also applies to a marble on a rotating disk.

The discussion below is overwhelming, so I am just going to stop worrying about pushing for this change. I'll just note that, as it currently stands, the Coriolis force page does not give any quick explanation for the meaning of the two terms in F_c that could be understood by someone with an introductory physics background (talking about how the planet turns beneath you doesn't help). It would be nice if it did.

Drchavas (talk) 02:08, 27 July 2018 (UTC)

May I remark that referring to "the planet turns beneath you" is strongly ambiguous and therefore not helpful for building a resilient and reasonable intuition. I suggest to start a new thread. Purgy (talk) 06:12, 27 July 2018 (UTC)

My primary suggestion is to get rid of headings, which imply that there might be some intuitively (=easy?) to grasp explanations for the behaviour of a spinning top. While most humans have, supposedly, at least some intuitive access to "forces on rigid bodies" in rotations in a plane, I doubt that there are many, capable to develop such an intuition about rotation in 3D, and even less about motions of fluids there. I am rather convinced that there are just examples, where the complex consequences of inertia in rotation may become observable, and, yes, experience and routine help in "understanding". I have a hard time in intuitive understanding, math to the rescue. Purgy (talk) 10:05, 18 July 2018 (UTC)

=========================================================

I have edited the "intuitive" text to get read of a blatant error on the page for a long time. The Coriolis force has absolutely nothing to do with the the circumfrence of latitude circle becoming smaller as a particle travels northward in the northern hemisphere. In other words it has nothing do do with trying to apply the concept of conservation of angular momentum, which anyway is not conserved in a non-inertial (rotating) reference frame. The mathematical derivation of Coriolis given in the maon body of the wikipage shows that angular momentum is not conserved in the rotating reference frame, so how is it conceivable that someone would write an "intuitive" explanation that is in direct contradiction of the mathematics?

Furthermore, just to be clear the Coriolis effect is the same on earth for an object that travels in any direction (east, west, north, or south, or any direction in between). This observational fact, backed up by the mathematical derivation given on the wikipage, directly contradicts the incorrect "intuitive" explanation that has been on the web page for a long time.

At it's heart, Coriolis in nothing other than perception of motion from a particular frame of reference. Objects tend to travel in straight lines in an inertial (stationary) frame of reference, yet, the very same object when viewed in a non-inertial (rotating) frame appears to travel in a curved path. If you think there is anything deeper to udnerstand about Coriolis than this, then you are thinking about the issue way too much.

Davidmholland (talk) 22:46, 23 July 2018 (UTC)davidmholland

=========================================================

There is nothing wrong with the "intuitive example". It does not apply conservation of momentum in the rotating frame, it applies it in an inertial frame (observing the rotating earth from non-rotating space). Aside from the fact that you're mistaken, you are also in violation of the ban against reverting more than 3 times in 24 hours. As such, you are likely to be blocked from editing. Rracecarr (talk) 23:10, 23 July 2018 (UTC)

I have reverted to the consensus version again: [5]. - DVdm (talk) 08:13, 24 July 2018 (UTC)

////

Reading through this thread, I see that Wikipedia has made the same mistake regarding Coriolis as on other web pages. For instance on Youtube and elsewhere one can see an elaborate animation of the intuitive argument as given in Wikipedia:

https://www.youtube.com/watch?v=i2mec3vgeaI

You would have to agree that the Youtube and the following Wikipedia arguments are the same: "For an intuitive explanation of the origin of the Coriolis force, consider an object moving northward in the northern hemisphere. Viewed from outer space, the object does not appear to go due north, but has an eastward motion (it rotates around toward the right along with the surface of the Earth). The further north you go, the smaller the "horizontal diameter" of the Earth, and so the slower the eastward motion of its surface. As the object moves north, to higher latitudes, it has a tendency to maintain the eastward speed it started with (rather than slowing down to match the reduced eastward speed of local objects on the Earth's surface), so it veers east (i.e. to the right of its initial motion).[4][5] Though not obvious from this example, which considers northward motion, the horizontal deflection occurs equally for objects moving east or west (or any other direction).[6]"

Wikipedia, drew this argument from references 4 and 5 and 6 for the 'eastward traveling speed up while going north' piece of the argument. References 4 & 5 are from some kind of solar engineering textbooks which provide no mathematics to back up the stated claims, and no references either. A while ago I had contacted the authors of these books to ask where they came up with their intuitive explanation of Coriolis, and they did not give a reply, as they just apparently just made up their arguments without any foundation. Basically, Wikipedia and Youtube video imply you can make up science facts about Coriolis and need not be constrained by physics and math. References 4 and 5 are not from the mainstream of geophysical fluid dynamics and earth sciences, and are not valid references. The authors in 4 and 5 provide their opinion on Coriolis and do not provide any mathematical or physical argument to defend (the indefensible) arguments.

Interestingly, reference 6 is from the MIT, and definitely does not support the Wikipedia claim "Though not obvious from this example, which considers northward motion, the horizontal deflection occurs equally for objects moving east or west (or any other direction)". The MIT reference does correctly state that the Coriolis force is the same in all directions i.e. " To an observer on the horizontal plane the Coriolis acceleration vector is horizontal and points due east for a northward movement and due west for a southward movement. By reference to Figure 7-12, the magnitude of the Coriolis acceleration is again 2vω sinφ. Although the mathematics is much more intricate, it turns out that the Coriolis acceleration has this same magnitude, 2vω sinφ, for any direction of movement in the horizontal plane." This text from reference 7 in no way supports the intuitive argument given in Wikipedia. The reason the Wikipedia text states "Though not obvious from this example" is because the Wikipedia arguments is a false intuitive argument that contradicts itself. It is very poor form to confuse the statements made in reference 7 into the desire to defend the bizzaro Wikipedia statement "Though not obvious from this example...". It is not obvious because it is not true. This kind of argument presented in Wikipedia if given say by a graduate student in a class would not pass, as it is indefensible and wrong. In other words, just citing a reference to back up a claim is not tolerable, if the reference does not support explicitly your claim. In the this case reference 7 actually contradicts the false intuitive argument given in Wikipedia.

Here is a simple argument to show arguments in references 4 and 5 from Wikipedia (and Youtube video) completely wrong. Following the specific argument made in the Youtube video, in Texas at latitude 30 degree north any object (like a paper airplane) is traveling at 860 mph eastward through space as it rotates with the earth. In Nebraska such an object would inherently be traveling slower at 760 mph. So the Wikipedia and Youtube arguments are saying that a paper airplane (or air parcel to be more realistic) traveling north from Texas to Nebraska would be traveling 100 miles per hour to the east when it reaches Nebraska. Well, yes it certainly has turned to the right in this case by this false argument, but if this was the actual case in nature, somebody would have noticed these ridiculously high wind speeds of 100 mph in Nebraska.

The false intuitive argument also falls on its face when considering a paper airplane going from Texas to Florida. In both Nebraska and Florida the paper airplane (or air parcel to be more realistic) would have the same eastward velocity (860 mph). So, there would be no Coriolis effect on the paper airplane. But, from the derivation of the Coriolis force we know that it is independent of the direction of travel on the earth, which proves the Wikipedia and Youtube intuitive arguments as wrong.

Also, the Wikipedia and PBS argument has no possibility of making the paper airplane (or air parcel) ever turn around and head south again. So a circular hurricane can never form on earth following the argument laid out in the Wikipedia and the video, which is the whole point of the argument. Instead, the airplane (or air parcel) will not stop heading north once it arrives in Nebraska but keeps going north and eventually arriving near the north pole moving eastward at 1000 mph. Just to restate that, the false intuitive argument has no possible mechanism to make air parcels travel in complete circles, in direct contradiction of the shape of hurricanes as seen in satellite pictures.

Air regularly circulates in large synoptic systems that cover north-south distances equivalent to Texas-Nebraska. Take a look at a typical weather briefing on the Weather Channel. The winds in these synoptic systems are not moving at 100 mph differences form one end of the system to the other, but generally at the same typical speed of 10 mph everywhere in the system. In a hurricane the winds do travel close to 100 mph, but this is the same speed at the north end of the hurricane as compared to the south end. A hurricane does not move 100 mph faster at one ed of the hurricane as compared to the other. This observational evidence itself completely trashes the Wikipedia and Youtube arguments.

Interestingly, the mathematical derivation of the Coriolis force shows that the Coriolis force has no dependence on the distance from the spin axis of the Earth (i.e. north pole). It only depends on the rotation rate of the Earth and the relative speed of an object to the spinning earth surface. The Centrifugal force does depend on the distance from the spin axis of the Earth, but not the Coriolis. So any intuitive argument of Coriolis that involves "latitude circles" and the distance to the north-pole is wrong on an mathematical and physical level, and therefore impossible to be claimed that intuitively the Coriolis depends on the north-south distance from the north-pole.

A better intuitive explanation to Coriolis is simply 'earth rotates beneath the atmosphere/ocean, so air/ocean which travel in straight paths appear to deflect when they move (i.e. Coriolis effect) relative to the spinning earth'. This intuitive argument does not depend on the false argument of distance north-south or the direction of travel, and is completely consistent with the physics of math.

RealCoriolis (talk) 15:49, 24 July 2018 (UTC)RealCoriolis

////

Hi. I believe there are valid reasons for including the "intuitive explanation" currently in the lead, or something similar, despite the fact that the mathematical expression is quite simple.

There are two reasons why I don't regard the explanation "the earth rotates beneath a moving object, making it appear to curve" as sufficient.

First, that explanation does not distinguish between the effects of the Coriolis force and that of the centrifugal force.

Second, it inevitably leads to the question of why the magnitude of the Coriolis force changes with latitude. You can try a line like: "the local rate of rotation about a vertical axis (half the 'planetary vorticity') is equal to the projection of the Earth's rotation vector onto the local vertical--so, effectively, the rotation rate increases toward the pole"; but, based on experience, this is not readily accepted by someone learning these concepts for the first time. The typical response is: "wait, but the rotation rate of the Earth is once per day, no matter where you are." The "intuitive example" at least makes an attempt to overcome these cognitive obstacles.

As to your claim that the lack of 100 mph winds in Nebraska disproves the validity of the example: when anything (such as an air parcel) moves over the surface of the earth with no horizontal external forces applied, that is "inertial motion". Due to the Coriolis force, such motion is circular. The diameter of the circles depends on the speed of the motion. In order for such a circle to stretch from Texas (northward motion) to Nebraska (eastward motion)--say, a radius of 400 miles--the speed would indeed need to be in the range of 100 mph (as the inertial period at that latitude is around a day).

The current example is not immutable. If you can suggest improvements that take the above points into account, I would welcome them.

Rracecarr (talk) 18:01, 24 July 2018 (UTC)

Note that user RealCoriolis was blocked for block evasion as user Davidmholland. - DVdm (talk) 18:10, 24 July 2018 (UTC)

And likewise new username Efdl.wiki. - DVdm (talk) 21:39, 24 July 2018 (UTC)

Is there any harm in engaging with his socks as long as he confines himself to the talk page? (Er, just noticed the edits to other articles. They are mainly not bad, but clearly flout the block. I won't respond further until block is cleared.) Rracecarr (talk) 22:03, 24 July 2018 (UTC)

@DavidMHolland: You can spout all the hyperbole you like about how completely incorrect it is--just shows you're not willing to consider that the same thing can be explained in many ways. Your understanding of the Coriolis force seems to be correct; however, your continued assertions that it has "nothing to do" with latitude circles, or that the example offered is a "confused misunderstanding" don't hold up. The statement that the speed of a point closer to the equator is larger than one on a smaller circle of latitude further from the equator is just another way of saying that the ground is effectively rotating underneath one's feet. Not wrong: just a different, less mathematical approach.

I agree with you that a shallow rotating parabolic dish is a good model for developing an understanding of the Coriolis force as a fictitious force arising in a rotating reference frame, which, appropriately, is how it's presented throughout most of the article. But the fact is that in the overwhelming majority of cases in which most people run across the concept of Coriolis force the relevant rotating reference frame is the earth, which is spherical. My feeling is that to the extent that a simple example can be provided describing the effect on the Earth's surface (away from the pole), it will be more useful to these readers than one on a turntable. In any case, there are plenty of other turntable examples in the article.Rracecarr (talk) 22:03, 24 July 2018 (UTC)

Good edit, this. And I agree with the above. Let's keep it at an intuitive explanation, without complications. Any "improvement" to this is likely going to make it less intuitive, even if strictly correct. Strict correctness is not the subject of this section, on the contrary. I propose to just close this thread already. - DVdm (talk) 09:04, 25 July 2018 (UTC)

Rotating sphere figure

The arrows don't look right, esp. the y and x vectors. We need a better diagram. Betaneptune (talk) 18:26, 26 October 2018 (UTC)

Why the negative sign?

Just an innocent question. Why is there customarily a negative sign in the equation for Coriolis acceleration and force?

${\boldsymbol {F}}_{C}=-2\,m\,{\boldsymbol {\Omega \times v}}$

It could be got rid of by reversing the order of ${\boldsymbol {\Omega }}$ and $v\,$ Then the direction of Coriolis force could be defined by the right-hand rule. Just wondering why it is normally written this way. --Chetvorno^TALK 11:50, 18 June 2015 (UTC)

You normally use your thumb for the rotation vector and your index for the velocity. So keeping with the right-hand rule it's more natural to write Omega x v and put a negative sign Sergefranchoo (talk) 14:13, 27 June 2018 (UTC)

In what follows, G, omega, r, and v are vectors. x is the cross-product operator.

It's because of the rotation operator. For a general vector G

(dG)_space = (dG)_body + (dG)_rot

(dG/dt)_space = (dG/dt)_body + omega x G

where G is an arbitrary "General" vector. So if you know how G is changing in time in the body frame, you add omega X G, which then gives you how G is changing in the space frame.

This can be generalized to the operator expression

(d/dt)_space = (d/dt)_rot + omega X

So you get omega X as part of the operator and you end up with cross products that start with omega.

Apply the above operator to v and to get

v_space = v_rot + omega X r # v_rot is v as seen in the body, or rotating frame.

Then apply the operator again to get the acceleration in the space frame:

a_space = (d/dt v_space)_rot + omega x v_space

       = a_rot + 2(omega x v_rot) + omega x (omega x r)

Multiply by m to get the force. In the end you get

F_space = F_rot + 2m(omega x v_rot) + m omega x (omega x r)

That equation is the force as seen in the space frame. But we're looking for what's seen in the rotating frame, e.g., the earth. So we then get

F_rot = F_space - 2m (omega x v_rot) - m (omega x (omega x r))

and that's why you get the minus signs. To keep things consistent, you keep omega first, with a cost of the minus signs.

I got this from Classical Mechanics by Goldstein, and I think he might have gotten the _body and _rot confused, or maybe I did. Bottom line: The final equation is right and the stuff before it, even if the _body and _rot might be wrong in places, you can still see why we get the minus signs. Sorry for any goofs I might have done here.

Betaneptune (talk) 18:24, 26 October 2018 (UTC) Betaneptune (talk) 04:22, 1 November 2018 (UTC)

A suggestion

Balance between gravitational an centrifugal force on the Earth surface

In the introduction it says "Though not obvious from this example, which considers northward motion, the horizontal deflection occurs equally for objects moving east or west (or any other direction)."

The deflection east/west is in fact due to another cause! A part of the "coriolis force" is in fact the change in the "centrifugal force" for a mass element MOVING relative the rotating reference system (i.e. here the Earth). If an object (i.e. atmosphere) moves towards east its "rotational speed" relative the Earth axis is higher and the gravitation no longer balances the "centrifugal force" resulting in a drift towards the equator. The balance between the gravitational force and the centrifugal force is illustrated in the figure (click to enlarge).

I would be willing to add some sentences explaining this deflection of east/west motion towards and away from the equator. Stamcose (talk) 21:23, 12 December 2018 (UTC)

References

Pardon, I took the freedom to refactor the above.Purgy (talk) 08:00, 13 December 2018 (UTC)

I looked at the article again! It certainly is a typical "grown" Wikipedia article with contributions from many (uncoordinated!) authors! Anyway, as the the main or at least one of the most important application of the concept is for meteorology I think it is important to explain the balance between gravitational och centrifugal force on the surface of the rotating Earth. I would therefore propose to replace the text under "Applied to the Earth" with the following

++++++++++++++++

The concept "Coriolis force" is specially suitable for the description of motion of atmosphere (i.e. winds) over the surface of the Earth. The Earth (like all rotating celestial bodies) has taken an oblate shape such that the gravitational force is slightly off-set towards the Earth axis as illustrated in the figure.

Balance between gravitational an centrifugal force on the Earth surface

For a mass point at rest on the Earth surface the horizontal component of the gravitation counteracts the "centrifugal force" preventing it to slide away towards the equator. This means that the vector term of the "equation of motion" above

$\omega ^{2}{\boldsymbol {r}}_{ort}\ +{\boldsymbol {f}}$

is directed straight down, orthogonal to the surface of the Earth. The force affecting the motion of air "sliding" over the Earth surface is therefore (only) the horizontal component of the Coriolis term

$-2\,{\boldsymbol {\Omega \times v}}$

++++++++++++++++

But for this it is necessary to expand the text under "Formula" somewhat! This I think also should be done "in its own right". My proposed new text:

++++++++++++++++

The Newtonian equation of motion for a mass point in an inertial system is

${\boldsymbol {a}}={\boldsymbol {f}}$

where ${\boldsymbol {a}}$ is the acceleration of the mass point relative to the inertial system and ${\boldsymbol {f}}$ is the force (per unit mass) acting on the mass point. Transforming this equation to a rotating system it takes the form

${\boldsymbol {a}}_{C}=-2\,{\boldsymbol {\Omega \times v}}+\omega ^{2}{\boldsymbol {r}}_{ort}\ +{\boldsymbol {f}}$

where

${\boldsymbol {a}}_{C}$ is the acceleration relative to the rotating reference system

${\boldsymbol {\Omega }}$ is the rotation vector of the rotating system relative to inertial space

${\boldsymbol {v}}$ is the velocity relative to the rotating reference system

$\omega$ is the (scalar) rotation rate of the rotating system relative to inertial space

${\boldsymbol {r}}_{ort}$ is the projection of the position vector ${\boldsymbol {r}}$ on the plane orthogonal to ${\boldsymbol {\Omega }}$

${\boldsymbol {f}}$ is the force (per unit mass)

See fictitious force or for a derivation.

The term

$\omega ^{2}{\boldsymbol {r}}_{ort}$

which (only) depends on the position in the rotating system is known as the "centrifugal force" and the term

$-2\,{\boldsymbol {\Omega \times v}}$

which (only) depends on the velocity relative to the rotating system is known as the "coriolis force"

The Coriolis effect is the behavior added by the Coriolis acceleration. The formula implies that the Coriolis acceleration is perpendicular both to the direction of the velocity of the moving mass and to the frame's rotation axis. So in particular:

• if the velocity is parallel to the rotation axis, the Coriolis acceleration is zero. (For example, on Earth, this situation occurs for a body on the equator moving north or south relative to Earth's surface.)
• if the velocity is straight inward to the axis, the acceleration is in the direction of local rotation. (For example, on Earth, this situation occurs for a body on the equator falling downward, as in the Dechales illustration above, where the falling ball travels further to the east than does the tower.)
• if the velocity is straight outward from the axis, the accBut whn the atmosphere is movingeleration is against the direction of local rotation. (In the tower example, a ball launched upward would move toward the west.)
• if the velocity is in the direction of local rotation, the acceleration is outward from the axis. (For example, on Earth, this situation occurs for a body on the equator moving east relative to Earth's surface. It would move upward as seen by an observer on the surface. This effect (see Eötvös effect below) was discussed by Galileo Galilei in 1632 and by Riccioli in 1651.)
• if the velocity is against the direction of local rotation, the acceleration is inward to the axis. (On Earth, this situation occurs for a body on the equator moving west, which would deflect downward as seen by an observer.)

+++++++++++++++++++

I think this is a useful update keeping the text from other contributors to the largest possible extent!

Stamcose (talk) 17:44, 18 January 2019 (UTC)

I now made the update as it obviously is a significant improvement!

In addition I must say that I think there is a quite a lot of "round about" text in the article that ideally should be removed! After all it is an article with 1000s of accesses each day, it is a pity if it is "sub-optimal".

Stamcose (talk) 11:20, 19 January 2019 (UTC)

Personally, I am not a fan of the whole force per mass formulation. I cannot recall any derivation in any of the textbooks I've seen use that for this concept. I think it also muddles the distinction between force and acceleration. A force is what goes into the summation of forces on the lefthand side of Newton's equation, whereas the acceleration is a single vector on the other side. We can break up the acceleration into different terms like the centrifugal/centripetal or Coriolis terms but, imo, that leads to confusions like the fringe idea that the centrifugal force is a real force in the inertial frame just because of the way you can write the acceleration in polar coordinates. Maybe in specialized meteorological sources they do this, but I believe it's rare in general physics texts.

I've taken some wording from the centrifugal force and fictitious force articles and followed the pattern there a bit. I don't think we need to go into much detail of the centrifugal force - that's why we link to that article. I think it is sufficient to point out that it also pops out of the same derivation and why we make a distinction between the centrifugal and Coriolis forces. --FyzixFighter (talk) 03:34, 20 January 2019 (UTC)

Continued improvement?

I think it is not possible to have an adequate "Intuitive explanation" without referring to the fundamental role of the Earth gravitation that together with the Earth rotation is the cause of the "Coriolis effects" for the atmospheric motion. What about the following text referring to the figure illustrating the basic balance of forces?

++++++++++++++++++++++++++++++++++++++++++++++=

Intuitive explanation

If there is wind towards east the inertial velocity of the atmosphere (relative to the Earth center) is higher then the velocity of the Earth surface below. The horizontal component of the gravitational force is then not sufficient to prevent the atmosphere from being accelerated towards the equator. If there is wind towards west the the centrifugal effect is instead lower and the horizontal component of the gravitational force accelerates the atmosphere away from the equator. If there is wind in the direction "away from the equator" the atmosphere will reach areas where the eastward velocity of the ground is lower. Relative the ground the atmosphere therefore has an increasing eastward component. At the same time the centrifugal effect decreases the original velocity component "away from the equator". If there is wind in the direction "towards the equator" the atmosphere will reach areas where the eastward velocity of the ground is higher. Relative the ground the atmosphere therefore have an increasing westward component. At the same time the horizontal component of the gravitational force decreases the original velocity component towards the equator.

A detailed description of an "inertial circle" resulting from the "Coriolis effects" described above can be found in (based on exact numeric integration of the equation of motion)

Stamcose (talk) 17:00, 19 January 2019 (UTC)

References

I do not intend to interfere with what you consider to be an improvement of this article. However I am perplexed by some terminology, of which I do not know whether it is general meteorologic lingo or not: isn't a force per unit mass simply an acceleration, doesn't the surface normal in a point on the earth's surface simply deviate from the direction to the barycenter, so it might be better to be explicit about what is meant under "horizontal", instead of stating some "tilt" to the equator, the notion "exact numerical integration" sounds a bit idiosyncratic, I never heard of "inertial velocities" and of an "inertial circle" that should should result from "Coriolis effects", ... Coriolis force/effect certainly exists, and deserves an article (with explanations) in WP, even when it not occurred in the context with meteorology.

Should this be off-limits for non-meteorologists? Purgy (talk) 17:55, 19 January 2019 (UTC)

1

Force per unit mass is the concept, specially when gravitational forces from different masses are added up. That force => acceleration is Newtons law!

2

Offset is relative the surface normal for the reference ellipsoid (geoid). Has nothing to do with the Earth centre

3

"Exact numerical integration" is what is done with differential equations. Central in applied mathematics!

4

"Inertial velocities" as opposed to velocities relative a non-inertial reference system (here rotating reference system) is the concept

5

Read further down (or Google!) what "inertial circles" is in meterology

Stamcose (talk) 18:28, 19 January 2019 (UTC)

Maybe this is the smallest bubble of yours to get out of by googling for the meaning of "numerical integration" (of DEs): this is a technique for approximating a solution, and in no context something exact.

As said, I wont interfere with your "significant improvements", but maybe you should take the opinion of others more seriously. In any case, I left a note here. Purgy (talk) 07:42, 21 January 2019 (UTC)

Interference by user "FyzixFighter"

My original formula was

${\boldsymbol {a}}_{C}=-2\,{\boldsymbol {\Omega \times v}}+\omega ^{2}{\boldsymbol {r}}_{ort}\ +{\boldsymbol {f}}$

Because user "FyzixFighter" is "not a big fan of the force per unit mass formulation" because he thinks that "it tends to "muddy the distinction between force and acceleration" he changed it to

${\boldsymbol {F}}-m{\frac {\operatorname {d} {\boldsymbol {\Omega }}}{\operatorname {d} t}}\times {\boldsymbol {r}}-2m{\boldsymbol {\Omega }}\times {\boldsymbol {v'}}-m{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}})$ $=m{\boldsymbol {a'}}$

1 - I disagree, there is no risk for any "muddy"

2 - If one really does not like " force per unit mass" simply write

${\boldsymbol {a}}_{C}=-2\,{\boldsymbol {\Omega \times v}}+\omega ^{2}{\boldsymbol {r}}_{ort}\ +{\frac {\boldsymbol {F}}{m}}$

or if preferred

${\boldsymbol {a'}}=-2\,{\boldsymbol {\Omega \times v'}}+\omega ^{2}{\boldsymbol {r}}_{ort}\ +{\frac {\boldsymbol {F}}{m}}$

3 - He even screved it up, what he meant was

${\boldsymbol {F}}-2m{\boldsymbol {\Omega }}\times {\boldsymbol {v'}}-m{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}})$ $=m{\boldsymbol {a'}}$

but it is certainly better for the reader to see my

$\omega ^{2}{\boldsymbol {r}}_{ort}$

rather then the more mysterious "double cross product" of user "FyzixFighter":

${\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}})$ 

what is the same, only more complicated!

I would therefore propose to use (as a compromise!)

${\boldsymbol {a'}}=-2\,{\boldsymbol {\Omega \times v'}}+\omega ^{2}{\boldsymbol {r}}_{ort}\ +{\frac {\boldsymbol {F}}{m}}$

To multiply the Coriolis term and the Centrifugal term with the mass to be able call them "forces" is uttermost nonsense!

Am I right? If I do not receive any protests I will change it (back!) to this correct and more readable format

Stamcose (talk) 17:23, 20 January 2019 (UTC)

Anyway, I do not have the time nor the nerve to fight an "editing war" with this user "FyzixFighter" (fighter!!!). I know this "Wikipedia problem" from before! Astonishing that it works relatively well although anybody can write and and change anything!

Stamcose (talk) 17:33, 20 January 2019 (UTC)

Dude, chill. No one is interfering. This is a collaborative effort. "Interference" can only happen if you think you own the article or if my edits are malicious. Interference would be behavior characteristic of User:FDT/David Tombe or some other fringe pusher or User:Brews ohare. I apologize if I was too terse in my explanation or if I communicated my rationale poorly. Let me try to be a bit more clear to the points you raise above:

1. We're probably going to agree to disagree on if it muddies the distinction. Beyond that, I would point to the number of physics textbooks and other technical sources that describe the formula without using "force per mass". I think I've only seen it once in a specialized meteorology textbook. Why is "force per mass" preferable? Why should we ignore the way this is described in numerous reliable sources?
2. Similar to the above, because that's not how it is treated in reliable sources. The article is about the Coriolis force, not the Coriolis force per unit mass and not the Coriolis acceleration.
3. Are you talking about the first term, which is the Euler force? The Euler force pops out of the general derivation if you don't assume the rotation rate is constant. We use the same formula on the fictitious force article and the centrifugal force article. Why do you feel we should not include the Euler force? I did go back and forth on $\omega ^{2}{\boldsymbol {r}}_{ort}$ and ${\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}})$. I think the latter is better because it is the more general way to write it and is consistent with the use of $\omega$ and $\Omega$ used in the rest of the article. Also, ${\boldsymbol {r}}_{ort}$ seems to come out of nowhere - at least if you start from the vector cross product you can see why we only care about the orthogonal distance. But in the end, this is an article about the Coriolis force, not the centrifugal force, so deep diving into the centrifugal force seems a bit out of scope.

Are there any third opinions or thoughts from other editors? --FyzixFighter (talk) 20:00, 20 January 2019 (UTC)

1. I am from profession Spacecraft Flight Dynamics Specialist! I did not only read text books in the beginning of my career, I am also the author of numerous scientific papers about satellite orbits and interplanetary flight! Nobody in this environment (spacecraft flight/astro-dynamics) would ever talk about anything else then "force per mass unit" as almost all forces are due to gravitation! It would be ridiculous to drag around a symbol "m" for mass in all formula. Here the situation is the same! The "atmospheric circulation" for which the Coriolis effect is relevant is also an effect of gravitation, rotation and shape of the planet!
2. The "Euler force" is not relevant for this discussion as there is no reason to involve accelerating rotating systems when the Coriolis Term is discussed. Here one should restrict oneself to uniformly rotating system with one Coriolis term and one Centrifugal term. The atmospheric circulation depends on these two terms, an "Euler force" is irrelevant here!
3. It should rather be stressed that the Coriolis term is no force but a term resulting from mathematical formula manipulation. As it is no force it has in fact nothing to do with any "mass"

Stamcose (talk) 20:52, 20 January 2019 (UTC)

1. But the Coriolis force/effect is not strictly an atmospheric effect or gravitational effect. It appears in all rotating frames regardless of the application. In the more specialized sections that follow I think it would make sense to make use of the shorthands you suggest. But when we are first introducing and defining and describing the general concept, imo we should not fall into the trap of specialized language or presentation.
2. By that same argument, shouldn't it be irrelevant to discuss the centrifugal term? In the general transformation from a inertial frame to a rotating frame there is an Euler term. For example if you are analyzing an object in an elliptical orbit and transform to a frame which rotates with the object (so that ${\dot {\theta }}=0$ for the object in the rotating frame) you do need to include all three (Euler, Coriolis, and centrifugal) terms. Again this is a general presentation of the formula that should be agnostic as possible about the application. Hence why I advocate for a brief inclusion of the Euler force term.
3. Agreed, the Coriolis force is an artifact of transforming the equation of motion to the rotating frame and not a true Newtonian force. It's a pseudoforce / fictitious force / inertial force - take your pick. However, most of the definitions I've seen for it include m in its definition. Do you have general sources that present it otherwise?

--FyzixFighter (talk) 22:12, 20 January 2019 (UTC)

Offhand, I can't recall "force per unit mass" from any of the classical-mechanics textbooks that I've used. It would not surprise me to hear that other fields, more specialized than physics, have their own vocabularies and approaches. We should cover such differences, because that helps bring clarity. On the whole, though, I agree with FyzixFighter's point above, that when we are first introducing and defining and describing the general concept, imo we should not fall into the trap of specialized language or presentation. And I don't find ${\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}})$ all that mysterious; of course, being a physicist, I wouldn't. XOR'easter (talk) 18:18, 21 January 2019 (UTC)

In the "intuitive explanation": Radius of what?

"This means the object will take a path of increasing radius due to centripetal acceleration." Radius of what? — Preceding unsigned comment added by Betaneptune (talk • contribs) 01:29, 30 March 2019 (UTC)

Caption of the Fig.1

In caption of Fig.1, I proposed to change the present caption by: "In an inertial frame of reference, as, for example, when you see the upper part of the picture without rotate your head or your eyes respect to the screen, the black ball moves in a straight line (upper part of the picture). However, an observer (red dot) who is standing in a rotating/non-inertial frame of reference (upper part of the picture again) sees (as depicted in the lower part of the picture) the object as following a curved path due to the fictitious Coriolis and centrifugal forces present in this frame" Crystallizedcarbon undid two times my proposal, but I think that it clarifies the straight line that we see in the upper part of the picture, but only if we see fixedly the ball trajectory. Thanks, Co-scienza (talk) 14:57, 7 June 2019 (UTC)

Thank you @Co-scienza: for bringing it here. I think "without rotate your head or your eyes respect to the screen" is not needed, grammatically incorrect and I think it could confuse the reader. Same goes for "(upper part of the picture again)" the red dot is the same in both cases, it is just a matter of the frame of reference used. I do not understand your comment that it clarifies the straight line in the upper part of the picture. it is not a matter of what you look at but a matter of from where you look at it. The circle is rotating in both cases (top and bottom). for the top image, please imagine the red dot is placed at the end of a seconds hand of a very large watch in a wall moving faster than usual and counter-clockwise, and the black ball is falling in front of it from its center if you place a camera in front of the center of the watch you would record the top image. If you now place the camera at the place where the red dot (so that it rotates along with it) then you would record the bottom image. I hope this helps to clarify it. Regards. --Crystallizedcarbon (talk) 16:06, 7 June 2019 (UTC)

Exactly, Crystallizedcarbon, I meant that our eyes must be fixed ìnto the center, like your camera. My eyes constitute the non-rotating reference, as your camera, whereas the rotating red point the rotating non-inertial frame. I would say that if I see my screen while I'm rotating my eyes (clockwise or counter-clockwise (rotating the neck is more difficult)) or if I rotate my touchscreen, I see the straight line as a curving line, as the red point says. Co-scienza (talk) 18:39, 7 June 2019 (UTC)

I also don't see how the proposed text is an improvement. Talking about the reader's eyes and head make it seem like the Coriolis force is an optical illusion, and not the result of describing the motion in a non-inertial frame. It also addresses the reader directly, which is not appropriate for wikipedia (see MOS:NOTED and WP:TONE). How is the current caption deficient? --FyzixFighter (talk) 16:25, 7 June 2019 (UTC)

A force is not a kinematic effect, but a dynamic quantity. To address to the reader, is useful in my opinion to call him in cause as an observer, if his eyes are fixed (or if his touchscreen is not rotating during the watching to the GIF animation): he is an inertial reference frame Co-scienza (talk) 18:39, 7 June 2019 (UTC)

I disagree. The Coriolis force (and other similar fictitious forces) are at root kinematic effects resulting from the use of a rotating frame (see John Taylor, "Classical Mechanics", pg 350). In textbooks and other instructional materials, it might be appropriate to address the reader directly, but the manuals of style for Wikipedia say explicitly not to do it (see WP:TONE and MOS:NOTED). Figure out another way to say it. It would again help for you to clearly state the deficiency of the current text - you've given your proposed text, but you've never stated why it is better than the current text. If you explain why the current text is lacking, then maybe we can all work together here rather than you constantly being reverted because you are unable to collaborate constructively. --FyzixFighter (talk) 21:33, 7 June 2019 (UTC)

I agree, just wanted to note that the example figure is illustrating just a matter of perception as the ball is not travelling within the rotating frame of reference. it is travelling in a straight line in the inertial frame of reference unaffected by the rotation of the disk. Relative to a viewer within the rotating frame of reference that straight path is curved. This is different from a better example: What happens when we walk towards the center of a marry-go-round in which we are standing. when we do so, besides the centrifugal force we also feel a sideways acceleration within our rotating frame of reference in the direction of rotation and proportional to how fast we try to reach the center. --Crystallizedcarbon (talk) 17:03, 7 June 2019 (UTC)

You are right, Crystallizedcarbon, that the picture could be misunderstood: the plate drags only the red dot point, not the black ball. In my opinion also this possible misundertanding should be dissipated in the caption Co-scienza (talk) 18:39, 7 June 2019 (UTC)

Hello @Co-scienza: We both have the same understanding, but I don't see in which way is the current caption misleading or incomplete. The ball goes clearly on a straight path on the inertial frame (independent of the rotation). I think is safe to asume that readers will keep their head still when looking at the top of the figure (and also at the bottom). For a caption I don't think we should add an excessive level of detail, so I don't think it would be correct to explain that fact or that if you rotate your Head or the screen along with the disk you will perceive a curved path, even though I agree with you that both statements are correct. Regards. --Crystallizedcarbon (talk) 06:38, 10 June 2019 (UTC)

Substantially I agree: it is better to leave the caption as simpler as possible ≈≈≈≈≈ — Preceding unsigned comment added by Co-scienza (talk • contribs) 13:51, 11 June 2019 (UTC)

I am glad we could reach a consensus. Thank you. --Crystallizedcarbon (talk) 15:37, 11 June 2019 (UTC)

It's not a fictitious force.

Physics is about reality, not fiction. Goldstein, in his graduate physics text Classical Mechanics, calls it an effective force. If you are in the rotating frame of reference, it is quite real. Non-powered moving objects will in fact, not in fiction, deviate from a straight line path. I recommend it be changed to effective force or inertial force. I could even, perhaps, go with pseudo-force -- maybe. But not fictitious force, because it isn't. Betaneptune (talk) 07:06, 27 August 2019 (UTC)

I understand your reasoning, however these types of forces appear to be referred to as "fictitious forces" throughout Wikipedia. Perhaps the talk page archives for that article explains the rational. There's no question the phenomena is real, our cannoneer observes an acceleration to the right. It's useful to assign a "force" to this acceleration. The problem is the cannon ball also appears to be gaining kinetic energy, but there is no source for this energy. That can't be, thus this "force" we've assigned is performing no work, and so isn't a real force. When Goldstein is writing to Physics graduate students, he can assume this is well understood, here on Wikipedia we're writing to the more general public and can't assume that. Meteorology uses the prefix pseudo- for a few things, so I think pseudo-force is best. That's highly specific to the subject material, and this article has to serve a much broader range of interest. -- Watchwolf49z (talk) 14:35, 27 August 2019 (UTC)

Within our rotating frame of reference we perceive a deflection, Coriolis accounts for that perceived deflection. We also perceive that the sun and most stars are describing various orbits around us. If we are inside of a car and and we turn left we feel a "fictitious" force to the right within the frame of reference of the car, while the real force is being applied by the car on to us to change our inertial path on the opposite direction. If you throw a ball towards the center of a merry go round you will perceive that it deviates from a straight line path, but in absence of real external forces (gravity..) its path as soon as it leaves your hand will be straight in the inertial frame of reference. I think that the fictitious term accounts for that difference in perception within the rotating frame of reference. In any case, the lead does describe it as inertial or fictitious. --Crystallizedcarbon (talk) 17:11, 27 August 2019 (UTC)

Recommended change: left/right

There are mentions of deflection to the 'right' (in northern hemisphere) and 'left' (in southern one) in this page. This is bad term to use since it depends entirely on which way the observer is facing. I strongly recommend that a consistent description of orientation be used for the Earth: either east/west, or clockwise/anticlockwise at a specific pole.TonyP (talk) 11:47, 28 November 2019 (UTC)

These terms are not ambiguous at all. They are relative to the direction of movement. So East or West are unusable. (anti)clockwise is also confusing, because that would be at most the result of continued deflection. The force itself is perpendicular to the direction of movement. in the literature left/right is the standard wording. −Woodstone (talk) 04:02, 29 November 2019 (UTC)

Thanks Woodstone. I'm thinking about it again and I see what you're saying. At the time, I was thinking about the conservation of angular momentum (which can be explained in terms of inertial forces) but was getting confused by the rotation of the Earth.TonyP (talk) 10:54, 29 November 2019 (UTC)

Do not overstate or understate the effect

This sentence from the article is wrong. In fact it is contradicted by its own reference.

> However, the theory that the effect influences draining water to rotate anti-clockwise in the northern hemisphere and clockwise in the southern hemisphere has been repeatedly disproven by modern-day scientists

The Scientific American article cited includes this quote

> "Do bathtubs drain in different directions in the two hemispheres? If you had a specially prepared bathtub, the answer would be yes.

Of course the effect influences draining water to rotate. In any typical bath or toilet it is negligible but it can be demonstrated.

The experiments have been done on a large enough tub in the southern hemisphere (Shapiro 1961) and the southern hemisphere (Trefethen et al 1965 https://www.nature.com/articles/2071084a0) and the experiments confirmed the theory. — Preceding unsigned comment added by Emmelaich (talk • contribs) 03:49, 3 June 2020 (UTC)

The proper name is "Coriolis Effect" it is a fictional force

Just as "centrifugal force" is actually conservation of momentum, the Coriolis Effect is not a force.

Since I don't understand why some incorrect entry names (such as "Coriolis force" or "Mark Twain") are chosen, I will not dare to change the main entry. However, the editors should look at these entries and correct them.

No page about a person should be titled by a pseudonym. Instead, the pseudonym should redirect to the person's name.

Pages about science should stick to scientific terminology for titles. Alternate names in common use should redirect.

See Talk:Coriolis_force/Archive_7#Proposed_move_to_'Coriolis_Force'. for the discussion on why this page is at "Coriolis force". --FyzixFighter (talk) 02:35, 17 June 2020 (UTC)

acceleration

Only the forces are fictional not the accelerations. This part of the article is Nonsense!--Wruedt (talk) 14:59, 2 February 2020 (UTC)

Force applied to objects causes acceleration. Could you please elaborate? --Crystallizedcarbon (talk) 15:09, 2 February 2020 (UTC)

The fictional Forces are "assumed" because an "observer" realize an acceleration and according to Newton II some people "assume" that this acceleration might caused by a force that das not satisfy Newton III. These acceleration are pure Kinematics. So the accelerations are all real!--Wruedt (talk) 16:08, 2 February 2020 (UTC)

As an example, to an observer on top of a very large rotating disk, an object moving at constant speed on a straight line in the inertial frame of reference just above him, towards the center would seem to be accelerating. In that example, Coriolis accounts for that perceived acceleration in the rotating frame of reference. --Crystallizedcarbon (talk) 19:59, 2 February 2020 (UTC)

The acceleration observed (perceived) in the rotating System is real. The Coriolisforce is asumed to be responsabel for this acceleration. The force is fictional (das not exist in the sense of a real force (Newton I-III)), the accelerations are real. This section is Nonsens. fictional accelerations ar TF.--Wruedt (talk) 20:33, 2 February 2020 (UTC)

I think what the original author of the section may have meant is that acceleration expressed in rotating coordinate system has additional terms that due not appear when it is expressed in the stationary frame coordinates. I would agree that really doesn't make the accelerations "fictional", just expressed in a non-stationary frame. In all honesty, the whole section tries to be too textbook-y due to the influence of a now-banned editor who, while very knowledgeable and able to make nice images, tried to turn most articles into textbook chapters and did not seem able to work cooperatively with other editors. The whole section needs to be pared down, imo. --FyzixFighter (talk) 04:09, 3 February 2020 (UTC)

if we describe Coriolis as a Fictitious force, the same should apply to the acceleration it accounts for. In the example above, illustrated by the first image of the article, Coriolis is needed to account for that "perceived" acceleration by an observer within the rotating frame of reference of an object that is really just moving in a straight line with constant velocity and 0 acceleration. The one that is actually subject to acceleration is the observer. Within the rotating frame of reference we assume that an observer subject to acceleration is stationary, the fictitious forces and accelerations are needed to counter that assumption. --Crystallizedcarbon (talk) 08:26, 3 February 2020 (UTC)

+1 FyzixFighter: @Crystallizedcarbon: You don't need any "observer". You can obtain these accelerations only pure with geometrie or kinematik. Nobody need's a force or have to assume any thing. These acceleration can be calculated straightforward. You must give a reference for the expression fictional acceleration. I suppose there is none.--Wruedt (talk) 08:41, 3 February 2020 (UTC)

Right. Does the object in the example moving in a straight line with constant speed have any "real" acceleration? --Crystallizedcarbon (talk) 09:02, 3 February 2020‎ (UTC)

Yes zero. There are no "unreal" accelerations--Wruedt (talk) 10:11, 3 February 2020 (UTC)

In the inertial frame of reference (upper part of the picture), the black ball moves in a straight line. However, the observer (red dot) who is standing in the rotating/non-inertial frame of reference (lower part of the picture) sees the object as following a curved path due to the Coriolis and centrifugal forces present in this frame.

But from the point of view of the observer within the rotating frame of reference that same object with zero "real" acceleration is actually accelerating... --Crystallizedcarbon (talk) 11:25, 3 February 2020 (UTC)

Of course!!! This acceleration is called relative acceleration and is as real as any other acceleration in a reference system. This relativ acceleration is at the beginning of the motion the coriolis-acceleration. The curved motion is a result of the accelerations and only some people asume that there must be a force. But this is a fictious force because this force does not exist.--Wruedt (talk) 12:07, 3 February 2020 (UTC)

Right, but because as you said, its real acceleration in the inertial frame of reference is zero, it can be called a "relative acceleration" or "perceived acceleration", fictional, etc within the rotating frame of reference, because the fact is that it's actually the observer and not the object that is actually accelerating. Same as you perceive an acceleration towards the right when inside of a car turning left but what "really" accelerated was the car in the oposite direction. --Crystallizedcarbon (talk) 17:54, 3 February 2020 (UTC)

When you sit in a car you dont "perceive an acceleration towards the right when ... a car turning left". You perceive as well the acceleration to the left caused by a force from the seat, also the relative accelaration zero in the car (Optic). The Diskussion is hopeless. You shoud study Perception--Wruedt (talk) 18:19, 3 February 2020 (UTC)

Change you by your head, or by a ball on top of the dashboard... To you (from inside the car), they do not seem to accelerate to the right??... OK, lets agree to disagree... --Crystallizedcarbon (talk) 18:45, 3 February 2020 (UTC)

This section theorie finding. What you call "apparent Coriolis acceleration" is the tangential component of the coriolis-acceleration calculated with the radial velocity v in your notation. Why do you revert changes wich are right and nessecary WP:VANDAL.--Wruedt (talk) 09:39, 4 February 2020 (UTC)

Sorry i forgot. There is no declared Notation. Sometimes v is a (konstant) velocity in the intertial system, sometimes the radial velocity to produce "an additional component of acceleration perpendicular to rB(t)". This section has to rewritten complete.--Wruedt (talk) 10:01, 4 February 2020 (UTC)

Also "Bug": "true centripetal force". Since Newton the centripetal force is a physical force (vis impressa). In this example there is no physical force present.--Wruedt (talk) 10:23, 4 February 2020 (UTC)

Only "strange" references use "fictious acceleration". WP here ist one of it. In generell this term is not used and has to be erased.--Wruedt (talk) 12:00, 4 February 2020 (UTC)

Please remember to assume good faith. Accusing other editors of vandalism over a content dispute is against our policies. Why do you consider the book from Universal publishers The pendulum paradigm, to name one example, or Cambridge University Press to be "strange references"? --Crystallizedcarbon (talk) 17:12, 4 February 2020 (UTC)

First because this is not "state of the art" in Technical mechanics and in physics. Second because something what can be calculated straightforward or derived by geometrie can not be fictious. This is the difference to the fictious force which only is assumed to have an expression similar (analog) to Newton II.--Wruedt (talk) 17:56, 4 February 2020 (UTC)

Try to search in WP for "fictitious acceleration". The result: one Artikle.--Wruedt (talk) 15:09, 7 February 2020 (UTC)

These accelerations are real before this quantities are brought on the other side of an equation. ==> They never can be named as "fictitious"--Wruedt (talk) 10:48, 19 March 2020 (UTC)

With due respect to those who've studied dynamics, I want to support @Wruedt assertions here. Coriolis acceleration may be described in the study of kinematics. Kinematics is the study of position, velocity, and acceleration of bodies without respect to forces. If we create geometry and movement where a coriolis acceleration exists, we can talk about this without resorting to forces, because the acceleration is inherent in the movement of the bodies, without respect to the causes of the movement. It is as real as any other acceleration. If we talk about "force", we need to understand, in the convention of mechanics (Newton I), that forces such as "centripetal force" producing cenripetal acceleration are "real" and forces such as "centrifugal force" are imaginary. If we use d'Alembert's principle, we can turn this on it's head, and treat the otherwise "imaginary" forces as "real". In any case,the acceleration exists and can be analyzed in kinematics, without resort to forces. The title of the article might better be changed to "Coriolis acceleration", and talk about forces in some secondary sense. — Preceding unsigned comment added by Pdr0663 (talk • contribs) 04:56, 13 July 2020 (UTC)