Cube

This article is about the geometric shape. For other uses, see Cube (disambiguation).

Template:Reg polyhedron stat table In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and of trigonal trapezohedron. The cube is dual to the octahedron. It has cubical symmetry (also called octahedral symmetry).

A cube is the three-dimensional case of the more general concept of a hypercube.

It has 11 nets. If one were to colour the cube so that no two adjacent faces had the same colour, one would need 3 colours.

If the original cube has edge length 1, its dual octahedron has edge length ${\sqrt {2}}$.

Cartesian coordinates

For a cube centered at the origin, with edges parallel to the axes and with an edge length of 2, the Cartesian coordinates of the vertices are

(±1, ±1, ±1)

while the interior consists of all points (x₀, x₁, x₂) with −1 < x _i < 1. it all so has wat u you call 3-d shape

Formulae

For a cube of edge length $a$,

surface area	$6a^{2}$
volume	$a^{3}$
face diagonal	${\sqrt {2}}a$
space diagonal	${\sqrt {3}}a$
radius of circumscribed sphere	${\frac {\sqrt {3}}{2}}a$
radius of sphere tangent to edges	${\frac {a}{\sqrt {2}}}$
radius of inscribed sphere	${\frac {a}{2}}$
angles between faces	${\frac {\pi }{2}}$

As the volume of a cube is the third power of its sides a×a×a, third powers are called cubes, by analogy with squares and second powers.

A cube has the largest volume among cuboids (rectangular boxes) with a given surface area. Also, a cube has the largest volume among cuboids with the same total linear size (length + width + height).

Uniform colorings and symmetry

The cube has 3 uniform colorings, named by the colors of the square faces around each vertex: 111, 112, 123.

The cube has 3 classes of symmetry, which can be represented by vertex-transitive coloring the faces. The highest octahedral symmetry O_h has all the faces the same color. The dihedral symmetry D_4h comes from the cube being a prism, with all four sides being the same color. The lowest symmetry D_2h is also a prismatic symmetry, with sides alternating colors, so there are three colors, paired by opposite sides. Each symmetry form has a different Wythoff symbol.

Name	Regular hexahedron	Square prism	Cuboid	Trigonal trapezohedron
Coxeter-Dynkin
Schläfli symbol	{4,3}	{4}x{}	{}x{}x{}
Wythoff symbol	3 | 4 2	4 2 | 2	| 2 2 2
Symmetry	Oh (*432)	D4h (*422)	D2h (*222)	D3d (2*3)
Symmetry order	24	16	8	12
Image (uniform coloring)	(111)	(112)	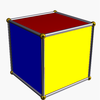(123)

Geometric relations

These familiar six-sided dice are cube-shaped.

The cube is unique among the Platonic solids for being able to tile Euclidean space regularly. It is also unique among the Platonic solids in having faces with an even number of sides and, consequently, it is the only member of that group that is a zonohedron (every face has point symmetry).

The cube can be cut into 6 identical square pyramids. If these square pyramids are then attached to the faces of a second cube, a rhombic dodecahedron is obtained.

Other dimensions

The analogue of a cube in four-dimensional Euclidean space has a special name—a tesseract or (rarely) hypercube.

The analogue of the cube in n-dimensional Euclidean space is called a hypercube or n-dimensional cube or simply n-cube. It is also called a measure polytope.

There are analogues of the cube in lower dimensions too: a point in dimension 0, a segment in one dimension and a square in two dimensions.

Related polyhedra

The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron. These two together form a regular compound, the stella octangula. The intersection of the two forms a regular octahedron. The symmetries of a regular tetrahedron correspond to those of a cube which map each tetrahedron to itself; the other symmetries of the cube map the two to each other.

One such regular tetrahedron has a volume of ⅓ of that of the cube. The remaining space consists of four equal irregular tetrahedra with a volume of 1/6 of that of the cube, each.

The rectified cube is the cuboctahedron. If smaller corners are cut off we get a polyhedron with 6 octagonal faces and 8 triangular ones. In particular we can get regular octagons (truncated cube). The rhombicuboctahedron is obtained by cutting off both corners and edges to the correct amount.

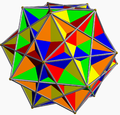
A cube can be inscribed in a dodecahedron so that each vertex of the cube is a vertex of the dodecahedron and each edge is a diagonal of one of the dodecahedron's faces; taking all such cubes gives rise to the regular compound of five cubes.

If two opposite corners of a cube are truncated at the depth of the 3 vertices directly connected to them, an irregular octahedron is obtained. Eight of these irregular octahedra can be attached to the triangular faces of a regular octahedron to obtain the cuboctahedron.

• 
  Two tetrahedra in the cube (stella octangula)
• 
  The rectified cube (cuboctahedron)
• 
  Truncated cube
• 
  Cantellated cube (rhombicuboctahedron)
• 
  Omnitruncated cube (truncated cuboctahedron)
• 
  Snub cube
• 
  Compound of three cubes
• 
  Compound of five cubes
• 
  An alternately truncated cube

All but the last of the figures shown have the same symmetries as the cube (see octahedral symmetry).

The cube is a special case in various classes of general polyhedra:

Name	Equal edge-lengths?	Equal angles?	Right angles?
Cube	Yes	Yes	Yes
Rhombohedron	Yes	Yes	No
Cuboid	No	Yes	Yes
Parallelepiped	No	Yes	No
quadrilaterally-faced hexahedron	No	No	No

Combinatorial cubes

A different kind of cube is the cube graph, which is the graph of vertices and edges of the geometrical cube. It is a special case of the hypercube graph.

An extension is the 3-dimensional k-ary Hamming graph, which for k = 2 is the cube graph. Graphs of this sort occur in the theory of parallel processing in computers.

See also

• Unit cube
• Tesseract
• Cube (film)
• Trapezohedron
• Yoshimoto Cube
• The Cube (game show)
• Prince Rupert's cube
• OLAP cube

External links

• Cube: Interactive Polyhedron Model
• K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• The Uniform Polyhedra
• Virtual Reality Polyhedra
• Volume of a cube, with interactive animation