7-demicube

Demihepteract (7-demicube)
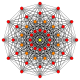
Petrie polygon projection
Type	Uniform 7-polytope
Family	demihypercube
Coxeter symbol	141
Schläfli symbol	{3,34,1} = h{4,35} s{21,1,1,1,1,1}
Coxeter diagrams	=
6-faces	78	14 {31,3,1} 64 {35}
5-faces	532	84 {31,2,1} 448 {34}
4-faces	1624	280 {31,1,1} 1344 {33}
Cells	2800	560 {31,0,1} 2240 {3,3}
Faces	2240	{3}
Edges	672
Vertices	64
Vertex figure	Rectified 6-simplex
Symmetry group	D7, [34,1,1] = [1+,4,35] [26]+
Dual	?
Properties	convex

In geometry, a demihepteract or 7-demicube is a uniform 7-polytope, constructed from the 7-hypercube (hepteract) with alternated vertices removed. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.

E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as HM₇ for a 7-dimensional half measure polytope.

Coxeter named this polytope as 1₄₁ from its Coxeter diagram, with a ring on one of the 1-length branches, and Schläfli symbol $\left\{3{\begin{array}{l}3,3,3,3\\3\end{array}}\right\}$ or {3,3^4,1}.

Cartesian coordinates

Cartesian coordinates for the vertices of a demihepteract centered at the origin are alternate halves of the hepteract:

(±1,±1,±1,±1,±1,±1,±1)

with an odd number of plus signs.

Images

orthographic projections

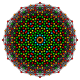
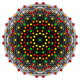
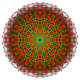
Coxeter plane	B7	D7	D6
Graph
Dihedral symmetry	[14/2]	[12]	[10]
Coxeter plane	D5	D4	D3
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

As a configuration

This configuration matrix represents the 7-demicube. The rows and columns correspond to vertices, edges, faces, cells, 4-faces, 5-faces and 6-faces. The diagonal numbers say how many of each element occur in the whole 7-demicube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.

The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing one mirror at a time.

D7		k-face	fk	f0	f1	f2	f3		f4		f5		f6		k-figures	notes
A6		( )	f0	64	21	105	35	140	35	105	21	42	7	7	041	D7/A6 = 64*7!/7! = 64
A4A1A1		{ }	f1	2	672	10	5	20	10	20	10	10	5	2	{ }×{3,3,3}	D7/A4A1A1 = 64*7!/5!/2/2 = 672
A3A2		100	f2	3	3	2240	1	4	4	6	6	4	4	1	{3,3}v( )	D7/A3A2 = 64*7!/4!/3! = 2240
A3A3		101	f3	4	6	4	560	*	4	0	6	0	4	0	{3,3}	D7/A3A3 = 64*7!/4!/4! = 560
A3A2		110		4	6	4	*	2240	1	3	3	3	3	1	{3}v( )	D7/A3A2 = 64*7!/4!/3! = 2240
D4A2		111	f4	8	24	32	8	8	280	*	3	0	3	0	{3}	D7/D4A2 = 64*7!/8/4!/2 = 280
A4A1		120		5	10	10	0	5	*	1344	1	2	2	1	{ }v( )	D7/A4A1 = 64*7!/5!/2 = 1344
D5A1		121	f5	16	80	160	40	80	10	16	84	*	2	0	{ }	D7/D5A1 = 64*7!/16/5!/2 = 84
A5		130		6	15	20	0	15	0	6	*	448	1	1		D7/A5 = 64*7!/6! = 448
D6		131	f6	32	240	640	160	480	60	192	12	32	14	*	( )	D7/D6 = 64*7!/32/6! = 14
A6		140		7	21	35	0	35	0	21	0	7	*	64		D7/A6 = 64*7!/7! = 64

Related polytopes

There are 95 uniform polytopes with D₆ symmetry, 63 are shared by the B₆ symmetry, and 32 are unique:

References

• H.S.M. Coxeter:
  • Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
• Klitzing, Richard. "7D uniform polytopes (polyexa) x3o3o *b3o3o3o3o - hesa".

External links

• Olshevsky, George. "Demihepteract". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• Multi-dimensional Glossary