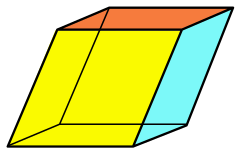
Rhombohedron

Rhombohedron
Type	prism
Faces	6 rhombi
Edges	12
Vertices	8
Symmetry group	Ci , [2+,2+], (×), order 2
Properties	convex, equilateral, zonohedron, parallelohedron

In geometry, a rhombohedron (also called a rhombic hexahedron or, inaccurately, a rhomboid) is a special case of a parallelepiped in which all six faces are congruent rhombi. It can be used to define the rhombohedral lattice system, a honeycomb with rhombohedral cells. A rhombohedron has two opposite apices at which all face angles are equal; a prolate rhombohedron has this common angle acute, and an oblate rhombohedron has an obtuse angle at these vertices. A cube is a special case of a rhombohedron with all sides square.

Special cases

The common angle at the two apices is here given as $\theta$. There are two general forms of the rhombohedron: oblate (flattened) and prolate (stretched).

Oblate rhombohedron	Prolate rhombohedron

In the oblate case $\theta >90^{\circ }$ and in the prolate case $\theta <90^{\circ }$. For $\theta =90^{\circ }$ the figure is a cube.

Certain proportions of the rhombs give rise to some well-known special cases. These typically occur in both prolate and oblate forms.

Form	Cube	√2 Rhombohedron	Golden Rhombohedron
Angle constraints	$\theta =90^{\circ }$
Ratio of diagonals	1	√2	Golden ratio
Occurrence	Regular solid	Dissection of the rhombic dodecahedron	Dissection of the rhombic triacontahedron

Solid geometry

For a unit (i.e.: with side length 1) rhombohedron, with rhombic acute angle $\theta ~$, with one vertex at the origin (0, 0, 0), and with one edge lying along the x-axis, the three generating vectors are

e₁ : ${\biggl (}1,0,0{\biggr )},$

e₂ : ${\biggl (}\cos \theta ,\sin \theta ,0{\biggr )},$

e₃ : ${\biggl (}\cos \theta ,{\cos \theta -\cos ^{2}\theta \over \sin \theta },{{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }} \over \sin \theta }{\biggr )}.$

The other coordinates can be obtained from vector addition of the 3 direction vectors: e₁ + e₂ , e₁ + e₃ , e₂ + e₃ , and e₁ + e₂ + e₃ .

The volume $V$ of a rhombohedron, in terms of its side length $a$ and its rhombic acute angle $\theta ~$, is a simplification of the volume of a parallelepiped, and is given by

$V=a^{3}(1-\cos \theta ){\sqrt {1+2\cos \theta }}=a^{3}{\sqrt {(1-\cos \theta )^{2}(1+2\cos \theta )}}=a^{3}{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }}~.$

We can express the volume $V$ another way :

$V=2{\sqrt {3}}~a^{3}\sin ^{2}\left({\frac {\theta }{2}}\right){\sqrt {1-{\frac {4}{3}}\sin ^{2}\left({\frac {\theta }{2}}\right)}}~.$

As the area of the (rhombic) base is given by $a^{2}\sin \theta ~$, and as the height of a rhombohedron is given by its volume divided by the area of its base, the height $h$ of a rhombohedron in terms of its side length $a$ and its rhombic acute angle $\theta$ is given by

$h=a~{(1-\cos \theta ){\sqrt {1+2\cos \theta }} \over \sin \theta }=a~{{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }} \over \sin \theta }~.$

Note:

$h=a~z$₃ , where $z$₃ is the third coordinate of e₃ .

The body diagonal between the acute-angled vertices is the longest. By rotational symmetry about that diagonal, the other three body diagonals, between the three pairs of opposite obtuse-angled vertices, are all the same length.

Relation to orthocentric tetrahedra

Four points forming non-adjacent vertices of a rhombohedron necessarily form the four vertices of an orthocentric tetrahedron, and all orthocentric tetrahedra can be formed in this way.

Rhombohedral lattice

Main article: Rhombohedral lattice

The rhombohedral lattice system has rhombohedral cells, with 6 congruent rhombic faces forming a trigonal trapezohedron:

See also

• Lists of shapes

External links

• Weisstein, Eric W. "Rhombohedron". MathWorld.
• Volume Calculator https://rechneronline.de/pi/rhombohedron.php