Wikipedia:Reference desk/Archives/Mathematics/2008 June 13

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

June 13

Mandelbrot set

A mathematician's depiction of the Mandelbrot set M, a point c is coloured black if it belongs to the set, and white if not. Re[c] and Im[c] denote the real and imaginary parts of c.

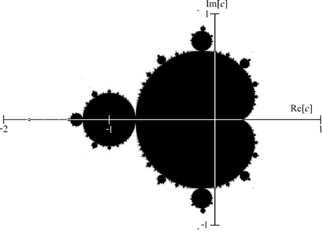
I'm looking at only real values of c i.e. along the horizontal axis of the graph. Black and white describe whether this iteration goes to infinity or not:

x_n+1 = x_n² + c

Consider the points (1,0) and (-1,0). In the iteration they are squared.

1² = 1

-1² = 1

Since squaring these real values gives the same result, how is it that one point is in the Mandelbrot set and the other isn't ? Cuddlyable3 (talk) 17:30, 13 June 2008 (UTC)

You seem to be confusing the roles of c and . The Mandelbrot set is the set of values c for which the sequence doesn't diverge, starting from x₀=0. For c = 1, the sequence starts 0,1,2,5,26..., which diverges, but for c = -1 it starts 0,-1,0,-1,..., which does not. What you are thinking of is more like a Julia set. --169.230.94.28 (talk) 17:50, 13 June 2008 (UTC)

Um, technically, the sequence 0,-1,0,-1,... does diverge, which simply means that it does not converge. I think the criterion you want is that c is in the set if the corresponding sequence is bounded. --Trovatore (talk) 19:00, 13 June 2008 (UTC)

Thank you for clarifying this. My error was supposing x₀ to start as c. The intro to Mandelbrot set does not state x₀=0, it only implies this by examples. Cuddlyable3 (talk) 18:17, 13 June 2008 (UTC)

Actually it does, but in very technical terminology. It talks about the "orbit of 0", which means all the numbers you can get to by starting at zero and applying the formula. It could be explained much better, I'll have a go now. --Tango (talk) 18:57, 13 June 2008 (UTC)

It does not matter: if $x_{0}=0$ then $x_{1}=x_{0}^{2}+c=c$ so you could think of starting from $c$ (as long as you do it consistently). – b_jonas 15:27, 14 June 2008 (UTC)

You don't even need to be consistent. If a sequence is bounded, the same sequence with the index offset by 1 is still bounded, and that's all that's required to be in the Mandelbrot set. If you want to do it with pretty colours showing how quickly it goes to infinity, then you need to be consistent. --Tango (talk) 16:22, 14 June 2008 (UTC)

Second Order Differntial Equation

Can anyone offer advice on how to go about solving the equation;

$y^{2}\left[1+{\bigg (}{\frac {dy}{dx}}{\bigg )}^{2}\right]^{3}={\bigg (}{\frac {d^{2}y}{dx^{2}}}{\bigg )}^{2}$

thanks. Philc 0780 20:21, 13 June 2008 (UTC)

Well, I can say that y=0 is a nice solution to it... But otherwise, not offhand. -mattbuck (Talk) 21:59, 13 June 2008 (UTC)

Mathematica is able to "solve" it, but I don't know if the solution would be at all useful. It looks quite complicated. Mathematica gives two solutions that are almost the same. Both are given in terms of the inverse function x(y). Here is one of them:

$x[y]=C[2]-{\sqrt {\frac {2}{-1+C[1]}}}\left((-1+C[1]){\text{EllipticE}}\left[i{\text{ArcSinh}}\left[y{\sqrt {\frac {1}{2+2C[1]}}}\right],{\frac {1+C[1]}{-1+C[1]}}\right]+{\text{EllipticF}}\left[i{\text{ArcSinh}}\left[y{\sqrt {\frac {1}{2+2C[1]}}}\right],{\frac {1+C[1]}{-1+C[1]}}\right]\right)$

You can set the constants C[1] and C[2] to anything. I doubt that this is very helpful. Oded (talk) 22:51, 13 June 2008 (UTC)

Express ${\frac {d^{2}y}{dx^{2}}}={\frac {d(y')}{dx}}={\frac {dy}{dx}}{\frac {d(y')}{dy}}=y'{\frac {d(y')}{dy}}={\frac {1}{2}}{\frac {d\left({y'}^{2}\right)}{dy}}$. You get a separable equation:

$2y\,dy=\pm {\frac {d\left({y'}^{2}\right)}{\left(1+{y'}^{2}\right)^{\frac {3}{2}}}}$  — Pt _(T) 13:49, 14 June 2008 (UTC)

Nice! I guess that's basically how Mathematica does it. Is the ${\frac {d^{2}y}{dx^{2}}}={\frac {1}{2}}{\frac {d\left({y'}^{2}\right)}{dy}}$ trick standard? Oded (talk) 21:36, 15 June 2008 (UTC)

I think it is standard. I learnt it once from a differential calculus textbook, but I don't have it around right now, so can't look it up. — Pt _(T) 23:12, 15 June 2008 (UTC)

An example of lecture notes describing briefly the technique is [1], look at the last section. — Pt _(T) 23:25, 15 June 2008 (UTC)

It is a reasonably common technique to use in second order ODEs that do not include the independent variable (i.e. of the form f(y, y', y'') = 0). The substitution may also be written as ${\frac {d^{2}y}{dx^{2}}}={\frac {d}{dy}}\left({\frac {dy}{dx}}\right)\cdot {\frac {dy}{dx}}={\frac {dy'}{dy}}y'$. Confusing Manifestation(Say hi!) 00:28, 16 June 2008 (UTC)