V curve

V curve for a synchronous motor

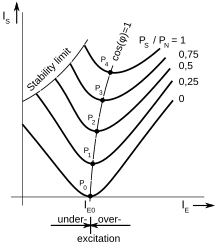
In synchronous machines, the V curve (also spelled as V-curve) is the graph showing the relation of armature current as a function of field current in synchronous motors keeping the load constant. The name comes from an observation made by W. M. Mordey in 1893 that the curve resembles a letter V.

The lowest point of the curve corresponds to the unity power factor. For a motor, points on the left of the minimum correspond to underexcitation (and therefore the armature current would "lag" the voltage), on the right - to overexcitation (and "lead"). Typically multiple V curves are plotted based on the experiments, each corresponding to its own load value.

The minimum at unity power factor ($\cos \phi$) is due to the general formula for the power P of a synchronous motor, $P={\sqrt {3}}V_{A}I_{A}\cos \phi$. In order to keep the power constant, with the line voltage at the terminals of the armature $V_{A}$ also constant, any decrease in power factor has to be accommodated by a corresponding increase in the armature current $I_{A}$. At the low values of the field current, the power factor is low, so the armature current is high (and lagging). As the field current increases, the power factor increases too, until the unity power factor is reached (the the armature current decreases to its minimum when the motor reaches this normal excitation). If the field current is increased beyond this point, the armature current becomes leading, power factor decreases, and $I_{A}$ grows again.

The data from the V curves can be used to set up the synchronous motor to correct the power factor of the overall system, as the power factor of the motor can be changed by simply adjusting the field current. While performing the correction, the motor can either provide the mechanical power also, or run in the idle mode ("float"), working as a synchronous condenser.

Inverted V curve

The inverted V curve is a graph showing the relation of power factor as a function of field current. The shape of this curve resembles a dome.

See also

• Synchronous motor

Sources

• Dawes, C.L. (1916). Jameson, J. M. (ed.). Electrical Measurements and Testing, Direct and Alternating Current. The Wiley technical series. J. Wiley & sons, Incorporated. Retrieved 2024-12-03.
• M.I.E.E. (1906). "The Electric Transmission of Power". English Mechanics and the World of Science. 83. E. J. Kibblewhite: 590–592. Retrieved 2024-12-03.
• Dawes, C.L. (1922). A Course in Electrical Engineering: Alternating currents. A Course in Electrical Engineering. McGraw-Hill Book Company, Incorporated. Retrieved 2024-12-03.
• Saadat, Hadi. 2004. Power Systems Analysis. 2nd Ed. McGraw Hill. International Edition. ISBN 978-0-07-128184-3.