User:Travm808/Systems Biology

Creating Biological Models

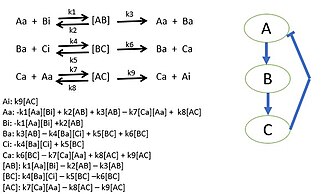
Researchers begin by choosing a biological pathway and diagramming all of the protein interactions. After determining all of the interactions of the proteins, mass action kinetics is utilized to describe the speed of the reactions in the system. Mass action kinetics will provide differential equations to model the biological system as a mathematical model in which experiments can determine the parameter values to use in the differential equations.^[1]These parameter values will be the reaction rates of each proteins interaction in the system. This model determines the behavior of certain proteins in biological systems and bring new insight to the specific activities of individual proteins. Sometimes it is not possible to gather all reaction rates of a system. Unknown reaction rates are determined by simulating the model of known parameters and target behavior which provides possible parameter values.^[2]^[3]

^ Chellaboina, V.; Bhat, S. P.; Haddad, W. M.; Bernstein, D. S. (2009-08). "Modeling and analysis of mass-action kinetics". IEEE Control Systems Magazine. 29 (4): 60–78. doi:10.1109/MCS.2009.932926. ISSN 1941-000X. {{cite journal}}: Check date values in: |date= (help)
^ Brown, Kevin S.; Sethna, James P. (2003-08-12). "Statistical mechanical approaches to models with many poorly known parameters". Physical Review E. 68 (2). doi:10.1103/physreve.68.021904. ISSN 1063-651X.
^ ^a ^b Transtrum, Mark K.; Qiu, Peng (2016-05-17). "Bridging Mechanistic and Phenomenological Models of Complex Biological Systems". PLOS Computational Biology. 12 (5): e1004915. doi:10.1371/journal.pcbi.1004915. ISSN 1553-7358.{{cite journal}}: CS1 maint: unflagged free DOI (link)

[1] Chellaboina, V.; Bhat, S. P.; Haddad, W. M.; Bernstein, D. S. (2009-08). "Modeling and analysis of mass-action kinetics". IEEE Control Systems Magazine. 29 (4): 60–78. doi:10.1109/MCS.2009.932926. ISSN 1941-000X. {{cite journal}}: Check date values in: |date= (help)

[2] Brown, Kevin S.; Sethna, James P. (2003-08-12). "Statistical mechanical approaches to models with many poorly known parameters". Physical Review E. 68 (2). doi:10.1103/physreve.68.021904. ISSN 1063-651X.

[:0-3] Transtrum, Mark K.; Qiu, Peng (2016-05-17). "Bridging Mechanistic and Phenomenological Models of Complex Biological Systems". PLOS Computational Biology. 12 (5): e1004915. doi:10.1371/journal.pcbi.1004915. ISSN 1553-7358.{{cite journal}}: CS1 maint: unflagged free DOI (link)

[1]

[2]

[3]