User:Phlsph7/Integer arithmetic

Integer arithmetic

Integer arithmetic is the branch of arithmetic that deals with the manipulation of positive and negative whole numbers. The set of integers is represented by the symbol $Z$ and can be expressed as {..., -3, -2, -1, 0, 1, 2, 3, ...}.

Simple one-digit operations can be performed by following or memorizing a table that presents the results of all possible combinations, like an addition table or a multiplication table. Other common methods are verbal counting and finger-counting.

Addition table

+	0	1	2	3	4	...
0	0	1	2	3	4	...
1	1	2	3	4	5	...
2	2	3	4	5	6	...
3	3	4	5	6	7	...
4	4	5	6	7	8	...
...	...	...	...	...	...	...

Multiplication table

×	0	1	2	3	4	...
0	0	0	0	0	0	...
1	0	1	2	3	4	...
2	0	2	4	6	8	...
3	0	3	6	9	12	...
4	0	4	8	12	16	...
...	...	...	...	...	...	...

Example of addition with carry. The black numbers are the addends, the green number is the carry, and the blue number is the sum.

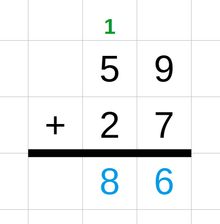
For operations on numbers with more than one digit, different techniques can be employed to calculate the result by using several one-digit operations in a row. For example, in the method addition with carries, the two numbers are written one above the other. Starting from the rightmost digit, each pair of digits is added together. The rightmost digit of the sum is written below them. If the sum is a two-digit number then the leftmost digit, called the "carry", is added to the next pair of digits to the left. This process is repeated until all digits have been added. Other methods used for integer additions are the number line method, the partial sum method, and the compensation method. A similar technique is used for subtraction: it also starts with the rightmost digit and uses a "borrow" or a negative carry for the column on the left if the result of the one-digit subtraction is negative.

Example of long multiplication. The black numbers are the multiplicand and the multiplier. The green numbers are intermediary products gained by multiplying the multiplicant with only one digit of the multiplier. The blue number is the total product calculated by adding the intermediary products.

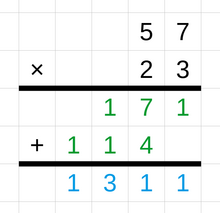
A basic technique of integer multiplication uses repeated addition. For example, the product of 3 × 4 can be calculated as 3 + 3 + 3 + 3. A common technique for multiplication with larger numbers is called long multiplication. This method starts by writing the multiplicand above the multiplier. The calculation begins by multiplying the multiplicand only with the rightmost digit of the multiplier and writing the result below, starting in the rightmost column. The same is done for each digit of the multiplier and the result in each case is shifted one position to the left. As a final step, all the individual products are added to arrive at the total product of the two multi-digit numbers. Other techniques used for multiplication are the grid method and the lattice method. Computer science is interested in multiplication algorithms with a low computational complexity to be able to efficiently multiply very large integers, such as the Karatsuba algorithm, the Schönhage-Strassen algorithm, and the Toom-Cook algorithm. A common technique used for division is called long division. Other methods include short division and chunking.

Integer arithmetic is not closed under division. This means that when dividing one integer by another integer, the result is not always an integer. For example, 7 divided by 2 is not a whole number but 3.5. One way to ensure that the result is an integer is to round the result to a whole number. However, this method leads to inaccuracies as the original value is altered. Another method is to perform the division only partially and retain the remainder. For example, 7 divided by 2 is 3 with a remainder of 1. These difficulties are avoided by rational arithmetic, which allows for the exact representation of fractions.

A simple method to calculate exponentiation is by repeated multiplication. For example, the exponentiation of 3⁴ can be calculated as 3 × 3 × 3 × 3. A more efficient technique used for large exponents is exponentiation by squaring. It breaks down the calculation into a number of squaring operations. For example, the exponentiation 3⁶⁵ can be written as ((((3²)²)²)²)²)² × 3. By taking advantage of repeated squaring operations, only 7 individual operations are needed rather than the 64 operations required for regular repeated multiplication. Methods to calculate logarithms include the Taylor series and continued fractions. Integer arithmetic is not closed under logarithm and under exponentiation with negative exponents, meaning that the result of these operations is not always an integer.

References

• Kupferman, Raz (29 October 2015). Elementary School Mathematics For Parents And Teachers - Volume 1. World Scientific Publishing Company. ISBN 978-981-4699-93-8.
• Uspenskii, V. A.; Semenov, A. L. (2001). "Solvable and Unsolvable Algorithmic Problems". In Tabachnikov, Serge (ed.). Kvant Selecta: Combinatorics, I: Combinatorics, I. American Mathematical Soc. ISBN 978-0-8218-2171-8.
• Geary, David C. (11 May 2006). "Development of Mathematical Understanding". In Damon, William; Lerner, Richard M.; Kuhn, Deanna; Siegler, Robert S. (eds.). Handbook of Child Psychology, Cognition, Perception, and Language. John Wiley & Sons. ISBN 978-0-470-05054-5.
• Ma, Liping (6 January 2020). Knowing and Teaching Elementary Mathematics: Teachers' Understanding of Fundamental Mathematics in China and the United States. Routledge. ISBN 978-1-000-02734-1.
• Resnick, L. B.; Ford, W. W. (12 November 2012). Psychology of Mathematics for Instruction. Routledge. ISBN 978-1-136-55759-0.
• Quintero, Ana Helvia; Rosario, Hector (2 March 2016). Math Makes Sense!: A Constructivist Approach To The Teaching And Learning Of Mathematics. World Scientific. ISBN 978-1-78326-866-5.
• Klein, Elise; Moeller, Korbinian; Dressel, Katharina; Domahs, Frank; Wood, Guilherme; Willmes, Klaus; Nuerk, Hans-Christoph (September 2010). "To carry or not to carry — Is this the question? Disentangling the carry effect in multi-digit addition". Acta Psychologica. 135 (1). doi:10.1016/j.actpsy.2010.06.002.
• Ebby, Caroline B.; Hulbert, Elizabeth T.; Broadhead, Rachel M. (23 November 2020). A Focus on Addition and Subtraction: Bringing Mathematics Education Research to the Classroom. Routledge. ISBN 978-1-000-22087-2.
• Sperling, Abraham; Stuart, Monroe (1981). Mathematics. Elsevier Science. ISBN 978-0-7506-0405-5.
• Mooney, Claire; Briggs, Mary; Hansen, Alice; McCullouch, Judith; Fletcher, Mike (10 June 2014). Primary Mathematics: Teaching Theory and Practice. Learning Matters. ISBN 978-1-4739-0707-2.
• Klein, Andreas (8 April 2013). Stream Ciphers. Springer Science & Business Media. ISBN 978-1-4471-5079-4.
• Muller, Jean-Michel; Brunie, Nicolas; Dinechin, Florent de; Jeannerod, Claude-Pierre; Joldes, Mioara; Lefèvre, Vincent; Melquiond, Guillaume; Revol, Nathalie; Torres, Serge (2 May 2018). Handbook of Floating-Point Arithmetic. Birkhäuser. ISBN 978-3-319-76526-6.
• Davis, Andrew; Goulding, Maria; Suggate, Jennifer (17 February 2017). Mathematical Knowledge for Primary Teachers. Taylor & Francis. ISBN 978-1-317-21901-9.
• Haylock, Derek; Cockburn, Anne D. (14 October 2008). Understanding Mathematics for Young Children: A Guide for Foundation Stage and Lower Primary Teachers. SAGE. ISBN 978-1-4462-0497-9.
• Prata, Stephen (2002). C Primer Plus. Sams Publishing. ISBN 978-0-672-32222-8.
• Koepf, Wolfram (11 July 2021). Computer Algebra: An Algorithm-Oriented Introduction. Springer Nature. ISBN 978-3-030-78017-3.
• Romanowski, Perry (2008). "Arithmetic". In Lerner, Brenda Wilmoth; Lerner, K. Lee (eds.). The Gale encyclopedia of science (4th ed.). Detroit: Thompson Gale. pp. 302–305. ISBN 978-1-4144-2877-2.
• Hindry, Marc (2011). Arithmetics. London: Springer. ISBN 978-1-4471-2130-5.
• Hafstrom, John Edward (10 June 2013). Basic Concepts in Modern Mathematics. Courier Corporation. ISBN 978-0-486-31627-7.
• Goodstein, R. L. (14 July 2014). Fundamental Concepts of Mathematics. Elsevier. ISBN 978-1-4831-5405-3.
• Cafaro, Massimo; Epicoco, Italo; Pulimeno, Marco (21 August 2018). "Techniques for Designing Bioinformatics Algorithms". Encyclopedia of Bioinformatics and Computational Biology: ABC of Bioinformatics. Elsevier. ISBN 978-0-12-811432-2.
• Reilly, Norman R. (2 November 2009). Introduction to Applied Algebraic Systems. Oxford University Press. ISBN 978-0-19-970992-2.
• Mahajan, Sanjoy (5 March 2010). Street-Fighting Mathematics: The Art of Educated Guessing and Opportunistic Problem Solving. MIT Press. ISBN 978-0-262-26559-1.
• Cuyt, Annie A. M.; Petersen, Vigdis; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (12 April 2008). Handbook of Continued Fractions for Special Functions. Springer Science & Business Media. ISBN 978-1-4020-6949-9.
• Kay, Anthony (14 September 2021). Number Systems: A Path into Rigorous Mathematics. CRC Press. ISBN 978-0-429-60776-9.