User:Nightmark/sandbox
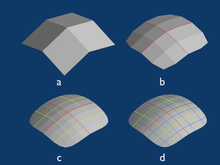
V Počítačovej grafike je delenie povrchov technika, pri ktorej sa vytvára z jednej plôšky alebo polygónu viac plôšok. Touto technikou získame jemnejší povrch. Prvýkrát bola predstavená spoločnosťou Pixar v krátkom animovanou filme s názvom Geri’s Game[1]. Bolo to na konferencii Siggraph v roku 1998.
Detaily
[edit]Na začiatku schéma vezme povrch alebo akýkoľvek model vytvorený z trojuholníkov, štvoruholníkov alebo viacuhoľníkov. Tento začiatočný povrch voláme kontrolná sieť. Potom je táto sieť rozdelená na základe sady pravidiel[2]. Pravidlá sa líšia od jedného delenia k druhému. Určujú koľko nových vrcholov bude pridaných do kontrolnej siete a na akú pozíciu budú posunuté. Následne sa tento nový povrch stane novou hladšou kontrolnou sieťou pre ďalšiu iteráciu delenia. Po každej iterácii dostávame jemnejší povrch pridaním vrcholou a nových plôšok. Nevýhodou je pri vyšších iteráciách veľký počet vrcholov, ktoré môžu zapríčinit’ spomalenú odozvu v reálnom čase. V počítačovej grafike sa pre delenie povrchov používa termín Surface subdivision. V súčasnej dobre sa rozsiahlo používajú v 3D modelovaní a animácii.
Pravidlá delenia – Topologické
[edit]Pravidlo delenia je predpis ktorý priraďuje skupine vrcholov rozsiahlejšiu skupinu vrcholov. Deliaca schéma má dva typy pravidiel topologické a váhové. Topologické udávajú ako získame graf vylepšeného objektu z grafu objektu vstupného tým, že generujeme nové vrcholy, hrany a plôšky.
Pravidlá delenia – Váhové
[edit]Špecifikujú ako vypočítať pozíciu nových vrcholov na základe interpolácie medzi vrcholmi vstupného povrchu.
Spojitost delenia Cn
[edit]Je stupeň parametrické spojitosti krivky v danom bode. Je to jedna z charakteristík deliacich schém. n nám hovorí koľko derivácii je spojitých.
Valencia vrcholu a výnimočné vrcholy
[edit]Valencia, stupeň vrcholu označuje počet hrán ktoré do vrcholu zasahujú. Regulárne vrcholy schémy voláme tie, ktorých je vyprodukovaných najviac počas delenia a majú tú istú valenciu. Hocijaké iné vrcholy nazývame výnimočné. To aké majú tieto vrcholi efekt na výslednú plochu, záleží na deliacej schéme. Niekedy nastanú problémy keď chceme analyzovať lmitu povrchu v blízkosti týchto výnimočných vrcholov. Väčšina schém neprodukuje výnimočné vrcholi počas delenia, a tak ich počet je daný controlnou sieťou, ktorú dostaneme na vstupe na začiatku delenia.
Typy delenia
[edit]- Aproximačné schémy delenia - Pri tomto type delenia sa pozície vrcholov upravia tak ako budú najlepšie vyhovovať novému povrchu
- Catmull-Clark[3] - Delenie ktoré sa dá použiť na hocijaký typ povrchu. Po prvej iterácii vždy vzniknú štvorsteny. Generovaný povrch je C2 spojitý, všade až na výnimočné vrcholi. Tento typ delenia je v súčasnej dobe najviac používaný v 3D aplikáciách a animácii.
- Doo-Sabin[4] - Dokáže spracovať ľubovoľnú topológiu. Môže vytvárať nove plôšky s ľubovolným počtom vrcholov.
- Loop - Pracuje iba na povrchoch poskladaných z trojuholníkov, a po každej iterácii vzniknú iba trojuholníky. V súčasnej dobe sa moc nepoužíva.
- Sqrt3
- Interpolačné schémy delenia - Pri interpolácii sa od vrcholov vyžaduje aby zodpovedali pôvodným pozíciám
- (Motýľ) Butterfly
- MidEdge
- Doo-sabin
Externé odkazy
[edit]- ^ DeRose, Tony; Kass, Michael; Truong, Tien. "Subdivision Surfaces in Character Animation" (PDF). pixar.com. Pixar Animation Studios. Retrieved 24 May 2015.
- ^ Sharp, Brian. "Subdivision Surface Theory". www.gamasutra.com. Gamasutra. Retrieved 24 May 2015.
- ^ Teorell Loop, Charles. "Smooth Subdivision Surfaces Based on Triangles" (PDF). http://research.microsoft.com/. The University of Utah. Retrieved 24 May 2015.
{{cite web}}: External link in|website= - ^ Teorell Loop, Charles. "Smooth Subdivision Surfaces Based on Triangles" (PDF). http://research.microsoft.com/. The University of Utah. Retrieved 24 May 2015.
{{cite web}}: External link in|website=

