User:Lakeratatat/sandbox

This is a Wikipedia user page.
This is not an encyclopedia article or the talk page for an encyclopedia article. If you find this page on any site other than Wikipedia, you are viewing a mirror site. Be aware that the page may be outdated and that the user in whose space this page is located may have no personal affiliation with any site other than Wikipedia. The original page is located at https://en.wikipedia.org/wiki/User:Lakeratatat/sandbox.

Please see User talk:Lakeratatat/sandbox for more information.--Guy vandegrift (talk) 19:37, 27 January 2016 (UTC)

Attribution

https://wiki.riteme.site/w/index.php?title=Hooke%27s_law&oldid=699300499 Special:Permalink/699300499 (Permalink to Hook's law

Article

Hooke's law: the force is proportional to the extension

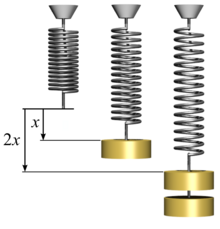
Hooke's law is a principle of physics that states that the force $F$ needed to extend or compress a spring by some distance $X$ is proportional to that distance. That is: $F = kX$ , where $k$ is a constant factor characteristic of the spring: its stiffness, and $X$ is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1660 as a Latin anagram.^[1]^[2] He published the solution of his anagram , sic vis ("as the extension, so the force" or "the extension is proportional to the force").

Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, a musician plucking a string of a guitar, and the filling of a party balloon. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean.

Hooke's law is only a first-order linear approximation to the real response of springs and other elastic bodies to applied forces. It must eventually fail once the forces exceed some limit, since no material can be compressed beyond a certain minimum size, or stretched beyond a maximum size, without some permanent deformation or change of state. Many materials will noticeably deviate from Hooke's law well before those elastic limits are reached.

On the other hand, Hooke's law is an accurate approximation for most solid bodies, as long as the forces and deformations are small enough. For this reason, Hooke's law is extensively used in all branches of science and engineering, and is the foundation of many disciplines such as seismology, molecular mechanics and acoustics. It is also the fundamental principle behind the spring scale, the manometer, and the balance wheel of the mechanical clock.

The modern theory of elasticity generalizes Hooke's law to say that the strain (deformation) of an elastic object or material is proportional to the stress applied to it. However, since general stresses and strains may have multiple independent components, the "proportionality factor" may no longer be just a single real number, but rather a linear map (a tensor) that can be represented by a matrix of real numbers.

In this general form, Hooke's law makes it possible to deduce the relation between strain and stress for complex objects in terms of intrinsic properties of the materials it is made of. For example, one can deduce that a homogeneous rod with uniform cross section will behave like a simple spring when stretched, with a stiffness $k$ directly proportional to its cross-section area and inversely proportional to its length.

Formal definition

Editorial comment by Guy vandegrift

Why was it necessary to tell the reader that Hook's law can be written as F=kx or F=-kx. I think readers should be able to figure that out. This is why we need a mechanism for abridging WP articles. Wikiversity allows limited POV, and a "guild" of independent online journals like v:Wikiversity Journal of Medicine and Wikiversity:Second Journal of Science permits wikimedia to decentralize (and democratize) the process of creating these abridgments. A Wikiversity journal could be created in less than a day, and the "editor/creator" of a journal can register an ISSN number for about $10 per year.

Note to Lakerattattat: Please keep the silly duplication of the same equation for a while so that this comment will be read by those who wonder why Wikipedia articles should be reformatted by these journals.--Guy vandegrift (talk) 17:19, 27 January 2016 (UTC)

For linear springs

Plot of applied force F vs. elongation X for a helical spring according to Hooke's law (red line) and what the actual plot might look like (dashed line). At bottom, pictures of spring states corresponding to some points of the plot; the middle one is in the relaxed state (no force applied).

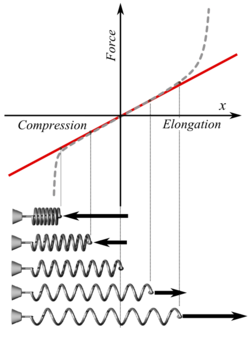
Consider a simple helical spring that has one end attached to some fixed object, while the free end is being pulled by a force whose magnitude is $F$ . Suppose that the spring has reached a state of equilibrium, where its length is not changing anymore. Let $X$ be the amount by which the free end of the spring was displaced from its "relaxed" position (when it is not being stretched). Hooke's law states that

F=kX\,

where $k$ is a positive real number, characteristic of the spring. Moreover, the same formula holds when the spring is compressed, with $F$ and $X$ both negative in that case. According to this formula, the graph of the applied force $F$ as a function of the displacement $X$ will be a straight line passing through the origin, whose slope is $k$ .

Hooke's law for a spring is often stated under the convention that $F$ is the restoring (reaction) force exerted by the spring on whatever is pulling its free end. In that case the equation becomes

F=-kX\,

since the direction of the restoring force is opposite to that of the displacement.

General "scalar" springs

Hooke's spring law usually applies to any elastic object, of arbitrary complexity, as long as both the deformation and the stress can be expressed by a single number that can be both positive and negative.

For example, when a block of rubber attached to two parallel plates is deformed by shearing, rather than stretching or compression, the shearing force $F$ and the sideways displacement of the plates $X$ obey Hooke's law (for small enough deformations).

Hooke's law also applies when a straight steel bar or concrete beam, supported at both ends, is bent by a weight $F$ placed at some intermediate point. The displacement $X$ in this case is the deviation of the beam, measured in the transversal direction, relative to its unloaded shape.

The law also applies when a stretched steel wire is twisted by pulling on a lever attached to one end. In this case the stress $F$ can be taken as the force applied to the lever, and $X$ as the distance traveled by it along its circular path. Or, equivalently, one can let $F$ be the torque applied by the lever to the end of the wire, and $X$ be the angle by which that end turns. In either case $F$ is proportional to $X$ (although the constant $k$ is different in each case.)

Vector formulation

In the case of a helical spring that is stretched or compressed along its axis, the applied (or restoring) force and the resulting elongation or compression have the same direction (which is the direction of said axis). Therefore, if $F$ and $X$ are defined as vectors, Hooke's equation still holds, and says that the force vector is the elongation vector multiplied by a fixed scalar.

Units of measurement

In SI units, displacements are measured in metres (m), and forces in newtons (N or kg·m/s²). Therefore, the spring constant $k$ , and each element of the tensor $\kappa$ , is measured in newtons per metre (N/m), or kilograms per second squared (kg/s²).

For continuous media, each element of the stress tensor $\sigma$ is a force divided by an area; it is therefore measured in units of pressure, namely pascals (Pa, or N/m², or kg/(m·s²). The elements of the strain tensor $\epsilon$ are dimensionless (displacements divided by distances). Therefore, the entries of $c_{ijk\ell }$ are also expressed in units of pressure.

Derived formulae

Spring energy

The potential energy $U_{el}(x)$ stored in a spring is given by

U_{el}(x)={1 \over 2}kx^{2}

which comes from adding up the energy it takes to incrementally compress the spring. That is, the integral of force over displacement. Since the external force has the same general direction as the displacement, the potential energy of a spring is always non-negative.

Whenever you get a turn in the graph, represented as a maximum or minimum, it will almost always represent the shape of the parabola. This fact also allows us to use parabolic equations to estimate the values at these turns.

Relaxed force constants (generalized compliance constants)

Relaxed force constants (the inverse of Grunenberg`s generalized compliance constants) are uniquely defined for molecular systems, in contradistinction to the usual “rigid” force constants, and thus their use allows meaningful correlations to be made between force fields calculated for reactants, transition state, and product of a chemical reaction. Just as the potential energy can be written as a quadratic form in the internal coordinates, so it can also be written in terms of generalized forces. The resulting coefficients are termed compliance constants. The suitability of relaxed force constants (inverse compliance constants) as covalent bond strength descriptors was demonstrated as early as ~1980, at the University of Cambridge. Recently, the suitability as non-covalent bond strength descriptors was demonstrated, too.^[3]

Harmonic oscillator

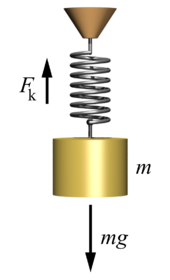
A mass m attached to the end of a spring is a classic example of a harmonic oscillator. By pulling slightly on the mass and then releasing it, the system will be set in sinusoid oscillating motion about the equilibrium position. To the extent that the spring obeys Hooke's law, and that one can neglect friction and the mass of the spring, the amplitude of the oscillation will remain constant; and its frequency $f$ will be independent of its amplitude, determined only by the mass and the stiffness of the spring:

f={1 \over 2\pi }{\sqrt {k \over m}}

This phenomenon made possible the construction of accurate mechanical clocks and watches that could be carried on ships and people's pockets.

Rotation in gravity-free space

If the mass $m$ were attached to a spring with force constant $k$ and rotating in free space, the spring tension ( $F t$ ) would supply the required centripetal force ( $F c$ ):

F_{t}=kx

F_{c}=m\omega ^{2}r

Since $F t = F c$ and $x = r$ , then:

k=m\omega ^{2}

Given that $ω = 2 π f$ , this leads to the same frequency equation as above:

f={1 \over 2\pi }{\sqrt {k \over m}}

Notes

^ The anagram was given in alphabetical order, ceiiinosssttuv, representing Ut tensio, sic vis — "As the extension, so the force": Petroski, Henry (1996). Invention by Design: How Engineers Get from Thought to Thing. Cambridge, MA: Harvard University Press. p. 11. ISBN 0674463684.
^ See [1], where one can find also an anagram for the catenary.
^ Alla G. Ponomareva, Yevgen P. Yurenko , Roman O. Zhurakivsky, Tanja van Mourik and Dmytro M. Hovorun Phys. Chem. Chem. Phys., 2012,14, 6787-6795

[1] The anagram was given in alphabetical order, ceiiinosssttuv, representing Ut tensio, sic vis — "As the extension, so the force": Petroski, Henry (1996). Invention by Design: How Engineers Get from Thought to Thing. Cambridge, MA: Harvard University Press. p. 11. ISBN 0674463684.

[2] See [1], where one can find also an anagram for the catenary.

[3] Alla G. Ponomareva, Yevgen P. Yurenko , Roman O. Zhurakivsky, Tanja van Mourik and Dmytro M. Hovorun Phys. Chem. Chem. Phys., 2012,14, 6787-6795

[1]

[2]

[3]