User:J kay831/Donut Theory

Doughnut Theory of the Universe The doughnut theory of the universe describes the shape of the universe to be similar to that of a doughnut. The technical name for the geometric shape of a doughnut is a torus. The structure of a torus allows for two ways to perform a loop in the torus: a loop around the outer edge and a loop around the tube of the torus. Therefore, a doughnut shaped universe would allow for two ways to travel in a seemingly straight path and end up at the starting point. The geometry of a torus may also be described algebraically.
The foundation for the doughnut theory started with Bell Lab’s discovery of cosmic microwave background (CMB). With the information provided from the study of CMB, Dr. Alexi Starobinski conceived the doughnut theory of the universe along with his mentor, Dr. Yakov B. Zeldovich, in 1984 from the Landau Institute in Moscow. With the study of CMB as the best source for information on the universe’s geometry, NASA launched two explorer satellites, the Cosmic Background Explorer (COBE) in 1989 and the Wilkinson Microwave Anisotropy Probe (WMAP) in 2001, to map CMB. The information from these satellites led many cosmologists to believe the universe is shaped like a torus.
Despite evidence supporting a finite, torus shaped universe, contradicting theories provide opposing evidence to the doughnut theory. Although neither theory is proven, the Big Bang inflation theory is the most popular and threatening theory to the doughnut theory. The doughnut theory’s finite, torus shaped universe is a complete contradiction to the infinitely expanding Big Bang inflation theory.

The Geometry of The Universe

Overview

A torus

While visualizing the universe in the structure of a doughnut is an easy and general way to understand the doughnut theory, the technical name for a doughnut-like structure is a torus. Additionally, any closed curve rotated around an axis is referred to by the general term toroid. If a toroidal universe existed, there would be two perpendicular ways to travel in a straight path and perform a complete loop around the universe. The first loop around the universe could be performed by traveling around the outer edges of the torus, while the second loop could be performed by traveling from the outside of the torus through the center hole, out the other side, and back up to the top the torus. Another, proposal for the structure of the universe is a flat torus. A flat torus appears to be a contradiction; however, a flat torus is possible much in the same way a paper cylinder may be cut to appear flat when laid on a table. While the loop around the outer edge of a flat torus would remain the same regardless of the torus’ curvature, the loop around the tube of the torus may be pictured similarly to the arcade game Asteroids. In the Asteroids (video game), when the ship left one side of the screen, it would appear on the other side. Similar to Asteroids, a journey around the tube in a flat torus universe would appear linear until the journeyers arrived where they started. Thus, the loop is still completed despite the lack of connectivity between the inner and outer edges of the flat torus.

The torus consists of two circles in which one may theoretically loop around the universe

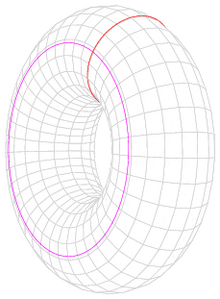
Equations of a Torus

To understand the mathematical expressions of a torus certain variables must be defined:

• α is the radius of the cylinder that makes up the tube of the torus
• β is the radius from the center of the torus to the center of the tube
• x is the x-coordinate on the Cartesian coordinate system with X = 0 on the direction of the torus axis of symmetry
• y is the y-coordinate on the Cartesian coordinate system with Y = 0 on the direction of the torus axis of symmetry
• z is the z-coordinate on the Cartesian coordinate system with Z = 0 on the direction of the torus axis of symmetry
• ν is the angular parameter variation that represents time

1) The surface equation in Cartesian coordinates is

(β − (x^2 + y^2)^(1/2))^2 + z² = α²

2) The parametric equations are

x = cosφ(β + αcosν)

y = sinφ (β + αcosν)

z = αsinν

3) The Riemannian metric equation is

ds² = (β + αcosν)² dφ² + α²dν²

4) The position of a point on the torus surface is specified in spherical coordinates by

x = Rsinθcosφ

y = Rsinθsinφ

z = Rcosφ

5) From (2) and (4)

R² − 2Rβsinθ + β² − α² = 0

Supporting Evidence

Dr. Alexi Starobinski first proposed the doughnut theory of the universe along with his mentor, Dr. Yakov B. Zeldovich in 1984 from the Landau Institute in Moscow; however, the basis for his theory began much earlier than 1984. The foundation for any knowledge of the shape of the universe began in the mid-1960s with the discovery of cosmic microwave background (CMB) by Bell Labs. Greater understanding of the universe's CMB provided greater understanding of the universe's geometry; therefore, in a quest for cosmic understanding, NASA supported two explorer satellites, the Cosmic Background Explorer (COBE) in 1989 and the Wilkinson Microwave Anisotropy Probe (WMAP) in 2001, which have gathered more information on CMB.

Cosmic Microwave Background (CMB)

Cosmic microwave background (CMB) is radiation found uniformly throughout the universe that was leftover from the Big Bang. Discovered in 1965 by Arno Penzias and Robert Wilson at Bell Labs while observing an unknown microwave signal in their radio telescope, CMB laid the foundation for the emergence of the doughnut theory that occurred years later. Although the discovery of CMB alone did not provided enough information to conclude anything about the shape of the universe, it laid a foundation for future scientists attempting to explain cosmic geometry. Cosmologist Robert Dicke and Jime Peebles of Princeton University were the first researchers to decipher the implications of CMB, as they proved the temperature of the universe was evenly 2.7 Kelvin. The uniformity of the CMB is referred to as isotropic radiation or black body. Dicke and Peebles proved that the near perfect black body of the CMB meant the universe began much denser and hotter than it is today. Despite Dicke and Peebles contributions to humanity’s understanding of the universe, they were unable to obtain a concrete understanding of the shape of the universe. Rather, the cosmologists' research allowed Dr. Alexei Starobinski to devise the doughnut theory. With the knowledge provided from the greater understanding of CMB, Dr. Starobinski believed the most probable shape of the cosmos that complied with known rules of the universe resembled that of a doughnut. ”

Cosmic Background Explorer (COBE)

The Cosmic Background Explorer was an explorer satellite launched in 1989 by NASA that used a Far Infrared Absolute Spectrometer (FIRAS) to measure the radiation of the universe. Led by researchers John Mather and George Smoot, COBE was able to obtain precise readings of radiation frequencies across the universe. With data on the universe’s radiation distribution, Mather and Smoot discovered small discrepancies in temperature fluctuation known as anisotropies throughout the universe. The finding of anisotropies led Mather and Smoot to conclude the universe consists of regions of varying densities. In the early stages of the universe, these denser regions of the cosmos were responsible for attracting the matter that ultimately became galaxies and solar systems. . In “Microwave Background Anisotropy in a Troidal Universe” by Daniel Stevens, Douglas Scott, and Joseph Silk of University of California Berkeley, the cosmologists proposed the isotropic universe suggests a complicated geometric structure. The researchers argued the density fluctuations reported by COBE proved “multiply connected universes are possible, [and] the simplest [and most probable multiply connected universe] is the three-dimensional torus.” Additionally, the journal concludes a torus shaped universe is compatible with COBE data if the diameter of the torus' tube is at least 80% greater than the torus’ horizontal diameter . Thus, COBE provided researchers with the first concrete evidence of the doughnut theory. COBE was eventually decommissioned by NASA on December 23, 1993.

Wilkinson Microwave Anisotropy Probe (WMAP)

WMAP cosmic microwave background map

The Wilkinson Microwave Anisotropy Probe (WMAP) was launched in 2001 as NASA’s second explorer satellite intended to map the precise distribution of CMB across the universe. Improving on the design of COBE, WMAP was able to represent an extremely accurate, fine resolution map of the universe’s CMB. Such accuracy of WMAP’s CMB charts provided cosmologists with new data to analyze. The analysis of WMAP data in “A high resolution foreground cleaned CMB map from WMAP” by Max Tegmark, Ange ́lica de Oliveira-Costa, and Andrew J. S. Hamilton of University of Colorado provides further evidence of a doughnut shaped universe. The research team discovered that if the WMAP CMB map is analyzed while eliminating the radiation from stars and our own galaxy, the CMB of the universe appears more concentrated in one direction than the other. This concentration of CMB forms a straight line in the universe, which is believed to be characteristic of a compact, finite universe. Tegmark proposes that if his data does prove the universe is finite, then the amount of radiation in one area would be limited to size of the area in that direction. If the radiation exceeded the size of that area, the universe would overflow in that direction creating a plane in other directions. The perpendicular to the direction of the plane would create the loop of the doughnut, or torus. Therefore, Tegmark suggests a torus geometry is the most probable shape consistent to his analysis of WMAP CMB maps.

Opposing Evidence

The most significant opposing argument to the doughnut theory is evidence supporting the more popular Big Bang inflation theory. A finite, torus shaped universe is a strict contradiction of the inflation theory’s infinitely expanding universe. Developed by Alan Guth, Andrei Linde, Paul Steinhardt, and Andy Albrecht, the inflation theory states the universe expanded extremely fast (increase of 10^26 in linear size per second) prior to the slower expansion of the Big Bang. The inflation theory is really a revision to the Big Bang theory that incorporates the greater understanding of the universe learned from satellites such as NASA’s COBE and WMAP. Three main issues of the Big Bang theory came from this increased understanding of the universe: the flatness problem, the horizontal problem, and the monopole problem. WMAP data suggests the universe is flat. A flat universe contradicts the Big Bang theory, as the Big Bang theory states the universe becomes more curved with time. As a solution, the inflation theory states despite a slight curve, the universe extends so long that the curve is negligible. The horizontal problem of the Big Bang theory involves the interaction of matter from opposite sides of the universe. While the Big Bang states the universe is too large for the matter on opposite sides of the universe to have interacted, CMB data proves otherwise. The inflation theory fixes this problem by suggesting that during the initial Big Bang expansion, the universe was much smaller than previously believed. A smaller universe would allow all matter to interact. The last issue with the Big Bang theory, the monopole problem, involves the Big Bang theory’s prediction that the universe should be littered with heavy, stable magnetic monopoles. A monopole is a particle that has one magnetically charged side. Despite COBE’s and WMAP’s detailed analysis of the universe’s CMB, no monopoles have been found. The inflation theory states monopoles may have existed before inflation expansion, but inflation expansion decreased the density of these monopoles to undetectable levels. Thus, the convincing evidence supporting the Big Bang inflation theory is the greatest threat to the validity of the doughnut theory.

External links

• “A Rotating Black Ring Solution in Five Dimensions”
• “The Topology of the Universe: The Biggest Manifold of Them All”