User:Halibutt/Spacetime/Gravitation

Gravitation

Click here for a brief section summary

This introductory section has focused on the spacetime of special relativity, since it is the easiest to describe. Minkowski spacetime is flat, takes no account of gravity, is uniform throughout, and serves as nothing more than a static background for the events that take place in it. The presence of gravity greatly complicates the description of spacetime. In general relativity, spacetime is no longer a static background, but actively interacts with the physical systems that it contains. Spacetime curves in the presence of matter, can propagate waves, bends light, and exhibits a host of other phenomena. A few of these phenomena are described in the later sections of this article.

Return to Introduction

Basic mathematics of spacetime

Galilean transformations

Main article: Galilean group

Click here for a brief section summary
Note: To avoid navigation issues with the internal wikilinks, mobile phone users should pre-expand all sections from Section Summaries back to the Introduction.

A basic goal is to be able to compare measurements made by observers in relative motion. Say we have an observer O in frame S who has measured the time and space coordinates of an event, assigning this event three Cartesian coordinates and the time as measured on his lattice of synchronized clocks (x, y, z, t) (see Fig. 1‑1). A second observer O′ in a different frame S′ measures the same event in her coordinate system and her lattice of synchronized clocks (x′, y′, z′, t′). Since we are dealing with inertial frames, neither observer is under acceleration, and a simple set of equations allows us to relate coordinates (x, y, z, t) to (x′, y′, z′, t′). Given that the two coordinate systems are in standard configuration, meaning that they are aligned with parallel (x, y, z) coordinates and that t = 0 when t′ = 0, the coordinate transformation is as follows:

$x'=x-vt$

$y'=y$

$z'=z$

$t'=t.$

Figure 3-1. Galilean Spacetime and composition of velocities.

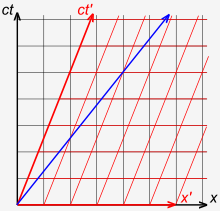
Fig. 3-1 illustrates that in Newton's theory, time is universal, not the velocity of light. Consider the following thought experiment: The red arrow illustrates a train that is moving at 0.4 c with respect to the platform. Within the train, a passenger shoots a bullet with a speed of 0.4 c in the frame of the train. The blue arrow illustrates that a person standing on the train tracks measures the bullet as traveling at 0.8 c. This is in accordance with our naive expectations.

More generally, assume that frame S′ is moving at velocity v with respect to frame S. Within frame S′, observer O′ measures an object moving with velocity u′. What is its velocity u with respect to frame S? Since x = ut, x′ = x − vt, and t = t′, we can write x′ = ut − vt = (u − v)t = (u − v)t′. This leads to u′ = x′/t′ and ultimately

$u'=u-v$  or  $u=u'+v,$

which is the common-sense Galilean law for the addition of velocities.

Return to Introduction

Relativistic composition of velocities

Main article: Velocity addition formula

Click here for a brief section summary

Figure 3-2. Relativistic composition of velocities

The composition of velocities is quite different in relativistic spacetime. To reduce the complexity of the equations slightly, we introduce a common shorthand for the ratio of the speed of an object relative to light,

$\beta =v/c$

Fig. 3-2a illustrates a red train that is moving forward at a speed given by v/c = β = s/a. From the primed frame of the train, a passenger shoots a bullet with a speed given by u′/c = β′ = n/m, where the distance is measured along a line parallel to the red x′ axis rather than parallel to the black x axis. What is the composite velocity u of the bullet relative to the platform, as represented by the blue arrow? Referring to Fig. 3‑2b:

1. From the platform, the composite speed of the bullet is given by u = c(s + r)/(a + b).
2. The two yellow triangles are similar because they are right triangles that share a common angle α. In the large yellow triangle, the ratio s/a = v/c = β.
3. The ratios of corresponding sides of the two yellow triangles are constant, so that r/a = b/s = n/m = &beta′. So b = u′s/c and r = u′a/c.
4. Substitute the expressions for b and r into the expression for u in step 1 to yield Einstein's formula for the addition of velocities:

$u={v+u' \over 1+(vu'/c^{2})}.$

The relativistic formula for addition of velocities presented above exhibits several important features:

• If u′ and v are both very small compared with the speed of light, then the product vu′/c² becomes vanishingly small, and the overall result becomes indistinguishable from the Galilean formula (Newton's formula) for the addition of velocities: u = u′ + v. The Galilean formula is a special case of the relativistic formula applicable to low velocities.
• If u′ is set equal to c, then the formula yields u = c regardless of the starting value of v. The velocity of light is the same for all observers regardless their motions relative to the emitting source.

Return to Introduction

Time dilation and length contraction revisited

Main articles: Time dilation and Length contraction

Figure 3-3. Spacetime diagrams illustrating time dilation and length contraction

Click here for a brief section summary

We had previously discussed, in qualitative terms, time dilation and length contraction. It is straightforward to obtain quantitative expressions for these effects. Fig. 3‑3 is a composite image containing individual frames taken from two previous animations, simplified and relabeled for the purposes of this section.

To reduce the complexity of the equations slightly, we see in the literature a variety of different shorthand notations for ct :

$\mathrm {T} =ct$ and $w=ct$ are common.

One also sees very frequently the use of the convention $c=1.$

Figure 3-4. Lorentz factor as a function of velocity

In Fig. 3-3a, segments OA and OK represent equal spacetime intervals. Time dilation is represented by the ratio OB/OK. The invariant hyperbola has the equation w = √x² + k² where k = OK, and the red line representing the world line of a particle in motion has the equation w = x/β = xc/v. A bit of algebraic manipulation yields ${\textstyle OB=OK/{\sqrt {1-v^{2}/c^{2}}}.}$

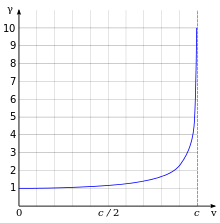
The expression involving the square root symbol appears very frequently in relativity, and one over the expression is called the Lorentz factor, denoted by the Greek letter gamma $\gamma$:

$\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}$

We note that if v is greater than or equal to c, the expression for $\gamma$ becomes physically meaningless, implying that c is the maximum possible speed in nature. Next, we note that for any v greater than zero, the Lorentz factor will be greater than one, although the shape of the curve is such that for low speeds, the Lorentz factor is extremely close to one.

In Fig. 3-3b, segments OA and OK represent equal spacetime intervals. Length contraction is represented by the ratio OB/OK. The invariant hyperbola has the equation x = √w² + k², where k = OK, and the edges of the blue band representing the world lines of the endpoints of a rod in motion have slope 1/β = c/v. Event A has coordinates (x, w) = (γk, γβk). Since the tangent line through A and B has the equation w = (x − OB)/β, we have γβk = (γk − OB)/β and

$OB/OK=\gamma (1-\beta ^{2})={\frac {1}{\gamma }}$

Return to Introduction