User:FishOnWiki/Sandbox

An Euler diagram does not need to show all possible intersections.

A Venn diagram shows all possible intersections.

Euler diagrams are a diagrammatic means of representing sets and their relationships. They are the modern incarnation of Euler circles, which were invented by Leonhard Euler.

Euler diagrams usually consist of simple closed curves in the plane which are used to depict sets. The spatial relationships between the curves (overlap, containment or neither) corresponds to set-theoretic relationships (intersection, subset and disjointness).

Euler diagrams generalise the well-known Venn diagrams which represent all possible set intersections available with the given sets. The intersection of the interior of a collection of curves and the exterior of the rest of the curves in the diagrams is called zone. Thus, in Venn diagrams all zones must be present (given the set of curves), but in an Euler diagram some zones might be missing.

In a logical setting, one can use model theoretic semantics to interpret Euler diagrams, within a universe of discourse. In the examples on the right, the Euler diagram depicts that the sets Animal and Mineral are disjoint since the corresponding curves are disjoint, and also that the set of Animals with Four Legs is a subset of the set of Animals. The Venn diagram which uses the same categories of Animal, Mineral and Four Legs does not encapsulate this information. Traditionally this emptiness of a set in Venn diagrams is depicted by shading in the region. Euler diagrams represent emptiness either by shading or by the use of a missing zone.

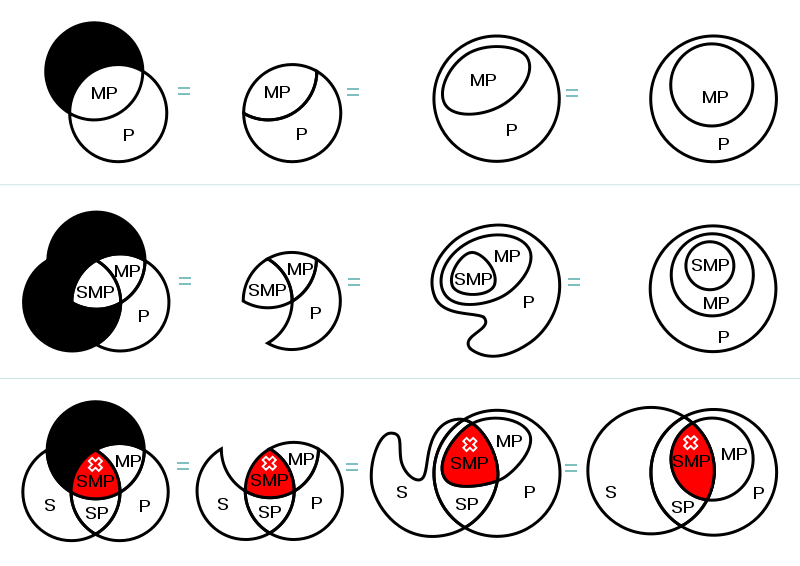
Often a set of well-formedness conditions are imposed; these are topological or geometric constraints imposed on the structure of the diagram. For example, connectedness of zones might be enforced, or concurrency of curves or multiple points might be banned, as might tangential intersection of curves. In the diagram below, examples of small Venn diagrams are transformed into Euler diagrams by sequences of transformations; some of the intermediate diagrams have concurrency of curves. However, this sort of transformation of an Venn diagram with shading into an Euler diagram without shading is not always possible. There are examples of Euler diagrams with 9 sets which are not drawable using simple closed curves without the creation of unwanted zones since they would have to have non-planar dual graphs.

Examples of small Venn diagrams with shaded regions representing empty sets that are easily transformed into Euler diagrams.

External links

Euler Diagrams. Brighton, UK (2004).What are Euler Diagrams?
Visualisation with Euler diagrams project

See also

External links