User:Dedhert.Jr/sandbox/3

Definition

A binary operation is said to be commutative if every two elements commute without noticing the order of elements. Equivalently, the first element commutes with another element under the binary operation. Mathematically speaking, let $x$ and $y$ be the elements of a set, then a binary operation $*$ is said to be commutative if, for every $x$ and $y$ in the set, $$x*y=y*x.$$ More generally, it is said to be commutative if there are $n$ elements in a set that may randomly commute to each other.

Examples

The cumulation of apples, which can be seen as an addition of natural numbers, is commutative.

The addition of vectors is commutative, because ${\vec {a}}+{\vec {b}}={\vec {b}}+{\vec {a}}$.

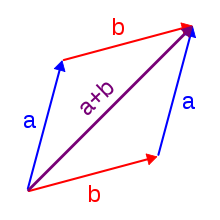
Operations in many branches of mathematics are said to be either commutative or not, depending on the given elements and mathematical structures:

• In calculation, addition and multiplication are commutative in real numbers, complex numbers, or every field in general. An example is $5+3=3+5$. Operations such as subtraction, division, and exponents are not always commutative; as in $5-7\neq 7-5$.
• In algebra, the commutative operations are not always commutative. This can be found in vectors: the addition of vectors is commutative, but the cross product is not.. The addition operation of matrices is commutative, but the multiplication is not, as in

$${\begin{bmatrix}0&2\\0&1\end{bmatrix}}={\begin{bmatrix}1&1\\0&1\end{bmatrix}}{\begin{bmatrix}0&1\\0&1\end{bmatrix}}\neq {\begin{bmatrix}0&1\\0&1\end{bmatrix}}{\begin{bmatrix}1&1\\0&1\end{bmatrix}}={\begin{bmatrix}0&1\\0&1\end{bmatrix}}.$$

• In set theory,
• In logic, the law of Boolean algebra states that the variables are commutative under the truth operator of conjunction ($\wedge$) and disjunction ($\vee$).

History and etymology

Records of the implicit use of the commutative property go back to ancient times. The Egyptians used the commutative property of multiplication to simplify computing products. Euclid is known to have assumed the commutative property of multiplication in his book Elements. Formal uses of the commutative property arose in the late 18th and early 19th centuries when mathematicians began to work on a theory of functions. Nowadays, the commutative property is a well-known and basic property used in most branches of mathematics.

The first known use of the term was in a French Journal published in 1814

The first recorded use of the term commutative was in a memoir by François Servois in 1814, which used the word commutatives when describing functions that have what is now called the commutative property. The word is a combination of the French word commuter meaning "to substitute or switch" and the suffix -ative meaning "tending to" so the word literally means "tending to substitute or switch". The term then appeared in English in 1838, in Duncan Farquharson Gregory's article entitled "On the real nature of symbolical algebra" published in 1840 in the Transactions of the Royal Society of Edinburgh.

Related property

The associative property is closely related to the commutative property. The associative property of an expression containing two or more occurrences of the same operator states that the order operations are performed does not affect the final result, as long as the order of terms does not change. When the associative property holds, the commutative property states that the order of the terms does not affect the final result.

Graph showing the symmetry of the addition function

Some forms of symmetry can be directly linked to commutativity. When a commutative operation is written as a binary function $z=f(x,y),$ then this function is called a symmetric function, and its graph in three-dimensional space is symmetric across the plane $y=x$. For relations, a symmetric relation is analogous to a commutative operation, in that if a relation R is symmetric, then $aRb\Leftrightarrow bRa$.

See also

• Quasi-commutative property

References

• Allaire, Patricia R.; Bradley, Robert E. (2002). "Symbolical Algebra as a Foundation for Calculus: D. F. Gregory's Contribution". Historia Mathematica. 29: 395–426. doi:10.1006/hmat.2002.2358.
• Barbeau, Alice Mae (1968). A Historical Approach to the Theory of Groups. Vol. 2. University of Wisconsin--Madison.
• Cooke, Richard G. (2014). Infinite Matrices and Sequence Spaces. Dover Publications. ISBN 978-0-486-78083-2.
• Gay, Robins R.; Shute, Charles C. D. (1987). The Rhind Mathematical Papyrus: An Ancient Egyptian Text. British Museum. ISBN 0-7141-0944-4.
• Gregory, D. F. (1840). "On the real nature of symbolical algebra". Transactions of the Royal Society of Edinburgh. 14: 208–216.
• Heath, Thomas L. (1956) [1925]. The Thirteen Books of Euclid's Elements. Vol. 2 (2nd ed.). New York: Dover Publications. ISBN 0-486-60088-2.
• O'Regan, Gerard (2008). A brief history of computing. Springer. ISBN 978-1-84800-083-4.
• Posamentier, Elaine; Farber, William; Germain-Williams, Terri L.; Paris; Thaller, Bernd; Lehmann, Ingmar (2013). 100 Commonly Asked Questions in Math Class. Corwin Press. ISBN 978-1-4522-4308-5.
• Rice, Adrian (2011). "Introduction". In Flood, Raymond; Rice, Adrian; Wilson, Robin (eds.). Mathematics in Victorian Britain. Oxford University Press. ISBN 9780191627941.
• Rosen, Kenneth (2013). Discrete Maths and Its Applications Global Edition. McGraw Hill. ISBN 978-0-07-131501-2.
• Saracino, Dan (2008). Abstract Algebra: A First Course (2nd ed.). Waveland Press Inc.
• Sterling, Mary J. (2009). Linear Algebra For Dummies. John & Sons Wiley. ISBN 978-0-470-43090-3.