Conjecture

For text reconstruction, see Conjecture (textual criticism).

The real part (red) and imaginary part (blue) of the Riemann zeta function along the critical line Re(s) = 1/2. The first non-trivial zeros can be seen at Im(s) = ±14.135, ±21.022 and ±25.011. The Riemann hypothesis, a famous conjecture, says that all non-trivial zeros of the zeta function lie along the critical line.

In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's conjecture (now a theorem, proven in 1995 by Andrew Wiles), have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.

Resolution of conjectures

Proof

Formal mathematics is based on provable truth. In mathematics, any number of cases supporting a universally quantified conjecture, no matter how large, is insufficient for establishing the conjecture's veracity, since a single counterexample could immediately bring down the conjecture. Mathematical journals sometimes publish the minor results of research teams having extended the search for a counterexample farther than previously done. For instance, the Collatz conjecture, which concerns whether or not certain sequences of integers terminate, has been tested for all integers up to 1.2 × 10¹² (1.2 trillion). However, the failure to find a counterexample after extensive search does not constitute a proof that the conjecture is true—because the conjecture might be false but with a very large minimal counterexample.

Nevertheless, mathematicians often regard a conjecture as strongly supported by evidence even though not yet proved. That evidence may be of various kinds, such as verification of consequences of it or strong interconnections with known results.

A conjecture is considered proven only when it has been shown that it is logically impossible for it to be false. There are various methods of doing so; see methods of mathematical proof for more details.

One method of proof, applicable when there are only a finite number of cases that could lead to counterexamples, is known as "brute force": in this approach, all possible cases are considered and shown not to give counterexamples. In some occasions, the number of cases is quite large, in which case a brute-force proof may require as a practical matter the use of a computer algorithm to check all the cases. For example, the validity of the 1976 and 1997 brute-force proofs of the four color theorem by computer was initially doubted, but was eventually confirmed in 2005 by theorem-proving software.

When a conjecture has been proven, it is no longer a conjecture but a theorem. Many important theorems were once conjectures, such as the Geometrization theorem (which resolved the Poincaré conjecture), Fermat's Last Theorem, and others.

Disproof

Conjectures disproven through counterexample are sometimes referred to as false conjectures (cf. the Pólya conjecture and Euler's sum of powers conjecture). In the case of the latter, the first counterexample found for the n=4 case involved numbers in the millions, although it has been subsequently found that the minimal counterexample is actually smaller.

Independent conjectures

Not every conjecture ends up being proven true or false. The continuum hypothesis, which tries to ascertain the relative cardinality of certain infinite sets, was eventually shown to be independent from the generally accepted set of Zermelo–Fraenkel axioms of set theory. It is therefore possible to adopt this statement, or its negation, as a new axiom in a consistent manner (much as Euclid's parallel postulate can be taken either as true or false in an axiomatic system for geometry).

In this case, if a proof uses this statement, researchers will often look for a new proof that does not require the hypothesis (in the same way that it is desirable that statements in Euclidean geometry be proved using only the axioms of neutral geometry, i.e. without the parallel postulate). The one major exception to this in practice is the axiom of choice, as the majority of researchers usually do not worry whether a result requires it—unless they are studying this axiom in particular.

Conditional proofs

Sometimes, a conjecture is called a hypothesis when it is used frequently and repeatedly as an assumption in proofs of other results. For example, the Riemann hypothesis is a conjecture from number theory that — amongst other things — makes predictions about the distribution of prime numbers. Few number theorists doubt that the Riemann hypothesis is true. In fact, in anticipation of its eventual proof, some have even proceeded to develop further proofs which are contingent on the truth of this conjecture. These are called conditional proofs: the conjectures assumed appear in the hypotheses of the theorem, for the time being.

These "proofs", however, would fall apart if it turned out that the hypothesis was false, so there is considerable interest in verifying the truth or falsity of conjectures of this type.

Important examples

Fermat's Last Theorem

Main article: Fermat's Last Theorem

In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers $a$, $b$, and $c$ can satisfy the equation $a^{n}+b^{n}=c^{n}$ for any integer value of $n$ greater than two.

This theorem was first conjectured by Pierre de Fermat in 1637 in the margin of a copy of Arithmetica, where he claimed that he had a proof that was too large to fit in the margin. The first successful proof was released in 1994 by Andrew Wiles, and formally published in 1995, after 358 years of effort by mathematicians. The unsolved problem stimulated the development of algebraic number theory in the 19th century, and the proof of the modularity theorem in the 20th century. It is among the most notable theorems in the history of mathematics, and prior to its proof it was in the Guinness Book of World Records for "most difficult mathematical problems".

Four color theorem

Main article: Four color theorem

A four-coloring of a map of the states of the United States (ignoring lakes).

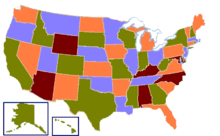
In mathematics, the four color theorem, or the four color map theorem, states that given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map—so that no two adjacent regions have the same color. Two regions are called adjacent if they share a common boundary that is not a corner, where corners are the points shared by three or more regions. For example, in the map of the United States of America, Utah and Arizona are adjacent, but Utah and New Mexico, which only share a point that also belongs to Arizona and Colorado, are not.

Möbius mentioned the problem in his lectures as early as 1840. The conjecture was first proposed on October 23, 1852 when Francis Guthrie, while trying to color the map of counties of England, noticed that only four different colors were needed. The five color theorem, which has a short elementary proof, states that five colors suffice to color a map and was proven in the late 19th century; however, proving that four colors suffice turned out to be significantly harder. A number of false proofs and false counterexamples have appeared since the first statement of the four color theorem in 1852.

The four color theorem was ultimately proven in 1976 by Kenneth Appel and Wolfgang Haken. It was the first major theorem to be proved using a computer. Appel and Haken's approach started by showing that there is a particular set of 1,936 maps, each of which cannot be part of a smallest-sized counterexample to the four color theorem (i.e., if they did appear, one could make a smaller counter-example). Appel and Haken used a special-purpose computer program to confirm that each of these maps had this property. Additionally, any map that could potentially be a counterexample must have a portion that looks like one of these 1,936 maps. Showing this with hundreds of pages of hand analysis, Appel and Haken concluded that no smallest counterexample exists because any must contain, yet do not contain, one of these 1,936 maps. This contradiction means there are no counterexamples at all and that the theorem is therefore true. Initially, their proof was not accepted by mathematicians at all because the computer-assisted proof was infeasible for a human to check by hand. However, the proof has since then gained wider acceptance, although doubts still remain.

Hauptvermutung

Main article: Hauptvermutung

The Hauptvermutung (German for main conjecture) of geometric topology is the conjecture that any two triangulations of a triangulable space have a common refinement, a single triangulation that is a subdivision of both of them. It was originally formulated in 1908, by Steinitz and Tietze.

This conjecture is now known to be false. The non-manifold version was disproved by John Milnor in 1961 using Reidemeister torsion.

The manifold version is true in dimensions m ≤ 3. The cases m = 2 and 3 were proved by Tibor Radó and Edwin E. Moise in the 1920s and 1950s, respectively.

Weil conjectures

Main article: Weil conjectures

In mathematics, the Weil conjectures were some highly influential proposals by André Weil (1949) on the generating functions (known as local zeta-functions) derived from counting the number of points on algebraic varieties over finite fields.

A variety V over a finite field with q elements has a finite number of rational points, as well as points over every finite field with q^k elements containing that field. The generating function has coefficients derived from the numbers N_k of points over the (essentially unique) field with q^k elements.

Weil conjectured that such zeta-functions should be rational functions, should satisfy a form of functional equation, and should have their zeroes in restricted places. The last two parts were quite consciously modeled on the Riemann zeta function and Riemann hypothesis. The rationality was proved by Dwork (1960), the functional equation by Grothendieck (1965), and the analogue of the Riemann hypothesis was proved by Deligne (1974).

Poincaré conjecture

Main article: Poincaré conjecture

In mathematics, the Poincaré conjecture is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space. The conjecture states that:

Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere.

An equivalent form of the conjecture involves a coarser form of equivalence than homeomorphism called homotopy equivalence: if a 3-manifold is homotopy equivalent to the 3-sphere, then it is necessarily homeomorphic to it.

Originally conjectured by Henri Poincaré in 1904, the theorem concerns a space that locally looks like ordinary three-dimensional space but is connected, finite in size, and lacks any boundary (a closed 3-manifold). The Poincaré conjecture claims that if such a space has the additional property that each loop in the space can be continuously tightened to a point, then it is necessarily a three-dimensional sphere. An analogous result has been known in higher dimensions for some time.

After nearly a century of effort by mathematicians, Grigori Perelman presented a proof of the conjecture in three papers made available in 2002 and 2003 on arXiv. The proof followed on from the program of Richard S. Hamilton to use the Ricci flow to attempt to solve the problem. Hamilton later introduced a modification of the standard Ricci flow, called Ricci flow with surgery to systematically excise singular regions as they develop, in a controlled way, but was unable to prove this method "converged" in three dimensions. Perelman completed this portion of the proof. Several teams of mathematicians have verified that Perelman's proof is correct.

The Poincaré conjecture, before being proven, was one of the most important open questions in topology.

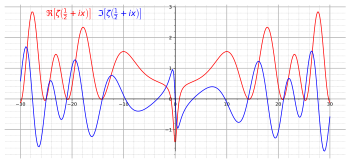
Riemann hypothesis

Main article: Riemann hypothesis

In mathematics, the Riemann hypothesis, proposed by Bernhard Riemann (1859), is a conjecture that the non-trivial zeros of the Riemann zeta function all have real part 1/2. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields.

The Riemann hypothesis implies results about the distribution of prime numbers. Along with suitable generalizations, some mathematicians consider it the most important unresolved problem in pure mathematics. The Riemann hypothesis, along with the Goldbach conjecture, is part of Hilbert's eighth problem in David Hilbert's list of 23 unsolved problems; it is also one of the Clay Mathematics Institute Millennium Prize Problems.

P versus NP problem

Main article: P versus NP problem

The P versus NP problem is a major unsolved problem in computer science. Informally, it asks whether every problem whose solution can be quickly verified by a computer can also be quickly solved by a computer; it is widely conjectured that the answer is no. It was essentially first mentioned in a 1956 letter written by Kurt Gödel to John von Neumann. Gödel asked whether a certain NP-complete problem could be solved in quadratic or linear time. The precise statement of the P=NP problem was introduced in 1971 by Stephen Cook in his seminal paper "The complexity of theorem proving procedures" and is considered by many to be the most important open problem in the field. It is one of the seven Millennium Prize Problems selected by the Clay Mathematics Institute to carry a US$1,000,000 prize for the first correct solution.

Other conjectures

• Goldbach's conjecture
• The twin prime conjecture
• The Collatz conjecture
• The Manin conjecture
• The Maldacena conjecture
• The Euler conjecture, proposed by Euler in the 18th century but for which counterexamples for a number of exponents (starting with n=4) were found beginning in the mid 20th century
• The Hardy-Littlewood conjectures are a pair of conjectures concerning the distribution of prime numbers, the first of which expands upon the aforementioned twin prime conjecture. Neither one has either been proven or disproven, but it has been proven that both cannot simultaneously be true (i.e., at least one must be false). It has not been proven which one is false, but it is widely believed that the first conjecture is true and the second one is false.
• The Langlands program is a far-reaching web of these ideas of 'unifying conjectures' that link different subfields of mathematics (e.g. between number theory and representation theory of Lie groups). Some of these conjectures have since been proved.

In other sciences

Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is related to hypothesis, which in science refers to a testable conjecture.

See also

• Bold hypothesis
• Futures studies
• Hypotheticals
• List of conjectures
• Ramanujan machine

References

Works cited

• Deligne, Pierre (1974), "La conjecture de Weil. I", Publications Mathématiques de l'IHÉS, 43 (43): 273–307, doi:10.1007/BF02684373, ISSN 1618-1913, MR 0340258, S2CID 123139343
• Dwork, Bernard (1960), "On the rationality of the zeta function of an algebraic variety", American Journal of Mathematics, 82 (3), American Journal of Mathematics, Vol. 82, No. 3: 631–648, doi:10.2307/2372974, ISSN 0002-9327, JSTOR 2372974, MR 0140494
• Grothendieck, Alexander (1995) [1965], "Formule de Lefschetz et rationalité des fonctions L", Séminaire Bourbaki, vol. 9, Paris: Société Mathématique de France, pp. 41–55, MR 1608788

External links

• Media related to Conjectures at Wikimedia Commons
• Open Problem Garden
• Unsolved Problems web site