Talk:Pi/Archive 11
| This is an archive of past discussions about Pi. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 5 | ← | Archive 9 | Archive 10 | Archive 11 | Archive 12 | Archive 13 | → | Archive 15 |
Featured article status update
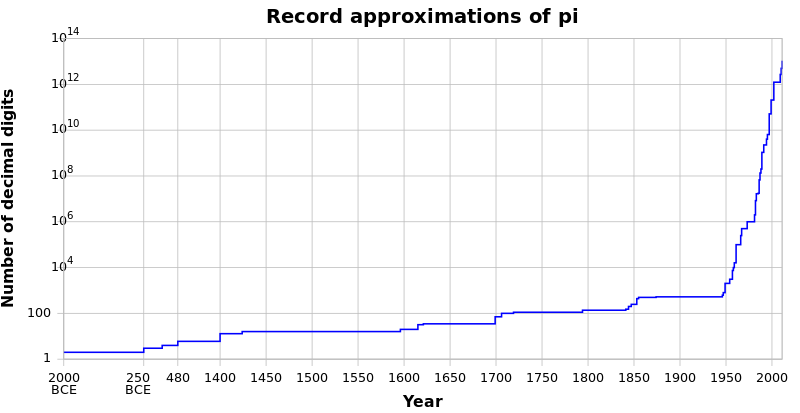
Update on progress towards FA: Thanks to all the editors that have recently improved the article. User Jakob.scholbach did a great review (above) and there have also been some good suggestions from user Nageh. The article meets all the formalistic FA requirements (cites, links, illustrations, MOS, etc); and the prose has been reviewed by several editors, so the prose is probably as good as it is going to get. The only remaining tasks I'm aware of are implementing 3 or 4 remaining suggestions from the review, and polishing the "speed of convergence" subsection. After than, perhaps in late May, I'll nominate the article for FA. All other editors are welcome to review and improve the article as they see fit, of course. If anyone out there is a graphics wizard, it would be great if you could create an English version the graph File:Rekordaj alproksimighoj al pi.png. That is a nice graph that should be in this article, but its axis labels are not in English ... all you have to do is translate the labels from Esperanto to English. --Noleander (talk) 18:03, 1 May 2012 (UTC)
- I can certainly replace the axis labels easily. Are you sure you don't want to do it yourself so you can decide exactly how you want everything? I'm just going to open it in MS Paint, erase the old labels, and put new ones in with the text tool. Use Flip/Rotate to do the vertical one. It's no trouble, but if you'd rather I did it, let me know your preferences. Should I keep it all black and white, or maybe use blue for the labels and title to add a little color? I could also color the graph plot using the fill tool. Preferred font? Should the labels be bigger than they are now? Should I leave off the title, since it'll have a caption on the page? Lots of little decisions like these. Tell me what you prefer, and I'll just use my own judgment on the rest.
- I don't know Esperanto, but I presume the title says "Record approximations of pi", and the x-axis label says "year". I would guess the y-axis label says "decimal position", but that doesn't make sense. Tell me the exact wording you want, including how it's capitalized. --Joseph Lindenberg (talk) 18:04, 2 May 2012 (UTC)
- Thanks for volunteeering:
- Colors: a simple black-on-white would be best. WP sort of has a policy to avoid relying on colors, due to color-blind readers.
- Axes: The vertical axis should be "Number of digits" and the horiz axis "Year".
- Scale: the vertical axis has to be logarithmic. Horiz axis should probably keep the "breaks" so the graph is not flat for centuries.
- Year axis: the labels on the vertical axis are too hard to read (to get the number of zeros); suggest use scientific notation e.g. 1012 etc
- Font: use Arial or Helvetica.
- File format: Ideally, the picture should be in SVG vector format, not a pixel format like GIF/PNG/TIFF. That way, future editors can edit the file, and tweak individual graphic elements (for example, as new records are set, future editors could add new points onto the end of the graph). I've used InkScape in the past to create SVG pictures: InkScape is free, mature, and works on Mac or PC. To get to SVG Format would entail re-drawing the picture from scratch.
- Data: Another reason to re-draw the picture from scratch is because we don't know what source the original picture creator used: their data may be suspect. the WP:V policy applies to data in graphs as well: we must be able to identify a source. I'd suggest the data points from Chronology of computation of π are the best data to use. The Arndt book has a great table (in an appendix) summarizing the num digits over time, and it is consistent with the Chronology of computation of π data, so I'd just use the latter as a starting point.
- Newest data: it would be great if you could extend the old graph to include the newest data through 2011 (as shown in Chronology of computation of π)
- Thanks! --Noleander (talk) 18:17, 2 May 2012 (UTC)
- Thanks for volunteeering:
- I realize SVG is preferable, but I don't know anything about working with vector graphics. I assumed we were just talking about replacing the labels on the existing graph. I was surprised you were seeking a volunteer to do something so simple. (And wondering how in the world it could be that you didn't know how to use MS Paint.) Maybe we should continue to look for another volunteer. Sorry I misunderstood. (By the way, on the color issue, three other graphs in the article do use blue for the actual plot line. So you might want to consider doing that for consistency.) --Joseph Lindenberg (talk) 18:51, 2 May 2012 (UTC)
- No problem. At first I thought just replacing the labels would be okay, but the more I think about it, it probably needs to be redrawn from scratch. Or, the graph could be left out of the article ... I don't think its absence is a bar to FA status. Thanks for considering it anyway. --Noleander (talk) 18:54, 2 May 2012 (UTC)
- I posted a request at Wikipedia:Graphic_Lab/Illustration_workshop#Pi_graph:_convert_from_PNG_to_SVG to see if anyone there could help. Not sure how active that group is, though. --Noleander (talk) 19:05, 2 May 2012 (UTC)
- User Nageh drew a great illustration of the hunt for digits, :And it is in vector format, so it can be easily updated in the future. Great job! --Noleander (talk) 16:22, 3 May 2012 (UTC)
- I posted a request at Wikipedia:Graphic_Lab/Illustration_workshop#Pi_graph:_convert_from_PNG_to_SVG to see if anyone there could help. Not sure how active that group is, though. --Noleander (talk) 19:05, 2 May 2012 (UTC)
- No problem. At first I thought just replacing the labels would be okay, but the more I think about it, it probably needs to be redrawn from scratch. Or, the graph could be left out of the article ... I don't think its absence is a bar to FA status. Thanks for considering it anyway. --Noleander (talk) 18:54, 2 May 2012 (UTC)
- I realize SVG is preferable, but I don't know anything about working with vector graphics. I assumed we were just talking about replacing the labels on the existing graph. I was surprised you were seeking a volunteer to do something so simple. (And wondering how in the world it could be that you didn't know how to use MS Paint.) Maybe we should continue to look for another volunteer. Sorry I misunderstood. (By the way, on the color issue, three other graphs in the article do use blue for the actual plot line. So you might want to consider doing that for consistency.) --Joseph Lindenberg (talk) 18:51, 2 May 2012 (UTC)
FA nomination initiated
This article has been nominated for FA status at Wikipedia:Featured article candidates/Pi/archive1. If anyone would like to review the article, please do so there. --Noleander (talk) 02:31, 15 May 2012 (UTC)
"Correct title" template?
I removed the {{Correct title}} template from the top of the article, which read:
- The correct title of this article is π. It appears incorrectly here because of technical restrictions
First, I think that is super ugly to put such a notice at the top of a high-quality article. Second, many, many articles & books about π use "pi" in their titles, and π in their body - this article is following suit. Third, I don't think there is consensus that "pi" as a title is "wrong" or "incorrect": "pi" is a valid alternative to π within a title. The "technical restrictions" are just one factor that causes "pi" to be a valid title. Thoughts? --Noleander (talk) 16:14, 3 May 2012 (UTC)
- I agree, it should not be there unless the title is seriously wrong and confusing (like the old title for C Plus Plus). Some editors think that hatnotes are some kind of an interactive game where you scour the encyclopedia for any possible use for them, even if they contribute nothing and resolve no confusion. The threshold for ugly notices should be very high, since a professionally edited work contains exactly none. —Designate (talk) 23:35, 17 May 2012 (UTC)
- More than that, the claim is just false. There are no technical restrictions in play. If we wanted the title to be π we could make it be that; the question has been debated and the decision made. (I don't know whether we could get it to display this incongruous-looking π thingie, which I dislike for other reasons, but I think we could.) --Trovatore (talk) 23:41, 17 May 2012 (UTC)
irrational number
The link to irrational in the section irrationality and transcendence section points to the wrong article. It should be irrational. (ie irrational_number)128.97.68.15 (talk) 19:45, 18 May 2012 (UTC)
- Thanks for reporting that. I've fixed it. --Noleander (talk) 19:50, 18 May 2012 (UTC)
Featured article
The article was promoted to FA status today. Thanks to all who helped, particularly those that helped with the Peer Reviews! --Noleander (talk) 18:04, 4 June 2012 (UTC)
- Excellent. Maybe suggest a Main Page entry for 22 July?—A bit iffy (talk) 19:35, 4 June 2012 (UTC)
- Seems reasonable to me. Let's hope the Americans don't feel strongly about it ;-) Sławomir Biały (talk) 19:38, 4 June 2012 (UTC)
- Actually, I was thinking of pi day (March 14, 2013) ... US centric as it is. What is the signfificance of 22 July? --Noleander (talk) 19:45, 4 June 2012 (UTC)
- I think the idea is that it's 22/7. All these pi-ish days are kind of silly, based on artificial and meaningless interpretations of date notations. How about the anniversary of some significant event related to the number? Admittedly I don't know what event that might be. --Trovatore (talk) 19:48, 4 June 2012 (UTC)
- Well, there's really no reason to put it on any kind of special day. But since 22/7 is one coming up, I suggest that one, unless there is one of more significance that someone else suggests. 3/14/2013 seems too far off to me, but if Noleander is ok with that, I don't mind it. Sławomir Biały (talk) 12:53, 5 June 2012 (UTC)
- Sure, 22/7 is fine. Nine months is a bit long to wait, and I favor the European/military date convention ... I don't want to do anything to support the 3/14 convention :-) I'll put it on TFAR for 22 July. --Noleander (talk) 13:59, 5 June 2012 (UTC)
- It is in the WP:TFAR holding area now. --Noleander (talk) 14:05, 5 June 2012 (UTC)
- Sure, 22/7 is fine. Nine months is a bit long to wait, and I favor the European/military date convention ... I don't want to do anything to support the 3/14 convention :-) I'll put it on TFAR for 22 July. --Noleander (talk) 13:59, 5 June 2012 (UTC)
- Well, there's really no reason to put it on any kind of special day. But since 22/7 is one coming up, I suggest that one, unless there is one of more significance that someone else suggests. 3/14/2013 seems too far off to me, but if Noleander is ok with that, I don't mind it. Sławomir Biały (talk) 12:53, 5 June 2012 (UTC)
- I think the idea is that it's 22/7. All these pi-ish days are kind of silly, based on artificial and meaningless interpretations of date notations. How about the anniversary of some significant event related to the number? Admittedly I don't know what event that might be. --Trovatore (talk) 19:48, 4 June 2012 (UTC)
- Actually, I was thinking of pi day (March 14, 2013) ... US centric as it is. What is the signfificance of 22 July? --Noleander (talk) 19:45, 4 June 2012 (UTC)
- Seems reasonable to me. Let's hope the Americans don't feel strongly about it ;-) Sławomir Biały (talk) 19:38, 4 June 2012 (UTC)
Well done everyone! Martin Hogbin (talk) 16:08, 7 June 2012 (UTC)
- I was unaware that it was expressed as 22/7 in Europe. In that case, I suppose it's fine, but I much prefer 3/14. Mind you, I've never touched the article, so w/e. This is also Sven Manguard 14:22, 8 June 2012 (UTC)
- Irrespective of notational preferences, March 14 is certainly the date best known for being pi day, and I think we could get everyone to agree on it if it were coming up soon. But it isn't, and 22 July is. --Trovatore (talk) 18:38, 8 June 2012 (UTC)
"Exploiting" numbers?
Have changed these two instances of "exploited"; not sure numbers should be subjected to exploitation, even if they are inanimate.
- "Although infinite series were exploited for π most notably by European mathematicians..." and
- "Lambert's proof exploited a continued-fraction representation of the tangent function...."
Have run across this same construction elsewhere recently, so maybe it's not as pejorative in BrE than AmE, where I take the meaning to be something like "searched for a weakness in order to misuse". Not sure what to replace it with. engaged? employed? riffed off of? improvised? elaborated? refactored? Maybe someone who understands what is happening to these numbers can suggest something more descriptive, so to be more informative for the international reader, or revert. Neotarf (talk) 14:39, 12 June 2012 (UTC)
- In mathematics, "exploited" just means "used", but perhaps with a suggestion of "used in a particularly unusual or interesting way". Gandalf61 (talk) 15:31, 12 June 2012 (UTC)
- The alternatives for exploited that were used, "elaborated on" and "engaged", respectively, are both manifestly inferior alternatives. It's not even clear what "Infinites series were elaborated on for π" in supposed to mean! Sławomir Biały (talk) 15:54, 12 June 2012 (UTC)
- No argument. "Exploit" is a perfectly good English word whose meaning is precise. As such it is there to be exploited. After all, mathematics is not for the pure-hearted and those of upright morals, it's for evil people only. --Matt Westwood 21:14, 12 June 2012 (UTC)
- I do not think there is any English-variety issue here. Exploit is a word with multiple nuances depending on context. Exploiting people is almost always bad (but then, so is using people), but exploiting, say, a regularity or a symmetry, is perfectly normal and even praiseworthy. --Trovatore (talk) 19:41, 12 June 2012 (UTC)
volume vs diameter?
Lambiam: Regarding the number of digits sufficient for computing universe's volume etc: Can you supply the quote from Arndt on that? I no longer have the book, but I my notes say "diameter" not "volume". Thanks. --Noleander (talk) 14:47, 12 June 2012 (UTC)
- I included the quote in this edit. --Lambiam 23:17, 12 June 2012 (UTC)
Too many examples in "rate of convergence" section.
An editor just added a 3rd example to the "rate of convergence" section. I removed it, because it clouds the point that the section is making. That section is intended to be a concise explanation of why mathematicians kept searching for better series. It illustrates the point by comparing to simple series. Providing a 3rd example in that section would do nothing other than confuse readers. There are scores, perhaps hundreds, of series that could be listed in that section. But we have an entire article for that purpose: List of formulae involving π. --Noleander (talk) 05:40, 15 June 2012 (UTC)
- I also removed a simplification of Nilakantha's series. Again, the point of that section is focused: show two simple series, compare them, and show the reader how one converges faster than the other. Presenting alternative versions is just confusing things for lay readers. --Noleander (talk) 05:50, 15 June 2012 (UTC)
how about the lexarithm in ancient greek
each lettre is a number so that¦ Α=1, Β=2, Γ=3, Δ=4, Ε=5, F=6, S΄= 6, Ζ=7, Η=8, Θ=9, Ι=10, Κ=20, Λ=30, Μ=40, Ν=50, Ξ=60, Ο=70, Π=80, Q=90, Ρ=100, Σ=200, Τ=300 Υ=400, Φ=500, Χ=600, Ψ=700, Ω=800, ΣΑΜΠΙ=900
given this each word is an adittion of numbers numer. given this: ΜΗΚΟΣ (length) = 40+8+20+70+200 = 338 ΠΕΡΙΦΕΡΕΙΑΣ (circumference) =80+5+100+10+500+5+100+5+10+1+200 = 1016 ΚΥΚΛΟΥ (circle) = 20+400+20+30+70+400 = 940 and finally
ΔΙΑΜΕΤΡΟΣ (diameter) = 4+10+1+40+5+300+100+70+200 = 730
so the tlngth of the circumferance of a cirle or (if you prefer) ratio of a circle's circumference = ΜΗΚΟΣ ΠΕΡΙΦΕΡΕΙΑΣ ΚΥΚΛΟΥ = 338+1016+940 = 2294 and diameter = ΔΙΑΜΕΤΡΟΣ = 730
SO
ratio of a circle's circumference / diameter = pi
= ΜΗΚΟΣ ΠΕΡΙΦΕΡΕΙΑΣ ΚΥΚΛΟΥ / ΔΙΑΜΕΤΡΟΣ = Π
= 2294 / 730 = 3.14...
quite funny isn't it? funniest part is the the same applies for the golden ratio Φ and that it was first pointed out by the pythagorean school of thought. — Preceding unsigned comment added by 85.75.67.238 (talk) 18:25, 24 June 2012 (UTC)
- I do think it's funny, and pretty cool if applicable! It might even give a clue that the Greeks knew Pi at some very early point, and used it as the basis for making up some or all of these Greek words! But first: Where did you discover that each of those Greek words means what you indicated they mean? I used Google Translate (iffy at times), and it said: ΜΗΚΟΣ (length)—Google Translate agrees. ΠΕΡΙΦΕΡΕΙΑΣ (circumference)—Google Translate says "region". ΚΥΚΛΟΥ (circle)—Google Translate says "value". And finally, ΔΙΑΜΕΤΡΟΣ (diameter)—Google Translate agrees. I checked all the Greek-letter-for-number portions you included, and checked all the calculations you listed just above this for Pi, and they appear to be CORRECT. :) The full final calculation to complete decimal points came to 3.14246575342466, but at least the first 3 digits are right, which is intriguing! QUESTIONS: What Greeks used these words in the way you did above, all? When is the earliest place in time that these Greek words are they found used to mean this, for Mathematics? SOURCES? Links? Thanks! (Btw, I didn't look into or check the "Golden Ratio" part.) Misty MH (talk) 05:53, 25 June 2012 (UTC)
- I hope you don't mind: I turned your contribution into its own section, I think, lol. Misty MH (talk) 05:57, 25 June 2012 (UTC)
- Yep! It worked. :) Misty MH (talk) 05:59, 25 June 2012 (UTC)
- To Google translate, "Greek" means "Modern Greek", but the Pythagoreans would have used Ancient Greek, in which περιφέρεια did mean "circumference". (The form περιφέρειας is the genitive: "of the circumference".) However, to include material in Wikipedia, we need be able to cite it to a reliable source, something that is lacking here. --Lambiam 21:17, 28 June 2012 (UTC)
What did people call Pi throughout history?
The article states in the first/intro section that "It has been represented by the Greek letter "π" since the mid-18th century." Okay, if that is true, and implies it might not have been used before that, then: What did people call Pi throughout history? Was it called that but they simply spelled it out rather than using the single letter for it? For those interested in studying this throughout history, the answer to this would seem pretty important. What it was called or referred to in various cultures seems important to the research and study of this topic, so that people can actually find the topic in old or ancient texts. Wondering if the depth of this question might warrant a separate article. In any case, I myself would like to know here what it was called! References? Thanks! Misty MH (talk) 05:34, 25 June 2012 (UTC)
- Yes, if you find that someone had a name for it before then, that would be interesting. Dicklyon (talk) 06:09, 25 June 2012 (UTC)
- In Japanese, for example (I guess Chinese the same), "pi" is "called" enshuuritsu (円周率) which is literally circle-circumference-ratio. Because of the particular feature of Chinese word-construction it's possible to get a description into a single word. The curious thing is that in English in particular we simply have no normal word for it.
- Imaginatorium (talk) 12:49, 25 June 2012 (UTC)
- @Misty: My recollection from reading the sources was there there was (at least in the Western world) no uniform term. Every mathematician used their own personal notation for pi, and for many other constants and operations. And, some did not use circum/diameter ratio at all. --Noleander (talk) 14:07, 25 June 2012 (UTC)
- Thanks all. It would be cool to see what the ancients did use! Misty MH (talk) 04:48, 28 June 2012 (UTC)
Bible material?
Misty: Could you provide some quotes from the secondary sources that support the Bible material you want to include? Then we can look at the material and see what would be the best way to represent it in the article. Thanks. --Noleander (talk) 14:04, 25 June 2012 (UTC)
- The article itself referred to the Bible already. When I tried to add a verse below for context, you deleted my edit! Reverting it makes it look like those Bible passages say the value of Pi is three, when it clearly does not. I explained this not only in my reasons for the changes (twice) but on your Talk page. Are you trying to DELIBERATELY misrepresent the Bible? because there is no justification for reverting a clear correction of fact. This isn't a POV or Personal Research issue. It's a misrepresentation issue. And such a correction doesn't require secondary sources or citations. Please change it back, and if you like, reword it to fit your idea of encyclopedic style (mentioned in your reversion); I don't care how it's worded stylistically, as long as it's accurate and not misleading. Thanks. Misty MH (talk) 22:59, 25 June 2012 (UTC)
- Note also that secondary sources were mentioned already in a note (which I mentioned on your Talk page before your second reversion), where the note says "Suggestions that the pool had a hexagonal shape or an outward curving rim have been offered to explain the disparity. See Borwein, Jonathan M.; Bailey, David H. (2008), Mathematics by Experiment: Plausible Reasoning in the 21st century (revised 2nd ed.), A. K. Peters, ISBN 978-1-56881-442-1, pp. 103, 136, 137." (This note was there before I recently edited the article.) However, the wording in the article itself needed correcting, which I did, and which you undid, twice, and without discussion. Misty MH (talk) 23:06, 25 June 2012 (UTC) Edit Misty MH (talk) 23:12, 25 June 2012 (UTC) Edit Misty MH (talk) 23:13, 25 June 2012 (UTC) Edit: Typo correction only. Misty MH (talk) 00:59, 26 June 2012 (UTC)
- The issue is that the cited source (which is "Pi-Unleashed" by Arndt and Haenel) supports the article as presently worded. The same cited source mentions various attempts to portray the value offered in the Bible in a more favorable light, including the hypothesis that the pool was hexagonal (which dates to the 19th century), but it clearly doesn't attach much significance to these attempts. Sławomir Biały (talk) 23:21, 25 June 2012 (UTC)
- Agreed; it does say that, for I checked a ©2000 version of the book Pi-Unleashed, by Jörg Arndt and Christoph Haenel, in the chapter called Antiquity (between 13.4 and 13.6). It is clear that the author (and possibly other people mentioned) did not bother to check the Bible itself. For just a few verses later, 1 Kings 7:26 says that it was "a handbreadth thick; and its brim was shaped like the brim of a cup, like a lily blossom" (NKJV, also in 2 Chronicles 4:5). However, no mention of this is made in the passage by the author. This makes the Pi article clearly in error about what the Bible actually says. If someone wants to fix it in a way that's acceptable, please do. I comment more below. Misty MH (talk) 01:53, 26 June 2012 (UTC)
- MistyMH: I have no objection to including more material about pi in the Bible, but it is best if the the material comes from some secondary source about pi. If you have a source that discusses pi in the Bible, go ahead and post some quotes from that source here in the Talk page, and we can go from there. We could maybe add another sentence, but not too much or it starts to get a bit out of proportion (that is, pi in the Bible is just not that important, so the article cannot devote too much space to it, per WP:UNDUE). --Noleander (talk) 01:07, 26 June 2012 (UTC)
- Agreed, though I have no interest in adding more material from the Bible, only correcting what it currently says about the Bible. Do I REALLY need a source to justify an obvious correction?? See my comment just above. Misty MH (talk) 01:53, 26 June 2012 (UTC)
- Yeah, sources are needed because this is a matter of interpretation of an ancient text. Therefore, editors are really not permitted to select verses to illustrate a point: the secondary sources have to select the verses. Look at it this way: if that "lily blossom" verse is important in relation to pi, there will be a source about pi that quotes it in that regard. If you cannot find such a source, then it is probably best to leave the article alone. --Noleander (talk) 02:03, 26 June 2012 (UTC)
- Agreed, though I have no interest in adding more material from the Bible, only correcting what it currently says about the Bible. Do I REALLY need a source to justify an obvious correction?? See my comment just above. Misty MH (talk) 01:53, 26 June 2012 (UTC)
I've moved the external links to the reference, as they should not be in the article body. And are there any better links for them? Looking at e.g. the Kings one it redirects to [1] which has three lines of text with headings, surrounded by twelve adverts/commercial links. Surely there is a Bible source which isn't so ad-laden; these would be removed if they were just external links, not refs, because of the advertising.--JohnBlackburnewordsdeeds 23:18, 25 June 2012 (UTC)
- Interesting idea, though now maybe almost no one will bother to check the accuracy of the statement in the article, which is simply and plainly wrong. See 1 Kings 7:26 and 2 Chronicles 4:5. (IGNORE what follows there, which is another topic anyway, as a literal rendering of the Hebrew may indicate "thousands" rather than "two thousand".) Misty MH (talk) 01:53, 26 June 2012 (UTC)
- Someone edited it. Thanks. Misty MH (talk) 20:28, 27 June 2012 (UTC)
- Important: The passages in 1 Kings 7 and 2 Chronicles 4 do not indicate Pi, because the diameter measurement isn't stated anywhere. This also means that Pi cannot be derived from the passages. Crucial passages 1 Kings 7:26 and 2 Chronicles 4:5 are not directly referred to in the notes or article, I think. These contextual-verses indicate that the shape of the rim was like a cup's brim, curved outward; while vss. 23 and 2 (respectively) say the stated distance was from brim to brim (wider than the diameter) NOT from side to side (the actual diameter). Therefore, the passages in 1 Kings 7 and 2 Chronicles 4 do NOT indicate Pi because the diameter measurement isn't stated. And therefore the article, as worded, is wrong on this point. Misty MH (talk) 20:28, 27 June 2012 (UTC)
- I have to ask this, but what relevance does an ancient collection of bronze-age fairy stories have to an article about a mathematical concept? Might as well discuss J.R.R.Tolkien's ents in the entry on trees. --Matt Westwood 13:06, 5 July 2012 (UTC)
- I would not quite put it the same way, but I also feel that the discussion of the Bible is a bit out of place. Nowhere does it actually discuss the value of Pi as it was known at the time. The only conclusions drawn from it are by pure exegesis. It seems much more likely that the priests of Solomon's temple had made much more accurate measurements than those now reported in the Bible. I would suggest either that some more authoritative source be found, or than the discussion of the Bible be removed. Sławomir Biały (talk) 15:05, 5 July 2012 (UTC)
- Several authoritative secondary sources on pi discuss the bible's text in relation to pi. They all use it as an example of how the ratio of circumference-to-diameter was perceived in ancient times. Since secondary sources devoted to pi discuss it in relation to pi, it is appropriate for the article. Now, if the secondary sources did not discuss it, of course it would be WP:OR or WP:SYNTH for an editor to include the material. --Noleander (talk) 15:25, 5 July 2012 (UTC)
- I really don't think I would consider any of the sources presented to be authorities on the history of mathematics, nor (as far as I can tell) do they provide references to such sources. Sławomir Biały (talk) 15:38, 5 July 2012 (UTC)
- Hmm. They seem like pretty good sources to me. What makes you think they are not reliable for the history of pi? --Noleander (talk)
- Usually one expects scholastic sources for the history of mathematics, not pop science sources. There are textbooks and journals on the subject. Arndt & Haenel seem to lack any credible literature review on the subject of pi in ancient Judaism. At a minimum, one would expect this. Instead, they refer disparagingly to all other literature on the subject, and the only item they bother to reference is just so they can make it a target of their ridicule. This is not what one expects from a serious, scholarly work. Sławomir Biały (talk) 17:04, 5 July 2012 (UTC)
- Just about every source on the history of pi (including Beckman, Schepler, Posamentier, and Arndt) mention the Bible's circumference/diameter material. Of course those sources are more than sufficient, so I must be missing your point. --Noleander (talk) 18:14, 5 July 2012 (UTC)
- I'm much more satisfied with the Schepler source. Schepler says that it is likely that the Hebrews had adopted the value of 3 from the Semites. Furthermore, the value of three is stated very unambiguously in the Talmud. Sławomir Biały (talk) 19:41, 5 July 2012 (UTC)
- Just about every source on the history of pi (including Beckman, Schepler, Posamentier, and Arndt) mention the Bible's circumference/diameter material. Of course those sources are more than sufficient, so I must be missing your point. --Noleander (talk) 18:14, 5 July 2012 (UTC)
- Usually one expects scholastic sources for the history of mathematics, not pop science sources. There are textbooks and journals on the subject. Arndt & Haenel seem to lack any credible literature review on the subject of pi in ancient Judaism. At a minimum, one would expect this. Instead, they refer disparagingly to all other literature on the subject, and the only item they bother to reference is just so they can make it a target of their ridicule. This is not what one expects from a serious, scholarly work. Sławomir Biały (talk) 17:04, 5 July 2012 (UTC)
- Hmm. They seem like pretty good sources to me. What makes you think they are not reliable for the history of pi? --Noleander (talk)
- I really don't think I would consider any of the sources presented to be authorities on the history of mathematics, nor (as far as I can tell) do they provide references to such sources. Sławomir Biały (talk) 15:38, 5 July 2012 (UTC)
- Several authoritative secondary sources on pi discuss the bible's text in relation to pi. They all use it as an example of how the ratio of circumference-to-diameter was perceived in ancient times. Since secondary sources devoted to pi discuss it in relation to pi, it is appropriate for the article. Now, if the secondary sources did not discuss it, of course it would be WP:OR or WP:SYNTH for an editor to include the material. --Noleander (talk) 15:25, 5 July 2012 (UTC)
- I would not quite put it the same way, but I also feel that the discussion of the Bible is a bit out of place. Nowhere does it actually discuss the value of Pi as it was known at the time. The only conclusions drawn from it are by pure exegesis. It seems much more likely that the priests of Solomon's temple had made much more accurate measurements than those now reported in the Bible. I would suggest either that some more authoritative source be found, or than the discussion of the Bible be removed. Sławomir Biały (talk) 15:05, 5 July 2012 (UTC)
The point is that religion of any kind has no relevance to modern society, as nobody with a modicum of intelligence can possibly take it seriously. It's interesting from a sociological perspective, and vital to get an overview in a study of history, but in the context of mathematics and science has absolutely no place at all. --Matt Westwood 19:32, 5 July 2012 (UTC)
- Tut tut, verifiability not truth ;-) The bit about the Bible wouldn't have much weight but I think a little extra about it probably is justified. Pi is a mathematical constant but that does not justify excluding non-mathematical material about it. Dmcq (talk) 18:13, 6 July 2012 (UTC)
- Matt Westwood's comments do not appear to be aimed at improving this article but rather at attacking ideas and people he disapproves of. Wikipedia is not a forum for him to engage in attacking other editors and their beliefs. Probably he is deliberately trolling. 212.118.224.148 (talk) 13:04, 7 July 2012 (UTC)
- This seems to be an old chestnut and was written about back in the day. I have added the following, citing The Scientific & the Divine.
| “ | Rabbi Nehemiah explained the discrepancy as being due to the thickness of the vessel. His early work of geometry, Mishnat ha-Middot, was written around 150 AD and takes the value of π to be three and one seventh. | ” |
Pi repeats?
Hagar Dronbecker, an amateur mathematician, has apparently discovered that Pi does repeat, at the hyper-thousandth level.
Before going further, I'll be the first to admit that not a single one of the sources I've found is what I would consider reliable. If I were to submit my doctoral thesis on the sources I've thus far found, I've no doubt that I'd be (quite literally) laughed off campus! But perhaps it might be prudent to add to the article that it's possible that Pi might indeed repeat?
Just a thought. And yes, it's 00:38hrs here, and my brain is indeed tired.
Happy Trails! --Dr. Entropy (talk) 04:38, 22 July 2012 (UTC)
- Thanks for the suggestion, but the article needs to limit itself to mainstream conclusions. See WP:FRINGE. --Noleander (talk) 05:02, 22 July 2012 (UTC)
- In case there's any doubt, the non-repeatability of pi is one of those things that mathematicians are certain about, see Proof that π is irrational, and per Irrational number it easily follows that pi does not repeat. Johnuniq (talk) 07:47, 22 July 2012 (UTC)
Hiya, Johnuniq! Thank you for the proof article; it brought back memories and made my brain hurt more. Thanks again. :) Happy Trails! --Dr. Entropy (talk) 22:40, 22 July 2012 (UTC)
π memorization records
The chart in the article doesn't seem to match the information in the text at all. Kaldari (talk) 08:10, 22 July 2012 (UTC)
- Thanks for pointing that out. I've removed the chart, to be on the safe side. The chart doesnt have, for example, the 67K record. The data in the chart may actually be pretty accurate, but I don't see a source for the data points, so it is probably not worth the risk. --Noleander (talk) 15:09, 22 July 2012 (UTC)
Digits "appear to be random"?
Why not more positive and say that the digits are random? Isn't indexing the digits of pi a acceptable way of returning truly random numbers? Thanks. JMOprof (talk) 15:12, 22 July 2012 (UTC)
- No proof has yet been found that the digits are random (or "normal"). The digits appear to be random/normal, but without a proof, the article cannot say the digits are random. --Noleander (talk) 15:17, 22 July 2012 (UTC)
- The digits really aren't random- for example, the first digit after the decimal point is always "1". The word random isn't technically appropriate in this context, which is why it says the digits "appear to be random". The proper technical statement, as Noleander says, is that pi is a normal number, which is almost universally believed but hasn't been proved. Staecker (talk) 15:27, 22 July 2012 (UTC)
- Thanks. I now get it. As written, it seems to wait for "a shoe to drop" as in "appear to be random, but are not, as shown by Noleander and Staecker in 2012..." ☺ May I suggest "appear to be random, but haven't been proved so"? Well deserved featured article. JMOprof (talk) 17:51, 22 July 2012 (UTC)
- The wording in the article was the result of quite a bit of discussion. Much of it revolving around the fact that "random" should be avoided in this context, because it does not apply to sequences (such as the digits of pi) which have a deterministic algorithm for generation. Thus, the emphasis is on tests like the test for normality. --Noleander (talk) 18:12, 22 July 2012 (UTC)
- Lesson for me. The wording differs between the Wikipedia home page and the article. I've no comments about the article. ☺ thanks. JMOprof (talk) 18:16, 22 July 2012 (UTC)
- The wording in the article was the result of quite a bit of discussion. Much of it revolving around the fact that "random" should be avoided in this context, because it does not apply to sequences (such as the digits of pi) which have a deterministic algorithm for generation. Thus, the emphasis is on tests like the test for normality. --Noleander (talk) 18:12, 22 July 2012 (UTC)
- Thanks. I now get it. As written, it seems to wait for "a shoe to drop" as in "appear to be random, but are not, as shown by Noleander and Staecker in 2012..." ☺ May I suggest "appear to be random, but haven't been proved so"? Well deserved featured article. JMOprof (talk) 17:51, 22 July 2012 (UTC)
Pyramid material - need quotes from sources.
Dave Light: could you please post some quotes from sources here about the pyramid material you want to add to the article? The sources I've seen indicate that such material is fringe science, so it needs to be vetted carefully. We may have to start a discussion at WP:RS, but lets see the quotes from the sources first. Thanks. --Noleander (talk) 15:02, 22 July 2012 (UTC)
- Well, I'm at the 3RR limit for reverting this Fringe info ... if any other editors want to help out, please pitch in. --Noleander (talk) 15:16, 22 July 2012 (UTC)
- Removed it again and repaired the formatting. It's not just a dubious addition but disagrees with the sourced information that's already there. It really needs discussing here.--JohnBlackburnewordsdeeds 16:01, 22 July 2012 (UTC)
Hi Noleander. I am not sure what your sources are or who you have been talking to, but the sources that are referenced on this matter, supporting the correct information, are Professors Flinders Petrie, Professor Verner, Professor I E S Edwards. There is a misconception in some circles that this issue is fringe. It is not fringe. The surveys and documents are quite clear on this matter. I have studied this subject in detail for 10 years, published a book and a paper, and spoken at several conferences on this matter. Professors Petrie, Verner and Edwards were the acknowledged authorities on this matter, and their conclusions are still supported today. The publications by Rossi was refuted in my own publication and Lego had already refuted her argument in 1991. I don't want to enter into an edit war, but it is a requirement that Wikipedia reflects the authoritative sources and facts. — Preceding unsigned comment added by Dave Light (talk • contribs) 16:17, 22 July 2012 (UTC)
Here are some quotes to support the facts:
1/Possibly the greatest authority on the pyramids of Egypt was Egyptologist Professor I.E.S Edwards, author of ‘The Pyramids of Egypt’ and of whom Dr Mark Lehner, author of ‘The Complete Pyramids’, referred to as ‘the great pyramid authority’, (Lehner 1997: 34). Edwards wrote: “The normal angle of incline was about 52° - a slope which, in the Pyramid of Meidum and in the Great Pyramid, would have resulted if the height had been made to correspond with the radius of a circle the circumference of which was equal to the perimeter of the Pyramid at ground level. The northern stone Pyramid at Dashur, with its gradient of 43°35’, provides the only striking exception to this rule” (Edwards 1979: 269).
2/Possibly the other greatest pyramid authority of the second half of the 20th century was Egyptologist Professor Miroslav Verner, author of ‘The Pyramids, their Archaeology and History”. He wrote: "…the ancient Egyptians' constructions are the best evidence of their mathematical capabilities. Let us take for instance, the Great Pyramid in Giza. If we imagine a circle whose radius is the height of the pyramid, then the circumference is identical with the base of the pyramid. This could be achieved only if the wall had the correct angle, and everything had to be calculated in advance. We can conclude that although the ancient Egyptians may have never precisely defined the value of pi, in practice they used it.” (Verner 2001: 70).
3/ To further support this, see also page 454 where Verner writes “Today, Egyptologists rightly ask whether Archimedes, to whom the discovery of Pi is attributed, might have become acquainted with that principle during his stay in Egypt.”
4/Egyptologist Dr Bojana Mojsov, in her recent book about the Egyptian funerary god "Osiris", wrote about pyramids and Old Kingdom architecture saying: (2005: 26): "The architects seem have been aware of the mathematical properties now represented by the letter "Pi". Possibly obtained from practical experience, this knowledge had a profound influence on their ability to design and build complex structures." (Mojsov 2005).
5/The greatest pyramid authority of the late 19th century and the first half of the 20th century was undoubtedly Flinders Petrie, and was author of ‘The Pyramids and Temples of Gizeh” and the survey of the Meidum pyramid. He was the first accurate surveyor of Giza and the excavator and surveyor of the Pyramid of Meidum, he concluded, after many years in the field in Egypt: "but these relations of areas and of circular ratio are so systematic that we should grant that they were in the builder’s design" (Petrie 1940: 30). Earlier in the chapter quoted above, he wrote more specifically, that: “We conclude therefore that the approximation of 7 to 22 as the ratio of diameter to circumference was recognised” (Petrie 1940: 27).
6/ W M Flinders Petrie - The Pyramids and Temples of Gizeh - 2nd edition 1885 republished in a new and revised edition, 1990. Summary of probable theories Page 94 – The’ King’s’ Chamber: "The king’s chamber walls are determined by the same π proportions which rules the exterior of the Pyramid; the circuit of the side of the chamber being equal to a circle described by its width as a radius; and further, the length of the side of the chamber is equal to diameter of its circuit."
7/ W M Flinders Petrie, Nature Journal 1925 wrote: “The bases of some of the other pyramids are also known from my surveys. That of king Snefru and Meydum immediately preceded the Great Pyramid, and was planned on a similar system of measures. Both have the proportions resulting from the height being the radius of a circle equal to the circuit of the base, the angles found being: By Pi theory: 51*51’14”.3 Khufu’s pyramid 51* 50’ 40” +/- 1’5” Sneferu’s pyramid 51* 52’ +/-2” ? The dimensions found are: Khufu’s, height 7, circuit 44, x 40 cubits. Sneferu’s, “ 7, “ 44, x 25 cubits. The modulus of design, being thus 40 or 25 cubits shows the deliberate intention to embody the proportions of 7 : 22.”
References: (not alphabetical)
Legon,, J.A.R. ' 1979 The Plan of the Giza Pyramids', Archaeological Reports of the Archaeology Society of Staten Island, Vol.10 No.1. New Yor.
Edwards, I. E. S.
1979 The Pyramids of Egypt. Middlesex: Penguin.
Lehner, M.
1997 The Complete Pyramids. London: Thames & Hudson Ltd
Petrie, W. M. F.
1883 The Pyramids and Temples of Gizeh. London: Field & Tuer.
Petrie, W.M.F 1892 Medum. London. Field and Tuer Petrie, W.M.F 1925 Surveys of the Great Pyramid, Nature Journal. Pp942-943 Verner, M.
2003 The Pyramids: Their Archaeology and History. London: Atlantic Books.
Cole, J.H.
1925. Determination of the Exact Size and Orientation of the Great Pyramid of Giza.
Cairo: Government Press. Survey of Egypt paper no. 39.
Clarke, S. and R. Engelbach 1991 Ancient Egyptian Construction and Architecture Dover Publications.
Edwards, I. E. S. 1979 The Pyramids of Egypt. Middlesex: Penguin.
Lehner, M. 1997 The Complete Pyramids. London: Thames & Hudson Ltd
Mojsov, B. 2005 Osiris. London: Blackwell Publishing.
Petrie, W. M. F. 1940 Wisdom of the Egyptians. London: British School of Archaeology in Egypt and B. Quaritch Ltd.
Verner, M. 2003 The Pyramids: Their Archaeology and History. London: Atlantic Books. — Preceding unsigned comment added by Dave Light (talk • contribs)
- These citations are all from Egyptologists, and not mathematicians. The quote given by Verner gives this away when he uses the word "identical" whereas in reality it is only approximate.
- As such I believe the existing paragraph on the pyramids is probably adequate, but no more weight should be given it than currently, as Egyptology has even less relevance to mathematics than numerology does. --Matt Westwood 16:27, 22 July 2012 (UTC)
Dave Light: this section in question is discussing the history of the concept, not the mathematics. This is historical fact. In fact the correspondence is extremely close. The question here is not Verner's use of the english language, it is the Egyptian's abilities, which are well attested. Flinders Petrie was an expert surveyor. He was well trained in mathematical principles.
- Okay, so we see that there are several pyramid experts that assert that the size may have been motivated by the number pi. The problem is that (1) there is no evidence that the egyptians knew about pi; and (2) people that study pyramids tend to be very enthusiastic about finding meaning where there is none. Numerology is filled with examples that look persuasive, but are just conincidental. But, in the spirit of compromise, how about this change:
The Great Pyramid at Giza, constructed circa 2589–2566 BC, was built with a perimeter of approximately 1760 cubits and a height of 280 cubits; the ratio 1760/280 ≈ 6.2857 is about equal to 2π ≈ 6.2832. Some
pyramidologistsEgyptologists conclude that the pyramid builders had knowledge of π and deliberately designed the pyramid to incorporate the proportions of a circle.MostOther historians dispute that ancient Egyptians had a concept of π and state that the correspondence is merely coincidental.
- I still maintain that the pi assertion is fringe, but unless the sources are shown to be not reliable, I have no objection to changing the wording. --Noleander (talk) 17:49, 22 July 2012 (UTC)
- He's been blocked for 24 hours, so he won't be replying here today. Dougweller (talk) 18:24, 22 July 2012 (UTC)
- Comment: The proposed change in wording seems reasonable to me. "Most historians" is in fact an unreferenced assertion because no specific data on the proportion of Egyptologists who agree with the position is provided in the accompanying references in the article. Clearly though "other historians" is entirely justifiable in light of the existing references. --Mike Agricola (talk) 00:34, 23 July 2012 (UTC)
- The current wording "Most historians dispute that ancient Egyptians had a concept of π ..." is absurd as it is immediately contradicted by the following paragraph, "The earliest written approximations of π are found in Egypt ...". The book The Shape of the Great Pyramid seems to be a good source for this issue as it provides a comprehensive review of the literature and various theories. It provides a good account of the pi-theory in chapter 9 and says "...of all the theories concerning the shape of the Great Pyramid, it is the pi-theory which is the best known." I shall try a different wording to this effect. Andrew Davidson (talk) 11:42, 23 July 2012 (UTC)
- Andrew: The book you cite explicitly rejects the theory that pi was used in the pyramid design (pp 165-166). --Noleander (talk) 13:38, 23 July 2012 (UTC)
- Andrew: Could you please revert your change, since you are using the source to represent a statement which implies to the reader the opposite of what the source is stating? Thanks. --Noleander (talk) 13:48, 23 July 2012 (UTC)
- I was looking at that on Google books earlier today - I also found this:[2]" Herz-Fischler describes fifteen such proposals for the design plan of the Great Pyramid, all of which highlight correlations in dimensional details that Egyptologists regard as unimportant. This shows an important aspect of archaeology and science, that the selection of data is influenced by the theories that one already believes. And sometimes this can degrade the objectivity of the process, if selecting evidence is self-serving. But in this case, Herz-Fischler uses an independent means of evaluating the relevance of these data. He provides a statistical analysis of the proposed correlations and shows that none of the fifteen stands out as being more significant than any of the others (ibid.: 29)." (from Archaeological Fantasies: How Pseudoarchaeology Misrepresents the Past and Misleads the Public ). Dougweller (talk) 13:35, 23 July 2012 (UTC)
- I added this sentence: Skeptics maintain that the suggested relationship to π is merely a coincidence, because the pyramid is missing its outer layer of stones, and thus the shape cannot be accurately analyzed - citing a book by Michael Shermer. --Noleander (talk) 13:48, 23 July 2012 (UTC)
- Andrew: The book you cite explicitly rejects the theory that pi was used in the pyramid design (pp 165-166). --Noleander (talk) 13:38, 23 July 2012 (UTC)
Euler buckling formula error?
The quoted formula defines the variable "L", but uses the variable "s".
I believe that the variable "s" should be replaced with "k L", where L is defined as in the current text and k is a variable determined by the nature of the end connections of the column... At least that's what I gather from the Wikipedia "Buckling" entry... NitPicker769 (talk) 02:25, 23 July 2012 (UTC)
- Thanks for finding that. It has been fixed. --Noleander (talk) 15:18, 23 July 2012 (UTC)
Pi
Have just read all the way through the article, and now my head hurts. I am going for a lie down! WillE (talk) 11:30, 25 July 2012 (UTC)
Dr who reference
In 'midnight', the Dr does not recite pi to 30 places, rather its square root http://www.youtube.com/watch?v=QWboRfYGhpI — Preceding unsigned comment added by 101.165.24.192 (talk) 16:48, 15 August 2012 (UTC)
Inconsistency.
Why should there not be a section on the inconsistency of defining pi by the ratio of the circumference by the diameter? I mean a circle is defined by the radius, the radians are defined by the radius, a sphere is defined by its radius, .... Why is pi the only mathematically defined notion related to a circle not defined by the radius? Yes, I know that the diameter is two times the radius. But that does not explain the question. So, there needs to be a section which explains why pi is only half 6.283185307179.... No where in this article mentions this, why? — Preceding unsigned comment added by Reddwarf2956 (talk • contribs) 06:18, 17 August 2012 (UTC)
- Oh no let's not start this lame old argument again. --Matt Westwood 18:17, 17 August 2012 (UTC)
- Oh great, a lame answer. Reddwarf2956 (talk) 04:48, 19 August 2012 (UTC)
- Sorry, but it's a mega-lame question which has been done to death on the discusson on Tau. Let's all puke in synchrony. --Matt Westwood 05:22, 19 August 2012 (UTC)
- If you are going to reply, please make it a mathematical reason why pi should not have a section dealing with the inconsistency of its definition. Reddwarf2956 (talk) 12:00, 19 August 2012 (UTC)
- Wikipedia is only here to represent what the consensus "out there" is. Perhaps English would be better off with a more funetik speling sistm. But that does not mean we write all of articles that way. Currently the article's coverage of tau is commensurate (quite generous, even) with the attention it has received, wouldn't you say? Leonxlin (talk) 16:14, 19 August 2012 (UTC)
- Repeat, if you are going to reply with an argument against the suggested section, please make it a mathematical reason why pi should not have a section dealing with the inconsistency of its definition. Until then, the request stands. Also note, that without this section, pi is in violation of WP:DUE in that there is no minority viewpoint in which "controversies regarding aspects of the minority view should be clearly identified and explained". Reddwarf2956 (talk) 19:38, 19 August 2012 (UTC)
- In my opinion this article gives due weight to the "τ" constant already, inside the "in popular culture" section. Once we begin to see mainstream textbooks use τ instead of π the article will need to be changed, but at the moment the due weight for τ is very low, and certainly does not extend to an entire section. — Carl (CBM · talk) 21:02, 19 August 2012 (UTC)
- We are easily giving more than WP:DUE weight to tau in this article. I have never seen a reliable scientific source use the constant τ for 2π. Sławomir Biały (talk) 23:49, 19 August 2012 (UTC)
- We are still dealing with opinions here. I keep saying pi has a "inconsistency of its definition" I have not brought up tau, but it is a mathematical constant which has not been formally named. You call it tau, so I will too. I have seen that constant tau is used in programming as names like twopi, two_pi, TWOPI, TWO_PI, ... for example MATHEMATICA: 2Pi, FORTRAN: http://naif.jpl.nasa.gov/pub/naif/toolkit_docs/FORTRAN/spicelib/twopi.html . Or, as here a way numbering software versions: https://wiki.riteme.site/wiki/Pugs#Version_numbering . It is at the OEIS as A058291, and A019692. A simple search on Google will find many, many more examples of the constant tau by other names and used as 6.2831853.... And, tau is mathematically consistent. Yet here on Wikipedia, there is a pious bias against tau or anything that looks like tau in value. Every where I look for the constant there is no references back to tau, two pi, or even 6.2831853. They all redirect back to pi or do not exist. The above commentators reference tau and know what it is and what its value is, yet you expect me to talk about it as if it was numerology, sorry if any number here is consider numerology that is pi because as a Wikipedia topic it has the lack of consistency. And, this Wikipedia topic "pi" does not reference any of these references above or any of many other places that I did not state. In fact there is the act of hijacking 2pi and saying that it, pi, in a lot of places http://wiki.riteme.site/wiki/List_of_formulae_involving_%CF%80 . But, that does not change the problem pi has as stated here earlier, it is inconsistent in that it does not use radius for consistency sake. And, no one wants to agree that tau is not the issue here, it is the unnecessary bias against tau because it is mathematically a better constant to deal with things like pi. Just look at how both pi and tau is used in spherical coordinates. On the x and y axes the use of the maximum value is tau. The maximum angle from the positive z axis is pi. Yet here you insist on C/d and ignore the facts. Just do a search for the number of times an even and odd multiples of pi are used in the period of functions, or just in functions here http://wiki.riteme.site/wiki/List_of_formulae_involving_%CF%80 .
- Oh great, a lame answer. Reddwarf2956 (talk) 04:48, 19 August 2012 (UTC)
- Now pi is not the first mathematically inconsistent thing. Just look at when 1 was called prime and 2 was called not prime. http://planetmath.org/HistoryOfPrimeNumbers.html
- So, do you want to continue or do you want to fix this issue that tau, while not formal, is a mathematical constant more fundamental than pi. Put it in another way, when you see the "Equation of a Circle" stated with diameters in a text book, then I will except pi as mathematically consistent until then pi needs to explain itself in this encyclopedia as to why it is inconsistent. Yes, I know this means using tau as a more fundamental constant, as in tau radians make a circle. But, it helps, not hurts, the writing to be understood by the readers. And, to say that tau does not need its own space to express all of the uses of 6.2831853... is a lie.
Reddwarf2956 (talk) 02:28, 20 August 2012 (UTC)
- You are spouting the most utter complete and utter blethering claptrap. Nothing you say has any coherence whatsover. --Matt Westwood 05:13, 20 August 2012 (UTC)
- There is no need to argue any of these points. In the sense that the scientific world uses the constant π rather than some other constant, there is a bias in favor of π. This doesn't invalidate your opinion that 2π is a more natural choice. But that's irrelevant for an encyclopedia. We just reiterate what reliable sources have to say on a subject. Sławomir Biały (talk) 13:45, 20 August 2012 (UTC)
Irrational and Transcendence
There is a formula for Pi squared divided by 6 being the sum of the inverse squares of the integers. I just wanted to point out that Pi squared divided by 6 is also the surface area for a 4-sphere of diameter 1. 4-sphere being a 5d sphere... if I read the article right Hypersphere. The 4-sphere has a surface area of 8/3 * Pi^2 * R^4. So with R=1/2, we have 8/48 * pi^2 or 1/6 * pi^2. This probably has no real meaning as Pi is going to be involved in circular objects anyway. In fact the 4 formulas for surface and volume of the 3-sphere and 4-sphere would all work with a proper selection of the radius. But the 4-sphere surface area is the simplest. I just thought I would add this in case someone was looking for something tangible to relate to Pi squared. Maybe it has some further meaning that is beyond me, but Im sure someone else would have discovered this relationship and exploited its importance if that was true. I just thought it was interesting that the relationship between the primes and pi squared is also the value of a surface area of a basic object with a length value (diameter) of '1'. Also, vice-versa... a simple n-sphere diameter 1 has a surface area of the sum of the inverse squared integers. — Preceding unsigned comment added by 96.49.55.157 (talk) 01:51, 4 September 2012 (UTC)
- π appears in many formula, not least all of the formulae for the sizes of the n-sphere and n-ball in two more dimensions. And as these formula are quite simple it's possible to relate them, to each other or other expressions involving π. But I don't think there's any deeper meaning to this.--JohnBlackburnewordsdeeds 01:58, 4 September 2012 (UTC)
pi is too random in a sense — Preceding unsigned comment added by 58.8.105.29 (talk) 03:13, 9 September 2012 (UTC)
"Approximately equal to?"
The article states in the lede: "The constant, sometimes written pi, is approximately equal to 3.14159." That isn't entirely accurate wording. Depending on usage, pi can approximately equal 3.14 or even just 3. Could the sentence be reworded to better reflect this fact? Perhaps something like, "The constant, sometimes written pi, to five decimal places is 3.14159." I'm just really leery of saying pi equals something -- even "approximately," as pi can approximately equal 3 -- given that different uses call for different degrees of accuracy. JayHubie (talk) 02:17, 17 September 2012 (UTC)
- Formally you are right: "approximately" has no meaning without defining the accuracy. Nevertheless, it is a common convention that the number of digits defines the accuracy: all the digits (possibly but the last one) are supposed to be exact. Thus I believe that everybody will understand correctly the sentence, namely that the given digits are correct (Note that if one digit less have been given, there would be an ambiguity for the last digit). Thus the sentence follows perfectly the instructions of MOS:MATH which asserts that the lead should contain "an informal introduction to the topic, without rigor, suitable for a general audience". IMO there is nothing to change in this sentence.D.Lazard (talk) 08:25, 17 September 2012 (UTC)
- I respectfully disagree. People who've been through elementary math can understand the phrase "to five decimal places." My concern stands, since pi still can be said to be "approximately" equal to 3. The wording is inaccurate. JayHubie (talk) 19:23, 19 September 2012 (UTC)
- I agree that the wording seems slightly inappropriate. Perhaps better to say something like: "The value of pi is approximately 3.1415926535..." (but no need to state the number of significant figures). I think your instinct is correct, because "approximately equal" sort of implies two values that just happen to be close, as in (music) "Twelve perfect fifths (1.5^12) is approximately equal to seven octaves (2^7)" (see Pythagorean comma) Imaginatorium (talk) 19:35, 19 September 2012 (UTC)
Phi
In the "about" template at the top of the article, i think you should add a link to the number Phi as well- many people confuse between them.
80.230.2.55 (talk) 17:45, 18 September 2012 (UTC)
Choice of glyph for the Greek letter pi in this article
The number π /paɪ/ is a mathematical constant that is the ratio of a circle's circumference to its diameter. The constant, sometimes written pi, is approximately equal to 3.14159.
Common (not only mathematician, but there it is coined) notation/typografic is or π (a lower Greek letter). Sadly, very uncommon article typograhy is used here. — Preceding unsigned comment added by 2001:638:504:C00E:214:22FF:FE49:D786 (talk • contribs)
- You are unhappy with how {{pi}} is rendered on the page? At present it gives π. Which of the alternatives you mentioned do you like better? EdJohnston (talk) 17:35, 19 September 2012 (UTC)
- Yes, this bugged me too. The normal mathematical symbol for pi is a Greek lowercase letter pi (that's a bizarrely redundant statement actually). Somehow the symbol used here appears as a square shape, like an uppercase Roman numeral 'II' with a bar across the top. I guessed that this was some bizarre property of the font on my computer (or something) combined perhaps with a different Unicode value for "mathematical pi" as opposed to "Genuine Greek pi". If so I submit it is an error, either by font designers or the Unicode lot or both. But I don't know how to find out exactly what the WP *triple-quoted-pi* is supposed to mean.
- I grabbed the first mathematical book to hand (Penguin Dictionary of Mathematics) and scanned the first three lines of the definition of 'pi': you can see it here - http://imaginatorium.org/private/pi.jpg You will see that the symbol is a Greek lowercase pi, and this I submit is what WP should show pi as, to conform with standard usage.
- Imaginatorium (talk) 18:33, 19 September 2012 (UTC)
- I
agree;add that π looks awful on my setup (Firefox 15.0.1 running under Ubuntu 12.4). The whole project of trying to put serif math into sans-serif running text should just be scrapped, and we should go back to using π inline and in displayed text. --Trovatore (talk) 18:45, 19 September 2012 (UTC)- I share the distaste of others with the symbol rendered by {{pi}} and agree with Trovatore that the conventional sans-serif lower-case Greek pi is a better choice for use in running text in this article. EdJohnston (talk) 19:14, 19 September 2012 (UTC)
- That is exactly what it should look like; a serif Greek lowercase pi as shown on your scan. {{pi}} uses the HTML entity
π; it's not unicode, and it's set infont-family: serif;. If that doesn't show correct on your system, there is a problem with your fonts setup; your default serif font in your browser may be set to something different then the default 'Times'. The reason serif is used is not for aestethic reasons; it is used because math formulae and symbols are illegible and indiscernable (think I vs. l vs. 1) in sans-serif. It is more important to be able to see what is actually represented on screen then care about aestethics. (btw: the triple quote is the wiki markup equivalent of<b>...</b>; it simply makes π bold: π.) — Edokter (talk) — 20:50, 19 September 2012 (UTC)- "Times" is a proprietary font, I think. Wikipedia is part of the open-content movement, broadly construed, and should not be making decisions based on the way proprietary systems render things. --Trovatore (talk) 21:15, 19 September 2012 (UTC)
- It doesn't. As I said, the template (and math) uses
sans-serif, which on most systems (even open source ones!) maps to Times. — Edokter (talk) — 21:22, 19 September 2012 (UTC)
- It doesn't. As I said, the template (and math) uses
- "Times" is a proprietary font, I think. Wikipedia is part of the open-content movement, broadly construed, and should not be making decisions based on the way proprietary systems render things. --Trovatore (talk) 21:15, 19 September 2012 (UTC)
- I
- Imaginatorium (talk) 18:33, 19 September 2012 (UTC)
Edokter more or less hit this one on the head, but I think there are a few misconceptions here that need addressing. First and foremost, Wikipedia doesn't choose the glyph to be displayed. It can't. (Well, except when using images -- which is what the <math>\pi</math> tags do -- but that's undesirable in running text.) Your browser chooses the glyph (more precisely, it chooses the font which gives the glyph), based on what Wikipedia says it should do.
Secondly, contrary to what the anonymous user at the top of this section appears to be saying, there is no "mathematical symbol" pi. There is only the Greek letter, which is subject to different styles of writing. There are conventions for which style should be used, but that's analogous to the convention that we write e in italics for its mathematical meaning -- it's still a lowercase Latin letter E. (Unicode accordingly has just one codepoint for the pi character in both its alphabetic and mathematical meanings, so that can't be the source of Imaginatorium's problems.)
The preferred style for "mathematical" pi, with the horizontal stroke overhanging the (usually) curved legs, is the style used in serif typefaces, and (with individual variations, of course) in handwritten Greek. On the other hand, the "square" pi that Imaginatorium describes, which looks like three sides of a rectangle, is a perfectly standard sans-serif letter form, suitable for everyday Greek text, but not for mathematical expressions. I don't know why it's appearing for Imaginatorium, but Trovatore's statement that we should be using a sans-serif face instead is the opposite of solving the problem.
Here's where Edokter was wide of the mark; we don't use serif typefaces for mathematical typesetting because it makes characters like 1, I and l easier to distinguish (though that's often true and a worthy benefit). We use serif fonts because that's the style that's customary in maths. Specifically, it's very often customary to use italic characters, and there's another reason to avoid sans-serif typefaces; oblique type is not the same thing as italic type. Having a bit of visual dissonance between the typeface of the maths expression and that of the text around it is better than violating this convention and having a sans-serif "square" pi!
Which is why Wikipedia tells your browser it should use a serif typeface to write pi. Actually, the {{pi}} template doesn't try to directly manage the appearance of pi; it applies a style called "texhtml". I'm not fully certain of what magic this style applies (aside from requesting a serif typeface)... but I'm fairly sure it will make some suggestions to the browser to try and get a font suitable for mathematical typesetting (as hinted by the mention of "tex" in the style name). I'm pretty sure it's more than just asking for the default serif typeface (which, by the way, is more likely to be Times New Roman than Times per se; in many *nix systems it'll probably be something like DejaVu Serif unless the Microsoft web fonts have been installed). -- Perey (talk) 17:22, 8 October 2012 (UTC)
- There’s no magic going on. If I didn’t miss anything, all texhtml does in the default skin is to set "font-family: serif" (common/shared.css), "white-space: nowrap" (MediaWiki:Common.css), and "font-size: 118%" (MediaWiki:Vector.css).—Emil J. 17:45, 8 October 2012 (UTC)
- OK, first of all, I disagree with Perey and Edokter that "a little visual dissonance" is not so bad. I think it looks completely unprofessional. But that's a general consideration and maybe more important in the rendering of e (a separate gripe) than for this article.
- So getting down to specifics, here's what I see:
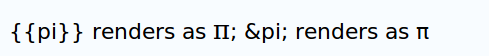
- Anticipating Edokter's response, this is on a bog-standard (at least, for these purposes) installation of Ubuntu 12.4, running Firefox. Ubuntu is probably the most popular free-software operating system, version 12.4 is the latest long-term stable version, and Firefox the most popular browser for it. There is nothing unusual in my setup; presumably, this is what most people running Ubuntu 12.4 see. --Trovatore (talk) 19:15, 8 October 2012 (UTC)
- (I hope that not the bog-standard font size on your system...) If I'm not mistaken, that's DejaVu Sans. I can't tell what the default serif font on your system is, but I guess that would be DejaVu Serif. These fonts do have a funny way of displaying pi, using pillars in serif, yet having a decent sans-serif pi. I don't know how to handle this properly. All I can tell is that I try to cater to most systems on the planet, and I cannot please them all. What would help is reset your font-size for .texhtml to 100%, as DejaVu fonts have the same x-height, and/or possibly actually use Times or Computer Modern as you maths font. — Edokter (talk) — 20:19, 8 October 2012 (UTC)
- What would help would be to stop using these misguided templates. --Trovatore (talk) 20:21, 8 October 2012 (UTC)
- That would help for you, but it would also be detrimental to the majority of users/readers. I'm still looking for a way to have better font managment on Wikipedia, either in the form of an extension or gadget, so people don't have to mess with their local font setup on skin files. — Edokter (talk) — 20:31, 8 October 2012 (UTC)
- What would help everyone is to get rid of the idea of mixing serif and sans-serif fonts inline. That was an unfortunate decision from the get-go and needs to be reversed. Without that, there is little rationale left for the templates. --Trovatore (talk) 20:56, 8 October 2012 (UTC)
- Please don't asume that what's good for you is good for everyone; too many people make that mistake. I go what is good for most. The situation is not ideal, but it is better then having math displayed in a sans-serif font that strips it of all meaning and context. Readability outweighs any aesthetical motivations. — Edokter (talk) — 21:40, 8 October 2012 (UTC)
- It seems to me that you're the one who's assuming you know what is good for most. I dispute the accuracy of your claim; I do not think it is in fact good for most, though even if it were, you have not established that that is the correct criterion to use. --Trovatore (talk) 22:30, 8 October 2012 (UTC)
- Please don't asume that what's good for you is good for everyone; too many people make that mistake. I go what is good for most. The situation is not ideal, but it is better then having math displayed in a sans-serif font that strips it of all meaning and context. Readability outweighs any aesthetical motivations. — Edokter (talk) — 21:40, 8 October 2012 (UTC)
- What would help everyone is to get rid of the idea of mixing serif and sans-serif fonts inline. That was an unfortunate decision from the get-go and needs to be reversed. Without that, there is little rationale left for the templates. --Trovatore (talk) 20:56, 8 October 2012 (UTC)
- That would help for you, but it would also be detrimental to the majority of users/readers. I'm still looking for a way to have better font managment on Wikipedia, either in the form of an extension or gadget, so people don't have to mess with their local font setup on skin files. — Edokter (talk) — 20:31, 8 October 2012 (UTC)
- What would help would be to stop using these misguided templates. --Trovatore (talk) 20:21, 8 October 2012 (UTC)
- (I hope that not the bog-standard font size on your system...) If I'm not mistaken, that's DejaVu Sans. I can't tell what the default serif font on your system is, but I guess that would be DejaVu Serif. These fonts do have a funny way of displaying pi, using pillars in serif, yet having a decent sans-serif pi. I don't know how to handle this properly. All I can tell is that I try to cater to most systems on the planet, and I cannot please them all. What would help is reset your font-size for .texhtml to 100%, as DejaVu fonts have the same x-height, and/or possibly actually use Times or Computer Modern as you maths font. — Edokter (talk) — 20:19, 8 October 2012 (UTC)
Edokter is right -- you are seeing DejaVu Sans and DejaVu Serif, Trovatore. And it does look bad for the serif. The serif pi lacks the slightly "cursive" look customary in mathematical rendering (and it doesn't have a true italic, just an oblique). But have a look at this selection of free fonts (and Times New Roman), all available for Ubuntu (I can no longer remember how many of these were pre-installed and how many I added).
| Asana Math | Computer Modern | DejaVu Sans | DejaVu Serif | Liberation Sans | Liberation Serif | STIXGeneral | Times New Roman | Nimbus Roman No9 L | Ubuntu |
|---|---|---|---|---|---|---|---|---|---|
| π | π | π | π | π | π | π | π | π | π |
| π | π | π | π | π | π | π | π | π | π |
If you have all, or even some of these fonts installed, you should be able to see what I mean. The DejaVu Serif pi is uniquely unsuitable for mathematical use. Yes, the DejaVu Sans pi is better, but that's because almost anything is better than DejaVu Serif. ;-) It's emphatically not a reason to go and switch to sans-serif typefaces for pi. Most of the sans-serif pi glyphs look acceptable for mathematical use, but not good, compared with serif fonts (even those not made with mathematical typesetting in mind), and some sans-serif typefaces are definitely not suitable (like Ubuntu) -- they have the simple three-sided rectangular pi. -- Perey (talk) 14:00, 9 October 2012 (UTC)
- (Reply to Trovatore) I do not asume to know what's best; my findings are based on extensive research in web typography (and it's shortcomings). I gather statistical data from here, here, here and here among other places, combine these with other data like this and make an analysis that would suit most users. Not so long ago, .texhtml was hardcoded to use Times New Roman; it may be a good idea to go back to that, as it now turns out that DejaVu Serif sucks as a default serif font. But it will always be impossible to make it perfect for all users. — Edokter (talk) — 16:30, 9 October 2012 (UTC)
- Who bloody asked you? You do have an impressive array of facts about typography at your fingertips, and I acknowledge your expertise in that sense. But what is "best" for "most users" is a value judgment, and I do not agree with yours. --Trovatore (talk) 17:52, 16 October 2012 (UTC)
- No-one "bloody" asked me, and I resent that tone. This is Wikipedia, remember? I'm sorry if my aproach does not meet your preference, but it does enjoy the approval of most editors here. It has been discussed before and there is consensus for using serif for pi and formulae in general. — Edokter (talk) — 18:10, 16 October 2012 (UTC)
- It's a response to your ownership attitude, which I resent. --Trovatore (talk) 19:04, 16 October 2012 (UTC)
- You're welcome to start an RFC then. I certainly do not see an ownership issue here; this is simply a matter of someone's preference clashing with consensus, one I happen to defend. You just continue to complain about how you don't like how it looks, without providing any rational arguments. So at this point I have nothing more to say to you. — Edokter (talk) — 21:11, 16 October 2012 (UTC)
- If I may interject... Trovatore, perhaps what you're seeing as Edokter's "ownership attitude" of this issue stems from the fact that Edokter is an administrator and is involved with maintaining Wikipedia's CSS styles. In that sense, he/she does "own" this issue; if there's a problem with how pi appears, Edokter is in a position to fix it, and has the right to use his/her judgement to decide on a solution. You, in turn, have the right to dispute Edokter's decision. Edokter mentioned RFC as an option, to which I'll add that Dispute Resolution lists a number of alternatives. -- Perey (talk) 17:10, 20 October 2012 (UTC)
- Perey, I think you misunderstand the role of administrator on Wikipedia. A WP admin has no special authority whatsoever. He has extra tools; that's it. His admin status counts for precisely nothing in disputes. --Trovatore (talk) 19:55, 20 October 2012 (UTC)
- I don't think I do. I may disagree somewhat with the idea that admin status counts for nothing -- as they say, with great power comes great responsibility, or in this case, with a little bit of CSS-related power comes a little bit of CSS-related responsibility. ;-) But that's not actually the point. I'm not saying that being an admin makes Edokter right; I'm saying that being an admin justifies any "ownership" of the problem by Edokter. What I described as "the right to use his/her judgement" is not because of any special admin authority -- it's just "Be bold" applied to an admin's tools: "If you can do it, and you think it's right, go ahead and do it." -- Perey (talk) 09:44, 25 October 2012 (UTC)
- I don't know what you're talking about. There is nothing here to which the tools are even relevant; neither {{pi}} nor {{math}} is protected. And I reiterate that admin status counts for nothing, zero times zero times zero, in disputes. --Trovatore (talk) 09:47, 25 October 2012 (UTC)
- As regards to adminship, Trovatore is absolutely right. Adminship confers no special rights or authority in this context. Paul August ☎ 21:12, 29 October 2012 (UTC)
- Both of those templates rely on the
texhtmlCSS style class, though, which (unless I've been looking at this completely wrong all along) is only editable by admins. -- Perey (talk) 06:52, 29 October 2012 (UTC)- Even if that's so, nothing says the templates need to use that CSS style class, nor that we need to use the templates. --Trovatore (talk) 20:43, 29 October 2012 (UTC)
- I don't know what you're talking about. There is nothing here to which the tools are even relevant; neither {{pi}} nor {{math}} is protected. And I reiterate that admin status counts for nothing, zero times zero times zero, in disputes. --Trovatore (talk) 09:47, 25 October 2012 (UTC)
- I don't think I do. I may disagree somewhat with the idea that admin status counts for nothing -- as they say, with great power comes great responsibility, or in this case, with a little bit of CSS-related power comes a little bit of CSS-related responsibility. ;-) But that's not actually the point. I'm not saying that being an admin makes Edokter right; I'm saying that being an admin justifies any "ownership" of the problem by Edokter. What I described as "the right to use his/her judgement" is not because of any special admin authority -- it's just "Be bold" applied to an admin's tools: "If you can do it, and you think it's right, go ahead and do it." -- Perey (talk) 09:44, 25 October 2012 (UTC)
- Perey, I think you misunderstand the role of administrator on Wikipedia. A WP admin has no special authority whatsoever. He has extra tools; that's it. His admin status counts for precisely nothing in disputes. --Trovatore (talk) 19:55, 20 October 2012 (UTC)
- If I may interject... Trovatore, perhaps what you're seeing as Edokter's "ownership attitude" of this issue stems from the fact that Edokter is an administrator and is involved with maintaining Wikipedia's CSS styles. In that sense, he/she does "own" this issue; if there's a problem with how pi appears, Edokter is in a position to fix it, and has the right to use his/her judgement to decide on a solution. You, in turn, have the right to dispute Edokter's decision. Edokter mentioned RFC as an option, to which I'll add that Dispute Resolution lists a number of alternatives. -- Perey (talk) 17:10, 20 October 2012 (UTC)
- You're welcome to start an RFC then. I certainly do not see an ownership issue here; this is simply a matter of someone's preference clashing with consensus, one I happen to defend. You just continue to complain about how you don't like how it looks, without providing any rational arguments. So at this point I have nothing more to say to you. — Edokter (talk) — 21:11, 16 October 2012 (UTC)
- It's a response to your ownership attitude, which I resent. --Trovatore (talk) 19:04, 16 October 2012 (UTC)
- No-one "bloody" asked me, and I resent that tone. This is Wikipedia, remember? I'm sorry if my aproach does not meet your preference, but it does enjoy the approval of most editors here. It has been discussed before and there is consensus for using serif for pi and formulae in general. — Edokter (talk) — 18:10, 16 October 2012 (UTC)
- Who bloody asked you? You do have an impressive array of facts about typography at your fingertips, and I acknowledge your expertise in that sense. But what is "best" for "most users" is a value judgment, and I do not agree with yours. --Trovatore (talk) 17:52, 16 October 2012 (UTC)
- FWIW, in the table you show above, the only glyphs in IE 7 running on Windows XP that are rendered with serifs or "cursive style" are Times New Roman (all of the rest are sans serif style), and those are the only ones that look "proper" as a mathematical font symbol. (I'm using IE 7 at work, so I assume that the OS fonts are those we got straight out of the box.) — Loadmaster (talk) 16:50, 9 October 2012 (UTC)
- That;s normal for IE; it falls back to the parent font if the specified font is not available. Chrome will fall back to it's default webpage font, which is serif. — Edokter (talk) — 17:30, 9 October 2012 (UTC)
I've restored the Times fontstack for .texhtml ("Times New Roman", Times, FreeSerif, serif;), which now includes FreeSerif for Linux. But, I'd rather use Nimbus Roman No9 because it has near 100% installed base on Linux. However, I'm not sure how to exactly reference that font in CSS; there are are multiple versions around. I even have two version installed that like to be called "NimbusRomanNo9" and "NimbusRomNo9L" (they are TrueType versions though). This page lists it as "Nimbus Roman No9 L"; in other words, what is the proper font-family name for this font? — Edokter (talk) — 21:05, 12 October 2012 (UTC)
- Never mind. It should be "Nimbus Roman No9 L". — Edokter (talk) — 21:28, 12 October 2012 (UTC)
spelling of Madhava of Sangamagrama
If you'd indicated at the start that spelling without the diacritics is according to the manual of style, and not a "typo", I would not have wasted my time "correcting" it back to "Mādhava of Saṅgamagrāma". Calling the latter a "spelling mistake" is misleading and can be considered inflammatory. --Matt Westwood 22:17, 24 September 2012 (UTC)
Edit request on 3 November 2012
This edit request has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
(There is a bottom)I wish to change the way you think of Pi. As you say in the article, Pi is the number 3.14159, but really its(I typed this):
Extended content
|
|---|
|
3.141592653589793238462643383279502884197169399375105820974944592307816406286 208998628034825342117067982148086513282306647093844609550582231725359408128481 117450284102701938521105559644622948954930381964428810975665933446128475648233 786783165271201909145648566923460348610454326648213393607260249141273724587006 606315588174881520920962829254091715364367892590360011330530548820466521384146 951941511609433057270365759591953092186117381932611793105118548074462379962749 567351885752724891227938183011949129833673362440656643086021394946395224737190 702179860943702770539217176293176752384674818467669405132000568127145263560827 785771342757789609173637178721468440901224953430146549585371050792279689258923 542019956112129021960864034418159813629774771309960518707211349999998372978049 951059731732816096318595024459455346908302642522308253344685035261931188171010 003137838752886587533208381420617177669147303598253490428755468731159562863882 353787593751957781857780532171226806613001927876611195909216420198938095257201 065485863278865936153381827968230301952035301852968995773622599413891249721775 283479131515574857242454150695950829533116861727855889075098381754637464939319 255060400927701671139009848824012858361603563707660104710181942955596198946767 837449448255379774726847104047534646208046684259069491293313677028989152104752 162056966024058038150193511253382430035587640247496473263914199272604269922796 782354781636009341721641219924586315030286182974555706749838505494588586926995 690927210797509302955321165344987202755960236480665499119881834797753566369807 426542527862551818417574672890977772793800081647060016145249192173217214772350 141441973568548161361157352552133475741849468438523323907394143334547762416862 518983569485562099219222184272550254256887671790494601653466804988627232791786 085784383827967976681454100953883786360950680064225125205117392984896084128488 626945604241965285022210661186306744278622039194945047123713786960956364371917 287467764657573962413890865832645995813390478027590099465764078951269468398352 595709825822620522489407726719478268482601476990902640136394437455305068203496 252451749399651431429809190659250937221696461515709858387410597885959772975498 930161753928468138268683868942774155991855925245953959431049972524680845987273 644695848653836736222626099124608051243884390451244136549762780797715691435997 700129616089441694868555848406353422072225828488648158456028506016842739452267 467678895252138522549954666727823986456596116354886230577456498035593634568174 324112515076069479451096596094025228879710893145669136867228748940560101503308 617928680920874760917824938589009714909675985261365549781893129784821682998948 722658804857564014270477555132379641451523746234364542858444795265867821051141 354735739523113427166102135969536231442952484937187110145765403590279934403742 007310578539062198387447808478489683321445713868751943506430218453191048481005 370614680674919278191197939952061419663428754440643745123718192179998391015919 561814675142691239748940907186494231961567945208095146550225231603881930142093 762137855956638937787083039069792077346722182562599661501421503068038447734549 202605414665925201497442850732518666002132434088190710486331734649651453905796 268561005508106658796998163574736384052571459102897064140110971206280439039759 515677157700420337869936007230558763176359421873125147120532928191826186125867 321579198414848829164470609575270695722091756711672291098169091528017350671274 858322287183520935396572512108357915136988209144421006751033467110314126711136 990865851639831501970165151168517143765761835155650884909989859982387345528331 635507647918535893226185489632132933089857064204675259070915481416549859461637 180270981994309924488957571282890592323326097299712084433573265489382391193259 746366730583604142813883032038249037589852437441702913276561809377344403070746 921120191302033038019762110110044929321516084244485963766983895228684783123552 658213144957685726243344189303968642624341077322697802807318915441101044682325 271620105265227211166039666557309254711055785376346682065310989652691862056476 931257058635662018558100729360659876486117910453348850346113657686753249441668 039626579787718556084552965412665408530614344431858676975145661406800700237877 659134401712749470420562230538994561314071127000407854733269939081454664645880 797270826683063432858785698305235808933065757406795457163775254202114955761581 400250126228594130216471550979259230990796547376125517656751357517829666454779 174501129961489030463994713296210734043751895735961458901938971311179042978285 647503203198691514028708085990480109412147221317947647772622414254854540332157 185306142288137585043063321751829798662237172159160771669254748738986654949450 114654062843366393790039769265672146385306736096571209180763832716641627488880 078692560290228472104031721186082041900042296617119637792133757511495950156604 963186294726547364252308177036751590673502350728354056704038674351362222477158 915049530984448933309634087807693259939780541934144737744184263129860809988868 741326047215695162396586457302163159819319516735381297416772947867242292465436 680098067692823828068996400482435403701416314965897940924323789690706977942236 250822168895738379862300159377647165122893578601588161755782973523344604281512 627203734314653197777416031990665541876397929334419521541341899485444734567383 162499341913181480927777103863877343177207545654532207770921201905166096280490 926360197598828161332316663652861932668633606273567630354477628035045077723554 710585954870279081435624014517180624643626794561275318134078330336254232783944 975382437205835311477119926063813346776879695970309833913077109870408591337464 144282277263465947047458784778720192771528073176790770715721344473060570073349 243693113835049316312840425121925651798069411352801314701304781643788518529092 854520116583934196562134914341595625865865570552690496520985803385072242648293 972858478316305777756068887644624824685792603953527734803048029005876075825104 747091643961362676044925627420420832085661190625454337213153595845068772460290 161876679524061634252257719542916299193064553779914037340432875262888963995879 475729174642635745525407909145135711136941091193932519107602082520261879853188 770584297259167781314969900901921169717372784768472686084900337702424291651300 500516832336435038951702989392233451722013812806965011784408745196012122859937 162313017114448464090389064495444006198690754851602632750529834918740786680881 833851022833450850486082503930213321971551843063545500766828294930413776552793 975175461395398468339363830474611996653858153842056853386218672523340283087112 328278921250771262946322956398989893582116745627010218356462201349671518819097 303811980049734072396103685406643193950979019069963955245300545058068550195673 022921913933918568034490398205955100226353536192041994745538593810234395544959 778377902374216172711172364343543947822181852862408514006660443325888569867054 315470696574745855033232334210730154594051655379068662733379958511562578432298 827372319898757141595781119635833005940873068121602876496286744604774649159950 549737425626901049037781986835938146574126804925648798556145372347867330390468 838343634655379498641927056387293174872332083760112302991136793862708943879936 201629515413371424892830722012690147546684765357616477379467520049075715552781 965362132392640616013635815590742202020318727760527721900556148425551879253034 351398442532234157623361064250639049750086562710953591946589751413103482276930 624743536325691607815478181152843667957061108615331504452127473924544945423682 886061340841486377670096120715124914043027253860764823634143346235189757664521 641376796903149501910857598442391986291642193994907236234646844117394032659184 044378051333894525742399508296591228508555821572503107125701266830240292952522 011872676756220415420516184163484756516999811614101002996078386909291603028840 026910414079288621507842451670908700069928212066041837180653556725253256753286 129104248776182582976515795984703562226293486003415872298053498965022629174878 820273420922224533985626476691490556284250391275771028402799806636582548892648 802545661017296702664076559042909945681506526530537182941270336931378517860904 070866711496558343434769338578171138645587367812301458768712660348913909562009 939361031029161615288138437909904231747336394804575931493140529763475748119356 709110137751721008031559024853090669203767192203322909433467685142214477379393 751703443661991040337511173547191855046449026365512816228824462575916333039107 225383742182140883508657391771509682887478265699599574490661758344137522397096 834080053559849175417381883999446974867626551658276584835884531427756879002909 517028352971634456212964043523117600665101241200659755851276178583829204197484 423608007193045761893234922927965019875187212726750798125547095890455635792122 103334669749923563025494780249011419521238281530911407907386025152274299581807 247162591668545133312394804947079119153267343028244186041426363954800044800267 049624820179289647669758318327131425170296923488962766844032326092752496035799 646925650493681836090032380929345958897069536534940603402166544375589004563288 225054525564056448246515187547119621844396582533754388569094113031509526179378 002974120766514793942590298969594699556576121865619673378623625612521632086286 922210327488921865436480229678070576561514463204692790682120738837781423356282 360896320806822246801224826117718589638140918390367367222088832151375560037279 839400415297002878307667094447456013455641725437090697939612257142989467154357 846878861444581231459357198492252847160504922124247014121478057345510500801908 699603302763478708108175450119307141223390866393833952942578690507643100638351 983438934159613185434754649556978103829309716465143840700707360411237359984345 225161050702705623526601276484830840761183013052793205427462865403603674532865 105706587488225698157936789766974220575059683440869735020141020672358502007245 225632651341055924019027421624843914035998953539459094407046912091409387001264 560016237428802109276457931065792295524988727584610126483699989225695968815920 560010165525637567856672279661988578279484885583439751874454551296563443480396 642055798293680435220277098429423253302257634180703947699415979159453006975214 829336655566156787364005366656416547321704390352132954352916941459904160875320 186837937023488868947915107163785290234529244077365949563051007421087142613497 459561513849871375704710178795731042296906667021449863746459528082436944578977 233004876476524133907592043401963403911473202338071509522201068256342747164602 433544005152126693249341967397704159568375355516673027390074972973635496453328 886984406119649616277344951827369558822075735517665158985519098666539354948106 887320685990754079234240230092590070173196036225475647894064754834664776041146 323390565134330684495397907090302346046147096169688688501408347040546074295869 913829668246818571031887906528703665083243197440477185567893482308943106828702 722809736248093996270607472645539925399442808113736943388729406307926159599546 262462970706259484556903471197299640908941805953439325123623550813494900436427 852713831591256898929519642728757394691427253436694153236100453730488198551706 594121735246258954873016760029886592578662856124966552353382942878542534048308 330701653722856355915253478445981831341129001999205981352205117336585640782648 494276441137639386692480311836445369858917544264739988228462184490087776977631 279572267265556259628254276531830013407092233436577916012809317940171859859993 384923549564005709955856113498025249906698423301735035804408116855265311709957 089942732870925848789443646005041089226691783525870785951298344172953519537885 534573742608590290817651557803905946408735061232261120093731080485485263572282 576820341605048466277504500312620080079980492548534694146977516493270950493463 938243222718851597405470214828971117779237612257887347718819682546298126868581 705074027255026332904497627789442362167411918626943965067151577958675648239939 176042601763387045499017614364120469218237076488783419689686118155815873606293 860381017121585527266830082383404656475880405138080163363887421637140643549556 186896411228214075330265510042410489678352858829024367090488711819090949453314 421828766181031007354770549815968077200947469613436092861484941785017180779306 810854690009445899527942439813921350558642219648349151263901280383200109773868 066287792397180146134324457264009737425700735921003154150893679300816998053652 027600727749674584002836240534603726341655425902760183484030681138185510597970 566400750942608788573579603732451414678670368809880609716425849759513806930944 940151542222194329130217391253835591503100333032511174915696917450271494331515 588540392216409722910112903552181576282328318234254832611191280092825256190205 263016391147724733148573910777587442538761174657867116941477642144111126358355 387136101102326798775641024682403226483464176636980663785768134920453022408197 278564719839630878154322116691224641591177673225326433568614618654522268126887 268445968442416107854016768142080885028005414361314623082102594173756238994207 571362751674573189189456283525704413354375857534269869947254703165661399199968 262824727064133622217892390317608542894373393561889165125042440400895271983787 386480584726895462438823437517885201439560057104811949884239060613695734231559 079670346149143447886360410318235073650277859089757827273130504889398900992391 350337325085598265586708924261242947367019390772713070686917092646254842324074 855036608013604668951184009366860954632500214585293095000090715105823626729326 453738210493872499669933942468551648326113414611068026744663733437534076429402 668297386522093570162638464852851490362932019919968828517183953669134522244470 804592396602817156551565666111359823112250628905854914509715755390024393153519 090210711945730024388017661503527086260253788179751947806101371500448991721002 220133501310601639154158957803711779277522597874289191791552241718958536168059 474123419339842021874564925644346239253195313510331147639491199507285843065836 193536932969928983791494193940608572486396883690326556436421664425760791471086 998431573374964883529276932822076294728238153740996154559879825989109371712621 828302584811238901196822142945766758071865380650648702613389282299497257453033 283896381843944770779402284359883410035838542389735424395647555684095224844554 139239410001620769363684677641301781965937997155746854194633489374843912974239 143365936041003523437770658886778113949861647874714079326385873862473288964564 359877466763847946650407411182565837887845485814896296127399841344272608606187 245545236064315371011274680977870446409475828034876975894832824123929296058294 861919667091895808983320121031843034012849511620353428014412761728583024355983 003204202451207287253558119584014918096925339507577840006746552603144616705082 768277222353419110263416315714740612385042584598841990761128725805911393568960 143166828317632356732541707342081733223046298799280490851409479036887868789493 054695570307261900950207643349335910602454508645362893545686295853131533718386 826561786227363716975774183023986006591481616404944965011732131389574706208847 480236537103115089842799275442685327797431139514357417221975979935968525228574 526379628961269157235798662057340837576687388426640599099350500081337543245463 596750484423528487470144354541957625847356421619813407346854111766883118654489 377697956651727966232671481033864391375186594673002443450054499539974237232871 249483470604406347160632583064982979551010954183623503030945309733583446283947 630477564501500850757894954893139394489921612552559770143685894358587752637962 559708167764380012543650237141278346792610199558522471722017772370041780841942 394872540680155603599839054898572354674564239058585021671903139526294455439131 663134530893906204678438778505423939052473136201294769187497519101147231528932 677253391814660730008902776896311481090220972452075916729700785058071718638105 496797310016787085069420709223290807038326345345203802786099055690013413718236 837099194951648960075504934126787643674638490206396401976668559233565463913836 318574569814719621084108096188460545603903845534372914144651347494078488442377 217515433426030669883176833100113310869042193903108014378433415137092435301367 763108491351615642269847507430329716746964066653152703532546711266752246055119 958183196376370761799191920357958200759560530234626775794393630746305690108011 494271410093913691381072581378135789400559950018354251184172136055727522103526 803735726527922417373605751127887218190844900617801388971077082293100279766593 583875890939568814856026322439372656247277603789081445883785501970284377936240 782505270487581647032458129087839523245323789602984166922548964971560698119218 658492677040395648127810217991321741630581055459880130048456299765112124153637 451500563507012781592671424134210330156616535602473380784302865525722275304999 883701534879300806260180962381516136690334111138653851091936739383522934588832 255088706450753947395204396807906708680644509698654880168287434378612645381583 428075306184548590379821799459968115441974253634439960290251001588827216474500 682070419376158454712318346007262933955054823955713725684023226821301247679452 264482091023564775272308208106351889915269288910845557112660396503439789627825 001611015323516051965590421184494990778999200732947690586857787872098290135295 661397888486050978608595701773129815531495168146717695976099421003618355913877 781769845875810446628399880600616229848616935337386578773598336161338413385368 421197893890018529569196780455448285848370117096721253533875862158231013310387 766827211572694951817958975469399264219791552338576623167627547570354699414892 904130186386119439196283887054367774322427680913236544948536676800000106526248 547305586159899914017076983854831887501429389089950685453076511680333732226517 566220752695179144225280816517166776672793035485154204023817460892328391703275 425750867655117859395002793389592057668278967764453184040418554010435134838953 120132637836928358082719378312654961745997056745071833206503455664403449045362 756001125018433560736122276594927839370647842645676338818807565612168960504161 139039063960162022153684941092605387688714837989559999112099164646441191856827 700457424343402167227644558933012778158686952506949936461017568506016714535431 581480105458860564550133203758645485840324029871709348091055621167154684847780 394475697980426318099175642280987399876697323769573701580806822904599212366168 902596273043067931653114940176473769387351409336183321614280214976339918983548 487562529875242387307755955595546519639440182184099841248982623673771467226061 633643296406335728107078875816404381485018841143188598827694490119321296827158 884133869434682859006664080631407775772570563072940049294030242049841656547973 670548558044586572022763784046682337985282710578431975354179501134727362577408 021347682604502285157979579764746702284099956160156910890384582450267926594205 550395879229818526480070683765041836562094555434613513415257006597488191634135 955671964965403218727160264859304903978748958906612725079482827693895352175362 185079629778514618843271922322381015874445052866523802253284389137527384589238 442253547265309817157844783421582232702069028723233005386216347988509469547200 479523112015043293226628272763217790884008786148022147537657810581970222630971 749507212724847947816957296142365859578209083073323356034846531873029302665964 501371837542889755797144992465403868179921389346924474198509733462679332107268 687076806263991936196504409954216762784091466985692571507431574079380532392523 947755744159184582156251819215523370960748332923492103451462643744980559610330 799414534778457469999212859999939961228161521931488876938802228108300198601654 941654261696858678837260958774567618250727599295089318052187292461086763995891 614585505839727420980909781729323930106766386824040111304024700735085782872462 713494636853181546969046696869392547251941399291465242385776255004748529547681 479546700705034799958886769501612497228204030399546327883069597624936151010243 655535223069061294938859901573466102371223547891129254769617600504797492806072 126803922691102777226102544149221576504508120677173571202718024296810620377657 883716690910941807448781404907551782038565390991047759414132154328440625030180 275716965082096427348414695726397884256008453121406593580904127113592004197598 513625479616063228873618136737324450607924411763997597461938358457491598809766 744709300654634242346063423747466608043170126005205592849369594143408146852981 505394717890045183575515412522359059068726487863575254191128887737176637486027 660634960353679470269232297186832771739323619200777452212624751869833495151019 864269887847171939664976907082521742336566272592844062043021411371992278526998 469884770232382384005565551788908766136013047709843861168705231055314916251728 373272867600724817298763756981633541507460883866364069347043720668865127568826 614973078865701568501691864748854167915459650723428773069985371390430026653078 398776385032381821553559732353068604301067576083890862704984188859513809103042 359578249514398859011318583584066747237029714978508414585308578133915627076035 639076394731145549583226694570249413983163433237897595568085683629725386791327 505554252449194358912840504522695381217913191451350099384631177401797151228378 546011603595540286440590249646693070776905548102885020808580087811577381719174 177601733073855475800605601433774329901272867725304318251975791679296996504146 070664571258883469797964293162296552016879730003564630457930884032748077181155 533090988702550520768046303460865816539487695196004408482065967379473168086415 645650530049881616490578831154345485052660069823093157776500378070466126470602 145750579327096204782561524714591896522360839664562410519551052235723973951288 181640597859142791481654263289200428160913693777372229998332708208296995573772 737566761552711392258805520189887620114168005468736558063347160373429170390798 639652296131280178267971728982293607028806908776866059325274637840539769184808 204102194471971386925608416245112398062011318454124478205011079876071715568315 407886543904121087303240201068534194723047666672174986986854707678120512473679 247919315085644477537985379973223445612278584329684664751333657369238720146472 367942787004250325558992688434959287612400755875694641370562514001179713316620 715371543600687647731867558714878398908107429530941060596944315847753970094398 839491443235366853920994687964506653398573888786614762944341401049888993160051 207678103588611660202961193639682134960750111649832785635316145168457695687109 002999769841263266502347716728657378579085746646077228341540311441529418804782 543876177079043000156698677679576090996693607559496515273634981189641304331166 277471233881740603731743970540670310967676574869535878967003192586625941051053 358438465602339179674926784476370847497833365557900738419147319886271352595462 518160434225372996286326749682405806029642114638643686422472488728343417044157 348248183330164056695966886676956349141632842641497453334999948000266998758881 593507357815195889900539512085351035726137364034367534714104836017546488300407 846416745216737190483109676711344349481926268111073994825060739495073503169019 731852119552635632584339099822498624067031076831844660729124874754031617969941 139738776589986855417031884778867592902607004321266617919223520938227878880988 633599116081923535557046463491132085918979613279131975649097600013996234445535 014346426860464495862476909434704829329414041114654092398834443515913320107739 441118407410768498106634724104823935827401944935665161088463125678529776973468 430306146241803585293315973458303845541033701091676776374276210213701354854450 926307190114731848574923318167207213727935567952844392548156091372812840633303 937356242001604566455741458816605216660873874804724339121295587776390696903707 882852775389405246075849623157436917113176134783882719416860662572103685132156 647800147675231039357860689611125996028183930954870905907386135191459181951029 732787557104972901148717189718004696169777001791391961379141716270701895846921 434369676292745910994006008498356842520191559370370101104974733949387788598941 743303178534870760322198297057975119144051099423588303454635349234982688362404 332726741554030161950568065418093940998202060999414021689090070821330723089662 119775530665918814119157783627292746156185710372172471009521423696483086410259 288745799932237495519122195190342445230753513380685680735446499512720317448719 540397610730806026990625807602029273145525207807991418429063884437349968145827 337207266391767020118300464819000241308350884658415214899127610651374153943565 721139032857491876909441370209051703148777346165287984823533829726013611098451 484182380812054099612527458088109948697221612852489742555551607637167505489617 301680961380381191436114399210638005083214098760459930932485102516829446726066 613815174571255975495358023998314698220361338082849935670557552471290274539776 214049318201465800802156653606776550878380430413431059180460680083459113664083 488740800574127258670479225831912741573908091438313845642415094084913391809684 025116399193685322555733896695374902662092326131885589158083245557194845387562 878612885900410600607374650140262782402734696252821717494158233174923968353013 617865367376064216677813773995100658952887742766263684183068019080460984980946 976366733566228291513235278880615776827815958866918023894033307644191240341202 231636857786035727694154177882643523813190502808701857504704631293335375728538 660588890458311145077394293520199432197117164223500564404297989208159430716701 985746927384865383343614579463417592257389858800169801475742054299580124295810 545651083104629728293758416116253256251657249807849209989799062003593650993472 158296517413579849104711166079158743698654122234834188772292944633517865385673 196255985202607294767407261676714557364981210567771689348491766077170527718760 119990814411305864557791052568430481144026193840232247093924980293355073184589 035539713308844617410795916251171486487446861124760542867343670904667846867027 409188101424971114965781772427934707021668829561087779440504843752844337510882 826477197854000650970403302186255614733211777117441335028160884035178145254196 432030957601869464908868154528562134698835544456024955666843660292219512483091 060537720198021831010327041783866544718126039719068846237085751808003532704718 565949947612424811099928867915896904956394762460842406593094862150769031498702 067353384834955083636601784877106080980426924713241000946401437360326564518456 679245666955100150229833079849607994988249706172367449361226222961790814311414 660941234159359309585407913908720832273354957208075716517187659944985693795623 875551617575438091780528029464200447215396280746360211329425591600257073562812 638733106005891065245708024474937543184149401482119996276453106800663118382376 163966318093144467129861552759820145141027560068929750246304017351489194576360 789352855505317331416457050499644389093630843874484783961684051845273288403234 520247056851646571647713932377551729479512613239822960239454857975458651745878 771331813875295980941217422730035229650808917770506825924882232215493804837145 478164721397682096332050830564792048208592047549985732038887639160199524091893 894557676874973085695595801065952650303626615975066222508406742889826590751063 756356996821151094966974458054728869363102036782325018232370845979011154847208 761821247781326633041207621658731297081123075815982124863980721240786887811450 165582513617890307086087019897588980745664395515741536319319198107057533663373 803827215279884935039748001589051942087971130805123393322190346624991716915094 854140187106035460379464337900589095772118080446574396280618671786101715674096 766208029576657705129120990794430463289294730615951043090222143937184956063405 618934251305726829146578329334052463502892917547087256484260034962961165413823 007731332729830500160256724014185152041890701154288579920812198449315699905918 201181973350012618772803681248199587707020753240636125931343859554254778196114 293516356122349666152261473539967405158499860355295332924575238881013620234762 466905581643896786309762736550472434864307121849437348530060638764456627218666 170123812771562137974614986132874411771455244470899714452288566294244023018479 120547849857452163469644897389206240194351831008828348024924908540307786387516 591130287395878709810077271827187452901397283661484214287170553179654307650453 432460053636147261818096997693348626407743519992868632383508875668359509726557 481543194019557685043724800102041374983187225967738715495839971844490727914196 584593008394263702087563539821696205532480321226749891140267852859967340524203 109179789990571882194939132075343170798002373659098537552023891164346718558290 685371189795262623449248339249634244971465684659124891855662958932990903523923 333364743520370770101084388003290759834217018554228386161721041760301164591878 053936744747205998502358289183369292233732399948043710841965947316265482574809 948250999183300697656936715968936449334886474421350084070066088359723503953234 017958255703601693699098867113210979889707051728075585519126993067309925070407 024556850778679069476612629808225163313639952117098452809263037592242674257559 989289278370474445218936320348941552104459726188380030067761793138139916205806 270165102445886924764924689192461212531027573139084047000714356136231699237169 484813255420091453041037135453296620639210547982439212517254013231490274058589 206321758949434548906846399313757091034633271415316223280552297297953801880162 859073572955416278867649827418616421878988574107164906919185116281528548679417 363890665388576422915834250067361245384916067413734017357277995634104332688356 950781493137800736235418007061918026732855119194267609122103598746924117283749 312616339500123959924050845437569850795704622266461900010350049018303415354584 283376437811198855631877779253720116671853954183598443830520376281944076159410 682071697030228515225057312609304689842343315273213136121658280807521263154773 060442377475350595228717440266638914881717308643611138906942027908814311944879 941715404210341219084709408025402393294294549387864023051292711909751353600092 197110541209668311151632870542302847007312065803262641711616595761327235156666 253667271899853419989523688483099930275741991646384142707798870887422927705389 122717248632202889842512528721782603050099451082478357290569198855546788607946 280537122704246654319214528176074148240382783582971930101788834567416781139895 475044833931468963076339665722672704339321674542182455706252479721997866854279 897799233957905758189062252547358220523642485078340711014498047872669199018643 882293230538231855973286978092225352959101734140733488476100556401824239219269 506208318381454698392366461363989101210217709597670490830508185470419466437131 229969235889538493013635657618610606222870559942337163102127845744646398973818 856674626087948201864748767272722206267646533809980196688368099415907577685263 986514625333631245053640261056960551318381317426118442018908885319635698696279 503673842431301133175330532980201668881748134298868158557781034323175306478498 321062971842518438553442762012823457071698853051832617964117857960888815032960 229070561447622091509473903594664691623539680920139457817589108893199211226007 392814916948161527384273626429809823406320024402449589445612916704950823581248 739179964864113348032475777521970893277226234948601504665268143987705161531702 669692970492831628550421289814670619533197026950721437823047687528028735412616 639170824592517001071418085480063692325946201900227808740985977192180515853214 739265325155903541020928466592529991435379182531454529059841581763705892790690 989691116438118780943537152133226144362531449012745477269573939348154691631162 492887357471882407150399500944673195431619385548520766573882513963916357672315 100555603726339486720820780865373494244011579966750736071115935133195919712094 896471755302453136477094209463569698222667377520994516845064362382421185353488 798939567318780660610788544000550827657030558744854180577889171920788142335113 866292966717964346876007704799953788338787034871802184243734211227394025571769 081960309201824018842705704609262256417837526526335832424066125331152942345796 556950250681001831090041124537901533296615697052237921032570693705109083078947 999900499939532215362274847660361367769797856738658467093667958858378879562594 646489137665219958828693380183601193236857855855819555604215625088365020332202 451376215820461810670519533065306060650105488716724537794283133887163139559690 583208341689847606560711834713621812324622725884199028614208728495687963932546 428534307530110528571382964370999035694888528519040295604734613113826387889755 178856042499874831638280404684861893818959054203988987265069762020199554841265 000539442820393012748163815853039643992547020167275932857436666164411096256633 730540921951967514832873480895747777527834422109107311135182804603634719818565 557295714474768255285786334934285842311874944000322969069775831590385803935352 135886007960034209754739229673331064939560181223781285458431760556173386112673 478074585067606304822940965304111830667108189303110887172816751957967534718853 722930961614320400638132246584111115775835858113501856904781536893813771847281 475199835050478129771859908470762197460588742325699582889253504193795826061621 184236876851141831606831586799460165205774052942305360178031335726326705479033 840125730591233960188013782542192709476733719198728738524805742124892118347087 662966720727232565056512933312605950577772754247124164831283298207236175057467 387012820957554430596839555568686118839713552208445285264008125202766555767749 596962661260456524568408613923826576858338469849977872670655519185446869846947 849573462260629421962455708537127277652309895545019303773216664918257815467729 200521266714346320963789185232321501897612603437368406719419303774688099929687 758244104787812326625318184596045385354383911449677531286426092521153767325886 672260404252349108702695809964759580579466397341906401003636190404203311357933 654242630356145700901124480089002080147805660371015412232889146572239314507607 167064355682743774396578906797268743847307634645167756210309860409271709095128 086309029738504452718289274968921210667008164858339553773591913695015316201890 888748421079870689911480466927065094076204650277252865072890532854856143316081 269300569378541786109696920253886503457718317668688592368148847527649846882194 973972970773718718840041432312763650481453112285099002074240925585925292610302 106736815434701525234878635164397623586041919412969769040526483234700991115424 260127343802208933109668636789869497799400126016422760926082349304118064382913 834735467972539926233879158299848645927173405922562074910530853153718291168163 721939518870095778818158685046450769934394098743351443162633031724774748689791 820923948083314397084067308407958935810896656477585990556376952523265361442478 023082681183103773588708924061303133647737101162821461466167940409051861526036 009252194721889091810733587196414214447865489952858234394705007983038853886083 103571930600277119455802191194289992272235345870756624692617766317885514435021 828702668561066500353105021631820601760921798468493686316129372795187307897263 735371715025637873357977180818487845886650433582437700414771041493492743845758 710715973155943942641257027096512510811554824793940359768118811728247215825010 949609662539339538092219559191818855267806214992317276316321833989693807561685 591175299845013206712939240414459386239880938124045219148483164621014738918251 010909677386906640415897361047643650006807710565671848628149637111883219244566 394581449148616550049567698269030891118568798692947051352481609174324301538368 470729289898284602223730145265567989862776796809146979837826876431159883210904 371561129976652153963546442086919756737000573876497843768628768179249746943842 746525631632300555130417422734164645512781278457777245752038654375428282567141 288583454443513256205446424101103795546419058116862305964476958705407214198521 210673433241075676757581845699069304604752277016700568454396923404171108988899 341635058515788735343081552081177207188037910404698306957868547393765643363197 978680367187307969392423632144845035477631567025539006542311792015346497792906 624150832885839529054263768766896880503331722780018588506973623240389470047189 761934734430843744375992503417880797223585913424581314404984770173236169471976 571535319775499716278566311904691260918259124989036765417697990362375528652637 573376352696934435440047306719886890196814742876779086697968852250163694985673 021752313252926537589641517147955953878427849986645630287883196209983049451987 439636907068276265748581043911223261879405994155406327013198989570376110532360 629867480377915376751158304320849872092028092975264981256916342500052290887264 692528466610466539217148208013050229805263783642695973370705392278915351056888 393811324975707133102950443034671598944878684711643832805069250776627450012200 352620370946602341464899839025258883014867816219677519458316771876275720050543 979441245990077115205154619930509838698254284640725554092740313257163264079293 418334214709041254253352324802193227707535554679587163835875018159338717423606 155117101312352563348582036514614187004920570437201826173319471570086757853933 607862273955818579758725874410254207710547536129404746010009409544495966288148 691590389907186598056361713769222729076419775517772010427649694961105622059250 242021770426962215495872645398922769766031052498085575947163107587013320886146 326641259114863388122028444069416948826152957762532501987035987067438046982194 205638125583343642194923227593722128905642094308235254408411086454536940496927 149400331978286131818618881111840825786592875742638445005994422956858646048103 301538891149948693543603022181094346676400002236255057363129462629609619876056 425996394613869233083719626595473923462413459779574852464783798079569319865081 597767535055391899115133525229873611277918274854200868953965835942196333150286 956119201229888988700607999279541118826902307891310760361763477948943203210277 335941690865007193280401716384064498787175375678118532132840821657110754952829 497493621460821558320568723218557406516109627487437509809223021160998263303391 546949464449100451528092508974507489676032409076898365294065792019831526541065 813682379198409064571246894847020935776119313998024681340520039478194986620262 400890215016616381353838151503773502296607462795291038406868556907015751662419 298724448271942933100485482445458071889763300323252582158128032746796200281476 243182862217105435289834820827345168018613171959332471107466222850871066611770 346535283957762599774467218571581612641114327179434788599089280848669491413909 771673690027775850268664654056595039486784111079011610400857274456293842549416 759460548711723594642910585090995021495879311219613590831588262068233215615308 683373083817327932819698387508708348388046388478441884003184712697454370937329 836240287519792080232187874488287284372737801782700805878241074935751488997891 173974612932035108143270325140903048746226294234432757126008664250833318768865 075642927160552528954492153765175149219636718104943531785838345386525565664065 725136357506435323650893679043170259787817719031486796384082881020946149007971 513771709906195496964007086766710233004867263147551053723175711432231741141168 062286420638890621019235522354671166213749969326932173704310598722503945657492 461697826097025335947502091383667377289443869640002811034402608471289900074680 776484408871134135250336787731679770937277868216611786534423173226463784769787 514433209534000165069213054647689098505020301504488083426184520873053097318949 291642532293361243151430657826407028389840984160295030924189712097160164926561 341343342229882790992178604267981245728534580133826099587717811310216734025656 274400729683406619848067661580502169183372368039902793160642043681207990031626 444914619021945822969099212278855394878353830564686488165556229431567312827439 082645061162894280350166133669782405177015521962652272545585073864058529983037 918035043287670380925216790757120406123759632768567484507915114731344000183257 034492090971243580944790046249431345502890068064870429353403743603262582053579 011839564908935434510134296961754524957396062149028872893279252069653538639644 322538832752249960598697475988232991626354597332444516375533437749292899058117 578635555562693742691094711700216541171821975051983178713710605106379555858890 556885288798908475091576463907469361988150781468526213325247383765119299015610 918977792200870579339646382749068069876916819749236562422608715417610043060890 437797667851966189140414492527048088197149880154205778700652159400928977760133 075684796699295543365613984773806039436889588764605498387147896848280538470173 087111776115966350503997934386933911978988710915654170913308260764740630571141 109883938809548143782847452883836807941888434266622207043872288741394780101772 139228191199236540551639589347426395382482960903690028835932774585506080131798 840716244656399794827578365019551422155133928197822698427863839167971509126241 054872570092407004548848569295044811073808799654748156891393538094347455697212 891982717702076661360248958146811913361412125878389557735719498631721084439890 142394849665925173138817160266326193106536653504147307080441493916936326237376 777709585031325599009576273195730864804246770121232702053374266705314244820816 813030639737873664248367253983748769098060218278578621651273856351329014890350 988327061725893257536399397905572917516009761545904477169226580631511102803843 601737474215247608515209901615858231257159073342173657626714239047827958728150 509563309280266845893764964977023297364131906098274063353108979246424213458374 090116939196425045912881340349881063540088759682005440836438651661788055760895 689672753153808194207733259791727843762566118431989102500749182908647514979400 316070384554946538594602745244746681231468794344161099333890899263841184742525 704457251745932573898956518571657596148126602031079762825416559050604247911401 695790033835657486925280074302562341949828646791447632277400552946090394017753 633565547193100017543004750471914489984104001586794617924161001645471655133707 407395026044276953855383439755054887109978520540117516974758134492607943368954 378322117245068734423198987884412854206474280973562580706698310697993526069339 213568588139121480735472846322778490808700246777630360555123238665629517885371 967303463470122293958160679250915321748903084088651606111901149844341235012464 692802880599613428351188471544977127847336176628506216977871774382436256571177 945006447771837022199910669502165675764404499794076503799995484500271066598781 360380231412683690578319046079276529727769404361302305178708054651154246939526 512710105292707030667302444712597393995051462840476743136373997825918454117641 332790646063658415292701903027601733947486696034869497654175242930604072700505 903950314852292139257559484507886797792525393176515641619716844352436979444735 596426063339105512682606159572621703669850647328126672452198906054988028078288 142979633669674412480598219214633956574572210229867759974673812606936706913408 155941201611596019023775352555630060624798326124988128819293734347686268921923 977783391073310658825681377717232831532908252509273304785072497713944833389255 208117560845296659055394096556854170600117985729381399825831929367910039184409 928657560599359891000296986446097471471847010153128376263114677420914557404181 590880006494323785583930853082830547607679952435739163122188605754967383224319 565065546085288120190236364471270374863442172725787950342848631294491631847534 753143504139209610879605773098720135248407505763719925365047090858251393686346 386336804289176710760211115982887553994012007601394703366179371539630613986365 549221374159790511908358829009765664730073387931467891318146510931676157582135 142486044229244530411316065270097433008849903467540551864067734260358340960860 553374736276093565885310976099423834738222208729246449768456057956251676557408 841032173134562773585605235823638953203853402484227337163912397321599544082842 166663602329654569470357718487344203422770665383738750616921276801576618109542 009770836360436111059240911788954033802142652394892968643980892611463541457153 519434285072135345301831587562827573389826889852355779929572764522939156747756 667605108788764845349363606827805056462281359888587925994094644604170520447004 631513797543173718775603981596264750141090665886616218003826698996196558058720 863972117699521946678985701179833244060181157565807428418291061519391763005919 431443460515404771057005433900018245311773371895585760360718286050635647997900 413976180895536366960316219311325022385179167205518065926351803625121457592623 836934822266589557699466049193811248660909979812857182349400661555219611220720 309227764620099931524427358948871057662389469388944649509396033045434084210246 240104872332875008174917987554387938738143989423801176270083719605309438394006 375611645856094312951759771393539607432279248922126704580818331376416581826956 210587289244774003594700926866265965142205063007859200248829186083974373235384 908396432614700053242354064704208949921025040472678105908364400746638002087012 666420945718170294675227854007450855237772089058168391844659282941701828823301 497155423523591177481862859296760504820386434310877956289292540563894662194826 871104282816389397571175778691543016505860296521745958198887868040811032843273 986719862130620555985526603640504628215230615459447448990883908199973874745296 981077620148713400012253552224669540931521311533791579802697955571050850747387 475075806876537644578252443263804614304288923593485296105826938210349800040524 840708440356116781717051281337880570564345061611933042444079826037795119854869 455915205196009304127100727784930155503889536033826192934379708187432094991415 959339636811062755729527800425486306005452383915106899891357882001941178653568 214911852820785213012551851849371150342215954224451190020739353962740020811046 553020793286725474054365271759589350071633607632161472581540764205302004534018 357233829266191530835409512022632916505442612361919705161383935732669376015691 442994494374485680977569630312958871916112929468188493633864739274760122696415 884890096571708616059814720446742866420876533479985822209061980217321161423041 947775499073873856794118982466091309169177227420723336763503267834058630193019 324299639720444517928812285447821195353089891012534297552472763573022628138209 180743974867145359077863353016082155991131414420509144729353502223081719366350 934686585865631485557586244781862010871188976065296989926932817870557643514338 206014107732926106343152533718224338526352021773544071528189813769875515757454 693972715048846979361950047772097056179391382898984532742622728864710888327017 372325881824465843624958059256033810521560620615571329915608489206434030339526 226345145428367869828807425142256745180618414956468611163540497189768215422772 247947403357152743681940989205011365340012384671429655186734415374161504256325 671343024765512521921803578016924032669954174608759240920700466934039651017813 485783569444076047023254075555776472845075182689041829396611331016013111907739 863246277821902365066037404160672496249013743321724645409741299557052914243820 807609836482346597388669134991978401310801558134397919485283043673901248208244 481412809544377389832005986490915950532285791457688496257866588599917986752055 455809900455646117875524937012455321717019428288461740273664997847550829422802 023290122163010230977215156944642790980219082668986883426307160920791408519769 523555348865774342527753119724743087304361951139611908003025587838764420608504 473063129927788894272918972716989057592524467966018970748296094919064876469370 275077386643239191904225429023531892337729316673608699622803255718530891928440 380507103006477684786324319100022392978525537237556621364474009676053943983823 576460699246526008909062410590421545392790441152958034533450025624410100635953 003959886446616959562635187806068851372346270799732723313469397145628554261546 765063246567662027924520858134771760852169134094652030767339184114750414016892 412131982688156866456148538028753933116023229255561894104299533564009578649534 093511526645402441877594931693056044868642086275720117231952640502309977456764 783848897346431721598062678767183800524769688408498918508614900343240347674268 624595239589035858213500645099817824463608731775437885967767291952611121385919 472545140030118050343787527766440276261894101757687268042817662386068047788524 288743025914524707395054652513533945959878961977891104189029294381856720507096 460626354173294464957661265195349570186001541262396228641389779673332907056737 696215649818450684226369036784955597002607986799626101903933126376855696876702 929537116252800554310078640872893922571451248113577862766490242516199027747109 033593330930494838059785662884478744146984149906712376478958226329490467981208 998485716357108783119184863025450162092980582920833481363840542172005612198935 366937133673339246441612522319694347120641737549121635700857369439730597970971 972666664226743111776217640306868131035189911227133972403688700099686292254646 500638528862039380050477827691283560337254825579391298525150682996910775425764 748832534141213280062671709400909822352965795799780301828242849022147074811112 401860761341515038756983091865278065889668236252393784527263453042041880250844 236319038331838455052236799235775292910692504326144695010986108889991465855188 187358252816430252093928525807796973762084563748211443398816271003170315133440 230952635192958868069082135585368016100021374085115448491268584126869589917414 913382057849280069825519574020181810564129725083607035685105533178784082900004 155251186577945396331753853209214972052660783126028196116485809868458752512999 740409279768317663991465538610893758795221497173172813151793290443112181587102 351874075722210012376872194474720934931232410706508061856237252673254073332487 575448296757345001932190219911996079798937338367324257610393898534927877747398 050808001554476406105352220232540944356771879456543040673589649101761077594836 454082348613025471847648518957583667439979150851285802060782055446299172320202 822291488695939972997429747115537185892423849385585859540743810488262464878805 330427146301194158989632879267832732245610385219701113046658710050008328517731 177648973523092666123458887310288351562644602367199664455472760831011878838915 114934093934475007302585581475619088139875235781233134227986650352272536717123 075686104500454897036007956982762639234410714658489578024140815840522953693749 971066559489445924628661996355635065262340533943914211127181069105229002465742 360413009369188925586578466846121567955425660541600507127664176605687427420032 957716064344860620123982169827172319782681662824993871499544913730205184366907 672357740005393266262276032365975171892590180110429038427418550789488743883270 306328327996300720069801224436511639408692222074532024462412115580435454206421 512158505689615735641431306888344318528085397592773443365538418834030351782294 625370201578215737326552318576355409895403323638231921989217117744946940367829 618592080340386757583411151882417743914507736638407188048935825686854201164503 135763335550944031923672034865101056104987272647213198654343545040913185951314 518127643731043897250700498198705217627249406521461995923214231443977654670835 171474936798618655279171582408065106379950018429593879915835017158075988378496 225739851212981032637937621832245659423668537679911314010804313973233544909082 491049914332584329882103398469814171575601082970658306521134707680368069532297 199059990445120908727577622535104090239288877942463048328031913271049547859918 019696783532146444118926063152661816744319355081708187547705080265402529410921 826485821385752668815558411319856002213515888721036569608751506318753300294211 868222189377554602722729129050429225978771066787384000061677215463844129237119 352182849982435092089180168557279815642185819119749098573057033266764646072875 743056537260276898237325974508447964954564803077159815395582777913937360171742 299602735310276871944944491793978514463159731443535185049141394155732938204854 212350817391254974981930871439661513294204591938010623142177419918406018034794 988769105155790555480695387854006645337598186284641990522045280330626369562649 091082762711590385699505124652999606285544383833032763859980079292284665950355 121124528408751622906026201185777531374794936205549640107300134885315073548735 390560290893352640071327473262196031177343394367338575912450814933573691166454 128178817145402305475066713651825828489809951213919399563324133655677709800308 191027204099714868741813466700609405102146269028044915964654533010775469541308 871416531254481306119240782118869005602778182423502269618934435254763357353648 561936325441775661398170393063287216690572225974520919291726219984440964615826 945638023950283712168644656178523556516412771282691868861557271620147493405227 694659571219831494338162211400693630743044417328478610177774383797703723179525 543410722344551255558999864618387676490397246116795901810003509892864120419516 355110876320426761297982652942588295114127584126273279079880755975185157684126 474220947972184330935297266521001566251455299474512763155091763673025946213293 019040283795424632325855030109670692272022707486341900543830265068121414213505 715417505750863990767394633514620908288893493837643939925690060406731142209331 219593620298297235116325938677224147791162957278075239505625158160313335938231 150051862689053065836812998810866326327198061127154885879809348791291370749823 057592909186293919501472119758606727009254771802575033773079939713453953264619 526999659638565491759045833358579910201271320458390320085387888163363768518208 372788513117522776960978796214237216254521459128183179821604411131167140691482 717098101545778193920231156387195080502467972579249760577262591332855972637121 120190572077140914864507409492671803581515757151405039761096384675556929897038 354731410022380258346876735012977541327953206097115450648421218593649099791776 687477448188287063231551586503289816422828823274686610659273219790716238464215 348985247621678905026099804526648392954235728734397768049577409144953839157556 548545905897649519851380100795801078375994577529919670054760225255203445398871 253878017196071816407812484784725791240782454436168234523957068951427226975043 187363326301110305342333582160933319121880660826834142891041517324721605335584 999322454873077882290525232423486153152097693846104258284971496347534183756200 301491570327968530186863157248840152663983568956363465743532178349319982554211 730846774529708583950761645822963032442432823773745051702856069806788952176819 815671078163340526675953942492628075696832610749532339053622309080708145591983 735537774874202903901814293731152933464446815121294509759653430628421531944572 711861490001765055817709530246887526325011970520947615941676872778447200019278 913725184162285778379228443908430118112149636642465903363419454065718354477191 244662125939265662030688852005559912123536371822692253178145879259375044144893 398160865790087616502463519704582889548179375668104647461410514249887025213993 687050937230544773411264135489280684105910771667782123833281026218558775131272 117934444820144042574508306394473836379390628300897330624138061458941422769474 793166571762318247216835067807648757342049155762821758397297513447899069658953 254894033561561316740327647246921250575911625152965456854463349811431767025729 566184477548746937846423373723898192066204851189437886822480727935202250179654 534375727416391079197295295081294292220534771730418447791567399173841831171036 252439571615271466900581470000263301045264354786590329073320546833887207873544 476264792529769017091200787418373673508771337697768349634425241994995138831507 487753743384945825976556099655595431804092017849718468549737069621208852437701 385375768141663272241263442398215294164537800049250726276515078908507126599703 670872669276430837722968598516912230503746274431085293430527307886528397733524 601746352770320593817912539691562106363762588293757137384075440646896478310070 458061344673127159119460843593582598778283526653115106504162329532904777217408 355934972375855213804830509000964667608830154061282430874064559443185341375522 016630581211103345312074508682433943215904359443031243122747138584203039010607 094031523555617276799416002039397509989762933532585557562480899669182986422267 750236019325797472674257821111973470940235745722227121252685238429587427350156 366009318804549333898974157149054418255973808087156528143010267046028431681923 039253529779576586241439270154974087927313105163611913757700892956482332364829 826302460797587576774537716010249080462430185652416175665560016085912153455626 760219268998285537787258314514408265458348440947846317877737479465358016996077 940556870119232860804113090462935087182712593466871276669487389982459852778649 956916546402945893506496433580982476596516514209098675520380830920323048734270 346828875160407154665383461961122301375945157925269674364253192739003603860823 645076269882749761872357547676288995075211480485252795084503395857083813047693 788132112367428131948795022806632017002246033198967197064916374117585485187848 401205484467258885140156272501982171906696081262778548596481836962141072171421 498636191877475450965030895709947093433785698167446582826791194061195603784539 785583924076127634410576675102430755981455278616781594965706255975507430652108 530159790807334373607943286675789053348366955548680391343372015649883422089339 997164147974693869690548008919306713805717150585730714881564992071408675825960 287605645978242377024246980532805663278704192676846711626687946348695046450742 021937394525926266861355294062478136120620263649819999949840514386828525895634 226432870766329930489172340072547176418868535137233266787792173834754148002280 339299735793615241275582956927683723123479898944627433045456679006203242051639 628258844308543830720149567210646053323853720314324211260742448584509458049408 182092763914000854042202355626021856434899414543995041098059181794888262805206 644108631900168856815516922948620301073889718100770929059048074909242714101893 354281842999598816966099383696164438152887721408526808875748829325873580990567 075581701794916190611400190855374488272620093668560447559655747648567400817738 170330738030547697360978654385938218722058390234444350886749986650604064587434 600533182743629617786251808189314436325120510709469081358644051922951293245007 883339878842933934243512634336520438581291283434529730865290978330067126179813 031679438553572629699874035957045845223085639009891317947594875212639707837594 486113945196028675121056163897600888009274611586080020780334159145179707303683 519697776607637378533301202412011204698860920933908536577322239241244905153278 095095586645947763448226998607481329730263097502881210351772312446509534965369 309001863776409409434983731325132186208021480992268550294845466181471555744470 966953017769043427203189277060471778452793916047228153437980353967986142437095 668322149146543801459382927739339603275404800955223181666738035718393275707714 204672383862461780397629237713120958078936384144792980258806552212926209362393 063731349664018661951081158347117331202580586672763999276357907806381881306915 636627412543125958993611964762610140556350339952314032311381965623632719896183 725484533370206256346422395276694356837676136871196292181875457608161705303159 072882870071231366630872275491866139577373054606599743781098764980241401124214 277366808275139095931340415582626678951084677611866595766016599817808941498575 497628438785610026379654317831363402513581416115190209649913354873313111502270 068193013592959597164019719605362503355847998096348871803911161281359596856547 886832585643789617315976200241962155289629790481982219946226948713746244472909 345647002853769495885959160678928249105441251599630078136836749020937491573289 627002865682934443134234735123929825916673950342599586897069726733258273590312 128874666045146148785034614282776599160809039865257571726308183349444182019353 338507129234577437557934406217871133006310600332405399169368260374617663856575 887758020122936635327026710068126182517291460820254189288593524449107013820621 155382779356529691457650204864328286555793470720963480737269214118689546732276 775133569019015372366903686538916129168888787640752549349424973342718117889275 993159671935475898809792452526236365903632007085444078454479734829180208204492 667063442043755532505052752283377888704080403353192340768563010934777212563908 864041310107381785333831603813528082811904083256440184205374679299262203769871 801806112262449090924264198582086175117711378905160914038157500336642415609521 632819712233502316742260056794128140621721964184270578432895980288233505982820 819666624903585778994033315227481777695284368163008853176969478369058067106482 808359804669884109813515865490693331952239436328792399053481098783027450017206 543369906611778455436468772363184446476806914282800455107468664539280539940910 875493916609573161971503316696830992946634914279878084225722069714887558063748 030886299511847318712477729191007022758889348693945628951580296537215040960310 776128983126358996489341024703603664505868728758905140684123812424738638542790 828273382797332688550493587430316027474906312957234974261122151741715313361862 241091386950068883589896234927631731647834007746088665559873338211382992877691 149549218419208777160606847287467368188616750722101726110383067178785669481294 878504894306308616994879870316051588410828235127415353851336589533294862949449 506186851477910580469603906937266267038651290520113781085861618888694795760741 358553458515176805197333443349523012039577073962377131603024288720053732099825 300897761897312981788194467173116064723147624845755192873278282512718244680782 421521646956781929409823892628494376024885227900362021938669648221562809360537 317804086372726842669642192994681921490870170753336109479138180406328738759384 826953558307739576144799727000347288018278528138950321798634521611106660883931 405322694490545552786789441757920244002145078019209980446138254780585804844241 640477503153605490659143007815837243012313751156228401583864427089071828481675 752712384678245953433444962201009607105137060846180118754312072549133499424761 711563332140893460915656155060031738421870157022610310191660388706466143889773 631878094071152752817468957640158104701696524755774089164456867771715850058326 994340167720215676772406812836656526412298243946513319735919970940327593850266 955747023181320324371642058614103360652453693916005064495306016126782264894243 739716671766123104897503188573216555498834212180284691252908610148552781527762 562375045637576949773433684601560772703550962904939248708840628106794362241870 474700836884267102255830240359984164595112248527263363264511401739524808619463 584078375355688562231711552094722306543709260679735100056554938122457548372854 571179739361575616764169289580525729752233855861138832217110736226581621884244 317885748879810902665379342666421699091405653643224930133486798815488662866505 234699723557473842483059042367714327879231642240387776433019260019228477831383 763253612102533693581262408686669973827597736568222790721583247888864236934639 616436330873013981421143030600873066616480367898409133592629340230432497492688 783164360268101130957071614191283068657732353263965367739031766136131596555358 499939860056515592193675997771793301974468814837110320650369319289452140265091 546518430993655349333718342529843367991593941746622390038952767381333061774762 957494386871697845376721949350659087571191772087547710718993796089477451265475 750187119487073873678589020061737332107569330221632062843206567119209695058576 117396163232621770894542621460985841023781321581772760222273813349541048100307 327510779994899197796388353073444345753297591426376840544226478421606312276964 696715647399904371590332390656072664411643860540483884716191210900870101913072 607104411414324197679682854788552477947648180295973604943970047959604029274629 920357209976195014034831538094771460105633344699882082212058728151072918297121 191787642488035467231691654185225672923442918712816323259696541354858957713320 833991128877591722611527337901034136208561457799239877832508355073019981845902 595835598926055329967377049172245493532968330000223018151722657578752405883224 908582128008974790932610076257877042865600699617621217684547899644070506624171 021332748679623743022915535820078014116534806564748823061500339206898379476625 503654982280532966286211793062843017049240230198571997894883689718304380518217 441914766042975243725168343541121703863137941142209529588579806015293875275379 903093887168357209576071522190027937929278630363726876582268124199338480816602 160372215471014300737753779269906958712128928801905203160128586182549441335382 078488346531163265040764242839087012101519423196165226842200371123046430067344 206474771802135307012409886035339915266792387110170622186588357378121093517977 560442563469499978725112544085452227481091487430725986960204027594117894258128 188215995235965897918114407765335432175759525553615812800116384672031934650729 680799079396371496177431211940202129757312516525376801735910155733815377200195 244454362007184847566341540744232862106099761324348754884743453966598133871746 609302053507027195298394327142537115576660002578442303107342955153394506048622 276496668762407932435319299263925373107689213535257232108088981933916866827894 828117047262450194840970097576092098372409007471797334078814182519584259809624 174761013825264395513525931188504563626418830(etc...) |
When you said "π is an irrational number, which means that it cannot be expressed exactly as a ratio of two integers (such as 22/7 or other fractions that are commonly used to approximate π); consequently, its decimal representation never ends and never repeats."-Pi Article. You didn't really explain it as much as an infinite nubmer. You really should have put something like that. I would like it if you used that in the place of 3.14159 when you began. Thanks. TheGeneralOfFisher 1234567890 (talk) 20:02, 3 November 2012 (UTC)
- Pi is not an "infinite number", but it is irrational. This means that writing 3.14159265... (for example) is just as appropriate as your (frankly silly) suggestion. The edit should not be made; and I think your comment should be severely truncated (but I'm not sure if there are "principles" about editing other people's comments). Note that the external links include a reference to the first billion digits of pi. Imaginatorium (talk) 20:17, 3 November 2012 (UTC)
 Not done: The top of the article says that PI is approximately 3.14159 and that it goes on forever. There is no need to put a larger approximation into the article. RudolfRed (talk) 20:18, 3 November 2012 (UTC)
Not done: The top of the article says that PI is approximately 3.14159 and that it goes on forever. There is no need to put a larger approximation into the article. RudolfRed (talk) 20:18, 3 November 2012 (UTC)
- Tau is the rival irrational number to Pi. This tells us that Pi is wrong. ElliottBelardo (talk) —Preceding undated comment added 01:59, 19 November 2012 (UTC)