Talk:Merkle–Damgård construction

	This article is within the scope of WikiProject Cryptography, a collaborative effort to improve the coverage of Cryptography on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.CryptographyWikipedia:WikiProject CryptographyTemplate:WikiProject CryptographyCryptography
???	This article has not yet received a rating on the importance scale.
	This article is supported by WikiProject Computer science.

Oops

I just read through source code for about ten of the more well known hash algorithms. It seems they do not work exactly as I thought. That is, there are some factual errors in this article. (All my fault, I inserted those errors.) I will correct those errors in the article after I thought a bit more about it and done some checking in my books. --David Göthberg 19:31, 22 February 2006 (UTC)[reply]

So no one things anything else: I did correct those errors some days later.

--David Göthberg (talk) 14:56, 26 June 2008 (UTC)[reply]

Name of this article

How about "Merkle-Damgård hash construction"?

I originally choose the name "Merkle-Damgård construction" for this article since that is what Handbook of Applied Cryptography by Menezes & Co calls it. (Note that Merkle-Damgård strengthening just means the length padding, not the whole construction.)

User:Mangojuice changed it to "Merkle-Damgård hash function". I agree that using the term "hash" in the name is very nice. But in itself it is not a hash function. It only becomes a hash function when used together with a compression function. Of course hash functions that use Merkle-Damgård (just about all hash functions out there) are "Merkle-Damgård hash functions". So perhaps we should use the name "Merkle-Damgård hash construction" or "Merkle-Damgård hash construct"? Oh, and is there any difference in meaning between "construction" and "construct"? As far as I can understand from the dictionaries I have both can be used in this case.

--David Göthberg 11:13, 6 March 2006 (UTC)[reply]

I think "construction" is more idiomatic within the field. — Matt Crypto 12:32, 6 March 2006 (UTC)[reply]

Here is the result of the Google test:

1,190 for "Merkle-Damgard construction" -Wikipedia

488 for "Merkle-Damgård construction" -Wikipedia

6 for "Merkle-Damgard hash construction" -Wikipedia

6 for "Merkle-Damgård hash construction" -Wikipedia

6 for "Merkle-Damgard construct" -Wikipedia

3 for "Merkle-Damgård construct" -Wikipedia

85 for "Merkle-Damgard hash function" -Wikipedia

36 for "Merkle-Damgård hash function" -Wikipedia

2 for "Merkle-Damgard function"

No results found for "Merkle-Damgård function".

To filter out most of the hits from sites that copy Wikipedia I used the additional search criteria "-Wikipedia". Note that results for "Damgard" automatically include results for "Damgård" when Google is used. And searches for "Merkle-Damgard" and "Merkle Damgard" gives the same results. The hyphen has no effect.

It is clear that "Merkle-Damgård construction" by far is the most used name. But to make the article name clearer I think we perhaps can deviate somewhat from common practise and use "Merkle-Damgård hash construction", even though that name is rarely used.

--David Göthberg (talk) 16:06, 16 September 2008 (UTC)[reply]

On second thought, we are an encyclopaedia, we should name things with their proper name. Unless of course there is a name collision, such as for the Tiger hash, which we currently have named Tiger (cryptography). But there are nothing else named "Merkle-Damgård construction" so we don't need to name it "Merkle-Damgård hash construction".

So, today I moved this article back to Merkle-Damgård construction.

--David Göthberg (talk) 09:30, 20 September 2008 (UTC)[reply]

Earliest use?

References 1 and 2 are dated 1989, but Merkle used the construction in his 1979 Ph.D. thesis (see http://www.merkle.com/papers/Thesis1979.pdf, chapter 2). Unless there's a reference to something earlier than 1979, Merkle's thesis would be the first use (and the text should be changed accordingly). —Preceding unsigned comment added by 68.209.119.202 (talk • contribs) 05:53, 28 May 2006

As far as I remember when I checked it both independently published the idea the same year just some month apart, back in the 1970's. But note, I just double checked it since I was curious, the crypto books I have state that they invented it independently. And both men are in the now widely used name for this algorithm.

And Wikipedia references are often not to the first publication, but instead to a good to read reference describing the technique. Since the first paper about something usually is not the best paper about it.

--David Göthberg (talk) 14:50, 26 June 2008 (UTC)[reply]

I just reread the article and noticed we doesn't really state one important fact:

Hash functions that used a compression function by breaking up the input into a series of blocks already existed long before Merkle and Damgård wrote their papers. I am not sure, but I think some hashes even already had the "10000" padding. What Merkle and Damgård did was to add the length padding, that is the adding of "00009" in the example in the article. And they wrote proofs for how and why that makes the hash secure. So it is the whole construct with compression and length padding together that is the "Merkle-Damgård construction".

We probably should make that clearer in the article.

--David Göthberg (talk) 18:06, 9 November 2008 (UTC)[reply]

Example

In the example, both the length and a terminating '1' are used. If the length is given then surely the terminator is unnecessary. Perhaps it could be either changed or a note added explaining why both are required if it is so. penagate _{[talk|contribs]} 08:55, 26 June 2008 (UTC)[reply]

Right, it is probably secure enough to only use one of the two padding techniques. However, in crypto (and any other security or safety related field) we like to use multilayer defence since you never know what kind of new cracks people will invent. So we use both, just in case. When I wrote that example I checked the code for about 10 different crypto algorithms and they all used both pads.

I don't think it is necessary to state such a basic thing about security/safety. But in the text we have written "To harden the hash even further" which kind of says it is multilayer defence. But hey, every now and then I have had arguments with some of my students who wanted to use a single line of defence, so some people don't seem to know/understand that basic security/safety thing.

As far as I remember it is only considered cryptographically "proven" that one of the pads are secure (I think it was the size value), but both are believed to be secure. However, remember that such "proofs" are not absolute, they might contain mistakes and someone might invent some brand new cracking method that the proof didn't take into consideration. And especially in computing it happens all the time that people invent new methods that make things possible that previously were considered "proven" to be impossible, but it also happens every now and then in other science fields. Most who have worked long enough in research know that "proven" just means "we are pretty darn sure about this, and we think it will hold for some time".

--David Göthberg (talk) 14:50, 26 June 2008 (UTC)[reply]

Don't be an idiot. In cryptography, just as in the rest of mathematics, "proven" means exactly that, proven (beyond any doubt). If you really have students (hope not), stop teaching them any nonsense to the contrary (better yet, stop teaching). As the article makes abundantly clear, the appending of the message length makes the hashing secure as long as the compression function itself is secure, and that (according to the article text) is rigourously established. This means the "bit-1" thing is unnecessary as far as security is concerned, and probably subsists for historical reasons. — Preceding unsigned comment added by 85.240.50.25 (talk) 02:39, 27 February 2013 (UTC)[reply]

Security Characteristics

Aren't points 1 and 3 equivalent or a subset/superset of the other? 87.254.83.229 (talk) 03:36, 23 December 2008 (UTC)[reply]

No, but the distinction isn't clear in the article. Length extension depends on the colliding sets of messages having the same prefix, whereas multicollision attacks can find multiple collisions for messages of the same length. --David-Sarah Hopwood ⚥ (talk) 15:32, 11 October 2009 (UTC)[reply]

Wide-pipe construction

Since I am not in the mood and currently don't have the time to edit the article itself, here goes:

I disagree with parts of the content in the new "Wide pipe construction" section in this article:

The section currently states that "Stefan Lucks proposed the use of the wide-pipe hash" and links to a paper from 2004. However, the idea of using a larger internal state in the Merkle-Damgård construction for added security has been well known for decades. And some of the well known hash algorithms designed in the 1980's and 1990's do use a larger internal state. So I think Stefan Lucks' name should be removed. (He graduated in 1992 so I doubt he influenced hash designs in the 1980's.)
Such compressing of a larger internal state to a smaller final output state is also mentioned in the Handbook of Applied Cryptography in chapter 9. That book was written in 2001. And it is part of the graphs used to describe the Merkle-Damgård construction in that book and other cryptography books.
I disagree with wording such as "instead of Merkle–Damgård construction", since the wide-pipe construction still is the Merkle-Damgård construction. It is just a small extension that usually is shown together with the Merkle-Damgård construction in most books and graphs.

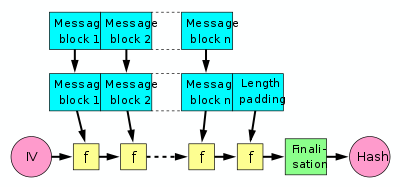
Even before the "wide-pipe" section was added to this article the image used in this article already showed the "finalisation function" (the green box in the image) and the first section already described it:

To harden the hash further the last result is then sometimes fed through a finalisation function. The finalisation function can have several purposes such as compressing a bigger internal state (the last result) into a smaller output hash size or to guarantee a better mixing and avalanche effect on the bits in the hash sum. The finalisation function is often built by using the compression function. (Note that in some documents instead the act of length padding is called "finalisation".)

The wide-pipe section also says: "Therefore, in final step a second compression function compresses the last internal hash value to the final hash value." I disagree with the wording "a second compression function" since usually it is the same compression function that is used to do the finalisation, and then simply parts of its output is discarded to get the shorter output. The reason that the same compression function is used is that otherwise the hash function would use about twice the amount of code.
And a minor note: The "Fast wide pipe construction" section mentions that "Widepipe hash function can be made approximately twice faster". However, if the same one-way compression function is used that method only makes the hashing 50% faster. And it makes the hashing less secure than using full wide-pipe.

--David Göthberg (talk) 07:24, 24 July 2011 (UTC)[reply]

Confusing aspects of the diagram, and suggested improvements

Though having a basic familiarity with hash functions, I went to Wikipedia to brush up on the Merkle-Damgard construction. Two aspects of the current diagram

(which also appears in the article on cryptographic hash functions) at first confused me. The n'th message block is depicted as the same length as all the others, when in fact it is usually shorter; and the two upper rows, with arrows going e.g. from block 1 to block 1 below, made me think some processing of contents was happening, rather than a no-op. Though lacking the nice colors, the former diagram

is free of the first of these confusing features, and in addition nicely indicates the compression of the data by using trapezoids to represent the compression function. The present figure is visually nicer, and available in different resolutions, so the best thing would be to redraw it to 1) eliminate the top row, 2) represent message block n by a visibly shorter rectangle, and 3) use trapezoids to indicate compression. I would try to draw this myself, but lack the necessary skills. If someone undertakes revision of the drawing to incorporate some or all of these suggestions, here's another thing to consider. The construction of the padding is a rather subtle matter, depending on the length of the whole message, not just the last block. The fact that the padding depends on all the preceding blocks might be indicated graphically, e.g. by a large horizontally oriented brace symbol "}" at the top, spanning all n original message blocks, with a arrow labeled "MD-compliant padding" extending from the brace to the padding that extends the last block to the same length as the others. But this may be more trouble than it's worth, because the text example explains it so well, and my suggested drawing would not capture cases where the original last block is only slightly too short, causing the padding to overflow into an n+1'st block.CharlesHBennett (talk) 14:43, 15 September 2015 (UTC)[reply]

two years passed, nothing happened. i support that change, i find the image incorrect too. but i suggest further tweaks, because it *is* possible that you need one more block. it could be marked as optional on the picture. Krisztián Pintér (talk) 21:31, 3 August 2017 (UTC)[reply]

Apparent Contradiction

Not long ago there was a flurry of methods for producing collisions in MD5 (and others), a once popular hash function that uses the MD construction. These were perfected to the point that a modest laptop took only some minutes to find instances of colliding messages, and led to the mandatory deprecation of MD5 for, basically, all new applications. Now, IIRC, these methods all worked by finding 2 pairs of consecutive message blocks (say, A:B and A':B') such that any differences between the intermediate hash values after blocks A and A' were nullified after blocks B and B', respectively. That is, roughly, one had H(A:B)==H(A':B') even though H(A)!=H(A'), meaning, this method found collisions in the full hash function without giving any hint of an instance of a collision for the compression function. Doesn't this conflict with what is claimed in Merkle's thesis, namely, that a secure compression function plus the MD construction generates a secure hash? As far as i see it, the only way to reconcile these 2 facts is to admit that MD5's compression function has thus been proven to be insecure, even though nobody knows of a single instance of compression-function collision, nor any way to obtain it that is better than the birthday attack (which must work against all functions). Or am i misunderstanding something here? — Preceding unsigned comment added by 89.180.144.158 (talk) 21:02, 1 February 2017 (UTC)[reply]

(Same girl as above, despite different IP.) Well, after having had a chance to go through the wonderful (but in dire need of extensive copy-editing) lecture notes by Goldwasser&Bellare, referenced in this article, i've realised that the source of the contradiction was my misunderstanding that the final XOR operation after every application of the compression function is part of the compression function. Probably influenced from wherever i first learned about the structure of MD5 and similar hashes, i was under the impression that 'compression function' referred only to the (actually reversible, at least in MD5's case) function that computes, from the current hash value and message block, the 'XOR-difference', if you will, to be applied to the current hash value to generate the next one. I thought that this final XOR was part of, and actually mandated by, the Merkle-Damgard construction. So: Nevermind. — Preceding unsigned comment added by 81.193.5.173 (talk) 13:17, 13 February 2017 (UTC)[reply]

Nostradamus

After reading the CWI site referenced in the paragraph about the Nostradamus, or 'herding' attack, i decided to change said paragraph because the previous version (which alluded to 'committing to an output h') might mislead the reader into thinking that significant progress had been made in finding preimages for MD5, as 'output' usually refers to the final result of the hash calculation. I believe the altered version to be both significantly more descriptive and more correct. — Preceding unsigned comment added by 89.180.151.104 (talk) 21:53, 1 February 2017 (UTC)[reply]

Broken source

The first source has a broken link 46.114.111.156 (talk) 07:49, 23 February 2022 (UTC)[reply]