Talk:Magnus effect
| This article is rated C-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||||||||||||
| |||||||||||||||||||||
|
This page has archives. Sections older than 90 days may be automatically archived by ClueBot III when more than 4 sections are present. | |
The missing surface
[edit]Nowhere in the article as it stands does the article discuss why the surface of the object (such as a rotating cylinder) interacts with the fluid in the first place. It surely not because a rotating cylinder has non constant displacement or any macroscopic wing.
Is it because of atomic structure that the surface of the cylinder is not finally cylindrical after all? If you polish like hell, does this effect diminish or disappear? What about in a superfluid, does this effect exist there? After polishing like hell?
If the magnitude of the "shoveling effect" isn't due to surface deformity, is it due to electrostatic considerations?
Well, no-one will walk away informed on this matter from this article, as things now stand. — MaxEnt 00:15, 23 September 2022 (UTC)
- I will attempt to satisfy your curiosity here on the Talk page, and then I will investigate what I can insert into the article to fill the gaps.
- When two solid objects are in contact and moving relative to one another, the motion is called slipping. The velocity of each object is the same for all particles in the object, including at the interface. For a fluid moving relative to a solid surface, the opposite is true - the particles of fluid in contact with the solid surface do not move relative to that surface; they do not slip past the solid surface and this is called the no-slip condition. The layer of fluid close to the solid surface but not actually in contact with it, moves slowly relative to the solid surface but not at a speed equal to the speed of the free stream. This is due to viscosity and it leads to the presence of a boundary layer between the solid surface and the free stream.
- Where a sphere or cylinder has a circular cross-section, and that sphere or cylinder is spinning in air or water, a boundary layer forms like a skin around the sphere or cylinder. The air or water is stationary, but close to the surface the boundary layer is also spinning, dragged around by the spinning surface. Gradually the boundary layer thickens and a more substantial body of fluid is circulating around the sphere or cylinder. Formation of this body of circulating fluid can be promoted by having a roughened surface such as the dimpled exterior of a golf ball or the furry skin on a tennis ball.
- When this spinning sphere or cylinder is moving through a stationary fluid or immersed in a flowing fluid, the sphere or cylinder experiences a force perpendicular to the vector representing the relative velocity between the free stream and the sphere or cylinder, and this force is called lift. This phenomenon is called the Magnus effect.
- The streamlines are skewed by the circulating boundary layer. The result is that the streamlines are closer together on one side of the sphere or cylinder than on the other. Reduced streamline spacing is associated with reduced pressure, and increased spacing is associated with increased pressure, and this is one plausible explanation of the origin of the Magnus effect. Other equally plausible explanations also exist. Dolphin (t) 07:36, 23 September 2022 (UTC)
Newton's 3rd law does not explain the Magnus effect
[edit]The section Magnus effect#Physics begins with the sentence An intuitive understanding of the phenomenon comes from Newton's third law, that the deflective force on the body is a reaction to the deflection that the body imposes on the air-flow.
The paragraph, including this sentence, is unsourced. I will insert the "Citation needed" tag.
It is technically unsound to offer Newton’s 3rd Law of Motion as an explanation for the existence of a force. All forces occur in pairs, and all pairs of forces demonstrate the truth of Newton’s 3rd law. Some forces are gravitational in origin, some are magnetic, some are hydraulic etc.; it is unsound to suggest that some forces have Newton’s 3rd law as the explanation of their origin.
In some force pairs (but not all) it is clear that one of the forces is the action and the other is the reaction. One form of Newton’s 3rd law states that the action force and the reaction are equal in magnitude but opposite in direction. In this situation it is reasonable to explain the magnitude and direction of the reaction in terms of Newton’s 3rd law but it is unsound to attempt to also explain the origin of the action force as being caused by Newton’s 3rd; this leads to the circular argument that the force exerted on B by A is caused by Newton’s 3rd, and the force exerted on A by B is also caused by Newton’s 3rd!
The Magnus effect consists of two observations – on the spinning body there is a force perpendicular to the direction of the oncoming fluid flow, and on the fluid there is a force causing it to be deflected in a direction opposite to the force on the spinning body. These two observations invite two questions – what causes the force on the spinning body; and what causes the oncoming fluid to be deflected? It would be unsound to suggest that the answer to both these questions is “Newton’s 3rd law”. The paragraph under discussion suggests that one of these forces can be explained by Newton’s 3rd law but offers nothing to explain the other force. The Magnus effect may be an illustration of Newton’s 3rd law, but Newton’s 3rd law is not an explanation of Magnus.
Newton’s laws of motion are applicable to point particles, and rigid bodies that can be represented as point particles. These laws of motion are not ideally applied to the motion of fluids. When a flow of fluid experiences a continuous acceleration, either change in direction or change in speed, it is usually quantified using the momentum equation which is based on Newton’s 2nd law and the law of conservation of momentum. In the case of the Magnus effect, the momentum equation can be used to calculate the magnitude of the force necessary to deflect the oncoming fluid flow through the observed angular deflection, but it does not explain why the fluid flow is deflected. Consequently it would be equally unsound to suggest that the Magnus effect is caused by, or has its origins in, Newton’s 2nd law or the momentum equation.
The Magnus effect in air is a manifestation of the viscosity of the air. In an inviscid flow there would be no Magnus effect. Any suggestion of the origin of Magnus is unsound if it does not take viscosity into account. Suggestions based on Newton’s laws of motion, if used alone, imply inviscid flow and do not acknowledge the role of viscosity; such suggestions are therefore unsound.
If there is no suitable response after a period of time I will erase the paragraph. Dolphin (t) 13:18, 11 September 2024 (UTC)
- Like nearly everything else surrounding aerodynamic phenomena, there are multiple ways to explain them, some more detailed or precise than others. The simple, intuitive approach of air is deflected in one direction and consequently the object experiences a reaction force and is accelerated in the opposite direction is fine for an intuitive explanation of many aerodynamic phenomena, including this one. This explanation is certainly incomplete, and in most cases another analytical approach provides a better path to making quantitative predictions. And as you point out, it begs the question of what causes the air to be deflected which is one of its omissions; but for an intuitive simple explanation, because the ball is spinning is probably enough for most people.
- I've added a cite to [[1]] which includes this quote from Isaac Newton himself where he describes it as a reaction force:
- Isaac Newton is said to have been the first to explain the motion of a tennis ball in relation to its spin. In his letter to Oldenburg in 1671, writing about the dispersion of light, he explained “I remembered that I had often seen a tennis ball struck with an oblique racket describe such a curved line. For a circular as well as progressive motion being communicated to it by that stroke, its parts on that side where the motions conspire must press and beat the contiguous air more violently, and there excite a reluctancy and reaction of the air proportionately greater”
- I think this paragraph under discussion is sufficiently sourced, and that the article would not be improved by removing it. Mr. Swordfish (talk) 17:35, 11 September 2024 (UTC)
- I agree that these cases have multiple explanations and different ones may suit different purposes.
- I disagree that the quotation of Newton in the ref implies that Newton's Third law makes the Magnus effect intuitive. First, the effect is obviously not intuitive: much ink has been devoted to explain it. Second, the quote only says that the rotation adds a force. Third, the action/reaction law does not explain where the force comes from, its direction, or magnitude. To me these are the ingredients in an explanation. The ref is excellent and I think we can use it more effectively. Johnjbarton (talk) 16:41, 14 September 2024 (UTC)
- The fact that "much ink has been devoted to explain it" is orthogonal to the whether there is a simple, intuitive explanation. For example, Russell and Whitehead's Principia Mathematica goes on at quite some length before proving that 1+1=2, which they do on page 379. Does this make 1+1=2 something that can't be explained simply and intuitively?
- Agree that the quote from Newton does not necessarily establish that his 3rd law makes the Magnus effect intuitive, so perhaps we can leave that claim out of the article unless we find a source that supports it.
- I have more to say below about using Newton's 3rd and the concept of reaction force to explain the Magnus effect. Mr. Swordfish (talk) 18:43, 16 September 2024 (UTC)
- Here is a draft paragraph to replace the current one. If this is sorta ok I can put it in and let others improve it.
- The Magnus effect or Magnus force acts on a rotating body moving relative to a fluid. Examples include a "curve ball" in baseball or a tennis ball hit obliquely. The rotation alters the boundary layer between the object and the fluid. The force is perpendicular to the relative direction of motion and oriented towards the direction of rotation, for example the direction the "nose" of the ball will point. The magnitude of the force depends primarily on the rotation rate, the relative velocity, and the geometry of the body; the magnitude also depends upon the body's surface roughness and viscosity of the fluid. Accurate predictions of the force are difficult.(ref Seifert here): 20
- Johnjbarton (talk) 23:30, 14 September 2024 (UTC)
- Thanks John. I think your draft paragraph is good. My suggestions for further improvement are:
- Try switching the sentence “The rotation alters the boundary layer ...” with the sentence “The force is perpendicular to the relative ... “.
- Around a uniform, non-spinning cylinder or sphere the boundary layers adjacent to the upper and lower surfaces are symmetric so the upper and lower flow patterns are also symmetric and pressures and velocities are identical. The consequence of altering both boundary layers (plural) is that they become asymmetric. Flow patterns, pressures and velocities change too.
- Dolphin (t) 05:50, 15 September 2024 (UTC)
- I put my version in, please try your changes. Johnjbarton (talk) 15:33, 15 September 2024 (UTC)
- Thanks John. I think your draft paragraph is good. My suggestions for further improvement are:
We do the readers a disservice by not mentioning the simple, easy to understand explanation based on Newton's 3rd law. Take a look at this diagram that is included in the article:

It is obvious from the picture that air is being deflected downward; anyone who paid the slightest bit of attention on the first day of PHYSICS 101 would be able to see that there must be a reaction force opposite in direction from the air's deflection. This is the Magnus effect. Presented in a way that anyone can understand.
Granted, this is dependent on the diagram being correct, and it doesn't explain why the air flows the way that it does - more sophisticated analysis is needed for that, and I think the article does a good job of addressing that. Note that the second sentence of the first section is:
- The wake and trailing air-flow have been deflected downwards.
It is a simple matter to modify it to say:
- The wake and trailing air-flow have been deflected downwards; according to Newton's third law of motion there must be a reaction force in the opposite direction.[1]
For the reference, I've added my undergraduate Physics text, Halliday and Resnick 3rd ed. with the following quote:
- The result is that the wake is not symmetrical; the airflow is deflected to one side, and the sphere experiences a reaction force in the opposite direction (Fig. 4). The direction and strength of this force will depend on the rate and direction of spin. This phenomenon is known as the Magnus effect...
This should be sufficient to establish the use of Newton's 3rd as an explanation of the Magnus effect. We can leave out the part about how it's a simple or intuitive approach to the problem. — Preceding unsigned comment added by Mr swordfish (talk • contribs) 22:37, 16 September 2024 (UTC)
- Newton's laws of motion says
- If two bodies exert forces on each other, these forces have the same magnitude but opposite directions.
- In the case of the Magnus for, what is the second body? The air? The boundary layer? The turbulent wake? What causes the second body to exert such a force? I don't see how this law adds anything beyond "sphere experiences a reaction force" Johnjbarton (talk) 23:12, 16 September 2024 (UTC)
- Mr Swordfish has written
Granted, this is dependent on the diagram being correct …
The diagram is amateurishand was soundly criticised back in July 2012.A replacement diagram was offered at that time but, perhaps unfortunately, we didn’t incorporate it into the article. See Talk:Magnus effect/Archive 1#Figure. 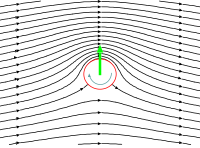
- This new diagram is a classic in aerodynamics and can be seen in other sites on the internet – for example, the one by Prof Richard Fitzpatrick of the University of Texas shown at the following website:
- We are all inclined to write “the air is deflected downwards”. This is one of the inaccuracies often seen in explanations of aerodynamic lift, including the Magnus force. If the air were deflected downwards the atmosphere between the lifting body and the Earth’s surface would become compressed, and that above the body would become rarified. That doesn’t happen and this new diagram shows why in the case of a spinning cylinder. As each parcel of air approaches the cylinder from the left it is deflected anti-clockwise (or upwards) through an angle of θ/2. As it passes the cylinder it is deflected clockwise (or downwards) through an angle of θ; and as it departs from the cylinder it is again deflected anti-clockwise (or upwards) through an angle of θ/2. The combined effect of these three regions is that there is no net deflection. In the remote stream each parcel of air approaches the cylinder moving horizontally at height h1 above the Earth’s surface, and departs from the cylinder still moving horizontally at height h1 above the Earth’s surface. There has been a strong clockwise rotation in the immediate vicinity of the cylinder but there has been no net deflection of the air towards the Earth's surface or away from it. The Kutta-Joukowski theorem shows that the Magnus force is not associated with an upwards or downwards linear deflection of the flow, but with the circulation in the flow pattern around the spinning cylinder.
- The streamlines shown in this new diagram are based on potential flow, including the influence of a clockwise circulation added to simulate the consequence of the net clockwise vorticity that is the legacy of the asymmetric boundary layers above and below the cylinder when it is spinning in a viscous fluid. These streamlines show the primary flow around a spinning cylinder. The Magnus force is evident in this primary flow. Notice the axis of symmetry - a vertical line through the center of the spinning cylinder. The existence of this symmetry shows that the Magnus force is a lifting force and there is no drag in evidence; also it shows that there is no net deflection upwards or downwards.
- Photographs and some of the diagrams depicting the Magnus force show distinctly unsteady flow, and a conspicuous deflection of the wake due to the finite span of the cylinder or sphere. This conspicuous deflection downstream of the cylinder is most likely associated with trailing vortices and is associated with lift-induced drag rather than the Magnus lifting force. These are all secondary effects and are not necessary for the Magnus force to exist. Dolphin (t) 01:33, 17 September 2024 (UTC)
- The reference seems to be concerned with fluid flow around a cylinder without the rotation? Johnjbarton (talk) 02:23, 17 September 2024 (UTC)
- Which reference? We have identified several - Newton in 1671, Resnick & Halliday, Prof Richard Fitzpatrick. Dolphin (t) 02:50, 17 September 2024 (UTC)
- Prof. Fitzpatrick Johnjbarton (talk) 18:49, 18 September 2024 (UTC)
- Which reference? We have identified several - Newton in 1671, Resnick & Halliday, Prof Richard Fitzpatrick. Dolphin (t) 02:50, 17 September 2024 (UTC)
- @Dolphin51 Where to start here...
- 1) The diagram currently in the article was not "roundly criticized" in July 2012, since it did not get uploaded to Wikimedia until 16 February 2014.
- 2) The comment at Talk:Magnus effect/Archive 1#Figure was about a previous diagram, which can be viewed here [2]
- 3) With only one comment and no replies, it's quite a stretch to say that anything was "roundly criticized".
- Let's try to keep things factual.
- Moving on to the gist of your argument, it is based on two-dimensional potential flow, as is the diagram at Flow Past a Cylindrical Obstacle. 2D potential flow is a model that when paired with the Kutta–Joukowski theorem gives surprisingly accurate estimates of lift given all the simplifying assumptions made to reduce the math to solving Laplace's equation. But it's just a model, and not a terribly accurate one: 2-D potential flow has been said be so unphysical that the only fluid to obey the assumptions is "dry water".
- The largest practical problem with 2-D potential flow is that it does not predict stall; this is also a failing of any inviscid model such as the more detailed Euler equations. Now, if you were to go over the the article on stall and claim that you have proved that stall is impossible since the 2-D potential flow model predicts no such thing I don't think it would be received very favorably.
- Similarly, one of the failings of 2-D potential flow is that it does not predict that the flow is deflected. That's an issue with the model, and using it to argue that there is no deflection of the air does not logically follow.
- Earlier, you say:
- The Magnus effect in air is a manifestation of the viscosity of the air. In an inviscid flow there would be no Magnus effect. Any suggestion of the origin of Magnus is unsound if it does not take viscosity into account.
- and then go on to use a model that assumes inviscid flow to make your argument. This is also hard to follow logically.
- Bottom line here is that the law of conservation of momentum says that if an object is deflected by the Magnus force, then there must be some other mass that is deflected in the opposite direction. When you say "That doesn’t happen..." you are describing a violation of conservation of momentum. I understand that "air goes one way, object is deflected in the opposite direction" is not a satisfying explanation for everyone. That does not mean it is false, or that it does not help some readers understand the physics. OTOH, leaving it out does a disservice to the readers. Mr. Swordfish (talk) 13:30, 17 September 2024 (UTC)
- Mr Swordfish: I agree with your explanation that the current diagram was not soundly criticized. That was my error and I have struck out the erroneous words.
- When I wrote the words
That doesn’t happen ...
I was referring to the fact that the passing of a lifting body does not cause an increase in pressure below the body and a rarefaction of the air above the body. The passing of a lifting body does not alter the density profile of the atmosphere. If the air is “deflected downwards” without being deflected upwards somewhere nearby, the density profile, and hence also the pressure profile, must be altered. Doug McLean makes this point somewhere in “Understanding Aerodynamics”; I hope to provide a quotation of his words in coming days. - One of the elegant features of the horseshoe vortex is that it allows us to see that everywhere there is some upwash, there is an equivalent amount of downwash nearby, so we can see that the vortex system of a 3-D lifting body does not make a net relocation of air from above the altitude of the lifting body to below it; nor does it alter the density profile of any column of air through which the body passes. The same is true of 2-D flow around a lifting body of infinite span. The same cannot be said of “the air is deflected downwards.” If the response is “but the air is deflected upwards somewhere else to balance things out”, what and where is the downwards force “predicted by Newton’s 3rd law”?
- I’m not opposed to mentioning Newton’s laws of motion as part of a simple, easy way of explaining Magnus to a lay audience. We do this over at Lift (force) where such explanations have their own section with its own title. My objection is to presenting Newton’s 3rd law as the substance of the first paragraph in the section titled “Physics”. I think we are moving in a suitable direction. Dolphin (t) 14:16, 17 September 2024 (UTC)
- I am not opposed to reorganizing the order of presentation of the various explanations; the preferred ordering of material on Wikipedia is to go from simple to complex, so presenting the simpler versions earlier would be consistent with the preferred style.
- Currently, we state in the third sentence of the lead:
- The deflection can be explained by the difference in pressure of the fluid on opposite sides of the spinning object.
- But we never get around to clearly providing that explanation; I think this is a shortcoming of the article's current state.
- My take is that there are three simple ways to explain the Magnus effect.
- 1) Newton's 3rd law:
- The wake and trailing air-flow have been deflected downwards; according to Newton's third law of motion there must be a reaction force in the opposite direction.
- That's what's there now; I don't know that we need to go into further detail.
- 2) Bernoulli's Principle:
- Due to the rotation, the air on one side of the sphere or cylinder is moving faster than the air on the other side; by BP there must be lower pressure on that side, hence a net force. (note that for a spinning object there's a good, correct, intuitive reason why the air is faster on one side than the other - attempts to start with speed differences around a wing are typically either false (e.g. Equal transit time fallacy) or useless tautologies (e.g. "the wing is designed to make the air go faster on the top")
- 3) The Streamline curvature theorem:
- Again, the air is faster on one side than the other due to the rotation. Higher velocities imply larger pressure gradients so there is a pressure imbalance due to the difference in speed. Unfortunately, I'm unaware of any reliable source that explains it this way, so we probably have to leave this one out.
- Perhaps there are others, depending on the value of "simple". Currently, the article does not go into the mathematical details of the physics along the same lines as the Lift(force) article does. I'm ok with that, and since I don't think we need more than a sentence or two to treat item's 1) and 2) above creating separate one-sentence sections or sub-sections would seem superfluous. As for how much detail to provide re more sophisticated mathematical analyses, my take is to keep that short too and link to the relevant articles that further explain.
- I would suggest that the physics material be removed from the lede and the Description sections and moved to the Physics section. That section would begin with a brief one or two sentence to address items 1) and 2), followed by a brief synopsis of the more detailed treatments. The Description section would then need to be rewritten to include a brief description of the phenomena since there wouldn't be much left after moving the physics material. Mr. Swordfish (talk) 15:59, 17 September 2024 (UTC)
- In one of my recent edits I promised a quotation from Doug McLean’s ‘’Understanding Aerodynamics’’ to support my comments that a lifting body does not change the density profile of the atmosphere in which it is generating lift; so every region of downwash is accompanied by an equivalent region of upwash nearby.
- In 7.3.1.12 Lanchester’s Explanation McLean writes
Because there can be “no permanent change of density or accumulation of matter in the lower strata of the atmosphere,” the downward current above and below the plate must be accompanied by upward currents around the edges of the plate, driven by the difference in pressure.
The quotation marks show where McLean is directly quoting Lanchester. - Later In 7.3.1.12 McLean writes
Lanchester concludes that the vertical velocity of the air particles far ahead of and far behind the airfoil is zero, by the same argument as before, that a nonzero velocity would result in an accumulation of matter.
- In 7.3.1.12 Lanchester’s Explanation McLean writes
- Dolphin (t) 02:28, 18 September 2024 (UTC)
- This is a short postscript to my earlier post. The notion that upwash and downwash must be equivalent is totally related to mass continuity and mass flow rates. It doesn’t impose any constraint on momentum flux, and the momentum in upwash and downwash May be very different! In the case of a hovering helicopter the momentum flux in the downwash greatly exceeds that in the upwash outside the rotor disk with the result that the helicopter can support its own weight using aerodynamic lift. Dolphin (t) 06:43, 18 September 2024 (UTC)
- "the air on one side of the sphere or cylinder is moving faster than the air on the other side;"
- Sorry, I do not understand this claim or why it is relevant. Air does not just magically get faster because the object is rotating. There must be an interaction.
- The references clearly show that the Magnus effect depends on surface roughness. In fact smooth surface show inverse effect. Thus any proposed cause must include the rotating object surface.
- This is a complex effect. It's okay to say that and discuss the issues as raised in the references. It's no okay to assert it is simple. That seems like misinformation to me. Johnjbarton (talk) 04:30, 18 September 2024 (UTC)
- Yep. We should include the dependence on surface roughness.
- And we don't need to claim anything is "simple"; if we include an explanation that is easily understood that's sufficient.
- My copy of Halliday and Resnick contains non-quantative expositions using both 1) and 2) above. I'll take a stab at paraphrasing them and post a draft. Mr. Swordfish (talk) 13:50, 18 September 2024 (UTC)
- I think the quote you put in from Halliday and Resnick:
- The result is that the wake is not symmetrical; the airflow is deflected to one side, and the sphere experiences a reaction force in the opposite direction.
- should just be in the text. Johnjbarton (talk) 18:48, 18 September 2024 (UTC)
- Well, we can't just use the wording; we either need to paraphrase it or put quotation marks around it with an attribution. See WP:PLAG. I think the latter is distracting to the reader, so I'd prefer the paraphrase approach. Mr. Swordfish (talk) 22:15, 18 September 2024 (UTC)
- I think the quote you put in from Halliday and Resnick:
- Johnjbarton Yes, there is an interaction. The conventional wisdom is that when a cylinder (or ball) is stationary relative to the surrounding air but is made to spin, the air's viscosity leads to a boundary layer and that layer exerts a shear force on the cylinder, acting in the direction to try and slow the cylinder's angular velocity. The boundary layer also exerts a shear force on the surrounding air, acting in the direction to try give the surrounding air an angular velocity. The surrounding air does not achieve anywhere near the angular velocity of the cylinder but it does acquire an angular velocity which immediately establishes itself as a free vortex. (In a free vortex, the speed at all points a distance r from the center of the vortex is directly proportional to the inverse of r. Close to the center of the vortex the speed is higher than at a greater distance from the center; think of the velocity profile in a hurricane (tornado, cyclone etc.))
- When a cylinder is set spinning, it creates about itself a free vortex. In such a vortex the streamlines are concentric circles.
- When a spinning cylinder is immersed in an otherwise uniform flow, the flow pattern can be obtained by the principle of superposition - the parallel streamlines of the uniform flow are added to the concentric circles of the free vortex surrounding the spinning cylinder. See the diagram which I inserted above on 17 September (time 01:33). The streamlines are closer together on one side of the cylinder than on the other. Where the streamlines are closer together, the speed is faster and the static pressure is lower. Where the streamlines are further apart, the speed is slower and the static pressure is higher. The pressure imbalance manifests as a lift force (perpendicular to the direction of the oncoming flow) and is called the Magnus force. This is the primary flow pattern.
- The secondary flow pattern includes such flow features as unsteady flow; transition; and separation. These secondary features modify the precise magnitude of the Magnus force, either to make it stronger or weaker, but they don't eliminate the Magnus force evident in the primary flow pattern. Dolphin (t) 13:52, 18 September 2024 (UTC)
- The first part of this description, the creation of a transition region (boundary layer) between a stationary rotating object and the more distant air, makes sense to me. The rotation of the object causes the rotation of this boundary layer, which tails off as we move away from the object. So now we have the air velocity changed by a force, the force caused by the object rotation interacting with the boundary layer. (Newton's third law tells us that the object experiences a back force that works against the angular momentum of an unpowered object per Newton's 2nd law.)
- The second part is less clear. It requires understanding meaning of "streamlines" and "potential lines". I also assume that a non-rotating object in a flow will also have a boundary layer complicating the story. Johnjbarton (talk) 18:45, 18 September 2024 (UTC)
- Streamlines are easy and intuitive in steady flow. See Streamlines, streaklines, and pathlines. (In an unsteady flow the analogue of the streamline is the streakline and the pathline. It is easiest to ignore unsteady flow.) Potential lines are more challenging! I barely begin to comprehend them in fluid flow so I ignore them!
- In the case of a non-spinning cylinder, and a symmetric body aligned with an otherwise uniform stream, the boundary layers adjacent to the upper and lower surfaces are symmetric (identical?). The two boundary layers each have an influence on the flow pattern but those influences are symmetric so the flow pattern remains symmetric and circulation around the body is zero. Pressures are symmetric on either side of the body so there is no lift force.
- When the body is a spinning cylinder, or a symmetric body with a sharp trailing edge and the body is no longer aligned with the flow, the two boundary layers are no longer symmetric, pressures are no longer symmetric, a circulation is evident in the flow around the body, and a lifting force (perpendicular to the relative velocity vector) acts on the body. The Kutta-Joukowski theorem tells us that the lifting force per unit of span of the body is directly proportional to the circulation (which is the measure of the strength of the free vortex embedded in the flow surrounding the body.) Dolphin (t) 21:59, 18 September 2024 (UTC)
- I have begun a draft of a new section titled "Magnus effect in potential flow". It concludes with a comment about Newton's 3rd law. See User:Dolphin51/Sandbox2. Any comments will be most welcome. Dolphin (t) 12:23, 19 September 2024 (UTC)
- Wikipedia already has an article on Potential_flow_around_a_circular_cylinder, so I don't know that we need to reiterate that here.
- That said, your exposition is simpler and clearer to a layperson, so this might be a good addition to the article - this article is a bit light on the physics at this point, so a short section like you have drafted would be an improvement.
- A few comments
- I'd add a brief sentence explaining what potential flow is, along with a link to potential flow. I don't think we can assume the reader is familiar with potential flow.
- A flaw in most streamtubes-based explanations is that they don't adequately explain why the streamtubes change size. Here, the streamtube pinching is the result of a mathematical model, so there's a reason, although not an easily understood or intuitive one.
- We should still cover items 1) and 2 above somewhere in the article.
- Mr. Swordfish (talk) 14:06, 19 September 2024 (UTC)
- The basic problem with the draft is the references which don't support the text. Johnjbarton (talk) 03:16, 20 September 2024 (UTC)
- Are you talking about the draft in my sandbox, or the draft of the new section as proposed by Dolphin?
- Regardless, do you have specific examples? I'm fairly certain I can provide cites to support anything that I've added. I can't speak for the majority of the article that I left intact. Dolphin's draft looks correct, but there may be some assertions that are not currently supported by citations; I'm fairly certain those can be addressed too. But we'd need specific examples. Mr. Swordfish (talk) 13:17, 20 September 2024 (UTC)
- I have begun a draft of a new section titled "Magnus effect in potential flow". It concludes with a comment about Newton's 3rd law. See User:Dolphin51/Sandbox2. Any comments will be most welcome. Dolphin (t) 12:23, 19 September 2024 (UTC)
- In one of my recent edits I promised a quotation from Doug McLean’s ‘’Understanding Aerodynamics’’ to support my comments that a lifting body does not change the density profile of the atmosphere in which it is generating lift; so every region of downwash is accompanied by an equivalent region of upwash nearby.
- The reference seems to be concerned with fluid flow around a cylinder without the rotation? Johnjbarton (talk) 02:23, 17 September 2024 (UTC)
- Mr Swordfish has written
I've created a draft in my sandbox incorporating the new section on potential flow around a cylinder and addressing the suggestions above. Take a look at User:Mr_swordfish/sandbox.
I started with the article as-is, added the new section as-is, and made incremental edits that can be reviewed in the edit history. Major changes include:
- additon of potential flow around a cylinder section (with a few minor additions o Dolphin's work
- moving most of the lede to the description section
- removing physics material from the lede and Description sections and adding it to the Physics section
- added subsections on flow deflection and pressure differences
- broke out remaining Physics material into two new subsections, wake turbulence and Kutta–Joukowski lift
- adding a bit of text to one of the diagrams so that it covers pressure differences in addition to flow deflection.
Mr. Swordfish (talk) 16:34, 19 September 2024 (UTC)
- Per discussion at my user talk page re this draft, making the changes live. Mr. Swordfish (talk) 14:30, 22 September 2024 (UTC)
References
- ^ Halliday, David (1988). Fundamentals of Physics (3rd Extended ed.). John Wiley and Sons. pp. E6 – E8.
The result is that the wake is not symmetrical; the airflow is deflected to one side, and the sphere experiences a reaction force in the opposite direction (Fig. 4). The direction and strength of this force will depend on the rate and direction of spin. This phenomenon is known as the Magnus effect...
Pressure gradient force
[edit]The section "Pressure gradient force" is an odd interjection in the article. The first part describes "Pressure gradient force" which AFIACT is just "pressure gradient". The second part gives the somewhat trivial observation that a pressure gradient creates a force proportional to the area of an object. The reference is to a German language textbook. I propose to delete this section despite the reference (which is not useful IMO).
There are alternative explanations of the Magnus effect expressed in terms of pressure gradients but ultimately the cause of the gradient has to be some interaction between the object and the fluid. Without the interaction there is no gradient. Johnjbarton (talk) 16:07, 15 September 2024 (UTC)
- The phrase "pressure gradient force" is technical jargon that is probably best avoided. Pressure gradients lead to pressure differences, and pressure differences lead to forces, but there are better ways to say it.
- I'm not finding that phrase in the current article; I don't quite know where it went, but I don't miss it. Mr. Swordfish (talk) 19:11, 25 September 2024 (UTC)
- I previously deleted that section.
 Done Johnjbarton (talk) 19:19, 25 September 2024 (UTC)
Done Johnjbarton (talk) 19:19, 25 September 2024 (UTC)
- I previously deleted that section.
Wake turbulence section
[edit]There are no citations in the section. Granted, we just added this section heading, but the material there is basically unchanged from before the recent spate of edits. We should either find some references or remove the section. Mr. Swordfish (talk) 14:57, 24 September 2024 (UTC)
- Well spotted! The material in this sub-section is not specific to the Magnus effect (except possibly the last sentence.) Mostly it could have been copied from Wake (physics).
- The Magnus effect is evident in the primary flow around a spinning cylinder, as shown in the diagram of potential flow. In potential flow there is no wake, which tells us that a wake is not a pre-requisite for the Magnus force to exist. The Magnus force occurs in spite of a wake, not because of it.
- I recommend removing the entire sub-section. Dolphin (t) 22:50, 24 September 2024 (UTC)
- Sounds reasonable. We can always restore it if there's consensus and someone produces some cites.
- Done. Mr. Swordfish (talk) 14:14, 25 September 2024 (UTC)



