Talk:High-performance sailing/Archive 6

Archive 1

←

Archive 4

Archive 5

Archive 6

Propeller vs. rotor

The High-performance sailing#Directly down wind faster than the wind (DDWFTTW) vehicle section uses the word, "propeller", frequently, as if the propeller were driving the vehicle in the conventional sense with aircraft and ships. Instead, the rotor is acting more like a wind turbine, directing wind energy to power the vehicle's wheels (instead of an electric generator). I feel that this term is misleading and would recommend "rotor", instead. Wind-powered vehicle uses "wind turbine". User:HopsonRoad 16:29, 23 January 2017 (UTC)

Actually it's the opposite. In the case of sailing downwind faster than the wind, the wheels are driving the propeller. The propeller provides thrust to enable the wheels to continue driving it. It almost sounds like perpetual motion, but it isn't; the whole thing needs the energy of the wind to keep moving. ~Anachronist (talk) 16:36, 23 January 2017 (UTC)

I realize that this has been the subject considerable archived discussion, Anachronist, but take the directly-into-the-wind case. Then it's clearly not the wheels driving the propeller. As one comes around to any point of "sail", it's still the effect of the apparent wind on the airfoil, which must be driving it, not the other way around. There is no magic moment when that flips to the wheels driving the "propellor" at a speed faster than the wind, noting that the apparent wind is still forward.

Remember, "wind-powered" means that the device is capturing kinetic energy from the air at a rate sufficient to overcome resistance to forward motion. The only element outside the device with kinetic energy is the air. The ground doesn't have kinetic energy.

If you consider a free-wheeling propeller on a moving platform, it rotates in one direction, when the apparent wind is from behind; it rotates in the opposite direction, when the apparent wind is in front; when the speed of the craft cancels the true wind and the apparent wind is zero, the propeller stops spinning. To this, we must now add deriving power from the propeller. Apparently, if the device is going faster than the true wind, downwind, it's still possible to obtain kinetic energy from the air.

Sadak Ali Khan, et al. report that "The propeller is connected to the wheels of the vehicle through a chain/belt drive, so that when the vehicle moves forward, the propeller spins in such a way to provide a thrust that will speed up the vehicle if there is energy available from a tailwind,...." They cite other papers that describe energy being obtained from a tailwind. The conclude that there is not theoretical limit to speed and recommend a variable-pitch propeller for optimum performance.

Cheers, User:HopsonRoad 17:15, 23 January 2017 (UTC)

References

Yes, in the case of heading upwind, the propeller acts as a rotor. In the case of heading downwind, the wheels drive the propeller. Even the source you cite refers to it as a propeller. The wind on the airfoil does not drive the vehicle, particularly when it starts from a standstill, the wind on the entire vehicle is what drives the vehicle forward and starts moving the propeller, which at first just acts as a stationary drag object. As it speeds up, the propeller becomes the dominant force resisting the tailwind.

There is also a flip observed in a graph of velocity over time. The vehicle experiences a fairly constant acceleration, with velocity increasing linearly as the vehicle approaches the wind speed, at which point the acceleration flips from constant to increasing, with velocity increasing exponentially until friction and drag take over to limit the terminal speed. ~Anachronist (talk) 23:32, 23 January 2017 (UTC)

Thank you for your reply, Anachronist. Perhaps you could supply a reliable reference that shows the graph that you describe. You seem now to be agreeing that the propeller supplies the motive power to the wheels downwind and not vice versa. If not, please supply a reliable reference for that.

As to propeller vs. rotor, I've seen that different sources use different terms. The paper that I cited is by a group from Hyderabad, Pakistan, whose lexicon may vary from others. I don't believe that there's one "correct" choice. I'm only trying to obtain consensus from other editors what a preferred choice would be. If, indeed, the wind drives the rotor and not vice versa, "rotor" or "turbine" would seem to be a better choice than "propeller".

In "Theory and Design of Flow Driven Vehicles Using Rotors for Energy Conversion", the authors use "rotor" to cover two types, a "turbine"—a rotor with a shroud, and a "propeller"—a rotor without a shroud.

Sincerely, User:HopsonRoad 02:21, 24 January 2017 (UTC)

I studied this in some depth when the Blackbird first made its run and saw the research reports. I tried to find the original graphs of the speed runs. Unfortunately the website for the project http://www.fasterthanthewind.org/ appears to have lost its domain name and now belongs to some Chinese group, and all the research reports are behind paywalls, so I cannot find a copy of that graph. If I find it, I'll post it.

And no, the propeller definitely doesn't supply motive power to the wheels when traveling downwind, it's just the opposite. The propeller draws power from the wheels. Sources are easy to find, such as: "The flaw in thinking about this is usually the feeling that the propeller drives the wheels and the wheels drive the vehicle. This sounds like circular reasoning, and it is. The wheels do not drive the vehicle's forward motion, but they do drive the propeller's rotation."[1] Or here: "the key to understanding going downwind faster than the wind is that the wheels are turning the propeller and that the propeller needs to only produce enough lift in still air to overcome the forces required to turn it."[2] The source you cite also agrees; the vehicle has "a propeller that pushes it along like an aircraft's propeller does." And finally, Rick Cavallaro, the man who built the Blackbird, explained: "the car is able to move faster than the wind because the propeller is not turned by the wind. The wind pushes the vehicle forward, and once moving the wheels turn the propeller."[3] Can't get much more reliable than the designer's own words. There is really no mistaking in any of the sources that "propeller" actually means exactly that. ~Anachronist (talk) 05:28, 24 January 2017 (UTC)

Found the graph! Archive.org to the rescue: http://web.archive.org/web/20120107072642/http://www.fasterthanthewind.org/2010/05/testing-graph.html - click on the graph to expand. Note the point labeled "5"; this is where the vehicle reaches wind speed. Velocity stops increasing momentarily and then takes on a very different exponential profile up to nearly 3X wind speed. ~Anachronist (talk) 05:43, 24 January 2017 (UTC)

I very much appreciate your patience on this, Anachronist. I feel that it will be rewarded by a clearer explanation in the article. Of course, I have never doubted that the vehicle goes downwind faster than the wind, I have only struggled to understand why. The DWFTTW Blogspot (unfortunately not a reliable source) makes the best case for the wheels driving the rotor with a balloon/Prius/cart analogy, which I find unconvincing for two reasons: 1) it isn't a steady-state example (the Prius is decelerating) and 2) it fails if windspeed is zero (there's no free kinetic energy available).

The real test of which drives which would be if the vehicle hit a patch of ice. Would the wheels spin forward with a surplus of power from the rotor or would the rotor falter from a lack of power from the wheels? I suggest the former, but the sources that you cite suggest the latter.

While I applaud the sources cited for changing the frame of reference to the cart, I feel that the only helpful change in frame of reference is to the rotor blade. This is where, as with a close-hauled iceboat sailing well off the wind, the rotor still experiences an apparent wind that is providing free kinetic energy. Unfortunately it would be both WP:OR and above my pay grade to explain this further.

For now, I'm content to call the rotor a propeller in the case of the DDWFTTW vehicle.

Sincerely, User:HopsonRoad 13:47, 24 January 2017 (UTC)

@HopsonRoad: I think there's still a misunderstanding. In the case of traveling downwind, the propeller does not drive the wheels. Every source you have posted, including the quote from Drela below, supports that contention. The propeller provides thrust, just like an aircraft propeller. That thrust translates into forward motion of the vehicle. Because the wheels are in non-slip contact with the ground, that forward motion turns the wheels. The gear ratio between the wheels and the propeller translates the wheel rotation into faster propeller rotation. And so on. The wheels resist the forward motion — that's the key point that seems to be missed in your comments.

In the absence of friction (such as driving over a patch of ice), the wheels, which are resisting the forward motion, would slip. If the vehicle drove over a completely frictionless surface, its speed would eventually match the wind speed, like a balloon traveling through the air (imagine the vehicle levitating off the ground while traveling at any initial speed). Non-slip interaction with the ground is required for this to work. If you propped a stationary Blackbird up on jacks so the wheels turn freely without any interaction with the ground, and let the wind blow against its back, the propeller would become a windmill rotor, turning the wheels backward. If you then set the vehicle back down on a non-slip surface, the wind forces on the propeller will still try to turn the wheels backward (which would drive the vehicle upwind), but the gear ratio combined with the wind resistance on the entire vehicle (including the propeller) forces it forward instead, forcing the wheels to turn forward, which drives the propeller against the wind. Once forward motion has begun, causing the propeller to resist the wind even more, the forward motion increases.

I find it strange that you would say below that "Cavallaro may not even understand what he succeeded in doing." He's the chief scientist at Sportvision (if you recall the cool graphics overlayed on the 2012 America's Cup in San Francisco Bay, that was them), and he has degrees in aerospace engineering as well as dynamics and controls. Considering his academic background and the fact that he built the Blackbird, he's certainly a source who understands the underlying physics and knows what he's talking about. ~Anachronist (talk) 20:16, 25 January 2017 (UTC)

@Anachronist: Thank you for your concerns about my comment on Cavallaro. I regret having said that. As to Drela, your description fits his Example 1 frame of reference. My comments correspond to his Example 2 frame of reference. He said in his communication to me that Gaunaa describes the physics well, using both frames of reference. (See 2.2 and 2.3.) The underlying issue is that there must be a contrast in speed between two media—in this case the ground and the air—for power to be transferred through the cart, as viewed from any frame of reference. Sincerely, User:HopsonRoad 03:57, 26 January 2017 (UTC)

HopsonRoad, your icepatch example was good for noting two possibilities, and for noting that the RS answer doesn't match your expectation. The RS are right. This is a weird design. It violates all normal expectations. Nothing will makes sense until you mentally demolish several obvious (but wrong) expectations in a row. If something sounds weird, let go of your initial belief and power forwards. I'll give an OR summary here. Maybe it will help us improve one or both of the articles. You're having trouble with it, which makes you the expert on what would make the article(s) clearer. Chuckle.

You mentioned the the directly-into-the-wind case. This is a dangerous starting point. Everything runs in the opposite direction. It will look very very broken until you reverse everything you think you know. The wheels and the rotor reverse roles.

The only difference between an upwind design and a downwind design is the gear ratio. The wheels and rotor want to turn in opposite directions. If the rotor is geared to win, you have a turbine driving the wheels, the cart goes upwind. If the wheels are geared to win, everything spins the opposite way, power flows the opposite way, the wheels drive the rotor as a fan, the cart goes downwind.

Upwind:

• Important note: The rotor blades drag in the wind. At high speed, this drag fights really hard trying to slow the cart.
• The air passing over the cart forces the rotor to turn.
• The rotor is a windmill (turbine).
• The rotor forces the wheels to turn.
• The wheels drive the cart upwind.

Downwind, full reversal:

• Important note: The wheels drag on the ground. At high speed, the wheels fight really hard trying to slow the cart.
• The ground passing under the cart forces the wheels to turn.
• The rotation of the wheels forces the rotor to turn.
• The rotor is a fan (propeller).
• The fan drives the cart forwards.

Starting a parked downwind cart, simple wind-drag gets the cart to start moving a little. The movement of the cart forces the wheels to turn. That forces the prop to turn. The prop pushes the cart forwards. That forces the wheels to turn. That forces the prop to turn. That pushes the cart forwards. If this sounds like a perpetual motion machine loop, then you're understanding it correctly. Grin. Yep, it is a power loop. That is partly why it's so controversial. There is an important key here. A perpetual motion machine design will run if you attach a motor and power supply to it. When the power supply is shut off, the machine stops. Machines with circular power loops are weird, but they are perfectly legal. You just need a power input to feed it. This cart has a circular power loop. It looks just like a perpetual motion loop. It does have a power input. If the wind stops blowing, the cart coasts to a stop.

The final weird bit is how the wind power gets into the cart. That is extremely hard to explain without getting into physics calculations. The simplest way to "prove" it happens is to consider it from the point of view of someone on the ground. They see the propeller pushing against the wind, slowing the wind down. If the wind slows down, the wind is losing energy. The only place for that energy to go is into the cart. At perfect efficiency, the propeller would blow the wind to a perfect halt, extracting 100% of the wind's energy. The force between the prop and the wind acts to slow the wind and speed up the cart. The wind loses energy, the cart gains energy.

The next step would be to do the physics calculations. You can find those in Blackbird (land yacht) refs to MIT professor Mark Drela. Alsee (talk) 00:27, 25 January 2017 (UTC)

I very much appreciate the energy that you put into the above, Alsee. I actually feel that the pickings are pretty slim, when it comes to the credibility of the sources. Some contradict themselves, e.g. Sadak Ali Khan, et al., the analysis of others comes from students, e.g. Mac Gaunaa. Drela appears to be self-published. The DWFTTW Blogspot is definitely not a RS. Isshiki's article is riddled with spelling errors and uses Wikipedia for the bulk of its references, which casts doubt on the quality of the journal. And Cavallaro may not even understand what he succeeded in doing. So I find much of the discussion to be an echo chamber that doesn't explain where the free kinetic energy comes from, which is all I require. In every other sailing and aerodynamics problem, either the free energy is in the form of wind flowing past an airfoil, resisted by a surface (e.g. water, ice or land), or an airfoil falling through a sometimes rising medium, pulled by gravity (e.g. a wing on a sail plane). Nothing here passes the test unless the explanation is that the wind-powered rotor drives the cart via the wheels, not vice versa.

When you say, "the wheels fight really hard trying to slow the cart", this illustrates the problem. What causes the cart to continue forward on a sustained basis? It's the wind. But for that the wheels would succeed in slowing the cart down, as they would with no wind. So, now that it's the wind, how does it sustain motion? Answer: through driving the rotor that drives the wheels, which is what your final paragraph appropriately describes, especially with "The only place for that energy to go is into the cart", which can happen only by the rotor transferring wind energy to the wheels as it encounters the apparent wind in its rotational frame of reference with sufficient angle of attack to create forward lift.

Cheers, User:HopsonRoad 01:38, 25 January 2017 (UTC)

HopsonRoad I'm not well familiar with sailing so my terminology may be poor, but maybe it will help if I try to give the sailing-based explanation. It is well established that a ship can go faster than the wind, sailing at an angle to the wind. Sailing can reach a downwind destination, faster than the wind, as long as as the ship tacks back and forth across the wind. The airfoil on the propeller is equivalent to a ship's sail. The fact that the propeller shaft rotates ensures that this sail is always travelling cross-wind. Instead of having the entire craft tack back and forth across the wind, the Blackbird has just the sail tack across the wind in a continuous spiral. The wheels are comparable to the keel. The keel supplies a force pushing the ship (and it's sail) to move on the particular crosswind course. The wheels are similar, driving the prop's airfoil on a crosswind course. The prop's airfoil is able to generate a lift in the downwind direction because the airfoil is never travelling directly downwind. This airfoil lift pulls the cart forwards. A portion of that lift pays the cost of the wheel drag (keel drag) needed to maintain the airfoil's cross-wind course.

In case I botched that explanation, here's a Reliable Source Wired magazine article on DDWFTTW which includes the sailing explanation. It also has nice illustrations depicting of how a sailboat could mimic DDWFTTW, if it sailed on a specially shaped planet. Alsee (talk) 04:25, 25 January 2017 (UTC)

Thanks, Alsee. I'm very familiar with sailing faster than the wind. (I wrote Forces on sails.) The article that you linked has it right and is completely consistent with what I've said above. The key phrase is: "The lift the propellers provided would pull the cart forward, with the wind. That forward motion would feed back into the system through the wheels, which would turn the prop even faster, creating even more lift, or, as it’s usually called vis-é-vis a propeller, thrust. The propeller—on its continuous rotational “tack”—would then simply screw itself through the zero wind." The wind is driving the rotor, the rotor drives the wheels, which drive the rotor faster, which allow the rotor to encounter the wind ever faster, which continues to drive it. This I've understood all along. I feel that others have mistaken the fact that the linkage with the wheels means with increased speed they are driving the rotor and obtaining energy through the ground. No, the ground supplies the reactive force that I described above, not the free kinetic energy. There is no magic reversal at any point of sail. Your "upwind" example also applies downwind and on any other point of sail. The wheels are always supplying a reactive force and turning with the rotor, ever faster until forward resistive forces equilibrate. Cheers, User:HopsonRoad 13:14, 25 January 2017 (UTC)

User:HopsonRoad, sounds good. Just two minor things. It's probably best to avoid using the words "free" and "energy" in the same sentence, chuckle. It too easily feeds into the perpetual motion misunderstanding. The other thing is a physics technicality:

"I feel that others have mistaken the fact that the linkage with the wheels means with increased speed they are driving the rotor and obtaining energy through the ground. No" We're getting into physics technicalities, but that objection isn't really valid. Per physics, the air and ground are simply two masses. Both are moving - they both orbit the sun at 30km/s. There is zero available energy in the wind, there is zero available energy in the ground. The energy exists in the difference between the two. We extract power by changing the velocity of both masses, making them more equal. Getting energy from the ground is just as valid (or just as invalid) as getting energy from the wind. For some people, the concept of "getting energy from the ground" really does aid their understanding. Physics says that it's perfectly valid to swap reference frames, and to swap your viewpoint regarding air and ground. Alsee (talk) 19:08, 25 January 2017 (UTC)

Thank you, Alsee. Your physics remarks are consistent with the helpful summary from Mark Drela (below). As to terminology, how does "available kinetic energy from the wind" sound? Cheers, User:HopsonRoad 19:44, 25 January 2017 (UTC)

HopsonRoad, "available kinetic energy" is an excellent term. And the Mark Drela section below is also excellent. One of the fun things about this topic is how it almost always ends up with hyper-agreement. This one got there really fast. Alsee (talk) 20:45, 25 January 2017 (UTC)

From Mark Drela

I asked MIT Professor Mark Drela to help resolve this discussion. Here is what he wrote:

Short summary:

Power extraction from a mass occurs when the mass's velocity is decreased somehow. But velocity depends on the observer, so where the power to the DDW vehicle comes from depends on the observer. Specific examples:

1. To an observer suspended in a free hot-air balloon, the airmass is fixed and the earth moves. The DDW vehicle's wheel traction force decelerates the moving earth (however slightly), and thus the DDW vehicle appears to extract power from the earth-mass.

2. To an observer standing on the ground, the earth is fixed and the airmass moves. The DDW vehicle's propeller decelerates the fluid passing through the prop disk, and thus the vehicle appears to extract energy from the airmass.

3. To the DDW vehicle pilot, both the earth and the air appear to move. Some power always appears to come from the moving earth which is driving the wheels. But the power from the airmass depends on the vehicle's speed:

3a. DDW vehicle is slower than the wind (like a DDW sailboat). Additional power comes from prop decelerating the airmass.

3b. DDW vehicle is moving at the wind speed. This is exactly the same as case 1 above, since the pilot and the balloon observer move in unison.

3c. DDW vehicle is faster than the wind. The prop now sends some of the power provided by the earth into the airmass.

All the above cases are somewhat idealized. Specifically, they assume that velocities are nearly steady, so the various accelerations are very small. They also assume that the propeller disk is very large, so the velocity increment or decrement of the air after it passes through the disk is very small compared to the other velocities. But these complications don't change the basic physics as seen by cases 1,2,3a,3b,3c.

The more sophisticated statement on the situation, which is observer-independent, is that the DDW vehicle (or landsailer, or iceboat, or sailboat) extracts power from the air-earth or air-water interface. Specifically, there is available mechanical power in the delta(V) across the interface, and each vehicle extracts this power by reducing this delta(V). Ultimately, this extracted power appears as heat in both masses once the vehicle is long gone.

So, what I was describing, above, corresponds to Drela's Example 2, the frame of reference with which most readers would identify. Drela recommends Gaunaa, et al. as a reliable source: Gaunaa, Mac; Øye, Stig; Mikkelsen, Robert (2009), "Theory and Design of Flow Driven Vehicles Using Rotors for Energy Conversion", Proceedings EWEC 2009, Marseille{{citation}}: CS1 maint: location missing publisher (link). Cheers, User:HopsonRoad 19:23, 25 January 2017 (UTC)

Proposed new text

I propose to substitute the text found at: Rotor-powered vehicles that exceed wind speed for the section at "Directly down wind faster than the wind (DDWFTTW) vehicle", which I suggest should be moved to Wind-powered vehicle. I look forward to the input of other editors, here. User:HopsonRoad 15:43, 26 January 2017 (UTC)

Having reviewed it I think those changes make sense to me. - Ahunt (talk) 15:24, 27 January 2017 (UTC)

Beta theorem

Hi Charco21, thank you for your interest in this article. I appreciate that you feel the contributions that you made are obvious derivations of what's published. Nonetheless, they are still your work, not concepts that you have paraphrased from reliable sources. Furthermore, your contributions mentioned a variety of sailing craft from whose un-cited performance characteristics you made conclusions.

The article is already written on a subject and at a level that is difficult for the average reader to understand. So, what's obvious to you, is not obvious to most readers. I also appreciate that you were trying to help the reader with your contributions. My suggestion would be for you could tackle the article as it is and see if you can make what's there more accessible to a less technically knowledgeable reader. That would be very welcome and would earn the removal of the template at the beginning of the article, were it successful. Cheers, HopsonRoad (talk) 02:25, 30 July 2020 (UTC)

Hi HopsonRoad, many thanks for the note. Fair enough. Yes it is a complex topic and the articles I think need to have a mix of both easy to understand descriptions of high efficiency sailing as well as some of the complexities because without both the topic is incomplete. I guess that is why I was trying to introduce real-life examples like foiling mono-hulls and speed sailing craft to help an understanding of the topic by somehow connecting every-day news to the gritty maths.

I often get asked how a yacht can sail faster than the wind and my explanation is that the yacht is like a slippery lemon pip - the lemon pip when squeezed slowly, shoots forward quickly - the slippery yacht when squeezed between wind and foils does likewise.

I have looked far and wide for publication of the maximum speed course to no avail, but I will keep trying. This concept was shown to me by an Auckland University lecturer circa 1987, so I can vouch that this is not an original idea of mine!!

The Course Theorem, or Beta Theorem as I have probably mis-named it, outside of Garrett also does not seem to have much traction, but nevertheless it seems strongly fundamental to the maths of sailing, and I am keenly interested in it's simplicity and relevance to all sailing, but especially in the way it helps me understand high performance sailing.

Another corollary of the Course Theorem is that the apparent wind angle of a yacht sailing in its fastest direction, is given by:

β = (180/pi) / (craft speed as a multiple of wind-speed)

eg

ice yacht capable of 10x windspeed -> apparent wind angle 5.7 deg

AC75 capable of 5x windspeed, -> apparent wind angle 11.5 deg

AC50 capable of 4x windspeed, -> apparent wind angle 14.3 deg

windsurfer and blokart and AC62 capable of 3x windspeed -> apparent wind angle 19.1 deg

Cheers to all, and looking forward to further discussion on this great topic

Charco21 (talk) 07:06, 30 July 2020 (UTC)Charco21

Hi Charco21, thank you for your thoughtful and considerate reply! Indeed, it is a mystery to many how a sailing craft can go faster than the wind that it's using for propulsion. Perhaps another way of explaining it is that the craft is deriving power from the wind, which is a function of the airfoil—whether sail or propellor—to continue to generate lift at the combined speeds and directions of the wind and sailing craft. People are limited in thinking of a sail as an object blown upon in what I call "parachute mode", rather than blown across in what I call "wing mode", which makes it difficult to appreciate the manner in which sails most efficiently harvest power. I think that better understanding can be built from the simple to the complex, as you suggest. Cheers, HopsonRoad (talk) 13:54, 30 July 2020 (UTC)

Unsourced, but possibly pertinent material

I have not found a source for the material, below. It appears to be germane, but difficult to follow. It also appears to be WP:OR. I have hidden it in a collapsible box to avoid taking up too much space. Please find a supporting reference, before moving it back into the article.

Unsourced, but possibly pertinent material is here

{{ Surface resistance If hull speed is not a limiting factor, and if the strength of the wind is sufficient to overcome the surface resistance, then the speed of the boat as a multiple of the wind speed depends only on how close it can sail to the wind. For example, assuming that surface resistance is negligible (as for an iceboat), if a boat sails at 90° to the true wind, but at 45° to the apparent wind, then it must be sailing at the same speed as the true wind. That is, if the wind speed is V, then the boat's speed is also V. Elementary trigonometry and elementary vector operations can be used to show that, if a boat sails perpendicular to the true wind, but at angle alpha (α) to the apparent wind, and the wind speed is V, then the boat's speed must be V×cotangent(α). The table below shows the values of this function, as a multiple of windspeed. The actual speed of a sailing craft depends on the wind speed, how close to the wind it is sailing, the resistance of the surface (water or ice), and leeway (downwind drift). Alpha (α) Multiple of windspeed 45° 1.00 40° 1.19 35° 1.43 30° 1.73 25° 2.14 20° 2.75 15° 3.73 10° 5.67 The table and diagram below illustrate this situation. The vector labelled "boat speed" represents the relative wind resulting from the boat's progress through the water, that is, the wind that is induced by the boat's motion: its speed is the same as the speed of the boat and its direction is directly opposite to the direction of the boat's motion. Both boat speed and apparent wind speed are shown as a fraction (or multiple) of true wind speed, which is represented by the vertical vector at the left of the diagram. Boat speed Alpha (α) Apparent wind speed 0.10 131° 0.93 0.30 120° 0.82 0.50 106° 0.74 0.71 90° 0.71 1.00 68° 0.77 1.41 45° 1.00 2.00 29° 1.47 3.00 17° 2.40 4.00 12° 3.37 5.00 9° 4.35 Note that, if a boat can accelerate until it is sailing at 45° off the apparent wind when sailing 135° off the true wind, then its speed is 1.41 times the speed of the true wind. Thus its velocity made good downwind is equal to the velocity of the true wind. If it can accelerate until it is sailing closer than 45° to the apparent wind, then its velocity made good downwind is greater than the velocity of the true wind: see section Velocity made good below. Maximum speed course sailing angle The maximum speed potential of a sailing craft is reached when the apparent wind and the true wind are at right angles. This course sailing theory applies only to high performance sailing craft (those that can sail at least 41.4% faster than the wind), since a low performing sailing craft may never go fast enough for the apparent wind to swing 90 degrees to its true course. The course sailing angle conclusion for maximum speed is shown to be a corollary of the Beta Theorem, with the assistance of Figures 1–3. Beta Theorem Vectors that determine β. Velocity of craft for arbitrary β. β for greatest velocity. Figure 1 shows the relationship of the true wind and apparent wind vectors as differing by the sailing craft velocity. Also shown is the angle β, which is the "apparent wind angle", i.e., the angle between the sailing craft heading and the apparent wind on the craft. Although β is assumed to be constant, this is not perfectly true in practice. However, in the quest for maximum speed, it could be made to be true—i.e., by setting the size of the craft's sails and fin or centreboard for each speed run so as to maintain the same (optimal) operating points, and therefore the same lift to drag ratios, and correspondingly a constant β for each heading under test. Having accepted the constraints for a constant β, then it is simple maths (a constant angle is subtended on the arc of a circle) that we arrive with the locus of a circle for one end of the vector showing sailing craft velocity, as in Figure 2. The maximum sailing craft velocity clearly occurs when the vector Vy lies across the diameter of the circle, as shown in Figure 3. In this figure, the apparent wind and the true wind are at right angles. Also note that the optimum speed sailing angle is equal to the apparent wind angle (β) below a beam reach. Vt and Va appear equal in figure 3, where Vy is about 1.4x Vt. This is not the general case. The more efficient the sailing craft, the smaller β is, and the closer to a beam reach is the optimum speed sailing course. The ultimate ratio of sailing craft speed to wind speed therefore also gives rise to β by inverse cosine, e.g., speed-sailing at twice the wind speed corresponds to a 30° apparent wind angle, i.e., β = 30°. Speed sailing windsurfers have an apparent wind angle somewhat worse (greater than) 30°, and accordingly their speed sailing courses are set for a broad reach at least as broad as 120 deg. Speed sailing kite boards prefer an even broader course than windsurfers. In contrast to windsurfers and kites, the highly efficient Vestas Sailrocket has a β of about 20°, noting that the hull is offset this amount from the centreline to align with the apparent wind. Vestas Sailrocket would have been sailing at close to a 110 deg course to set her incredible world speed record of 65.45 knots in 25 knots of wind. Velocity made good (VMG) Most sailing is not done in order to achieve a maximum speed, but in order to go from one point to another. In most sailboat racing the objective is to sail a certain distance directly upwind (to a point called the upwind mark), and then to return downwind, as fast as possible. Since sailboats cannot sail directly into the wind, they must tack in order to reach the upwind mark (this process is called beating or working to the mark). This lengthens the course, thus the boat takes longer to reach the upwind mark than it would if it could have sailed directly towards it. The component of a sailboat's velocity that is in the direction of the next mark is called the velocity made good. If a boat sails perpendicular to the wind, it will never reach the upwind mark. So, in racing, speed is not everything. What counts is the velocity made good, that is, the progress towards the upwind mark. Again, simple trigonometry can be used to calculate the velocity made good. The tables below show velocity made good, again as a multiple of windspeed, and again assuming negligible surface resistance. The first column indicates the course as an angle off the true wind; α is the closest angle to the apparent wind at which the boat can sail. The calculation assumes that the boat accelerates until the apparent wind is at angle α off the bow. Speed made good as multiple of windspeed Alpha (α) Upwind Course 10° 15° 20° 25° 30° 35° 40° 45° 10° 20° 0.94 0.32 30° 1.71 0.87 0.44 0.18 40° 2.21 1.25 0.77 0.47 0.27 0.12 50° 2.38 1.42 0.94 0.64 0.44 0.29 0.17 0.08 60° 2.21 1.37 0.94 0.68 0.50 0.37 0.27 0.18 70° 1.71 1.08 0.77 0.57 0.44 0.34 0.27 0.20 80° 0.94 0.61 0.44 0.34 0.27 0.21 0.17 0.14 90° 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 Alpha (α) Downwind Course 10° 15° 20° 25° 30° 35° 40° 45° 100° 1.00 0.67 0.50 0.40 0.33 0.27 0.23 0.20 110° 1.94 1.32 1.00 0.81 0.67 0.58 0.50 0.44 120° 2.71 1.87 1.44 1.18 1.00 0.87 0.77 0.68 130° 3.21 2.25 1.77 1.47 1.27 1.12 1.00 0.91 140° 3.38 2.42 1.94 1.64 1.44 1.29 1.17 1.08 150° 3.21 2.37 1.94 1.68 1.50 1.37 1.27 1.18 160° 2.71 2.08 1.77 1.57 1.44 1.34 1.27 1.20 170° 1.94 1.61 1.44 1.34 1.27 1.21 1.17 1.14 180° 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 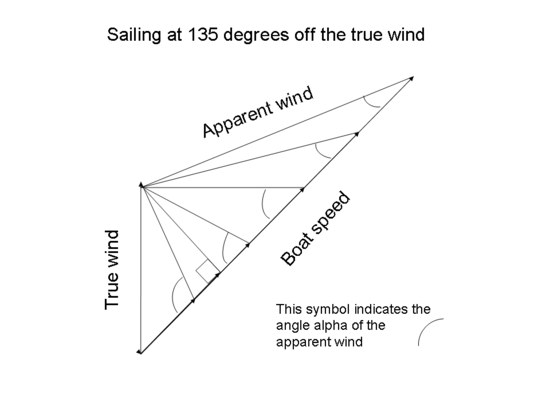It can be seen that a boat that can sail closer than 20° to the apparent wind can make good upwind faster than the real wind. Vector diagrams and formulas As explained in the article on apparent wind, a boat's forward motion creates a corresponding head wind of the same strength in the opposite direction. That head wind must be combined with the true wind to find the apparent wind. The drawing below shows the vector operations and resulting calculations for sailing upwind. Alpha (α) is the angle of the apparent wind. Beta (β) is the course of the boat with respect to the true wind. The true wind is assumed to be equal to 1 in order to simplify the formulas. Note that the true wind is added using vector addition to the head wind created by the boat's speed. The drawing below shows the vector operations and resulting calculations for sailing downwind. Alpha (α) is the angle of the sails to the apparent wind. Beta (β) is the course of the boat with respect to the true wind. The true wind is assumed to be equal to 1 in order to simplify the formulas. Note that the true wind is added to the head wind created by the boat's speed. The drawing below shows apparent wind angles and speeds for different boat speeds for a boat sailing downwind at 135°. Note that for both the upwind and downwind cases, the apparent crosswind (the component of true wind perpendicular to the heading of a boat) is true wind speed x sin(β), independent of the boat's speed. The maximum speed of a sail boat is a function of how fast it can travel for a given apparent crosswind and the drag from the water (or land or ice) related to the boat's true speed. Since the drag from the water (or land or ice) increases with the boat's true speed, the boat achieves its maximum apparent wind on an upwind tack, where its true speed is the slowest. This is why minimum β for a boat is smaller upwind than it is downwind. Vector diagrams and resulting speed of sailing craft Upwind course. Downwind course of 135°. Boat speed as a multiple of true wind speed for various angles of apparent wind. Vector operations and calculations to find the speed of a craft sailing on each course shown. The formula for the apparent wind is (using the symbols shown in the vector diagrams) tan(α)=sin(β)/ (Boat speed+cos(β)). The figures shown for the angle of the apparent wind assume a boat speed around 0.3 times windspeed, say 6 knots (11 km/h; 6.9 mph) for a keelboat in 18-knot (33 km/h; 21 mph) winds. The figures for the angle of the true wind are from the main article on sailing. The maximum multiple of windspeed is achieved at an angle of 90°+α off the true wind. For α = 45°, the maximum multiple of windspeed is 1.41 at an angle of 135° off the true wind. Broad reach As stated in the introduction of the book High Performance Sailing, in the section Tacking Downwind, "... any boat which runs 'square' must necessarily sail downwind at some speed less than the wind's speed whereas any boat which tacks downwind has no theoretical limit to its speed. Iceboats, for example, can tack downwind at average speeds many times the wind speed." From the detailed data provided for the 2009 record set by a sand yacht, it can be seen that the record was achieved when the craft's course was about 120° off the true wind. That is, the craft was moving faster than the wind although the true wind was behind it. This is possible because the speed of the craft results in a large forward wind shift, so that the craft is close hauled with respect to the apparent wind. Suppose that a boat is at a standstill, then starts to sail on a course that is 135° off the true wind (the value 135° is chosen for this explanation in order to simplify certain calculations). The boat accelerates, so the apparent wind is less than the true wind and shifts forward of the true wind. If the boat can reach a speed equal to about 71% of the true windspeed, then the apparent wind is perpendicular to the boat's course and its speed is about 71% of the true windspeed. If that reduced apparent windspeed still generates sufficient force to overcome the resistance of the surface, then the boat continues to accelerate. That is, the situation is the same as the one explained above, because the boat is still accelerating after having reached a course perpendicular to the apparent wind. In practice, most boats sailing on the water cannot overcome the resistance of the water in order to reach speeds equal to the speed of the wind. However, iceboats can do so, because the resistance of the surface is very small. Thus, an iceboat that starts sailing on a broad reach continues to accelerate until it is close-hauled with respect to the apparent wind. References }}

Sincerely, HopsonRoad (talk) 11:19, 31 July 2020 (UTC)