Talk:Gravitational potential/Archive 1

Archive 1

Gravitational potential and gravitational potential energy

Gravitational potential is NOT the same as gravitational potential energy. The writer has mixed these two things. Needs fixoring ASAP. —The preceding unsigned comment was added by 130.234.6.46 (talk • contribs) on 06:59, 9 January 2006.

What, specifically, do you believe is incorrect about the article as it presently stands? --Christopher Thomas 07:46, 9 January 2006 (UTC)

The article is just fine, it's just named incorrectly. Gravitational potential energy (U) is equal to the mass of the body multiplied by the gravitational potential (Φ) => U = m * Φ -- the same —Preceding unsigned comment added by 130.234.202.80 (talk • contribs) on 15:39, 31 January 2006

Merge with potential energy

Most of the material on this page is covered at potential energy in the "gravitational potential energy" subsection. I've added "merge" tags to get discussion on what, if any, advantage there is to keeping this material on its own page. --Christopher Thomas 07:59, 9 January 2006 (UTC)

sign (+ or -) of the gravitational potential P

L.S.,

According to me (and others: see other pages of Wikipedia; also Vector Methods, D.E. Rutherford) the formula for P schould be: P=+GM/r and not P=-GM/r.

Here follows the reason. For P=+GM/r the accelleration is indeed given by the gradient of P. The components of the gradient of P are:(in ax the x is subscript, so the x-component) ax=-GMx/r3 ay=-GMy/r3 az=-GMz/r3. Suppose y=0 and z=0. Then ax=-GMx/r3. So for positive x, ax is negative (towards the left, so towards the pointmass) For negative x, ax is positive (towards the right, so also towards the pointmass. As it should be, of course: gravitation is an attractive force.

Now, if you should have have: P=-GM/r,then ax= + GMx/r3. For positive x that value is positive, so to the right, away from the point mass. For negative x that value is negative, so to the left,also away from the point mass. That would make gravity a repulsive force.

So, P=+GM/r gives the correct value for the acceleration by a=gradient P. The + or - sign is not trivial and should be correctly chosen in Wikipedia. There must me no ambiguity at this point(unless there should be ambiguity in the scientific litterature; in that case the ambiguity should be mentioned in the page).

Besides i remark, as is done by previous contributors, that the potential is not the same as the potential energy of a mass of 1kg (in that case you would not need the concept). The value of the concept is that it gives the acceleration by means of its gradient.

Fransepans (talk) 22:32, 21 September 2009 (UTC)

This is a case of differing sign convention. Per potential, the usual convention is to define a potential $U({\vec {x}})$ such that $F=-\nabla \cdot U({\vec {x}})\cdot Q$, where Q is the charge upon which the force is acting (in this case, mass). This convention gives the change in potential energy $\Delta E_{p}$ over some path $P$ as $\Delta E_{p}(P)=\int _{P}\nabla \cdot U({\vec {x}})\cdot Q\cdot d{\vec {x}}$. Because a force moves a particle in the direction of decreasing potential energy, a minus sign results in the expression for force. --Christopher Thomas (talk) 23:59, 21 September 2009 (UTC)

L.S., I can agree with the convention (although the literature is not unanimous at this point). I conclude that, according to that convention, in the article a minus sign must be added to the word "gradient": The gravitational field equals MINUS the gradient of the potential. We agree on that. I will edit the page accordingly.

Dimensions are very important

The dimensions such as force, mass, time, and distance are very important from an engineering point of view. Although the pure mathematician may think dimensions are irrelevant, there are engineering oriented people who read the Wikipedia. Therefore it is important that we give adequate attention to dimensions in Wikipedia articles such as this. RHB100 (talk) 02:23, 27 February 2010 (UTC)

This is a case where too much detail is as bad as too little. The article currently emphasizes the dimensions of the gravitational constant, which is not relevant to understanding the potential, and is written in a potentially confusing manner. Sławomir Biały (talk) 11:11, 27 February 2010 (UTC)

It certainly is not too much emphasis to merely state the dimensions of the gravitational constant. If anything it is too little emphasis since only the dimensions, not the units, are stated and the value is not stated. RHB100 (talk) 21:52, 27 February 2010 (UTC)

It is important that at least the dimensions be stated since it aids the reader in verifying the dimensional compatibility of the equation. One of the first and most important things that one should do upon encountering a new equation is verify the dimensional compatibility. Every well educated engineer with degrees from one or more of the better American universities understands this. As a licensed professional engineer I know the importance of dimensional compatibility. RHB100 (talk) 21:52, 27 February 2010 (UTC)

I find it distracting from the much more meaningful point that the potential has units of energy per unit mass. Also, when saying "which has dimensions", the referent is unclear: the reader is expecting dimensions of the potential (the subject of this article), but is instead given the dimensions of the gravitational constant. This sort of information belongs in a footnote, if in the article at all. Surely professionalism also demands the ability to follow footnotes (if not wikilinks to the gravitational constant article). Sławomir Biały (talk) 23:53, 27 February 2010 (UTC)

Update. I have started a dedicated section on Units and dimension. Please populate this with information that would be useful to "professionals". Sławomir Biały (talk) 00:17, 28 February 2010 (UTC)

It needs to be in the main section not relegated to a footnote. The reader needs to see the dimensions or units of all the factors on the right side of the equation and verify that they are compatible with the left side of the equation.

Sławomir Biały, don't you know, dx^3 is not a differential element of mass. Any competent mathematician should know this. Where did you study math?

Here ρ(x) is the distribution function, and d^3x is the volume element. Sławomir Biały (talk) 02:20, 28 February 2010 (UTC)

I believe this notation, using ρ for the mass density, is a fairly standard one. I will wait a few days for others to comment, and then restore the original version of the formula. Also, back to the original topic of the thread, I don't think the value of the gravitational constant G needs to be right next to the formula for V. It seems to be that the better place for that is in the new section that I have created for a fuller discussion of the units and dimensions. Sławomir Biały (talk) 03:15, 28 February 2010 (UTC)

I'd suggest that giving the exact value of G right beside the formula for V is distracting (the wikilink is sufficient). I also don't think the dimensions of G are necessary either. I do think it's a good idea to give the dimensions of the potential right after giving the formula. Regarding the notation switch from ρ(x)d³x to dm, I'm ambivalent: in some sense dm is more conceptual, on the other hand, the notation ρ(x)d³x is more friendly to the less experienced reader. So who is the target audience?

I'd also suggest that in the newly added expansion of the denominator the article should not assume that the reader is aware of the convention that if v is a vector quantity then v is its magnitude. Either something should be said about this, or the notation should be changed.

I also think the first thing someone should think about when seeing an equation for a physical quantity is what it says about the dependence of the quantity on others. I would place verifying the dimensional consistency of a >200 year old equation low on my list.

As a last comment, I find it generally better in a content dispute to revert the article back to the previously held "consensus" version of the article and to use the discussion page to build a new consensus (this would appear to be this). RobHar (talk) 03:57, 28 February 2010 (UTC)

Comments:

• I don't see any problem with giving the numerical value of G, including units, in the 'Mathematical form' section. It's true that the article is supposed to be about potential and not about the gravitational constant, but I don't think that giving the value is crossing the bounds of WP:TOPIC. Don't don't agree entirely with RHB100's reasons for including it, but since this is essentially a physics article it seems appropriate to include the values of constants used. However, the placement on the same line as the formula is awkward. Perhaps it can be incorporated into the text by rewording the paragraph.

I took a stab at a rewording that may work as a compromise. Not claiming it's perfect but hopefully it's a step towards addressing everyone's concerns. It's a small point but the previous wording had M being used both as a position in space and as a mass value; there's not much harm in confusing the two for a point mass but it shows the previous wording wasn't perfect either.--RDBury (talk) 05:09, 28 February 2010 (UTC)

• I've always seen the volume element written as dV, but this would be problematic in this article because V is also used for the potential. The dm form is correct but in practice it would just be factored as ρdV anyway. If there is a way to work around the coincidence of V being used to mean two different things then I think that would be the best way of writing it, otherwise I don't really have a preference.

It appears that Φ is also commonly used for the potential, so using it instead of V would allow using V for volume as is customary. So I vote to replace all the Vs with Φs and use dV as the volume element.--RDBury (talk) 05:39, 28 February 2010 (UTC)

• The 'Units and dimension' and section that was added, seems inappropriate per WP:TOPIC whether or not the value of G is included in the other section. This is an exercise in dimensional analysis anyway so I don't think it adds value.

--RDBury (talk) 04:45, 28 February 2010 (UTC)

The use of the differential element of mass, dm, is more common than what some people realize. Dynamics professor, Dr. Peter W. Likins, taught at UCLA before going on to become Dean of Engineering at Columbia, and President of Lehigh and Arizona. In his dynamics text, "Elements of Engineering Mechanics", Likins used dm wherever appropriate such as in defining angular momentum. In the dynamics text, "Methods of Analytic Dynamics" by Leonard Meirovitch, dm is used wherever appropriate. I think that in dynamics texts used in engineering schools, the use of dm is fairly standard. RHB100 (talk) 23:32, 28 February 2010 (UTC)

I, for one, am not contending that dm is uncommon. In fact, it is very common in sufficiently advanced physics texts as well (by which I mean textbooks that would be used in sophomore physics and beyond). However, ρ(x)d³x is much more likely to be understood by anyone who has taken some calculus, without necessarily moving on to higher level physics courses. Another matter is that dm is really mostly a shorthand for ρ(x)d³x. Were one to actually compute an integral, one would, in most cases, immediately rewrite dm as ρ(x)d³x. RobHar (talk) 22:41, 28 February 2010 (UTC)

I have several problems with "dm". First, the integral is still over physical space, but the notation does not emphasize this. It should at the very least be $\int _{\mathbb {R} ^{3}}dm(\mathbf {x} )$. Secondly, I do not like the way in which the integral with respect to "dm" is treated as though it were something well-defined in its own right. If this is an ordinary Riemann integral, then it is the integral of a distribution function (and so we should write the simpler ρ(x)dx). If it is a Lebesgue integral of a mass measure, then that should be indicated instead. But it is not explained at all what the "integral over the extent of the differential mass elements, dm" means. Also, the fact that this is a convolution is significant, and should be mentioned, although that fact was removed in the recent round of edits. Sławomir Biały (talk) 23:08, 28 February 2010 (UTC)

The problems you have with dm are due to your own lack of understanding and education. You should go back and repeat undergraduate dynamics for rigid bodies. RHB100 (talk) 21:11, 1 March 2010 (UTC)

The expression, d³x, is not a meaningful expression for a differential volume. dx dy dz is a proper expression for a differential element of volume, a differential cube. I think that a student who had studied calculus would be confused by d³x. The elements of dx dx dx are not orthogonal, they are all in the same direction and it is thus not a meaningful expression of a differential element of volume and it is confusing to say the least. RHB100 (talk) 00:07, 1 March 2010 (UTC)

The notation d³x is completely standard in physics texts, by the way, and it is not meant to mean dx dx dx=(dx)³, but rather the 3 symbolizes the fact that the integral is over three dimensions. It is true that from the point of view of making this article at least accessible to people who have done calculus, it would be better to use dxdydz. RDBury above also suggested dV instead which I have certainly seen a lot, but is not necessarily standard, so I might be reticent to use that. RobHar (talk) 00:28, 1 March 2010 (UTC)

I have not read all physics books but I did take a survey of 4 physics books that I own. All 4 used the differential element, dm, in connection with angular momentum and moments of inertia. I did not observe the notation, d³x in these particular books but again I confess I have not read all physics books. The books I surveyed are "Elements of Physics" by Shortley and Williams, "University Physics" by Sears and Zemansky, "Fundamentals of Physics" by Haliday and Resnick, and "Physics for Science and Engineering" by McKelvey and Grotch. RHB100 (talk) 01:52, 1 March 2010 (UTC)

I have added an explanation of the unexplained notation, since from the earlier version, is was not even clear that the integration was over ordinary physical space. I also felt the need to explain what "dm" is, and link to the appropriate notion of integral. Sławomir Biały (talk) 12:01, 1 March 2010 (UTC)

Physics and engineering books use integrals with dm as the differential element and manage to make it clear to the intelligent student without a lot of extra explanation. We should use mathematics to explain not to confuse. RHB100 (talk) 21:11, 1 March 2010 (UTC)

There isn't "a lot of extra explanation", we simply state correctly (and now with a reference) what "dm" refers to in the notation. Saying that "dm" is a "mass measure" is mathematically much more satisfactory than referring to fictional "differential elements of mass", and is not likely to lead to any greater confusion than the latter. (However, it still seems simpler to me to work with a distribution function instead.) The latest version now also includes a brief discussion of the role of Poisson's equation, which was strangely lacking from the earlier revision. Also, I have corrected the recently-introduced errors that put R=r−r_i as incorrect and incoherent. Sławomir Biały (talk) 22:06, 1 March 2010 (UTC)

Look at the definition of R. Try to understand it. One of the things we now need to do is add a figure showing R, x, and r. To avoid ambiguity we need to talk in terms of point a and point b rather than just talk about the point, the point, ... .

—Preceding unsigned comment added by RHB100 (talk • contribs)

Please stop adding this, it is both incoherent and incorrect. Also, you continue to remove sourced content. The potential is a function of a point r in space. There is no need to talk about the center of mass of the system when defining it. Of course, if one picks a coordinate system that places that origin at the center of mass, then one recovers what you have written, but that does depend on choices that are irrelevant to the definition of the potential. Sławomir Biały (talk) 01:32, 2 March 2010 (UTC)

The current revision is wrong. Also, sourced content was removed, I don't know if you are aware of that. (I keep pointing this out, but you keep ignoring it, and just reverting every edit that I make, which is getting to be really aggravating.) Sławomir Biały (talk) 02:01, 2 March 2010 (UTC)

Comment. I tried to make various compromises in the article, including using RHB's preferred "dm" notation, but I also felt it important to include the case of a continuous mass distribution ρ, and a discussion of the Poisson equation. My efforts to achieve compromise have been systematically reverted, often without any edit summary or talk page explanation, by RHB. On top of that, RHB has introduced conceptual errors into the article, as well as unnecessary and unexplained formulas (like the formula that pretends to be an integral in spherical coordinates, but fails to say what any of the variables are), and removed sourced content. I ask that we should either go back to the earlier consensus version of the section, or that a new consensus should emerge. The current version of the article is totally unacceptable. Sławomir Biały (talk) 02:08, 2 March 2010 (UTC)

Let me add that this formula

$V(\mathbf {r} )=-\sum _{i}{\frac {GM_{i}}{|\mathbf {R} -\mathbf {r} _{i}|}}\,{\rm {where\ \mathbf {r} =|\mathbf {R} -\mathbf {r} _{i}|\ }}$ and where R is a vector from the center of mass to point b.

is extremely unclear, since the vector r appears on the left-hand side as the argument of the function and on the right as a scalar (which is one reason I changed these rs to x: they were persistently being misunderstood by an editor). The equation r = |R − r_i| is also questionable, because on the left is something that does not involve i and the right clearly depends on i. Happily, I see that my preferred (correct) revision has been restored that has none of these problematic issues. Sławomir Biały (talk) 11:49, 2 March 2010 (UTC)

I have to add that I don't see how any formula involving the center of mass can be anything non-trivial. I thought about this last night, and I have an example that I'd like others here to think about: Suppose I'm standing at the origin. There are two point masses, each 1 kg. One point mass is 1 m directly to my left, and the other point mass is 1 m directly to my right. I'm at the center of mass of the system of the two point masses. But the potential is not singular there; instead it is singular at the locations of the two point masses. So the center of mass really doesn't appear naturally in the potential; you can always change your coordinate system, as I think RHB100 wants to do, but there's no reason why the center of mass is a better place than any other (from a mathematical perspective). Ozob (talk) 12:44, 2 March 2010 (UTC)

I had a similar problem as well, and initially tried to post it, but my explanation failed utterly to convey the sense of it. For me the bottom line is that the potential is currently defined in a totally coordinate-independent manner, which is how it should be. Sławomir Biały (talk) 13:00, 2 March 2010 (UTC)

I think terms such as my left and my right are ambiguous. You need to talk about point a and point b. Another thing I rely on vectors. Vectors are independent of any coordinate system in which they happened to be expressed. I like to rely on vectors since it often eliminates the need for consideration of a coordinate system. It is important to give consideration to the center of mass when expanding the potential in terms of Legendre Polynomials as I have done below. RHB100 (talk) 03:14, 3 March 2010 (UTC)

Your bold text is using up all my electronic ink.

Here is a more formal statement of what I would like: Suppose that there is a point mass of 1 kg located at (1 m, 0, 0) and a point mass of 1 kg located at (1 m, 0, 0). For each point (x, y, z), what is the gravitational potential at (x, y, z)?

Which revision?

We need to develop a consensus. I propose my most recent revision [1] as a suitable starting point. I have attempted to take into consideration the comments of the preceding section, including RHB's preference of the "dm" notation, as well as RDBury's suggestion of using "dV" and what seems to be a consensus that a distribution function should be presented. (Not to rehash old arguments, but most of the physics books that I checked which used "dm" in an intuitive setting almost immediately explained this with a distribution function.) In addition, I had made a number of edits to address some of RHB's misunderstandings of the text as it had stood. The other revision, which I feel to be substantially inferior, is this one (here is a diff between the two revisions). I would ask that some consensus should develop on which revision should be the "stable" one. Sławomir Biały (talk) 02:21, 2 March 2010 (UTC)

Hmm. While you wrote this, I was working on a new revision myself. It's pretty similar to yours; as of now it's on the page itself, but in case the article changes my version can be seen at [2]. Ozob (talk) 04:47, 2 March 2010 (UTC)

Looks fine to me, clear progress over the version I had suggested. Sławomir Biały (talk) 11:22, 2 March 2010 (UTC)

Sławomir Biały, you are not qualified to accuse me of misunderstanding anything. I am a Licensed Professional Engineer in the field of control systems engineering. I hold advanced engineering degrees from two of the better quality engineering schools in America. I have had a career designing autopilots for American missiles. I don't believe you could get an undergraduate degree from one of the better quality American Universities. You are not qualified to accuse me of misunderstanding anything. The errors I have pointed out are due to sloppy writing and errors on your part not any misunderstanding on my part. RHB100 (talk) 23:43, 2 March 2010 (UTC)

Wow, that's some bold text.

I don't understand why you're even interested in qualifications. Isn't it more important to be correct? I for one plan to never reveal my identity or my qualifications. If I'm wrong, I want to be told I'm wrong, and I don't care whether the person doing it is a certified genius or a bored teenager.

RHB100, your version of the article is wrong. The formula V = -Σ GM_i / |R - r_i| is incorrect. I gave an example above: Suppose that you are standing at the origin and that there is a 1 kg mass 1 m to your left and a 1 kg mass 1 m to your right. What is the potential? Ozob (talk) 01:37, 3 March 2010 (UTC)

In the example above you had V(r), now you have V without an argument. V without an argument is correct. The notation with V(r) is incorect since r is a dummy variable of summation. I have added a diagram below for the continuous case which should also make it clear for the discrete case if you keep in mind that x in the continuous case replace the discrete, r_i. RHB100 (talk) 02:46, 3 March 2010 (UTC)

Could you explain for me how my example would look in your fomulas? Ozob (talk) 02:59, 3 March 2010 (UTC)

V(r) means V at point r. By the way, an additonal additional notation b is not needed for this point.--Patrick (talk) 11:50, 3 March 2010 (UTC)

You still have not answered my question. In my example: V(r) = ? Please be specific. I don't know how to interpret your formula in this context. Ozob (talk) 23:24, 3 March 2010 (UTC)

Mathematical form is poorly written

The mathematical form section is poorly written at present. Expressions such as "where r is a vector of length r pointing from the origin" indicate the general sloppiness with which the article is written since the origin is not even defined. The article below indicates some of the ways the article could be improved. A diagram has been added to this new version to clearly show the relationship of R, r, and x to supplement the verbal definition. Also the integral for the continuous case has been expanded into a series of Legendre Polynomials in the new version. The comments on mass measure serve only to add confusion and should be removed.

—Preceding unsigned comment added by RHB100 (talk • contribs)

Mathematical form, New

See section titled, Gravitational potential expanded in series of Legendre Polynomials. RHB100 (talk)

Perhaps it is better to put the power series in a separate section, choosing here the origin at the center of mass, and to work out the first few terms: main term n=0. term n=1 which vanishes due to the center of mass being at the origin, and n=2, the main deviation from the main term.--Patrick (talk) 11:59, 3 March 2010 (UTC)

Patrick, I have already worked out the first few terms in a Taylor series expansion. RHB100 (talk) 21:31, 4 March 2010 (UTC)

The Laplace series is valid whether or not the origin coincides with the center of mass (in contrast to what RHB asserted in an earlier post). I do think this deserves a place in the article, though, but I think it is better to introduce spherical coordinates a little more explicitly than is done here. Sławomir Biały (talk) 12:05, 3 March 2010 (UTC)

Here we again see the vague and ambiguous writing of Sławomir Biały. The accusation that I made a statement regarding Laplace series is totally untrue. If you want to accuse me of saying something wrong then quote exactly what I said rather than make vague allegations with regard to something I did not say. I said absolutely nothing about Laplace series. Your failure to make clear and precise statements causes a lot of confusion. RHB100 (talk) 19:40, 3 March 2010 (UTC)

There is no need to get defensive. I agree with what you wrote below, but I misinterpreted your statement in an earlier thread regarding the center of mass. Sławomir Biały (talk) 22:58, 3 March 2010 (UTC)

The fact is that in order to put the Legendre Series expansion in the proper form for applications, the vectors R and x should emanate from somewhere close to the center of mass. This helps to assure that x < R, a necessary condition for the convergence of the infinite series expansion. RHB100 (talk) 19:40, 3 March 2010 (UTC)

May I ask what the point is of introducing a vector r and even drawing a diagram for it, which does not appear in any of the equations used? TimothyRias (talk) 20:39, 3 March 2010 (UTC)

$V=-\int {\frac {G}{r}}\ dm=-\int {\frac {G}{|\mathbf {R} -\mathbf {x} |}}\ dm,$ where r is a vector from the differential element of mass to point b. r is very important since it is a vector from the mass element to the point at which the potential is being computed. The potential is inversely proportional to r. RHB100 (talk) 01:38, 4 March 2010 (UTC)

Note: an improved diagram has replaced the old diagram to more clearly show the meaning of r. RHB100 (talk) 01:38, 4 March 2010 (UTC)

Notational question

Is anybody opposed to using ${\vec {x}}$ instead of $\mathbf {x}$ for vectors. Due to the difference in font-weight between the normal text and the rasterized TeX it is sometimes hard to distinguish bolded from non-bold TeX. No such confusion is possible with the overhead arrow. Both notations are fairly common in the literature. (I've never quite been able to figure out which communities use what notation. Is it a math vs. physics thing? Or a US vs. EU thing? Or is it purely personal preference?)

Also to me ${\hat {\mathbf {x} }}$ for a unit vector seems like a pleonasm. TimothyRias (talk) 15:27, 3 March 2010 (UTC)

I was under the impression that the manual of style discouraged using notation that would be forcibly rendered inline as a PNG image (like ${\vec {x}}$). At least with my settings, this aligns very poorly with the surrounding text. The article doesn't use mathbf inline, as $\mathbf {x}$, but rather the html bold x, which should be easily distinguishable from the surrounding unbolded text. Sławomir Biały (talk) 18:26, 3 March 2010 (UTC)

Explanation of edit

I have recently edited the article for a number of issues. First of all, the notation of the new section was not consistent with the notation of the previous section (detailed discussion about what notation to use appears in an earlier thread—if you can manage to ignore all of the insults). I also removed some extraneous details on the construction of the Taylor series of the generating function of the Legendre polynomials, this is a well-known expansion and is already amply dealt with in the dedicated article Legendre polynomials. I got rid of the diagram as confusing and unnecessary (this seems to have already been pointed out by other editors above). I also made other tweaks, including an explicit remark on the change to spherical coordinates, and I have corrected to the explanation of why the first moment vanishes. Sławomir Biały (talk) 14:22, 11 March 2010 (UTC)

Sławomir Biały, your editing has degraded my well written section. I am a licensed professional engineer in the field of control system engineering. I hold advanced engineering degrees from both the University of Arkansas and UCLA. What are your qualifications? Just because you by your own admission do not understand the diagram does not mean other people have the same shortcomings as you. Any professional quality person knows that a diagram is absolutely essential in explaining a topic of this type. Note that Meirovich includes a diagram for this topic in the book, "Analytic Dynamics". You need to learn that other people are better able to comprehend and understand than you. Other people do not have the same shortcomings as you. RHB100 (talk) 02:33, 13 March 2010 (UTC)

Ok, so from the above post, the reason you prefer your revision is that there is a diagram in a book. But as I have already pointed out, Patrick has remarked briefly about the lack of need for additional notation (b,r,R,cm), and TimothyRias remarked on the lack of necessity of the diagram. The diagram and additional notation simply make the treatment more complicated, not less so. Sławomir Biały (talk) 12:12, 13 March 2010 (UTC)

I like it better for many reasons, the clarity with which it is written, the generally better quality writing, ... . RHB100 (talk) 21:08, 13 March 2010 (UTC)

Sławomir Biały has the arrogance to destroy my writing by replacing it with his own poor quality writing. But he refuses to tell us the basis of his arrogance. He damages the Wikipedia with his destructive activities but I see nothing in the way of solid accomplishments. RHB100 (talk) 21:08, 13 March 2010 (UTC)

Sławomir Biały is guilty of taking comments out of context in his paragraph above. Neither of the comments Bialty referred to above had any relevance to the diagram, dated 5 March 2010 removed by Bialty, since they were made before the diagram. Furthermore I answered both of the comments and had a useful dialogue with Patrick. RHB100 (talk) 21:16, 13 March 2010 (UTC)

(edit conflict) My modest contributions to the project are a matter of public record, although they are not especially pertinent to the present discussion. Obviously which revision constitutes better writing is a somewhat subjective matter that would benefit from further outside input. User:Ozob has already weighed in favor of this revision (well, one fairly close to that). But subjective issues aside, there are a number of things that can be said quite objectively about this revision, which I would not consider to be a model of good writing. There are unattached sentence fragments, and the formatting is of substandard quality—e.g., $cos\beta \,$ instead of $\cos \beta \,$, $({\frac {x}{R}})$ instead of $\left({\frac {x}{R}}\right)$. The style of referencing is quite homespun. Finally, the notation should at least be made to conform to that of the preceding section, which was ultimately a compromise if you recall. There are also other more subjective things that I had attempted to correct, including: (1) the issue of the diagram (that others at the very least have commented on here), and (2) a mathematically correct explanation for the vanishing of the first-order correction term in the series. Sławomir Biały (talk) 21:26, 13 March 2010 (UTC)

Sławomir Biały, your statement that, others have commented on the diagram is untrue. The diagram that you chose to remove thereby depriving others of the benefits of using is dated 5 March 2010. Others have not commented on this diagram. RHB100 (talk) 22:07, 13 March 2010 (UTC)

TimothyRias' comment: [3]. Patrick's comment on the irrelevance of the proposed "b" notation: [4]. Seems pretty clear to me what they were referring to, but I suppose I might have misunderstood their intentions. At any rate, it is not my intention at all to be dishonest in this discussion. Sławomir Biały (talk) 22:14, 13 March 2010 (UTC)

Bad writing of Sławomir Biały 1: A vector does not designate a point

There are many things wrong with the writing of Biały. One place we can start is by pointing out that a vector does not designate a point. Biały makes the mistake of referring to the point, x, where x is a vector.

A vector has only a direction and a magnitude. It does not have a location. A vector beginning at the point (x,y,z) = (0,0,0) and ending at the point, (x,y,z) = (2,0,0), is exactly the same as a vector beginning at the point (x,y,z) = (5,0,0) and ending at the point, (x,y,z) = (7,0,0). This is true since they both have the same magnitude and direction.

Thus a vector certainly does not designate a point and the writing of Biały shows a failure to understand very basic fundamentals on the nature of vectors and points. RHB100 (talk) 21:55, 13 March 2010 (UTC)

Perhaps this is something of a difference of cultures, but the potential as we have defined it is a function of the point designated by x = (x,y,z). As you say, this is not a vector. Once an origin is chosen, however, then of course x also denotes a position vector: the displacement from the origin to x. There doesn't seem to be much benefit in belaboring this point, although perhaps a link to position vector in the article at the appropriate place would be helpful. Sławomir Biały (talk) 22:07, 13 March 2010 (UTC)

Article needs improvement and is not well written

The article is not well written at present. If you think it is good then you are kidding yourself. Sławomir Biały has managed to destroy the research and original writing of the section, "Gravitational potential expanded in series of Legendre polynomials". RHB100 (talk) 23:17, 14 March 2010 (UTC)

I agree that the article is not particularly well written. This goes for your contributions in particular. Your formatting is extremely sloppy, and your put emphasis on extremely simple things while ignoring the physical relevance of any arguments. Case in point is your in conclusion of a derivation of an expansion of the gravitational potential in spherical coordinates. Instead of focussing on the relevant physics and naming this by its name;(it is a multipole expansion of the potential, which useful far away from the mass distribution, telling you that if your are far away enough you can treat an mass distribution as a point mass, etc.) , you focus on technical details of showing that Legendre polynomial are involved. This could have just as easily have been dealt with by say "For points far away from the mass distribution the gravitational potential can be developed in spherical harmonics" and then giving the expression. And leaving it to the spherical harmonics article to explain the relation with Legendre polynomials. TimothyRias (talk) 08:47, 15 March 2010 (UTC)

Thank you TimothyRias, I will give consideration to what you say. However, I must say that I no longer have a contribution. Although I am the original writer of the section, "Gravitational potential expanded in series of Legendre polynomials", another editor has chosen to completely obliterate my vector diagram and my writing introducing mathematical errors in the process. I wrote the section to take care of an unsymmetrical mass distribution such as the earth. RHB100 (talk) 19:36, 16 March 2010 (UTC)

But if you look at the article you can tell that it is not the work of a Licensed Professional Engineer. The fact that no vector diagram is used indicates that it is probably written by someone who doesn't even have an engineering degree from a top quality American University. The fact that the units of the gravitational constant are not given at the beginning of the section, called "Mathematical Form" indicates that it is not written by a competent engineer, perhaps an unemployed mathematician wrote it but certainly not a competent engineer. RHB100 (talk) 23:58, 16 March 2010 (UTC)

Sorry, but you are only demonstrating the somewhat limited scope of engineers here. Your continuous stressing of your credentials as an engineer is not impressing anyone here (there are plenty of editors around with a lot more impressive credentials.) You do know that the general preconception of engineers in the scientific world is that they are great at calculating stuff, but generally only have a very basic understanding of what they are doing. Your contributions so far have done little to refute that preconception. TimothyRias (talk) 08:56, 17 March 2010 (UTC)

Exactly.

• Consider the target audience of Wikipedia. Consider WP is intended as an encyclopedia. Quibbling over which form of Legendre Polynomial expansionis preferred is missing the point.
• A long expansion is difficult to justify -- if it's copied from a source it's likely a copyright violation, if it's not, it's possibly original research.
• It says right below the "Save page" button If you do not want your writing to be edited, used, and redistributed at will, then do not submit it here. Therefore claims of original ownership and obliteration are irrelevant.
• Anyone can edit. Degrees are not relevant.
• Surrounding discussion points with three single quotes (i.e. bold text) does not make them more compelling.

I've taken a stab at rewriting the lead. Potential is applicable to all classical mechanics, not just celestial, and all objects with mass will create a field, not just massive ones. I've also reordered the sections to, I think, be the most useful for the casual Wikipedia user without advanced math or science education. Gerardw (talk) 12:24, 17 March 2010 (UTC)

Deliberately introduced confusion or poor quality writing

I think it is becoming obvious that the lack of clarity in the article is to a significant degree due to deliberately introduced confusion. Sławomir Biały (alias Slawekb) has removed the diagram which depicted the vectors. If you look at the version in the history of RHB100 on 13 March 2010, you will see that the presence of the diagram certainly makes it clearer and easier to understand.

It therefore becomes pretty much completely obvious that Sławomir Biały (alias Slawekb) has the goal not of clarifying and making more understandable but instead of making the article more confusing and difficult to understand. We don't know the reason for this destructive activity. There are some people who like to send out computer viruses just for the joy of causing problems. There are also people who would like to make less information available on the Internet in order to sell more books.

The statement, "The denominator in the integral can be expanded in terms of the dot product to give ...", is misleading and confusion. The statement, "Expanding the denominator by taking the square root of the square, carrying out the dot product, and factoring R out of the denominator we get the more useful expression,", is much more understandable.

Quoting from the article, "where in the last integral we have changed to spherical coordinates (r,θ,φ) in which r is the distance to the origin and θ is the axial angle with respect to the axis in the direction of x ". This is ambiguous. "r is the distance to the origin", from where to the origin? And why use the indirect language speaking of the origin rather than the center of mass. "axial angle" is a meaningless expression. "with respect to the axis in the direction of x " is meaningless.

RHB100 (talk) 21:38, 14 March 2010 (UTC)

Regarding the explanation of the dot product expansion, I obviously prefer my own version as shorter and more to the point, but there aren't really strong objective reasons for preferring one over the other; a third opinion at least should be required to establish a consensus. Regarding the terminology of spherical coordinates, the present version of the article at least says that spherical coordinates are being used in the integral, which is a significant point that the earlier revision most certainly did not even think worth mentioning. Now while there are obviously some slight variations in how members of different professions (and geographical origins) refer to their spherical coordinates, is this really such an alien concept? Some outside input would be appreciated on this point. (I see that our article spherical coordinates uses the term "inclination angle", "polar angle", or "zenith angle" to refer to θ, any of which is also acceptable to me, although I have no strong preference.) Sławomir Biały (talk) 23:37, 14 March 2010 (UTC)

No consensus

Contrary to the statement [[5]], there's no evidence of consensus. You all should discuss more and edit less, and consider an RFC if you can't come to a reasonable compromise/consensus. Gerardw (talk) 02:15, 15 March 2010 (UTC)

Three different editors reverted RHB's attempts to restore the old revision. I believe this is the consensus that Ozob referred to. If RHB doesn't like this small consensus, then the correct course of action is of course to start an RfC. But as far as my own obligations to discuss, I have discussed every action that I have made to the article. I have made attempts to incorporate every reasonable criticism of the content. And I have done this amid a torrent of insults. Forgive me if I say that I find your unsolicited admonishment most frustrating and unhelpful. Have you actually read this discussion page? Sławomir Biały (talk) 02:47, 15 March 2010 (UTC)

Also, you might care to review the portion of WP:CONSENSUS that refers to how consensus emerges as a part of the normal editing process (this includes the role of reverts in building consensus). My impression is that editors without a lot of mainspace experience typically are unaware of the precise consensus policy, and would do well to review it. Editing and discussion work hand-in-hand, so the solution does not boil down to a facile mantra of "edit less, talk more". Both are necessary parts of the consensus-building process. In the current dispute, RHB made an edit, then I made some edits to that to attempt to seek a compromise. I also posted here for a discussion of what I had changed, and responded to points in turn. Then RHB reverted my edits, but this action was subsequently overruled by two other editors (and then myself just recently). This process is perfectly within the parameters of the normal consensus-building process—and Ozob's observation that a new consensus had emerged is also supported in Wikipedia's notion of consensus as it is codified in our policy. Now while I do share a certain amount of your frustration that other editors do not seem to be participating in discussion (so that the consensus that currently exists had to be achieved through the less desirable WP:BRD-style process), it is perfectly reasonable that the editors might not be willing to "join in the fray" that this discussion page has unfortunately been reduced to. Sławomir Biały (talk) 03:38, 15 March 2010 (UTC)

What the Wikipedia article on Gravitational Potential could be

I add the section below to provide an indication of what the Wikipedia could be. As a licensed professional engineer with advanced engineering degrees from both the University of Arkansas and UCLA, it is clear to me that it is certainly better than the section being used at the time of this writing. In order to make the section clear and understandable, it is absolutely essential that a vector diagram be included. The vector diagram should include the vector from the center of mass to point b, the vector from the center of mass to the element of mass, dm, and the vector from the element of mass, dm, to point b, where point b is the point for which the potential is being computed. The angle between the vector from the center of mass to point b and the vector from the center of mass to the element of mass, dm, should also be included. No coordinate system, not even an origin should be defined since a coordinate system is not needed and would introduce an unnecessary complication. It is only necessary to talk in terms of points in space not points on a coordinate system. The mathematical equations should be written based on the elements in the vector diagram so that the reader can refer to the vector diagram as the equations are read thereby enhancing understanding. RHB100 (talk) 21:00, 15 March 2010 (UTC)

We unfortunately have destructive editors who appear to want to degrade the quality of the Wikipedia. RHB100 (talk) 20:22, 15 March 2010 (UTC)

If you have any suggestions for improvement of the section below then please enter your comments below or perform your editing below. RHB100 (talk) 21:37, 16 March 2010 (UTC)

The below text represents an earlier revision of the article, prior to my own contributions (which were an attempt to streamline and correct this treatment) as well as those of Patrick, and several other editors who contributed to a lesser extent. If you still wish to go back to this, then the correct approach is either to convince people here that the new stable version represents a step backwards over the old one, or to start a RfC to engage other editors in the discussion. I, for one, would rather continue to make improvements to the article's version of the text. Sławomir Biały (talk) 22:23, 16 March 2010 (UTC)

Is thee anybody with good sense who does not believe the section below is far superior to the one that is now in the article? If you believe that the section below is not far superior to the one that is now in the article, then state the reason and your qualifications. Keep in mind that Sławomir Biały did nothing more than essentially copy my original work making changes that greatly degraded the quality of the section. He did not discuss the proposed changes prior to making them. He instead made a sneak attack without allowing for prior discussion. Sławomir Biały contributed nothing but degradation of the Wikipedia through such activities as destroying the vector diagram. It is clear to me as a Licensed Professional Engineer that my original work is far superior to the copying of Sławomir Biały. RHB100 (talk) 02:39, 17 March 2010 (UTC)

Thus far Sławomir Biały's contributions have been of a much higher quality then yours. You should really review the goals of wikipedia in writing articles. The goal of wikipedia articles is not to convince the reader that the material presented is true. (The truth of the material is simply asserted though references.) As such, the extended arguement you give for expanding the potentical in Legendre polynomials is out of place. In the context of wikipedia it is much clearer to simply state that the potential can be expanded is such a way and give the result with a proper reference to literature. Much more important for the wikipedia article is to explain why this expansion is useful. TimothyRias (talk) 09:08, 17 March 2010 (UTC)

I would prefer to keep a very brief description of the Taylor expansion since it may be less intimidating than just saying you can expand in Legendre polynomials. The basic idea is quite simple, even if a straightforward calculation of the coefficients is laborious. Many mathematical articles state things in so much generality that the basic idea is obscured to readers who are unfamiliar with the subject. Obviously the Legendre polynomials should be mentioned as well.

Recent edits and discussion reminded me that people with physics and engineering backgrounds use mathematical terminology slightly differently than those from a mathematical background. Mathematicians tend to switch to nondimensional units as soon as possible, use the word vector in the sense of just a member of a linear vector space, without regard to an inner product, how that vector transforms under coordinate transformations etc. They typically say just integral where a physicist might say volume integral, unless the context requires it. It would be good to formulate this article in such a way that it is accessible to as broad an audience as possible, not just to a specialised mathematical audience. Martijn Meijering —Preceding undated comment added 11:54, 17 March 2010 (UTC).

Gravitational potential expanded in series of Legendre polynomials

For the continuous case the potential, V at point b is computed as an integral over the distributed mass,

$V=-\int {\frac {G}{r}}\ dm=-\int {\frac {G}{|\mathbf {R} -\mathbf {x} |}}\ dm,$

where dm equals density times differential volume, where x is a vector from the center of mass to the differential element of mass, where r is a vector from the differential element of mass to point b i.e. $\mathbf {r} =\mathbf {R} -\mathbf {x} \,$, , and where R is a vector from the center of mass to point b as shown in figure.

Diagram showing vectors, R, x, and r

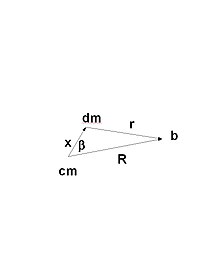
Expanding the denominator by taking the square root of the square, carrying out the dot product, and factoring R out of the denominator we get the more useful expression,

$V=-\int {\frac {G}{\sqrt {R^{2}-2\mathbf {R} \cdot \mathbf {x} +x^{2}}}}\,dm\ =$

$-{\frac {1}{R}}\int G\,{\bigg /}\,{\sqrt {1-2cos(\beta )\left({\frac {x}{R}}\right)+\left({\frac {x}{R}}\right)^{2}}}\,dm.\$ V can be expanded in a series of Legendre Polynomials

Consider the function,

$f({\frac {x}{R}})=\left(1-2cos(\beta )\left({\frac {x}{R}}\right)+\left({\frac {x}{R}}\right)^{2}\right)^{-{\frac {1}{2}}}\ .$

Expanding $f({\frac {x}{R}})$ in a Taylor series about $\left({\frac {x}{R}}\right)=0$, we get the approximation,

$f({\frac {x}{R}})\approx 1+\left({\frac {x}{R}}\right)\ cos(\beta )+\left({\frac {x}{R}}\right)^{2}{\frac {3cos(\beta )^{2}-1}{2}}\ .\$

The coefficients are Legendre polynomials with argument $cos(\beta )$:

$f({\frac {x}{R}})\approx P_{0}(cos(\beta ))+\left({\frac {x}{R}}\right)\ P_{1}(cos(\beta ))+\left({\frac {x}{R}}\right)^{2}\ P_{2}(cos(\beta ))\$.

The appearance of the first three terms of the Taylor series expansion for $f({\frac {x}{R}})$ suggests that the infinite series might follow the same pattern. On page 454, section 10.8 of Theorem 2 which states that $\left(1-2XZ+Z^{2}\right)^{-{\frac {1}{2}}}\ =\sum _{n=0}^{\infty }Z^{n}P_{n}(X)\$, is proven. Also see Applications of Legendre polynomials in physics. Applied to the notation used here Theorem 2 states that

$\left(1-2cos(\beta )\left({\frac {x}{R}}\right)+\left({\frac {x}{R}}\right)^{2}\right)^{-{\frac {1}{2}}}\ =\sum _{n=0}^{\infty }\left({\frac {x}{R}}\right)^{n}P_{n}(cos(\beta ))\ .$

We thus get the result,

$V=-{\frac {G}{R}}\int \sum _{n=0}^{\infty }\left({\frac {x}{R}}\right)^{n}P_{n}(cos(\beta ))\,dm\ {\rm {,}}$

where the $P_{n}(cos(\beta ))$ are Legendre Polynomials of degree n and argument $cos(\beta )\,.$ This is a form which is quite useful for applications as shown in section 11.7 Gravitational Potential ... of . Taking integrals of terms in the series we get:

$V=-{\frac {G}{R}}\int (1+\left({\frac {x}{R}}\right)\ cos(\beta )+\left({\frac {x}{R}}\right)^{2}{\frac {3cos(\beta )^{2}-1}{2}}\ dm+...$

Note that $\int x\ cos(\beta )dm=0.$ This is true since $x\ cos(\beta )$ is the component of the location with respect to the point cm of the differential element of mass along the direction of R as can be seen from the figure. But the point cm is the location of the center of mass. Therefore we get the desired result that $\int x\ cos(\beta )dm=0\$ and that $\int \left({\frac {x}{R}}\right)\ cos(\beta )dm=0\$ since R is invariant over the integral. We therefore get

$V=-{\frac {GM}{R}}-{\frac {G}{R}}\int \left({\frac {x}{R}}\right)^{2}{\frac {3cos(\beta )^{2}-1}{2}}dm+...$

RHB100 (talk) 20:22, 15 March 2010 (UTC)

Comments on Legendre polynomials section in article

This is the beginning of an attempt to merge the best features of the section on Legendre Polynomial expansion as it was originally written with the new version. Some good features of the original version were deleted and some new features have now been added.

The denominator in the integral is expressed as the square root of the square.

There is no conversion to spherical coordinates. There is only a change in notation. Zenith angle does not give any useful information.

Since r =|y|, for simplicity let just call what is now called y, the vector r from the outset.

It is not necessary to understand generating functions.

Although it had looked bad before, with a few edits I think it is already looking much better. Hopefully we don't get any destructive edits.

The statement in article was incorrect, the correct statement is $\int r\cos \theta dm$ is the component of the center of mass in the x direction. The error is attributed to the failure to use a vector diagram. —Preceding unsigned comment added by RHB100 (talk • contribs)

But spherical coordinates are indeed being used: the variables of integration have been replaced by r (distance to the origin) and θ (a zenith angle). While it is also true that it is just a "change in notation", the nature of the change is in specifying a spherical coordinate system, and this is of course significant if one actually wanted to do any kind of calculation. However, it might be easiest simply to eliminate any specification of the coordinate system, and leave the entire thing in terms of the dot products, rather than the cosine of an angle. I think this is probably more satisfactory, since it leaves one free to perform the resulting integral in any convenient coordinate system. This is also very much consistent with the philosophy of using vector notation whereever possible. Ultimately, the point about elongated bodies would obviously require a change to spherical coordinates, but this can probably done at the very end for the purposes of making this single point.

I agree that there is no need to specify a coordinate system. The angle can be easily defined and supplemented with a vector diagram. RHB100 (talk) 19:06, 17 March 2010 (UTC)

While I don't feel tremendously attached to mentioning the notion of the "generating function", this is the standard way to refer to the expansion in physics, mathematics, and (yes) engineering.

But many engineers don't study generating functions and it is not necessary to understand them to use the Theorem. There is still a link to generating functions for those who want to use them. RHB100 (talk) 19:06, 17 March 2010 (UTC)

But the statement of the theorem is exactly that it is the generating function of Legendre polynomials. There is nothing more to it than that. TimothyRias (talk) 21:39, 17 March 2010 (UTC)

The quantity $\int r\cos \theta dm$ is the first moment of the mass distribution about the plane through the origin perpendicular to x (or "moment in the direction of x"). This is the same thing that you are describing, so there was no error. Sławomir Biały (talk) 18:45, 17 March 2010 (UTC)

Why was the statement, "Thus since x is invariant over the mass of the body, the second term in the above expansion vanishes" removed ? RHB100 (talk) 19:37, 17 March 2010 (UTC)

The preceding sentence already explains why the second term in the expansion is zero. This sentence is only likely to cause confusion (since it is not true that the second order term is zero—even though this is the third term of the series). Sławomir Biały (talk) 21:29, 17 March 2010 (UTC)

But how do we know the second term in the series under the integral sign, $\int {\frac {r}{|\mathbf {x} |}}\cos \theta dm=0=$ $\int r\cos \theta dm$ if we do not point out that x is invariant over the mass of the body. I am using some bold here because you have put in so much that it is hard to respond to each of your individual points. RHB100 (talk) 00:21, 18 March 2010 (UTC)

x is just a fixed point (or vector, whatever) for the purposes of computing the integral. I think things are made slightly less clear with the introduction of spherical coordinates, because now there are variables floating around whose precise relationships do not appear in the notation. I am beginning to feel more strongly about the need to change this. Sławomir Biały (talk) 00:39, 18 March 2010 (UTC)

Is it really simpler to belabor the distinction between points and vectors in order to define the integral? Thinking in terms of vectors, r−x is a vector difference. Thinking in terms of points, it is a displacement and |r−x| is just the distance between those points. The latter, it seems to me, is a much more natural way to view it. Now the better part of a paragraph is spent distinguishing between points and vectors, together with the introduction of additional notation that does not appear in any of the equations, diagrams, and so on. For me it is a stretch to think of this as a simplification of the earlier treatment (see my many comments above that have already addressed some of these issues). Also, details indicating that the integral is being taken in a spherical coordinate system have been removed, and to me this is much more relevant. This is obviously a "difference of cultures" between engineering and math/physics. I would be curious to see what other editors have to say. But my druthers is to restore the version of the second sentence:

"The potential can be expanded in a series of Legendre polynomials. For simplicity, assume the origin is chosen to coincide with the center of mass of the system, and identify the points x and r with the associated position vectors relative to this choice of origin."

and leave it at that. Sławomir Biały (talk) 21:43, 17 March 2010 (UTC)

I don't know what I did to elicit the comment, "belabor the distinction between points and vectors". I don't see why there is a problem with talking about r−x a vector instead of |r−x| a distance. I think in terms of both of them more or less at the same time. The paragraph just defines the vectors in simple easy to understand terms. What is the problem? You don't need to talk about an origin. Just talk about points in space, the cm etc. RHB100 (talk) 00:50, 18 March 2010 (UTC)

Now we have already agreed that we don't need coordinate systems. Thus we don't need to define an origin. All we need to do is talk about the center of mass, cm. We don't need to define an origin and then say the cm is the origin. We don't need a coordinate system. We should just talk about vectors and points in space. RHB100 (talk) 00:50, 18 March 2010 (UTC)

If I take this reply at face-value, then it is an agreement that we can go ahead and replace cosθ with ${\vec {x}}\cdot {\vec {y}}/|{\vec {x}}|\,|{\vec {y}}|$ in the expansion? Sławomir Biały (talk) 01:07, 18 March 2010 (UTC)

No, I didn't say that. The use of cosθ certainly does not require the definition of a coordinate system. RHB100 (talk) 01:22, 18 March 2010 (UTC)

Ok, then we are obviously talking past each other here, because that's what I was referring to above. Sławomir Biały (talk) 01:30, 18 March 2010 (UTC)

Another thought: perhaps we should incorporate a suggestion of Tim's systematically. Use ${\vec {x}}$ for vectors and x for points. (I don't like the ad hoc notation of px for the point.) Are there any thoughts one way or another on this suggestion? The first few formulas would then depend on ${\vec {r}}$, and the latter on x (the potential is a function of a point, and the integral is an integral over the points of space). Thoughts? Sławomir Biały (talk) 22:13, 17 March 2010 (UTC)

I've gone ahead and implemented this change, along with some of my other suggestions. Sławomir Biały (talk) 00:39, 18 March 2010 (UTC)

Well you are the one who insists as I understand it that we use the same notation for vectors and points. I chose px to please you. Bold text is best on diagrams for readability. If you don't want to use another notation for points such as point b, then you are forced to use something like px. RHB100 (talk) 00:50, 18 March 2010 (UTC)

I don't really have any recollection of a conversation in which I insisted on using the same notation for points and vectors, although I didn't really see anything wrong with the slight abuse of notation that my older revision indulged in, identifying points with their position vectors relative to a choice of origin. But this is the nature of compromise... Sławomir Biały (talk) 01:07, 18 March 2010 (UTC)

Let's discuss these changes and let's allow other editors to participate before summarily removing my changes. I have tried to make all the notation consistent. RHB100 (talk) 01:14, 18 March 2010 (UTC)

I did not "summarily remove your changes". I reversed one of the edits, because using x to refer to the distance to the origin seems much less natural than using the more standard r. (Indeed, this is very likely to lead to confusion.) I also incorporated what I thought of as the better parts of your edit with some of my suggestions above, but removed other things that I had felt were already adequately discussed (e.g., your diagram). I am perfectly happy to wait a few days for others to comment, but let's agree not to edit the article further during that time. Also, I think you will find that the notation is consistent in this revision of the article, contrary to the implication of your last assertion. Sławomir Biały (talk) 02:18, 18 March 2010 (UTC)

I do not see the need to have separate notations for position vectors and other vectors. "${\vec {r}}$ is a vector pointing from the point mass towards the small body" is almost the same as saying "Let the point mass be at the origin, and let ${\vec {r}}$ be the position vector of the small body". --Patrick (talk) 02:47, 18 March 2010 (UTC)

I was also talking about the section on the monopole expansion. I'm not married to the idea of having separate notations for vectors and points. But RHB has asserted that a firm distinction is necessary. But still, the following line of text seems to me to be quite unnecessarily pedantic:

The vector difference, x - r, thus emanates from the differential element of mass to the "point x" as can be seen in the vector diagram to the right where the "point x" is denoted as px.

Am I the only one that preferred the earlier revision? Sławomir Biały (talk) 03:24, 18 March 2010 (UTC)

Moving on

While I find that being told not to edit until others have had a chance to comment is somewhat contrary to my own vision of Wikipedia, I will honor that request, at least for the time being. For reference, the revisions under dispute here are:

• The old revision, prior to the latest round of RHB's edits [6]
• The current revision, without my modifications, that RHB seems to prefer [7] [8]
• The revision that I made on top of RHB's draft (which was then reverted by RHB): [9]

Please comment. Sławomir Biały (talk) 01:20, 18 March 2010 (UTC)

Update: I have updated the above post to reflect what seems to be RHB's newest favored version, that includes a diagram that I had previously removed (and which is the topic of much of the foregoing discussion). I would ask that, in order to more easily honor RHB's request for comment, that RHB please also refrain from editing the article in the mean time. Sławomir Biały (talk) 02:13, 18 March 2010 (UTC)

I would like to add that I would like to create a new vector diagram for the Mathematical Form section with slightly more appropriate notation as time permits. I put the same version in the Mathematical Form section since there did not seem to be a clear understanding of what we need for notational consistency. I put the diagram in quickly in order to mitigate the damage. RHB100 (talk) 03:10, 18 March 2010 (UTC)

Let's just go back to the notation the way it was before, ok? Then perhaps you can carefully explain why a change was needed in the first place. Sławomir Biały (talk) 03:25, 18 March 2010 (UTC)

Proposed edit

I have sandboxed a version of the article here; diff with current revision. It keeps what I consider to be the better features of RHB's latest round of edits, and eliminates the ones that I think are not as good. As I've already said, this includes the issue of the poor diagram, which has been discussed by several editors. It eliminates the special notation to refer to points, and the somewhat pedantic carping on the "points" versus "vectors" issue. I intend to be WP:BOLD in a few days, and make this edit if there are no cogent objections to it. Sławomir Biały (talk) 03:43, 18 March 2010 (UTC)

What are you talking about you are going to be WP:BOLD . We have just gotten into the process of merging the best features of my original writing of the section with the latest version of the article. This was done with discussion. Many compromises were made to get this done and there are still several issues to be discussed. Among the most contentious is the issue of vague references versus precise references. Also we still have not resolved the issue of showing that the integral of a term in the Legendre Polynomial expansion is zero. You should not make radical changes to your sandbox version. You have done this before causing problems in getting back to where we are now. You should not do it again. You should participate in the discussion and make only consensus changes. RHB100 (talk) 18:58, 18 March 2010 (UTC)

Please, the boldface type is not necessary. I fail to see anything resembling reasonable discussion in the above. At any rate, I agree with some of your edits, and disagree with others. I don't see any discussion about being pedantic about the nature of points and vectors. At any rate, I do disagree with at least this portion of the text, and it is absolutely acceptable for me to undo that portion of your recent edit, as I do not find it an improvement over the older revision. Sławomir Biały (talk) 22:04, 18 March 2010 (UTC)

Comments on Mathematical Form section in article

Notation should be made consistent.

The diagram

I'm very unhappy with the diagram as it currently stands.

• it is included twice
• it doesn't look very nice
• the distinction between position vectors and direction vectors adds little to the article
• it messes up the layout of the article

I suggest we remove it at least until the above points are addressed and until we can find someone who will second its inclusion. Martijn Meijering —Preceding undated comment added 02:23, 18 March 2010 (UTC).

It is included twice because there were some people who did not understand what we need for consistent notation. It doesn't make any difference if it is included twice. It is stored as one file. Your point that it is shown twice is totally irrelevant. RHB100 (talk) 02:53, 18 March 2010 (UTC)

Clarity and precision are far more important than looking pretty. Furthermore I completely disagree with your statement that it doesn't look very nice. I think it looks great. This is nothing more than an opinion on your part. RHB100 (talk) 02:53, 18 March 2010 (UTC)

It doesn't have anything to do with the distinction between position vectors and direction vectors. RHB100 (talk) 02:53, 18 March 2010 (UTC)

It does not mess up the layout of the article. It is small and fits very well into the article. This is nothing more than an opinion on your part. RHB100 (talk) 02:53, 18 March 2010 (UTC)

Please judge more on substance rather than superficial criteria of this type. RHB100 (talk) 02:52, 18 March 2010 (UTC)

I am a licensed professional engineer with advanced engineering degrees from both the University of Arkansas and UCLA.

Would you care to state your background and qualifications. RHB100 (talk) 02:53, 18 March 2010 (UTC)

There's no need to get all defensive (or rude) and especially no need to get personal and to tell people what to do. I found this very annoying. At any rate this diagram looks much better. If other people like it, I'm fine with it. It addresses the points I mentioned. The layout problem only happened if you choose a very large font size. Martijn Meijering —Preceding undated comment added 11:48, 18 March 2010 (UTC).

Such a diagram is fine to me. For flexibility with respect to notation the text could be overlaying the image, e.g. with Template:Annotated image, see Template:Annotated_image/doc/Samples#Simplest. Some irregular example shape around cm containing dm could also be drawn, instead of underlining dm. And some excess white space can be removed.--Patrick (talk) 08:48, 18 March 2010 (UTC)

The diagram to the right is fine provided that y is changed to r, names are given to the points at which the vector x originates and terminates, and preferably the vector x - r is added as a line only. The later may be difficult unless theta is changed from an obtuse to an acute angle. RHB100 (talk) 18:36, 18 March 2010 (UTC)

I have uploaded this diagram and added it to the proposed revision that I announced above. Sławomir Biały (talk) 11:07, 18 March 2010 (UTC)

If the differential mass notation is to stay (see the discussion I started below) it would be good to mark some small area at the end of y to represent the differential mass dm. TimothyRias (talk) 11:20, 18 March 2010 (UTC)

Your working on it i see. TimothyRias (talk) 11:21, 18 March 2010 (UTC)

Yep. I'm not sure why the parentheses are funny. I've seen this on SVG graphics on Wikipedia before. It has something to do with the way Wikimedia processes the thumbnail file (I think). I've asked someone who I think can help. Sławomir Biały (talk) 11:49, 18 March 2010 (UTC)

One option would be to convert the text to path in inkscape. TimothyRias (talk) 12:25, 18 March 2010 (UTC)

Hans just fixed it, but I prefer your solution since the θ isn't rendering in all browsers. Sławomir Biały (talk) 12:35, 18 March 2010 (UTC)

Another minor comment, I think it would look better if the y vector pointed to the center of the mass element.TimothyRias (talk) 15:05, 18 March 2010 (UTC)

Arbitrary break

A new image

I have made another image. This one could go into the "Mathematical form" section, although I admit it is not as pretty as the other one. Sławomir Biały (talk) 23:21, 18 March 2010 (UTC)

dm vs ρ(r)dV

There are basically two options for describing integration measure either dm(r) or ρ(r)dV. Both options occur in the literature and both have advantages and disadvantages. The dm notation as a differencial mass stresses that the integral is a generalization of the sum over a number of discrete masses. On the other hand, it requires knowledge if Lebesgue integrals to make sense of mathematically, making it somewhat inaccessible. Moreover, it obscures where the physical data about the mass distribution is entering in the formulas.

The ρ(r)dV notion, makes it very explicit where the data about the mass distribution is. It is in the distribution (mathematics) ρ(r) (note that this does not have to be a proper function, it can also contain delta peaks, etc.). Moreover, it only requires knowledge of Riemann integrals, as cover in high school calculus. It think the latter is going to be familiar to a much larger group of readers, since most readers that understand the differential mass integral notation, will also understand the volume integral notation. Therefore the latter is preferable on wikipedia to the former, although it is good to mention both.

The only remaining issue is what notation to use for the differential volume element. Common choices include dV, dv, and d³r. The latter is very common in physics literature. It has the advantage of explicitly stating what the integration variable is (r in this case) On the other hand people unfamiliar with the notion tend to get confused by it. TimothyRias (talk) 11:17, 18 March 2010 (UTC)

All good points. I've been a proponent of the ρ(r) notation from the beginning of these discussions. I have a slight personal aversion to using the integral notation with distributions because it can (and does) lead to some very egregious abuses, but obviously I should check these personal feelings at the door. The point about allowing ρ to be a distribution seems to be a very good one. But let me ask, are there any situations in physics where one considers a mass distribution that is not a measure? Sławomir Biały (talk) 11:37, 18 March 2010 (UTC)

I don't think so. Although, there might be some exotic areas where people might consider using something like δ'(x) as an energy distribution. TimothyRias (talk) 12:22, 18 March 2010 (UTC)

I guess if one imposes boundary conditions in some bounded region of space, then there will be a single and double layer corresponding to a monopole and dipole distribution on the boundary of the region. Even so, I think these are both measures, but it might be more natural to treat them as distributions. Sławomir Biały (talk) 12:29, 18 March 2010 (UTC)

Links to Multipole Expansion and Spherical Multipole Expansion

Spherical_multipole_moments linked to what appeared to be a reasonably good article. However, the article linked to by Multipole Expansion did not appear to be as good in my opinion. I suggest we retain the link, Spherical_multipole_moments and remove the link, Multipole Expansion. RHB100 (talk) 19:28, 18 March 2010 (UTC)

The current state of target articles is not a point of consideration in deciding whether to link to a target article. Remember that wikipedia is (and will be for a considerable amount of time) a work in progress. I also disagree that multipole expansion article is bad. It may be a bit technical and abstract, but it contains some good content.TimothyRias (talk) 19:43, 18 March 2010 (UTC)

Alright, if you want to keep it that is fine with me. However, please note I did not offend people by saying it was bad. I only said that it was not as good in my opinion. RHB100 (talk) 20:05, 18 March 2010 (UTC)

Vague reference versus precise reference

I propose that the reference to Wylie be made more specific so that it reads as follows:

The calculations can be simplified by observing that the integrand is the generating function for the Legendre polynomials. Also without knowing anything about generating functions Theorem 2 in section 10.8 on page 454 of can be used which proves that

$\left(1-2XZ+Z^{2}\right)^{-{\frac {1}{2}}}\ =\sum _{n=0}^{\infty }Z^{n}P_{n}(X)$

The time of the engineer, physicist, mathematician, or other worker is valuable. I don't want that worker to have to spend time searching through a long book. I want that worker to be able to pick up a book and go to the specific page that has the specific theorem that he or she needs. This also saves money for the employer and helps to maximize profits. —Preceding unsigned comment added by RHB100 (talk • contribs)

This style of referencing within the text is quite questionable because the sentence "Also without knowing anything about generating functions Theorem 2 in section 10.8 on page 454 of ^[1]" conveys no useful information relevant to the content of the article to the most prospective readers. In fact, it is totally useless to someone without the textbook in question. It seems to me that the pertinent information, that this can be done by Taylor expansion, has already been adequately conveyed in an earlier sentence. So, while I have no objection to referencing this book, it should be done in a less obtrusive manner. So I have moved these bibliographical details into a footnote. Sławomir Biały (talk) 21:58, 18 March 2010 (UTC)

What a line of baloney ! It saves time for the engineer. It helps to maximize profits for the employer. Profits man profits. That is what it is all about. Can't you understand the importance of profits? Are you from a communist country. The Taylor series is only good for a finite number of terms. You say "done in a less obtrusive manner" when profit maximization is involved. What a completely idiotic argument. RHB100 (talk) 22:32, 18 March 2010 (UTC)

I concur with Sławomir. Also, let's not get personal again. I thought we had put that behind us. Mmeijeri (talk) 22:41, 18 March 2010 (UTC)

I checked the Wylie source. It seems to me better to mention the way that he computes the series rather than just give a bald page and theorem reference in the text. I have gone ahead and done this, as well as making a few copyedits that hopefully tighten the text somewhat. Sławomir Biały (talk) 13:41, 20 March 2010 (UTC)

I like this edit. It shows how we can add value by collaborating. I've added another edit to show there are at least three ways of arriving at the same result, from a brute force elementary method, to a much easier but slightly less elementary method using the binomial theorem and finally by a yet more advanced method namely generating functions. Martijn Meijering (talk) 15:30, 20 March 2010 (UTC)

Explanation of edit 2

I see the moratorium on editing is over. In addition to adding the new diagram discussed above, I have addressed the following fairly mundane issues:

1. I changed back to r in the first paragraph of the Mathematical form section. Using x to refer distance to the point seems like more trouble than it is worth. Later in that same section, I have embraced the notation dv(r) as consistent with dm(r), and with the advantage of showing what the variable of integration is.
2. I have removed the pedantry over points versus vectors, and restored the simpler "center of mass at the origin" that was in the article before. (My sense is that there was never consensus of any kind about the need to be pedantic about this: rather I am told that this was inserted because of something that I wrote. So I retract whatever it is that gave this impression. I have given ample time to comment on this above.)
3. Moved the recently-added bibliographic details into a footnote, where they belong.
4. Moved "volume integral" to what seems to be a more natural place—where we are integrating with respect to the volume element.
5. I have removed the diagram from the Mathematical form section, since here x and r do not need to be vectors emanating from the center of mass. In fact, as the article says, they are points in the space, not necessarily regarded as vectors at all. (I believe I have already made this comment earlier. At any rate there seems to be some consensus that understanding is not further served by having this particular image in the "Mathematical form" section, and I do not think the new image is well-suited to it either, although I could easily fix it up given suitable parameters for a good image.)

Please wait before reverting this edit, allowing other editors to comment. Sławomir Biały (talk) 21:49, 18 March 2010 (UTC)

This is not a discussion. This is simply a series of statement without allowance for response. The statement, "I have removed the pedantry over points versus vectors," is not supported by quotes. If you think there is a single example of this then provides quotes and allow me to respond. You are also changing text that you agreed to in a discussion section above. This accusation you make may be something that is due to the superior quality of my education RHB100 (talk) 00:30, 19 March 2010 (UTC)

I already did discuss the pedantry in question. The ironic thing is, I even included a quote of part of the objectionable passage in one of the many threads that you have started above. But again, the following is what I was referring to:

"x is a vector from the center of mass to the point (i.e. "point x") at which the potential is being computed. r is a vector from the center of mass to the differential element of mass. The vector difference, x - r, thus emanates from the differential element of mass to the "point x" as can be seen in the vector diagram to the right where the "point x" is denoted as px."

I think you will find that, similarly, I have brought up each of these points in earlier discussions. And more than one of them had other editors weigh in as well. So, rather than wholesale revert, it might be better to respond to this piece by piece. Sławomir Biały (talk) 01:00, 19 March 2010 (UTC)

You now have a quote but there is absolutely nothing wrong with these statements that I can see. You have failed to show that there is anything whatsoever wrong with these statements. These are perfectly clear definitions of vectors. The x-r vector is very important since the fundamental principle of physics being used in the article is based on the magnitude of this vector. You accusation of pedantry is invalid. RHB100 (talk) 01:36, 19 March 2010 (UTC)

Rebuttal to five points:

I changed back to r in the first paragraph of the Mathematical form section. Using x to refer distance to the point seems like more trouble than it is worth. Later in that same section, I have embraced the notation dv(r) as consistent with dm(r), and with the advantage of showing what the variable of integration is.

To be consistent with the rest of the article, x is used as the vector from the concentrated mass to the point at which the potential is being computed. It has already been done. RHB100 (talk) 03:35, 19 March 2010 (UTC)

I suppose it is not a terribly big deal, but certainly one usually uses r for this. In mathematics, usually x denotes one of the three coordinates in a Cartesian coordinate system, so likely this will lead to confusion. I'm less concerned about the consistency issue. Are there any books that use x instead? Sławomir Biały (talk) 11:37, 19 March 2010 (UTC)

I have removed the pedantry over points versus vectors, and restored the simpler "center of mass at the origin" that was in the article before. (My sense is that there was never consensus of any kind about the need to be pedantic about this: rather I am told that this was inserted because of something that I wrote. So I retract whatever it is that gave this impression. I have given ample time to comment on this above.)

This accusation of pedantry is totally untruee. I have used clear, precise definitions of the vectors involved in the equations. RHB100 (talk) 03:35, 19 March 2010 (UTC)

The issue isn't whether it's precise, rather it is whether it is focused on trivial aspects of the thing (see wikt:pedantic). It is much simpler just to say that we have chosen the center of mass to be the origin and then identified the points x and r with their associated position vectors. I would be happy with a compromise wording, but I am certainly not happy with a paragraph whose only purpose it is to distinguish between points and vectors: this level of detail is clearly inappropriate for an article on the "Gravitational potential". Sławomir Biały (talk) 11:37, 19 March 2010 (UTC)

Moved the recently-added bibliographic details into a footnote, where they belong.

Section and page number are already in reference. RHB100 (talk) 03:35, 19 March 2010 (UTC)

Moved "volume integral" to what seems to be a more natural place—where we are integrating with respect to the volume element.

No comment at this time. RHB100 (talk) 03:35, 19 March 2010 (UTC)

I have removed the diagram from the Mathematical form section, since here x and r do not need to be vectors.

Yes they do need to be vectors for clarity and professionalism. RHB100 (talk) 03:35, 19 March 2010 (UTC)

They can be represented as vectors if you like, but there is nothing about the definition that requires them to be so: much less vectors represented with respect to the center of mass. Thus one has V as a function of the point x in Euclidean space. Say one wanted to write the integral in terms of the observer's frame of reference at the point x. Then one would choose the origin at the point x and locate dm(y) with the vector displacement y−x. But I don't see a reason to make a mountain out of a molehill. The version of the article that I prefer simply does not insist that x and y are vectors measured with respect to the center of mass. I feel like we have already discussed this somewhere, and that we even had some level of agreement about this at some point. Sławomir Biały (talk) 11:37, 19 March 2010 (UTC)

Moving on, again

I would like to state my intention here to restore this revision of the article (diff with current). This edit was reverted by User:RHB100 with the assertion that "consensus" is against this edit. As this seems unlikely to me, I would like to solicit comment on precisely where the consensus lies. See my points 1-5 above (in addition, Ozob made a good edit that I agree with, but which was also reverted under the blanket of "no consensus"). As I've already said several times, some of these points are elaborated on in earlier discussions.

• Support edit, for reasons given. Sławomir Biały (talk) 01:33, 19 March 2010 (UTC)

With all these edits and reversions going on I'm having a hard time keeping track of what's in and what's out. It's also hard to see if any individual changes were lost in the process. Let's not do major edits in a single change. Martijn Meijering 01:40, 19 March 2010 (UTC) —Preceding unsigned comment added by Mmeijeri (talk • contribs)

That is certainly correct. "Let's not do major edits in a single change" It should be repeated again, Let's not do major edits in a single change". Instead of "Moving on, again", lets talk more and edit less as suggested earlier. —Preceding unsigned comment added by RHB100 (talk • contribs)

Well, I thought we were doing that. You even put a message on my page telling me not to edit, so I stopped. But then when you continued to edit the article, I assumed that meant that the time for discussion-not-editing was over. Now even as you post this remark though, you appear to be continuing to edit the article, so I just don't know what to think. Sławomir Biały (talk) 11:42, 19 March 2010 (UTC)

I suggest we discuss each and every issue and make changes only when we have agreement. With regard to the edit of Ozob, he said, "The denominator of the integrand is the square root of a dot product". I cannot tell what dot product he is talking about. It could be $\mathbf {x} \cdot \mathbf {r}$. It is vague, the dot product is a binary operator and therefore you must specify both operands. It is much more clear and concise to just say, "The denominator in the integral is expressed as the square root of the square". RHB100 (talk) 20:09, 19 March 2010 (UTC)

OK, let's go through them one by one. I prefer Ozob's edit. Martijn Meijering (talk) 20:17, 19 March 2010 (UTC)

You've got to do more than just say what you prefer. You must provide arguments and you must provide a precise statement which eliminates the ambiguity. RHB100 (talk) 20:38, 19 March 2010 (UTC)

Why so? Ozob made an edit. The default position of Wikipedia is not "revert all edits unless solid reasons are given on the talk page". This is simply not how it works. Usually good reasons should be given for reverting an edit. (Indeed, one of the pillars of Wikipedia is to be WP:BOLD and to make edits.) As for this particular edit, I don't have a strong opinion either way. But I don't see any compelling reason that Ozob's edit should not be allowed to stand. Sławomir Biały (talk) 21:11, 19 March 2010 (UTC)

Dot product is ambiguous. Dot product is ambiguous. Dot product is ambiguous. Dot product is ambiguous. RHB100 (talk) 00:47, 20 March 2010 (UTC)

Well, "square" is fairly ambiguous too. Probably you mean what some folks might call "vector square", but I don't know if there is any universally understood term for what you mean. Sławomir Biały (talk) 01:08, 20 March 2010 (UTC)

Concur on the similar ambiguity of the word square. I feel the dot product formulation sounds better, but it's not a big deal to me. However, I cannot escape the impression that RHB100 simply wants to retain his version precisely because it is his version. If I'm wrong about this I'd be happy to be better informed. If true, then that on the other hand would be a big deal to me. Nobody owns a Wikipedia page and original authors have no special privileges. I would be strongly opposed to rewarding such behaviour. Martijn Meijering (talk) 15:24, 20 March 2010 (UTC)

Now an important issue to discuss is the consistency of notation. I have gone through and established consistency of notation with regard to the meaning of the vectors. Vector x in all cases is a fixed vector which emanates from an interior point of the massive body to the point at which the potential is computed. The interior point could be the center of mass or a point mass. Vector r in all cases emanates from the same interior point to the differential element of mass. In the case of a concentrated mass, vector r is null. Now that we have this consistency of notation established, we should leave it as it is. Let us discuss this issue below. RHB100 (talk) 20:34, 19 March 2010 (UTC)

Well, as I keep saying (but you apparently continue to ignore) x and y r are just points in space. They do not need to be vectors emanating from any origin (much less the center of mass or a point located in the "interior of the mass distribution"—if by that you mean the support of the distribution). Indeed, a perfectly natural origin for computing the integral would be the point x itself. This isn't really such a huge deal, except that it makes things more complicated than they need to be because suddenly one needs to worry about a choice of origin for the vectors, and this adds an ancillary and totally irrelevant element to the definition of the potential. Sometimes it is convenient to choose an origin at or near the center of mass, such as when computing the multipole expansion, but this has nothing to do with the definition of the potential. See the second image that I presented above for discussion. Sławomir Biały (talk) 21:11, 19 March 2010 (UTC)

We don't have any y. We have x and r. It is very confusing when you talk about y. You are proposing a radical change which is likely to confuse readers. You drew a vector diagram which shows vectors x and r so I don't know what it is you are accusing me of ignoring. The article has been written using vectors. We should not make a radical change. To achieve convergence of the Legendre polynomial expansion, it is important that vectors, x and r emanate from an interior point and there is no reason for doing something weird like having it emanate from an exterior point in any other case. You have given no advantages for making a change. RHB100 (talk) 00:54, 20 March 2010 (UTC)

Sorry, I meant r, not y. Look, V is what physicists would call a scalar field. It depends on a point of space, not on a vector. (I am surprised at the need to be explaining this to an engineer, but I don't really understand all of the various cultural differences that pervade our various related-but-distinct quantitative disciplines.) There are plenty of sources for this; see, for instance, Marion and Thornton. It is not controversial in any way. Sławomir Biały (talk) 01:06, 20 March 2010 (UTC)

As an example of why vectors are necessary consider the case of a unit vector. A vector is characterized by a direction and a magnitude. The direction property of a vector is essential in understanding the meaning of a unit vector. A point does not have the property of direction. A point is neither a vector nor a scalar. It is just a primitive geometric entity.RHB100 (talk) 01:14, 20 March 2010 (UTC)

Yes, vectors are absolutely essential in many situations. But this isn't one of them. Sławomir Biały (talk) 01:18, 20 March 2010 (UTC)

Please compare the Google books search for "gravitational potential at a point" [10] (over 400 hits) with the Google books search for "gravitational potential at a vector" [11] (no hits). Sławomir Biały (talk) 01:27, 20 March 2010 (UTC)

I have my own books. Read section 11.7 of Meirovitch, "Methods of Analytical Dynamics". No professional quality person would attempt to describe gravitational potential without using vectors. RHB100 (talk) 03:02, 20 March 2010 (UTC)

Another reason you need vectors is because the need to perform a dot product arises in the derivation of the Legendre polynomial expansion. You certainly cannot take a dot product of two points since points have neither magnitude nor direction both of which are necessary for dot products. RHB100 (talk) 05:04, 20 March 2010 (UTC)

You say "Huh?" below. Let me repeat it, You certainly cannot take a dot product of two points since points have neither magnitude nor direction both of which are necessary for dot products. You certainly cannot take a dot product of two points since points have neither magnitude nor direction both of which are necessary for dot products. RHB100 (talk) 21:49, 20 March 2010 (UTC)

Got it! One more time in case you missed the first three. RHB100 (talk) 21:49, 20 March 2010 (UTC)

You certainly cannot take a dot product of two points since points have neither magnitude nor direction both of which are necessary for dot products. RHB100 (talk) 21:49, 20 March 2010 (UTC)

I never asserted that you could. This is probably part of the reason for my reaction below: you seem to be convinced that I have said things that I never have. Sławomir Biały (talk) 22:59, 20 March 2010 (UTC)

Huh? The potential at the point x is

$V(\mathbf {x} )=-\int _{\mathbb {R} ^{3}}{\frac {G}{|\mathbf {x} -\mathbf {y} |}}\,dm(\mathbf {y} ).$

There is no need to introduce a further point of origin in order to regard x and y as vectors, at least not unless one wants to perform a multipole expansion. Introducing an origin earlier on is just an unnecessary further complication to the definition. And you haven't answered my challenge above: why is it that in every book I have consulted, the potential is defined "at a point" rather than "at a vector"? You may want to compare our treatment with the article by the well-known Russian potential theorist: Solomentsev, E.D. (2001) [1994], "Newtonian potential", Encyclopedia of Mathematics, EMS Press. Also, some authors use a notation like

$V(X)=-\int _{\mathbb {R} ^{3}}{\frac {G}{r_{X,Y}}}\,dm(Y)$

or, possibly,

$V(X)=-\int _{\mathbb {R} ^{3}}{\frac {G}{d(X,Y)}}\,dm(Y)$

in which some auxiliary notation for the distance between two points has been introduced. This seems to me to be unnecessary. Sławomir Biały (talk) 10:50, 20 March 2010 (UTC)

Also, the repeated insinuation that I am not a "professional quality person" is not appreciated. I understand that you are frustrated—I am too. But there is no need to resort to personalized rhetoric. Sławomir Biały (talk) 11:08, 20 March 2010 (UTC)

Concur. Martijn Meijering (talk) 15:24, 20 March 2010 (UTC)

The accusation that I have engaged in pedantry is not appreciated. To make that dishonest accusation toward a licensed professional engineer is totally lacking in professionalism. RHB100 (talk) 21:45, 20 March 2010 (UTC)

There is no need to prove that vectors are absolutely essential. The fact is that vectors work. Vectors are what I used to create the section now called Multipole Expansion. When you start calling entities with magnitude and direction points, you are just showing that the writing was done by a poorly educated person who doesn't understand the important distinction between vectors and points. RHB100 (talk) 21:45, 20 March 2010 (UTC)

If by "poorly educated person", you mean someone that would define the potential as depending on a point of space, then I am afraid you will find nearly every physicist and most engineers wanting. I have already given you fairly compelling evidence to that effect in an earlier post. WP:IDIDNTHEARTHAT appears to be getting increasingly relevant to our discussion. Sławomir Biały (talk) 22:59, 20 March 2010 (UTC)

RHB, you are only betraying your own lack of education here. To most educated people (which sadly does not seem to include engineers) a vector is a point in a vector space. Many texts simply treat position space as a vector space, in which case any point in space IS a vector. This treatment may seem weird because addition of points in space is physically meaningless. The actual vector space structure is inherited from the tangent space at any point. Because position space is flat, exponential map which maps the tangent space at a point to a patch of position space is (locally) an isometry and can thus be used to induce a vector space structure on position space. This is a very useful trick, which used (without any really explanation) in almost any physics textbook. TimothyRias (talk) 10:54, 22 March 2010 (UTC)

I have a different favorite way of looking at position space, namely as a torsor (= principal bundle) over a point with structure group Rⁿ. This is almost the same as what you're doing. The advantage is that you really can take the difference of two points. The way to take this difference is to designate one of the points as the origin of a vector space (which you can do because a point is a section of the bundle), then find the vector space difference of the two points; of course the vector space structure that you get is the same as the one you get by exponentiating. This isn't relevant to the article, but I thought I'd point it out because you don't ever need to introduce the exponential or the tangent space in this approach, so it's a little simpler. Ozob (talk) 22:14, 22 March 2010 (UTC)

I do not know who did the editing and drawing but the figure, caption, and text description of x and r in the Mathematical form section display a complete lack of competence in understanding the difference points and vectors. Points have neither magnitude nor direction. The difference in points is not defined since points are just primitive geometric entities. If it is supposed to designate another point, then it is improper to take the magnitude of a point. RHB100 (talk) 03:20, 21 March 2010 (UTC)

I already indicated earlier, there are other notations that we can consider using for the distance between two points. You seem to feel very strongly that the notation |x − r| should be abandoned. I've already given one source in this discussion that uses this notation, and others can be given, and there are reasons for mathematicians to prefer this to the other ones, like r_xr or d(x,r), chiefly because the geometrical significance of the integral as a convolution becomes clearer. But I am not married to this notation, and I am open to a reasonable discussion here. Do you feel that using d(x,r) as the distance between the two points improves the clarity of the article? Sławomir Biały (talk) 12:20, 21 March 2010 (UTC)