Talk:Function (mathematics)/Archive 10

This is an archive of past discussions about Function (mathematics). Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page.

Archive 5

←

Archive 8

→

Towards GA status

I had asked Jakob.scholbach for advice on how to advance this article to Good Article (GA) status, because he has experience advancing several mathematics articles to GA and/or FA status. In the sequel, he gave suggestions for improving the article on the talk page and also carried out several of these proposed changes. From the discussion that followed, I gather that the new version of the article is basically ok, although a few concerns were raised:

I'd separate out the history section into something like "history of the function concept" first
Comment: Agree. There should be a summary of the present history section in this article with a link to the main article.
I'd like to say I think the example of apples is terrible. There is no implicit way of distinguishing them and also having both four colours and four apples is asking for trouble
Comment I'm not very convinced about this example either. I would suggest an example with a telephone list for the colleagues in an office (domain). All telephone numbers have a certain prefix (codomain). Two or more colleagues may share the same number, so the function is not 1-to-1.
Also the triple definition of a function seems to have disappeared and the function is a pure set of pairs has been moved to an alternative. I think it is right that the discussion of a function without saying f from A to B be done separately but it shouldn't be shoved to the end like that
Comment It seems reasonable to pick one valid definition for the first article section and discuss variants later, in order not to confuse the reader, but there has been a lengthy discussion about the formal definition and hopefully we can reach consensus soon.
there was an earlier agreement or understanding at least, that major changes to the article were to be the subject of discussion in here first. I remain with the impression that the net effect of recent changes has not resulted in an improvement of the article.
Comment The agreement was not to make major changes to the beginning of the lead without first discussing them. Also, the changes to the article were announced first on the talk page. If the recent changes have not affected the article quality substantially, it might be a sign that the article is ready for promotion soon.
The article needs to begin with a statement that is accurate but is something a non-mathematician can understand. All that is necessary at that level is an imput and an output and some examples. Where the input and output come from, and how one gets from one to the other, are questions that are too technical for the non-mathematician and already understood by the mathematician.
Comment This is an encyclopedia, not a textbook. Instead of simplifying the description to a machine with inputs and outputs, I think we should provide good everyday examples that illustrate the properties of a function without assuming too much mathematical background. However, feel free to suggest a statement that is accurate, yet easy to understand.

Are there more concerns regarding the present article at this stage? Isheden (talk) 13:35, 31 July 2012 (UTC)

I think there is (unfortunately) no getting away from the fact that there are two valid definitions in common use; the article does not reflect this reality properly. Formal definition should not begin by saying that a function is not a rule, it should start off by saying there are two definitions in common use.....Selfstudier (talk) 14:45, 31 July 2012 (UTC)

Also, Formal Definition(s) should be limited to precisely that, formal definitions; toy examples and other things should be in another place.Selfstudier (talk) 14:54, 31 July 2012 (UTC)

---

Per discussion above and apparent agreement I moved the history section to History of the function concept. Almost all the references and footnotes when with it. I suggest someone else write the summary, the effort needs new eyes, more a mathematician's eyes than a historian's. Here's a place to start: Historically there are a few deep trends. The first trend began with the intuitive notion of "mathematical formula" aka algebra (i.e. symbols as "unknowns") from this deriving analysis and the need to graph the behavior of a mathematical formula with respect to the "unknowns" when they're assigned values, then the idea of ordered pairs as derived from set theory, then the idea from computation of a "function box" and tabular lookup (e.g. Turing machines; I have not seen any earlier formal expression of a "state table" anywhere). With the Logicists we see the ernest attempt to axiomatize, formalize and locate the philosophical "essence" of mathematics, starting in ernest with Dedekind's The Nature and Meaning of Numbers, then Peano and Frege, culminating in Russell; here we see the formalization of the idea of a relation, and then its restricted form -- the functional relation -- that dodges consistency violations [cf Hartley Rogers 1967]. These ideas were taken further by the set theorists (not clear where the bifurcation began and why) in an attempt to resolve problems with PM, in particular the axiom of reducibility. Since Bourbaki 1939 we've see almost every mathematician on the face of the earth creating their own symbolisms and formalisms and definitions.

The article's looking pretty thin now. Especially the references. BillWvbailey (talk) 15:09, 31 July 2012 (UTC)

That has really cleaned things up I think, thanks very much. I've done a tiny amount of tidying at the history article adding categories and suchlike, I'll copy your comment above over as a first comment on the talk page of the history article, hope that's okay with you. Dmcq (talk) 15:46, 31 July 2012 (UTC)

I deleted the fist sentences under Formal Definition, the stuff about not formally being a rule. One shouldn't start off the definition by stipulating what a function is not...; the Introduction and Definition section already has a rule based description and describes it as intuitive which should be sufficient. I suppose those sentences could go somewhere else, not sure where though...Selfstudier (talk) 17:01, 31 July 2012 (UTC)

I would like to suggest that we could perhaps usefully base our definitions on the following up-to-date text, available online [[1]] as well as from Amazon [[2]]. He has made a reasonable effort at catering for all interests.Selfstudier (talk) 23:16, 31 July 2012 (UTC)

I think the exposition in the chapter about functions is excellent. It's easy to read, yet accurate. We could use it as a basis fro this article also. What do other people think of it? Isheden (talk) 12:12, 1 August 2012 (UTC)

I see we are reverting to the usual edit war, think I will leave everyone to it, enjoy.....:-)Selfstudier (talk) 09:02, 1 August 2012 (UTC)

May I suggest that editing be done in phases like:

Phase 1 remove stuff or merge from elsewhere. Has been done by removing the history section.
Phase 2 move stuff around in the article till the structure is about right but not inserting or removing material.
Phase 3 add new material added or remove material without moving things around.
Phase 4 tidy up and fix the lead.
...go to the beginning again

The essential here is not to move things around at the same time as adding or removing material, doing both at the same time makes life extremely difficult. Are we happy that the overall order of the sections is right first before changing the material? I am not. I believe the pairs and triple definitions should be moved up to a separate section after the definition of a function which should deal with the common part of a function from X to Y. Dmcq (talk) 09:49, 1 August 2012 (UTC)

That sounds like a small change. Do you fear lack of consensus for such a change or does the article need more fundamental restructuring in your view? Isheden (talk) 10:10, 1 August 2012 (UTC)

@Selfstudier I think all your points raised above are good, so why not go ahead and expand the article based on the wealth of references that has been presented on this talk page? Perhaps you would be interested in working on a summary of History of the function concept, given your interest in the history? However, just deleting sourced statements is probably not the way forward right now, since we need more references at this stage, not less. Isheden (talk) 10:00, 1 August 2012 (UTC)

I agree with most of what's said above. At this stage, let's not worry too much about the level of this or that heading etc. This is details. Also, I can only invite everybody not to waste too much ink on the talk page, but rather work on individual sections of the article proper. In order to advance the article closer to GA level (it is currently far far away from that), we need, IMO:

flesh out the section on "Specifying a function"
flesh out the section on different types of functions. Here, we should focus on a few basic classes of functions. We should not attempt creating a complete glossary of [xxx function] (where xxx is any mathematical property applicable to functions).
Many of the sections are now in a roughly cleaned up state, but need more explanation. E.g. image and preimage should be illustrated with an example, possibly including the graph of a function etc.
Round off the generalizations section.

A final word about the "codomain-less" definition: I hear the sentiments of some editors that this is highly important. However, in the interest of an easily accessible article, we have to stick to one definition in the main part of the article. And this will be the "usual" definition of f: A to B. While the codomain-less definition may be of some interest to scholars etc., the quasi-totality of readers will rightfully(!) not be interested in formalities. Those will have a hard time digesting this (even if some claim this to be an easier definition). So, I'd suggest: carve out a clean and good presentation of the usual definition in the main part of the article. At most, give one hint that there is another definition given below at that point.

Jakob.scholbach (talk) 12:12, 1 August 2012 (UTC)

I agree we should give priority to the "usual" definition of f: A to B. However, all four groups define f: A to B, whether or not B is considered an attribute. In the Wiki spirit, we should have a reliable source pointing out which is indeed the most "usual" before we can decide on priorities. Boute (talk) 14:21, 1 August 2012 (UTC)

I see that someone replaced the "color-of-the-apple" by "color-of-the-shape" function, which is a good idea. Could someone volunteer to create an illustration? That would simplify explanations a lot. Jakob.scholbach (talk) 12:14, 1 August 2012 (UTC)

Boute, believe me that the quasi-totality of sources defines a function as as subset of X x Y with fixed X and fixed Y. There is no doubt that this is the major definition. See e.g. Encycl. of Maths. I am no longer inclined to discuss this issue. We do have a separate section on the domain-less definition and this is definitely enough and, from all I can see, this is the article design we need to take here. Jakob.scholbach (talk) 19:16, 1 August 2012 (UTC)

I do believe you, because I know you are right. However, it leaves open the question how much of that "fixed" X and Y can be inferred from individual functions. Given such a function (subset of X x Y) by itself as a mathematical object, without the introductory text, what is X and what is Y? We all know the answers to that, as well as the diverse design choices they entail. Boute (talk) 07:42, 2 August 2012 (UTC)

Illustrations

I don't have a decent vector-graphics program, only Autodesk SketchBook Pro which yields bit-map images. Also, I can't draw decent hexagons, so I drew a 6-sided polygon. The color yellow is very difficult, graphically, so that is why the shapes have black borders. Also, colorblind folks may find this example offputting. Anyway, what the example described is what I drew, with liberties re the order of the objects and the polygon. BillWvbailey (talk) 15:04, 1 August 2012 (UTC)

Looks good. Could we have five colours perhaps thanks?, say include purple or black. That way someone would be certain five refers to the coluurs and four to the shapes. p.s. perhaps the diagram should be checked against WP:Accessibilty somehow to check the shades are different in black and white though I don't suppose it maters much as there are arrows. Dmcq (talk) 17:13, 1 August 2012 (UTC)

Earlier, the article had the example of the function that sends A to 1, B to 2, C to 3, and so on. This was replaced with shapes to number of sides and apples to color. Then these were replaced by polygons to number of vertices and colored polygons to colors. Given the problem with accessibility to people who are color blind, why not go back to f(A) = 1, f(B) = 2, ... ? Rick Norwood (talk) 17:26, 1 August 2012 (UTC)

Thanks for creating it! I think the colors are OK, but User:KSmrq has the optimal colors as far as distinguishability for color blind people is concerned. Maybe we can use them? In any case, we need to accompany the picture with a careful text, so this will not be much of an issue. Jakob.scholbach (talk) 19:16, 1 August 2012 (UTC)

I didn't see your note re User:KSmrq until after I'd created the second image with 5 colors per Dmcq's question. I can probably come pretty close to KSmrq's colors (he uses only 4, ditto for the links re accessibility). I did look at the accessibility issue and it's really complicated because of luminosity as well as the { red, green, blue } pixelations of computer screens. I'll try Ksmrq's colors with a fifth (violet). Bill Wvbailey (talk) 20:40, 1 August 2012 (UTC)

Interesting. These are KSmrg's colors excepting the violet, which I toned down from true RGB (255, 0, 255). I have excellent color vision but I like this third image the best. "Yellow" is much better. BillWvbailey (talk) 21:06, 1 August 2012 (UTC)

I like the third image more, too, but I also have good color vision. More to the point I checked with a color-blind friend and he said the third image was much better: the green and yellow of the first two images are too close to each other. —David Eppstein (talk) 21:37, 1 August 2012 (UTC)

Excellent. Thanks, Bill. Would you be willing to create a picture illustrating "image" and "preimage", as well? This would help a lot, I guess (I'm thinking of a cubic function and highlighting parts of the axes). Jakob.scholbach (talk) 21:42, 1 August 2012 (UTC)

Bill, you may try [3] for svg export (free and quite good once you get in the swing of it) 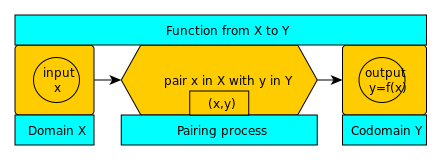— Preceding unsigned comment added by Selfstudier (talk • contribs) 22:56, 1 August 2012 (UTC)

Illustrations: image & preimage

This is the world through newbie eyes: I'd heard of "image", but not "preimage". So I have to read the lead sentences under "Image and preimage". Then I read it again. Then I read Image (mathematics) and then I go to bed. This AM I ask myself "What is the difference between codomain and image?" So I read the Codomain lead, and see the same drawing (exactly the same). In my undergrad days there was the "range" and that just adds to my confusion. So, I read further and I see that this confusion of terms is rampant. I take it, in the drawing above, the range/image/codomain is colors: { RED, YELLOW, GREEN }. If we pick the element RED, then the preimage is { red-triangle, red-square }, correct? Anyway the sketch is what I think, the preimage is when applied to a continuous function. I can't begin to imagine where the teensy dots came from. If this is what folks want to see, I'll see if I can rid the drawing of the dots. [BTW this was a challenging drawing]. BillWvbailey (talk) 16:35, 2 August 2012 (UTC)

Yes except the range can be either the image or the codomain dependent on the author, and the codomain is all five colours. The image of the function applied to the whole domain is the three colours red, green, and yellow. Yes the preimage of either red or the set containing just red is the set of the two red shapes, it's best to think of them as always applying to sets. You can get an image or preimage of any subset of the domain or codomain. Dmcq (talk) 16:48, 2 August 2012 (UTC)

Thanks, yes, I see now, I think: the image is a restriction of the codomain by the function. Here's another attempt at the continuous function drawing. The artifacts destroyed the bottom layer of the original tif drawing, but in trying to recover what wasn't corrupted, I find that this second drawing is quite a bit clearer. (This problem of artifacts has plagued me and I've written Autodesk about it but they could give a shit.) So lemme know what you think about this one. BillWvbailey (talk) 17:29, 2 August 2012 (UTC)

That's what I call learning by doing :) The illustration is tip top, however, the axes seem to be 2 pixels wide in a few spots and 1 in others. Can this be fixed? (Maybe create a bigger picture. It can always be shrunk by the thumbnail function of WP.) I would probably drop the (x-1)(x-3)(x-5), since this is not relevant to illustrating the preimage. If there is still space (or otherwise in a second picture), we could also use an illustration for the image: highlight a portion of the x-axis and the corresponding bit in the y-axis. Jakob.scholbach (talk) 17:38, 2 August 2012 (UTC)

The width-change of the X-axis was intended as emphasis -- mirrored at the bottom of the drawing with the closed intervals -- but I can fix the axes. (The drawing is already pretty large -- page-size (although the files aren't)). I'll see what I can do about adding the "image". I thought about this, but was worried about clutter. I'll give it a shot. Am working on the sqrt drawing, too, that was a weird one to graph in Excel, but I got it :). [I've removed the first drawing with the artifacts]. Bill Wvbailey (talk) 17:59, 2 August 2012 (UTC)

I've added the drawing with both the preimage and image indicated. BillWvbailey (talk) 19:01, 2 August 2012 (UTC)

I've added directional arrows. Perhaps this helps. Perhaps not. BillWvbailey (talk) 21:00, 2 August 2012 (UTC)

If you mean those on the x and y axis, I think not. I wondered what they were in aid of. Dmcq (talk) 22:11, 2 August 2012 (UTC)

I meant the colored ones. I don't like the arrow-heads on the x and y axes, either. BillWvbailey (talk) 23:19, 2 August 2012 (UTC)

No I'm not keen on the coloured arrows either sorry. What are they supposed to convey? Why would one go along the red ones down the green ones and back along the blue ones is the sort of obvious naive question I'd have though some people might think! Dmcq (talk) 09:40, 3 August 2012 (UTC)

I can't seem to make the axis arrows go away. For some reason wikipedia isn't honoring the revision. I may have to upload a whole new file. But I'll wait awhile; maybe there's a cache somewhere that has to be cleared (but it's not in my computer). As to the colored arrows: I see them as the same as the arrows on the "discrete" examples i.e. x to f(x) and f(x) to x. Plus they help me figure out where to start, especially wrt the preimage which is rather "unusual". I'll let you and Jakob.S et al work that out. (I understand your concern about the newbie wondering about whether they have to go around in a circle, a hazard of both image and preimage in the same illustration with the arrows). Bill Wvbailey (talk) 13:55, 3 August 2012 (UTC)

Actually I like the colored arrows. They give a more graphical imagination for the (pre)image than the mere definition. However, maybe we could rather have separate 2 pictures, one with the image, one with the preimage. This resolves the point raised by Dmcq, but also enables us to extend the green and yellow areas below and above the x-axis, respectively (which they should, exactly as in the first version). Jakob.scholbach (talk) 13:53, 3 August 2012 (UTC)

Another option is to just use two colours instead of four and keep the big arrows in the one diagram, one colour for image and the other for preimage. I'd vote for the red and blue. Dmcq (talk) 14:10, 3 August 2012 (UTC)

---

Here are 3 more, per the above discussion: image only, preimage only, both together (I'm part Scottish but this does not quite meet my requirements for the Innis plaid). BillWvbailey (talk) 18:53, 3 August 2012 (UTC)

Multi-valued functions

What is the simplest concrete (interesting) example of a multi-valued function? Currently I can only think of complex logarithms and roots, which are a bit beyond this article's intended audience. Ideally, we also have an illustration ... Jakob.scholbach (talk) 21:46, 1 August 2012 (UTC)

A circle? BillWvbailey (talk) 00:39, 2 August 2012 (UTC)

The concept of multi-valued functions could be introduced after the Inverse function section. The inverse of f(x) = x² is multi-valued. Gandalf61 (talk) 07:20, 2 August 2012 (UTC)

I guess by circle is meant point on circle to angle which is a good one. I can't see anything wrong with square root either myself. Dmcq (talk) 07:22, 2 August 2012 (UTC)

Inverse of x^2 is a good idea. Don't know why I didn't come up with this ... Someone up to writing a few words about it in the multi-valued section + creating a picture? Jakob.scholbach (talk) 08:09, 2 August 2012 (UTC)

The colleague to telephone example in fact sometimes is multi valued! I once had three different desks on three different floors of a building ;-) Dmcq (talk) 09:20, 2 August 2012 (UTC)

Here's the square-root function illustration. I'm trying to convey the idea that in goes +9 and out comes -3 and +3, and the "function box" is the blue curve. Clearly what appears to be a inconsistency violation has to be resolved. A good demo of a relation as opposed to a functional-relation. You gotta love it. Bill Wvbailey (talk) 19:58, 2 August 2012 (UTC)

Again, thank you. The illustration is good, except for the heading: sqrt(x) is commonly defined (only) as the positive square root. Can we have

f(x)=\pm {\sqrt {x}}

instead? Jakob.scholbach (talk) 08:32, 3 August 2012 (UTC)

Yes, we'll see how it looks. I removed the arrows from the axes, changed the "density" of the orange lettering just a hair. BillWvbailey (talk) 13:38, 3 August 2012 (UTC)

I remember a 1970's paper (when time permits, I'll look it up) stating that the term multi-valued function was being deprecated in mathematics and discouraged in education. Of course, older literature uses the term routinely, and we don't want to make that inaccessible. There are many ways to fulfil the role of the earlier multi-valued functions rigorously. The evident ones are

Relations, e.g., y iSqrt x <=> y² = x (suitably quantified, not pursued here)
Functions with sets as images, e.g., for real numbers,

Sqrt : R → Pow R with Sqrt(x) = {y : R | y² = x}, where Pow denotes powerset (set of subsets)

Obvious refinement: Sqrt : S → Pow T with Sqrt(x) = {y : T | y² = x}, where S and T can be separately chosen to be natural, rational, real, complex numbers, as desired.

Note: similar situations can arise with equations, e.g., for quadratic equations,

Sol : S³ → Pow T with Sol(a, b, c) = {x : T | a x² + b x + c = 0}.

If multiple roots are to be distinguished, multisets (bags) can be used instead of sets.

Maybe this helps. Boute (talk) 12:38, 3 August 2012 (UTC)

Well the everyday examples beside square root and complex numbers are the inverse trig functions and they are the inverse of straightforward functions. I'd guess most people just try and deal with a function on a covering surface instead if possible as it makes life much cleaner. Most other uses would just talk about a many to many relation. Anyway the article about that is where any material should go, and the subsection here mainly just copy the lead. Dmcq (talk) 17:49, 3 August 2012 (UTC)

I will be out of town for two weeks, so I cannot work on WP. However, I'm looking forward to finding a much improved article :) by you guys. Jakob.scholbach (talk) 18:07, 3 August 2012 (UTC)

this page was unclear, i made this edit -- http://wiki.riteme.site/w/index.php?title=Function_(mathematics)&diff=516518596&oldid=515853973

this page was unclear, i made this edit -- http://wiki.riteme.site/w/index.php?title=Function_(mathematics)&diff=516518596&oldid=515853973 — Preceding unsigned comment added by Coginsys (talk • contribs) 10:36, 8 October 2012 (UTC)

Unfortunately your version "a function is a group of inputs and outputs with each inputs corresponding to each output" is hard to understand because (1) in mathematics the word group has a specific technical meaning but you are probably not using it with this meaning and (2) the phrase "each inputs corresponding to each output" is ungrammatical and ambiguous. Your edit did not improve the article, and it was correctly reverted. Gandalf61 (talk) 11:52, 8 October 2012 (UTC)

What does f⊑g mean?

(Sorry to ask this here--it's a question on mathematics rather than this article, but I'm not sure where else to look for this.)

I recently read a paper that used the notation "f ⊑ g" without defining the symbol "⊑". f and g were functions. Does this notation mean anything to anyone? --Doradus (talk) 04:11, 4 November 2012 (UTC)

You may want to ask questions like this at the reference desk, or more specifically, the mathematics reference desk. The notation could refer to the order relation between partial functions, i.e., "f ⊑ g" could mean that g is "more defined" than f. If you identify functions with their graphs, this could also be written as "f ⊆ g". (The notation "f ≤ g" is often used to imply pointwise order.) — Tobias Bergemann (talk) 07:27, 4 November 2012 (UTC)

Thanks very much. I didn't know about the reference desk. --Doradus (talk) 22:48, 11 November 2012 (UTC)

Clarification needed in "Notation" section

It is my opinion that the Notation section of this article needs clarification so that novice readers like myself can understand it. For example, I had never seen the $f:X\rightarrow Y$ notation or the $x\mapsto {\text{'some expression'}}$ notation that sometimes followed it until I read this article. Could somebody add an explanation of where this notation came from to this section of the article or its counterpart in the article that discusses the History of function notation if he or she hasn't already? Also, does similar notation exist for single-line functions in a way that utilizes the more-common f(x) notation while still allowing the definition of a function's domain and range alongside its definition? It would help me in fixing an explicit definition that I have (most likely incorrectly) written down for the function $P(A:A\in {\mathcal {P}}(S))=({}^{|A|}/_{|S|}:P(A)\in [0,1])$ giving an event's probability in the case that the function's domain is the sample apace s containing such an event A and its range is the interval from 0 through 1, inclusive. Speaking of which, how would I fix this function with correct formatting as prescribed by set theory so as to evaluate only the function given such an event A inside its given sample space S without setting each side of the equation defining the function equal to each other? Should I ask at the mathematics reference desk? — Preceding unsigned comment added by BCG999 (talk • contribs) 21:58, 24 November 2012 (UTC)

Yes. Rick Norwood (talk) 00:29, 25 November 2012 (UTC)

Definition of a Function using Quantifier ∀ (for advanced readers)

Though not widely used for some reason, I have found the following definition of a function to be useful. Given sets A and B, f is said to be a function mapping A to B iff

∀x∈A (f(x)∈B)

or equivalently

∀x [x∈A → f(x)∈B]

Built into this notation is the fact that every element of A has unique image in B. By a simple substitution, we have:

f(a)=b ∧ f(a)=c → b=c

See First-Order Logic, Universal Quantification

I have made an edit to the Notation section.

Danchristensen (talk) 16:26, 5 December 2012 (UTC)

No, this is quite inaccurate, and surely misleading. First, to make it precise, you should clearly explain what a "function symbol" is in first order logic, which itself is at least as long as defining what a function is. Second, and more important, the

f

in the formula is not a function, but just a symbol "representing" a function, so you should deal with interpretation and so on and on...--78.15.205.92 (talk) 11:59, 8 December 2012 (UTC)

Incorrect introduction

I'm not sure I like the sentence there anyway, but "In the case of a function with just one input variable, the input and output of the function can be expressed as an ordered pair," isn't right. This "case" includes vector valued functions of a scalar argument. Can I leave it to the author of that part to fix it? — Preceding unsigned comment added by 132.206.112.10 (talk) 13:26, 18 February 2013 (UTC)

If the output of a function is a vector, then the input and output can still be expressed as an ordered pair - the second element of the ordered pair is simply the output vector. Similarly, if the input of a function is a vector, this vector can be the first element of the ordered pair. So the restriction to functions "with just one input variable" is unecessary. I have removed that phrase from the article. Gandalf61 (talk) 14:15, 18 February 2013 (UTC)

find out the rate of commission on items A,B and C

   month         sale of unit            total commission
   
                A    B    C                        Rs    
   january      90   100  20                      800
   
   february    130   50   40                      900

   march       60    100  30                      850  — Preceding unsigned comment added by 115.252.159.158 (talk) 11:20, 19 February 2013 (UTC)

We don't do puzzles here. This page is about improving the article. The closest we have to some place that might be vaguely interested is Wikipedia:Reference_desk/Mathematics but really that is supposed to be a reference desk rather than a puzzle forum. Dmcq (talk) 12:34, 19 February 2013 (UTC)

Alternate definition???

Calling an author's sloppiness in not mentioning the codomain of a function an alternate definition of the term "function" takes a simple concept and convolutes it to the point where it can and will confuse a novice reader. Most of the section that includes this should be deleted as pure fabrication - an elaboration of a non-existent difference. The definition of a function, a la Bourbaki (1937), has become standard and our article on it should reflect that fact. Bill Cherowitzo (talk) 17:14, 7 April 2013 (UTC)

The alternatives are well cited and quite common and that's all that's necessary in Wikipedia. We document what's out there. Alternatives are used quite frequently nowadays, Bourbaki wasn't the last word on the subject. The alternatives section is well marked as alternative so I don't see the problem with confusion. Dmcq (talk) 20:57, 7 April 2013 (UTC)

I would object to your use of well cited and quite common. I don't have a copy of Apostol to check, but the book is over 45 years old and is a bit dated. The Heins reference does not support the claim. In over 35 years of teaching this material using a large number of common texts, I have never seen this statement; if this was quite common I should have run across it. Of course a couple of good modern citations (say, published after 1990) would show me the error of my ways. I am not a big Bourbaki fan, but I will give them credit when it is due, and they nailed this definition. I am also not clear on why you would want to call this an alternative definition. This is not a different way of looking at an object or a different approach to understanding a concept, it is just being sloppy with a basic definition. Bill Cherowitzo (talk) 03:58, 8 April 2013 (UTC)

Try searching Google books for the phrase "function is a set of ordered pairs". It may make you sad (as it does to me) that they neglect to specify the codomain as part of the function, but it seems to be quite common. —David Eppstein (talk) 05:23, 8 April 2013 (UTC)

Thanks for that sobering suggestion, but I didn't really find anything that I wasn't expecting. The exercise did remind me that the vast majority of texts where this will come up are at the pre-college level. Let me be a little clearer about what is bothering me. The difference between what is found in this level of book and and a true mathematical definition is the level of formality. For quite valid pedagogical reasons, you do not introduce concepts in their most formal guise. Getting across the basic idea that a function is a set of ordered pairs (with a given property) should not be convoluted by introducing unnecessary vocabulary. I would object strongly to seeing the term codomain at an introductory level. It is not even clear to me that it should be mentioned that this set of ordered pairs is a subset of a Cartesian product. But, not saying it does not mean that it is not true! All we are doing, by being mum, is being less formal with our definition. What I am objecting to is calling the same definition stated at different levels of formality "alternative definitions." Under the "alternative" definition given in this article, all injections are bijections because every function is surjective. This nonsense statement comes about only because the level of formality in the definition is too low to support the abstraction of the concepts in the statement. This is not a legitimate alternative, it does not lead to the same conclusions. So, what does this mean for the article? I would strongly prefer to see, instead of these statements about alternative definitions, something more like, "When treated less formally, the codomain of a function may not be mentioned explicitly. This leads to ..." Bill Cherowitzo (talk) 23:37, 8 April 2013 (UTC)

The definition of a function as a set of ordered pairs is completely standard in set theory - all the way to the graduate level. It is the definition used by Halmos Naive Set Theory, Levy Basic Set Theory, Kunen Set Theory, Jech Set Theory - the latter two being the current standard graduate-level books on the subject. Moreover, I thought I don't have them here, there is a longer list of sources at [4] that included books by Apostol, Bartle, Krantz, Kolmogorov and Fomin, Royden, and others. It is completely standard to define a function simply as a set of ordered pairs, and also completely standard to define it as a triple consisting of domain, codomain, and graph. neither definition is more or less formal than the other.

In the setting where a function is just a set of ordered pairs, one does not talk about a function per se being surjective, one only talks about a "surjective function to a set B". Thus surjectivity is not treated as a property of a function, it is a property of a function and a set. — Carl (CBM · talk) 01:13, 9 April 2013 (UTC)

Thanks for the archive link. I clearly walked into this blindfolded and didn't realize it was a hornet's nest. I have no desire to stir up that pot again – far too much verbage has been spilled on what I would call an argument over the number of angels that could fit on a pinhead. Bill Cherowitzo (talk) 04:58, 9 April 2013 (UTC)

One thing that I have always found interesting about editing here is that in a few occasions I have found that the definitions I learned and thought were universal were actually only one of several formally distinct definitions used by different authors in print - and other people learned the other definitions and thought that the ones I learned were crazy. This seems to happen much more often with basic concepts. — Carl (CBM · talk) 12:06, 9 April 2013 (UTC)

Slowly (!) getting there -- but still full of inconsistencies

The article has much improved since I last saw it several months ago, but remains full of inconsistencies.

A major improvement is agreeing on the definition found in most present-day textbooks: "A function f from X to Y is a subset of the cartesian product X × Y subject to the following condition: every element of X is the first component of one and only one ordered pair in the subset".

Unfortunately, many logical inconsistencies remain, due to using disparate sources, and even internal inconsistencies in many present-day (say, post-2005) textbooks. The issue is muddled on this discussion page by throwing around names of authors without precise references (title, page), and often without having read them. Especially Bourbaki is a victim of such abuse. Hence we start with a few references. Firstly, for historical perspective:

(A) Tom P. Apostol, Calculus, Vol. I, 2nd ed. (Wiley, 1967), p. 53
(B0) Nicolas Bourbaki, Theorie des Ensembles (Hermann et. Cie, 1954), p. 76
(B1) ibid., p. 77
(Hl0) Paul R. Halmos, Naive Set Theory (Van Nostrand Reinhold 1960), p. 30
(Hl1) Paul R. Halmos, "Nicolas Bourbaki", in: Morris Kline, Ed., Mathematics in the modern world, pp. 77-81 (Scientific American, 1968), p. 80.

Some useful terminology for later observations: Bourbaki (B0) uses the neutral term functional graph for a set of pairs no two of which have the same first member.

Secondly, a sample of current textbooks, mostly after 2005.

(DG0) Ulrich Daepp and Pamela Gorkin, Reading, Writing and Proving: A Closer Look at Methematics (Springer, 2003) p. 147
(DG1) idem, 2nd. edition (Springer, 2011) p. 143
(K) Steven G. Krantz, Real Analysis and Foundations, 2nd ed. (Chapman et. Hall/CRC, 2005), p. 20
(Hm) Richard Hammack, Book of Proof, 2nd ed. (CC-BY-ND, 2009), p. 195 [5]
(R) Charles E. Roberts, Introduction to Mathematical Proofs -- A Transition (CRC Press, 2010), p. 220
(V) Daniel Velleman, How To Prove It: A Structured Approach, 2nd ed. (Cambridge, 2009), p. 226

All of these definitions (with one exception discussed later) are logically equivalent to the one in the current Wikipedia article (a function being a functional graph). Crucial implications are the following.

Since f is by definition a subset of X × Y where every element of X is represented (exactly once), only X, but not Y, is an attribute of f. This is why the ISO standard (referenced in the Wikipedia article) appropriately states that f : X $\rightarrow$ Y specifies that the domain of f is X and the range of f is a subset of Y.
Since f is a set by definition, function equality is determined by set equality. Any other characterization of function equality that is not logically equivalent is inconsistent with this definition. For instance, an equivalent (hence consistent) alternative characterization of function equality is found as a theorem in (A) p. 54 and as a "new" definition in (R) p. 223: " f = g iff Dom f = Dom g and f(x) = g(x) for all x in the domain". Adding extras (like Cod f = Cod g) is inconsistent. The reader can verify that similar contradictions are present in nearly all post-2005 references quoted here -- certainly reason for concern.

Clearly, making Y an attribute (called "codomain" or not) is inconsistent with the (well-chosen) definition in the Wikipedia article!

If (!) codomains are wanted, the only way to introduce them consistently is not defining a function as in the Wikipedia article as a functional graph, but as a pair consisting of a functional graph F and a codomain Y, so f = (F, Y). In passing (but not important): some authors use triples (F, X, Y) where X = Dom F, which is clearly redundant.

It is significant that Bourbaki briefly considers the triple-based definition in (B0), but immediately announces (B1) that "function" will often just stand for "functional graph". This illustrates Halmos' observation about the Bourbaki group that "weary of trying to remember their own innovation, the authors slip comfortably into the terminology of the rest of the mathematical world".

Hence the crucial question is: do we want the extra complication of a codomain, in the Wikipedia article or in mathematical usage? In both cases, the answer is a very definite "no".

For the Wikipedia article, because the definition in the current article is indeed the most frequently used and also the simplest (especially in Apostol's wording).
In mathematical usage, because

(i) In the entire literature no argument can be found why a codomain might serve a useful purpose at all (except an inconsistent argument in a paper by Shuard).

(ii) Functions defined without codomains lead to a more general and fundamentally as well as practically more useful properties.

Discussing the latter two items is beyond the scope of Wikipedia, but anyone interested in this matter can obtain a note (10 pages) by sending me an e-mail.

Of course, some disagreement about the above arguments is to be expected. However, good decisions require a spirit of logical reasoning rather than near-religious fervor. In particular, given the prevailing definition of "function" as reflected in the current Wikipedia article, codomains at best deserve only very secondary status.

To conclude, logically consistent arguments why codomains might be useful at all are indispensable before giving them more than a brief mention in passing, justified only because the word exists! The fact that Wikipedia is also used extensively by students at all levels imposes a heavy responsibility regarding accuracy, consistency and relevance. Boute (talk) 14:54, 7 June 2013 (UTC)

Discussion

If you look at the section immediately above this, you will see someone making exactly the opposite argument! There is no benefit in trying to work out which side is "right" -- both sides are very common in practice, and the article somehow has to represent both sides. Whether it does that well is another question, and would be worth discussing, but I see little reason to continue trying to argue that one of the two versions is wrong. I will simply quote from a 2011 Springer textwbook that gives the other side: Ethan D. Bloch, Proofs and Fundamentals: A First Course in Abstract Mathematics, Undergraduate Texts in Mathematics, 2nd ed. 2011. From pages 131-132:

It is important to observe that a function consists of three things: a domain, a codomain, and a subset of the product of the domain and the codomain satisfying a certain condition. Indeed, one way of defining a function is as a triple of sets (A,B,F) where F is a subset of A×B that satisfies the conditions given in Definition 4.1.1. However, we avoid this cumbersome triple notation by observing that in Definition 4.1.1 every function is defined as being from a set A to a set B, denoted f:A→B, and therefore the domain and codomain of a fuction are always specified in the definition of a function. Hence, to define a function properly, it is necessary to say "let A and B be sets and let f:A→B be a function." We will sometimes be more concise and just say "let f:A→B be a function," where is is understood from the notation that A and B are sets. It will not suffice, however, to write only "let f be a function" without specifying the domain and codomain, unless the domain and codomain are known from context.

The need to specify the domain and codomain of a function when defining a function is not a mere formality, but a necessity when treating functions rigorously. For example, consider the set F={(n,n²) : n ∈ Z}. The set F is a subset of Z×Z that satisfies the conditions given in Definition 4.4.1, and hence F can be though of a defining a function Z→Z. However, the set F is also a subset of Z×R that satisfies the conditions in the definition of a function, and hence F can be thought of as defining a function Z→R. Such ambiguity is not acceptable when we use functions in rigorous proofs, and so the domain and the codomain of a function must be specified as part of the definition of a function.

The opinion expressed there is very common, and the article needs to take it into account. — Carl (CBM · talk) 15:34, 7 June 2013 (UTC)

Of course, the article has to take into account many views, but the consistency obligation remains, and the decision about relative weights cannot be avoided (in your text, "very common" is still "much less common"!). Also, if you carefully check my observations, the word "wrong" never appears, although in mathematics inconsistency is wrong. Unfortunately, now I must say that the quoted statement "Such ambiguity is not acceptable when we use functions in rigorous proofs" where "such" refers to the explanation that immediately precedes it is entirely wrong. Indeed, the fact that, with the definition in the current Wikipedia article, a function type X → Z (Z for the integers) is a subtype of X → R (R for the reals) in no way hinders rigorous proofs (what an idea!); it does not reflect any ambuguity, but a richer algebra of fuctions and function types. Even more: the note I mentioned is precisely motivated by the concern for rigorous proofs, which is why I found the inconsistencies in the referenced textbooks (about proofs!) so disappointing. If you are interested in the link with formal proofs, feel free to send me an e-mail to receive the note (.pdf file). Boute (talk) 17:09, 7 June 2013 (UTC)

Note that the present Wikipedia article does not define the bare word "function" in the section "Definition". Instead, for all sets X and Y, the article defines "a function from X to Y". Formally, this is an infinite set of definitions, one definition for each pair of sets X and Y (or, it is a relation R(f,X,Y) between the object f being defined, X, and Y. Compare defining "A is a subset of B" versus trying to define "A is a subset" without reference to any other set.) Every "function from X to Y" does have a codomain specified, namely Y. The section "Alternative definition of a function", although it is not very well organized at the moment, talks about the options that are present when one tries to define a "function"; that is the point where different definitions enter the picture. — Carl (CBM · talk) 17:52, 7 June 2013 (UTC)

A small aside, has anyone ever written something good about what saying the set of integers is a subset of the set of reals actually means?Dmcq (talk) 23:26, 7 June 2013 (UTC)

The question of the aside leads to Dedekind cuts, and is similar to the question how integers are a subset of (or embedded in) rational numbers (formally defined as pairs). Dedekind cuts were common fare in high schools 50 years ago, but were at some time eliminated from the curriculum as being "too abstract". Sad but true. Anyway, back to the subject.

Let's assume your interpretation that starting a definition with "a function from X to Y" announces an infinite set of definitions (I rather see it as an attempt to cram 2 definitions into one sentence, but let that be). Even in that interpretation, if a function f from X to Y is defined as a subset of X × Y with the functionality property, f is also a subset of X × Z with the functionality property when Y is a subset of Z, in which case f is also a function from X to Z by an "other" (Z-based) definition in your infinite collection. That's fine by me and by the ISO standard. Hence, even with the infinite collection of definitions interpretation, if you want to associate a codomain consistently, you have to complicate things by defining a function as a pair (F, Y) or, with some redundancy, as a triple (F, X, Y), where F is a functional set of pairs. My main point earlier was how fortunate it is that, in the current literature, for each textbook using such triples (or pairs), there is a vast multiple using the simpler formulation as in the Wikipedia article or Bourbaki on page 77 (op. cit.), defining a function as just a functional set of pairs (the F in the triple). Also, although I have shown how to make the codomain-based definitions consistent, the crucial remark remains: the burden of the proof as to why codomains might be useful is on those who want it. Did you ever see a fitting justification for codomains? Boute (talk) 01:54, 8 June 2013 (UTC)

A commonly mentioned justification is that one cannot say whether a function itself is surjective unless there is a codomain associated with the function. So one is no longer able to ask just "Is that function a surjection?" if the function has no codomain associated with it. But in many fields, particularly algebra, it is completely common to say that a function itself is surjective. And the term "surjective", by the way, is due to Bourbaki, who do define a function as a triple. — Carl (CBM · talk) 02:11, 8 June 2013 (UTC)

(margin reset) The "commonly mentioned" argument in favor of codomains is indeed the only one I ever found in the literature (traceable to Shuard's paper) but its "advantage" (writing just "surjective" instead of "onto T" if the range is T) is rather illusory: arguably, "surjective" is coarser than "onto T"! Recall Halmos's remark (Hl1) that the Bourbaki authors apparently regretted some of their experimental definitions, which explains the decision in Bourbaki (op. cit, page 77) for often using the definition by which a "function" is simply just a functional set of pairs, as in the Wikipedia article. As regards algebra, most "modern algebra" textbook authors in the 1960's were well aware of Bourbaki's work, but (at that time) were careful in writing "onto T" rather than just "onto". Herstein's Topics in Algebra (Xerox Corporation, 1964), arguably the best introduction to algebra even today, is illustrative (definition halfway page 12). Many "completely common" practices might be just sloppiness (sometimes even leading to inconsistencies as mentioned earlier).

More important in this discussion are the genuine advantages of not tying down a function by a codomain. Just two examples (many more available on request).

(a) With codomains, composition g o f for f : X → Y and g : U → V is defined only for the special case when Y = U. This turns out to be very restrictive in actual usage. Without codomains, composition is defined for any pair of functions, the domain of the composition being the set of all x in X such that f(x) is in U. This definition is found in (A, p. 140), and many books not listed above, including most classical and modern calculus books (Axler 2008, Bartle 1964, Larson and Edwards 2009, Stewart 2007). In calculus, the codomain restriction would seem most unwelcome.

(b) With codomains, function typing is very inflexible. Avoiding codomains allows extreme flexibility, such as so-called dependent function types of the form

f : X::x → Y(x), where Y is a set-valued function allowing to express that the set constraining f(x) may depend on x.

See Halmos (Hl0), p. 36 for this view of the Cartesian product as a function space. Boute (talk) 08:55, 8 June 2013 (UTC)

The definition of a function as having a domain and codomain in mathematics corresponds quite closely with the definition of a function in strongly typed computer languages like Java. So you'd prefer a weakly typed language like LISP where anything goes. Fine for you. Lisp corresponds more closely with the set theory part of maths where functions as you like them are more appropriate and people want to do their own complicated things but don't cooperate with each other much. Python is an intermediate type language which is popular for getting work done quick, it is used in teams but typically where an occasional glitch isn't a problem. A language like Java or C++ is used more where people work in teams with each other and want to be able to depend on what they are using for robust applications that don't fall down. Yes your definition is flexible - but more often extra rigidity is what people really want, they don't want a funtion they want to talk about whole sets of functions of the same type. For everyday maths they want something like Python - tending towards being strongly typed but they fudge around and don't mind winging it a bit.

As to your integers being a subset or embedded in the reals. If you are going for a fully formal set theory approach that simply does not work. The natural numbers would be defined using sets of sets which don't at all match the pairs of a Dedekind cut. Dmcq (talk) 09:29, 8 June 2013 (UTC)

Sorry, Dmcq, but your inferences about what I personally like/dislike are simply wrong and likes/dislikes or programming languages are irrelevant in the effort to build a good Wikipedia article about mathematical functions. Also, linking weak/strong typing in programming languages to a codomain, as well as the idea that, without codomains, "anything goes" or program robustness is compromised goes beyond absurdity. Finally, observe that the aside which you designate as "your integers" was neither introduced by me, nor relevant to this article about the general notion of function. In other words, let's keep focus. Boute (talk) 10:17, 8 June 2013 (UTC)

Speaking of keeping focus: Boute, as far as I can tell you keep trying to argue that the definition without codomains is superior somehow. Such arguments are not really interesting to me, and they are irrelevant for writing this article. Both conventions are common in mathematics, and this article needs to cover both. I looked through the article again, and I didn't see any glaring "inconsistencies". If you focus on the actual content of the article, rather than arguments like "In calculus, the codomain restriction would seem most unwelcome.", it would help focus the discussion and move it forward. It would be a favor to everyone here if you could also keep your posts short and to the point, and avoid repeating arguments that have been covered before. — Carl (CBM · talk) 13:10, 8 June 2013 (UTC)

If you check, note that my observations contain significantly more examples, precise definitions and literature references "per line of text" than those of any other contributor thus far. So picking on the one sentence "In calculus, the codomain restriction would seem most unwelcome." is not serious. If it is a matter of wording, replace it by "The treatment of function composition in most current calculus textbooks indicates that the general form (defining g o f for arbitrary functions) is required, whereas the usual definition for g o f with codomains imposes the restriction that Dom g = Cod f ". In fact, saying "most" is most careful here, since it actually pertains to all current calculus textbooks I checked (about half a dozen, randomly chosen). — Preceding unsigned comment added by Boute (talk • contribs) 10:01, 9 June 2013 (UTC)

On the integers/reals business you said "Indeed, the fact that, with the definition in the current Wikipedia article, a function type X → Z (Z for the integers) is a subtype of X → R (R for the reals) in no way hinders rigorous proofs (what an idea!)" I disagree with saying a function like that is a subtype or subset of the other but if one is speaking loosely I wouldn't object in most circumstances. I brought in the programming languages analogy to try and step back a little and show a similar debate elsewhere and what it means. Your automatically changing reals into integers definitely counts as an operation in most programming languages even if implicit and they write stuff describing it. Dmcq (talk) 13:17, 8 June 2013 (UTC)

I certainly agree with the latter; considerable caution is needed. Note however, that the codomain issue is unrelated to degrees of formality, and "subtypes" are not a matter of "speaking loosely". The degree of formality is orthogonal to the choice of definition, and there are two clearly distinct definitions under consideration:

* (B0) Bourbaki p. 76: A function is a triple (F, A, B), where F is a functional graph and A = pr₁ F.

* (B1) Bourbaki p. 77: A function is a functional graph.

Both definitions are equally formal. Since, in Bourbaki (p. 71), a "graph" is defined as a set of pairs, (B1) is equivalent to the definition in the Wikipedia article, the ISO standard, Apostol's book and most current textbooks. Also, in view of (B1), calling f a subfunction of g iff f is a subset of g is formal and unambiguous, and so isis calling X → Y a subtype of X → Z in case X → Y is a subset of X → Z (or, for nonempty X, if Y a subset of Z), where X → Y is defined as the set of all functions from X to Y (see, e.g., Bertrand Meyer), written by Halmos as Y^X. Boute (talk) 14:18, 9 June 2013 (UTC)

Overall I agree with CBM. I think the alternatives section definitely could be improved and a contribution there would be most welcome. However arguments about the superiority of a way of doing things would need citations to people comparing the alternatives and would simply be reported in the article rather than mean we should go about proselytizing for their preferred scheme. Dmcq (talk) 15:30, 8 June 2013 (UTC)

This brings up one of the main difficulties, which is that although there are many textbooks that have some description of functions, they don't compare and contrast their definition with other definitions. If there was a source somewhere that actually discussed both definitions, it would be very valuable for the "alternative definitions" section. By the way, I think that the "definition" section does a good job of being written in a way that can be read either way, depending on the taste of the reader. — Carl (CBM · talk) 19:39, 8 June 2013 (UTC)

I wrote about these two definitions here: http://www.abstractmath.org/MM/MMFuncSpec.htm and in the book Handbook of Mathematical Discourse by Charles Wells, Infinity Publishing, 2003. A preliminary version of the latter is online at http://www.abstractmath.org/Books/handbkhyper.pdf.

SixWingedSeraph (talk) 22:28, 8 June 2013 (UTC)

May we assume that in "The value of F at 3, for example, is 2, because the definition says that F(2) = 3." the reversal of 2 and 3 is a typo? Boute (talk) 10:14, 9 June 2013 (UTC)

Infinity Publishing comes under WP:SPS doesn't it? I think Wikipedia will have to do something more about SPS in future because so many people are doing this sort of thing. Dmcq (talk)

How realistic is WP:SPS if any editor with hidden identity can ignore it? Especially given the absence of peer review, perhaps it is rather the hidden identity issue that requires scrutiny.Boute (talk) 13:19, 9 June 2013 (UTC)

The 'self' in SPS refers to the book in that it hasn't passed through editorial control. You're probably thinking of WP:COI. Dmcq (talk) 17:24, 9 June 2013 (UTC)

Some information about requiring codomains

I collected data from some math books published since 2000 that contain a definition of function; they are listed below. In this list, "typed" means function was defined as going from a set A to a set B, A was called the domain, and B was not given a name. If "typed" is followed by a word (codomain, range or target) that was the name given the codomain. One book defined a function essentially as a partial function. Some that did not name the codomain defined "range" in the sense of image. Some of them emphasized that the range/image need not be the same as the codomain.

As far as I know, none of these books said that if two functions had the same domain and the same graph but different codomains they had to be different functions. But I didn't read any of them extensively.

My impression is that modern mathematical writing at least at college level does distinguish the domain, codomain, and image/range of a function, not always providing a word to refer to the codomain.

If the page number as a question mark after it that means I got the biblio data for the book from Amazon and the page number from Google books, which doesn't give the edition number, so it might be different.

I did not look for books by logicians or computing scientists. My experience is that logicians tend to use partial functions and modern computing scientists generally require the codomain to be specified.

Opinion: If you don't distinguish functions as different if they have different codomains, you lose some basic intuition (a function is a map) and you mess up common terminology. For example the only function from {1} to {1} is the identity function, and is surjective. The function from {1} to the set of real numbers (which is a point on the real line) is not the identity function and is not surjective. Also a lot of modern math research is stated in terms of functors (particularly homotopy functors) which need to make the distinction.

THE LIST

Mathematics for Secondary School Teachers By Elizabeth G. Bremigan, Ralph J. Bremigan, John D. Lorch, MAA 2011 p. 6 (typed)

Oxford Concise Dictionary of Mathematics, ed. Christopher Clapham and James Nicholson, Oxford University Press, 4th ed., 2009. p. 184, (typed, codomain)

Math and Math-in-school: Changes in the Treatment of the Function Concept in ... By Kyle M. Cochran, Proquest, 2011 p74 (partial function)

Discrete Mathematics: An Introduction to Mathematical Reasoning By Susanna S. Epp, 4th edition, Cengage Learning, 2010 p. 294? (typed, co-domain)

Teaching Mathematics in Grades 6 - 12: Developing Research-Based ... By Randall E. Groth, SAGE, 2011 p236 (typed, codomain)

Essentials of Mathematics, by Margie Hale, MAA, 2003. p. 38 (typed, target).

Elements of Advanced Mathematics By Steven G. Krantz, 3rd ed., Chapman and Hall, 2012 p79? (typed, range)

Bridge to Abstract Mathematics By Ralph W. Oberste-Vorth, Aristides Mouzakitis, Bonita A. Lawrence, MAA 2012 p76 (typed, codomain)

The Road to Reality by Roger Penrose, Knopf, 2005. p. 104 (typed, target)

Precalculus: Mathematics for Calculus By James Stewart, Lothar Redlin, Saleem Watson, Cengage, 2011 p. 143. (typed)

The Mathematics that Every Secondary School Math Teacher Needs to Know By Alan Sultan, Alice F. Artzt , Routledge, 2010. p.400 (typed)

SixWingedSeraph (talk) 22:16, 8 June 2013 (UTC)

Thanks for that. Our article Binary relation has exactly the same problem as this article. There some people use the word 'correspondence' instead of relation for the triple and relation for the set of ordered pairs. And they have the exact same problem about saying if a relation is surjective etc. Personally I can't see why we should treat a set of ordered pairs as a function when we already have the term functional relation - but of course then the problem has been regressed to what definition of a relation one is using so one would have to have a relation not being a correspondence. Unfortunately that makes how all the terms apply different. Anyway I'm happy this article mainly talks about functions from X to Y and deals with 'function' on its own as the problem case. Dmcq (talk) 11:16, 9 June 2013 (UTC)

The addition by Charles Wells to previous lists is much appreciated. Perhaps all those lists should be collated somehow.

One potential subtlety requires closer scrutiny. Let's consider all definitions where a function is defined as a functional set of pairs whether ot not the sentence starts with the preamble "from X to Y " . and compare the two groups.

(PRE) With preamble (or "typed" in the terminology proposed by Wells), as in the Wikipedia article and most current textbooks: "A function f from X to Y is a subset of X × Y such that every element of X is the first component of one and only one pair in f.".

(NOPRE) Without preamble, as in Bourbaki (B1) and Apostol (A): "A function is a functional set of pairs, i.e., a set of pairs no two of which have the same first member."

Now, let f be a function from X to Y in the sense of (PRE). Clearly, f is a functional set of pairs, and hence also a function in the sense of (NOPRE). Conversely, let f be a function in the sense of (NOPRE), and define, as in Apostol p. 53, Dom f to be the set of first components and Ran f to be the set of second components. Let X = Dom f and Y a set such that Ran f is a subset of Y. Clearly f is a subset of X × Y, and every element of X is the first component of one and only one pair in f. Hence f is a function from X to Y in the sense of (PRE).

The resaoning is rigorous and can be fully formalized.

Finally, add to (NOPRE) the definition "A function f is said to be from X to Y iff Dom f = X and Ran f is a subset of Y (expressed by f : X → Y, as in the ISO standard). The bottom line is that both definitions are equivalent. If there is any problem, it is with (PRE), which tries to cram two definitions into one: what a "function" is, and when a function is from X to Y.

The psychological problem is that people who have not not fully grasped the cartesian product think that a function defined as a subset of X × Y somehow inherits X and Y in its DNA. For X this causes no problem, due to the extra stipulation in (PRE) that every element of X is represented (exactly once) as the first component. For Y, this does not hold.

Conclusion: rather than improving the definition, the preamble does not help understanding and makes (PRE) easy to misinterpret. A two-step approach, first (NOPRE) from Apostol, then the addition introducing X → Y, eliminates the problem. Boute (talk) 15:43, 9 June 2013 (UTC)

The proper function of an encyclopedia article is, among other things, to describe the usage of technical language in the subject of the article. It is clear to me the following usages for "function" are common:

A function $f:A\to B$ has a graph, which is a relation on $A\times B$ with the functional property. Thus it is "typed" in the sense of my previous post on this Talk Page.
Texts may or may not regard two functions with the same graph but different codomains as the same or different. Thus there are two different meanings of equality for functions and the particular text may not tell you which is being used, and (it appears to me) in many cases it does not even matter, and in other cases it is an important distinction.
Many texts define a function as a functional relation, period.
Some texts assume that "function" means what the rest of us call a "partial function".

The main Wikipedia article on functions should describe all these usages in understandable terms and using easy examples. (For example, is an identity function different from an inclusion function?) Mathematicians will continue to use common terms with varying definitions and there is no Terminology Academy to stop them.

I recommend the article use "function" for the typed case -- so there are two meanings of equality -- and "functional relation" for the other case. Some authors have recommended that the word "map" be used for the typed case with the stricter meaning of equality (so codomains matter). I think that it is an excellent idea, but it is not common practice.

Arguments for or against particular usages do not belong in Wikipedia. Of course, you can reference arguments in other texts.

Note: I wrote this post without reading the post by Boute

SixWingedSeraph (talk) 16:31, 9 June 2013 (UTC)

Here are several books that explicitly state the condition that the codomains must be equal when defining equality of functions. Although there are more, I tried to pick a sample to show that this usage goes beyond just abstract algebra.

Jacobson, Basic Algebra I, second edition, page 5 - a graduate level abstract algebra monograph
Devlin, Sets, Functions, and Logic: An Introduction to Abstract Mathematics, 3rd edition, page 92
MacLane and Birhoff, Algebra, 3rd edition, page 5
Eccles, An Introduction to Mathematical Reasoning, page 93
Joshi, Introduction to General Topology, page 33
Haddad, VijaySekhar Chellaboina, Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach, page 33

— Carl (CBM · talk) 14:16, 10 June 2013 (UTC)

A Modest Proposal

It is clear that after much good work by many people there is no longer a bull goose mathematician capable of settling the question of codomains -- the age when Hilbert said it, I believe it, and that settles it is long past. (The same is true of rings.)

I suggest: the article begin with a definiton for the non-specialist. A function assigns to any given input a unique output. We then need some examples. Later in the article, below the ToC, we need a statement that different authors use different definitions, and a clear statement of the three primary points of view: 1: a function is a set of ordered pairs, 2: a function is an ordered triple: domain, codomain, set of ordered pairs, 3: (the naive definition) a function is a rule.

I really do think that we can discuss this until the cows come home and not arrive at a single definition of "function".

Rick Norwood (talk) 17:29, 9 June 2013 (UTC)

I think the article does start off in a reasonably non-specialist way and it most deals with the case where the differences don't matter much, i.e. where X and Y are specified. I'm not too keen on confusing people by having say exp(x) be the same function whether we're talking about reals or complex numbers and I'm pretty certain students in the future will often have some exposure to computer languages which not only distinguish the two but have explicitly given possible inputs and outputs. The article used to be more up front about the two main variants where one said function without specifying X and Y and discussed them in parallel, but it was changed to the current form with a main and alternate view after having people come along arguing that one side or the other was the greatest most wonderful way and one side basically ran over the other - in fact I believe that argument was initiated by people arguing that not having a codomain was the main way so it kind of backfired on them. Dmcq (talk) 18:14, 9 June 2013 (UTC)

I agree with the proposal. Also, any explanation saying that exp(x) is the same function whether we're talking about reals or complex numbers would indeed be very confusing, but (fortunately) thus far no one has proposed such a thing. However, continuous personal remarks intending wanton misrepresentation are harmful to the final quality of the article. Indeed, in the preceding observations, I often unambiguously endorsed representing both views. Far from "running over" something, I even showed how to make the codomain-based view consistent (using pairs or triples), altbeit properly balanced with factual mathematical properties (no hyperboles!) indicating that choices do matter.

Unfortunately, the current Wikipedia article is very problematic. On one hand, the stated definition is indeed the simplest and most frequently used in modern texts, namely as a functional set of pairs, as in Bourbaki (B1) (no "extra's", as in the triple of B0). On the other hand, the same article without blinking talks about codomains as an attribute of such a function. This is inconsistent and, if diehards persist in denial, will backfire on the entire article.

Since apparently symbolic arguments are basically run over or simply not understood, I make a final attempt by providing an example and then stop wasting my time (ironic cheers predictable). The example comes literally from Hammack, chosen because it is freely available to everyone [Hammack, Book Of Proof], Example 12.2 page 196.

(Begin quote) Let

A=\{p,q,r,s\}

and

B=\{0,1,2\}

and

f=\{(p,0),(q,1),(r,2),(s,2)\}\subseteq A\times B

This is a function

f:A\rightarrow B

because each element of

A

occurs exactly once as the first coordinate of an ordered pair in

f

(End quote)

By definition 12.2 that precedes this example on the same page,

B

is the codomain. However, letting

C=\{0,1,2,3\}

, we also have

f=\{(p,0),(q,1),(r,2),(s,2)\}\subseteq A\times C

and hence

f:A\rightarrow C

, so

C

is the codomain. Since

C\neq B

, this is a contradiction.

Comparing the definitions shows that this is exactly the same situation as in the Wikipedia article. I rest my case. Boute (talk) 20:39, 9 June 2013 (UTC)

You stuck in f both times but that doesn't mean the two f's are the same. One f is a function from A to B, the other is a function from A to C.It is like in the real or complex number case saying that 1.0 is a real or 1.0 is a complex number. They may look the same but they're different. Of course that's working from the opposite viewpoint to you, you are right from your own viewpoint. Dmcq (talk) 21:33, 9 June 2013 (UTC)

In both cases, the function is simply the set

\{(p,0),(q,1),(r,2),(s,2)\}

, irrespective of the name. You can even rephrase the argument without the name, just in terms of this set. If you want to enforce a difference under Hammock's Definition 12.1, you have to use tagged sets or a similar device (as in the disjount union of a set with itself - see Meyer, Introduction to the Theory of Programmig Languages, 1990). In most of mathematics and engineering, enforcing a difference is restrictive. In programming, you can do it in the manner just explained when you need it. This is the advantage of not irrevocably building the difference into the definition from the start. Boute (talk) 05:26, 10 June 2013 (UTC)

You are still in the mode of trying to persuade us that one definition is better than the other. This is the wrong approach. You should be trying to persuade us that one definition is *more accepted* than the other. Or at least, that the level of coverage of one approach in our article is out of proportion to its level of acceptance in the literature. —David Eppstein (talk) 05:56, 10 June 2013 (UTC)

Don't patronize. I'm not trying to persuade anyone; people can only persuade themselves by careful thought about arguments given. I don't even believe that "the level of coverage of one approach in our article is out of proportion to its level of acceptance in the literature". To the contrary, I repeatedly emphasized that the current definition of a function in the article is, and even by far, the most accepted one, as I carefully checked. At worst, the coverage of codomains might be out of proportion, but judging that requires statistics that are not available.

So please stop wasting time and concentrate on the essence of the arguments I gave, which concerns the remaining inconsistencies in the current article. Try to get it right; it's easy for any mathematician used to formal reasoning. Boute (talk) 07:18, 10 June 2013 (UTC)

Afterthought: I consider it only polite to keep responding to remarks addressed directly or indirectly at me, but would prefer devoting my time to other things and see how the article stands in, say, a few months. Boute (talk) 07:29, 10 June 2013 (UTC)

The two functions are only the same because of your definition of a function. Most of the article talks about a function from X to Y rather than a function all on its own and does not try comparing it to some other function from A to B. It is only in the alternatives section it talks about functions without such a qualification. If a function from X to Y is considered as typed then its value can be given by a set of ordered pairs, that does not mean it is the same as some other type of function. It is only if you start with the assumption that it is completely defined by the set and the qualification is irrelevant that of course the qualification is irrelevant because we're assuming functions are untyped. To go back to your considering they are the same from the value without considering the type consider

2 in a representation of numbers using set theory may have the value 2={{}, {{}}}

When talking about ordered pairs a way of representing ordered pairs a short way is (a,b)={a,{a,b}}, this means for instance that (0,0)={{},{{}}}. And in a representation of the integers by the equivalence class of a-b that is 0.

However we do not conclude that 2=(0,0)=0 because the set represents different things each time. It is typed.

To fully specify a typed function complete with its type so we can say function on its own meaning some type of function then we need to specify a triple. But if one's not interested in specifying the domain and codomain and just want untyped functions then of course your way of doing it works. However outside of logic and set theory most people are more interested in sets of functions with a given source and destination set whatever about the flexibility of being completely free. Dmcq (talk) 09:04, 10 June 2013 (UTC)

(MARGIN RESET) Referring to the definition in the current Wikipedia article, also found in most present textbooks: the interpretation just described can be found nowhere in the literature. To the contrary, the notions of cartesian product, subsets and set equality are defined everywhere (i.e. in all references that came up in these discussions thus far) in a clear and unambiguous way that logically excludes this interpretation. Also, consider the analogy with the (PRE) style mentioned above: assume someone states: "DEFINITION: Let T be a set. A subset S of T is a set whose elements are all in T ". Now someone else might start arguing that T is an attribute of S, and that a set defined as a subset of T is somehow different from the same set defined as a subset of U in case U is different from T. However, equality between sets is defined as having the same elements, irrespective of the (many!) sets of which the considered sets might be a subset. Hence, if a function is defined as a subset of X × Y (with the extra property as in the article), it is a set and does not "change" if one defines it as a subset of X × Z -- assuming, of course, that the subset relation indeed holds. Note that using the same X is imperative, and that the function type that logically follows from the Wikipedia definition is that of the ISO standard, stating that the type definition f : X → Y specifies that Dom f = X and Ran f is a subset of Y. Such functions are not, in any meaningful sense, "less typed" than in the alternative definitions (e.g., as triples), only typed differently. In the example definition "sqrt : R_{>= 0} → R_{>= 0} defined by (sqrt x)^2 = x" the type specifies the nonnegative root. Obviously, in this setting, the "distinguishing effect" you are trying to obtain by a nonstandard view on set equality can be obtained simply by using tagged sets for Y and Z, as is common practice in programming language semantics (recall Meyer). Boute (talk) 13:42, 10 June 2013 (UTC)

As far as I can see, you are still talking about the definition of a "function" rather than "a function from X to Y". Instead of continuing that analysis, I would like to ask you to focus on describing any inconsistencies you see in the actual text of the article. You have claimed there are some, but I did not see them when I looked through the text. — Carl (CBM · talk) 14:10, 10 June 2013 (UTC)

(MARGIN RESET - long text by necessity!) I apologize for the length of this text, but please don't read it diagonally, look at all references provided (just 1 click away every time to make it easy) and, in case there is still disagreement, point specifically to the particular step in the arguments and state why you don't consider it logically valid.

I was definitely talking about "a function from X to Y" (or "A to B") as in Hammack's Definition 12.1, p. 195), in the current Wikipedia article and nearly all present-day textbooks. Let's call this definition (X2Y).

(I) I'd also prefer skipping the analysis, but some preliminary arguments in small steps are indispensable to see the inconsistencies in the rest of the article. For distinguishing definition variants, rigorous logic avoids (a) reading into a definition things that are not there, (b) overlooking things that are (already) there.

An illustration: by Example 12.2, p. 196, quoted literally earlier, Hammack demonstrates that he really means what he says in Definition 12.1 -- as befits a book about proofs. He concludes that the example function (a set of pairs) is really a function from A to B from two facts:

(i) the function is a subset of A × B;

(ii) each element of A occurs exactly once as a first component.

This is exactly what his (and the Wikipedia) definition says, nothing more, nothing less, leaving no room for other interpretations. Replacing B by any superset C of Ran f (or Im f) throughout Example 12.2 yields a proof that the same function (set of pairs!) is also a function from A to C under definition (X2Y).

Conclusion: all that (X2Y) says about the relationship between f : X → Y and the sets X and Y is that Dom f =X and Ran f (or Im f) is a subset of Y. This logically obvious point is made explicit in Bartle, p. 5, in Zakon, pp. 10--11 and by Labl, p. 14, referenced in the Wikipedia article on real analysis, and what the ISO standard says about the notation f : A → B. It is consistent with all modern texts using the (X2Y) definition, up to the point where some texts themselves contain internal inconsistencies (the latter's existence is quite scary).

Consequence A: making a codomain a function attribute in the sense that, given f : X → Y, one can write Cod f = Y is inconsistent with (X2Y), since it would allow Cod f = Y and Cod f = Z with Y /= Z. Obviously, this does not prevent calling Y the "codomain" of the area of discourse.

Consequence B: with (X2Y), "onto" is a preposition, as in "onto Y" (Halmos, Bartle, Kolmogorov etc.), and using "onto" as an adjective assumes Y from the context. Example: in the April 2013 Bulletin of the AMS, Kontorovich, pp. 199 and 210 uses both forms whereas Fuchs, pp. 241, 242, 244--246 uses "onto" as a preposition only.

Occasionally the remark surfaces that one cannot talk just about a "function" an sich but only about "a function from X to Y for given sets X and Y". Its validity critically depends on the definition variant. A complete analysis is skipped here, but consider:

(a) The definition in Apostol (A) and Bourbaki (B1) where a "function" an sich is simply a functional set of pairs is in no way problematic and is used formally in Suppes, Axiomatic Set Theory (Dover 1972), Definition 39, page 86 -- so let's call this definition (ABS).

(b) It has been shown that any function from X to Y as defined by (X2Y) is a function by (ABS), and that any function f as defined by (ABS) is a function from Dom f to any superset of Ran f by (X2Y). This follows from the definitions if one puts aside all dogmata other than rigorous logic. Conclusion: the remark that the phrase "from X to Y" is essential in the definition of a "function" does not pertain to the Wikipedia definition (which can be rephrased as ABS), but only to some other definitions that one might discuss in an "alternative definitions" section.

(II) This careful preparation allows to be more brief in discussing the residual inconsistencies in the Wikipedia article, and how to correct them with very minimal changes. Aside: keeping the "codomain" issue in a separate Wikipedia article is inviting inconsistencies due to incompatible editings.

(IIa) Inconsistencies in the "function" article In brief: residual inconsistencies in the article arise whenever it is said or implied that a function according to (X2Y) has a unique codomain. The text of the Definition section with (X2Y) is itself consistent, but the diagram is inconsistent with (X2Y), since the set of ordered pairs shown is the function by definition (X2Y), not just a component of it.

Similarly, saying that "A function is properly defined only when the domain and codomain are specified" is inconsistent with (X2Y), according to which a function is fully defined as a set of pairs.

(IIb) Correction with minimal changes It suffices to make clear that "codomain" in the context of (X2Y) is not an attribute of the function itself but a set assumed known in, or implied by, the context.

(i) In the introductory text. For instance, changing the text "called the domain, a set containing the outputs, called its codomain" into "called its domain, a set containing the outputs, called codomain" and adding "In some definitions, the codomain is part of the context only, in others it is also part of the function itself.

Definitely misleading is the suggestion that function spaces in real analysis involve codomains. I checked all references and links in that article where the definition of "function" was visible (Google Books is more irritating than Amazon): nearly all of them use definition (X2Y) but none of the (X2Y)-users mention the term "codomain", and the function space X → Y, also written Y^X, is simply as defined in the ISO standard. Note that this function space is isomorphic to the X → Y variant with codomain.

(i) In all the rest of the article: similar diligent care.

The codomain article, whether or not integrated in this "function" article, needs more references to compensate for its strong bias. I'll add them when time permits. Boute (talk) 06:49, 15 June 2013 (UTC)

The problem is encapsulated in the example of the problem you are having about whether you aredealing with a typed functionor just functions where the type is not specified. Now how about applying your own logic to

Natural number 2 ={{}{{{}}}

Ordered pair (0,0)={{{].{{}}}

Integer 0=0-0={{}.{{}}}

Therefore 0=2.

Two sets that look the same can mean two entirely different things if they are typed. If the domain and codomain are given then the function can be specified by a set of ordered pairs. That does not mean it is the same as a function to some other codomain. This applies to both the source and target for relations from one set to another. The big difference comes when one talks about a relation without assuming one is talking about a relation between one set and another. Some people say you map the relation on one pair of sets to the on one the other pair whereas your way is to say it is exactly the same relation. Even though that first reference you gave talked about the graph of a function you say they showed their true colours because they wrote f=set instead of graph(f)=set but you ignored the inclusion in the set product at the end of the line so in fact they were saying the f was a function from A to B. Don't you think it would be better to accept people might actually mean what they say they mean rater than try and find something to show they mean something other than what they say?

It is perfectly okay your path and for the 1={{},{{}}} I guess one aught to put extra brackets and operators round it like saying Graph(f) instead of f above if one were working in set theory and yet wanted to deal with functions from A to B. However trying to show what you want is better and interpreting other people's work in your way is not leading anywhere useful. Why can't you just try and improve the alternatives section rather than trying to prove a point of view? 12:50, 15 June 2013 (UTC)

I am quite aware of the problem you mentioned with natural numbers, ordered pairs etc. (just google "representational and denotational semantics"), but that is an entirely different issue. Indeed, that problem stems from representing quite different kinds of objects by sets. Unavoidably this causes artefacts, as also extensively discussed by Halmos in Naive Set Theory in various places, e.g., p. 25. Here we are dealing with function objects only.

The sentence in my analysis,

"(i) the function is a subset of A × B"

highlights rather than ignores (quote) "inclusion in the set product at the end of the line".

Moreover, this inclusion is the crux of the matter. If B is a subset of C then A × B is a subset of A × C. Hence, if f is a subset of A × B it is, by transitivity, a subset of A × C. Note that, in all the (X2Y) definitions in the ever-growing reference list, it is the function itself that is defined as a subset of A × B (not its graph, which is not even mentioned).

It may interest you learning that my own preferred definition of "function" (which I carefully avoided discussing at all on these pages) is quite more abstract than (X2Y) or (ABS), essentially to avoid artefacts as discussed by Halmos. So my arguments are not motivated in any way by "what I want" for definition, but by the importance of getting the Wikipedia article right. Boute (talk) 18:31, 15 June 2013 (UTC)

A function from A to B is completely represented by its graph but according to the first alternative in the article is typed a function from A to B. It is quite reasonable to represent it with a set of pairs. The product specified the A and B and the author went and specified them. It really makes very little sense that you go around saying an author really meant something else when they talk about domains codomains and graphs. There are other works that say differently and agree with the alternative view. As to being correct, we are not some sort of Bourbaki group. As WP:POV says we should present the significant views fairly and in proportion. Dmcq (talk) 20:10, 15 June 2013 (UTC)

I'm not talking about alternate views or which of them is "correct", I am talking only and exclusively about the definition of a function from X to Y as in the Definition section of the Wikipedia article, and in all the other texts that happen to use exactly the same definition. In each of my comments, I've added new references pertaining to this definition -- when will you give some as well? Please read Bartle, p. 5, Zakon, pp. 10--11 and Labl, p. 14. It's free! Anyway, the time I allotted for this is up. I'll see in a few months how it goes. Boute (talk) 21:10, 15 June 2013 (UTC)

I haven't Bartle but I looked at the other two and basically we just don't see eye to eye and we've gone over it all before. I believe the f:A->B description in the main part of the article covers both viewpoints quite adequately, and I really don't see why you keep on trying to say as far as I can see that one of the alternatives is wrong and the other is the only one that is truly consistent with the main part of the article. Dmcq (talk) 21:54, 15 June 2013 (UTC)

In view of the discussion above, wasn't the old version of the section Formal definition [6] actually better than the present one, which only mentions the definition of a function as a set of ordered pairs? Isheden (talk) 15:58, 30 June 2013 (UTC)

I put some work into that old section but it seemed people here wanted things more black and white confuse people with different possibilities. The article now has a main usage and an alternatives section. I believe the alternatives deserves a higher profile but the point of view warring like above has rather polarized the whole business. Dmcq (talk) 20:17, 30 June 2013 (UTC)