Talk:Euclidean algorithm/Archive 3

This is an archive of past discussions about Euclidean algorithm. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page.

Archive 1

Archive 2

Archive 3

Archive 4

Continued fractions and quotients

The article presently says,

"The quotients that appear when the Euclidean algorithm is applied to the inputs a and b are precisely the numbers occurring in the continued fraction representation of a/b"

But this is very strange because there are no quotients in the Euclidean algorithm, only remainders. If a > b are nonzero real numbers, the (real) remainder of dividing a by b is 0, so the Euclidean algorithm would halt after one step. But there is no greatest common divisor of two real numbers anyway.

Could someone who understands what the continued fractions sections is supposed to say rewrite it so that it makes sense? — Carl (CBM · talk) 05:14, 12 March 2009 (UTC)

Does it make sense now? — Emil J. 11:06, 12 March 2009 (UTC)

It's better, and I am not going to press this issue, but I still think that the article is somewhat vague about the changes needed to the algorithm in order to do the real number version. Michael Hardy also explained at WT:WPM the main issue, which is that the thing I have always called the Euclidean algorithm:

  function gcd(a, b)
    if b = 0 return a
    else return gcd(b, a mod b)

has to be replaced with a different algorithm that uses subtraction:

   function gcd(a, b)
     if b = 0 return a
     else   
       while ( a > b) 
         a = a - b
       return gcd(b, a)

The main area where the article is vague is in explaining how you get "quotients" from these. Yes, I see what is meant in each case, but the article itself is not very clear about it in the real-number case. — Carl (CBM · talk) 13:18, 12 March 2009 (UTC)

There is no reason to modify the algorithm to use subtraction instead of division, it works exactly the same way as for integers: a mod b is defined as

a-b\lfloor a/b\rfloor

. The quotients referred to are

\lfloor a/b\rfloor

, again the same as for integer inputs. Could you clarify what is vague about it? — Emil J. 13:38, 12 March 2009 (UTC)

I added an explicit definition of mod to the article, in case it helps. — Emil J. 13:56, 12 March 2009 (UTC)

Thanks. The article does a much better job at the moment of explaining what it means by quotient.

Here's the confusion. If you asked me, I would say that a mod b is the smallest nonnegative c such that there is an x such that a = bx + c. If a,b,c,x are all taken to be real numbers, this definition gives a mod b = 0 for all nonzero a,b, which makes sense because every real number is divisible by every other nonzero real number, so the remainder upon division will be 0. In the present context, the point is that x is required to be an integer, rather than a real number. That is a very different sort of "mod" than I am used to. If you redefine mod in your way, that does allow you to avoid switching to subtraction, but at the cost of introducing external concepts like division and floor into the definition of mod. — Carl (CBM · talk) 14:19, 12 March 2009 (UTC)

You see, I do not "redefine mod in my way", this is the standard definition of mod for reals. It is also used in other contexts, for example "mod 2π" is popular in Fourier analysis. If you do not restrict x to be an integer, then "the smallest c such that etc" is 0 even for integer a, b. I do not understand what do you mean by "introducing external concepts". You yourself wrote a division-free definition of mod above: in other words, it's the smallest nonnegative element of

a+b\mathbb {Z}

. Either way, you need to introduce the very same concepts in the integer case, so by the same objection you shouldn't use the mod-version of Euclidean algorithm at all. — Emil J. 14:50, 12 March 2009 (UTC)

I don't view the "mod 2π" as actual modular arithmetic; it's just slang for talking about a periodic function on [0,2π], or using a covering map from the reals to the circle, or similar operations. I am very used to the terminology, of course, I have just never thought of it as an actual modular operation.

What I mean by "external concept" is that to define the mod operation on the reals you are quantifying over the integers. In my jargon, an "internal" algebraic definition regarding a field or ring only uses the operations of the ring and only quantifies over all the elements of the ring. The definition of a mod b in the integers has this property: it uses only multiplication and addition and quantifies over the set of integers. If you than take this literal definition and replace the ring of integers with the ring of real numbers, you get the definition of "a mod b" for reals that I alluded to above. This is just about notation now, however; I understand what you're saying and I would guess you understand what I'm saying. — Carl (CBM · talk) 16:05, 12 March 2009 (UTC)

I see, the external concept here is not the division operation, but a predicate for the integers. That makes sense from the logical point of view. — Emil J. 16:44, 12 March 2009 (UTC)

(outdent) Just for completeness, Euclid's original definition of the algorithm uses subtraction, as you can read in Book 7 (esp. Propositions 1 and 2) and Book 10 (esp. Propositions 2 and 3) of his Elements. Here's a nice translation in parallel with the Greek. Given two real numbers a and b with a>b, you subtract from a an integer number q of b until the remainder r is less than b: r = a − qb where r<b. Michael Hardy's clarification at WT:WPM was exactly correct. Proteins (talk) 14:36, 13 March 2009 (UTC)

dash it all!

Why does McGraw–Hill have an en dash rather than a plain hyphen? —Tamfang (talk) 03:41, 13 March 2009 (UTC)

Because it is named after two people, James H. McGraw and John A. Hill. — Emil J. 11:12, 13 March 2009 (UTC)

Structure of the article?

Hi, I'd like to hear people's opinions about how the article should be structured. I'll present some ideas here, but I'm not married to them, and I can see several good alternatives. My general idea is that we should put the easiest stuff earliest in the article, to hold onto our readers as long as possible. Once we've lost them, I fear they won't keep reading for long in the hopes of finding something intelligible.

My initial thought is that we should put the code/pseudocode implementations in a special section "Implementations" at the end, similar to proofs and derivations. I believe that relatively few people will understand the code. In their place, I would an English description similar to the one in the lead.

I'm also tempted to move the History section to near the end, since I believe that more people will want to know how the algorithm works rather than its historical provenance. We can move some key historical details to the lead section, as I began to do already.

The main four elements of the article would seem to be: (1) motivate why the algorithm is notable and useful (applications); (2) describe how the algorithm works in different domains; and (3) discuss the method as an algorithm, e.g., its running time/efficiency, Gabriel Lamé's results, etc. and (4) its generalizations such as determining a Gröbner basis.

However, these need not be the main sections, nor the order. For example, we could devote the beginning of the article to integers, which might be easier to understand, and reserve the other domains to near the end. The algorithmic part could come after the integers, since it probably doesn't depend much on the domain. We might begin the body of the article with a short section on the greatest common divisor in integers, to help readers become familiar with the concept and motivate the need for the Euclidean algorithm.

I'd welcome other thoughts and suggestions on the article structure! Thanks, Proteins (talk) 15:05, 13 March 2009 (UTC)

Review

As requested by Proteins, I'm giving an informal review in preparation of GAN and/or FAC. Currently I have read til "Factorization algorithms" section. I think this is a nice article, featuring well-explained and very detailed explanations. My main point right now is a more coherent article structure. I think certain aspects should be carved out more clearly, notably how modular arithmetic works, and the role E.a. plays in it (namely calculate the generator of the principal ideal). (Technically, this could be done by little section introductions.)

Thanks for your detailed review! I'll intersperse my answers among your comments. Proteins (talk) 16:07, 8 April 2009 (UTC)

The lead is very long, I guess too long. I would probably remove the example from the lead. Overall, the lead should be a succinct overview of the article, and should not be overwhelmingly detailed, which it currently is. On the other hand, it does not cover the whole article, e.g. the efficiency aspects are not at all treated in the lead.

I added some material about the computational efficiency to the lead. Our colleague Michael Hardy has also consistently pushed for a concrete example in the lead. I see the sense of that, since the EA is taught in elementary school, usually to children of ages 9-13, who will not have had algebra. We should remember these younger readers, even if we have to stretch the MoS guidelines on the lead. Proteins (talk) 16:07, 8 April 2009 (UTC)

In general, the article is fairly long, too. I dont think it's too long, but it has come to a point where putting any additional stuff must be done with care. Actually, there are places where some trimming would be good, I think. As a general guideline, I would propose doing the following check with every paragraph or even sentence: is the material in question an additional piece of information which deepens the understanding of the E.a.. For example the discussion on lcm's "The GCD is related to the least common multiple (LCM) by the equation..." is never used again in the article, and should, IMO, be removed.

Point taken. I agree and, as a downpayment of brevity, LCM has been removed. Proteins (talk) 16:07, 8 April 2009 (UTC)

The background section is nice, but I miss an essential bit of information on the gcd, namely that you can read it off the prime factorization.

It was there, but perhaps you missed that paragraph? I moved it up to make it more prominent. Proteins (talk) 16:07, 8 April 2009 (UTC)

Sorry about that. Jakob.scholbach (talk) 16:49, 8 April 2009 (UTC)

The "division algorithm" section is odd. Especially "The Euclidean algorithm requires that ..." is wrong, at least if you use the subtraction implementation. I suggest removing the section or somehow merging it into the algorithm description.

Good suggestion — merged. Proteins (talk) 16:07, 8 April 2009 (UTC)

"Description" section: somehow I miss the statement "Let a and b be natural numbers. We want to compute gcd(a,b)". (This is given in the preceding section, but would be good to put it there again, (or just move it?)

Fixed. Proteins (talk) 18:34, 8 April 2009 (UTC)

"Each step k begins" - what is k? Perhaps reword somehow.

Good point — fixed. I may tweak it some more. Proteins (talk) 17:53, 8 April 2009 (UTC)

Eliminate the artificial distinction between the initial step k=0 and k=1 (by setting some x_0 := a, x_1 := b, x_{n+1} := ...)?

Stated general recursion formula with r₋₂=a and r₋₁=b. Led to a nice improvement in overall description; thanks! Proteins (talk) 17:53, 8 April 2009 (UTC)

"This chain of equations is the basis for a recursive implementation of Euclid's algorithm." -- why recursive? I think that chain is the basis/the justification of the E.a.

Removed unnecessary statement. Proteins (talk) 17:53, 8 April 2009 (UTC)

"Visualization": perhaps create an image. Would be nice.

Working on it. Images are not my forte. Proteins (talk) 17:53, 8 April 2009 (UTC)

I remember the guys at Wikipedia talk:WikiProject Mathematics/Graphics as very helpful. Jakob.scholbach (talk) 20:30, 8 April 2009 (UTC)

"The basic task in the Euclidean algorithm" ? -- perhaps: "The E.a. involves ..."

Fixed. Proteins (talk) 16:07, 8 April 2009 (UTC)

"... until the remainder rk is smaller than j. This approach is guaranteed to work in advanced number systems such as commutative rings, where the only defined operations are addition, subtraction and multiplication." -- I'm not sure what you mean by that. Commutative rings generally don't have a notion of "≤". Actually general commutative rings don't have an E.a. at all, right?

This was poor wording. I was trying to say that "integer division" and the "floor" operation aren't fundamental operations in rings, whereas subtraction, etc. were. The point wasn't really worth making, so I re-worded it. Proteins (talk) 16:07, 8 April 2009 (UTC)

I don't know how computers work, but "The usual approach is to use integer division and the modulo operation to calculate the quotient and remainder, respectively" does not really explain what a computer does differently than the subtraction approach. At least this needs a reference, if you want to make it a point.

These comments aren't mine, but I'll think more about them. I do know something about the electronics of computers, but it's not clear to me that it's relevant. There's probably a hardware/software difference between how mod is calculated for relatively small integers (say, less than 16 bytes, 2¹²⁸ = 2^2⁷) and numbers like 2^2¹⁶. Some clarification of this issue is probably a good idea. Proteins (talk) 16:07, 8 April 2009 (UTC)

"Worked example" -- I would move that up, right after the description. Try to match the notation of the description section ("For example, let a = ... ")

Good idea, fixed. Proteins (talk) 18:34, 8 April 2009 (UTC)

In the pseudocode, perhaps say a word what "b := a mod b" means.

Better, but could probably be improved further. Proteins (talk) 18:34, 8 April 2009 (UTC)

"This approach is well-suited to computers" -- again, this may well be right, but ad hoc sounds a bit like POV. Provide a reference to back up your claim (Actually I'm not sure this is right; you need a hack of memory to keep all the instances of the function alive, whereas the other implementations are less memory-expensive, I believe).

Computers usually keep a function-call stack that's pretty efficient. The number of steps in a typical Euclidean algorithm shouldn't overflow the stack. Proteins (talk) 16:07, 8 April 2009 (UTC)

I'm not convinced until you give a ref for that. Jakob.scholbach (talk) 16:49, 8 April 2009 (UTC)

Move the "algorithmic efficiency" in front of applications?

I think it's better to motivate why the algorithm is worth doing to the reader. That way, they'll want to see it made efficient. Proteins (talk) 16:07, 8 April 2009 (UTC)

"Bezout" -- a little ref, please.

Added a few references. Relatively few authors give this theorem a name, but it's convenient for exposition and enough authors call it Bezout's lemma or Bezout's identity to warrant calling it that, IMO. Proteins (talk) 18:15, 10 April 2009 (UTC)

"This definition is helpful in considering more sophisticated number fields" -- this sounds misleading. Number field has a particular meaning, so do you mean this is helpful for general number fields (instead of Q). Probably, anyway, you want to talk about rings, perhaps number rings or UFD's? Actually this whole section might be better off somewhere in the generalizations section.

Lame wording. Will fix. Proteins (talk) 16:07, 8 April 2009 (UTC)

Somehow the "Extended E.a." section is oddly organized, I find. (By the way, it is not at all mentioned in the lead!) Is the e.E.a. about the matrices or just about the additionl info of s and t. Also, I don't understand the purpose of doing all this with matrices. "The matrix M can be calculated efficiently," -- does this mean more efficiently than what you get by tracking all the variables in the usual algorithm?

That's a good suggestion. I added the more typical recursive formulation first, but I like the matrix formulation as an alternative viewpoint that other readers might find easier to understand. Proteins (talk) 17:48, 8 April 2009 (UTC)

In formulae, minus should be typed as − (−), not as a hyphen (-). E.g. in "extended E.a." section

Fix on sight, please. I've been going through the article looking for those, but a few may have escaped me. I'll keep looking. Proteins (talk) 17:48, 8 April 2009 (UTC)

"To prove unique factorization, assume the contrary,..." is one of the things I would remove. (It's all nice, but adds little to the E.a.)

Indulge me on this. Unique factorization is critical for many of the applications lower down in the article, and some readers will want to see exactly how it follows from Euclid's lemma. Proteins (talk) 17:48, 8 April 2009 (UTC)

A general organizational remark: much of the more "advanced" facets (like principal ideals, Euclid's lemma, inverses in GF(p), etc.) stakes on a more or less thorough understanding of modular arithmetic. If you agree on that, this means two things. First of all, write a little more about it. Secondly, and more importantly, center things more around that notion. So, I suggest to make this more of an organizational point, make a little intro in to m.a. and derive things (both mathematically and in terms of article organization) from there. Somehow, many of these things are one and the same thing, formulated differently. It would be nice if the article would convey that; currently it's a bit like a bouquet of flowers that smell differently (but very nicely :) each. I see, though, that it is challenging to convey a clear modular arithmetic picture without fading into technicalities like ideals and so on.

A brief introduction to basic modular arithmetic might go well as a subsection in "Background", but I'm wary of relying too heavily on advanced math to unify the article when I know that our readers will include smart 9-year-old children. I don't want to lose them early on. Let me think about it. Proteins (talk) 18:34, 8 April 2009 (UTC)

Sure. These are all just suggestions. I would probably do a "Linear Diophantine equations modular arithmetic" section and move general things like "the set of 13 numbers {0, 1, 2, ..., 12} using modular arithmetic. In this field, the results of any mathematical operation (addition/subtraction/multiplication/division) is reduced modulo 13; that is, multiples of 13 are added or subtracted until the result is brought within the range 0-12. For example, the result of 5×7 = 35 mod 13 = 9." up to that section, possibly write a little bit more about it. Later, e.g. in the finite field section, you simply say: "In the particular case n (the modulus) = p (a prime), and ... = 1, the algorithm can be used to compute the inverse in GF(p)." Actually, you probably would not even take a section then, just a single paragraph? Jakob.scholbach (talk) 20:30, 8 April 2009 (UTC)

"Factorization algorithms" section needs some refs.

Added a handful. Proteins (talk) 18:15, 10 April 2009 (UTC)

This may be trivial, but the gcd of multiple numbers might be worth mentioning?

Done. Proteins (talk) 16:07, 8 April 2009 (UTC)

Jakob.scholbach (talk) 21:16, 7 April 2009 (UTC)

Thanks again! I'm looking forward to the next part of your review. Proteins (talk) 16:07, 8 April 2009 (UTC)

I will read the rest later tonight or tomorrow. Right now, only one thing: the description of the inverses in finite fields of prime power (but not prime) cardinality is wrong. GF(p^m) (m > 1) is not just doing modular arithmetic modulo p^m (actually Z/p^m is not a field). GF(p^m) is a splitting field of GF(p) w.r.t. to a certain polynomial. Frankly, I would not talk about inverses in these more general fields, since this is basically part of the notion of splitting field. Jakob.scholbach (talk) 16:49, 8 April 2009 (UTC)

Thanks for your continued help. Re:the one thing, I do know the basics of working in GF(p^m), thanks to a misspent youth in algebraic coding theory. I think if you re-read the paragraph, you'll see that nothing's incorrect, although it might be misleading. I finessed the prime power issue with the proviso "using more sophisticated definitions,..." I agree, it might be better to just delete the GF(p^m) references. Proteins (talk) 17:48, 8 April 2009 (UTC)

I don't have youth coding experiences :), but I think this is still wrong. In GF(p^m), p * x = 0, for all x. So the notation "mod p^m" is at the very least misleading. Secondly, in order to make sense of statements like ax + my = 1, what bijection do you want to take between GF(p^m) and {0, 1, ..., p^m - 1}? Jakob.scholbach (talk) 20:30, 8 April 2009 (UTC)

"Worst-case number" section: wikilink induction. Or even better, write a little bit (just 2-3 lines) about induction, since this seems to be a recurring argument here.

Added wikilink, and new section in "Backgroun" on induction, recursion and infinite descent. Proteins (talk) 20:33, 9 April 2009 (UTC)

"first practical application" -- not terribly practical :)

Just quoting my reference, Knuth. He says, "This theorem has the historical claim of being the first practical application of the Fibonacci sequence". Perhaps it's practical for theoretical computer scientists? Proteins (talk) 20:33, 9 April 2009 (UTC)

"Average number" section - wikilink the O notation. Also, if you use O notation, you should write =, not ≈

Fixed. Proteins (talk) 21:39, 9 April 2009 (UTC)

"well-approximated" -- a bit POV. Perhaps make it more precise? (possibly by explaining the meaning of the O notation in that particular case)

Tried to explain this. Proteins (talk) 16:41, 10 April 2009 (UTC)

"it can be approximated by the formula" -- perhaps you put some ≈ sign instead of the = ?

Did so; the Knuth reference uses the approximation symbol as well. Proteins (talk) 16:41, 10 April 2009 (UTC)

In that section, it might be good to highlight that all measures lead to the same leading term. Is that obvious a priori?

It's not obvious to me, but I sense it should be derivable from τ(x) ~ ln x, the inversion formula

T(a)={\frac {1}{a}}\sum _{d|a}\phi (d)\tau (d)

and the von Mangoldt function

\log x=\sum _{d|x}\Lambda (d)

Computational expense per step should be referenced

Referenced to Knuth. Proteins (talk) 18:15, 10 April 2009 (UTC)

I think the efficiency section might be better structured into 1) Number of steps 1a) Worst 1b) Average 2) Single-step-analysis 3) Conclusion?

I'm not sure what you're suggesting? Is the repetition of "number of steps" in the subsection headings? Proteins (talk) 16:41, 10 April 2009 (UTC)

I'm not sure either anymore... Jakob.scholbach (talk) 17:37, 10 April 2009 (UTC)

"Consider the computation of " -- talking to the reader should be avoided as unencyclopledic language.

Improved, I hope. Proteins (talk) 16:41, 10 April 2009 (UTC)

I would briefly mention that h is more or less ln (n). (Knowledge of this is presupposed in the conclusion section). Also, is it standard to give the estimates in terms of ln(n) instead of n? For example "Prime factorization is also inefficient, and likely scales exponentially with the number of digits." is a bit odd. Also you probably mean "likewise" instead. Again, refs, please.

Will do; you're quite right about the "likewise". Proteins (talk) 16:41, 10 April 2009 (UTC)

I don't understand how O(h (log h)^2 (log log h)). can be the same as O(h^2). Do you mean roughly the same?

I believe I meant to say that the subquadratic methods all scaled in the same way. Proteins (talk) 20:33, 9 April 2009 (UTC)

You might merge the generalizations and "other domains of numbers" (the latter is a fairly odd title, I find)

I'm trying to move gradually for the non-mathematical reader. It's a smaller jump from integers to quadratic integers like 1 + 3√2, than to knots and ideals. Proteins (talk) 20:33, 9 April 2009 (UTC)

I like the "Real and rational number" section very much. Very neat. Do provide a reference, though. (I'm a bit picky perhaps, but this is sure to come up at FAC.)

Thank you! I'll be sure to find a ref.

(later) Added some refs. Proteins (talk) 18:15, 10 April 2009 (UTC)

The "Pythagorean triples" is one of those I'd trim down a bit. It is fairly long, and only weakly connected to E.a.; it's more about Gaussian integers.

Good point; gone. Proteins (talk) 20:33, 9 April 2009 (UTC)

I would probably put the material on Euclidean rings first, and put Gaussian integers, polynomials as examples (i.e., subsections) of that one.

If our readers were mathematicians, I would do exactly that (general theorem -> specific examples). But I think it will be easier for most readers to go in the opposite direction, understand a few concrete examples well and then generalize from them. Proteins (talk) 20:33, 9 April 2009 (UTC)

Describing the integral basis of Q[sqrt[D]] is a bit off-topic. On the other hand, I personally would appreciate a brief mention of the class number, including a brief hint where the differences between the Heegner numbers and the only 5 values for D (−11, −7, −3, −2, −1) where the ring is an Euclidean domain come from. (Actually, this may well be off-topic, too.)

This presumes that I understand what a class number is. :) I'll do my best, but... Proteins (talk) 21:39, 9 April 2009 (UTC)

Well, it's not terribly important here. You only need to know that class number one means that the ring has a unique factorization. There are 9 values for which imaginary quadratic fields are of this type (these are the Heegner numbers). For example -163 is one such, but apparently Q[sqrt(-163)] is not an Euclidean domain. I was simply wondering why not. But again, this is probably off-topic. Jakob.scholbach (talk) 10:35, 10 April 2009 (UTC)

Fermat's last theorem section seems also a bit off-topic, at least in this length. I would suggest highlighting the UFD property of rings very prominently, and briefly allude to a few cases where UFD is of interest (such as Fermat, class number).

Removed FLT discussion. Proteins (talk) 21:39, 9 April 2009 (UTC)

"two numbers from such a ring" -- perhaps two elements?

Done — thanks! Proteins (talk) 21:39, 9 April 2009 (UTC)

Jakob.scholbach (talk) 20:30, 8 April 2009 (UTC)

The "elementary school children" I was trying to reach in the lead are typical university graduates who need to exert painful effort to understand elementary-school-level mathematics. Most such people got good grades in algebra and calculus and cannot handle such problems as solving 5x + 3 = 2/x for x, but some of them are a little bit curious about mathematics at the elementary school level that they didn't properly learn as children even though they get good grades in it. They are perfectly capable of understanding that the if 252 − 105 = 153, then the GCD of 252 and 105 is the same as the GCD of 153 and 105. But they will be hopelessly lost if you tell them that the GCD of two numbers is the same as the GCD of the smaller of the two and the remainder upon division of the larger by the smaller. Or if you say anything in even the simplest algebraic notation. Michael Hardy (talk) 06:24, 10 April 2009 (UTC)

We all agree that the article should be accessible to readers, especially the lead, and that many likely readers will not know algebra. I agree that we should try to accommodate them, while keeping the article pithy and general, suitable as a reference work. Proteins (talk) 08:48, 10 April 2009 (UTC)

OK. I have put my 2c there. Jakob.scholbach (talk) 10:35, 10 April 2009 (UTC)

Much improved, kudos! Proteins (talk) 18:15, 10 April 2009 (UTC)

I have now read the rest of the article, which I found pretty cool. (I may also be a bit tired...) I would consider moving the history section up, after the description section. History is often a second, somewhat casual introduction to the topic.

So moved. Proteins (talk) 18:20, 10 April 2009 (UTC)

What is the meaning of the page numbers in the Stilwell reference, say? If this is a book, I would put page references to the footnotes where they are relevant.

They're meant as a suggestion for "Further reading". The footnotes give the exact page(s) that support the assertion, whereas the Bibliography highlights the relevant sections of the book. Proteins (talk) 18:15, 10 April 2009 (UTC)

Another suggestion concerning the references: it would be a service to the reader to use {{Harvard citations}} templates, they provide a hyperlink to the references.

I'm not experienced enough to know how that works. I'll try to read up on it. In my own work, I'm more used to superscripts, which are less obtrusive to reading. Proteins (talk) 18:15, 10 April 2009 (UTC)

See e.g. matrix (mathematics). But it's really just an option. Jakob.scholbach (talk) 18:42, 10 April 2009 (UTC)

Some of the external links should probably go. My personal rule is to remove all links that don't present additional material to this article. For example, the PlanetMath article is of this kind. Also, at some point they should be endowed with an accessdate, otherwise FAC reviewers will complain. (I personally don't need that.)

I agree, I just haven't gotten to reviewing them yet. Proteins (talk) 18:15, 10 April 2009 (UTC)

Again, congrats on the article, which is well on its way toward GA standards. Jakob.scholbach (talk) 17:33, 10 April 2009 (UTC)

I sense that this will an infinite recursion, but let me say thank you again for your help and patience. You've helped the article tremendously. Proteins (talk) 18:15, 10 April 2009 (UTC)

application to knot theory

Generalizations of Euclid's algorithm have been developed with these features. For example, generalized Euclidean algorithms have been used to prove several theorems of knot theory. Similar to the natural numbers, knots can be factored uniquely into "prime" knots.^[1] Knots can be mapped onto polynomials of one variable (such as the Jones polynomial),^[1] to which the Euclidean algorithm can be applied as shown above.

I admit to being greatly puzzled by this passage. I have no idea what it is trying to say. The second sentence would indicate we will see how theorems have been proven using the Euclidean algorithm. The third sentence then states a theorem which has nothing to do with the Euclidean algorithm. Then the fourth sentence brings up knot polynomials, and states Euclidean algorithm can be applied to polynomials, which is true, but seems like a pointless observation in this context. --C S (talk) 04:45, 8 April 2009 (UTC)

^ ^a ^b Adams C (2004). The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. American Mathematical Society. ISBN 0821836781.

Yes, it's a placeholder section while I read up more on the connections between knot theory and the EA. If you type "Euclidean algorithm knot theory" into Google (as some GA/FA reviewers are certain to do!), you'll find several theorems in knot theory that have been proven using a type of Euclidean algorithm, such as this one or this one. The reference to knot polynomials was inspired by this reference. Since I've begun reading up on knot theory in preparation for helping you with your FA, I have a vague impression of how and why the EA is being used, but I haven't studied those or any other knot-theory proofs involving the EA. There are doubtless many more references to the EA in the knot-theory literature. If you'd like to spare me some trouble, it would be a kind gesture if you would write that section yourself. But I'm sure it will be a serious investment of time/effort, even for you, so I'll understand if you can't commit to that. Proteins (talk) 09:24, 8 April 2009 (UTC)

If you're going to call any use of facts in knot theory like certain rings are PIDs an application of EA to knot theory (like in the Lickorish reference), that's really stretching. It's on the same level as calling any use of the prime factorization of numbers an application of EA. You might as well throw in an application to string theory while you're at it! The first two hits you give are what I would call direct, "legitimate" applications, but more complicated than what I would consider the "standard" simple application of EA to knot theory: the use of EA to either write elements of the mapping class group of the torus or four punctured sphere as a product of Dehn twists (which shows up in defining Conway's fraction of a rational tangle). The majority of applications of EA in knot theory will be based on this. We'll see about the investment issue :-) --C S (talk) 15:59, 8 April 2009 (UTC)

Prefer less material on Euclidean domains

The section on Euclidean domains is written in rather breezy language, and contains some inaccuracies and misleading statements. There is already a perfectly good article on Euclidean domains, so I don't see the need to attempt to duplicate this much content here. A sentence which links to Euclidean domain would have the same effect, I think.

What specifically is wrong with this section? First, the definition of a Euclidean domain is not given at the beginning of the section, and then is casually inserted at an intermediate point in the discussion. This is unfortunate, because there are many subtle variations on the definition. For instance, by a "Euclidean quadratic field" some people -- especially in older texts -- mean a quadratic field such that the standard norm function $a\mapsto |a\ \sigma (a)|$ is a Euclidean function on the ring of integers. In this restricted sense there are only finitely many Euclidean quadratic fields. However, the definition given in the article is much more general, and by this general definition it is a difficult open problem as to which (real) quadratic fields are Euclidean. For instance, just in 2004 Malcolm Harper proved that the ring of integers of Q(\sqrt{14}) is Euclidean. Moreover, by a theorem of Harper and Murty, it is now known that the generalized Riemann hypothesis implies that, except for imaginary quadratic fields, every class number one field is Euclidean. But whether there are infinitely many real quadratic fields of class number one has been open since Gauss' day...

Also the article discusses quadratic fields Q(\sqrt{D}) with D of the form 4k + 1 and of the form 4k+3: what about 4k+2? Also it, to my mind, overstates the importance of certain applications of the EA. For instance, it gives the idea that it is in some sense required to know the Euclidean algorithm for the Gaussian integers (resp. the Hurwitz quaternions) in order to prove the two (resp. four) squares theorems. But Fermat and Lagrange gave completely different proofs.

Do others agree that the article would be improved by removing most of the content on Euclidean domains? If so, I can take care of it, but I don't want to cut this much without asking for consensus. Plclark (talk) 01:28, 20 April 2009 (UTC)

First off, let me thank you for the expert attention that you've paid the article, and for being specific in your criticism. I would be very happy if other mathematicians would follow in your and Jakob's footsteps.

I agree with you on several points, although I disagree that the section should be deleted. Let's begin with the agreements. The present article does perhaps convey the impression to the unwary that the Euclidean algorithm is more essential than it is. That's true not only in the 2- and 4-square proofs, but also in other applications where the GCD is needed but not necessarily the EA. I didn't mean to say that the EA was irreplaceable, only useful and convenient. I'll try to comb through the article and tone down any misleading statements.

You didn't mention this specifically, but the 4-square section illustrating the Hurwitz quaternions is rather long and contains several basic statements about quaternions per se. I wrestled with that while writing this section. I decided to include that material, because I think it's good for the reader to see at least one example of how the EA can be exploited in a more advanced mathematical proof.

I do not think that replacing the Euclidean domain section to a redirect to the Euclidean domain would be helpful, for the following reasons. I agree very strongly that mistakes should be fixed and technical precision shouldn't be sacrificed for nothing. Yet I believe that the shortcomings you mention can be fixed within the context of the present article. Second, I feel that most lay-readers are unlikely to follow the link to the Euclidean domain, but we have an opportunity here to introduce them to more advanced mathematics. In my opinion, it's better to allow some redundancy in Wikipedia, especially in fundamental, often-read articles such as this one. Third, — and here we disagree — in my opinion, the present Euclidean domain article is not representative of Wikipedia's best work. Bluntly, the article seems likely to be impenetrable to anyone with less than a graduate education in mathematics. I feel that we have an obligation to write accessibly for lay-people, and I hope you agree. I can't claim that my writing is much better, but the breezy style was related to accessibility. Perhaps we can work on improving this section together. Proteins (talk) 11:19, 20 April 2009 (UTC)

After taking a look at Euclidean domain, I agree with you that it is in need of improvement. For instance, the lead makes the comment that any Euclidean domain is a Bezout domain. This is true but very strange: probably the majority of working mathematicians do not know what a Bezout domain is (for instance, I got a PhD in algebra / number theory in 2003 and only learned this term a couple of years ago). The more familiar statement, that a Euclidean domain is a PID, is in fact a stronger conclusion. When I have the time, I will work on Euclidean domain and will not suggest deleting material in the present article until/unless that article becomes more acceptable and accessible. Plclark (talk) 13:39, 20 April 2009 (UTC)

Thanks for your kind words, Dr. Clark, and your generous volunteering to improve the "Euclidean domain" article. For my part, I appreciate your insights and I'll commit myself to improving the "Euclidean domains" section of this article. In particular, I hadn't realized that the technical definition of a Euclidean domain had shifted subtly over the past few decades; I had just assumed that it would stay constant. I'll need to read up more on that. I've found this 2004 article by Harper and Murty, from which I'll begin to educate myself on the latest developments. I'd appreciate any other corrections or literature you might recommend. Proteins (talk) 14:16, 20 April 2009 (UTC)

The concept of a Euclidean domain is an important one in mathematics and I am glad that you have taken the intiative to improve it, User:Proteins! I think that the article is of great quality.

Euclidean domain and many other articles in the context of ring theory need to be developed to conform to the recent mathematical advances in algebra. In particular, articles of this nature lack anything further than the definition; they fail to describe the significance of the concept in mathematics. I am more than happy to improve Euclidean domain.

On a different note, I believe that the concept of a Euclidean domain should be given greater importance in the article because otherwise we are considering this concept to be a property unique only to the natural numbers. On the other hand, it is with no doubt that I understand the lack of people who have heard of "Euclidean domain". P.S. Is it really the case that many mathematicians have not heard of the concept of a "Bézout domain"? I am sure that the "Bézout identity" is a familiar term among mathematicians. On the other hand, rarely have I seen the concept of a "Bézout domain" being referred to in a textbook. --PS T 14:26, 20 April 2009 (UTC)

Thanks, PST, for your enthusiasm to help with Euclidean domain and your kind words; it helps to know that my amateur efforts aren't too misguided! I've enjoyed working on the EA, because it seems to me a keystone topic in mathematics: one that is basic and understandable to lay-people (some children learn it by age 10) but also deep and rich in consequence. This article seems like a wonderful opportunity to open readers' eyes and minds to modern mathematics, drawing them in with something easy and then expanding their horizons. That being so, we should do our utmost to improve the article both in technical correctness and accessibility. Proteins (talk) 15:06, 20 April 2009 (UTC)

I've re-arranged the section on Euclidean domains, and distinguished between Euclidean and norm-Euclidean domains, with a few references to recent work. How does that section seem now? Proteins (talk) 15:58, 20 April 2009 (UTC)

Euclidean domain

I have written a motivation section in the article Euclidean domain, the relavant parts of which, may possibly be included in this article. The section is very intuitive as far as the FA critieron goes but as I am not an expert on GA's and FA's, I would probably leave this up to User:Proteins. --PS T 11:04, 23 April 2009 (UTC)

Comment about quaternions and the four squares theorem

There is now some very nice content about using the Hurwitz quaternions to prove the four squares theorem. I suggest however that this material belongs in Lagrange's four-square theorem rather than here. Also one needs to be especially careful with concepts like divisibility and factorization in non-commutative rings: I would prefer a slightly more careful exposition, including a reference. Plclark (talk) 16:32, 26 April 2009 (UTC)

Thank you, Plclark, for these comments and your other improvements to the article! The material on the four-square theorem derive mainly from the Stillwell reference, which is cited just above. Parts of it also appear in the Joe Roberts reference, which is cited earlier for Euclid's game.

As mentioned above, I do see the reasoning for removing this material to Lagrange's four-square theorem, in the same way that we removed the Pythagorean triple and Fermat's Last Theorem material. The section is rather long, and I foresee that reviewers at FAC will demand its removal, anyway. But I haven't bowed yet to inevitability, mainly because I'd like to give the interested reader one full example of modern mathematics in which the EA is used. Perhaps we can inspire a future Gauss or Noether? On the other hand, I concede this isn't the best example, since the EA is merely ancillary to proving unique factorization. I'll move the material over, but perhaps we together can think of some other path to inspiration? Proteins (talk) 21:03, 26 April 2009 (UTC)

Second sentence makes no sense

The second sentence, which is supposed to give the main idea of the Euclidean algorithm, makes no sense:

"The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the smaller number is subtracted from the larger number. "

Well, duh! NOTHING changes the greatest common divisor of two given numbers -- it is what it is.

But of course, this was not the intended meaning. Since this article will be read by many people who won't know the intended meaning, it should be stated clearly. For example:

"The Euclidean algorithm is based on the principle that the greatest common divisor of two integers A and B, with B > A > 0, is the same as the greatest common divisor of A and B-A."

This is just one suggestion; there are many ways this could be stated clearly, none of them being the current sentence.Daqu (talk) 18:40, 4 May 2009 (UTC)

Further comments

Start of this list was taken from the FAC. More will be added if you (Proteins) are interested.

Thank you very much, and I am indeed interested in making the article as good as possible. I appreciate your thoughtful suggestions. Proteins (talk) 04:33, 23 May 2009 (UTC)

~~"For example, consider two measuring cups of volume a and b, respectively" Why "respectively"?~~
Gone. Proteins (talk) 04:33, 23 May 2009 (UTC)
~~"By assumption, this can be written as" I've never heard the term "by assumption" before. If it is indeed the correct term here, perhaps it should be wikilinked.~~
I spelled out the reasoning more fully. Proteins (talk) 04:33, 23 May 2009 (UTC)
The closing lines of Extended Euclidean algorithm (before Equivalent matrix method) are, to borrow a term of yours, a "wall of math". I think an example with real numbers would be very helpful here, something I'm sure you can find in any math textbook.
I'm too tired to work on this now, but I'll get back to it. Proteins (talk) 04:33, 23 May 2009 (UTC)
The term matrix should probably be wikilinked somewhere in the section Equivalent matrix method.
Done. Proteins (talk) 04:33, 23 May 2009 (UTC)
~~"The inverse is well-defined" I have the feeling "well-defined" is jargon that should either be wikilinked, explained, or reworded.~~
Re-worded and much better. Thanks for the prompting! Proteins (talk) 04:33, 23 May 2009 (UTC)
~~"Bézout's identity is essential to many higher applications" I think "higher" was supposed to be "higher-level", though omitting it entirely would also work.~~
Omitted. Proteins (talk) 04:33, 23 May 2009 (UTC)
~~"For if the greatest common divisor of u and w is 1, then integers s and t can be found such that" Extraneous "for" at the beginning of this sentence? Perhaps I'm misreading this section.~~
Reworded — is the logic clearer now? Proteins (talk) 04:33, 23 May 2009 (UTC)
Ah, yes. I set it off with a colon to make it even clearer. --Cryptic C62 · Talk 20:14, 26 May 2009 (UTC)
"Specifically, if a prime number p divides L, it must divide at least one factor of L" If you want to introduce a new letter for this sentence, be sure to actually use it: "Specifically, if a prime number p divides L, p must divide at least one factor of L". One the other hand, if you want to be brief and reduce the number of letters being thrown at the reader, try this: "Specifically, if a prime number divides L, it must divide at least one factor of L" or "Specifically, if a prime number p divides L, that prime number must also divide at least one factor of L".
Omitted p. Proteins (talk) 04:33, 23 May 2009 (UTC)
"L = p₁p₂…p_m = q₁q₂…q_n" This might be clearer to non-mathematicians and mathematicians who forgot to put their contacts in if the elements being multiplied had multiplication symbols between them. I distinctly remember "a₁×…×a_n" from my math reasoning course.
~~"where a, b and c are also integers" It may be helpful for the reader if "also" were swapped out for "given". This clarifies the distinction between the variables (x, y) and the constants (a, b, c).~~
Great suggestion. Proteins (talk) 04:33, 23 May 2009 (UTC)
"where s and t can be found by the extended Euclidean algorithm" Throughout the article, you've mentioned several times how the EA is extremely helpful in solving Diophantine equations. However, this is the only line (along with the bit about Bezout's identity, although that is arguably a separate topic) of the section Linear Diophantine equations that mentions the EA. Perhaps I may be missing something here, but it seems to me that whatever connections exist between the EA and linear Diophantine equations need to be spelled out more explicitly in this section.
I need to mull this one over. As the article states, the EA allows you to find one solution of a linear Diophantine equation. Without that, you have no solutions; and with that, you can get an infinite number of solutions. Hence, the EA is key to solving such equations. Proteins (talk) 04:33, 23 May 2009 (UTC)
Ah, I see. That should probably be made clearer in the article. As it currently reads (to someone who is not familiar with diophantine equations), it seems to just go off on an unrelated tangent after the first solution.
"The Euclidean algorithm has a close relationship with continued fractions" Suddenly Wikipedia has become an online dating site for mathematical concepts. How about "is closely related to" instead?
"The sequence of equations can be written in the form" Which sequence of equations?
The Factorization algorithms section is much shorter than any of the other of the Mathematical applications. This is probably because this section gives only a brief overview of several related factorization algorithms without providing a wall of math for any one of them. For those of us who don't know what a factorization algorithm is, it might be helpful to include some sort of mathematical sketch of what this all looks like.

--Cryptic C62 · Talk 03:32, 23 May 2009 (UTC)

Delectable praise

Wow -- This is a fan-tas-tic article. Well done !Pergamino (talk) 21:40, 24 May 2009 (UTC)

I prefer the House article (/joke). This article is great. Good job!! 125.238.148.250 (talk) 01:48, 18 June 2009 (UTC)

Distributive Property of Subtraction

Shouldn't this article mention the distributive property of subtraction, as that is the reason why it works? AB-AC=A(B-C) which is why this preserves any common factors. 69.178.101.144 (talk) 04:47, 18 June 2009 (UTC)

I decided just to add in a line, but I think that the math should be explained in a less confusing manner. Wikipedia tends to be very complicated when explaining mathematical concepts. 69.178.101.144 (talk) 04:59, 18 June 2009 (UTC)

Lead is seven paragraphs; shouldn't exceed four

Two paragraphs in the lead are one sentence each; the first paragraph is only two sentences. Per the style guideline at WP:LEAD#Length, the lead should be <= four paragraphs. At first glance, it seems that the lead could be rearranged to have more substantial paragraphs -- that is, the short 1-2 sentence paragraphs could be merged with the remaining four to meet the guideline. The lead length guideline is occasionally overlooked for articles of lower status, but I think a featured article should strive to fully meet WP:MOS. Making slightly beefier paragraphs than 1-2 sentences is also good prose in itself, in my opinion.Emw2012 (talk) 08:35, 18 June 2009 (UTC)

Agreed. I'll have a tweak. --Dweller (talk) 09:04, 18 June 2009 (UTC)

"first described"

Is there any proof of this? This is the earliest surviving description. Is there any basis for going further? Peter jackson (talk) 11:18, 18 June 2009 (UTC)

See Euclidean algorithm#Historical development. It seems 'first described' is misleading and should probably be changed. Algebraist 12:16, 18 June 2009 (UTC)

Wrong Euclid picture?

Which Euclid is this supposed to be?

The article and currently the Main page displays File:Euklid.jpg which is cut from File:Artgate Fondazione Cariplo - Cifrondi Antonio, Euclide.jpg where the artist calls the subject Euclid of Megara. He is not Euclid of Alexandria from the Euclidean algorithm. But the image caption at Euclid of Megara says "it is almost certainly trying to show Euclid the mathematician, and is typical of the medieval confusion surrounding his identity." Should the image be here and on the main page without comments about the identity? PrimeHunter (talk) 12:10, 18 June 2009 (UTC)

I personally don't much like the practice of illustrating historical personages with pictures which have no resemblance to them, but Wikipedia's 'images for all' practice seems well-established here. We could switch to a less equivocal image, such as File:Euklid-von-Alexandria 1.jpg. Algebraist 12:23, 18 June 2009 (UTC)

I was aware of the medieval mis-attribution when I added the image, but there seems little doubt that this image is intended to show Euclid of Alexandria, the most famous of all geometers and writer of the Elements, considered the most popular/influential textbook ever. The dividers indicate this, and the fact that the image is part of a series entitled "Famous Men". Euclid of Megara was an obscure philosopher/student of Socrates from whom little has survived. The medieval confusion of Euclid the mathematician's birthplace is well-known.

I agree with the disappointment that the Main Page shows an ahistorical image of Euclid, and not a depiction of the algorithm, but I don't feel the need to argue over that. Proteins (talk) 12:55, 18 June 2009 (UTC)

Actually, his birthplace is unknown, so it's conceivable he might really have been born in Megara. Peter jackson (talk) 15:55, 18 June 2009 (UTC)

Animation distracting?

I personally find the animation so distracting to my eye that I'm actually unable to read the lede with the animation in view. Does anyone else think this is a problem? Paul August ☎ 16:44, 18 June 2009 (UTC)

I agree. Besides, I think that is why it was hidden in the first place: [1]. Shreevatsa (talk) 17:53, 18 June 2009 (UTC)

Yes, that's true. Personally I don't find the animation distracting, but others do, which is why I added the "hidden" feature at FAC. Proteins (talk) 17:57, 18 June 2009 (UTC)

I also do not find it distracting. The way it was hidden before was hackish if nothing else... if you're going to have a lead image, it should be viewable imo. Stylistically it looks poor otherwise. I am not against moving it however, or switching with one of the other images. --Izno (talk) 18:27, 18 June 2009 (UTC)

In code

Anyone think we should add what's on [2] to this page?99.182.222.37 (talk) 22:13, 18 June 2009 (UTC) <--- Oops, forgot to log in, that's me Overthinkingly (talk) 22:15, 18 June 2009 (UTC)

The first thing here under Euclidean algorithm#Implementations is essentially identical. Algebraist 22:19, 18 June 2009 (UTC)

Would it not be better replaced with pseudo-code? Overthinkingly (talk) 22:26, 18 June 2009 (UTC)

What's wrong with the current pseudocode? Algebraist 22:33, 18 June 2009 (UTC)

Oh, nevermind. It just looked somewhat easier to understand.Overthinkingly (talk) 23:27, 18 June 2009 (UTC)

Incorrect subscripts for q in the recursive formulas in "Extended Euclidean algorithm"

The section Extended Euclidean algorithm contains the following recursive formulas:

s_k = s_k-2 + q_k-1 s_k-1

t_k = t_k-2 + q_k-1 t_k-1

In both of these, the term q_k-1 should be q_k. The proof of the formulas incorrectly says:

"The kth step of the algorithm gives the equation

r_k = r_k-2 - q_k-1 r_k-1 "

But the earlier section Procedure gives the recursive equation as

r_k-2 = q_k r_k-1 + r_k

So the subscript of q is k, not k - 1.

Note that the initial values for s and t don't make sense with q_k-1 is in the above formulas, because q_-1 is undefined.

Here's an example for a = 9, b = 2. Since 9 = 4*2 + 1, q_0 = 4 and r_0 = 1. So

s_0 = s_-2 + q_0 s_-1 = 1 - 4*0 = 1

t_0 = t_-2 + q_0 t_-1 = 0 - 4*1 = -4

Then r_0 = s_0 * a _ t_0 * b. Since 4 = 4*1 + 0, the algorithm terminates at the next step, which is N = 1. So r = 1, s = s_0 = 1 and t = t_1 = -4

The article says:

"Using this recursion, Bézout's integers s and t are given by s = s_N and t = t_N, where N + 1 is the step on which the algorithm terminates with r_N+1 = 0." — Preceding unsigned comment added by 88.70.136.177 (talk) 22:11, 13 August 2014 (UTC)

Note that this statement still doesn't handle the special case in which b divides a, for which the Euclidean algorithm terminates at step N = 0. In this case, a = q*b + 0, and r = b, s = 1 and t = 1 - q.

EGalois (talk) 22:48, 24 September 2009 (UTC)

Animation is confusing

No, I'm not talking about the problems of having a big animation in the article lead (that's got a section above). I'm talking about this: It doesn't illustrate GCD(252, 105). No, it illustrates GCD(12n, 5n) for some integer n, and if you looked at it without reading the caption you'd be justified in thinking that n = 1. The caption declares that each dash represents 21, which is the GCD -- which is also confusing, because that means the diagram relies on the GCD for scale before the GCD is shown to be calculated! Am I worried about nothing, or do you see it too? Perey (talk) 03:45, 14 January 2010 (UTC)

I too agree with Perey's argument; however, it seems that a simple re-writing of the caption would solve most problems. 130.238.58.123 (talk) 10:39, 2 August 2010 (UTC)

-- Moved my comments down to next section --

Distracting animation: Paste-in of Heath 1908, etc.

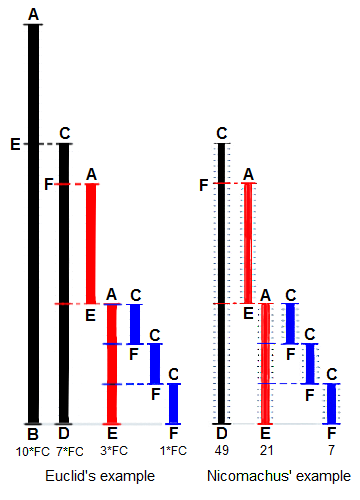
I put this in the article, but it may be too much, or located in the wrong place. Personally I like to see the "real deal" (the Greek would be even more interesting, especially side by side). I added Heath 1908 to the Bibliography. His commentary is very interesting. BillWvbailey (talk) 16:55, 1 February 2011 (UTC)

I don't see the purpose of a scan from a textbook, anywhere in the article but especially not as the first image. Those that trouble to read it will find the layout tiring and the language anachronistic ("But it also measures itself"). If it were historically interesting but the theorem dates back to Euclid: that it appears in a 1908 text book is entirely unnotable. Both captions are far too long: a caption should briefly describe the image, the article should cover the topic. And I can see nothing wrong with the animation: 'the animation is a pain' makes no sense at all so is not a reason to remove it, or replace it with a less clear image that needs a much longer explanation.--JohnBlackburne^words_deeds 17:42, 1 February 2011 (UTC)

I didn't expect anything different than a revert. Okay so you don't like the page from Heath. But here's the problem with the animation. It's not just me, see the above comments at more than one page. Apparently over the years it's been hidden, partly hidden, and now its back. (1) I derived NO insight or information whatsover from it. A close look at the drawing derived from Heath explains a lot, you can measure off as I explained above. (2) The animation is visually distracting; because the hopping images are viewed from the side they cause the eye to be diverted from the text. So I'm going to revert the animation again. I'll leave the page of text off. We need other opinions. Bill Wvbailey (talk) 18:03, 1 February 2011 (UTC)

I find the animation so visually distracting that I am unable to read the lead. Paul August ☎ 18:58, 1 February 2011 (UTC)

But the image and caption that are there now are worse: it's not clear from looking at the image what the two parts represent, and the overlong caption does little to help. It is unclear what it's referring to: it mentions Heath, Nicomachus (Nichmachus?), "Proposition 2" without saying what they are. It reads like the second or third paragraph of a far lengthier explanation. Mostly though it is too long, with far too much calculation detail that should be postponed until the worked example later. To me the image is a lot less clear than the animation, which shows much more clearly how the process proceeds and to me not at all distracting: such animations I find are very appropriate for illustrating mathematical proofs, algorithms and constructions which by their nature are not static. The current image also suffers from the same problem identified above: the scale in the left example is not clear. And it seems most contributors to the talk page find the animation is fine or that the problem is with the scale or description: there's no consensus to remove it.--JohnBlackburne^words_deeds 19:30, 1 February 2011 (UTC)

We're both experienced editors, and I've noted your points. There must be a way to make an illustration that isn't highly bothersome to some of us, and useless for at least one of us. Heath 1908 can be found at www.books.google.com. It's from Heath 1908 that Stephen Hawking's 2005 God Created the Integers draws his textual source (without decent attribution). Nicomachus was a ancient Greek mathematician. But his method (his illustration) uses numbers, shown on the right, and unlike Euclid's (shown on the left), allowed for more than 3 iterations (Euclid's "proof" stopped at three). Apparently Euclid's was done completely in terms of lengths (altho I haven't seen a literal facsimile in Greek), and he did not specify any example lengths (apparently intentionally), as did Nicomachus. Plus Nichomachus' method did not assume Euclid's Proposition 1: Two unequal numbers being set out, and the less being continually subtracted in turn from the greater, if the number which is left never measures the one before it until an unit is left, the original numbers will be prime to one another. In other words, here's the notion of "relatively prime" in algorithmic form. But Euclid assumed Prop. 1 in his demo of his Prop. 2, now known as the Euclid algorithm.

This is from what was immediately above, but I've moved it down here:

Here is a drawing that I've used in the Algorithm article. I too find the animation confusing because I can't "measure" the lengths; they're hopping around. With the still drawing I can see what's going on. It's pretty clear that there are 3 CF's making up 1 AE, 3 + 3 + 1 CF's making up DC, and 7 + 3 CF's making up BA. Thus the two numbers could be 10 and 7, relativiely-prime with CF = 1, but they could also be 20 and 14 so CF=2 units, or 30 and 21 so CF=3 units, etc, i.e. an infinite number of possibilities that result in this pattern. BillWvbailey (talk) 16:55, 1 February 2011 (UTC)

I worked on the description here on this page. As for its length, so what? It's there, it's information, a reader can read it or not. If it's inaccurate then it can be rewritten, + there's nothing saying that I couldn't do another illustration more suited, e.g. one example or the other. But I find the hopping animation no more worthy than a flasing side-advertisment on an internet page. BillWvbailey (talk) 20:39, 1 February 2011 (UTC)

The policy on captions is WP:CAP. In particular it says "More than three lines of text in a caption may be distracting". The description should be minimal: the image, which is there to illustrate the article, should be clear enough that a lengthy description is not needed. The caption should not give the source: use references for that. And there should be no lengthy explanation: that should be in the article body, at a font size that's not a strain on the eyes and where it can be placed in context so things like "Proposition 2" make sense – though referring so precisely to non-notable secondary sources is unnecessary; it's Euclid's algorithm not Heath's.--JohnBlackburne^words_deeds 20:57, 1 February 2011 (UTC)

--- We had an edit conflict. I trimmed the Euclid illustration and re-did the explanation (but it probably offends your succinctness police. I suppose we can work to rule, or we can try to do a good job.) Per "succinctness" I cut this out "3 CFs make up AE, 3 + 3 + 1 CFs make up DC, and 1 DC (i.e. 7 CFs) + 3 CFs make up BA; thus BA = 10 CFs and DC = 7 CFs. But CF can be 1, 2, 3, ... units; if CF is one unit then the numbers are relatively prime.(Illustration derived from Heath 1908:298-300)." Bill Wvbailey (talk) 21:15, 1 February 2011 (UTC)

Added another version. The image on the right plays off the image on the left. These are both historically attributed, so they have that content (historical) as well as avoiding any claims of O.R. Bill Wvbailey (talk) 23:49, 1 February 2011 (UTC)

Generating musical rhythms?

The lead says "[The Euclidian algorithm] may be used to generate almost all the most important traditional musical rhythms used in different cultures throughout the world". I know the phrase links to an article whose title says so much, but that does not make it clear to me what this means. The algorithm computes GCD's it does not generate any rhythm (or do the rhythms arise when you run the algorithm on equipment that actually makes noise as it performs the steps)? This point does not seem to be elaborated anywhere, so I feel it does not belong in the lead. Marc van Leeuwen (talk) 14:58, 13 February 2011 (UTC)

Section "induction, recursion and infinite descent"

I do not see why this section is relevant in this article. It amounts to redefine what is a proof in every mathematical article. I propose to remove it and, possibly, to add links to induction (mathematics), recursion and infinite descent where needed. D.Lazard (talk) 10:38, 26 April 2012 (UTC)

Sounds good. Glrx (talk) 15:50, 27 April 2012 (UTC)

Yuk

This article does everything but explain to a general reader what the Euclidean algorithm consists of. The first statement of the algorithm occurs way down in the Procedure section and uses dense, unnecessarily technical notation. The earlier "concrete example" also uses unnecessary function notation. The lede mostly engages in a lot of name dropping. We are told "If implemented using remainders of Euclidean division rather than subtractions, Euclid's algorithm computes the GCD of large numbers efficiently..." without being told what either the division or subtraction methods are. I'd like to take a stab at a rewrite but i don't want to start an edit war. Other's thoughts?--agr (talk) 17:20, 22 May 2012 (UTC)

I fully agree with the preceding post. I do not understand how it could become a FA. Here are some of its flaws:

The lead is too long and too technical
Section "Euclidean division" should appear (edited accordingly) as a subsection of section Backgrounds, before the description of the algorithm.
There are two Euclidean algorithms, the original one with subtractions and the one with remainders. Section Procedure should have a subsection for each one.
The difference between these two algorithms is that all the steps between two exchange of the r_k in the original algorithm are regrouped in a single step of the algorithm with remainders. This should be emphasized.
The proof is much too long: It suffices to remark that the set of the common divisors of two consecutive r_k is not changed during the algorithm. Thus the greatest one is also invariant.
It is said that "the algorithm is iterative". This is true for some implementations, but wrong for the simplest one which is recursive: GCD(a,b)== if b=0 then return a else return GCD(b, a mod b). For the record, the original algorithm is: GCD(a,b)== if b=a then return a else if a<b then return GCD(b, a) else return GCD(a-b,b).

I could rewrite the article myself, but I do not have enough time for doing it.

D.Lazard (talk) 20:37, 4 July 2012 (UTC)

@agr. Go ahead and edit the article. If somebody reverts the edits, we can discuss them on this talk page.

@D.Lazard. I agree with many points, but the syntactically recursive expressions are tail recursive and therefore iterative.

Glrx (talk) 19:19, 5 July 2012 (UTC)

@Glrx. I agree and I did know that the recursive description of Euclidean algorithm is tail terminal. But it is not the point, and I missed it in my previous post. The opposite of "recursive" is not "iterative" but "imperative". In fact, "iterative" is used here in a rather usual sense of "containing a loop such that the result of each iteration is used in the next one". Such a meaning is unusual. It is different of that defined in Iterative method. It is sourced to a rather old book that is not a book about algorithmic. It should thus be considered as WP:OR. D.Lazard (talk) 06:36, 6 July 2012 (UTC)

I don't see your point. We are discussing an algorithm where the usual sense of iteration is appropriate. Iterative method is about approximation/convergence; there are still iterations, and each iteration hopefully improves the result. I don't see an implicit/explicit distinction being important; reduction is the issue here. Glrx (talk) 16:39, 9 July 2012 (UTC)

The point is that the qualification of "iterative" for an algorithm is presently used only for iterative methods, and means "proceeding by successive numerical approximations (real or complex)", which is absolutely not the case here. I admits that, before the development of computer science and algorithmic as scientific fields, "iterative" may have had the meaning of "containing a loop". But using this meaning now is totally misleading for the reader. It suggest that there are non trivial algorithms that do not contain any loop, or, if "iterative" is linked to iterative method (where a definition of "iterative algorithm" is given that does not apply here), that it is an algorithm that works on real numbers. Thus, it is much better, here, to avoid the word of "iterative". D.Lazard (talk) 17:32, 9 July 2012 (UTC)

Many algorithms employ iteration -- not just those that involve convergence. Search algorithms (for roots or tables) employ iteration. Your argument seems inconsistent. You assign a usual meaning to "iterative" above, but then contradict that by assuming "iterative" is linked to iterative method. If there's a usual meaning, then why would an unusual meaning be selected? The quadratic formula is a nontrivial algorithm that finds the roots of a quadratic equation without obvious iteration (yes, there is that pesky square root). The obvious algorithm to compute the Ackermann function doesn't seem to iterative either. The Euclidean algorithm seems to be a fine example of an iterative algorithm that does not work on real numbers. I disagree with the latter linkage to a single class of methods. Glrx (talk) 15:58, 10 July 2012 (UTC)

Can you provide a reliable source where an accurate definition of iterative algorithm is given? If not, this word has to be avoid here. Personally, during more than thirty years of research in algorithmic and in algebra, the only use of "iterative", that I have encounter is that of iterative methods. I have also encountered iterative in some old fashioned texts of mathematics written before the development of algorithmic, or by mathematicians that believed that they could talk of algorithmic without knowing anything about it. D.Lazard (talk) 14:39, 13 July 2012 (UTC)

Move?

The following is a closed discussion of the proposal. Please do not modify it. Subsequent comments should be made in a new section on the talk page. No further edits should be made to this section.

The result of the proposal was not moved per WP:COMMONNAME. It is not for us to correct perceived errors in naming (fortunately or unfortunately!). --regentspark (comment) 20:48, 4 September 2012 (UTC)

Euclidean algorithm → Euclid's algorithm –

Euclid's algorithm is due to Euclid, unlike "Euclidean spaces" or "Euclidean rings". D.Lazard (talk) 10:27, 25 August 2012 (UTC)

Oppose: it really is most commonly referred to as the Euclidean algorithm. RobHar (talk) 04:47, 26 August 2012 (UTC)
Oppose My exposure is to the current name. I would search for COMMONNAME evidence, but that doesn't seem necessary until there is evidence to support a move. Johnuniq (talk) 08:59, 26 August 2012 (UTC)
Oppose - of the five number theory textbooks I just pulled from my bookshelf, four use the term "Euclidean algorithm", and only one (Davenport's Higher Arithmetic) calls it "Euclid's algorithm". Gandalf61 (talk) 09:10, 26 August 2012 (UTC)
Support: When a mathematician's name has an adjective form, the current usage is to use it for notions and objects that are not fully specified (normally preceded by the article "a"), while noun form is used for theorems, formulas, algorithms and other well specified objects (implicit article "the"). IMO this should apply also for Euclid. I do not see any reason to talk of "the Euclidean algorithm" instead of "Euclid's algorithm". "An Euclidean algorithm" is a nonsense, and "the Euclidean algorithm" does not clearly credit Euclid for it. D.Lazard (talk) 15:41, 27 August 2012 (UTC)
Support: But only because the eminence gris Donald Knuth 1973:2 refers to it as "Euclid's algorithm". I am vaguely persuaded to a limited degree by D.Lazard's argument, above: Turing's theorem, Goedel's theorem, etc whereas it's a "Turing machine", not a "Turing's machine". Knuth's context here is his discussion of his characterization of the notion of "algorithm"; he states that "By 1950, the word algorithm was most frequently associated with "Euclid's algorithm," a process for finding the greatest common divisior of two numbers which appears in Euclid's Elements (Book 7, Propositions 1 and 2.) [etc. Knuth repeats his usage "Euclid's algorithm" twice more, so it's not a random occurrence.] BillWvbailey (talk) 19:21, 27 August 2012 (UTC)
Ooh, so he does. And Robert Sedgewick does the same in his Algorithms. I mentioned this proposal at WT:WikiProject Mathematics#Euclidean algorithm. Johnuniq (talk) 01:34, 28 August 2012 (UTC)
Both are perfectly respectable terms, but the fact that Knuth prefers "Euclid's algorithm" impresses me. Michael Hardy (talk) 04:13, 28 August 2012 (UTC)

BTW, in case anyone doesn't know: look at Donald Knuth. Michael Hardy (talk) 04:14, 28 August 2012 (UTC)

Another moniker: I have three old "number theory" books that, when they discuss this particular algorithm of Euclid's, label it this way -- Uspensky and Haselet 1939:26 "Euclid's algorithm", Ore 1948:41 "Euclid's algorism" [sic], and Hardy and Wright 1939, 1979:136 "Euclid's algorithm". BillWvbailey (talk) 21:28, 28 August 2012 (UTC)
google search: 78,000 for "Euclid's algorithm" in quotations, 193,000 for "Euclidean algorithm" in quotations. One "front-page" article seems to mix the two. BillWvbailey (talk) 21:41, 28 August 2012 (UTC)

Oppose Personally I'd prefer Euclid's algorithm and I also dislike 'Pythagorean theorem', but the evidence seems fairly clear to me that Euclidean is significantly more commonly used even in recent books and we're supposed to reflect the world not correct it. Dmcq (talk) 07:47, 28 August 2012 (UTC)
Oppose "Euclidean algorithm" is the standard term. "Euclidean" is the standard proper adjective from the proper noun Euclid, and is used in the related "Euclidean domain". The alternative "Euclid's algorithm" is acceptable but inferior generally; it is preferable when the emphasis is on Euclid. Kiefer.Wolfowitz 09:49, 28 August 2012 (UTC)
Oppose "Euclidean algorithm" is commoner. "Euclid's lemma" is also standard. Really, it doesn't matter as long as there's cross-references - Virginia-American (talk) 13:23, 28 August 2012 (UTC)
Support: All other algorithms named after people that come to mind use the genitive form in case of one person (Dijkstra, Tarjan, Risch) or nominative in case of more than one (Robinson-Schensted, Wilf-Zeilberger), never an adjective. So Consistency would favour Euclid's algorithm, which is quite all right and in fact slightly better for Recognizability, Naturalness, Precision, and Conciseness as well. That is not to say "Euclidean algorithm" is problematic, but I would say it more properly describes a class of algorithms in Euclidean rings than the algorithm on positive (in fact >1) integers that Euclid describes. The large majority if the current article is specifically about integers, so "Euclid's algorithm" is appropriate. It would be good to know if this distinction was kept in mind when tallying common use. On the downside I should note that Euclid's algorithm uses repeated subtraction as basic operation, rather than "Euclidean division" as does much (but not all) of this article. All in all "Euclid's algorithm" seems better to me. Marc van Leeuwen (talk) 13:26, 28 August 2012 (UTC)
Oppose: While the standard in naming concepts after their inventors nowadays is to use the possessive form rather than an adjective, “Euclidean algorithm” is an established traditional name and we should follow it per WP:COMMONNAME. (Though in an encyclopedia that calls groupoids by the “magma” abomination, this hardly matters.)—Emil J. 14:00, 28 August 2012 (UTC)
Oppose: One of the beauties(?) of the English language is its charming ability to be inconsistent with its own rules. With all due respect to Don Knuth, he is known for bucking the tide and not following common usage when he has a point to make. This may be an instance of that. Bill Cherowitzo (talk) 16:44, 28 August 2012 (UTC)

Another point to consider – when the emphasis is on algorithms, there is no reason to write the names of some of them one way and others a different way. On the other hand, if you have a specific algorithm in mind (and are not trying to compare different ones in any sense) then the adjective form singles out this algorithm from all the other possible algorithms that you could associate with the individual author. The "Euclidean algorithm" means this algorithm, but "Euclid's algorithm" could refer to any algorithm associated with Euclid. It's not specific. Bill Cherowitzo (talk) 21:13, 28 August 2012 (UTC)

Quite to the contrary, "Euclid's algorithm" refers to the algorithm Euclid described, while "Euclidean algorithm" can be any algorithm vaguely inspired by or resembling it. I would consider calling an algorithm operating on polynomials "Euclid's algorithm" an anachronism. Knuth sticks to "Euclid's algorithm" a bit longer, speaking of "Euclid's algorithm for polynomials over a field" in TAOCP Vol 2 p.405 (4.6.1) but three pages further goes for "Generalized Euclidean algorithm". As for ambiguity in the term, in case a person is lucky enough to have multiple algorithms named after her, qualifications should be added to keep them apart, but this rarely happens. "Dijkstra's algorithm" is one specific algorithm, although without any doubt he thought of more than one in his lifetime; the situation with Euclid is no different. Marc van Leeuwen (talk) 13:36, 30 August 2012 (UTC)

I think I blurred the point that I was trying to make. In this case (and I don't want to make a general statement) the situation with Euclid is different. This becomes clear when you consider the fact that the expression "a Euclidean algorithm" is never used, it is always "the Euclidean algorithm" when referring to this particular algorithm of Euclid. One may wish that there was more consistency in the language, but our job is not to correct the world, just report it. Common usage prevails, whether it is correct or not. As an author I can decide whether to follow the flock or write things in what I consider to be their correct form, but as a WP editor I can't. Bill Cherowitzo (talk) 19:41, 31 August 2012 (UTC)

Oppose: "Euclidean algorithm" is the only term used, in my experience. (That means "Euclid's algorithm" might be used somewhere, it's just difficult to find after 10 years in the profession.) Rschwieb (talk) 14:18, 29 August 2012 (UTC)
Comment: All of the support votes are arguing that if we had a chance to name this algorithm, then we should clearly name it "Euclid's algorithm". And I tend to agree. I think this would be a good tie-breaker if the two terms were used equally, but "Euclidean algorithm" is by far the more common term. So, it doesn't matter what it should be called. RobHar (talk) 16:53, 30 August 2012 (UTC)
- Comments like this one seem to occur when people think of the article's title as a proper noun. When it's merely a noun phrase describing the topic, like analyticity of holomorphic functions, then discussions about the best title seem to involve things like comprehensibility, brevity, probability of its use as a search term, conformance with Wikipedia's style manuals, etc. I wonder if there's some rule about when a phrase is regarded as a proper noun and when it's just a description of the topic. Michael Hardy (talk) 18:23, 30 August 2012 (UTC)
- QUOTE if we had a chance to name this algorithm, then we should clearly name it "Euclid's algorithm" END OF QUOTE. I wonder to what degree we do have a chance to name things. Certainly whoever writes a book or a scholarly paper has a chance to name it within the paper, and some other writers may follow, especially if they think the name is better than any others that might get used. It's not unusual that the author of a Wikipedia article has some discretion in what to call it: look at the edit history of the article titled 2008 Beijing Drum Tower stabbings and you see that the title of the article was changed 28 times! Possibly none of the names violated any Wikipedia rules or customs, but at each step it was thought that another name is better. Michael Hardy (talk) 21:36, 1 September 2012 (UTC)

The above discussion is preserved as an archive of the proposal. Please do not modify it. Subsequent comments should be made in a new section on this talk page. No further edits should be made to this section.

If you use Euclidean algorithm on numbers A and B to produce gcf(A,B) but also coefficients C and D such that CA-DB=gcf(A,B), is it guaranteed that C<B/gcf(A,B) and D<A/gcf(A,B)?

If you keep track of the coefficients on A and B each step of the way, so A starts with the vector <1, 0> and B starts with the vector <0, 1> and suppose you subtract B from A 5 times, then A's new vector will be <1, 0> + 5*<0, 1> = <1, 5> (it actually doesn't matter if you subtract or add the vectors as long as you ALWAYS subtract or ALWAYS add - if you subtract them you get a solution to C*A+D*B=gcf(A,B) instead of C*A-D*B, but that's a minor distinction, you'll just get one of the numbers negated if you do that); then say you subtract the new value of A from B 3 times, B's new vector will be <0, 1> + 3*<1, 5> = <3, 16>. Once you get to 0, you go back a step to get to the GCF, you'll have a vector that goes along with it that represents the coefficients C and D on the original values of A and B that produce the GCF as C*A-D*B=+/-gcf(A,B). (It is + or - the gcf depending on whether A was being subtracted from B or B was being subtracted from A on the last step. If you get -gcf(A,B) and want them to add to +gcf(A,B), you can just negate both C and D.) But of course, more than one possible values of C and D solve that equation - if you add B/gcf(A,B) to C and also add A/gcf(A,B) to D, it works as well. In fact all solutions will be of the form <C+n*B/gcf(A,B), D+n*A/gcf(A,B)> for any arbitrary integer n. So since the solutions for C occur regularly and with a period of every B/gcf(A,B) there's exactly one solution involving a value of C between 0 and B/gcf(A,B) and it is accompanied by a value of D which is between 0 and A/gcf(A,B), and exactly one solution for C between B/gcf(A,B) and 2*B/gcf(A,B), exactly one between 2*B/gcf(A,B) and 3*B/gcf(A,B), etc. But does the one generated by the Euclidean algorithm always generate the first solutions? That is, the one between 0 and B/gcf(A,B) (or between -B/gcf(A,B) and 0 if you had to negate C and D because you got -gcf(A,B)) in preference to the solution between +B/gcf(A,B) and +2*B/gcf(A,B)? Does it always perhaps produce the smallest possible magnitude solutions and therefore will produce an answer between -.5*B/gcf(A,B) and +.5*B/gcf(A,B)? Could pot luck cause it to generate a solution for C that is between 4*B/gcf(A,B) and 5*B/gcf(A,B)? I know that if B is a multiple of A, then you get to 0 on the first try subtracting multiples of A from B, so the starting vector of A of <1, 0> is the winner, so C or D CAN be 0 (and if one number is 0, the other is 1). And I know that C and D can't be of opposite polarity - you can't have one positive and one negative, because that would require that A and B be less than gcf(A,B) and that violates the definition of gcf (also it's all positive numbers until you get to the end and possibly choose to negate BOTH C and D together if they produced -gcf(A,B)), but I can't seem to prove anything else about the actual range the values of C and D produced by this algorithm will be in, or find that anyone else states any results about it.

75.175.24.214 (talk) 15:22, 6 November 2012 (UTC)

Firstly, the method you describe is explained in the section Euclidean algorithm#Extended Euclidean algorithm and the article Extended Euclidean algorithm. It is a pity that none answers to your question.

The answer of your question is yes: The extended Euclidean algorithm produces C and D such that |C|<B/gcd(A,B) and |D|<A/gcd(A,B), and C and D are either both positive or both negative. Sketch of the proof: The quotient of the division of A by B is less than A/B, unless at the last step where it is equal. Thus the product of the quotients is less than A/gcd(A,B) and the product of the quotients but the first one is less than B/gcd(A,B). The successive values of the coordinates of the vector you consider are computed as s_i+1 = s_i-1 - q_is_i. It suffices to remark that the absolute values of the s_i are increasing and that their signs change at each step to obtain that |s_i+1| < |s_i q_i|, which gives easily the desired result. D.Lazard (talk) 19:57, 6 November 2012 (UTC)

Some practical problems

After the well written proofs of "Euclid's lemma" and the "Fundamental theorem of arithmetic" some practical problems would be wellcome. My students, from 13 year up to bachelor level, experienced difficulties in the following problems.

1. Simplify as far as possible the rational numbers 10759/15847 and 10760/15848.

2. Solve the linear diophantic equation 9x + 20y = -465 in Z<sup">- x Z<sup">-.

3. A shopkeeper bought in the beginning of a year 120 pieces of apparatus. In July 93 were already sold and his income on the sold articles was $ 15 more than the amount he had spent at the purchase. Find his cost price and his selling price a piece as the man sells nothing above $ 50.

4. Prove gcd(a, 2a + 3b) = gcd(b, 3a - 2b).

5. Gcd(a, b, c) = 1 and a<sup">2 + b<sup">2 = c<sup">2 → gcd(a, b) = gcd(b, c) = gcd(c, a) = 1

6. Gcd(a, b) = 1 → gcd(a<sup">2 - b<sup">2, a<sup">2 + b<sup">2) = 1 or 2. C.W. Vugs (talk) 16:53, 19 December 2012 (UTC)

Examples are too easy

I agree with all remarks written in the section review : too long, too long. Further I think that your examples are too easy and will not convince the readers of the importance of Euclid's algorithm.

Example 1 : GCD (252, 105) far too easy. Let this out. Readers will skip this up to and included Bezout's identity. They will see without any algorithm GCD (252, 105) = 21.

Example 2 : GCD (1386, 3213) is also too easy. Readers will discover that both numbers have a lot of small factors 2, 3, 7 and 11. They will factorize quikly.

Example 3 : The worked example : GCD (1386, 3213) the same. Once again too many small factors.

Start with a difficult one. How did Euclid find GCD (12769, 14803)?

(i) He divides 14803 by 12769 to get 14803 - 12769·1 = 2034.

(ii) He divides 12769 by 2034 to get 12769 - 2034·6 = 565.

(iii) He divides 2034 by 565 to get 2034 - 565·3 = 339.

(iv) He divides 565 by 339 to get 565 - 339·1 = 226.

(v) He divides 339 by 226 to get 339 - 226·1 = 113. He stops here. The next remainder will be 0. He states and proves GCD (14803, 12769) = 113.

{B} Going from (v) to (i) : 113 is a common divisor of 226 and 339 -----> 113 is a common divisor of 339 and 565 -----> 113 is a common divisor of 565 and 2034 -----> 113 is a common divisor of 2034 and 12769 -----> 113 is a common divisor of 12769 and 14803.

{C} Going from (i) to (v). Let d be any common divisor of 14803 and 12769 -----> d | 12769 and d | 2034 -----> d | 2034 and d | 565 -----> d | 565 and d | 339 -----> d | 339 and d | 226 -----> d | 113. {A} together with {B} explain the name : GCD (a, b) is the greatest among the common divisors of a and b.

{D} Going again from (v) to (i): 113 = 339 - 226•1 = 339 - (565 - 339•1) = 339•2 - 565 = (2034 - 565•3)•2 - 565 = 2034•2 - 565•7 = 2034•2 - (12769 - 20344•6)•7 = 2034•44 - 12769•7 = (14803 - 12769•1)•44 - 12769•7 = 14803•44 - 12769•51. This means that the equation 14803x - 12769y = 113 has solutions in Z⁺, namely x = 44 and y = 51.

For Euclid zero was nothing and certainly not a number. He didn't divide a number by 1 or by itself. The set of remainders is not empty and consists of a serie decreasing natural numbers. The set has a smallest element according to the principle of well ordening. This element is called the GCD of the two numbers. His method can easely be generalized and summarized.

THEOREM OF EUCLID'S ALGORITHM : Each pair a, b ε Z⁺ has a GCD (a, b), which can be calculated by Euclid's algorithm and has the following properties : {A} GCD (a, b) ε Z⁺. {B} GCD (a, b) is a common divisor of a and b. {C} Each common divisor of a and b is a divisor of GCD (a, b). {D} Moreover : the equation ax - by = GCD (a, b) can be solved for x and y ε Z⁺.C.W. Vugs (talk) 09:32, 15 April 2013 (UTC)

Even if Euclid did not know about 0 and negative numbers, it is not convenient to restrict a and b to positive values. If one is zero, the usual convention is gcd(a,0)=gcd(0,a)=a. On the other hand, your condition D is known as Bezout's identity and is commonly computed with extended Euclidean algorithm. D.Lazard (talk) 11:05, 15 April 2013 (UTC)

The difference between Euclid's algorithm and Bezout's identity. Euclid is working in Z⁺ and his equation ax - by = gcd (a, b) has exactly one solution in Z⁺. Bezout is working in Z and his equation ax + by = gcd (a, b) has infinitely many solutions in Z.C.W. Vugs (talk) 12:17, 15 April 2013 (UTC)

Take my example (x, y) = (44, 51) is a unique solution of 14803x - 12769y = 113. And (x, y) = (44, -51) + t(113, -131), t ε Z, are infinitely many solutions of 14803x + 12769y = 113. Note the + and the -. For instance (157, -182) is also a solution. Euclid didn't work with negative numbers but he could subtract.C.W. Vugs (talk) 12:49, 15 April 2013 (UTC)

The assertion that (what is now called) Euclidean algorithm works only for positive inputs is your opinion, which is not supported by any source. Your assertion is wrong, that x and y are positive in the solution of ax - by = GCD (a, b), which is provided by Euclidean algorithm (take a=5, b=3). On the other hand, Bezout's identity asserts the uniqueness of x and y such that ax + by = GCD (a, b) and |y|<a and |x|<b; this implies that they have opposite signs, but their exact sign depends on the parity of the number of iterations in Euclidean algorithm. D.Lazard (talk) 13:17, 15 April 2013 (UTC)

Your first example take a = 5 and b = 3 is an excellent example of Euclid's algorithm. GCD(5, 3) = 1 and the equation 5x - 3y = 1 has as solution x= 2 and y = 3. Even with the restrictions you added to Bezout's identity |y| < a, |x| < b there are still many solutions. Here is another one x = -69 and y = 80. Perhaps you can tell me how many there are?C.W. Vugs (talk) 15:02, 15 April 2013 (UTC)

given

5 x - 3 y = 1

substitute your proposed solutions of x = -69 and y = 80 gives

5 (-69) - 3 (80) = -345 - 240 = -585 ≠ 1

furthermore, |x| = |-69| = 69 and is not less than b = 3

|y| = | 80| = 80 and is not less than a = 5

Glrx (talk) 18:38, 15 April 2013 (UTC)

Does the writer of this article still agree with this comment ?C.W. Vugs (talk) 19:58, 15 April 2013 (UTC)

Subsequent

In the section "Examples are to easy" we discussed two Diophantine equations.

(i) Solve 14803x - 12769y = 113 in Z⁺. Using Euclid's algorithm I calculated the solution (x, y) = (44, 51).

D. Lazard wrote : Your assertion is wrong, that x and y are positive in the solution of ax - by = GCD (a, b) which is provided by Euclidean algorithm (take a = 5 and b = 3).

D. Lazard forgot to check if my solution was correct, in other words, if 14803•(44) - 12769•(51) = 113, yes or no.

(ii) Solve 14803x + 12769y = 113 in Z. Rewriting this to 14803x - 12769(-y) = 113 in Z and using Euclid's algorithm and a bit of analytical geometry I calculated the solution (x, y) = (44, -51) + t•(113, -131), t ε Z .

D. Lazard wrote : On the other hand, Bezout's identity asserts the uniques of x and y such that ax + by = GCD (a, b) and |y| < a and |x| < b; this imply that they have opposite signs, but their exact sign depends on the parity of the number of iterations in Euclidean algorithm.

D. Lazard forgot again to check if perhaps two of my solutions were correct. Is for t = 0 14803•(44) + 12769•(-51) = 113 an identity, yes or no. And is for t = 1 14803•(157) + 12769•(-182) = 113 an identity, yes or no. C.W. Vugs (talk) 17:56, 14 May 2013 (UTC)

Question : Is the number of my iterations in Euclid's algorithm odd or even? C.W. Vugs (talk) 18:02, 14 May 2013 (UTC)

Please add practical applications 1

I like to repeat the theorem of Euclid's algorithm, because this is the base of Euclidean number theory.

Theorem of Euclid's algorithm : Each pair a, b ε Z⁺ has an unique GCD (a, b) with the following properties. {A} GCD (a, b) ε Z⁺ can be calculated by Euclid's algorithm. {B} GCD (a, b) is a common divisor of a and b. {C} Each common divisor of a and b is a divisor of GCD (a, b) [and thus GCD (a, b) is the greatest common divisor of a and b]. {D} The equation ax - by = GCD (a, b) has an unique solution in Z⁺ x Z⁺.

Here is a practical application connected with the nice picture on top of the article.

A Greek, called P, was selling cords. He had two cords, a short one of a length 20 units and a long one of 284 units. Three customers Q, R and S entered his shop. Q was first and wanted to buy a lot of the 20 units cords. The shopkeeper took the 20 units cord and "measured" fourteen 20 units cords from the 284 cord and gave those to Q [284 = 14•20 + 4]. Q paid and grumbling left the shop because he wanted also the 20 units cord that the shopkeeper had used for measering, but P refused to sell that one. At that moment the shopkeeper was left with a very short 4 units cord and the longer 20 units cord. Fortunedly R was interested in a lot of 4 units cords. So the shopkeeper took the 4 units cord and "measured" five 4 units cords from the 20 units cord and gave these to R, but kept the 4 units cord, that he used as "measuring" instrument [20 = 5•4]. The shopkeeper didn't want to sell that one because then S should stay empty handed. R paid and left the shop slamming the door. The shopkeeper was left with one poor 4 units cord. To make things worse S told the shopkeeper that he didn't need a 4 units chord, but that he wanted a lot of 2 units cords. The shopkeeper P answered : "My friend, I knew that you have at home a lot of 20 units cords as well as 4 units cords. Fold simply this last 4 units cord and start "measering" 2 units cords from any of those. This left over of 4 units cord you get for nothing". S didn't pay anything and whristling left the shop.C.W. Vugs (talk) 21:09, 17 April 2013 (UTC)

The article contains an excellent application of Euclid's algorithm, namely the animation. Note that this animation has the stopping condition GCD(r_N-1, r_N-1) = r_N-1 and not GCD(r_N-1, 0) = r_N-1. Euclid didn't work with zero.C.W. Vugs (talk) 10:52, 26 April 2013 (UTC)

Interesting remark. The fact is that for division-based version of Euclidean algorithm (which was not Euclid's version) negative and zero input are allowed, and b=0 is the only possible stopping criterion. On the other hand, subtraction based version requires positive input (otherwise it may lead to endless loops) and passes through a step where a=b before to reach zero. I have edited the pseudo-code of the subtraction-based version of the algorithm and the caption of the animation for taking into account these remarks. By the way, I am not convinced that application is the right qualification for the animation, not for your pseudo-real-life example. Euclidean algorithm has many true applications in higher mathematics (like for computing the inverse modulo p, or defining the order of an element in a group). About elementary applications, the only ones I am thinking of are the simplification of fractions and the reduction of several fractions to the same (smallest) denominator. D.Lazard (talk) 12:34, 26 April 2013 (UTC)

How do you solve 2x = 3(mod 11)? Sorry I can't write the three lines.C.W. Vugs (talk) 14:50, 26 April 2013 (UTC)

One applies Extended Euclidean algorithm to 11 and 2:

r0:=11, r1:=2, s0:=1, s1:=0, t0:=0, t1:=1;

q1:=quotient of the division of r0 by r1, that is q1=5

r2:=r0-q1.r1=1, s2:=s0-q1.s1=1, t2:=t0-q1.t1=-5;

q2:=quotient of the division of r1 by r2, that is q2=2:

r3:=r1-q2.r2=0, s3:=s1-q2.s2=-2, t3:=t1-q2.t2=11;

For every i, one has ri=11.si+2.ti. As 11 and 2 are coprime, the last nonzero remainder is 1 (here r2=1). Thus

1=r2=11.s2+2.t2=11.1+2.(-5),

and thus 2.(-5)=1 mod 11. Multiplying by 3, we get 2.(-15)=3 mod 11. As -15 = 7 mod 11 (Euclidean division), we get the desired result

2.7=3 mod 11.

Note that the si's are used only for the proof of correctness of this algorithm. They do not need to be computed.

D.Lazard (talk) 16:05, 26 April 2013 (UTC)

I don't want to act like a schoolmaster but, without computation, it will be hard labour to solve 37x = 39 (mod 125). Concerning my pseudo-real-life example : Euclid didn't work with numbers but, indeed, with line segments.C.W. Vugs (talk) 17:28, 26 April 2013 (UTC)

To solve 37x = 39 (mod 125) is a true application in higher mathematics. Working this out (it is not that high) you will convince readers of the importance of Euclid's algorithm.C.W. Vugs (talk) 05:56, 28 April 2013 (UTC)

Solve 2x =₁₁ 3. Or solve -3 = 11k - 2x, k and x ε Ζ⁺. Calculate GCD (11, 2) : 11 - 2•5 = 1 ; 5 - 5•1 = nothing. Thus 11•(1) - 2•(5) = 1 and 11•(-3) - 2•(-15) = -3. Therefore x =₁₁ -15 =₁₁ 7.

Solve 37x =₁₂₅ 39. Or solve -39 = 125k - 37x, k and x ε Z⁺. Caculate GCD (125, 37) : 125 - 37•3 = 14 ; 37 - 14•2 = 9 ; 14 - 9•1 = 5 ; 9 - 5•1 = 4 ; 5 - 4•1 = 1 ; 4 - 1•4 = nothing. We can write 1 = 5 - 4•1 = 5 - [9 - 5•1]•1 = 5•2 - 9•1 = [14 - 9•1]•2 - 9•1 = 14•2 - 9•3 = 14•2 - [37 - 14•2]•3 = 14•8 - 37•3 = [125 - 37•3]•8 - 37•3 = 125•(8) - 37•(27) = 1. Thus 125•(8•-39) - 37•(27•-39) = -39. Solution x =₁₂₅ -1053 =₁₂₅ 72.C.W. Vugs (talk) 08:02, 3 May 2013 (UTC)

Important property of GCD : the linear Diophantine equation ax - by = GCD (a, b) a, b positive integers has a solution for positive integers x and y.

By giving in your article the congruence equation 37x = ₁₂₅ 39 and the well proved Euclid's lemma you have two applications that can convince readers of the importance of this property. C.W. Vugs (talk) 09:28, 6 May 2013 (UTC)

Another practical application : a shopkeeper bought in the beginning of this year x pieces of apparatus for $ 46 each and started selling them for $ 57 a piece. At the moment he has a left over of y exemplares but already a profit of $ 10. Find x and y. C.W. Vugs (talk) 10:04, 7 May 2013 (UTC)

Solution : 57(x - y) - 46x = 10 or 11x - 57y = 10. Calculate GCD (11, 57): 57 - 11•5 = 2 and 11 - 2•5 = 1.

GCD (11, 57) = 1 and 1 = 11 - 2•5 = 11 - [57 - 11•5]•5 = 11•(26) - 57•(5) = 1. Multiply this identity by 10 to get 11•(260) - 57•(50) = 10 Solution : x = 260 and y = 50. C.W. Vugs (talk) 05:58, 9 May 2013 (UTC)

Please add practical applications 2

Off topic

Up to now we discussed applications of the Diophantin equation ax - by = c and how Euclid's algorithm helps us to find an eventual solution. The properties (i) GCD (a, b) is a common divisor of a and b and (ii) each common divisor of a and b is a divisor of GCD (a, b) and the fact that in Z⁺ each divisor d is smaller or equal then the number of which it is a divisor are also very important. Fermat's proof (ca. 1650) of the insolvability of X⁴ + Y⁴ = Z⁴ in Z⁺ is full of GCD statements and proofs by contradiction. Here are two examples. Fermat worked in Z⁺.

Example 1 (easy) : GCD (b, c) ≥ GCD (a, b, c)

Example 2 (difficult) : a > b and GCD (a, b) = 1 <----> GCD (a² - b², a² + b²) is 1 or 2. C.W. Vugs (talk) 04:19, 10 May 2013 (UTC)

IS IT ALLOWED TO DELETE A CONTRIBUTION OF AN USER ? — Preceding unsigned comment added by C.W. Vugs (talk • contribs) 11:38, 10 May 2013 (UTC)

Previously, it was common to delete off topic material, but now putting them in a box is preferred. The material does appear to be off topic; It is about GCD in general rather than the algorithm. Glrx (talk) 04:07, 11 May 2013 (UTC)

First sentence of the article : This article is about the greatest common divisor. I give two examples of frequently used GCD statements and you delete the whole lot, because it is off topic . C.W. Vugs (talk) 21:33, 11 May 2013 (UTC)

1/ This is not the first sentence of the article, but a hatnote aimed to disambiguate . Unfortunately, it was ambiguous; I have edited the article to make it clear. 2/ You do not give examples but exercises; Wikipedia is not the place for them (see WP:NOTTEXTBOOK). 3/ In any cases, there are not related to this article (they do not involve Euclidean algorithm at all), but to Greatest common divisor. 4/ Your post has been restored. Too see it, click on the "show" button. D.Lazard (talk) 22:44, 11 May 2013 (UTC)

I believe the article already has quite enough applications. Any more should justify themselves as being notable uses rather than just that someone on Wikipedia noticed it was being used in passing. That's getting into trivia. There's far too much there to justify sticking in something like that as an illustrative example. It is just unnecessary and besides doesn't illustrate anything well. Dmcq (talk) 23:04, 11 May 2013 (UTC)

I READ AT THE BOTTOM OF THIS PAGE : THIS PAGE WAS LAST MODIFIED ON 14 MAY 2013 AT 20:04. IS IT POSSIBLE TO SHOW THESE CHANGES ON THIS TALK PAGE, BECAUSE I CAN'T FIND IT? C.W. Vugs (talk) 21:24, 14 May 2013 (UTC)

Please don't WP:SHOUT. Your contribution was moved to the end of the talk section you said it was relevant to, see #Subsequent added to Examples are too easy. Dmcq (talk) 00:14, 15 May 2013 (UTC)

Click the "View history" tab at the top of the page. It shows all of the edits and when they were made. Glrx (talk) 01:17, 15 May 2013 (UTC)

Thank you Dmcq, I will never shout again, but the two statements behind [show] are not trivial at all and the writer of Pythagorean triple needs them urgently. Look at the remarks of Arthur Rubin in that talk page.

Glrx, you will remember that we were talking about two equations (i) Solve 14803x - 12769y = 113 in Z⁺. Using Euclid's algorithm, I calculated the unique soltion (x, y) = (44, 51) and (ii) Solve 14803x + 12769y = 113 in Z. Again using Euclid's algorithm and a bit of analytical geometry, I found the general solution (x, y) = (44, -51) + t•(113, -131), t ε Ζ. Then D. Lazard told the world that in ax - by = GCD(a, b) x and y couldn't be positive, take a = 5 and b = 3. I wrote equation (iii) 5x - 3y = 1 in Z and gave the solution (x, y) = (2, 3).

To prove that my story was wrong you, Glrx, took a solution of equation (ii), namely x = -69 and y = 80, substituted x and y of equation (iii) by these x and y to get 5(-69) - 3(80) ≠ 1.

My question : "Does the writer of this article still agree with this comment?", was never answered. C.W. Vugs (talk) 09:40, 19 May 2013 (UTC)

The point about the examples is not that they are trivial. It is that they are not really relevant to the topic of the Euclidean algorithm. They are just some random uses of it, it is like saying the Empire State building used a lot of steel in its construction in the article about steel.

I'll leave the rest to whoever it is you're arguing with as I didn't see anything in it that looked to me like an improvement to the article. Dmcq (talk) 12:30, 19 May 2013 (UTC)

Back to the steel article, in this case Euclid's algorithm. In fact the writer has an example in his article. But it is too easy to convince the reader of the importance of the algorithm. Moreover it is very poorly worked out and gives little information about properties of the GCD.

Writer's example : (i) 1071 = 2•462 + 147; (ii) 462 = 3•147 + 21; (iii) 147 = 7•21 + 0. Since the last remainder is zero, the algorithm ends with 21 as the greatest common divisor of 1071 and 462. This agrees with the GCD (1071, 462) found by prime factorization above.

My example : (i) 1071 – 462•2 = 147; (ii) 462 - 147•3 = 21; (iii) 147 - 21•7 = 0. I claim 21 is the GCD (1071, 462). (a) From (iii) to (i) : 21 is a common divisor of 21 and 147, thus 21 a common divisor of 147 and 462 and also a common divisor of 462 and 1071. (b) From (i) to (iii) : Take any common divisor d of 1071 and 462, then d a common divisor of 462 and 147 and also a common divisor of 147 and 21. It means, any common divisor of 1071 and 462 is a divisor of GCD (1071, 462). (c) Properties (a) and (b) axplain the name greatest common divisor. (d) Moreover from (ii) to (i) : 21 = 462 - 147•3 = 462 - [1071 - 462•2]•3 = 462•(7) – 1071•(3) = 21. This means (x, y) = (7, 3) is a solution of 462x - 1071y = GCD (462, 1071). C.W. Vugs (talk) 15:19, 24 May 2013 (UTC)

My steel comment was in reference to the example hatted in the green box above as off topic. You seem to be sticking in yet another explanation of why the algorithm works when there are already as far as I can see three explanations above the example. Also examples are supposed to be illustrations and not introduce new ideas, which I guess is the case here as it is simply repeating the same old stuff yet again, but really all the text is simply obscuring the algorithm in use as far as I can see and turning it from being an example into yet another explanation. Dmcq (talk) 15:31, 24 May 2013 (UTC)

Today I banked my usual contributions to Wikipedia, but it will be the last time unless, you, people involved, find GCD (24389, 27889) and give a second solution of the equation 24389x + 27889y = 2 in integers. I give a first solution (x, y) = (-11809, 10327). C.W. Vugs (talk) 17:53, 29 May 2013 (UTC)

In the meantime we are a week further. Are your computers running out of paper? If that is the case, write a note on this talk page and I will consider a second donation this month, to buy more paper. C.W. Vugs (talk) 18:03, 6 June 2013 (UTC)

Is there any reason for inclusion of your of the additional text in GCD(1071, 462) or the inclusion of your new example GCD (24389, 27889)? (The section is also misnamed.... It's not specifically a "practical" application. — Arthur Rubin (talk) 03:58, 8 June 2013 (UTC)

The reason is that I doubt if D.Lazard, Glrx, Dmcq or Arthur Rubin can solve this problem and therefor are unable to answer critical remarks about this important article and so that I am intended to stop my contributions. C.W. Vugs (talk) 07:42, 8 June 2013 (UTC)

A second solution is (16080, −14062), which took no time flat in my head and you could probably do that too if you really understood what you were asking for. This is the wrong article, that's not a good example and the talk page is not for puzzles. Dmcq (talk) 09:04, 8 June 2013 (UTC)

Correct : You took -11809 + 27889 = 16080 and 10327 - 24389 = - 14062. You were lucky that I gave a solution. You know for sure analytical geometry. To proof that you can work with Euclid's algorithm : find one solution in Z of 4394x + 4107y = 2 C.W. Vugs (talk) 12:42, 8 June 2013 (UTC)

Please attend to the rest of what I said. There's three other articles which deal with that: Bézout's identity, Chinese remainder theorem and Extended Euclidean algorithm. This article is not about that. Nobody here need prove anything about their competence doing some arithmetic. And I really do not think that a more complicated example is needed. Dmcq (talk) 14:02, 8 June 2013 (UTC)

I like to repeat my question : Find a solution in Z of 4394x + 4107y = 2. C.W. Vugs (talk) 11:49, 18 June 2013 (UTC)

Please read WP:TALK. This talk page is for discussing improvements to the article, not to answer odd computational requests.—Emil J. 12:15, 18 June 2013 (UTC)

Due to difficulties with logging in I had to change my user name into Xoagus. The last part of the first edit of this article reads :

For example, 21 is the GCD of 252 and 105 (252 = 2x21, 105 = 5x21); since 252 - 105 = (12 - 5)x21 = 147, the GCD of 147 and 105 is also 21. By reversing the steps in the Euclidean algorithm, the GCD can be expressed as a sum of the two original numbers each multiplied by a positive or negative integer e.g. 21 = [5x105] + [(-2)x252].

I don't see any steps nor reversing of steps. Here follows how we learned this during 1962 in a first year algebra college in Utrecht.

We find GCD (252, 105): first division 252 - 105•2 = 42, second division 105 - 42•2 = 21, third division 42 - 21•2 = 0. GCD (252, 105) = 21. Second division 21 = 105 - 42•2. Fill in first division 21 = 105 - [252 - 105•2]•2 = 105•[5] - 252•[2]. Xoagus (talk) 13:11, 20 June 2013 (UTC)

Featured article review

Articles that have been tagged for cleanup for over four years do not meet the featured article criteria. Tagged material should be removed or cited. If the material can neither be removed nor cited, then the article should be taken to Wikipedia:Featured article review for demotion. DrKiernan (talk) 14:32, 23 November 2014 (UTC)

I have added the one citation that was requested. Are there any other parts of the article that have been "tagged for cleanup"? I do not see anywhere else. Sławomir Biały (talk) 13:33, 6 December 2014 (UTC)

Lead material

Does the following stub paragraph need to be in the lead, or can it be moved to interior sections?

"By the extension called extended Euclidean algorithm, the GCD can be expressed as a sum of the two original numbers each multiplied by a positive or negative integer, e.g., the GCD of 252 and 105 is 21, and 21 = [5 × 105] + [(−2) × 252]. This important property is known as Bézout's identity."

Just asking, Grandma (talk) 20:33, 7 December 2014 (UTC)

At least remove WP:PEACOCK "important". IMO, extended Euclidean algorithm must appear in the lead, as many usages of Euclidean algorithm that appear in the articles are, in fact, applications of extended Euclidean algorithm (Bezout's identity, modular inverse, ...). However this sentence is not necessarily the best one for presenting extended Euclidean algorithm. By the way the present form of this sentence results of my recent edit. Previously, the sentence was linked to extended Euclidean algorithm, but calling it wrongly "reversing Euclidean algorithm" (through a pipe). D.Lazard (talk) 21:20, 7 December 2014 (UTC)

D.Lazard, can you please, then, take care of this issue yourself? Thanks, Grandma (talk) 21:36, 7 December 2014 (UTC)

@D.Lazard, can you please have a look at the following content that forms the last half of the lead. It reads like a laundry list of subjects and I wonder how important it is to have such an unenlightening list when, we also, immediately after the lead have a "contents" section where this material is repeated again. I'd like to keep the lead rather general, so maybe we can shorten all of this to something like two sentences or so?

It is a key element of most cryptographic protocols, such as RSA algorithm, which are widely used for secure communication between computers. It is used to solve Diophantine equations, such as finding numbers that satisfy multiple congruences (Chinese remainder theorem) or multiplicative inverses in modular arithmetic. It can also be used to construct continued fractions, in the Sturm chain method for finding real roots of a polynomial, and in several modern integer factorization algorithms. Finally, it is a basic tool for proving theorems in modern number theory, such as Lagrange's four-square theorem and the fundamental theorem of arithmetic (unique factorization).

If implemented using remainders of Euclidean division rather than subtractions, Euclid's algorithm is efficient: it never requires more division steps than five times the number of digits (in base 10) of the smaller integer. This was proved by Gabriel Lamé in 1844, and marks the beginning of computational complexity theory. Methods for improving the algorithm's efficiency were developed in the 20th century.

By the extension called extended Euclidean algorithm, the GCD can be expressed as a sum of the two original numbers each multiplied by a positive or negative integer, e.g., the GCD of 252 and 105 is 21, and 21 = [5 × 105] + [(−2) × 252]. This important property is known as Bézout's identity.

Let me know, Grandma (talk) 22:22, 7 December 2014 (UTC)

I generally agree with your edits. Presently the lead is not yet at the level of a FA, but it is more acceptable than some parts of the body. For the moment, the main issues that I see in the lead are:

Too much place for the original version of the algorithm
The musical application has not its place in the lead
An important application deserve to be mentioned in the article, and probably in the lead: being one of the simplest algorithms involving a loop with a number of iterations which is not known in advance, it appears as example is almost every basic course of computer programming.
The distinction between the immediate consequences of Euclidean algorithm in elementary arithmetic (such as the existence of GCD, Euclid's lemma and unique factorization property) and its applications in math (such as modular inverse, cryptography, ...) deserve clarification.

However, it seems better to tune the lead only after upgrading the body. D.Lazard (talk) 13:17, 9 December 2014 (UTC)

[Adams_2004-1] Adams C (2004). The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. American Mathematical Society. ISBN 0821836781.

[1]