Talk:Convolution/Archive 4

Archive 1

Archive 2

Archive 3

Archive 4

Lead graphic implies convolution is not commutative, while properties sections says it is

The problem I have here is that the graphic to the right of the Lead paragraph shows f*g as different to g*f. Of course a less-casual reader should notice that the two situations have different headers (convolution and cross-correlation) and that the * of convolution is emphatically star-shaped while the * of cross-correlation is rather apologetically star-shaped. This may be a browser/font thing, but I think it would be very helpful were the cross-correlation one quite clearly a dot (since this is a sliding dot-product, is that the right symbol?). This may sound trivial, because most mathematical readers will already know what to expect, and know the difference anyway. But convolution is a really good example of a mathematical concept that's now very interesting to a broad range of non-mathematical or semi-mathematical readers. It's a place where an encyclopedia article has good reason to avoid assuming knowledge, and to make itself clear to those who are not very familiar with the terminology (for example, it would be no bad thing to state explicitly, even in the lead, that the asterisk is a special symbol - those who come here via computer programming may read an asterisk as multiplication without even being conscious of what they've done). In fact, I think it would be a better article if the applications section preceded the mathematical definition below (most general readers will be interested firstly in what it looks like, and what it does (why it's important), and only secondly in how the nuts and bolts of it work. By the way, I see the point that the sliding graphic animation does tend to look as though the overlap between the functions is what's evaluated rather than the integral of the product, but without the animation I can't see how any casual, non-specialist reader is going to understand the article at all - so it's useful. — Preceding unsigned comment added by 149.155.219.44 (talk) 12:10, 29 July 2020 (UTC)

I am a little short on time to help at the moment, but it sounds to me like you are basing your comments on the thumbnail picture instead of https://upload.wikimedia.org/wikipedia/commons/2/21/Comparison_convolution_correlation.svg. The remedy to prevent others from the same mistake might be to shrink the thumbnail down even smaller, forcing them to follow the link. But my personal opinion is that people who draw false conclusions from a thumbnail pic deserve what they get. I do agree about the potential confusion between using ∗ for both convolution and multiplication. But it's a fact of life that there are more mathematical operations than symbols to uniquely represent them all. And switching to a "dot" (which also means multiplication) is not a solution. Context and commentary (such as the figure caption) is what usually resolves such ambiguities. You might be right about moving the applications section above the mathematical definition. I am ambivalent on that point at the moment. But I think the tie-breaker will be consistency with many other WikiPedia articles. It is customary to lead with definitions before applications.

--Bob K (talk) 15:10, 29 July 2020 (UTC)

Bob, thanks for your very constructive comment. Yes, I realize now that the full asterisk and the five-pointed star are quite distinct, and are an important part of the nomenclature of cross-correlations and convolutions. Since their relationship is a big part of the Lead, and it's essential to the thumbnail, I've added (f*g) and (f /star g) to the Lead to try to help other novice readers such as myself. I'm very nervous of this edit as it's outside my field. Please feel free to revert if it's either incorrect, or just annoying. Also I may not have got the formatting right (as I nicked it off the cross-correlation page). 149.155.219.44 (talk) 13:36, 30 July 2020 (UTC)

Convolution vs modulation

Is modulation (such as AM or FM) a form of convolution? —Preceding unsigned comment added by 219.78.87.74 (talk) 11:02, 29 January 2011 (UTC)

Fig 1: An audio signal (top) may be carried by an AM or FM radio wave.

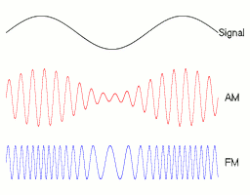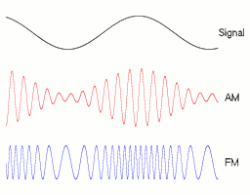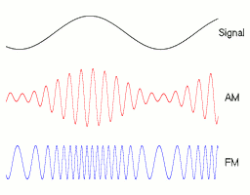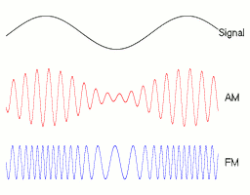
Good question; the answer is "no". Convolution can be thought of as replacing each sample in the time domain with a copy of a fixed kernel, scaled by that sample. In contrast, FM replaces each sample in the time domain with a signal that has an instantaneous frequency corresponding to that sample value. AM is more similar to convolution: In AM, you take a high-frequency sine wave and then scale each sample in that signal by the value of the signal you are encoding. This is a direct product. Imagine trying to cast AM as a convolution. Your kernel would presumably be a little wavelet of fixed frequency, but, e.g., a fixed nonzero signal as input would produce zero as output as each copy of the kernel canceled out the ones around it.

Put another way, each could be modeled like a convolution; with AM you'd change the phase of the kernel at every sample, and with FM you'd change the phase and frequency at each sample, but not the amplitude.

My intuition is that FM is nonlinear and that AM is a linear function of the carrier signal and the input signal, but nonlinear in the input signal alone, and so neither could possibly be described by a convolution, which is linear. —Ben FrantzDale (talk) 15:55, 31 January 2011 (UTC)

One of the more useful ways to use convolution is the connection to the Fourier transform. Convolution in one domain Fourier transforms to multiplication in the other domain. Since AM can be considered multiplication, it comes out convolution in the Fourier domain, or frequency domain in the case of time dependent signals. Gah4 (talk) 06:49, 11 July 2021 (UTC)