Talk:Calculus/Archive 1

Archive 1

Archive 2

Archive 3

→

Archive 5

DO NOT EDIT OR POST REPLIES TO THIS PAGE. THIS PAGE IS AN ARCHIVE.

This archive page covers approximately the dates from 21 July 2005 until 17 December 2006.

Post replies to the main talk page, copying or summarizing the section you are replying to if necessary.

This archive is no longer active. Please add new archivals to the latest archive on the talk page.

older comments

Regarding the note in "History": I think it would be wise to note that mathematics is a purely invented concept, and that the only way to "discover" some mathematical principle is to discover it as a facet of an invention (mathematics) rather than as a facet of nature. When it comes to calculus, this is especially true, because nowhere is nature does the concept of a perfectly curved surface exist; all things in nature are quantized down at an arbitrary level, even perfect spheres (and potentially even space itself). The notion of infinitely small changes in position to discover tangent lines, areas under curves, and lengths of curves has never been a part of reality, and only exists in the theoretical sense, so it cannot be a discovery in the traditional sense. In fact, I would suggest we change that entire sentence to something along the lines of, "Leibniz and Newton are usually designated the originators of calculus, mainly for their invention of the fundamental theorem of calculus." I understand the issue some will have with this, as they may view mathematics as a discovery not an invention, but as I said above, the things that calculus works on don't exist in nature, and cannot therefore be discovery. - Augur

While your assertion has some merit, it is very clear that calculus can be used to simply and accurately describe a great number of natural phenomena, and that its discovery was played a fundamental part in understanding such phenomena. Planetary motion, falling objects, water flowing from a tank, basically any kind of continuous dynamical system, and so on. Although some accepted notions of physics may state that, in some sense, space and matter are perfectly quantized, this is hardly a hands-on discovery either. And although I am no expert, I do know that there are several theoretical tools used in quantum mechanics that depend on calculus (Schrödinger's equation, for one). And just because physical objects are not shaped like smooth curves doesn't mean they, in addition to many other aspects of the natural world, aren't described accurately by calculus in many ways.

To address your concern more generally, mathematics is not "invented" in such a simple sense. Newton didn't sit down next to Leibniz and say "Hey, let's make up something new." Nature, as a concept, may be understood in many different ways, but when something like calculus is discovered through the study of physical motion of real-life objects, I would consider it a natural discovery. Similarly, when something is discovered in the context of mathematics that are based on natural, intuitive axioms, I would consider it a natural discovery. The structure of mathematics is built upon quite natural principles, no matter how "invented" those principles may be.

To object to mathematics' status as a natural discovery calls into question considering anything as a natural discovery. Reality as a whole is unknown to us, except in how we observe it through very limited means, and whenever we make statements about anything, we are "inventing" these things in some sense. To say "[t]he notion of infinitely small changes in position to discover tangent lines, areas under curves, and lengths of curves has never been a part of reality" makes a fair deal of assumptions about how we chose to define what is "a part of reality." The set of positive integers does not exist in reality, but we use it constantly, in some instances subconsciously. But an integer does not "exist" (by your terms) in any way. In fact, there are too many integers to exist, according to such an argument about a finite, quantized universe. But there's nothing unnatural about the integers, as far as I know.

I hope this helps you better understand why one can "discover" calculus, and why it is a natural discovery to have made. 149.43.x.x 03:15, 21 July 2005 (UTC)

---

I don't know how calculus is normally defined, but I prefer the definition "branch of mathematics involving the study of limits".

From what I have seen, infinite series are normally associated with calculus. This makes sense because of the summation notations ideas used while developing the concept of the definite integral, and because of the integral test.

This definition seems to include nicely differentiation, integration and infinite series.

Brianjd 07:13, Sep 12, 2004 (UTC)

'Limits' - their study is more accurately mathematical analysis. It's a bit different. Charles Matthews 08:32, 12 Sep 2004 (UTC)

---

I think a link to a truly functioning place to study calculus online makes a right thing to put on the calculus page. student person any ideas

---

Looking at the other languages, they look like they're a completely different encyclopedia... -User:Loisel

---

Old comments from calculus that I (Gareth Owen) have tried to take on board:

---

First, I think a page on Calculus should reflect current word usage in Mathematics. Therefore, functions are rules that assign to each member of a specified domain a value in a specified range. We do not speak of independent and dependent variables in Math, hardly ever, any more. I am not sure this terminolgy, while easy to remember, is the what we want a learner to retain.

Hmmm...I use the terms "independent variable", "dependent variable" quite a lot in my calculus classes, especially when students get truly mixed up in a problem over which variables represents domain elements and which codomain elements. In advanced math (analysis, topology, etc.) these terms are probably not as common, but in calculus and physical science classes they are still used quite a lot, and I don't see how they're harmful.

Second, Calculus, from the first day I opened my first book has always been both Differentiation and Integration and hopefully the relationship between them. Therefore, I see this entry as misleading.

For the above two reasons, I think it requires a major overhaul in terminology and content. This is a key entry in Math and only Math. In other areas in is ancillary. RoseParks

Well, RP, what's stopping you from rewriting it? How long can it take to rewrite two short articles about a subject you teach regularly (I'm guessing)? :-) --LMS---- Well it is 5:39 A.M. Wednesday, March 28,2001, I think and I am still dealing with copy edit problems. Any suggestion about when I might do this, not to mention sleep, food, a shower...Not all of us have time to come and write on wikipedia every day for a number of hours...HELP...RoseParks

---

What can I say? Thanks! Anyway, no rush on Wikipedia. If you don't make changes, eventually, someone else will, I'm sure. --LMS

---

Recently I added some other (very common?!) usage of "calculus" in mathematics, namely as a formal system of rules and axioms (which also is one general meaning of the word). This usage appears quite often in proof theory and symbolic logic. I also move the general calculi above into this section, since they are really different from the special calculus. --Markus[sorry, currently no login] 24 Jun 2003

---

I changed the "calculus series" table a bit. I think "topics in calculus" is more appropriate. The articles that have the old table need to be updated, of course. Thoughts? Fredrik 22:56, 27 Mar 2004 (UTC)

---

I would enjoy a page comparing various Calc textbooks. Personally I know Stewart's Calculus. Goodralph 02:18, 4 Apr 2004 (UTC)

---

Nearly 200 edits to this page so far and ... it's pretty bad. Charles Matthews 07:39, 5 Jun 2004 (UTC)

Heh. I think we need a page explicitly describing the differential calculus though - so far it is just a redirect to this page. Dysprosia 07:58, 5 Jun 2004 (UTC)

Charles, it is definitely better now. Don't you think the differentiation notation section is way too long now though? Some of it may have to be moved off to a sub article especially when all of the integral notation is included. - Taxman 19:20, Jun 23, 2004 (UTC)

Anything is possible - it was all in three places (four counting the full Leibniz notation page) and can be shuffled around later. All work-in-progress, really. Obviously the elements of differentiation and integration should be covered. They are in various places, and piecemeal, too. Charles Matthews 19:36, 23 Jun 2004 (UTC)

Kowa Seki

I only had time to read part of that article, but it doesn't seem to support that Seki had developed nearly as much of calculus as the two primary figures. Seki's method is referred to as a crude form of integral calculus and the article doesn't say that he even made any significant contributions to differential calculus. Newton and Leibniz had much more developed methods and notation. Just because he is referred to as Japan's Newton or Leibniz, does not mean he had the same level of contributions to the subject. The article even mentions that role is tenuous at best. I would support moving his role and citation to the lesser credit section. - Taxman 14:53, Aug 3, 2004 (UTC)

I have no problem with this. I'm not sure if I would characterize his methodology as "crude" given that the concept of area approximation by the use of rectangles is still practiced in the teaching of basic calculus; particularly since it appears his efforts were somewhat hampered by the inadequacy of his language. Moreover, I gather Kowa Seki did not have the same access to publication as his Western peers. Nonetheless, even though he may have been closer to formalizing integration than, say, Descartes, extant records are pretty meager. Lesser credit is fine with me. Mashford 12:45, 4 Aug 2004 (UTC)

I made the move, you can fix the phrasing if you think it needs it. Crude is not a denigrating term, its just that it seems clear Seki's method was a purely geometric one, not making use of functions and so forth that I believe were used in the west at the time. - Taxman 13:51, Aug 4, 2004 (UTC)

"key"?

The following appeared:

It was this realization by both Newton and Leibniz that was the key to the explosion of analytic results after their work became known.

An anonymous Wikipedian changed "that was the key" to "which was key". The latter seems inferior since it treats key as literally an adjective. It seems to me I've seen that a lot in the last couple of years. Has it now reached the point where, in addition to being merely acceptable, that usage is thought of as standard? Michael Hardy 22:54, 6 Dec 2004 (UTC)

It seems very standard to me. I hear that useage often. - Taxman 00:00, Dec 7, 2004 (UTC)

The OED only cites "key" as an adjective in this sense dating back to the early 20th Century, but it does have many citations for that sense. I think it's a standard usage, and preferable to the noun here because A. it's shorter, and B. it doesn't imply that the realization was the only key to the explosion (which would be debatable and probably false). 216.59.230.140 14:35, 13 December 2006 (UTC)

delta epsilon

Should we have a brief explanation of the formal definition of limit in terms of delta and epsilon, and the delta/epsilon proofs that have annoyed generations of math students? --Christofurio 01:42, Feb 16, 2005 (UTC)

the article is obscure

I went to the article to initiate my understanding of calculus. It failed completely. The article looks as if it was written by mathemeticians in order to impress other mathemiticians. The article was not written to introduce, or to instruct, the (previously uninitiated) into the idea(s).

As such, the article is worthless. Those who already have enough of an introduction to understand what the article is saying do not need to read an encyclopedia article on calculus. Those of us who need to read an article on calculus do not have the requisite understanding of what is being said to make reading the article of value. KeyStroke 20:18, 2005 Mar 17 (UTC)

You know, I agree with you. I will see if I can do better when I come back from vacation. --Pmeisel 22:21, 17 Mar 2005 (UTC)

I do not think the changes made were an improvement. They contained some good ideas, but they took out some other good ideas and made some things more vague.

I couldn't disagree with the above more strongly. I think Calculus' intro is well written and more readable than many of the other math articles. In fact, if I were to fault it, I'd fault it for not going into more detail on some of the technical aspects lower down... but at least those things are covered in other articles. Checkout articles like Hyperreal numbers to complain... there are many that lack a layman readable intro completely. --Gmaxwell 06:21, 14 Apr 2005 (UTC)

I agree with the opinion that the article is poor at introducing the subject to the unitiated. It is not much better at reacquainting the formerly initiated. For this reason, the suggestion below that this article was once ranked among Wikipedia's good articles surprises me. It's not much of a comfort to say that this is better written than other maths articles. They seem to me to suffer the same problem. I acknowledge that, as a newcomer to Wikipedia, I am disparaging the efforts of others when I have contributed none myself, but I do wonder whether all the mathematical articles should not be systematically reworked in two halves, an intro for beginners and something definitive for experts. David Colver 19:32, 30 April 2006 (UTC)

Yes, the definition of calculus involving limits is a very good one. The four main principals of calculus, as far as I'm concerned, are limits, derivatives, integrals, and series (which can be argued also as limits).

As far as I am concerned, with series we are getting in to a more specialized topic in calculus. If for example we restrict attention to taylor series, then the functions we discuss are pretty special - just analytic functions. If we aim a fourier series, then they are periodic. I love all this stuff - but for me I would put differential equations ahead of series in an ordering that begins with the fundamental topics in calculus.

French link

Someone that speaks French: The french link from this article goes to fr:Analyse (mathématiques). The link from there to English goes to Mathematical analysis. The link from there to french also goes to Analyse (mathématiques). Then, I found fr:Calcul infinitésimal, which seems to be somewhat of a translation of this article. The MS Office dictionary says that calcul means calculus (but, interestingly, not the other way round). I just thought I'd point this out at let someone that knows this stuff sort it out. Neonumbers 11:38, 3 May 2005 (UTC)

There is a similar problem with german and I think the core of the problem is just common usage: at least in german, when you learn this at school, it is called "Analysis" and a you probably hear of "Infinitesimalrechnung" (which is the topic fitting best what is descibed as calculus here) only at university. I think in english-speaking countries this is just the other way round. So I don't really know which page should be linked from here: for use as a dictionary (for looking up the word "calculus"), de:Analysis would be preferrable but when looking for an explanation of the same topic in german de:Infinitesimalrechnung will perhaps fit better (although it is on the german page only a short text mainly linking to de:Analysis. At least I would really like to have a short description of the relation of "calculus" to "mathematical analysis" in the text.--84.177.245.153 10:43, 11 July 2006 (UTC)

Father of calculus

To Oleg's Whatever he discovered was done much earlier and in isolation - Not in isolation and not much earlier to 'Indian' development of calculus . Madhava and others from the Kerala school picked up after him and developed it further. Please see [1] --Pranathi

I am not sure if this was clear from what you wrote in the article. So I thought of removing it because I was not sure if it belonged there. Oleg Alexandrov 23:42, 7 May 2005 (UTC)

Besides, that particular paragraph was concerned with the developement of the calculus in the west. I believe what you wrote belongs in a paragrph or article about calculus in India. 23:42, 7 May 2005 (UTC)

I agree, I did not make that clear. I don't agree with the paragraph being about calculus in the west. Calculus is global - it is not a cultural/local subject. Newton or Leibniz was first to come up with the important concepts of the calculus - this implies that they were the first in the world not just the west - right? also don't agree with though this was not known in the West at the time, and he had no contact with Western scholars. with regard to the Japanese mathematician. It is a Eurocentric sentence. Maybe it should say - "in isolation"? --Pranathi 03:04, 8 May 2005 (UTC)

Maybe. It was not me who wrote about the Japanese mathematician. Yes, calculus is global. The thing is, calculus, the way we know it, was developed in the West. So, there is some bias towards the West in this article, and maybe it does not expore well enough other attempts and insights in other times and other places. Oleg Alexandrov 03:27, 8 May 2005 (UTC)

I will agree though that I think Bhaskara being the Father of Calculus is not universally acknowledged by those familiar with Indian math history with Madhava being the other contender. But he is 'sometimes' described as the Father of calculus. --Pranathi

I find the "father of calculus" amusing to start with. I will now remove the mention of the other guy too. Oleg Alexandrov 23:42, 7 May 2005 (UTC)

Good idea. --Pranathi 03:04, 8 May 2005 (UTC)

RFC: Fundamental Theorem

I'm not quite happy with the FTOC section. I would certainly like to see the FTOC reprhased physically. Something along the lines of "If we consider the net area under the velocity curve we obtain displacement".

In modern US textbooks, there is no mention of 1st and 2nd fundamental theorems. They are typically called FTOC (part 1) and FTOC (part 2). What's more unusual is the ordering given. What's called the 2nd FTOC is typically dealt with first -- the 1st FTOC presented as a consequence. I suppose this is pretty arbitrary.

Each part should be explained in plain english! For example, the 2nd FTOC says every continuous function has an antiderivate, namely that funny integral that confuses students to no end!

Comments?

I find this topic very interesting. As far as I can recall, there has always been *one* fundamental theorem of calculus (ftoc) - there is no *part 1* and no *part 2*. The version stated as the 2nd part in the article of Wikipedia is *the* theorem - it says *everything* that needs to be said. It is also accurate (just compare mathworld's and many other sites which state the theorem incorrectly) and shows immediately the connection between the integral and the derivative.

What is happening here is that how you are taught the FTC depends on when you went to college. Most modern textbooks give the FTC in two parts. The first part says that if you define a function as a definite integral with constant lower bound, x as upper bound, and integrand f(t), then the derivative of that function is f(x). The second part says that if F(x) is any antiderivative of f(x), then the definite integral from a to b of f(x) is equal to F(b) - F(a). When I went to college, that second part was the FTC. But now it is taught in two parts, because so many important functions can only be defined in terms of definite integrals. Rick Norwood 16:08, 10 September 2005 (UTC)

History section

A number of things have gone into the history section that are almost right, but really wrong. I'm going to try to fix them. References would include Anton's Calculus, Rudin's Real and Complex Analysis, and various histories of mathematics. Rick Norwood 20:40, 25 September 2005 (UTC)

suggested rewrite

I would like to see the Calculus article one of the best in Wikipedia, and I do not think it is that as it stands. My major objection is that it does not give the reader any idea of the importance of calculus, and that it presents calculus as primarily a computational tool. I want to attempt a rewrite, a little at a time, and I'll begin by posting my proposed rewrite here, to see if it is acceptable, before posting it on the main page.

Calculus

Calculus is one of the most important breakthroughs in modern mathematics. In the Seventeenth Century calculus answered many questions that had puzzled mathematicians, scientists, and philosophers for more than two thousand years. In particular, calculus gave a clear and precise definition of infinity, both in the case of the infinitely large and the infinitely small. It provided an answer to Zeno's paradoxes and gave the first clear definition of what Aristotle called "the quality of motion".

Calculus was not discovered all at once. In the ancient world, Eudoxus and Archimedes proposed mathematical ideas that can now be seen as similar to calculus. In Twelfth Century India, Bhaskara, and in Seventeenth Century Japan, [Kowa Seki]], proposed ideas that would now be considered part of calculus. In Seventeenth Century Europe, Wallis and Barrow proposed ideas that would now be considered integrals, derivatives, and the Fundamental Theorem of Calculus. But it was Newton and Leibniz who brought all these ideas together, and they are usually credited with the independent and nearly simultaneous creation of calculus. Even so, it was generations after Newton and Leibniz that Cauchy and other mathematicians finally put calculus on a rigorous basis, with the definition of the limit.

From a mathematical standpoint, calculus gives the definitions and properties of three linear operators, the limit, the derivative, and the integral. All of these depend on the definition of the limit. Roughly speaking, the limit allows us to control an otherwise uncontrollable output, the derivative is the slope of a graph, and the integral is the area under a curve. In scientific applications, the derivative is often used to find the velocity given the displacement, and the integral is often used to find the displacement given the velocity. The Fundamental Theorem of Calculus, discussed more fully below, says roughly that the derivative and the integral are inverse operators.

Today, calculus is used in every branch of science and engineering, in business, in medicine, and in virtually every human endeavor where the goal is an optimum solution to a problem that can be given mathematical form.

Rick Norwood 22:54, 26 September 2005 (UTC)

Rick, much more readable. I think though that the first parah is eurocentric. Significant advances in calculus had been made before 17th century in India (with coresponding insights into infinity etc). Also, the second parah doesn't mention Madhava [2],[3], who preceded the European mathematicians in many of their methods and results. Eudoxus, Archemedes, Bhaskara and Kowa Seki are all put on equal footing and dismissed as having done something similar to calculus - each is significant and needs to be expanded (maybe you were planning on that in detail elsewhere). I think history needs to be tied together in a better fashion - maybe mention possibility of Indian calculus influencing European ideas [4], [5]. I agree that much more has been written about the development of calculus in Europe but significant contributions of the Kerala school need to be mentioned in more detail.--Pranathi 12:59, 27 September 2005 (UTC)

Thank you for your comments. The introduction should help the person who looks up the article understand what calculus is, with just a little bit of history, and a link to the article "History of calculus", where the topic of discovery can be expanded considerably. Rick Norwood 14:09, 27 September 2005 (UTC)

Rick, My comments can be incorporated without expanding on the history. 1. The first parah is still eurocentric. 2. Madhava, who has made significant contributions, has not been mentioned at all. 3. The 2 sentences on Exodus till Kowa Seki say the same thing, without revealing anything about their contributions.

May I propose:

Calculus is one of the most important breakthroughs in modern mathematics. It answers many questions that had puzzled mathematicians, scientists, and philosophers for more than two thousand years. In particular, calculus gives a clear and precise definition of infinity, both in the case of the infinitely large and the infinitely small. It provided an ... called "the quality of motion".

Calculus was not discovered all at once. In the ancient world, Eudoxus and Archimedes proposed the method of exhaustion that breaks down irregular shapes into traditional shapes to compute area or volume. In twelfth Century India, Bhaskara conceived of differential calculus and 2 centuries later, Madhava and the Kerala school studied infinite series, convergence, differentiation and other concepts that fall under calculus. In the 17th century, Kowa Seki in Japan elaborated some of the fundamental principles of integral calculus. Around the same time, Wallis and Barrow in Europe proposed ideas that correspond to integrals, derivatives, and the Fundamental Theorem of Calculus. ... with the definition of the limit.

If you find the second parah too detailed maybe we can do something like..

:Calculus was not discovered all at once. In the ancient world, Eudoxus and Archimedes proposed the method of exhaustion that constitutes integral calculus. In twelfth Century India, Bhaskara conceived of differential calculus and 2 centuries later, Madhava and the Kerala school invented many concepts of integral and differential calculus. In the 17th century, Kowa Seki in Japan elaborated some principles of integral calculus. In the same period, Wallis and Barrow in Europe proposed ideas that correspond to integrals, derivatives, and the Fundamental Theorem of Calculus. Newton and Leibniz brought all these ideas together, and ..of the limit. --Pranathi 17:25, 28 September 2005 (UTC)

Sounds good to me. I've added it to the article. But I think any further expansions on the history should go into the History of Calculus article. Rick Norwood 17:55, 28 September 2005 (UTC)

Thanks, Rick. I am going to harp on one more thing. The first parah mentions that Calculus answered questions etc in the 17th century. This ignores the advances made by Madhava and Bhaskara. For instance, Bhaskara suggested the differential coefficient vanishes at an extreme value , indicating knowledge of the infinitely small .. Since Madhava studied infinite series, he may have well been able to resolve Zeno's paradoxes, had he been aware of them.. Perhaps we remove the seventeenth century to make it generic to calculus and not calculus as known since the 17th century? --Pranathi 21:36, 28 September 2005 (UTC)

Done. Rick Norwood 23:11, 28 September 2005 (UTC)

i think that this is a too generalized way of teaching calculus.there is not much informationon the operations.however,it is a good article. rudraksh m. kulshreshtha,pathways world school,gurgaon,india rudrakshmk@yahoo.com,rudrakshmk@msn.com

(Moving discussion from Rick's talk tage) Rick, In recent edits, mention of Madhava, Bhaskara and Kowa seki were removed and replaced with a generic phrase for Indian and Japanese mathematicians. For a summary they may not be important, but I see you chose to keep reference to Wallis, Barrow and James Gregory. Madhava made some of the most significant advancements in the field, some exactly the same and 300 yrs earlier than the European counterparts that remain listed. Also, all mention of period (14th century, 17th century etc) was removed, while initially your parah mentioned 17th century only. Why the bias? or am I missing something? I am open to discussion. ----Pranathi 19:37, 28 October 2005 (UTC)

It's still there, just a little further down. Here it is from the history section:

"An Indian mathematician, Bhaskara (1114-1185), developed a number of ideas that can now be seen to be forerunners of calculus, including the idea now known as "Rolle's theorem". He was the first to conceive of differential calculus. The 14th century Indian mathematician Madhava, along with other mathematicians of the Kerala school, studied infinite series, convergence, differentiation, and iterative methods for solution of non-linear equations. Jyestadeva of the Kerala school wrote the first calculus text, the Yuktibhasa, which explores methods and ideas of calculus repeated in Europe only by the seventeenth century."

I still think the intro should be shorter. I may attempt that later on. I believe in taking things slowly, and giving them a lot of thought. Rick Norwood 22:35, 28 October 2005 (UTC)

I don't disagree, the intro can be shorter. But I disagree on cutting down the intro by chopping off selective segments. I propose something on the lines of :

Calculus was not discovered all at once. In the ancient world, Eudoxus and Archimedes proposed mathematical ideas that can now be seen as similar to calculus. In 12th Century India, Bhaskara conceived of differential calculus and in the 14th century Madhava and the Kerala school studied many concepts of modern calculus. In the 17th century, Kowa Seki in Japan, and Wallis, Barrow and James Gregory in Europe proposed many ideas of Calculus. But it is Isaac Newton and Gottfried Leibniz who are credited with bringing all these ideas together, and they are usually credited with the independent and nearly simultaneous creation of calculus. Even so, it was generations after Newton and Leibniz that Cauchy and other mathematicians finally put calculus on a rigorous basis, with the definition of the limit.

It is nearly the same length as the existing one. --Pranathi 00:30, 29 October 2005 (UTC)

Sounds good to me. Why don't you put it in the article and see if it survives. The only change I would make is in one sentence. To avoid using the word "credited" twice, how about "But it is Isaac Newton and Gottfried Leibniz who brought these ideas together and they are usually credited with the independent and nearly simultaneous creaton of calculus." Rick Norwood 22:17, 29 October 2005 (UTC)

definition of displacement and velocity

This sentence,

In scientific applications, the derivative is often used to find the velocity given the displacement, and the integral is often used to find the displacement given the velocity.

I don't find very clear. More specifically I don't understand what the word displacement means in its context.

The displacement is the distance moved. If you move the football (forgive the US-centric example) from the twenty yard line to the fifty yard line, the displacement is thirty yards. Is there another word that would make the example clearer? Rick Norwood 13:00, 14 October 2005 (UTC)

On consideration, I think "change in position" will be clearer. Thanks for the input. Rick Norwood 13:01, 14 October 2005 (UTC)

I disagree. Displacement is an important technical term used in physics and should be preserved. Perhaps linking to Displacement (vector) would be an agreeable solution, since the sentence already links to Velocity? Ferret-aaron 18:06, 24 October 2005 (UTC)

Sadly, most of the calculus textbooks I'm familiar with (Thomas, Anton, etc.) define velocity as a scalar rather than a vector. I know this doesn't make sense, but it is in fact what our students are being taught. (My students know better, because I tell them so, but most students go "by the book".) Rick Norwood 18:46, 24 October 2005 (UTC)

Infinity

What is said in the introduction is nonsense. Charles Matthews 22:49, 29 October 2005 (UTC)

I don't suppose you would care to elaborate? Rick Norwood 00:41, 30 October 2005 (UTC)

In particular, calculus gave a clear and precise definition of infinity, both in the case of the infinitely large and the infinitely small.

Where does that come from? Calculus, you could say, was born around the Great Fire of London. There was nothing in the way of precision on 'infinity' until after the Battle of Waterloo. That's 150 years of history just elided. Tell me, Rick, are we selling something here? We are not, in fact. So why put such tendentious stuff in article introductions. I'm going to put back the old, informative intro from September, move this down to an overview section, and try to take out the mistakes. Charles Matthews 10:26, 30 October 2005 (UTC)

The introduction you have provided seems perfectly reasonable. But you should read something carefully before you call it "nonsense".

The old introduction said that calculus gives definitions of infinity. It does. You react as if the introduction had claimed that calculus included definitions of infinity from the beginning. No such claim was made.

You objected to the claim that calculus was one of the most important breakthroughs in modern mathematics. It was. You statement that calculus was "early modern" has nothing to do with the fact that it was an important beakthrough in modern mathematics. Rick Norwood 21:38, 30 October 2005 (UTC)

Calculus is essentially a collection of algorithmic, semi-algorithmic and heuristic techniques. It has been like that since Euler, and nothing changes. Physicists still do Euler's way. It doesn't 'define infinity'. You have that quite wrong. Modern mathematics, if the phrase means anything, was initiated by Gauss. Mathematical analysis - say with Gauss and the hypergeometric function, or Abel and convergence testing, also dates from that time. And, yes, Cauchy too. Eliding the difference between that and calculus is completely wrong and historically barbarous. Charles Matthews 21:54, 30 October 2005 (UTC)

Your understanding of calculus is narrow. Were it not for your rudeness, I would not reply so bluntly. The idea that physicists still do mathematics the way Euler did places you at least a generation away from modern physicists, and apparently ignorant of the impact of operator theory on both modern physics and on the way calculus is taught. You say that calculus does not include the definition of infinity. There are an awful lot of books that define infinity that have the name calculus on the cover. True, it is the sideways eight kind of infinity instead of the aleph null kind, but the sideways eight is sufficient to answer Zeno. While one can divide up history in as many ways as you can slice a pie, it is common to divide mathematics into the ancient and the modern, with the ancient dribbling off around the time of Heron and with modern European mathematics beginning with Fibonnacci. You may have an opinion as to where early modern ends and middle modern begins, but it is your opinion, not an accepted standard. The same can be said for the difference between calculus and analysis. There is no generally agreed upon line where one ends and the other begins. You seem to think that if it is algorithmic or heuristic it is "calculus" and if it is rigorous and includes convergence testing then it is "analysis". If that is what you are saying, then it is idiosyncratic, and no cause to call people who disagree "barbarous".

There is nothing really wrong with the introduction you prefer, but it is dull, and unlikely to be of any use to anyone. I realize there are mathematicians who consider dullness the sine qua non of mathematical writing. I prefer a writer who does not shy away from saying something is important when it is important, and who allows for philosophical and logical points of view in addition to the merely utilitarian. That is why I liked the other introduction better than this one. Rick Norwood 23:51, 30 October 2005 (UTC)

moving the history section

I would have thought that a major change in the article such as moving the history section to the end would be discussed here first. Guess not. Rick Norwood 22:08, 31 October 2005 (UTC)

Well, we all have discretion. Shuffling sections into logical order is sometimes just sensible. Someone had merged the section after the lead, meaning that had become a long chunk of history. At the end is one standard place for history. Charles Matthews 22:45, 31 October 2005 (UTC)

publication

would you like to publish this article? -- Zondor 22:18, 27 November 2005 (UTC)

Depends of where, and why. Check the FAQ for questions about reprinting wikipedia articles.

where? still online. why? to achieve the high quality standard comparable to traditional encyclopaedias such as britannica and encarta. -- Zondor 23:00, 27 November 2005 (UTC)

If I understand you, you want to publish an on-line encyclopedia that isn't wikipedia but which quotes wikipedia. I don't see the point, but you need to consult the wikigods about this. Nor not. This is a wiki, after all. Rick Norwood 23:18, 27 November 2005 (UTC)

no, we are publishing wikipedia articles one by one. we are in the process of consultation. yes, it would not be a wiki because it is an extension of the wiki system. -- Zondor 23:36, 27 November 2005 (UTC)

I misunderstood. Any article I have contributed to I did so with the understanding that whatever I wrote belongs to wikipedia. Publication sounds good to me. Rick Norwood 02:13, 28 November 2005 (UTC)

Note that whatever you guys publish must be under the GFDL, the same license as Wikipedia. And you don't need to ask permission, as long as you respect the license. Oleg Alexandrov (talk) 05:14, 28 November 2005 (UTC)

which version of the article do you think is publication worthy? ie. appropriate for schools and as good as or better than the one in britannica or encarta in quality and accurateness? please quote the oldid. -- Zondor 05:50, 28 November 2005 (UTC)

I would like to attempt to put a little polish on the article. It is accurate, but I do not think the prose style is as good as Britannica or Encarta. On the other hand, there has been so much controversy that editing this article may produce a strong reaction. I'm going to try with the intro -- not changing any ideas but just trying to improve the flow. If it gets reverted, you'll know I failed, and the article is probably not ready for prime time. Rick Norwood 14:03, 28 November 2005 (UTC)

At least we now have agreement of subject and verb. I did add one additional example -- that there are applications of calculus to statistics. Rick Norwood 14:16, 28 November 2005 (UTC)

actually, it doesn't need to be featured article quality or a brilliant prose, though that is the ultimate aim. it is publishable if it meets standard articles. does the article meet the standard article quality? its not a stub. its organised and wikified. is the facts justified by the sources? if you say it is accurate. i can't say, though i did well in calculus in high school but that was quite a while ago. i will assume good faith. there is a see also and external links section. i think believe its in neutral point of view. it has no original research. its verifiable presumably. do you think it meets standard article quality? -- Zondor 14:53, 28 November 2005 (UTC)

In my opinion, the article meets the "standard article" standards. I would still like to give it a final polish before it appears in cold, hard print. What's the deadline? Rick Norwood 22:11, 28 November 2005 (UTC)

there is no deadline obligated unless if you consider people who come on to wikipedia not knowing which version of the article to trust in certainty. on your behalf and your support, i would like to put it through the Wikipedia:Requests for publication process. -- Zondor 03:48, 29 November 2005 (UTC)

"With my support, certainly. In my behalf -- for that I need more information. I notice you have made this request on several articles. Where are you going with this? Rick Norwood 21:55, 29 November 2005 (UTC)

Now named, Wikipedia:Stable versions, it now has a first candidate: Common Unix Printing System. Typically, when people come on to Wikipedia, they read through the article but does not have full faith in them. This process raises the standard of Wikipedia so they can comfortably quoted in court cases. -- Zondor 02:51, 30 November 2005 (UTC)

Inverse operation?

The intro paragraph says that differential and integral calculus are inverse operations of each other. I do not believe this is necessarily correct, or at least the wording and placement. First of all, at this stage in the article, calculus has only been described as complementary concepts, that is, the study of change and accumulation respectively. In the intro, calculus has not yet been described in terms of transformations (eg. taking a derivative) so referring to "operations" seems premature in the article. Secondly, I believe the statement itself isn't entirely correct anyway. Simply put, differentiating isn't an injective process and therefore it cannot have a clear inverse. To illustrate, consider $f(x)=0$ and $g(x)=1$ which are not equal functions but they both have the same derivative. I will wait a little while to see if anyone has anything else to say on the matter before I make the change. Soltras 19:20, 3 December 2005 (UTC)

The indefinite integral is not a full inverse of the derivative in the same way that the square root is not a full inverse of the square. Still, in an article on the square root, it is useful to say it is the inverse of the square, and get into details later. The inverse relationship between derivative and integral is certainly one of the most important theorems of calculus.

There has been, over the years, strong debate about the contents of this article, as you might expect for so important a topic. It may be hard for you to believe, but I had to fight long and hard to get the concept of the limit even mentioned in the introduction.

My way of looking at calculus is that it is the study of certain linear operators, the limit, the integral, and the derivative, defined on spaces of functions or on spaces of equivalence classes of functions. When defined in this way, it is possible to make the idea that the derivative and integral are inverse operators exact. Needless to say, my way of looking at calculus is not going to get into the article. Wiki, like politics, is the art of the possible. Rick Norwood 21:35, 3 December 2005 (UTC)

No other comments. I made a wording change that functions as an agreeable solution for myself. Soltras 00:32, 15 December 2005 (UTC)

Simetrical's edit

Semitrical has made major changes in the article without discussion. He has thrown away some useful formulas, and there are many errors in what he has written. My inclination is to revert his edit. Any objections? Rick Norwood 15:37, 8 December 2005 (UTC)

I don't know about the revert; you guys discuss. Or you may revert if you feel like it. But I surely don't like the long discussion about instantaneous speed. All that talking about what really happens in real life at the level of picoseconds is true but reduntant. It carries one way too far from the purpose of illustrating what the derivative is about (which is the point of that article). If I were you Rick, I would cut off all that new stuff and then discuss the rest. Oleg Alexandrov (talk) 16:33, 8 December 2005 (UTC)

Not really, I saw some stuff in there that wasn't terribly helpful. Just try to save the parts that were useful, don't clean revert. To Semitrical, your edits aren't backed up by any references, so they're not terribly helpful. It's not terribly important what you know about calculus, but reputable, published material is. - Taxman ^Talk 16:34, 8 December 2005 (UTC)

I think his changes need to be cleaned, as any major edits usually need a few extra outside edits to better integrate with the article (no pun intended). Obviously any actual errors he's made should be fixed as they are noticed. I also agree that he added too much unnecessary detail to the paragraph about instantaneous speed, which bloats the article. However, I don't believe a total revert is necessarily the appropriate move. For one thing, I agree with him in that the strict mathematical definitions of things (like the FTC) should be relegated to more specific articles, leaving this one as merely a cursory overview of calculus for the layman. Soltras 17:16, 8 December 2005 (UTC)

There seems to be a consensus that I should edit rather than revert. I'll see what I can do. I like the formulas. What they state is ... well, fundamental. Rick Norwood 21:11, 8 December 2005 (UTC)

I've done my best at a cleanup. Mainly, I took out a lot of stuff, especially distinctions between the small and the really small (and the really really small and...). Improvements are welcome as always. Rick Norwood 21:51, 8 December 2005 (UTC)

I do agree, in retrospect, that some of my additions bloated the article, but I think my example (or at least some example) would be useful either here or at Derivative/Integral. Good examples are important in allowing those not knowledgeable in the field to get a better understanding of the principles underlying the subject matter. Maybe my example was too convoluted or not phrased well, but surely there should be some kind of example there. (The paragraph about natural rates of change not having a true limit was stupid and pedantic, though, in retrospect—I agree it doesn't belong here, if it even belongs anywhere.)

As for the formulae of the fundamental theorem of calculus: as I see it, it's rather silly for an article explaining calculus to assume that the reader is familiar with calculus notation. Obviously if you're sufficiently familiar with calculus notation to understand the fundamental theorem of calculus, you know pretty much everything that's going to be contained within the basic Calculus article, which is only an overview. If you're going to include formulae, the definitions of derivatives and integrals should surely be added before the FToC! The latter is meaningless without the former. I say leave the FToC formulae at the FToC article, and I'd leave the definitions of derivative/integral to their respective articles as well; to explain them properly you'd need to devote a few paragraphs to each, which would bloat the article too much. Leave this article with concepts.

Two more things. First, Rick Norwood, you said what I wrote contained "many errors". What are some examples of errors that I made? I see some long-windedness and pedantry, perhaps, but no actual errors. (But incidentally, speaking of errors, odometers don't measure displacement last I checked. They measure distance traveled. If they measured displacement, they would reset to zero when driven to the place they were manufactured.  :) )

Second, Taxman, what material did I provide that you think needs to be backed up by references? I would have thought that pretty much everything I added could be found in any calculus textbook. And it's not like there are any references in the article at present, or at least no specific ones (i.e., not counting Further Reading). —Simetrical (talk) 07:17, 9 December 2005 (UTC)

Most math articles in wikipedia begin with something for the layman, move on to something for the student, and some get very advanced before the end.

Maybe I was wrong to accuse you of many errors. I spotted a few, but mostly I found your explanations confusing rather than out-and-out wrong. You are right about displacement vs. distance. I'll fix that, if somebody else has not already done so. Rick Norwood 14:44, 9 December 2005 (UTC)

Going back to think of it I can't think of anything in the material you added that really requires references, that part of my comment was really a misplaced comment on other portions of the article, and possibly a reaction to your wording not being terribly encyclopedic. The history section desperately needs references and the applications section would, especially if expanded. The general goal of Wikipedia:Verifiability is important, but for truly obvious or uncontroversial things like much of the basics of calculus, there isn't much reason to cite specific things. The foundations section could concievably use some citations if those assertions are not universally accepted. - Taxman ^Talk 23:04, 12 December 2005 (UTC)

Fundamental theorem of calculus

Having the fundamental theorem of calculus in is good I think. Yes, this is an introductory calculus article, however, some people reading this article would have known some calculus. So, while one should not offend the newbies, one should also write important things in, like the above-mentioned theorem, as long as it is not too proeminent or not too early in the article. One may lessen the impact by carefully providing links to all concepts involved. Oleg Alexandrov (talk) 19:26, 9 December 2005 (UTC)

But again, surely the more important things to define are the definitions of integrals and derivatives, if we're going to define anything? Yes, the fundamental theorem of calculus is fundamental, but not as fundamental as those two, despite the name. —Simetrical (talk) 03:11, 11 December 2005 (UTC)

Well, first two sections are about derivatives and integrals. So, I would say that your requirement is satisfied, as the fundamental theorem of calculus is in the third section. No? Oleg Alexandrov (talk) 05:25, 11 December 2005 (UTC)

Yeah, the order it is in now seems about right. I think you really have to cover the fundamental theorem, because it is after all, fundamental to the subject. But putting it later with more technical material is probably good too. The ideal technical article gives a balanced overview of the subject. The lead should be an accurate overview of the article with as few undefined terms as possible. Then each section should proceed from easier to understand overviews into the nitty gritty towards the end. Then order the sections from easiest to most difficult if possible without sacrificing having the article make sense. To that end I tried working the examples in the lead into prose instead of bullet point lists, otherwise they break up the flow too much. In any case the article is in a better state than it used to be, but needs some help. I guess we should proceed by deciding what are the high level topics an overview of calculus should cover. Definitely as it currently has, we need differential and integral calculus, history, applications, and a fundamental theorem/foundations section (could we combine those?). But I was also thinking the subject could use a section on how it is taught, it's impact on curriculum, etc. I was thinking the applications section needs expanding, but I suppose you could also argue that should instead be built into other sections. What do you guys think? - Taxman ^Talk 23:04, 12 December 2005 (UTC)

"Well, first two sections are about derivatives and integrals. So, I would say that your requirement is satisfied, as the fundamental theorem of calculus is in the third section." Yes, but the notation for the FTOC isn't given in the sections on derivatives and integrals. Without $\int _{a}^{b}f(x)\,dx$ being defined, the notation of the FTOC makes no sense to the readers. Explain the idea, don't use the formula. —Simetrical (talk) 05:19, 26 December 2005 (UTC)

Differential Calculus of the Emotions

Spinoza defined the terms "perfection"; "sorrow-boredom-joy"; "hate-indifference-love" by their causes; not by their properties. They can be expressed using a Calculus format—precise definition, rates-of-change at any one instant.

Yesselman 23:45, 9 December 2005 (UTC)

Happy happy, joy joy! Rick Norwood 22:09, 12 December 2005 (UTC)

Examples in the introduction

I don't thing we need two economic examples in the introduction, but I like the new example better than the old, which is vague. Replace? Rick Norwood 22:08, 12 December 2005 (UTC)

I cut it down to two examples for differential and two for integral, but the removed one could be worked back in if someone feels strongly about it. - Taxman ^Talk 23:07, 12 December 2005 (UTC)

I like the cut to two examples of each -- don't like combining paragraphs throughout the article. I think it was easier to read with shorter paragraphs, and examples in separate sentences. Rick Norwood 14:26, 13 December 2005 (UTC)

History

I have clarified the nature of the dispute between Newton and Leibniz in the history section. Also, I have highlighted the key importance of the first and second fundamental theorems of calculus. Perhaps we should explain the contributions of people like Descartes and Fermat a little bit more. It was Fermat's insight into integrating functions of the form x^r that gave Newton and Leibniz a vital insight into the development of the fundamental theorems. —the preceding unsigned comment is by Grokmoo (talk • contribs) 18:06, 16 December 2005

Examples in derivative/integral sections

I previously added this example to the derivative section:

The derivative answers the question: as we consider progressively smaller and smaller pieces of time, what does the average speed computed by Distance/Time approach? If the car moves one kilometer over a span of one specific minute (perhaps the minute 0 ≤ t ≤ 60), and half a kilometer over a span of half a minute (0 ≤ t ≤ 30), and a fourth of a kilometer over a span of a fourth of a minute, and so on for any useful measure of time, we say that the car's instantaneous speed is one kilometer per minute, or 60 km/h. If, on the other hand, the car was speeding up or slowing down over the examined timeframe, it might move one kilometer over the course of one minute, but only 250 meters over the course of 30 seconds, 100 over fifteen seconds, 40 over 5 seconds, and perhaps as the amount of time considered is reduced closer and closer to zero, we will come up with a limit of 9 m/min, getting closer and closer to that figure (but perhaps without ever quite reaching it). As this example shows, average speed over any interval is not necessarily equivalent to instantaneous speed.

Now, this example is a bit lengthy and confusing, perhaps, but I think that something like it would be appropriate. It would allow a layman to get an idea of what exactly is happening when you take the limit of a function's rate of change, and what an instantaneous rate of change is. Currently, the reader is told things like "[d]ifferential calculus can be used to determine the instantaneous speed at any given instant"—but not told what "instantaneous speed" is. This stuff really isn't obvious. —Simetrical (talk) 05:06, 26 December 2005 (UTC)

I'm sorry to have to say so, but I find your lengthy example confusing. I think the example of the speedometer as a measure of instantaneous speed is both shorter and easier to understand. Rick Norwood 17:35, 26 December 2005 (UTC)

My writing skills tend to be somewhat erratic. This is one of my worse pieces.  :) Maybe there's no good way to explain what I'm getting at, basically introducing the concept of a limit and a derivative at the same time. I think I'll see what I can come up with later. —Simetrical (talk • contribs) 04:51, 27 December 2005 (UTC)

A bit of history about this article. While I think the limit is the essense of calculus, a majority of the people contributing to this article take a more practical approach. I was able to get in a mention of the limit -- after having my material on the limit reverted several times -- but I doubt you will be able to go much further with the limit here. I think it is probably more practical to discuss the limit in the article of that title. Rick Norwood 15:38, 27 December 2005 (UTC)

when was calculus invented by newton,when was calculus invented by leibniz?

Vote for new external link

Here is my site with calculus example problems. Someone please put this link in the external links section if you think it's helpful and relevant. Tbsmith

http://www.exampleproblems.com/wiki/index.php/Calculus

Method of exhaustion

What does this has to do with calculus? Isn't this just a fancy name for a common-sensical idea which everyone across all civilizations must have known. Most of them would have considered it too obvious to even mention. deeptrivia (talk) 17:56, 8 January 2006 (UTC)

The key idea behind calculus is the idea of the limit. It may seem obvious to you, but it is not at all obvious to most students, and it has only been written down a very few times in history. The Method of Exhaustion is the earliest known expression of this idea. Rick Norwood 18:04, 8 January 2006 (UTC)

I've attempted to add a reference for the requested "fact" but the wikipedia explanation of how to add references is clear as mud. If I can understand calculus, and cannot understand how to add references to a wiki article, I think the section on how to add references needs rewriting. Rick Norwood 18:32, 8 January 2006 (UTC)

Wikipedia bias

Just look at these two paragraphs:

---

An Indian mathematician, Bhaskara (1114-1185), developed a number of ideas that are foundational to the development of calculus, including the statement of the theorem now known as "Rolle's theorem", which is a special case of one of the most important theorems in analysis, the Mean Value Theorem. He was the first to conceive of the derivative. The 14th century Indian mathematician Madhava, along with other mathematicians of the Kerala school, studied infinite series, convergence, differentiation, and iterative methods for solution of non-linear equations. Jyestadeva of the Kerala school wrote the first differential calculus text, the Yuktibhasa, which explores methods and ideas of calculus repeated in Europe only in the seventeenth century.

Calculus started making great strides in Europe towards the end of the early modern period and into the first years of the eighteenth century. This was a time of major innovation in Europe, making accessible answers to old questions. Calculus provided a new method in mathematical physics. Several mathematicians contributed to this breakthrough, notably John Wallis and Isaac Barrow. James Gregory proved a special case of the Second Fundamental Theorem of Calculus in 1668. Leibniz and Newton pulled these ideas together into a coherent whole and they are usually credited with the independent and nearly simultaneous creation of calculus. Newton was the first to apply calculus to physics and Leibniz developed much of the notation used in calculus today; he often spent days determining appropriate symbols for concepts. It was generations after Newton and Leibniz that Cauchy, Riemann, and other mathematicians finally put calculus on a rigorous basis, with the definition of the limit, and the formal definition of the Riemann integral.

---

The first is just a bland statement of facts, desperately trying to minimise any indication of achievement. It doesn't even explicitly mention Bhaskara's work of differential calculus. The second has no limits to romaticising it's invention in Europe, "started making great strides in Europe", "This was a time of major innovation in Europe, making accessible answers to old questions", "contributed to this breakthrough". And you think you're not biased?

Why not edit it to put more information in? It is encouraged Sceptre ^(Talk) 19:36, 15 January 2006 (UTC)

The fact of the matter is that whatever contributions the Indian scientists made about calculus, they had to be rediscovered in the West. And of course the time of Newton was a great time for mathematics. To put it differently, the discoveries of ancient Indian scientists does not seem to have made a worldwide impact, they were more or less forgotten. The discoveries of Newton, Leibniz, etc, were followed by a lot of great mathematics in Europe eventually leading to mathematics as we know it. Oleg Alexandrov (talk) 21:39, 15 January 2006 (UTC)

Is the Yuktibhasas available in an English translation? Rick Norwood 01:08, 16 January 2006 (UTC)

See [6] for translation. --Pranathi 21:16, 23 April 2006 (UTC)

Thanks. Rick Norwood 13:43, 24 April 2006 (UTC)

I'd just like to point out that none of the Indian sources mention anything about doing integrals. While Euxodus and Archimedes developed the method of exhaustian (which was also what Kowa Seki's work was in), the development of the modern method of doing integrals, i.e. the fundamental theorems of calculus, was what really made math and science take off. For example, it wasn't even possible to integrate most simple polynomials until Fermat did his work. When Newton and Leibniz tied everything together and developed these modern methods of integration, it allowed integration of a huge, very useful class of functions, simply by knowing how to compute primitives. This is why Newton was able to actually apply his laws of motion and law of gravity. Without this breakthrough, the vast majority of modern science and math could not be developed. There seems to be some misconception here that Indian mathematicians "invented calculus", and it was only rediscovered by western mathematicians. That is not the case.

Also, I removed a statement about Archimedes saying that he "came close to the breakthrough" and that "there was no development in calculus after him for a thousand years". That statement seems to be something of a myth. Archimedes developed Euxodus's method of exhaustion a great deal, but never had any inklings of the general theory developed by Newton. Also, there was certainly work being done by Indian and Arab scholars during the middle ages in Europe that could be called calculus. For example, the definition and use of the derivative. Grokmoo 15:02, 14 February 2006 (UTC)

In fact, the sentence you cut out said: "Of all the mathematicians of the ancient world, [Archimedes] was the closest to discovering integral calculus, but never made the breakthrough, and after him the study of calculus did not advance appreciably for more than a thousand years." It did not say that Archimedes came close to the breakthrough, nor did it say that there was no development at all. -- Jitse Niesen (talk) 15:42, 14 February 2006 (UTC)

I agree with Jitse; the removal of the sentence by Grokmoo is not justified by his own explanation. For example, the work by Indian and Arab scholars during the middle ages came more than 1000 years after Archimedes. I'm going to revert his change.

My main concern with the statement is not that "calculus did not advance appreciably for more than a thousand years", it is that "Archimedes was the closest to discovering integral calculus, but never made the breakthrough." If you read some of Archimedes, and also know a little modern calculus, you will realize that Archimedes was no where near any "breakthrough". He had no inkling of modern calculus and the fundamental theorems. He developed methods for integrating many different functions by the method of exhaustian, but was no where close to being able to proceed with the general theory developed by Newton and Leibniz. Considering how he did not have a decent notation, nor analytic geometry, nor even the notion of the derivative, I don't see how anyone can claim that he was "close to a breakthrough". Please, stop reinserting this blatant myth. Grokmoo 04:19, 19 February 2006 (UTC)

I think we should discuss how much material about mathematicians in India should be included in this article which is, after all, about calculus, not the history of calculus. One person has complained that there the material about mathematics in India is "desperately trying to minimise any indication of achievement". Another person complains that "There seems to be some misconception here that Indian mathematicians "invented calculus"." This is a question that can only be settled by someone who is impartial, and who can read the original texts. Rick Norwood 20:44, 14 February 2006 (UTC)

Article removed from Wikipedia:Good articles

This article was formerly listed as a good article, but was removed from the listing because the article lists none of its references or sources --Allen3 ^talk 20:38, 18 February 2006 (UTC)

Which is very strange, because now there is a substantial list of references and sources. Do we need more? Rick Norwood 01:20, 19 February 2006 (UTC)

I noticed a very long list of items under both the "Further reading" and "External links" sections, but as per Wikipedia:Citing sources#Further reading/external links these sections are for items which have not been used as sources for the article. If you know for sure that the texts that are listed are able to verify the article, please make the appropriate updates. --Allen3 ^talk 02:18, 19 February 2006 (UTC)

I've been active in wikipedia for quite a while, now, but I still find the rules for "sources", "references", and "bibliography" confusing and inconsistent from article to article. Also, some articles seem to use footnotes, other do not. Rick Norwood 13:40, 19 February 2006 (UTC)

I followed the link you gave and it is very informative. I will try to modify the articles I work on accordingly, starting with this one. Rick Norwood 13:47, 19 February 2006 (UTC)

The difference between a contribution and a near breakthrough

I trust Grokmoo will not mind my posting here his message to my mailbox:

"This is in reference to your recent revert on the history of calculus section of the calculus article. I was wondering if you read the discussion in the talk page on this topic. In any event, you reverted the article to saying Archimedes was near a breakthrough, without giving any explanation of why. As for Archimedes "contribution" to calculus, you must be aware that he did significant work developing the method of exhaustion. This method is conceptually quite similar to the modern Riemann Integral, and is also probably the first example of using a limiting process to compute area exactly, which was precisely what doing an integral was before the fundamental theorems came along. For example, this sort of process is how Fermat computed the integral of general power functions. As for a source backing this up, I don't know why you would need a reference from Barrow. As for a more contemporary reference, see any book with a little history of calculus. Here is a link with some information: [7]

For the time being, I changed the statement back to what I had before. If you would like to change the wording to something more agreeable to you, I won't mind, so long as you don't put back in the statement about Archimedes "almost making a breakthrough". Grokmoo 04:51, 20 February 2006 (UTC)"

It seems odd that Grokmoo asks if I read the discussion, since my name appears here so often, but, yes, I do read the discussion. I'm really not sure what your point is, since we both agree that Archimedes got as close to calculus as any of the ancients -- though of course the method of exhaustion was originally developed by Eudoxus.

Archimedes was near a breakthrough in that if original Hellic mathematics had continued, the discovery of calculus would have been the natural next step. There was no breakthrough because that didn't happen.

On the other hand, to denomstrate a "contribution" by Archimedes, Wallis or Barrow or Newton or Liebniz or somebody would have had to acknowledge reading Archimedes and being inspired by what he had done. If you know of a case where that was done, please reference it. Rick Norwood 13:37, 20 February 2006 (UTC)

I will ask you a specific question then. To what breakthrough are you referring? The "discovery" of calculus consists primarily of the development of the fundamental theorems linking differentiation and integration. Of course, this is not the only thing, but it is certainly of key importance. Hence, to say Archimedes was "close to a breakthrough", he would need to have been near to discovering the fundamental theorems. Seeing as how the ancient Greeks had no concept of the derivative beyond the tangent of a curve (certainly possessing no notion of a formal definition), I don't see how you can possibly argue that they were close to discovering calculus. Before this discovery could happen, many other things needed to be done. For example, development of some notation for algebra, and of course analytic geometry were both needed. Since the ancient Greeks had neither of these things, they were not "close to discovering calculus". I fail to see how this constitutes the "next natural step". The development of Hellenic mathematics did continue, in the Arab and Indian traditions. It still took another 1700 years.

As for wanting a specific quote by a developer of calculus, it is clear that the idea of the integral originated with the ancient Greeks. Archimedes did work on the development of this idea. What more could you want?

The reason I asked if you read the discussion is because you changed my edit with nary a post here, and with only a terse explanation in your edit summary. I would think it would be reasonable to expect some sort of explanation when editing a comment that has been recently edited several times. I will delay editing it again for the time being, awaiting your response, and not wanting to start any sort of revert war. Grokmoo 16:59, 20 February 2006 (UTC)

It is a little hard to be specific about which breakthrough did not occur. If you want to delete the part about "close to a breakthrough" I have no objection.

We, from our vantage point, can see that the Greeks were close to integral calculus. I would have no objection to a statement to that effect. There is a big difference, however, between one idea anticipating another and the earlier idea contributing to the later. Maybe it did. I'd love to see a reference. Rick Norwood 20:49, 20 February 2006 (UTC)

I removed the specific line, and am now fairly happy with the section as it stands. I don't feel the need to say "Archimedes contributed to calculus", since this seems to be more a question of semantics than anything, and doesn't really add anything informative to the encyclopedia. Grokmoo 05:19, 21 February 2006 (UTC)

Looks good to me. Rick Norwood 13:50, 21 February 2006 (UTC)

Redundant redundancy

"Differental and integral calculus...calculus has two basic principles: Differential... and integral calculus" This article's intro is redundent! Should we change the beginning to Calculus, instead of Differental and integral calculus?

Nah, there is a difference. While it is true that differential and integral calculus are linked, there is the obvious distinction between them. In particular, you might refer to developments by Euxodus and Archimedes as integral calculus, while developments by Madhava would be in differential calculus. Of course, developments by Newton, Leibniz and others linking the two would probably be in just "calculus", I guess. In any event, I think the intro is ok as it stands. Grokmoo 16:33, 8 March 2006 (UTC)

I also agree, and would also note that differential and integral calculus are are only two (closely related) types of calculus. There are several other types of calculus (e.g. propositional calculus, umbral calculus), and so we must be specific, despite the prevailing misconception that calculus means only differential and integral calculus.149.43.x.x 04:27, 9 March 2006 (UTC)

I don't know about umbral calculus, but I do know that propositional calculus (and predicate calculus) are now most often called "propositional logic" and "predicate logic" precisely because the meaning of the word "calculus" is becoming more specialized over time. Today it usually means the mathematics that follows from the introduction of the concept of the limit. A more mathematical approach to the same subject is often called "analysis" (but Spivac's Calculus on Manifolds is an obvious exception). Rick Norwood 14:22, 9 March 2006 (UTC)

I don't think its redundant. "Calculus" like "algebra" can have many meaning, depending on the context. For exmaple, college elgebra, linear algebra, mulitlinear algebra, abstract algebra, and the calculus of variations, tensor calculus, lambda calculus, differential and integral calculus. Although today what we normally refer to as "The Calculus" is a combination of both differential and integral calculi, until Newton/Leibitz, the connecxion was not realized as such and could be seen as constututing two different branches of math. The Funadamental Theorem is what connects the two. Arundhati bakshi 13:39, 29 March 2006 (UTC)

Indian mathematics

Paul August removed some links about discoveries of calculus in India. I've put them back, at least for the time being. Throughout wikipedia there are a large numbers of claims about mathematical discoveries in India that are very general in nature and which keep being pushed further and further back in time. We need evidence for those claims, and the two links in question purport to provide evidence. This is a subject that needs to be investigated further. Rick Norwood 22:39, 16 March 2006 (UTC)

On the other hand, it may have already been investigated further, but mainstream math history may have chosen to be silent on the issue - either not being keen on disturbing the existing status quo or it being eurocentric in nature. Just providing a friendly opposing pov to your scepticism.. : ). I would suggest a search in books.google.com for hardcopy references - it may provide you a better comfort level. --Pranathi 03:15, 18 March 2006 (UTC)

Your implication that mainstraim historians of math would "cover up" new discoveries does not jibe with my own experience, which is that math historians love new discoveries. Nobody I know doubts that India has made and is still making major contributions to mathematics. But there is a problem when one source dates a particular contribution as 200 CE and another source dates the same contribution as 600 BCE. Maybe you can suggest some reference books? Rick Norwood 02:04, 19 March 2006 (UTC)

Rick, Which contribution are you talking about? I don't see anything in this page that purports to be from India from the BC. I haven't come here in a while and I see that there have been a lot of updates though. --Pranathi 19:01, 19 March 2006 (UTC)

The problem is widespread, with increasingly older (often conflicting) dates appearing in many of the math articles. I attempted to research the dates on the web, and was met with a maze of conflicting dates for ancient manuscripts. It is really beyond my expertise, but I hope someone more knowledgable than I will try to at least bring the dates of Indian mathematical discoveries in Wikipedia into agreement with one another. Rick Norwood 00:18, 18 April 2006 (UTC)

Etymology

I didn't think the etymology of the word "calculus" was appropriate as the second sentence of the article's main paragraph, so I created a subsection of the History section and pasted it there. Soltras 05:07, 8 April 2006 (UTC)

History of

Hi, I was thinking of further fleshing out the history of section, with a list of some specific contributions by Newton, Fermat, Leibniz, and others, and also information about developments after Newton (which is mysteriously absent) when I realized something. The history section is already too long. We already have an article called the history of calculus. Detailed lists of contributions by Aryabhata, Madhava, and others should probably go there, not here. If we included this much detail on every contributer, we would be duplicating the entire history of calculus page here.

To me, this situation is misrepresentative. I'd like to wait for some feedback on this before I make any changes, since my changes here have often been repeatedly reverted without explanation, and I know a lot of people feel strongly about this Indian Mathematics issue. Grokmoo 21:48, 17 April 2006 (UTC)

Why not propose something specific. The key is to stay balanced, treating each topic in relation to their importance, and do some good research. Anything less wouldn't be much of an improvement. Per WP:V any claims that can't be substantiated with references can be removed, but to be balanced, needed bits need to be researched. - Taxman ^Talk 23:50, 17 April 2006 (UTC)

I think shortenning a bit the histry is fine. Too huge paragraphs on indian mathematics is too much in this article I think. Shortening the Newton-Leibniz saga a bit could be good too. All, as Rick says, to keep things balanced. Oleg Alexandrov (talk) 00:38, 18 April 2006 (UTC)

I shortened it a bit, although not too much. I think I have managed to pack in a lot more informative content, though, with now a brief bit on the development since Newton. To fit this all in, I removed some detail to the Indian mathematics and Newton-Leibniz section. This stuff probably goes better in the main history of calculus article. I hope the new section is agreeable. Grokmoo 01:14, 21 April 2006 (UTC)

Comment on GA nomination

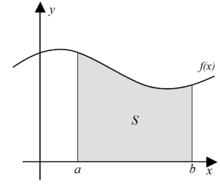
Calculus is a very important field and it's great to see that effort is being made to make this a great article. I think adding the following two images in their respective sections to graphically illustrate the difference between differential and integral calculus would greatly add to the strength of this article:

As a final comment, it would be great to be able to see which statements are supported by which reference. One commonly used way to do this is inline references, but I think there is some artistic freedom there. - Samsara (talk • contribs) 13:05, 26 May 2006 (UTC)

Two suggestions about the images. The first, to my eye at least, is misleading, because there is a "dot" on the tangent line that is not the point of tangency. In the second image, the area between a and b should be shaded, to distinguish it from the area between the y-axis and a. Rick Norwood 21:36, 26 May 2006 (UTC)

A desperate call to our Indian friends

Anybody claiming Indian priority in inventing calculus please quote the ancient sources. Don't tell me the dog ate them or the invading Turks burnt them. I want to see your proof! When I say sources I do not mean Hindutva booklets. Surely if some Indian mathematician 'long before Newton' used the notions of say derivative and integral in his work, he can be quoted directly.

By the way, I greatly appreciate Indian culture and science. Dear Indian friends, if you made me sick and tired of reading these endless passages about supposed Indian contributions to just about everything, think about disastrous impression it will make upon other readers. It's just like spam, nobody likes it. 212.199.22.126 01:12, 3 July 2006 (UTC)

I second the motion. We need authoritative sources. Rick Norwood 14:04, 3 July 2006 (UTC)

I think these are valid problems being raised here. Of course, it is well known that Euxodus and later Archimedes developed a sort of "integration" (although this was NOT the modern form of integration via the fundamental theorem). It is quite plausible that Indian mathematicians at least stated the definition of the derivative. (After all, this is a fairly straightforward extrapolation using Greek geometry and limiting processes.) However, some of the claims seem suspect. For example, it is currently stated in the article that Bhaskara stated Rolle's Theorem. While this is not that implausible, it is odd that we find no mention of the mean value theorem in this section, given that Rolle's Theorem is just a special case of the mean value theorem, and is really only of use in proving the more general theorem.

Also, some of the claims made seem inconsistent. It is stated that Aryabhata made use of a basic differential equation, yet we don't have the limit definition of the derivative until the 12th century! If we are just talking about the idea of a tangent line here, then Arybhata's contribution hardly seems worth mentioning.

Anyway, I've made a number of edits to this article and related ones in the past and have made little headway in trying to sort out fact from fiction, primarily due to the lack of good sources. I have read a number of "sources" in the form of webpages, but these are usually unsourced themselves, and often contain clearly erroneus statements.

I hope my above statements may be of some use to someone. Grokmoo 19:32, 3 July 2006 (UTC)

Did you read any of the references provided with those articles? I understand that it's hard to believe things not taught in school textbooks, and I've seen "comprehensive" Western "World history" books that don't bother to cover history beyond Europe, Egypt and a bit of China. Over the last centuries, biases like race, gender, etc. have been removed from these textbooks, and I'm positive that in another 50 years, they will become more globally balanced too. I'm sure everyone here understands that whatever is not on European and American textbooks is not automatically hoax. Anyway, just as an example, the reference for the Rolle's theorem bit is here. This was cited in the article, and is from a British university (in case Indian sources seem too boastful to rely on). The page itself doesn't have references, but the website does list all the references together on one page. deeptrivia (talk) 20:06, 3 July 2006 (UTC)

These are certainly interesting references, but they do not lay all the problems to rest. The history of Indian mathematics, for example, is by a grad student, Ian G Pearce, whose specialty is the study of insects. It seems to be very well researched, but to rely almost entirely on secondary sources. It would be nice to have a reference to a scholar who had read the originals, and who comments on their provenence, the methods by which they were dated, and the relationship between the notation used in the ancient sources and modern notation. For example, Pearce reports that in the 13th century, an Indian mathematician discovered that δ sin x = cos x δx. In what notation was this discovery expressed? In short, the reference answers some questions but raises others.

I certainly don't see any effort to belittle the mathematics of India. Every respectable history of mathematics mentions the Indian discovery of the decimal number system, of negative numbers, and of zero as a place holder. Rather, I think mathematicians are cautious, and want proof. Rick Norwood 21:44, 3 July 2006 (UTC)

So far 3 days have passed since my original call for a quotation. Nothing. The only valuable piece of information is from http://wiki.riteme.site/wiki/Talk:Indian_mathematics where I have asked the same question. According to thunderboltz a.k.a.Deepu Joseph "A lot of work and ideas by Indian scientists were disregarded due to Eurocentric views of Western scientists. Yuktibhasa is the ancient text by Jyeshtadeva of Kerala School describing Calculus". I am very interested in a relevant passage from this work, so let me address myself again to any Indian who can get access to this text - please, quote it! I have no anti-Indian agenda here, so I will be glad if this is really the first calculus text in the world. But if not - the false claims have to be removed, no matter what legends say. 212.199.22.219 22:56, 6 July 2006 (UTC)

You can read the contents of the book yourself — published by the Indian Institute of Advanced Studies (ISBN: 81-7986-052-3) (with analytic review). Or just download it in PDF from here. -- thunderboltz^{a.k.a.Deepu Joseph |TALK}07:25, 7 July 2006 (UTC)

Thank you for this wonderful link. The pdf file is very valuable for studying Indian science and I recommend to everybody reading this discussion to download and study it in depth. For me it was especially important as it contains numerous quotations in translaterated Sanskrit. Unfortunately there's no mention of anything related to calculus, so now I'm definitely baffled - how can anyone say this is the first calculus text in the world if a deep analysis of this book by a renowned Indian scholar does not mention calculus at all? Dear Indian friends, please help me understand your reasoning - you repeatedly claim Indian priority in inventing calculus, so in your country it must be common knowledge, written in every textbook. So why nobody has come with a quotation? 212.199.22.53 12:41, 7 July 2006 (UTC)

Of course you wont find the word "calculus" or "derivative" or "integral" in it. The entire text is in Malayalam — one of the prime reasons why these texts were for so long unknown to the world. See chapter VI (pages 72-142 in the original; or page no. 192 in the pdf). The earliest definition of Wallis product also occurs in the Yuktibhasa (a collection of works done by earlier Kerala School mathematicians Madhava of Sangamagrama and Nilakantha Somayaji). And here is a quote from the book itself:

“ The first term is the product of the given sine and radius of the desired arc divided by the cosine of the arc. The succeeding terms are obtained by a process of iteration when the first term is repeatedly multiplied by the square of the sine and divided by the square of the cosine. All the terms are then divided by the odd numbers 1, 3, 5, .... The arc is obtained by adding and subtracting respectively the terms of odd rank and those of even rank. It is laid down that the sine of the arc or that of its complement whichever is the smaller should be taken here as the given sine. Otherwise the terms obtained by this above iteration will not tend to the vanishing magnitude. ”

Jyesthadeva (the author) is decribing the Madhava series (better known as Gregory's series or perhaps Leibnitz' series) in the above quote.. -- thunderboltz^{a.k.a.Deepu Joseph |TALK}15:57, 7 July 2006 (UTC)

So what? Infinitesimal quantities were used by Ancient Greeks long before that. How can you compare this with groundbreaking results of Newton and Leibniz? 212.199.22.80 19:00, 7 July 2006 (UTC)

I apologize if my previous remark was perceived as rude. Thank you for your contributions to elucidating the history of Indian science. Of course the results obtained by Indian mathematicians at that time were excellent. But could these results be called calculus? 212.199.22.80 23:07, 7 July 2006 (UTC)

I don't want to open an ethnic editing war. The situation is unbearable. Only an Indian can check the sources. So please speak up! Do you think the quotation we got could be qualified as the first calculus text? 212.199.22.51 22:35, 8 July 2006 (UTC)

I dont agree with your claim that only an Indian can check the sources (why is that, may I ask?). What I had quoted, was a piece of translation of the text I got from this site. It is actually the Madhava Series, I think. Anyway, I am not a mathematics scholar, and I dont think I can help you any further in deciphering the calculus part in it. Perhaps this might interest you. Also, you could get more help on this front probably at Wikipedia:Reference_desk/Mathematics. -- thunderboltz^{a.k.a.Deepu Joseph |TALK}06:50, 9 July 2006 (UTC)

Please see the Yuktibhasa page now. Perhaps there is some calculus you can identify there? -- thunderboltz^{a.k.a.Deepu Joseph |TALK}14:32, 9 July 2006 (UTC)

And if you are still not conviced, then there is a direct quote of calculus in Yuktibhasa on this pdf file (first page, top middle coloumn). -- thunderboltz^{a.k.a.Deepu Joseph |TALK}15:47, 9 July 2006 (UTC)

OK. You are native speaker of Malayalam, aren't you? Can you help us with this, please: "Ekadyekothara pada sankalitam samam padavargathinte pakuti". Six words, piece of cake. Can you translate each word separately? 212.199.22.69 21:21, 10 July 2006 (UTC)

Its basically archaic Malayalam. But I think I can give a rough translation. (btw, it contains more than 6 words)

• Eka-dyekothara : Something that is singular or alone (here refering to a single variable)
• pada : term.
• sankalitam: summation; or as known to you and me — the integral.
• samam : equals
• pada-vargathinte : the term's square's
• pakuti : half

So in short, it means "The integral of x dx is x squared by 2". I dont understand why you are so skeptic about this. Also, why not create an account here? Anyway thank you for bringing this up. It helped me get the Yuktibhasa article onto the front page yesterday. :) -- thunderboltz^{a.k.a.Deepu Joseph |TALK}06:03, 11 July 2006 (UTC)

Thank you. Your efforts have obviously helped many people understand what exactly stands behind the recent wave of Indian priority claims in Wikipedia. Probably it won't come as a big surprise that I still think these claims are exaggerated (to use a polite definition). So far I have seen nothing in the field of "Kerala calculus" that was not done by Greeks. But I definitely will not edit these claims. They are a curious sample of exotic mentality quite foreign to mine. So let them live (probably not for long)! Sapienti sat :) Please continue your work on the Yuktibhasa article, that is very interesting. 212.199.22.127 21:46, 13 July 2006 (UTC)

If someone wants another better info on Indian Mathematics, please have a look at this research project from Scotland University of Mathematics.

Madhava and his history

http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Madhava.html

About Indian mathematics

http://www-groups.dcs.st-and.ac.uk/~history/Indexes/Indians.html

warm regards,

Source from,

School_of_Mathematics_and_Statistics University_of_St_Andrews,_Scotland

Formulas?

Am I the only one seeing "failure to parse" messages wherever there should be a formula? --Spangineer^es (háblame) 22:46, 30 July 2006 (UTC)

Everything seems fine to me. -- thunderboltz^{a.k.a.Deepu Joseph |TALK}05:33, 31 July 2006 (UTC)

Stable versioning tested on this article.

{{stablenotice}}

Stable versioning is being tested on this article. This means that all editing will be made on Calculus/development, and on a regular basis, good edits will be moved onto the consensus page. If you disagree with the current version, please let me know. Ral315 (talk) 05:27, 2 August 2006 (UTC)

I have to say that I'm rather miffed at your decision to try stable versioning on this article, without discussing it with the people that are actually interested in the article (i.e., on this talk page). Similarly, I'm annoyed with Splash's revert.

As to the proposal Wikipedia:Stable versions now itself, I think it is an interesting idea and that something like this will be good for Wikipedia eventually. Hence, I intend to implement stable versioning on this article unless there is opposition from the editors here. -- Jitse Niesen (talk) 15:01, 2 August 2006 (UTC)

Not really. The active editors of an article don't get to vote themselves an exemption from the m:Foundation issues, nor to decree that people shall not edit their article. The correct way to go about this is, for the umpteenth time, to go and build a workable, accepted proposal somewhere and then test to see if it works. It is wrong on many levels to take a proposal, the talk page for which is littered with objections, ruminations, alternatives, proposals and everything else and then say "right then, let's have some of that". You're doing it backwards, in the same way that these so-called 'test' earlier were backwards. Oppose, and object to the implication that only those who edit here should have anything to say. -Splash - tk 16:20, 2 August 2006 (UTC)

Oppose per WP:PROT and WP:OWN. Both of these trump a proposal that hasn't even achieved consensus support yet. Cynical 13:05, 4 August 2006 (UTC)

I guess Wikipedia is not ripe for it yet. -- Jitse Niesen (talk) 13:46, 8 August 2006 (UTC)

Eurocentric point of view

come out of your eurocentric point of view. Refferences are not readily available. But Lots of scholors(most of them western) have translated these texts and conclude that calculus in fact was from kerala much more than anyother place. Its easy to just deny ...when the world has just studied what you have. —The preceding unsigned comment was added by Vvn india (talk • contribs) 21:44, 15 August 2006.

Power of a function rule

Great article, but one suggestion, shouldn't we include the power of a function rule within the differentiation category on the right hand side. Or is there even such an article on Wikipedia yet? --Arsenous Commodore 00:15, 18 August 2006 (UTC)

I'm not sure what rule you mean. Are you thinking of the chain rule (when the outer function is a power)? 149.43.x.x 02:55, 18 August 2006 (UTC)

indian history of mathematics

i'm placing a request for references on the section in relation to india and calculus history. i've noticed a disturbing trend on a lot of history articles with a lot of POV pushing. these claims should be removed if they can not be verified because i have not read any of these supposed discoveries in any history book on mathematics. and please do not claim that the information was suppressed by the academic community... we need evidence for these claims. Truth100 01:43, 15 September 2006 (UTC)

Almost the whole article is unreferenced. I've added a couple of refs to the Indian claims. See the refs on Kerala School and Yuktibhasa article for more.-- thunderboltz^(Deepu) 08:00, 15 September 2006 (UTC)

Madhava and his history; about kerala school.

http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Madhava.html

About Indian mathematics

http://www-groups.dcs.st-and.ac.uk/~history/Indexes/Indians.html

From

School_of_Mathematics_and_Statistics University_of_St_Andrews,_Scotland

warm regards,

GA Re-Review and In-line citations

Note: This article has a small number of in-line citations for an article of its size and subject content. Currently it would not pass criteria 2b.
Members of the Wikipedia:WikiProject Good articles are in the process of doing a re-review of current Good Article listings to ensure compliance with the standards of the Good Article Criteria. (Discussion of the changes and re-review can be found here). A significant change to the GA criteria is the mandatory use of some sort of in-line citation (In accordance to WP:CITE) to be used in order for an article to pass the verification and reference criteria. It is recommended that the article's editors take a look at the inclusion of in-line citations as well as how the article stacks up against the rest of the Good Article criteria. GA reviewers will give you at least a week's time from the date of this notice to work on the in-line citations before doing a full re-review and deciding if the article still merits being considered a Good Article or would need to be de-listed. If you have any questions, please don't hesitate to contact us on the Good Article project talk page or you may contact me personally. On behalf of the Good Articles Project, I want to thank you for all the time and effort that you have put into working on this article and improving the overall quality of the Wikipedia project. Agne 05:57, 26 September 2006 (UTC)

Good article collaboration: a to do list

If we want to bring this article to FA status I think that the following things should be adressed:

1. Shorten the lead a bit. Add intro paragraph after the lead and put the overflow in there if need be.
2. More citations are needed, especially in the history section.
3. Expand on applications. There should be some comment regarding the fact that calculus is taught as a basic course in so many branches of education.
4. Check rigor and remove dubious bits (like the one about division by 0.

Feel free to add items to this list and to cross out those that have been adressed. Pascal.Tesson 18:40, 20 November 2006 (UTC)

Might I also suggest a peer review? The peer review bots might help us more on a quality scale. Tarret 22:36, 20 November 2006 (UTC)

It appears that the "bot" is only a semi-bot, and apparently uses a script that anyone can run on an article? Homestarmy 03:53, 21 November 2006 (UTC)

Interesting, I never noticed that I could have my own peer review bot. Heres what it gave me:

The following suggestions were generated by a semi-automatic javascript program, and might not be applicable for the article in question.

• The lead of this article may be too long, or may contain too many paragraphs. Please follow guidelines at WP:LEAD; be aware that the lead should adequately summarize the article.
• Per WP:MOS#Headings, headings generally should not repeat the title of the article. For example, if the article was Ferdinand Magellan, instead of using the heading ==Magellan's journey==, use ==Journey==.
• Please alphabetize the interlanguage links.
• Please make the spelling of English words consistent with either American or British spelling, depending upon the subject of the article. Examples include: behavior (A) (British: behaviour), meter (A) (British: metre), ization (A) (British: isation), isation (B) (American: ization), traveled (A) (British: travelled), travelled (B) (American: traveled).
• Watch for redundancies that make the article too wordy instead of being crisp and concise. (You may wish to try Tony1's redundancy exercises.)
  • Vague terms of size often are unnecessary and redundant - “some”, “a variety/number/majority of”, “several”, “a few”, “many”, “any”, and “all”. For example, “All pigs are pink, so we thought of a number of ways to turn them green.”
• Please ensure that the article has gone through a thorough copyediting so that it exemplifies some of Wikipedia's best work. See also User:Tony1/How to satisfy Criterion 1a.

Hope we can use it. Tarret 22:19, 21 November 2006 (UTC)

How is the lead too long, it seems about right to me..... Homestarmy 02:17, 24 November 2006 (UTC)

a branch of mathematics

Calculus isn't really a branch of mathematics, anymore than arithmetic is. Both are pretty much used in all of mathematics and just considered basic tools.

Also, it's nice to see all the physical applications mentioned, but very little is mentioned of its ubiquity in modern mathematics in general. --C S (Talk) 00:43, 26 November 2006 (UTC)

Re: Addition of Template:Calculus footer

Hello. While I have been on Wikipedia for a while now, I am still fairly new to the mathematics areas of Wikipedia, and I would like to make some contributions. I recently added a large (and hopefully comprehensive) footer navigation box to this article, Template:Calculus footer. There are a number of reasons why I support adding this template to this and other calculus-related articles. Currently, with the exception of a rare use of Template:Calculus as a side infobox, there is no easy way to navigate between calculus articles of different subjects. I have read previous discussions regarding infoboxes vs. categorization in the Wikiproject Mathematics, and saw that calculus was listed as a possible exception to the mainly anti-infobox opinion presented. As a result, I began creating side infoboxes for each branch (differential, integral, vector, etc.) until I realized that it is simply impossible to list even just the most important topics without having too-large-and-bloated infoboxex. At this point, I was lucky enough to stumble upon the World War II article; at the footer of each page of a World War II-related article, they have a comprehensive template (Template:World War II) that makes World War II articles, covering a vast topic in history, easy and user-friendly to navigate. Therefore, I decided to "be bold" and to do the same thing for the major topics of each branch of calculus, a vast total area in mathematics while using this World War II template as a base. While some things are probably still missing and others can be organized in a better fashion, I think this presents a much more user-friendly solution to those looking for information about calculus topics. Please let me know of any concerns you might have about this; barring any major objections, I would like to soon start putting this footer in other calculus articles. Thank you very much for your time and any feedback, Hotstreets 19:55, 8 December 2006 (UTC)

This template is huge! There is the Category:Calculus for that. I strongly disagreee agree with its addition. Oleg Alexandrov (talk) 17:27, 9 December 2006 (UTC)

Whoa, Oleg! It looks like you were typing too fast. Is that disagree? Or what? Anyway, I looked at the template and it's very nice. But I do think that tacking it onto the end of a large number of articles would be overkill. I also wonder how it would be updated as new articles are added. The Category tags work almost automatically.

What about just putting a link to it in "See also" sections? Could it be added at the end of several category tables that already exist? It would probably be welcome there. DavidCBryant 18:56, 9 December 2006 (UTC)

Sorry, I meant disagree. :) Oleg Alexandrov (talk) 20:03, 9 December 2006 (UTC)

I like Category:Calculus, but it does have the weakness that it doesn't present things in an order in which the topics may be taught. While this template doesn't solve this problem completely, I believe that it is a step in the right direction, by providing one-click access to the most commonly taught and known calculus topics (compared with four or more clicks to get to some vector topics via Category:Calculus). I will try to put some efforts into reducing the size of the template and report back my findings. Hotstreets 19:26, 9 December 2006 (UTC)

I agree it is too big, it might be possible to wrap it in a Wikipedia:NavFrame so the table is compressed by default and only shown when a reader requires it. --Salix alba (talk) 19:34, 9 December 2006 (UTC)

Either way, having both {{Calculus}} and {{Calculus footer}} is too much, they should be combined. And it should be short and sweet, with only the most necessary articles. Otherwise it is just link cruft multiplied by number of pages it shows at. Oleg Alexandrov (talk) 20:03, 9 December 2006 (UTC)

Yes, this is intended as a replacement for {{Calculus}}. And actually, using a series of NavFrames was exactly what I was thinking. I am not sure if this is possible (I will have to look into it), but I might try showing by default the category in which the article resides (an article in Category:Vector calculus will display the vector calculus list in the footer by default, etc.). This would require some restructuring, but would this be a good compromise? This would show the most necessary articles in the subtopic, and then have NavFrames to hide/show other topics as necessary. I will work on doing this. Hotstreets 20:13, 9 December 2006 (UTC)

(de-indenting) Having it at the bottom goes a long way to overcoming my dislike of navigation boxes. In my opinion, the list is clearly more useful than the category. It is huge though. If it's possible to hide it by default, that would be great. Otherwise, how about shortening it to two lines and linking to a separate page with the whole list? -- Jitse Niesen (talk) 02:40, 10 December 2006 (UTC)

After working to address concerns and suggestions, I have come up with a so-called "Version 2.0" of this template. The size has been dramatically reduced by hiding the lists of articles by default inside NavFrames - by clicking "Show" for a specific field, the list will become visible for that field. In addition, the font size of the text has been reduced, further shrinking the template. I think this is now a suitable addition to calculus-related articles. I think the one possible addition I would like to pursuit still, but would take additional time and effort is to:

• A: Clean up the code, as the recent changes have made it less edit-friendly.
• B: Find a way to show the list by default for the category/categories in which the article resides. (Example: the Differential calculus section of the box is automatically unhidden when viewing the Derivative of a function article)

Please let me know what you think of these changes, and what more can be tweaked or improved. Once again, thanks for all of the suggestions and feedback. Hotstreets 05:28, 10 December 2006 (UTC)

I like it! - grubber 05:30, 11 December 2006 (UTC)

I have further reduced the size of the template and put it all inside of a dynamic navigation box. I feel that I have addressed the major concern that prevented the template's inclusion in the article, its massive size. As of now, the template is about half of the original size, without sacrificing any of the topic links. Through use of NavFrames, major topics (differential, integral, etc.) are accessible immediately, and an article within one of these sections (Derivative or Green's theorem, for example), can now be accessed in two clicks. Also, the entire template can be collapsed if desired. Because of this, and the fact that no major objections have been raised since I last revised the template, I am once again including it in the article. Please let me know if you have any concerns, I hope this addresses most, if not all, of your feedback. Thanks! Hotstreets 20:37, 17 December 2006 (UTC)

Balance and accuracy concerning controversy concerning origins?

Article says, "When Newton and Leibniz first published their results, there was great controversy over which mathematician (and therefore which country) deserved credit." but I understand from the Wikipedia article on the controversy itself (to which this should link) that the controversy evolved many years after Leibniz published his results. Also, the slant of the story itself, as it is told here, seems to favor one side (Newton). — Preceding unsigned comment added by Rentstrike (talk • contribs) 18:25, 28 November 2012 (UTC)

Capitalization of Calculus

It is my understanding that the formal name for calculus is "The Calculus." While the "The" is generally dropped these days, isn't it still appropriate to capitalize the word Calculus?

"A calculus is a way of calculating, so mathematicians sometimes talk about the 'calculus of logic', the 'calculus of probability', and so on. But all are agreed there is really only one Calculus, pure and simple, and this is spelled with a capital C" (emphasis mine) (Crilly, Tony (2007). 50 Mathematical Ideas You Really Need to Know. London: Quercus Publishing Plc. p. 76, 208. ISBN 1-84724-147-6.)

Interestingly, the index of the book does not capitalize the word.

It would seem seems that we should at least mention the issue of capitalization in the article.

Billiam1185 (talk) 01:02, 4 March 2013 (UTC)

• Other common forms of calculus: There has been a general academic trend (20 years?) to not capitalize concepts, unless specifically discussing the "Ideals" of Plato ("Truth" or "Beauty"), and it has led to some confusion, such as any old "categorical imperative" versus "The Categorical Imperative" of Immanuel Kant. For types of calculus specializations, there is "differential calculus" versus "integral calculus" versus "tensor calculus" (similar to a type of algebra) verus "infinitesimal calculus". So, those are reasons to avoid capital "C" in "calculus". Does that make sense? -Wikid77 (talk) 20:01, 17 April 2013 (UTC)

There should be more technical information

Perhaps more examples on this matter. — Preceding unsigned comment added by Pedrovalle (talk • contribs) 13:11, 20 May 2013 (UTC)

Why is Leonhard Euler not mentioned ?

To be clear, most who add to the mathematical pages have probable forgotten more than I know about maths (I'm British, so I refuse to call it math). However it couldn't escape my notice that when Google put Leonhard Euler up in a Google doodle and specifically mentioned his historical significance to maths and his important work on infinitesimal calculus, that there is no mention of him whatsoever on the infinitesimal calculus page. Is Google incorrect in its highlighting the importance of Euler? Or is his work on infinitesimal calculus not as important as made out on his Wikipedia page? Either one or the other needs correction?

This is definitely an oversight. Euler should be mentioned both on calculus and infinitesimal calculus. Would you like to contribute a comment there? Tkuvho (talk) 15:05, 20 May 2013 (UTC)

The introduction should include when and who.

I think there should be something in the introduction about when it was invented and (gulp) who invented it. At the risk of being beaten over the head by all the history revisionists and refactorers out there, I think that should be the 17th century, Newton, and Leibniz. --Chetvorno^TALK 00:43, 27 July 2013 (UTC)

Quote hanging on Newton's edge

The Neumann quote box is hanging on Newton's image edge. Can someone fix it? Tried to, but got rolled-back. Formatting problems. --J. D. Redding 00:11, 28 July 2013 (UTC)

Really?

Come on, people, let's hold the line for general references. We don't have to give in to the inline-cite extremists, not here. For most aspects of the topic, all our refs are going to say the same thing, probably in almost the same words. Save the inline cites for the stuff that's a little particular, and don't make the reader work through a forest of little blue numbers. --Trovatore (talk) 19:14, 4 December 2013 (UTC)

My take on this... someone comes along and makes some subtle changes. Without inline refs it tends to be pretty hard—if not impossible—to check the sources, at least for me, having not significantly contributed to the article in the past. Inline refs make this much easier. - DVdm (talk) 19:22, 4 December 2013 (UTC)

I resist giving in to citation extremists on non-controversial facts, but having some citations are still useful. For instance, the large Principles section of this article has no citations. If a curious student wanted to learn more about principles of calculus, there are zero pointers to a good source or two on this. It's a flaw. I think the more relaxed citation guidelines in WP:SCICITE would be appropriate here: about one general ref per paragraph. --Mark viking (talk) 20:05, 4 December 2013 (UTC)

I am not a citation extremist. But this article doesn't even meet a one general reference per SECTION standard, much less one general ref per paragraph. Stigmatella aurantiaca (talk) 22:48, 4 December 2013 (UTC)

Orphaned references in Calculus

I check pages listed in Category:Pages with incorrect ref formatting to try to fix reference errors. One of the things I do is look for content for orphaned references in wikilinked articles. I have found content for some of Calculus's orphans, the problem is that I found more than one version. I can't determine which (if any) is correct for this article, so I am asking for a sentient editor to look it over and copy the correct ref content into this article.

Reference named "almeida":

• From Madhava of Sangamagrama: D F Almeida, J K John and A Zadorozhnyy (2001). "Keralese mathematics: its possible transmission to Europe and the consequential educational implications". Journal of Natural Geometry. 20 (1): 77–104.
• From Indian mathematics: Almeida, D. F.; John, J. K.; Zadorozhnyy, A. (2001), "Keralese Mathematics: Its Possible Transmission to Europe and the Consequential Educational Implications", Journal of Natural Geometry, 20: 77–104.
• From Kerala school of astronomy and mathematics: Almeida, D. F.; John, J. K.; Zadorozhnyy, A. (2001). "Keralese Mathematics: Its Possible Transmission to Europe and the Consequential Educational Implications". Journal of Natural Geometry. 20: 77–104.

I apologize if any of the above are effectively identical; I am just a simple computer program, so I can't determine whether minor differences are significant or not. AnomieBOT⚡ 21:02, 11 January 2014 (UTC)

Merger proposal

The following discussion is closed. Please do not modify it. Subsequent comments should be made on the appropriate discussion page. No further edits should be made to this discussion.

---

Request received to merge Infinitesimal calculus into Calculus. User:Unsigned request. Reason= unknown. Please discuss here. GenQuest ^{"Talk to Me"} 00:16, 30 March 2014 (UTC)

• Support, with qualifications. I think the main use of the term infinitesimal calculus is simply to mean the calculus; that is, the differential and integral calculus, as opposed to, say, the propositional calculus. So I think infinitesimal calculus should ultimately redirect to calculus. However, whether the content should be merged is a different question. Possibly the content should instead be moved to some title such as infinitesimal methods in the calculus, or else merged into nonstandard analysis, before pointing the redirect at calculus. --Trovatore (talk) 00:35, 30 March 2014 (UTC)
  • Update I wrote the above without really looking at the current content of infinitesimal calculus. As it stands, there's actually not that much about infinitesimal methods there, so I'm not sure how much there is to start another article with, or to merge to nonstandard analysis. Still, in principle, I stand by my remarks — for example, it could be (I haven't checked) that the article used to be more about infinitesimal methods, and in that case, that previous content could be used in the way I described. --Trovatore (talk) 00:48, 30 March 2014 (UTC)
• Support. There is not enough material specific to the use of infinitesimals in calculus to warrant an entire article on this topic. All the material presently in the infinitesimal calculus article should be in either the main calculus article or in some closely related article (such as on history, on derivatives or integrals specifically, on non-standard analysis, and so on). Ozob (talk) 02:01, 30 March 2014 (UTC)
  • Comment Even if there is enough material for such an article, I don't think infinitesimal calculus is the right name for it. Sorry to be picky about it when we're on the same "side", but I really think the point to stay focused on is, where should the search term infinitesimal calculus point? And in accordance with the "common name" principle, I think that term is more used for the integral and differential calculus (regardless of foundations) than it is for the use of infinitesimals in the foundations of calculus. --Trovatore (talk) 03:45, 30 March 2014 (UTC)
    • I think infinitesimal calculus should point to calculus. At this point I think that's what the term refers to; saying "infinitesimal calculus" distinguishes differential and integral calculus (considered together) from, say, propositional calculus. To me it also carries a hint of infinitesimal foundations; maybe they're Newtonian or Leibnizian instead of non-standard analysis, but regardless the term itself suggests that infinitesimals make an appearance in the theory somehow. Ozob (talk) 06:36, 30 March 2014 (UTC)
• Support. Theo (Talk) 10:00, 1 April 2014 (UTC)
• Support As far as I know as a math student with no background in history of math, calculus is essentially a shorthand for infinitesimal calculus. -- Taku (talk) 17:20, 1 April 2014 (UTC)
• Support I think infinitesimal calculus should be merged into calculus, with the redirect also pointing to calculus as the most common usage of the term. The infinitesimal calculus article is mostly redundant with calculus article, except for the "Non-standard calculus" and "Smooth infinitesimal analysis" sections--those could be usefully merged into the Calculus#Limits and infinitesimals section, which doesn't even mention the Non-standard calculus article. --Mark viking (talk) 17:38, 1 April 2014 (UTC)

The discussion above is closed. Please do not modify it. Subsequent comments should be made on the appropriate discussion page. No further edits should be made to this discussion.

Madhava sources

I have undone this edit. It is based on 4 sources, all of which i.m.o. unreliable:

• source [7]: "Categories:Types, School Work, Essays & Theses"
• source [8]: wp:primary self published website by Luke Mastin. Who is Luke Mastin?
• source [9] gives the view of one author, George Gheverghese Joseph, "on a mission to reclaim :India’s pride of place in the world of mathematics." Seems not sufficiently notable to be mentioned here.
• source [10] is wp:circular: "Based on materials from: Wikipedia."

Comments? - DVdm (talk) 10:47, 22 February 2015 (UTC)

Comments:

Regarding the third source (the Telegraph article), please read beyond the first sentence. George Gheverghese Joseph is an "emeritus professor at Manchester University in the UK" who was "awarded a Royal Society Visiting Fellowship". You can read more about him and his arguments here. Why is Joseph "not sufficiently notable"? Exactly what are your criteria for notability? — Preceding unsigned comment added by 71.106.229.93 (talk) 15:45, 22 February 2015 (UTC)

Please sign your talk page messages with four tildes (~~~~). Thanks.

Are there scholarly secondary sources who cite Joseph? See wp:secondary sources. - DVdm (talk) 15:49, 22 February 2015 (UTC)

Princeton University Press published Joseph's book "The Crest of the Peacock: Non-European Roots of Mathematics (Third Edition)" wherein he makes the arguments cited, and two positive reviews from New Scientist and Times Literary Supplement appear on the PUP website: http://press.princeton.edu/titles/9308.html His scholarly credentials are bona fide: http://www.sagepub.com/authorDetails.nav?contribId=649701 ~~~~ — Preceding unsigned comment added by 71.106.229.93 (talk • contribs) 16:02, 22 February 2015 (UTC)

Just the four tildes, without the nowiki-tags please (~~~~). Thanks.

Yes, but that is a wp:primary source. We need other scholar sources who cite the book. Such sources would establish notability. - DVdm (talk) 16:19, 22 February 2015 (UTC)

From the Wikipedia article on Secondary source: "In scholarship, a secondary source is a document or recording that relates or discusses information originally presented elsewhere. A secondary source contrasts with a primary source, which is an original source of the information being discussed; a primary source can be a person with direct knowledge of a situation, or a document created by such a person. However, as discussed in detail in the section below on classification, deciding how to classify a source is not always an obvious decision. Secondary sources involve generalization, analysis, synthesis, interpretation, or evaluation of the original information. Primary and secondary are relative terms, and some sources may be classified as primary or secondary, depending on how it is used." Princeton University Press and the reviewers at New Scientist and Times Literary Supplement would seem to agree that Joseph's scholarly credentials are unassailable; and his book published in 2010 contains "generalization, analysis, synthesis, interpretation, or evaluation of the original information" pertaining to events of the fourteenth and fifteenth centuries.

Has the citing by other scholarly sources been verified for other works cited on this page, such as those of Katz and Zill? Have their works been published by Ivy League universities? Where might we find Wikipedia's rules for what sources are acceptable and which ones are not? Too many articles on Wikipedia are treated as the private fiefdoms of their self-appointed guardians of correctness, and I've seen excellent scholarship repeatedly censored by such individuals who elsewhere in the same given article fail to abide by the "rules" they invent to set the bar far higher for facts and/or interpretations that they dislike. 71.106.229.93 (talk) 16:55, 22 February 2015 (UTC)

Please indent your messages along wp:talk page formatting guidelines. Thanks.

Reviews of a book don't really count as secondary sources for particular statements made in that book. The statements you like to add to the article should be found in other articles or books—preferably not newpapers—, referring to the primary source in question. If other poor or unacceptable sourcing has taken place here, perhaps remedial action should be taken, but it certainly does not warrant addition of more such content—see wp:otherstuffexists. - DVdm (talk) 17:52, 22 February 2015 (UTC)

I asked you specific questions, viz.: (i) Exactly what are your criteria for notability? (ii) Has the citing by other scholarly sources been verified for other works cited on this page, such as those of Katz and Zill? (iii) Have their works been published by Ivy League universities (as Joseph's work has)? (iv) Where might we find Wikipedia's rules for what sources are acceptable and which ones are not? 71.106.229.93 (talk) 18:12, 22 February 2015 (UTC)

George Gheverghese Joseph's book makes arguments in the general direction you are interested in, namely examining Indian contribution to the development of the calculus, but I am not convinced by your claim that Joseph "makes the [specific] arguments cited" in your proposed revision. If you can source these and replace some of the dubious references you provided by page numbers in Joseph this may strengthen your case for inclusion. Tkuvho (talk) 08:42, 23 February 2015 (UTC)

Fair enough. My interest is not geographically specific but rather the acknowledgement of contributions by great minds. Joseph's book covers "the deep influence that the Egyptians and Babylonians had on the Greeks, the Arabs' major creative contributions, and the astounding range of successes of the great civilizations of India and China". I will look further and propose material in the future.71.106.229.93 (talk) 16:00, 24 February 2015 (UTC)

Note that the reliability of Joseph is put into question in a detailed review by Jens Høyrup here. Tkuvho (talk) 08:49, 23 February 2015 (UTC)

@71.106.229.93: Re (i) and (iv): see wp:verifiability and wp:consensus. Re (ii) and (iii) see wp:otherstuffexists. - DVdm (talk) 11:36, 23 February 2015 (UTC)

Your link contains basic bibliographic information on Joseph's book and nowhere puts into question his reliability. I am well aware of Wikipedia's articles on sources, etc. and they do not answer the questions that I asked. Please reply in complete sentences: (i) Exactly what are your criteria for notability? (ii) Has the citing by other scholarly sources been verified for other works cited on this page, such as those of Katz and Zill? (iii) Have their works been published by Ivy League universities (as Joseph's work has)? (iv) Where might we find Wikipedia's rules for what sources are acceptable and which ones are not? 71.106.229.93 (talk) 16:00, 24 February 2015 (UTC)

Again, see wp:verifiability and wp:consensus. In a complete sentence: whether the content is notable or not, and whether the sources are reliable or not, is ultimately decided here by consensus on the article talk page. - DVdm (talk) 16:37, 24 February 2015 (UTC)

User 71.106.229.93, your claim that the link to the mathscinet review contains only "basic bibliographic information on Joseph's book" is in error. The review lists numerous inaccuracies, distortions, and tendentiousness in Joseph's book. Tkuvho (talk) 18:32, 24 February 2015 (UTC)

You have linked to a page that only shows basic bibliographic information on Joseph's book and that requires special access including a 'MathSciNet license'. Is this review freely available elsewhere? 71.106.229.93 (talk) 15:26, 25 February 2015 (UTC)

Ancient History Section

I've removed this from the article's Ancient History section since it should be dealt with here.

{{clarify|post-text=(Why mention this if not relevant? <-Perhaps it is a first/early instance of volume and area calculation, which the paragraph suggests would be the evolutionary antecedent of modern calculus, thus introducing a historical and logical progression, which would seem to be the purpose of this section.)|date=August 2015}}

Should something be added to the article in way of clarifying this point? Bill Cherowitzo (talk) 04:37, 30 August 2015 (UTC)

dx + Δx or just dx?

A question. Mesmerate (talk) 04:32, 22 November 2015 (UTC)

It is dx+Δx. Mesmerate (talk) 04:36, 22 November 2015 (UTC)

The context for that part of the article is the historical development of calculus through infinitesimals. At that time, dx was used to refer to an infinitesimal change in x. Such a change in x is too small to be represented by a real number. The replacement of infinitesimals by limits of real-valued increments Δx happened over a century later. The revival of infinitesimals by Robinson happened several centuries later, and his concept of infinitesimals was philosophically different from those used by the pioneers of calculus. Ozob (talk) 04:49, 22 November 2015 (UTC)

Sir, the idea is you're taking the limit as it gets really close to zero, and as it gets closer, that is what it gets closer and closer to. As it gets closer and closer, infinitely, it can be considered infinitesimal. Mesmerate (talk) 04:55, 22 November 2015 (UTC)

You are using a post-Weierstrass interpretation of infinitesimals as limits. That is a historical anachronism. It is not at all how Newton and Leibniz saw what they were doing. Ozob (talk) 04:58, 22 November 2015 (UTC)

Please tell me HOW they saw what they were doing? Mesmerate (talk) 05:05, 22 November 2015 (UTC)

The change in x, or Δx, can be defined to include infintely small or infinitely large numbers in its list of possible numbers. It commonly is, and that is partly why i think it is a just fine canidate for being an infinitesimal. Mesmerate (talk) 05:08, 22 November 2015 (UTC)

So, you think infinitesimals cannot be defined using limits? Mesmerate (talk) 05:11, 22 November 2015 (UTC)

For the inventors of calculus, dx (in Leibniz's notation) represented a change in x that was positive, but smaller than any number. This sounds paradoxical because we want to know what kind of thing dx is (it is by definition not a real number). It was just as paradoxical at the time it was introduced; see the article for some history of objections to calculus. Yet calculus seemed to work, so people went about using it. There were still open foundational questions even as calculus developed into a practical discipline. These foundational questions eventually spurred the work of Cauchy, Weierstrass, Riemann, Lebesgue, and so on, who all came much later than Newton and Leibniz and who gave us the definitions of limits, derivatives, and integrals that we use today. It would be historically incorrect to say that the discoverers of calculus understood it in the same way we do. They didn't. (It's also worth noting that the idea that all of mathematics should be rigorously derived from a small set of axioms did not develop until the 19th century, and it really only triumphed with the rise of Bourbaki.) Ozob (talk) 05:17, 22 November 2015 (UTC)

We are talking about modern calculus, where Δx is allowed to approach zero, and where dx is defined as Δx as dx. Mesmerate (talk) 05:25, 22 November 2015 (UTC)

Sorry. Mesmerate (talk) 05:26, 22 November 2015 (UTC)

• where dx is defined as Δx Mesmerate (talk) 05:26, 22 November 2015 (UTC)

The part of the article you edited is specifically about the history of calculus. Modern foundations are discussed in the following paragraph (and in other appropriate articles). Ozob (talk) 05:31, 22 November 2015 (UTC)

No it isn't, check. Mesmerate (talk) 05:35, 22 November 2015 (UTC)

It's under "principals". Mesmerate (talk) 05:37, 22 November 2015 (UTC)

@Mesmerate: dx and Δx as used in this article are quite different concepts. Letting Δx → 0 is most definitely not the same as simply having an infinitesimal quantity dx. See the hyperreal numbers for a rigorous discussion of the distinction. Any particular Δx is a finite real number. The operation of letting it approach zero does not make it the same as an infinitesimal, which on its own, without taking a limit, is smaller than any positive real number, yet nonzero. Phrases like "As it gets closer and closer, infinitely, it can be considered infinitesimal" are not mathematically rigorous and do not suffice.--Jasper Deng (talk) 06:33, 22 November 2015 (UTC)

I still argue otherwise, I argue in modern calculus dx itself can be considered as the change in x as it approaches 0. Mesmerate (talk) 12:37, 22 November 2015 (UTC)

And I have already clarified that we are talking about modern calculus, "principals" is not a sub heading of "history". Mesmerate (talk) 18:43, 22 November 2015 (UTC)

The meaning of dx depends on the context and the foundations. In modern differentiation, it is just a notational convenience and has no intrinsic meaning. In modern integration, it is a notation for the variable of integration or for a measure. As a differential form, dx stands for the exterior derivative of the identity function x → x. In Robinson's theory of infinitesimals, dx is a hyperreal number.

What I think you are proposing is that dx is a notation for "the limit of Δx as Δx → 0." But this is not what you want: lim_{Δx → 0} Δx = 0 for trivial reasons, and you do not want dx = 0. To derive anything useful, you must take the limit of some function of Δx. For example, the derivative is the result of taking the limit as Δx → 0 of the difference quotient (f(x + Δx) - f(x)) / Δx. In the difference quotient, Δx is not infinitesimal; it is just a real number. Taking the limit detects infinitesimal behavior but does not actually require the use of infinitesimals.

If you'd like to learn more about these topics, I suggest Rudin, Principles of Mathematical Analysis. Ozob (talk) 21:21, 22 November 2015 (UTC)

Sorry, nevermind. I read in a text book that the (dy/dx) could be seperated by multyplying by "dy" and as such, it had a page where it said "Who are we to throw around these numbers?" and defined dx as the change in x. I also understand that something getting infinitely cl in all the mess. I admitzero by itself. I still think that delta x equals zero, i just added a small note and got tangled up in it all. I still think something approaching zero still works like an infinitesimal, except for that one case in which it just goes to zero. Sorry i'm a little put of tune in calculus, plus, please tell me if i am right in "It acts like an infinitesimal, except for that one case.". Mesmerate (talk) 23:44, 22 November 2015 (UTC)

Sorry, i mean you can seperate the (dy/dx) by multyplying by dx, not dy. Mesmerate (talk) 23:46, 22 November 2015 (UTC)

Sorry my sentence 2 sentences ago was messed up. Mesmerate (talk) 23:47, 22 November 2015 (UTC)

I meant to say i got caught in it all, and in all cases except for that case "approaching" acts like an infinitesimal. Mesmerate (talk) 23:48, 22 November 2015 (UTC)

Sorry, by "two sentences ago" i meant two comments ago. Mesmerate (talk) 23:50, 22 November 2015 (UTC)

Also, to clarify, i admit i was wrong. I will stop editing that part of the page, and i am sorry for disrupting wikipedia. Mesmerate (talk) 23:53, 22 November 2015 (UTC)

The idea i had in mind was "dx=the change in x", "the change in x can act infinitesimal in most cases", "the change in x is fine, smd should be mentioned." Mesmerate (talk) 23:57, 22 November 2015 (UTC)

• and Mesmerate (talk) 23:57, 22 November 2015 (UTC)

Still, i believe that dx in integrals stands for "the change in x" in integrals,as the definition of the integral uses it alot. infact, it used "the change in x" an infinite number of times. and in both case, dx is short hand for "the limit of this using delta x" Mesmerate (talk) 00:00, 23 November 2015 (UTC)

And as such i would like to start a new discussion. I would like to discuss the idea of mentioning that the meaning of "dx" is different across modern and old calculus. Mesmerate (talk) 00:01, 23 November 2015 (UTC)

Explanation of the change of the meaning to the notation "dx" from meaning infintesimal, to meaning shorthand for the change in x, whether or not x approaches 0.

Read description. Mesmerate (talk) 00:06, 23 November 2015 (UTC)

I believe it is important enough to be mentioned. Is there any consensus? Mesmerate (talk) 00:07, 23 November 2015 (UTC)

It's explained in Leibniz notation. I'd support including that but not more. Also, by the way, please indent your comments (your next comment below should have two colons (::) appended before it, just like this comment has one before it).--Jasper Deng (talk) 04:13, 23 November 2015 (UTC)

The title of this section is misleading. Whether or not x approaches zero has nothing to do with dx and never did. If, for example, we take the limit as x approaches 7, then dx is still the change in x. Rick Norwood (talk) 12:23, 23 November 2015 (UTC)

On one hand, that entire section is historical - there are no infinitesimals in the real line. I would remove both the δx and the dx from that sentence, which is really only trying to say what an infinitesimal is. The symbol dx is not an infinitesimal in modern treatments of calculus. — Carl (CBM · talk) 12:37, 23 November 2015 (UTC)

It's in "principals", not "history". If it is historical, that's a mistake. Mesmerate (talk) 22:53, 24 November 2015 (UTC)

So we should remove the mention of "dx" meaning infinitesimal all together and only say it's just the change in x? I'm fine with that. Mesmerate (talk) 22:56, 24 November 2015 (UTC)

The h in the limit definition of a differential

What does h stand for in:

$f'=m={\frac {f(a+h)-f(a)}{(a+h)-a}}={\frac {f(a+h)-f(a)}{h}}...?$

Why don't we explain it in Calculus#Differential_calculus? Warmest Regards, :)—_thecurran Speak your mind ^{my past} 13:54, 6 December 2015 (UTC)

It is explained in the article: "If h is a number close to zero..." - DVdm (talk) 15:03, 6 December 2015 (UTC)

I think thecurran means "why do we call it h, particularly, and not some other letter?". I don't know the answer to that. If it turns out there's a known and sourceable explanation, do I think we should put it in the article? Maybe. I'd probably have to hear the explanation first. --Trovatore (talk) 20:40, 6 December 2015 (UTC)

When a fellow student asked why h was taken for Planck's constant, our prof said, because all other letters were already taken by that time. Perhaps it's the same in math: a, b, c, d were reserved for constants, e for the exponentials, f and g for functions (and gunctions ), and h was free. I have never seen a comment about it. - DVdm (talk) 21:10, 6 December 2015 (UTC)

The letter 'h' represents a simple exhalation of air, lesser than any of the other vocalizations that shape vowels or define consonants. It is used for Planck's constant because it's the smallest possible articulation of a meaningful utterance. Willondon (talk) 22:36, 6 December 2015 (UTC)

A glottal stop doesn't involve any air at all, but nobody uses the symbol ʔ for a variable. There may be other reasons for that, though. Ozob (talk) 23:52, 6 December 2015 (UTC)

The h used to be a delta x, but at some point someone decided that a two letter symbol might confuse students, and replaced it with h. I think Thomas was the first, at least the first I saw. I think the explanation "h was free" is as good as any. Rick Norwood (talk) 12:24, 7 December 2015 (UTC)

I'm not quite sure what you mean by "used to". This article used to have a Δx? Or authors used to use it? I'm not going to bother to check the history to see about the article. If you mean authors, I imagine that there are authors who still do — as far as I'm aware, there was no meeting held to decide what to do.

My personal take on the question is that using Δx is a suboptimal choice (and to keep this on topic, we should not use Δx in the article) because it invites learners to read too much into it. Δx can be read "the change in x", and in the indicated formula, it's true that it's the change in x. But that isn't necessary for understanding the formula; the formula itself does not ascribe any intensionality to the Δ symbol, or at least no such intensional reading is necessary. Therefore it's better to use a meaningless variable name like h, precisely because it's meaningless, to avoid giving the impression that the meaning is of the essence in the formula. --Trovatore (talk) 22:24, 7 December 2015 (UTC)