Talk:Archimedes/Archive 2
| This is an archive of past discussions about Archimedes. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 | Archive 2 | Archive 3 | Archive 4 |
New stuff about Archimedes and Calculus
http://www.sciencenews.org/articles/20071006/mathtrek.asp Gwen Gale 09:17, 8 October 2007 (UTC)
- Thanks, there are some good pictures in this article. --♦IanMacM♦ (talk to me) 09:28, 8 October 2007 (UTC)
In the opening paragraph there's a sentence that's probably spam, saying "for more information visit..." I can't believe it's in a featured article. Someone should clean that up. I'm viewing the page on Firefox and Archimedes' volume equations are coming up as errors (syntax). Is there a way to fix that?—Preceding unsigned comment added by 137.238.149.150 (talk) 01:28, 29 January 2008 (UTC)
It was fixed, may have just been a problem with the first load. —Preceding unsigned comment added by 137.238.149.150 (talk) 01:46, 29 January 2008 (UTC)
Unclear flash point relevancy
I commented out this text at the end of the penultimate paragraph of "Death ray", because I could discen no sense in it:
"However, the flash point of wood is around 300 degrees Celsius (572 degrees F), and this is hotter than the maximum temperature produced by domestic ovens."
This was reverted with a request to bring it to Talk. Is something preceeding missing that would give the However meaning? Also I still cannot see what the flash point nor domestic ovens has to do with the section. The sentence preceeding the However was "Critics of the MIT experiments have argued that the moisture content of the wood needs to be taken into consideration" so I was expecting something like "However, MIT used dry wood" (so contradicting the need for consideration). Finally I looked through the ref and it only supplies the flash point. -Wikianon 19:52, 19 October 2007 (UTC)
- The moisture content of wood affects its flash point, which is the temperature at which it bursts into flames. A piece of wood in a domestic oven on maximum temperature (usually 250 Celsius) would not catch fire. This is the most likely reason why the Mythbusters experiment failed, because it would take too long to get the wood to the flash point using the mirrors described. I'll have another look at the wording of this section, but do not think that it is particularly unclear. --♦IanMacM♦ (talk to me) 08:13, 20 October 2007 (UTC)
I see, and I don't see. The text makes no mention of any oven so a reader such as myself who is unaware of the Mythbusters experiment details will not understand. Even now I cannot make the connection - did MIT repeat the boat in the bay experiment using a boat in an oven? -Wikianon 01:30, 27 October 2007 (UTC)
- I have reworded the section and hopefully made it clearer. Wood does not catch fire until it reaches its flash point, and the comparison with an oven is given largely to show how hot wood needs to be before it will catch fire. --♦IanMacM♦ (talk to me) 07:34, 27 October 2007 (UTC)
- I didn't like the (reworded) oven reference either. Why is an oven mentioned? We all know that ovens get that hot, I don't think it's necessary to remind us. Tempshill (talk) 18:27, 29 January 2008 (UTC)
- Removed: ", and this is hotter than the maximum temperature produced by a domestic oven" Tempshill (talk) 18:39, 29 January 2008 (UTC)
a wonderful biography
I was astounded on the sheer volume of information that was provided in this article! I loved the fact the author added all of the mathematical info! That information is well beyond my ability! Thanks for a great article!Historybuffc13 (talk) 01:26, 29 January 2008 (UTC)
- I second that; great job to the chief editors here.--Pericles of AthensTalk 02:55, 29 January 2008 (UTC)
- Agreed, an excellent article on a topic of general notability. There should be more of it. -- Mattinbgn\talk 03:13, 29 January 2008 (UTC)
- Agreed. Yay for Archimedes, and boo for the "knife making guy" and "marching band of a college" featured articles. Tempshill (talk) 18:26, 29 January 2008 (UTC)
- Agreed, an excellent article on a topic of general notability. There should be more of it. -- Mattinbgn\talk 03:13, 29 January 2008 (UTC)
- I second that; great job to the chief editors here.--Pericles of AthensTalk 02:55, 29 January 2008 (UTC)
Protection
Did somebody forget to semi-protect this before it went up on the front page? I think the vandalism that just happened is a great example of why front page articles need to be at least semi-protected before they go up.Skywalkert65b (talk) 06:21, 29 January 2008 (UTC)
- They usually don't protect them on purpose because more editors and potentially new wikipedia users are going to be editing it. It makes sense, more people would be checking it for vandalism too. It may very temporarily impair a "perfect image" for wikipedia but is it worth it, and is it really that spotless in the first place? --fs 11:01, 29 January 2008 (UTC)
- See Wikipedia:Main Page featured article protection for more information. The current guideline is only to semi-protect in extreme cases. Consensus is unclear, some users (like me) support protection, others do not. Puchiko (Talk-email) 22:13, 29 January 2008 (UTC)
Archimedes screw
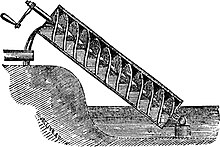
This article defines the 'Archimedes screw' as hand-driven. The article 'Archimedes screw' does not. Also it gives non-hand driven examples. I would like to change it here but I don't have any academic resources to back it up. I no one object I'll do it today. Pukkie (talk) 10:37, 29 January 2008 (UTC)
- In ancient times the screw would probably have been hand driven, and screws in developing countries are still operated like this today. However, modern screws are often driven by a motor. You can watch a video of a modern Archimedes screw here --♦IanMacM♦ (talk to me) 22:17, 30 January 2008 (UTC)
Reverts
I reverted the claim that the story about the sphere and cylinder on the tomb of Archimedes is a legend, as it is sourced to Cicero in the article. Also, I restored the quote from Gauss. Like many quotes from mathematicians, this lacks a direct source, but has often been quoted and is worth mentioning. --♦IanMacM♦ (talk to me) 08:11, 30 January 2008 (UTC)
- It's not the formal question of whether or not a link was given. Actually, if you care to read any standard source on history of mathematics, you'll find that the tomb story is a legend, and that the tomb was never found. Also, I did a bit of digging and found an attribution for the Gauss quote (it's not that hard; E.T. Bell, notoriously unreliable). My point was that the quote is a distraction: everyone agrees that Archimedes was the greatest scientist of the antiquity, this has never been in doubt. Gauss "endorsement" does not add anything there. On the contrary, it only raises more questions, for example, to state the most obvious, why Eisenstein occupies the third spot. Arcfrk (talk) 20:40, 30 January 2008 (UTC)
- Unless Cicero was inventing things, the story about the discovery of the tomb in 75BC is not a legend. [1] Unfortunately, many of the details of the life of Archimedes remain apocryphal by modern standards, but are given in the article so that people can find out what is usually said about his life and works.
I removed the comment about the Gauss quote because it is best to avoid adding HTML comments to Wikipedia articles, and to raise the matter on the talk page instead. If you have a direct source for the Gauss quote, please could you give it here. The Gauss quote has been in the article for a long time, and this is the first complaint. --♦IanMacM♦ (talk to me) 22:05, 30 January 2008 (UTC)
- Yes, Cicero might well have made up things, as was frequent with other writers of the period, e.g. Plutarch. To the best of my knowledge, the story that "At his [Archimedes'] request his tomb was carved with a sphere inscribed within a cylinder" has not been corraborated by other sources, and even Cicero speaks of it in a lot less certain terms that what's presently in the article.
- There two issues with the Gauss quote: first, and most important, is that it is not approprite, in my opinion. The fact that no "one complained before" is not a good argument for keeping it, or anything else on Wikipedia (e.g. many articles contain factually wrong statements for years), unless you want to permanently "lock" the article in its present state. (For what it's worth, I've read forceful complaints about this article's poor coverage of Archimedes' mathematical contributions. It is by no means perfect.) That sentence also doesn't fit with anything else in the lead, and it's not "what is usually said about his life and works". Second, the reason that I left an html comment in there is to simplify the sourcing task if it will be decided to keep it, the present source is below the lowest standard that can be imagined (a joculary comment in a hear-say format in a book review!) It appears from your comments and actions that you are not interested in improving the quality of the article, concentrating instead on creating hurdles for anyone else who is, or might be. I, on the other hand, only have limited time, and will concentrate on other projects. Arcfrk (talk) 22:59, 30 January 2008 (UTC)
There is an Error on his birth and death information
How did Archimedes become born 75 years after he died? AnaxMcShane (talk) 12:21, 30 January 2008 (UTC)
- It's BC. 287 BC is earlier than 212 BC. Just like -4 is more than -10. Puchiko (Talk-email) 14:32, 30 January 2008 (UTC)
I think you have it backwards, but no matter, backwards is correct too. 76.83.127.79 (talk) 18:50, 31 January 2008 (UTC)
- BC means before Christ so it is 287 years before Christ so therefore he did not die 75 years before he was born! 69.138.166.53 (talk) 23:35, 1 February 2008 (UTC)
Roman admiration for Archimedes?
Would anyone care to explain (and possibly, source) the following sentence in the lead:
- The historians of Ancient Rome showed a strong interest in Archimedes and wrote accounts of his life and works.
I am familiar with Plutarch's account of the siege of Syracuse, during which Archimedes installed terrible fear in Romans with his machines, and after which he was killed by a Roman soldier. Plutarch, however, was Greek. Historians of science wrote that "the works of Archimedes were not widely known in antiquity [except in Alexandria]". Who are these enlightened Romans, then? (Cicero?) There are many other similarly bold statements scattered throughout the article, including the lead. Since I was told that this article operates by the "complaint principle" (any changes not related to previously made complaints are reverted), I am going to complain. Arcfrk (talk) 00:48, 31 January 2008 (UTC)
Introduction of the article
The introduction has been through numerous versions in the past few months, and still seems to be attracting a lot of edits. According to WP:LEAD, the intro should summarise the article without going into too much detail. The current version aims to do this, and has maintained the previous material by making it more succinct and moving some of it elsewhere. --♦IanMacM♦ (talk to me) 12:55, 31 January 2008 (UTC)
- The aims are good, but if the introduction is as unstable as you are hinting, trying to lock it in may be premature. Longer articles can afford longer summaries. Often by adding just a few words, a vague and/or misleading claim can be transformed into an accurate statement. Obviously, editorial discretion is needed, but I disagree with some of your picks and think that quality and coherence, not "tradition" (whatever stayed the longest), should inform the decision. Arcfrk (talk) 16:53, 31 January 2008 (UTC)
Archimedes pop culture trivia
While Archimedes was Today's Featured Article (29 Jan 2008), the following nuggets of information were added:
- Archimedes appears in the Monty Python sketch International Philosophy. This is a spoof game of football between a team of German and Greek philosophers.
- In the film The Sword in the Stone, the name of Merlin's owl is Archimedes.
Both of these were reverted because they seemed to be trivia. What do other users think? --♦IanMacM♦ (talk to me) 20:12, 31 January 2008 (UTC)
- In the section that they were placed, they didn't fit. The Monty Python sketch for example, was placed in the legacy section. That doesn't seem like the correct place to put a comical reference to Archimedes. El Greco(talk) 21:44, 31 January 2008 (UTC)
- The IP user is very unwilling to discuss this at all. El Greco(talk) 22:23, 31 January 2008 (UTC)
- It is hard to discuss the history of Spam without mentioning the Monty Python sketch, but Archimedes plays only a small part in the sketch mentioned above. Also, apart from being called Archimedes, there is nothing particularly notable about the owl in The Sword and the Stone. So on balance, I think that the revert decisions were correct. --♦IanMacM♦ (talk to me) 08:38, 1 February 2008 (UTC
- ah but in greek mythology the owl is a sybol for being wise so they mean that archimedes is very wise that is why they chose the name for the owl69.138.166.53 (talk) 16:41, 24 February 2008 (UTC)
why is there such thing as the three edits only?
why are there the 3 edits only? i mean i need to make more changes but i'mm afraid to be booted from editing the article. 69.138.166.53 (talk) 23:45, 1 February 2008 (UTC)
- Three reverts only. A revert is sending the article back to a specific revision. Actually adding information is different from a revert, and there is no penalty, it is improving Wikipedia after all.--LWF (talk) 02:28, 2 February 2008 (UTC)
- For more information, see Wikipedia:Three-revert rule. For future reference, the best place to ask questions like this about using Wikipedia is the Wikipedia:Help desk. Since you seem to be new to Wikipedia, it may be helpful to read the Welcome page. --Lambiam 10:01, 2 February 2008 (UTC)
- thanks for helping and u above i am NOT NEW!69.138.166.53 (talk) 16:43, 24 February 2008 (UTC)
The Gauss quote
After being removed by User:Arcfrk, who objected strongly to its inclusion, the Gauss quote (as follows) was put back in the article by another user:
Carl Friedrich Gauss is said to have remarked that Archimedes was one of the three epoch-making mathematicians, with the others being Sir Isaac Newton and Ferdinand Eisenstein.
A couple of points here: I was unable to find a direct source for this quote, although Gauss has often been quoted as saying this. Also, some people might say that it is an example of WP:PEACOCK, although Archimedes needs few endorsements from Gauss or anyone else. If anyone has a direct source for this quote, could they add it to the article. Any other comments are welcome. --♦IanMacM♦ (talk to me) 09:06, 3 February 2008 (UTC)
- I removed the quote again as I agree with Arcfrk (the quote doesn't add to the article, the inclusion of Eisenstein distracts, it's dubious whether Gauss actually said this) and the IP editor did not give any reasons for reinstating the quote. -- Jitse Niesen (talk) 14:22, 3 February 2008 (UTC)
Error in the Sphere/Cylinder relationship discussed in the figure
There seems to be a mathematical error at two points in this article. Since I am new to Wikipedia, I thought I'd point it out and leave it to veterans to correct it. The surface area of the sphere and the cylinder are the same, so there is no factor of 2/3 involved in their relationship. The relationship is stated incorrectly in the caption of the figure, and in the section entitled `On the sphere and the cylinder'. The surface area of the sphere is correctly reported as . The latter section says the surface area of the circumscribing cylinder is , and below the figure it says "The sphere has 2/3 the surface area and volume of the circumscribing cylinder". I think what must be meant is "The sphere has 2/3 the volume, and the same surface area of the circumscribing cylinder" A simple argument is that the circumference of the circumscribing cylinder is , and its height is simply . So if you unroll it into a rectangle, its area is the product, . I hope someone can fix it so we don't have Archimedes giving blatantly absurd formulas. There is no other mathematician I find more impressive, and otherwise I find the article very informative. Bpalais (talk) 02:03, 5 February 2008 (UTC)
- There seems to be some confusion here about whether the cylinder is open or closed. Assuming that the cylinder is like a can of baked beans, it will have a lid at the top and the bottom. These will both have an area of , so when they are added to the area of the rolled out tube (), the total will be (example at [2]). Please could someone else comment on this. --♦IanMacM♦ (talk to me) 09:20, 5 February 2008 (UTC)
- That is correct. Does anyone know the ancient report on the (lost) inscription on the tombstone? --Lambiam 10:02, 5 February 2008 (UTC)
- The story about the tomb is sourced to Cicero, and can be found in English and the original Latin at [3]. Unfortunately, the exact wording of the inscription seems to be lost. --♦IanMacM♦ (talk to me) 10:19, 5 February 2008 (UTC)
- I am not sure that the previous version in Writings was incorrect, since it relied on the generally accepted definition of the surface area of a cylinder, which includes the area of the two lids (or congruent circular bases as they are formally known). Otherwise, you would be talking about the surface area of a tube rather than a cylinder. The current version in Writings is a bit long winded, and could probably go back to the previous version without too much potential for confusion. --♦IanMacM♦ (talk to me) 11:10, 5 February 2008 (UTC)
- At the time of writing, it seemed that the statement that Archimedes' cylinder has an area of was uncontroversial. The formal definition of a cylinder given at [4] is a space figure having two congruent circular bases that are parallel. Without the bases it would be a tube, so there is a risk of stating the obvious by including the information that the bases are included in the surface area. Archimedes' cylinder is a special case of the formula, since its two bases have an area exactly half of that of the connecting tube. --♦IanMacM♦ (talk to me) 16:06, 5 February 2008 (UTC)
- Thanks for the clarifications. I see this is correct with that interpretation of cylinder. Perhaps it would be helpful to note `including its bases' as I have seen elsewhere. Another current mathematical interpretation of the word cylinder that is consistent with other Wikipedia entries is a surface generated by parallel lines through some set, e.g., a `circular cylinder', `elliptical', `oblique' `square cylinder', etc. The `formal definition' above that I have never heard would exclude these and include any object however distorted as long as the ends were congruent, circular and parallel. The formulation with the closed circumscribing cylinder has the nice symmetry between the volume and surface area formulas, does give the area of the solid cylinder. The `open' finite cylinder formula has its own beauty too, and the reason I think of it that way is that it was the starting point of lectures by Sir Michael Atiyah several years ago on `area preserving geometry' (symplectic geometry) that became so important in mathematical physics. The amazing property is that not only the area of the open circumscribing cylinder and the sphere are the same, but the same is true for any subset of the sphere and the subset of the cylinder on which it projects! Archimedes knew this, as he gave formulas for the area of portions of the sphere between two parallel planes. This relation fails for the projection on the flat caps of course, and the lasting mathematical importance of the equality of spherical and cylindrical area is completely lost. Thanks again for clarifying the meaning! (Simon Donaldson also recalls Atiyah's talk entitled ”A generalisation of a theorem of Archimedes” in a paper called Geometry in Oxford 1980-1985 ) Bpalais (talk) 17:09, 5 February 2008 (UTC)
- After this issue was raised, it seemed like a good idea to see what Archimedes himself had to say about this. This can be done by looking at the complete works of Archimedes in English as translated by T.L. Heath, which can be downloaded in PDF form at [5]. Book One of On the Sphere and the Cylinder begins on page 191, while the key passage can be found on page 233:
| “ | From what has been proved it follows that every cylinder whose base is the greatest circle in a sphere and whose height is equal to the diameter of the sphere is 3/2 of the sphere, and its surface together with its bases is 3/2 of the surface of the sphere. | ” |
This shows that Archimedes considered the statement about the congruence between the volume and surface area to be at the heart of the theorem, and he uses the relationship 3/2 (2/3 is another way of expressing it).
A cylinder in geometry is usually considered to be a solid (like a sphere or cone), and several dictionary definitions that I consulted agreed with this. However, the word cylinder is also used to describe a hollow tube, notably when it describes the cylinder of an engine where fuel is burned. The wording on page 233 above includes the phrase its surface together with its bases to remove any ambiguity. --♦IanMacM♦ (talk to me) 20:00, 5 February 2008 (UTC)
That's very helpful. I agree that the `together with its bases' does assist the modern mathematician. It is interesting that Archimedes felt the coincidence of volume and surface area formulas was most interesting, while later mathematicians found the equality of spherical and cylindrical area (without the bases) was the only aspect that had far reaching and significant generalizations. I think the definition preference between solid vs. hollow cylinders was not at issue, just the definition of a cylinder as a space figure having two congruent circular bases that are parallel which can't be correct if it says nothing about what happens in between the bases. Thanks again. Bpalais (talk) 22:13, 5 February 2008 (UTC)
Archytas and the lever
I removed the statement that Archytas was the first person to describe the principle of the lever, mainly due to concerns about its reliability. We know even less about Archytas than we do about Archimedes, and again there is the problem of claims being made in Roman times long after his death. Some scholars argue that Aristotle's Mechanics is actually the work of Archytas, but nobody knows for sure. See also [6] for Marshall Clagett's view on this issue. Other comments welcome here. --♦IanMacM♦ (talk to me) 18:47, 17 February 2008 (UTC)
The lever
The replaced text sounds nonsensical: I am sure that people used the lever well before Archimedes came on the scene! What you probably mean is that he was one of the first to describe the principle of the lever, although recent scholarship seems to indicate that Archytas was the author of Mechanical Principles, and that theory should be mentioned at least. Presumably cave men were acquainted with levers, so Archimedes cannot be said to have invented the lever. Peterlewis (talk) 19:33, 17 February 2008 (UTC)
- The principle of the lever was almost certainly known well before Archimedes, even to the builders of Stonehenge. The question of who gave the first mathematical description is harder to answer, and the claim that it was Archytas is at best vague, as Marshall Clagett explains. There could be a compromise form of wording that brings in Archytas, but it should avoid weasel words, in view of the less than strong evidence of direct involvement by Archytas. --♦IanMacM♦ (talk to me) 19:48, 17 February 2008 (UTC)
Archimedes Movement
The reference to the Archimedes Movement seems to be non-notable and partly a promotional external link for the organization concerned. This should probably be removed, but other comments are welcome here. --♦IanMacM♦ (talk to me) 07:03, 24 April 2008 (UTC)
- The search term ["archimedes movement"] gets a respectable number of Google hits, and some local (Oregonian) news coverage. I can't quite judge which side of the edge its notability would land. The account that added this was not created for the purpose, this is the only edit from that account of this nature, and according to Special:Linksearch this is the only EL from Wikipedia to he organization's website. This does not have the look and feel of egregious linkspamming. --Lambiam 21:23, 26 April 2008 (UTC)
- I held off removing this because it was clearly added in good faith. The main concern was notability. As with the reference to Archimedes the owl in The Sword in the Stone, it is indirect and has nothing to do with mathematics or science. Also, since Wikipedia is read by people all over the world, access to health care in Oregon might not be all that interesting. The link is not linkspam but I still have concerns about whether the mention reaches the threshold of notability required for a Wikipedia article. --♦IanMacM♦ (talk to me) 06:01, 27 April 2008 (UTC)
- I do not like the idea to present a person out of context in a holy way. Archimdes archived a lot because he been wise, but he read and learned from his predecessors. (Tales23 (talk) 05:23, 12 January 2009 (UTC))
(O)stomachion
Things are getting a bit confused with the way that the article describes the origins of this word. The Archimedes Palimpsest spells the word as Stomachion, suggesting a link with the Greek word for stomach, although it has also been suggested that the actual meaning was based on the Greek words for "bone fight", making the correct spelling Ostomachion. Professor Chris Rorres gives the stomach explanation at [7] while the Early Puzzles website at [8] prefers the bone fight explanation. Due to the obscure nature of the word's origins, the article should avoid saying that one particular explanation is guaranteed to be the correct one. Also, the article currently says that the Greek word for throat is στόμαχος. Is this correct, since the standard Greek word for throat is λαιμός (laimos)? The article has run into issues with the Greek translations before, and this seems to be another example. --♦IanMacM♦ (talk to me) 06:52, 9 May 2008 (UTC)
- The present information that στομάχι is "the Greek word for stomach" is anachronistic: this is a Modern Greek word. Archimedes did not write in Modern Greek. In classical Greek στόμαχος means throat, gullet, or esophagus. Since this is a side issue I only gave the first meaning. When I put that in I gave a reference, A Greek-English Lexicon (LSJ), which is an authoritative source. The same information can be found in the Online Etymology Dictionary: [9]. LSJ also has an entry for ostomachion, and gives as its meaning: "a game played with fourteen pieces of bone". There can be no doubt that this is the same game that the manuscripts refer to as "stomachion". --Lambiam 23:24, 17 May 2008 (UTC)
- The origin of the game's name is obscure, since there are various ancient texts describing the game [10]. This link gives both spellings as follows:
Αρχιμήδους <Ὀ>στομάχιον (source: Greek palimpsest, from the Cloister of Saint Sabba [= Mar Saba], Jerusalem, then at Metochion of the Holy Sepulchre, Constantinopole, 1899 - The text is in Heiberg's edition of Archimedes, Opera, 2nd ed., Teubner, Leipzig, 1913, vol. II, pp. 415-424):
- The origin of the game's name is obscure, since there are various ancient texts describing the game [10]. This link gives both spellings as follows:
It is quite possible that the name was written wrongly by a monk or scribe at some stage, and the article should give both versions of the name so that readers can see how the difference arises. --♦IanMacM♦ (talk to me) 08:14, 18 May 2008 (UTC)
- I simply don't agree that "The origin of the puzzle's name is unclear". It is obvious that the Greeks called this game "bone game" because it was a game played with pieces of bone. The only thing that is not clear is why the initial letter "ο" was dropped in the manuscripts. --Lambiam 01:41, 21 May 2008 (UTC)
- The lexicon is citing the preface of Ausonius, Opusc. XVII, for this word. You can read the passage (Latin and English). See the Loeb, vol. 1 (PDF here), p. 374, and the discussion in an appendix (p. 395). But despite the fact that the Loeb and other editions print ostomachion, the codex Tilianus and editio princeps of Ausonius both have stomachion (see H.J. Rose 1956: he seems quite unconfusedly confident that the "true reading" is sans o-). Ostomachion may thus be modern editors' lectio facilior or Ausonius' rationalization of a strange name. Unless we can find a truly scholarly discussion (not math professors, obviously) of more recent vintage, we should give full representation to the possibility that the original title is the harder one to understand. Wareh (talk) 03:18, 21 May 2008 (UTC)
- I can freely admit to not being an expert on the Ancient Greek language. The article tries to give an accurate summary of the sources that were consulted, and after doing this it was apparent that there was no consensus on the "correct" spelling of the word. Further comments here are welcome. --♦IanMacM♦ (talk to me) 07:12, 21 May 2008 (UTC)
Archimedes Death Ray - Myth or Reality?
Added info to the opposition, requires sources.
Why the Death Ray Mirror is a myth, and why the Heat/Light Ray Mirror might have existed but still is impractical
- 1. Setting fire to something 100 feet away is exponentially more difficult than setting something on fire 10 inches away. Even if it was a giant parabolic mirror and not 1000 soldiers holding mirrors, you need progressively bigger and more precise parabolic mirrors to set something farther away on fire. And it's extremely difficult to create large parabolic mirrors even with modern technology. Furthermore, mirrors (and bronze metal) in the ancient world were extremely EXPENSIVE. Building catapults and ballistas would've been a far more efficient use of resources.
- 2. MIT and other groups have succeeded in setting fire to a ship by having a huge complex array of mirrors aiming at a single point in the wooden ship - made possible because the ship was stationary and at a "close distance."
- 3. The problem is a fleet has more than 1 ship, and it doesn't remain stationary in the water waiting for a parabolic mirror or 1000 soldiers with mirrors to set them on fire. The ship wouldn't be defenseless either.
- 4. Even if a single Roman ship kindly stood still for the mirrors to set them on fire, it'd take 10 minutes for each ship. By the time you set one or two ships on fire, the rest of the ships would've conquered half the city.
- 5. Even if they used mirrors to blind an enemy - like the Mythbusters stated, Syracuse faces east, meaning they would only have the sunrise as a time slot to use the mirrors effectively. Also, this mirror device is easily be defeated by clouds/bad weather. Furthermore, as a weapon that reflects light, they would have to shine the light accurately and directly onto the sailors on the decks of the ship, and could only do this one at a time...and the sailors could just as easily not look directly into the light.
- 6. Last but not least, historians of his time never mentioned anything about mirrors/lense weapons. This polished shield story was made up by people HUNDREDS of years after the event. I believe the Mythbusters stated this myth was first mentioned over 800 years after the actual event occurred.
Archimedes death ray myth, invented hundreds of years after the event. Here's a logical analysis: We can have ballistas or catapults that can hurl deadly flaming pots from a quarter mile away or archers that can launch thousands of flaming arrows from 1000 feet away. Instead let's spend all our time and money building an expensive mirror/lens contraption that might not work, will slowly kill one enemy at a time, only has a range of 100 feet, and only works if the enemy kindly stands still for us.
Also, MIT trial results: http://web.mit.edu/2.009/www/experiments/deathray/10_ArchimedesResult.html
Intranetusa (talk) 22:10, 12 May 2008 (UTC)
- The article tries to be fair to both sides of the argument, and avoids saying outright that the heat ray was a myth. There is a tendency in some quarters to concentrate excessively on the MythBusters episode about the heat ray, and to ignore the result of the Sakkas experiment in 1973. The claim about the heat ray appears in Roman times and has always been controversial, but may have some underlying truth. As mentioned before, the device (if built) may have been intended to temporarily blind or frighten the attacking Romans rather than to set the ships on fire. It is clear that it would have been difficult for the mirrors to have enough power to set a ship on fire at a distance of 100 feet, due to the inverse-square law of light propagation. This means that the amount of light received at a given point falls off with the square of the distance. Even a large parabolic reflector would have difficulty in creating a powerful point of focus 100 feet away, so it is understandable that doubts have been expressed about the viability of the heat ray. However, due to the fog of war and possible exaggerations during the retelling of the tale, it is not possible to rule out the story as entirely false. --♦IanMacM♦ (talk to me) 07:20, 13 May 2008 (UTC)
- I do not know whether it is a myth or not, but I have strong doubts of using the TV show "MythBusters" as a reliable source! And yes I have watched the episode! I would recommend either remove it or at least make a simple note or footnote. Here are images and the conclusions from the MIT group here and here. In both cases the final conclusion was inconclusive. A.Cython (talk) 15:17, 10 June 2008 (UTC)
- The experiment that MIT carried out for MythBusters was fair and well designed, so it is worth a mention in the article (if it were removed from the article, someone would only put it back). By mentioning the MythBusters experiment from 2005 and the Sakkas experiment from 1973 in the article and giving external links, people have both sides of the argument and can make up their own minds. --♦IanMacM♦ (talk to me) 17:19, 10 June 2008 (UTC)
- Still, (without me wanting to cause a problem) I think we should focus more on the MIT team rather than on the TV show... that is my two cents A.Cython (talk) 20:40, 10 June 2008 (UTC)
Heron's Formula
Some confusion has arisen over the citation. Abū Rayhān al-Bīrūnī was an 11th century Iranian scholar, while the reference to an Arab scholar with a similar name comes from [11]. Some clarification is needed here. --♦IanMacM♦ (talk to me) 09:32, 22 June 2008 (UTC)
- What is the issue? Whether the designation Abu'l Raihan Muhammed al-Biruni (also used at MathWorld, with citations) refers to the same person as Abū Rayḥān Muḥammad ibn Aḥmad al-Bīrūnī? See e.g. here and here. What is interesting is that according to Morris Kline (1972), Mathematical Thought from Ancient to Modern Times Volume 1, pp. 116–117, Heron himself credits the formula to Archimedes. --Lambiam 15:21, 27 June 2008 (UTC)
- The article was edited to avoid the possibility of confusion or inaccuracy. During the period that Archimedes was a Featured Article Candidate last year, someone objected to the use of MathWorld as a reliable source. This may or may not be fair, but as a Featured Article the citations should be from primary sources wherever possible. I have not seen the Morris Kline quote, but if it is from a book that you have read in the original version, it could be added to the article as a citation. --♦IanMacM♦ (talk to me) 19:50, 27 June 2008 (UTC)
- I see I misread the statement; Kline just states – without revealing a source for his knowledge – that the formula credited to Heron is actually due to Archimedes. The passage can be read online here. --Lambiam 07:31, 2 July 2008 (UTC)
Archimedes Movement
The reference to the Archimedes Movement seems to be non-notable and partly a promotional external link for the organization concerned. This should probably be removed, but other comments are welcome here. --♦IanMacM♦ (talk to me) 07:03, 24 April 2008 (UTC)
- The search term ["archimedes movement"] gets a respectable number of Google hits, and some local (Oregonian) news coverage. I can't quite judge which side of the edge its notability would land. The account that added this was not created for the purpose, this is the only edit from that account of this nature, and according to Special:Linksearch this is the only EL from Wikipedia to he organization's website. This does not have the look and feel of egregious linkspamming. --Lambiam 21:23, 26 April 2008 (UTC)
- I held off removing this because it was clearly added in good faith. The main concern was notability. As with the reference to Archimedes the owl in The Sword in the Stone, it is indirect and has nothing to do with mathematics or science. Also, since Wikipedia is read by people all over the world, access to health care in Oregon might not be all that interesting. The link is not linkspam but I still have concerns about whether the mention reaches the threshold of notability required for a Wikipedia article. --♦IanMacM♦ (talk to me) 06:01, 27 April 2008 (UTC)
(O)stomachion
Things are getting a bit confused with the way that the article describes the origins of this word. The Archimedes Palimpsest spells the word as Stomachion, suggesting a link with the Greek word for stomach, although it has also been suggested that the actual meaning was based on the Greek words for "bone fight", making the correct spelling Ostomachion. Professor Chris Rorres gives the stomach explanation at [12] while the Early Puzzles website at [13] prefers the bone fight explanation. Due to the obscure nature of the word's origins, the article should avoid saying that one particular explanation is guaranteed to be the correct one. Also, the article currently says that the Greek word for throat is στόμαχος. Is this correct, since the standard Greek word for throat is λαιμός (laimos)? The article has run into issues with the Greek translations before, and this seems to be another example. --♦IanMacM♦ (talk to me) 06:52, 9 May 2008 (UTC)
- The present information that στομάχι is "the Greek word for stomach" is anachronistic: this is a Modern Greek word. Archimedes did not write in Modern Greek. In classical Greek στόμαχος means throat, gullet, or esophagus. Since this is a side issue I only gave the first meaning. When I put that in I gave a reference, A Greek-English Lexicon (LSJ), which is an authoritative source. The same information can be found in the Online Etymology Dictionary: [14]. LSJ also has an entry for ostomachion, and gives as its meaning: "a game played with fourteen pieces of bone". There can be no doubt that this is the same game that the manuscripts refer to as "stomachion". --Lambiam 23:24, 17 May 2008 (UTC)
- The origin of the game's name is obscure, since there are various ancient texts describing the game [15]. This link gives both spellings as follows:
Αρχιμήδους <Ὀ>στομάχιον (source: Greek palimpsest, from the Cloister of Saint Sabba [= Mar Saba], Jerusalem, then at Metochion of the Holy Sepulchre, Constantinopole, 1899 - The text is in Heiberg's edition of Archimedes, Opera, 2nd ed., Teubner, Leipzig, 1913, vol. II, pp. 415-424):
- The origin of the game's name is obscure, since there are various ancient texts describing the game [15]. This link gives both spellings as follows:
It is quite possible that the name was written wrongly by a monk or scribe at some stage, and the article should give both versions of the name so that readers can see how the difference arises. --♦IanMacM♦ (talk to me) 08:14, 18 May 2008 (UTC)
- I simply don't agree that "The origin of the puzzle's name is unclear". It is obvious that the Greeks called this game "bone game" because it was a game played with pieces of bone. The only thing that is not clear is why the initial letter "ο" was dropped in the manuscripts. --Lambiam 01:41, 21 May 2008 (UTC)
- The lexicon is citing the preface of Ausonius, Opusc. XVII, for this word. You can read the passage (Latin and English). See the Loeb, vol. 1 (PDF here), p. 374, and the discussion in an appendix (p. 395). But despite the fact that the Loeb and other editions print ostomachion, the codex Tilianus and editio princeps of Ausonius both have stomachion (see H.J. Rose 1956: he seems quite unconfusedly confident that the "true reading" is sans o-). Ostomachion may thus be modern editors' lectio facilior or Ausonius' rationalization of a strange name. Unless we can find a truly scholarly discussion (not math professors, obviously) of more recent vintage, we should give full representation to the possibility that the original title is the harder one to understand. Wareh (talk) 03:18, 21 May 2008 (UTC)
- I can freely admit to not being an expert on the Ancient Greek language. The article tries to give an accurate summary of the sources that were consulted, and after doing this it was apparent that there was no consensus on the "correct" spelling of the word. Further comments here are welcome. --♦IanMacM♦ (talk to me) 07:12, 21 May 2008 (UTC)
Archimedes Death Ray - Myth or Reality?
Added info to the opposition, requires sources.
Why the Death Ray Mirror is a myth, and why the Heat/Light Ray Mirror might have existed but still is impractical
- 1. Setting fire to something 100 feet away is exponentially more difficult than setting something on fire 10 inches away. Even if it was a giant parabolic mirror and not 1000 soldiers holding mirrors, you need progressively bigger and more precise parabolic mirrors to set something farther away on fire. And it's extremely difficult to create large parabolic mirrors even with modern technology. Furthermore, mirrors (and bronze metal) in the ancient world were extremely EXPENSIVE. Building catapults and ballistas would've been a far more efficient use of resources.
- 2. MIT and other groups have succeeded in setting fire to a ship by having a huge complex array of mirrors aiming at a single point in the wooden ship - made possible because the ship was stationary and at a "close distance."
- 3. The problem is a fleet has more than 1 ship, and it doesn't remain stationary in the water waiting for a parabolic mirror or 1000 soldiers with mirrors to set them on fire. The ship wouldn't be defenseless either.
- 4. Even if a single Roman ship kindly stood still for the mirrors to set them on fire, it'd take 10 minutes for each ship. By the time you set one or two ships on fire, the rest of the ships would've conquered half the city.
- 5. Even if they used mirrors to blind an enemy - like the Mythbusters stated, Syracuse faces east, meaning they would only have the sunrise as a time slot to use the mirrors effectively. Also, this mirror device is easily be defeated by clouds/bad weather. Furthermore, as a weapon that reflects light, they would have to shine the light accurately and directly onto the sailors on the decks of the ship, and could only do this one at a time...and the sailors could just as easily not look directly into the light.
- 6. Last but not least, historians of his time never mentioned anything about mirrors/lense weapons. This polished shield story was made up by people HUNDREDS of years after the event. I believe the Mythbusters stated this myth was first mentioned over 800 years after the actual event occurred.
Archimedes death ray myth, invented hundreds of years after the event. Here's a logical analysis: We can have ballistas or catapults that can hurl deadly flaming pots from a quarter mile away or archers that can launch thousands of flaming arrows from 1000 feet away. Instead let's spend all our time and money building an expensive mirror/lens contraption that might not work, will slowly kill one enemy at a time, only has a range of 100 feet, and only works if the enemy kindly stands still for us.
Also, MIT trial results: http://web.mit.edu/2.009/www/experiments/deathray/10_ArchimedesResult.html
Intranetusa (talk) 22:10, 12 May 2008 (UTC)
- The article tries to be fair to both sides of the argument, and avoids saying outright that the heat ray was a myth. There is a tendency in some quarters to concentrate excessively on the MythBusters episode about the heat ray, and to ignore the result of the Sakkas experiment in 1973. The claim about the heat ray appears in Roman times and has always been controversial, but may have some underlying truth. As mentioned before, the device (if built) may have been intended to temporarily blind or frighten the attacking Romans rather than to set the ships on fire. It is clear that it would have been difficult for the mirrors to have enough power to set a ship on fire at a distance of 100 feet, due to the inverse-square law of light propagation. This means that the amount of light received at a given point falls off with the square of the distance. Even a large parabolic reflector would have difficulty in creating a powerful point of focus 100 feet away, so it is understandable that doubts have been expressed about the viability of the heat ray. However, due to the fog of war and possible exaggerations during the retelling of the tale, it is not possible to rule out the story as entirely false. --♦IanMacM♦ (talk to me) 07:20, 13 May 2008 (UTC)
- I do not know whether it is a myth or not, but I have strong doubts of using the TV show "MythBusters" as a reliable source! And yes I have watched the episode! I would recommend either remove it or at least make a simple note or footnote. Here are images and the conclusions from the MIT group here and here. In both cases the final conclusion was inconclusive. A.Cython (talk) 15:17, 10 June 2008 (UTC)
- The experiment that MIT carried out for MythBusters was fair and well designed, so it is worth a mention in the article (if it were removed from the article, someone would only put it back). By mentioning the MythBusters experiment from 2005 and the Sakkas experiment from 1973 in the article and giving external links, people have both sides of the argument and can make up their own minds. --♦IanMacM♦ (talk to me) 17:19, 10 June 2008 (UTC)
- Still, (without me wanting to cause a problem) I think we should focus more on the MIT team rather than on the TV show... that is my two cents A.Cython (talk) 20:40, 10 June 2008 (UTC)
Heron's Formula
Some confusion has arisen over the citation. Abū Rayhān al-Bīrūnī was an 11th century Iranian scholar, while the reference to an Arab scholar with a similar name comes from [16]. Some clarification is needed here. --♦IanMacM♦ (talk to me) 09:32, 22 June 2008 (UTC)
- What is the issue? Whether the designation Abu'l Raihan Muhammed al-Biruni (also used at MathWorld, with citations) refers to the same person as Abū Rayḥān Muḥammad ibn Aḥmad al-Bīrūnī? See e.g. here and here. What is interesting is that according to Morris Kline (1972), Mathematical Thought from Ancient to Modern Times Volume 1, pp. 116–117, Heron himself credits the formula to Archimedes. --Lambiam 15:21, 27 June 2008 (UTC)
- The article was edited to avoid the possibility of confusion or inaccuracy. During the period that Archimedes was a Featured Article Candidate last year, someone objected to the use of MathWorld as a reliable source. This may or may not be fair, but as a Featured Article the citations should be from primary sources wherever possible. I have not seen the Morris Kline quote, but if it is from a book that you have read in the original version, it could be added to the article as a citation. --♦IanMacM♦ (talk to me) 19:50, 27 June 2008 (UTC)
- I see I misread the statement; Kline just states – without revealing a source for his knowledge – that the formula credited to Heron is actually due to Archimedes. The passage can be read online here. --Lambiam 07:31, 2 July 2008 (UTC)
density formula
The density formula is mass divided by volume, not weight divided by volume. Weight and mass are 2 different things.Jlaskey (talk) 01:13, 8 October 2008 (UTC)
- This is strictly true, but if Archimedes did perform this experiment, he would have divided the measured weight of the crown by the volume of the water displaced. The wording in the article is not substantially incorrect, and there is a link to the article density given for more detailed information.--♦IanMacM♦ (talk to me) 08:03, 8 October 2008 (UTC)
Should we consider updating the Palimpsest section to be more historically interesting and significant?
According to Stephen Hawking in his book, God Created The Integers, he quotes Archimedes in the beginning of The Method as saying:
"For, though these properties were also naturally inherent in the figures all along, yet they were in fact unknown to all the many able geometers who lived before Eudoxus, and had not been observed by anyone. Now, however, it will be open to those who possess the requisite ability to examine these discoveries of mine."
Hawking goes on to say that, "Descartes, in fact, suspected Archimedes of suppressing The Method so that no one else would be able to benefit from it." (p. 123) This is really a testament to the type of character contained within the heart of Archimedes since, of course, he did not hold anything back from his fellow countrymen and mathematicians - neither proofs nor methods for discovering new theorems to be proven.
Carl Boyer in his book, A History of Mathematics, supports this quality in Archimedes (p. 136):
"The Method of Archimedes is of particular significance because it discloses for us a facet of Archimedes' thought that is not found elsewhere. His other treatises are gems of logical precision, with little hint of the preliminary analysis that may have led to the definitive formulations. So thoroughly without motivation did his proofs appear to some writers of the seventeenth century that they suspected Archimedes of having concealed his method of approach in order that his work might be admired the more. How unwarranted such an ungenerous estimate of the great Syracusan was became clear in 1906 with the discovery of the manuscript containing The Method. Here Archimedes had published, for all the world to read, a description of the preliminary "mechanical" investigations that had led to many of his chief mathematical discoveries."
In his final analysis, Hawking explains (p. 125), "The full title of this work, The Method of Archimedes Treating of Mechanical Problems, underscores Archimedes' view that the proofs contained in the works did not qualify as mathematical proofs. The proofs in The Method depend on physical assumptions about the figures involved and the principle of the lever, a mechanical principle!"
- If not an update to the importance of the Palimpsest being discovered, then at least to both the great character of Archimedes and the importance of The Method itself (describing the importance of the discovery, not just that it was discovered). What say you? Thanks, Andrew Turner [17] **
- God Created The Integers, Edited, with commentary, by Stephen Hawking, (c)2005 by Stephen Hawking, Running Press, Hardcover
- A History of Mathematics, Second Edition, by Carl Boyer, Revised by Uta C. Merzbach, (c) by 1991 John Wiley & Sons, Inc., Paperback —Preceding unsigned comment added by ThinkArchimedes (talk • contribs) 00:56, 12 October 2008 (UTC)
- All we know for sure about the Method is that it was lost to modern scholars until the Archimedes Palimpsest turned up in Constantinople in 1906. We know that it was available to the Greek Orthodox monks who copied it in the 10th Century AD, and it is reasonable to assume that it was available to the Arab mathematicians of medieval times (the palimpsest may have been translated from an Arabic version, as were a number of Archimedes' works.) The claim that Archimedes deliberately suppressed knowledge of the Method does not seem very plausible. It is more likely that the loss of the relatively few manuscripts of his work caused the Method to go missing. The article lists the other works by Archimedes known to be missing from references elsewhere. The main article for this area is Archimedes Palimpsest. The comments of Stephen Hawking and Carl Boyer are perhaps a personal analysis rather than encyclopedic content. The Method is important because it shows the line of reasoning that led to some of Archimedes' proofs, and the article could mention this in more detail. --♦IanMacM♦ (talk to me) 06:45, 12 October 2008 (UTC)
Archimedes Cattle problem
How about adding a link to http://wiki.riteme.site/wiki/Archimedes%27_cattle_problem in the "See Also Section"
68.12.62.107 (talk) 06:07, 15 October 2008 (UTC)
- Several of Archimedes' works have their own article, including Archimedes' cattle problem. This is wikilinked from within the article, so it is not really necessary to have it in the see also section as well. --♦IanMacM♦ (talk to me) 07:30, 15 October 2008 (UTC)
Shouldn't it be pointed out that Archimedes is probably not the author? It's not in his style or in his domains of interest, and it is mathematically trivial.Likebox (talk) 01:14, 27 December 2008 (UTC)
- This is a good point. Some doubts have been raised about whether the Cattle Problem really was invented by Archimedes, or whether it is another example of a later attribution. We may never know the answer to this question, but it could be added to the article if a WP:V source could be found questioning its origins. --♦IanMacM♦ (talk to me) 10:20, 28 December 2008 (UTC)
- After a look around the web, the best source that I could find was here. It describes the Cattle Problem as "generally attributed to Archimedes", which is about right. Nobody really knows, as it does not feature in works like the Archimedes Palimpsest. The Book of Lemmas (Liber Assumptorum) is usually regarded as having doubtful authorship by Archimedes in its current form, but the Cattle Problem is more of a mystery.--♦IanMacM♦ (talk to me) 12:14, 28 December 2008 (UTC)
Surviving Works: "On the Equilibrium of Planes"
The quoted text is not the Law of the Lever. It is in fact the first postulate that Archimedes uses in this text. The actual law of the lever should read "Two magnitudes, whether commensurable or incommensurable balance at distances reciprocally proportional to the magnitudes." This is taken from the same source that the current text is cited from.
Additionally, in the two volumes, Archimedes finds centers of gravity for triangles, parallelograms, and parabolas. He does not in any way address paraboloids or hemispheres. That fell to later mathematicians.
Linking to http://wiki.riteme.site/wiki/Principle_of_moments#Principle_of_Moments might also be useful as this is the modern generalization of the Law of the Lever.
- Thanks for your comments. The article has taken these suggestions on board. The text being referred to here is the Works of Archimedes in English by T. L. Heath (1897), which can be downloaded in PDF form at [18]. In Propositions 6 and 7 of Book I, Archimedes states: "Two magnitudes, whether commensurable or incommensurable balance at distances reciprocally proportional to the magnitudes." This seemed a bit hard to follow for the average reader, so a simpler modern version is given in the article. The suggestion of linking to torque has also been followed. --♦IanMacM♦ (talk to me) 10:53, 14 November 2008 (UTC)
On the Death Ray

This is ruining this article. I can't believe this was one of the featured articles. The death ray is missing so much information that logically disproves it had ever been made. I find it shameful that the death ray takes up so much of the page (almost more than the mathematics sections) while it is unimportant and false. Fix it somehow. Foozy101 (talk) 02:15, 14 March 2008 (UTC)
- It is hard to see the problem here. The wording of the "Death Ray" section points out that the claim about Archimedes and the death ray appears during Roman times and may be of doubtful authenticity. Nevertheless, it is described in the article due to the amount of historical interest that it has generated, including experiments to prove or disprove it. It is an exaggeration to say that MythBusters proved that the death ray was never built. The MIT experiment showed that it was unlikely that an array of mirrors would be powerful enough to have the effect described. The Sakkas experiment in 1973 [19] had a different result, which is given in the article as a counterbalance to the MythBusters experiment. If you have information that "logically disproves that it had ever been made", it can be added to the article. --♦IanMacM♦ (talk to me) 08:22, 14 March 2008 (UTC)
- I've been thinking that Jamie and Adam (mythbusters) got this all wrong. They tried to re-create the death-ray-by-mirrors myth, but isn't it more likely that the mirrors was used to blind the crew of the ship set on fire? I thought this was obvious when I first saw MB try to set a boat on fire and ended up busting the myth saying that it was more likely that they used other weapons (bow and arrow or catapults) to set the ships on fire. So why not keep the mirrors in the myth?
I read a book many years ago about anti-tank-warfare. 1. Stop the tank. The claim was that an antipersonellmine would disable the tracks enough to force it to stop. 2. Blind it. Using smoke grenades to stop the crew seeing you move outside the tank. 3. Blow it up. Stopped and blinded the tank would be an easy target for heavier explosives that would disable/destroy the tank for good. (Paraphrased from memory, the book was written in the 60s as soldiers manual. I'll try to dig up more references if needed.)
So, what's wrong with the combined mirrors/fire arrows theory? If your attacking a harbour with a ship, you wouldn't just sail in without expecting to be counter attacked by the defenders? You have soldiers ready to ward off attackers in boats, archers ready to take out archers on land with or without fire arrows and probably a crew of fire fighters just in case arrows hits the ship. A small fire team consisting of an archer, one or a small hand full of mirror operators and an assistant feeding lit arrows to the archer should be able to rain fire down on a ship if they can use the mirror to disable the ship's defensive archers? On the ship it would probably look as if the mirrors caused the fire. Obviously this could be configured in any number of ways, depending of availability of mirrors, archers and the coast line being defended. —Preceding unsigned comment added by 129.240.6.29 (talk) 22:11, 19 March 2008 (UTC)
- This is a reasonable point, and it has been suggested before that if it was ever built, the death ray acted as a non-lethal weapon. Temporarily blinding (or simply scaring) the enemy could have had the desired effect of repelling the attack. The idea is still used today, with weapons like the active denial system (BBC News story). There are also weapons that use beams of sound, known as sonic weaponry (USA Today news story). We may never know the truth of the death ray story, but it should not be ruled out entirely. --♦IanMacM♦ (talk to me) 07:42, 20 March 2008 (UTC)
- If I am correct (on the "ray" you are speaking of) it is believed by the manufacturers of educational video tapes (I do not recall the name of the specific one that discusses Archimedes) that he indeed made a "heat ray" that would make people feel uncomfortably hot (and, it leaves one to conclude that the subject on whitch the ray was aimed would believe her or she was about to burst into flames and die, despite the fact that this is simply not possible).
I would like to aplogise if I misunderstood what you were talking about, however changing it to "Heat Ray" may be a good idea. (It indeed could not kill anyone, but if you yelled "Do not invade us, we have a death ray" and made people feel very hot by shining light on them, it would indeed be thought of as a death ray.) --Abominable Toaster (talk) 04:17, 26 March 2008 (UTC)
- The title of the section has been changed to "Heat ray" (this matches the caption of the image in the section). The phrase "death ray" was used by MIT and MythBusters [20] but it is overdramatic because it is unlikely that the device would kill anyone, even if it did repel an attack successfully. --♦IanMacM♦ (talk to me)
11:57, 26 March 2008 (UTC)
- I added a link in the See also section to Diocles. As Gerald Toomer has pointed out, it is believed that Diocles showed that light striking a parabolic mirror would be reflected on to a focal point. This is similar to the idea behind the heat ray, and it is not out of the question that Archimedes could have built a similar device. By tradition, the Olympic flame is lit in Greece using a parabolic mirror. There is a photo of this on the website HowStuffWorks at [21]. The page says:
An actress dressed as a ceremonial priestess, in the robes of the ancient Greeks, lights the torch via the same technique used in the original Games. She uses a parabolic mirror to focus light rays from the sun. The parabolic mirror has a curved shape. When it is held toward the sun, the curvature focuses the rays to a single point. The energy from the sun creates a great deal of heat. The priestess holds a torch in the center of the parabolic mirror, and the heat ignites the fuel in the torch, sparking a flame.
This undoubtedly does work, since the torch is held close to the mirror bowl at the focal point. This is similar to the way that a solar barbecue works [22]. I have always wanted to own one of these to see how well it works on a cloudy day, and the one mentioned in the link costs US $250. --♦IanMacM♦ (talk to me) 16:15, 26 March 2008 (UTC)
When MythBusters broadcast the result of the San Francisco experiment in January 2006, the claim was placed in the category of "busted" (or failed) because of the length of time and the ideal weather conditions required for combustion to occur. It was also pointed out that since Syracuse faces the sea towards the east, the Roman fleet would have had to attack during the morning for optimal gathering of light by the mirrors.
Many of the posts above also seem to repeatedly talk about the Romans "attacking". Are we not talking about the Siege of Syracuse here? Who attacks during a siege. Maybe I have missed something, but would the Romans have not been blockading Syracuse and therefore have anchored their ships? If so, would not Archimedes have had all the time in the world to set their ships alight or at least burn holes in the hulls near the waterline? From the MIT article, the result seemed effective enough to disable or cripple a blockading navy. If the blockade could not be maintained, how could the siege be maintained? Perhaps the attack was carried out while the Romans were still sleeping off the previous night's spirits.
In any case, claiming this is a "busted myth" is incorrect to say the least. It is quite possible, although it would have taken a genius to manage. But how many great feats of history are precisely so?
LuYu (talk) 18:19, 15 April 2008 (UTC)
- This YouTube video is worth a look. It shows a parabolic reflector in action, and although setting a cardboard box on fire at a distance of twelve inches is not the same as setting a ship on fire at a distance of 100 feet, it does show that the basic principle works. --♦IanMacM♦ (talk to me) Also, this YouTube video is very silly but worth watching. It features Barbie and Ken recreating the death ray story. Not very scientific, but a measure of how well known the story is in popular culture. 13:28, 9 May 2008 (UTC)
If a person had access to one large parabolic mirror, I bet they had at least one smaller mirror. The geometry of a telescope allows to create a pencil of concentrated light that astronomers have used to light fires and break their equipment unintentionally. Ever been told that you need special filters to look at the sun? The density of the output power is related to the ratio of the larger to smaller focal lengths and the larger both mirrors are, the more light will be collected and transfered. It would be quite easy to design a method to allow safe and accurate targeting. Even better, since the light is concentrated into a beam, the energy drops off more linearly as the light passes through the air as opposed to the inverse square drop with the radial pattern from a single mirror system. 129.107.28.119 (talk) 19:19, 16 July 2008 (UTC)
ARCHIMEDES DEATH RAY
a concave metal lense acting as a mirror such as the one shown in the illustration will focus the heat of the sun into a concentrated beam. what the article has not yet mentioned is the use of glass combined with the metal to magnify the heat further still. we had been making glass for a long time before Archimedes and I am sure that he would have been aware of this. a series of these devices arranged around a simple lantern would provide a beacon that could act as a light-house at night. the proof of Archimedes death-ray is that such a device existed in Alexandria, the one which protected the port but was tragically turned upon the city itself during the revolt/sacking of Alexandria, which burnt the Great Library to the ground and lost us a thousand years of records including papyrus scrolls from egypt and texts from china as well as many other books gathered from all over the known world at the time.
- Most of the details of the Death Ray - including whether it was built at all - are speculative. The claims here would need to be referenced to a reliable published source. --♦IanMacM♦ (talk to me) 19:47, 6 September 2008 (UTC)
- DO not forget about the scenario, which was a 2 year siege scenario! So i do not know much about the population amount, but after 2 years of war, it is likly that the moral and military units been - little. Archimdes archived the first automatic defence weapon, run just with the renewable forces of nature.
- So think about it as a device which was stationery and passiv. They could be able to use thousands of them - reflecting diffrent angles! So if you see an approaching ship at the horizon, you have a defined corridor of angles. SO lets assume the ships apporaches the corridor, than we have a first phalanx of shilds focusing the start of the corridor - the way the ships have to approach very down till they reach the beach and here might bows add an outome aswell (mythbuster arguement) BUT attcking siege ships would have been prepared for arrows - so and it would be atsted as acrhers not anything related to machines or devices! So i herby debunk, Mythbuster.
- And i theorem this should be replicable with conventional burning glas on a small scale too!
- And than we DO know that the enemy king wanted Archimdes alive, so conclusion they had to fight 2 years because of Archimedes, and the soldier killed him because he was propably instructed todo so, there would not be such a lame soldier to guard the most valuable traget *which he made of himself, when starting useing high techologies - to defeat the barbars. (Tales23 (talk) 05:23, 12 January 2009 (UTC))
The mythbuster by MIT students was conducted in San Francisco. As a resident of San Francisco, I can attest that the conditions at most times include significant wind chill that even if you had a fire, it would be put out. The experiment was done at ambient temperature of 20 deg C. Were these conditions present during Roman times? Would the mythbuster experiment have yielded different results under 40 deg C summer weather, no wind chill and under dryer conditions in the Mediterranean? —Preceding unsigned comment added by Sb445 (talk • contribs) 21:16, 25 May 2009 (UTC)
Crown story
As many scholars have pointed out, it is next to impossible to accurately measure the volume of a small object like a crown by means of water displaced. Theoretically, it could work, but in practice it won't. The king wouldn't execute a goldsmith on the basis of shoddy evidence. Archimedes discovered the law of bouyancy, and considers it one of the great discoveries of his life. This is what this story is about. Bouyancy provides a precision test for the purity of the crown, with readily available instruments.Likebox (talk) 01:04, 27 December 2008 (UTC)
- The story about the golden crown is an popular anecdote rather than an "official" work by Archimedes. The article stresses this, unlike some biographies of Archimedes. Strictly speaking, the method used by Archimedes to determine the density of the crown has nothing to do with the principle of buoyancy as described in his works. It is also true that it would not be a very accurate method, and the one described by Chris Rorres here would have been more elegant and accurate. --♦IanMacM♦ (talk to me) 10:15, 28 December 2008 (UTC)
- Yes, I agree, but it unlike most anecdotes, this one is very likely to be true. I heard that the goldsmith got executed. There is also little doubt that Archimedes did what Rorres suggests, not what other secondary sources claim. So why not fix the anecdote here? I don't know what the primary sources say, but whatever, we know what he was thinking, and it has been published in many places (I don't even remember where I read it).Likebox (talk) 05:18, 29 December 2008 (UTC)
- It is far from certain that Archimedes did what Chris Rorres suggested, and implying that he did could be seen as original research not supported by the cited text. The primary source of the golden crown story is Vitruvius at [23] (section 9). Some versions of the story say that the king had the goldsmith executed on discovering the fraud, but Vitruvius does not. Like "do not disturb my circles", the golden crown story is attractive and believable, but needs to be approached as an anecdote rather than a verifiable fact. --♦IanMacM♦ (talk to me) 09:13, 29 December 2008 (UTC)
- It doesn't have to be OR. You can say it something like this "Vituvius says blah blah blah, but others (like Rorres) believe Archimedes did this (cite Rorres)". The reason I say it is likely is because it is more in Archimedes' style.
- There are other ways to make the measurement more accurate. For example, Archimedes could have also used a container with a lid which narrows to a very small tube to get an accurate comparison for the two volumes. With a narrow enough cross section, he could get a reasonably accurate volume comparison. But it just seems obvious to me that he did what Rorres suggested.Likebox (talk) 09:45, 29 December 2008 (UTC)
- "It just seems obvious to me" is not really a WP:V statement. Chris Rorres is acknowledged as the world's foremost authority on Archimedes, but his golden crown method is still speculative, just as proposed method for the heat ray at MIT is speculative. Chris Rorres at [24] stops short of implying that Archimedes actually did this, because it would not be supported by the published sources. However, his alternative method could be added to the external links section.--♦IanMacM♦ (talk to me) 09:58, 29 December 2008 (UTC)
(deindent) "It just seems obvious to me" is perfectly verifiable if it also seems obvious to somebody else who wrote a book. I didn't know Rorres was an authority on Archimedes, but it makes no difference. I read about the bouyancy test when I was little, and I don't believe it's original to Rorres. I don't remember where I read about it, but I'll try.Likebox (talk) 19:26, 29 December 2008 (UTC)
I read the Vituvius original--- it is much more detailed about this than I ever imagined! So the article should definitely say that Vituvius relays Archimedes measured volume, sorry for erasing that. But I agree that it is likely that the story is garbled, because Archimedes' work is all about bouyancy.Likebox (talk) 19:36, 29 December 2008 (UTC)
Yes but Archimedes never jumped out of his bath and shouted Eureka. That is the bit of the story that pisses me off. IT NEVER HAPPENED! Pythagoras was the first to say it after having discovered the Golden Triangle (3,4,5) Theorem. It links in with Gematria. —Preceding unsigned comment added by Styx6 (talk • contribs) 23:50, 18 February 2009 (UTC)
I have added an explanation of the "hydrostatic scale" to this section, as well as created an animated drawing demonstrating the method. Rorres includes Galileo's treatise on the subject (now cited in the article), where he says, "I think it probable that this method is the same that Archimedes followed, since, besides being very accurate, it is based on demonstrations found by Archimedes himself." (Translation as provided by Rorres.) —Tonyle (talk • contribs) 08:23, 24 March 2009 (UTC)
- This is an interesting area, because it shows how other people have attributed to Archimedes things that he may or may not have done. It is worth mentioning that Galileo considered this to be the method used by Archimedes, although there is an element of speculation. Strictly speaking, the Bilancetta idea is a piece of original research by Galileo, since it is quite different from the bath story as told by Vitruvius. The important thing for the article is that a reader does not get the impression that Archimedes actually did do this, since it is a departure from the "Eureka" story that is commonly told in conjunction with the Golden Crown.--♦IanMacM♦ (talk to me) 20:43, 24 March 2009 (UTC)
Checkers on Diagram
May I ask that somebody please remove the gray checkers on the full-version of the heat-ray diagram? They are annoying and make the diagram harder to see. Thanks. (If they are not removable, then please put the old bit-mapped version back.) —Preceding unsigned comment added by 4.231.173.207 (talk) 05:08, 15 February 2009 (UTC)
- The checkerboard does not appear in the thumbnail version in the article, only in the image page. SVG images can be scaled to different sizes, but there is nothing much wrong with the PNG version at [25]. Any objections to using this, or I will put back the PNG version?--♦IanMacM♦ (talk to me) 08:52, 15 February 2009 (UTC)
Archimedes death ray and Mythbusters
Since the TV show the Myth Busters is not a scientific show, I believe this reference needs to be deleted. Weather conditions in San Francisco do NOT mimick those commonly seen on the coast of Sicily. Anyone who has ever been to Sicily knows that cloudless and dry conditions are very common there unlike San Francisco. The results yielded by Sakkos in 1973 therefore validate Archimedes "death Ray" very accurately, meaning that the American TV show is far from the truth.
Again, this only allows the conclusion that the reference to the TV show must be deleted because its methods are flawed leading to the wrong conclusions.
Please take out the reference to MYTHBUSTERS because it is absolutely WRONG. 70.20.87.90 (talk) 05:11, 21 March 2009 (UTC)
- The article tries to achieve neutral point of view. The MythBusters experiment was conducted by a team from MIT and was well designed. It is hard to disagree with the basic conclusion of the MIT team that it would have been difficult to set a ship on fire under battle conditions, but the article also mentions the Sakkas experiment in 1973 (often overlooked today), which was more successful. The purpose of the section is to give both sides of the argument so that readers can make up their own minds, rather than to insist that a particular view is the "correct" one. Everything that is said about the "heat ray" contains an element of speculation, since there are no contemporary records to confirm that it was ever built.--♦IanMacM♦ (talk to me) 08:05, 21 March 2009 (UTC)
- To get off on a tangent a bit, I have been to Sicily and it rained every day. My fault for going during the rainy season. Sicily's climate is more like Los Angeles than San Francisco though.
- I do think it's appropriate to mention the MythBusters segment since many people are familiar with the show. The show does not follow accepted scientific standards, so I would be reluctant to use the show as a reference, as in "X is a myth because it said so on MythBusters." But I don't think there is a problem with having a statement like "X appeared as a segment on MythBusters and their verdict was Busted."--RDBury (talk) 18:26, 20 July 2009 (UTC)
Surviving Works: "On the Sphere and the Cylinder"
There seems to be a typo. "... and 4πr2 for the cylinder (including its two bases) ..." should read "... and 6πr2 for the cylinder (including its two bases) ..." This gives credence to the 2/3 statement in the next sentence. The surface area of the cylinder is "A = 2πrh + πr2 + πr2 = 2πr2r + 2πr2 = 6πr2" Yalitzot (talk) 04:14, 20 July 2009 (UTC)Yalitzot
- Thanks for pointing this out. There was a long argument about how to calculate the surface area of a cylinder some time back [26]. It is clear that the bases should be included for the 2/3 ratio to be valid.--♦IanMacM♦ (talk to me) 06:55, 20 July 2009 (UTC)
an ingenious system for expressing very large numbers
I'd like to see a cite on this topic. Or examples. Is it the exponential concept ? He was a physics and complex math person - I suspect - but want a verification on the topic.
Martin —Preceding unsigned comment added by 64.92.35.246 (talk) 18:38, 11 August 2009 (UTC)
- This is a reference to The Sand Reckoner. It does not have a source in the lead at the moment, but is discussed and sourced in its own section.--♦IanMacM♦ (talk to me) 18:46, 11 August 2009 (UTC)
Development of Pi value
If They were so concerned about the Pi value in Archimedes' day, why didn't they just closely approximate it (as they did) and then just put a notch in their instrument of measurement and indicate that that was the Pi value, in the same way as the notch they put in it to indicate the unit value. Or they could have talked about the Pi value as part of the plane geometry curriculum. After all who knows why the volume of a cone is 1/3 the volume of a cylinder if he doesn't know what Pi is?WFPM (talk) 22:13, 23 August 2009 (UTC)
But the fact that the volume of a cone is 1/3 the volume of a cylinder is independent of the value of pi is it not? Adrionwells (talk) 08:24, 7 November 2009 (UTC)
Infinitesimals
The article says that Archimedes used infinitesimals. That is misleading. He postulated that if x and y are unequal, then |x - y|n can be made indefinitely large by choosing n large enough. This implies that x = y if and only if |x -y| < 1/n for all integers n, and that rules out infinitesimals. This is the Archimedean property of the real numbers and it should be mentioned. —Preceding unsigned comment added by Adrionwells (talk • contribs) 08:52, 7 November 2009 (UTC)
Legacy section
Archimedes also lends his name to the Acorn range of computers by the same name, by way of the Eureka! story. Acorn's description at the time was that the creation of the machine was a Eureka moment, and that its users would experience similar moments when they realised the power of the machine and what they could do with it, hence the name choice. This information could do with adding to the article, along with a link to the relevant WP article. —Preceding unsigned comment added by WikiPhu (talk • contribs) 23:36, 24 January 2010 (UTC)
I've now added this. My post above took me over the 10-post mark, and allowed me to edit the semi-protected page. —Preceding unsigned comment added by WikiPhu (talk • contribs) 23:42, 24 January 2010 (UTC)
Archimedes and the Lever
The unsourced claim that Archimedes authored the first rigorous explanation of the principles of the lever is incorrect. A much better explanation appears in Aristotle's Mechanica, a work that predates Archimedes birth.
I recognize that there is controversy over who actually authored Mechanica, but that is irrelevant to the point at hand. It definitely contains a rigorous explanation of the lever, and it definitely was not authored by Archimedes.
I am therefore removing the incorrect claim, and adding a (sourced) statement re: the above. FellGleaming (talk) 03:59, 20 March 2010 (UTC)
- The wording on this issue has stood for a long time, partly because it avoids the use of black/white terms like correct/incorrect, which implies that there is a single "correct" view on the issue, and that others are "incorrect". Archimedes' role in the development of the lever is noted in the WP:LEAD as it is an important part of his work, and should not be removed in favour of stressing a much more poorly sourced claim attributed to Archytas. Marshall Clagett's view on this issue has been taken into account, as he is regarded as one of the key authorities on this subject. The article stresses that Archimedes did not invent the lever (neither did Archytas), and the wording points out that Archimedes gave a rigorous mathematical proof of the principle of the lever, rather than simply a mechanical description. The claims about the lever involving Archytas may have been made by later authors, whereas Archimedes' proof in On the Equilibrium of Planes is known to be part of his canonical work. The article should not give undue weight to the poorly sourced claims involving Archytas, although it is worth mentioning his role somewhere. This article is about the work of Archimedes, and his work should take precedence. There is a parallel with the steam engine, because it is sometimes said that Heron of Alexandria invented the steam engine, although his version is nothing like a modern steam engine. Claims that Person A was the first person to do something are always hard to source reliably, which is why the article should steer clear of doing this with the lever, particularly when there is a debate about when and how Mechanica was written.--♦IanMacM♦ (talk to me) 06:38, 20 March 2010 (UTC)
- None of the above has any bearing on my original complaints, or the original edit. The "wording which stood for a long time" incorrectly stated-- in black and white terms, without source or attribution -- that Archimedes was the first to rigorously describe the lever. Drawing a parallel between earlier incarnations of the steam engine are far off base; a lever is a lever. The lever described in Mechanica certainly was not "substantially different" from the ones conceived by Archimedes. Further, your focus on Archytas is irrelevant. It doesn't matter who authored Mechanica; what matters is that the text predates Archimedes, and thus giving him credit for the first definition of the lever is false.
- The new version of the text merely points out that Archimedes gave "a" description of the lever. That is both correct, and in context. FellGleaming (talk) 20:13, 20 March 2010 (UTC)
- The new wording looks at both sides of the argument, and it should mention the earlier works including the possible link with Archytas. What is interesting is that Chris Rorres and Marshall Clagett have taken different views on the importance of the earlier works. Clagett argues that Archimedes' work was more rigorous, while Rorres does not. With both sources, people can make up their own minds.--♦IanMacM♦ (talk to me) 20:39, 20 March 2010 (UTC)





