Specific potential energy

Specific potential energy
Specific potential energy
Common symbols	pe, or eu
SI unit	J/kg
In SI base units	m2/s2
Derivations from; other quantities	eu = g h

Specific potential energy is potential energy of an object per unit of mass of that object. In a gravitational field it is the acceleration of gravity times height, $e_{u}=gh$ .

Mathematical form

The gravitational potential V at a distance x from a point mass of mass M can be defined as the work W that needs to be done by an external agent to bring a unit mass in from infinity to that point:^[1]^[2]^[3]^[4]

$V(\mathbf {x} )={\frac {W}{m}}={\frac {1}{m}}\int _{\infty }^{x}\mathbf {F} \cdot d\mathbf {x} ={\frac {1}{m}}\int _{\infty }^{x}{\frac {GmM}{x^{2}}}dx=-{\frac {GM}{x}},$ where G is the gravitational constant, and F is the gravitational force. The product GM is the standard gravitational parameter and is often known to higher precision than G or M separately. The potential has units of energy per mass, e.g., J/kg in the MKS system. By convention, it is always negative where it is defined, and as x tends to infinity, it approaches zero.

The gravitational field, and thus the acceleration of a small body in the space around the massive object, is the negative gradient of the gravitational potential. Thus the negative of a negative gradient yields positive acceleration toward a massive object. Because the potential has no angular components, its gradient is $\mathbf {a} =-{\frac {GM}{x^{3}}}\mathbf {x} =-{\frac {GM}{x^{2}}}{\hat {\mathbf {x} }},$ where x is a vector of length x pointing from the point mass toward the small body and ${\hat {\mathbf {x} }}$ is a unit vector pointing from the point mass toward the small body. The magnitude of the acceleration therefore follows an inverse square law: $\|\mathbf {a} \|={\frac {GM}{x^{2}}}.$

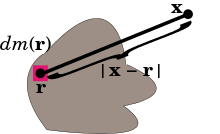
The potential associated with a mass distribution is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points x₁, ..., x_n and have masses m₁, ..., m_n, then the potential of the distribution at the point x is $V(\mathbf {x} )=\sum _{i=1}^{n}-{\frac {Gm_{i}}{\|\mathbf {x} -\mathbf {x} _{i}\|}}.$

If the mass distribution is given as a mass measure dm on three-dimensional Euclidean space R³, then the potential is the convolution of $- G /| r |$ with dm.^{[citation needed]} In good cases^{[clarification needed]} this equals the integral $V(\mathbf {x} )=-\int _{\mathbb {R} ^{3}}{\frac {G}{\|\mathbf {x} -\mathbf {r} \|}}\,dm(\mathbf {r} ),$ where $| x - r |$ is the distance between the points x and r. If there is a function ρ(r) representing the density of the distribution at r, so that $dm (r) = ρ (r) dv (r)$ , where dv(r) is the Euclidean volume element, then the gravitational potential is the volume integral $V(\mathbf {x} )=-\int _{\mathbb {R} ^{3}}{\frac {G}{\|\mathbf {x} -\mathbf {r} \|}}\,\rho (\mathbf {r} )dv(\mathbf {r} ).$

If V is a potential function coming from a continuous mass distribution ρ(r), then ρ can be recovered using the Laplace operator, $Δ$ : $\rho (\mathbf {x} )={\frac {1}{4\pi G}}\Delta V(\mathbf {x} ).$ This holds pointwise whenever ρ is continuous and is zero outside of a bounded set. In general, the mass measure dm can be recovered in the same way if the Laplace operator is taken in the sense of distributions. As a consequence, the gravitational potential satisfies Poisson's equation. See also Green's function for the three-variable Laplace equation and Newtonian potential.

The integral may be expressed in terms of known transcendental functions for all ellipsoidal shapes, including the symmetrical and degenerate ones.^[5] These include the sphere, where the three semi axes are equal; the oblate (see reference ellipsoid) and prolate spheroids, where two semi axes are equal; the degenerate ones where one semi axes is infinite (the elliptical and circular cylinder) and the unbounded sheet where two semi axes are infinite. All these shapes are widely used in the applications of the gravitational potential integral (apart from the constant G, with 𝜌 being a constant charge density) to electromagnetism.

References

^ Marion, J.B.; Thornton, S.T. (1995). Classical Dynamics of particles and systems (4th ed.). Harcourt Brace & Company. p. 192. ISBN 0-03-097302-3.
^ Arfken, George B.; Weber, Hans J. (2005). Mathematical Methods For Physicists International Student Edition (6th ed.). Academic Press. p. 72. ISBN 978-0-08-047069-6.
^ Sang, David; Jones, Graham; Chadha, Gurinder; Woodside, Richard; Stark, Will; Gill, Aidan (2014). Cambridge International AS and A Level Physics Coursebook (illustrated ed.). Cambridge University Press. p. 276. ISBN 978-1-107-69769-0.
^ Muncaster, Roger (1993). A-level Physics (illustrated ed.). Nelson Thornes. p. 106. ISBN 978-0-7487-1584-8.
^ MacMillan, W.D. (1958). The Theory of the Potential. Dover Press.

This physics-related article is a stub. You can help Wikipedia by expanding it.

[1] Marion, J.B.; Thornton, S.T. (1995). Classical Dynamics of particles and systems (4th ed.). Harcourt Brace & Company. p. 192. ISBN 0-03-097302-3.

[2] Arfken, George B.; Weber, Hans J. (2005). Mathematical Methods For Physicists International Student Edition (6th ed.). Academic Press. p. 72. ISBN 978-0-08-047069-6.

[3] Sang, David; Jones, Graham; Chadha, Gurinder; Woodside, Richard; Stark, Will; Gill, Aidan (2014). Cambridge International AS and A Level Physics Coursebook (illustrated ed.). Cambridge University Press. p. 276. ISBN 978-1-107-69769-0.

[4] Muncaster, Roger (1993). A-level Physics (illustrated ed.). Nelson Thornes. p. 106. ISBN 978-0-7487-1584-8.

[5] MacMillan, W.D. (1958). The Theory of the Potential. Dover Press.

[1]

[2]

[3]

[4]

[5]