B6 polytope
Appearance
(Redirected from List of B6 polytopes)
 6-cube |
 6-orthoplex |
 6-demicube |
In 6-dimensional geometry, there are 64 uniform polytopes with B6 symmetry. There are two regular forms, the 6-orthoplex, and 6-cube with 12 and 64 vertices respectively. The 6-demicube is added with half the symmetry.
They can be visualized as symmetric orthographic projections in Coxeter planes of the B6 Coxeter group, and other subgroups.
Graphs
[edit]Symmetric orthographic projections of these 64 polytopes can be made in the B6, B5, B4, B3, B2, A5, A3, Coxeter planes. Ak has [k+1] symmetry, and Bk has [2k] symmetry.
These 64 polytopes are each shown in these 8 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.
| # | Coxeter plane graphs | Coxeter-Dynkin diagram Schläfli symbol Names | ||||||
|---|---|---|---|---|---|---|---|---|
| B6 [12] |
B5 / D4 / A4 [10] |
B4 [8] |
B3 / A2 [6] |
B2 [4] |
A5 [6] |
A3 [4] | ||
| 1 |  |
 |
 |
 |
 |
 |
 |
{3,3,3,3,4} 6-orthoplex Hexacontatetrapeton (gee) |
| 2 |  |
 |
 |
 |
 |
 |
 |
t1{3,3,3,3,4} Rectified 6-orthoplex Rectified hexacontatetrapeton (rag) |
| 3 |  |
 |
 |
 |
 |
 |
 |
t2{3,3,3,3,4} Birectified 6-orthoplex Birectified hexacontatetrapeton (brag) |
| 4 |  |
 |
 |
 |
 |
 |
 |
t2{4,3,3,3,3} Birectified 6-cube Birectified hexeract (brox) |
| 5 |  |
 |
 |
 |
 |
 |
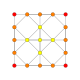 |
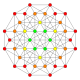
t1{4,3,3,3,3} Rectified 6-cube Rectified hexeract (rax) |
| 6 | 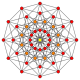 |
 |
 |
 |
 |
 |
 |
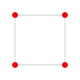
{4,3,3,3,3} 6-cube Hexeract (ax) |
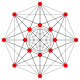
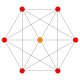
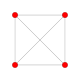
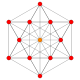
| 64 |  |
 |
 |
 |
 |
 |
|
h{4,3,3,3,3} 6-demicube Hemihexeract |
| 7 |  |
 |
 |
 |
 |
 |
 |
t0,1{3,3,3,3,4} Truncated 6-orthoplex Truncated hexacontatetrapeton (tag) |
| 8 |  |
 |
 |
 |
 |
 |
 |
t0,2{3,3,3,3,4} Cantellated 6-orthoplex Small rhombated hexacontatetrapeton (srog) |
| 9 |  |
 |
 |
 |
 |
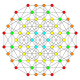 |
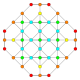 |
t1,2{3,3,3,3,4} Bitruncated 6-orthoplex Bitruncated hexacontatetrapeton (botag) |
| 10 |  |
 |
 |
 |
 |
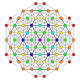 |
 |
t0,3{3,3,3,3,4} Runcinated 6-orthoplex Small prismated hexacontatetrapeton (spog) |
| 11 |  |
 |
 |
 |
 |
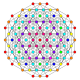 |
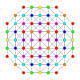 |
t1,3{3,3,3,3,4} Bicantellated 6-orthoplex Small birhombated hexacontatetrapeton (siborg) |
| 12 |  |
 |
 |
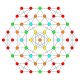 |
 |
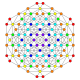 |
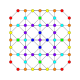 |
t2,3{4,3,3,3,3} Tritruncated 6-cube Hexeractihexacontitetrapeton (xog) |
| 13 |  |
 |
 |
 |
 |
 |
 |
t0,4{3,3,3,3,4} Stericated 6-orthoplex Small cellated hexacontatetrapeton (scag) |
| 14 |  |
 |
 |
 |
 |
 |
 |
t1,4{4,3,3,3,3} Biruncinated 6-cube Small biprismato-hexeractihexacontitetrapeton (sobpoxog) |
| 15 |  |
 |
 |
 |
 |
 |
 |
t1,3{4,3,3,3,3} Bicantellated 6-cube Small birhombated hexeract (saborx) |
| 16 |  |
 |
 |
 |
 |
 |
 |
t1,2{4,3,3,3,3} Bitruncated 6-cube Bitruncated hexeract (botox) |
| 17 |  |
 |
 |
 |
 |
 |
 |
t0,5{4,3,3,3,3} Pentellated 6-cube Small teri-hexeractihexacontitetrapeton (stoxog) |
| 18 |  |
 |
 |
 |
 |
 |
 |
t0,4{4,3,3,3,3} Stericated 6-cube Small cellated hexeract (scox) |
| 19 |  |
 |
 |
 |
 |
 |
 |
t0,3{4,3,3,3,3} Runcinated 6-cube Small prismated hexeract (spox) |
| 20 |  |
 |
 |
 |
 |
 |
 |
t0,2{4,3,3,3,3} Cantellated 6-cube Small rhombated hexeract (srox) |
| 21 |  |
 |
 |
 |
 |
 |
 |
t0,1{4,3,3,3,3} Truncated 6-cube Truncated hexeract (tox) |
| 22 |  |
 |
 |
 |
 |
 |
 |
t0,1,2{3,3,3,3,4} Cantitruncated 6-orthoplex Great rhombated hexacontatetrapeton (grog) |
| 23 |  |
 |
 |
 |
 |
 |
 |
t0,1,3{3,3,3,3,4} Runcitruncated 6-orthoplex Prismatotruncated hexacontatetrapeton (potag) |
| 24 |  |
 |
 |
 |
 |
 |
 |
t0,2,3{3,3,3,3,4} Runcicantellated 6-orthoplex Prismatorhombated hexacontatetrapeton (prog) |
| 25 |  |
 |
 |
 |
 |
 |
 |
t1,2,3{3,3,3,3,4} Bicantitruncated 6-orthoplex Great birhombated hexacontatetrapeton (gaborg) |
| 26 |  |
 |
 |
 |
 |
 |
 |
t0,1,4{3,3,3,3,4} Steritruncated 6-orthoplex Cellitruncated hexacontatetrapeton (catog) |
| 27 |  |
 |
 |
 |
 |
 |
 |
t0,2,4{3,3,3,3,4} Stericantellated 6-orthoplex Cellirhombated hexacontatetrapeton (crag) |
| 28 |  |
 |
 |
 |
 |
 |
 |
t1,2,4{3,3,3,3,4} Biruncitruncated 6-orthoplex Biprismatotruncated hexacontatetrapeton (boprax) |
| 29 |  |
 |
 |
 |
 |
 |
 |
t0,3,4{3,3,3,3,4} Steriruncinated 6-orthoplex Celliprismated hexacontatetrapeton (copog) |
| 30 |  |
 |
 |
 |
 |
 |
 |
t1,2,4{4,3,3,3,3} Biruncitruncated 6-cube Biprismatotruncated hexeract (boprag) |
| 31 |  |
 |
 |
 |
 |
 |
 |
t1,2,3{4,3,3,3,3} Bicantitruncated 6-cube Great birhombated hexeract (gaborx) |
| 32 |  |
 |
 |
 |
 |
 |
 |
t0,1,5{3,3,3,3,4} Pentitruncated 6-orthoplex Teritruncated hexacontatetrapeton (tacox) |
| 33 |  |
 |
 |
 |
 |
 |
 |
t0,2,5{3,3,3,3,4} Penticantellated 6-orthoplex Terirhombated hexacontatetrapeton (tapox) |
| 34 |  |
 |
 |
 |
 |
 |
 |
t0,3,4{4,3,3,3,3} Steriruncinated 6-cube Celliprismated hexeract (copox) |
| 35 |  |
 |
 |
 |
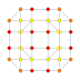 |
 |
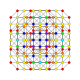 |
t0,2,5{4,3,3,3,3} Penticantellated 6-cube Terirhombated hexeract (topag) |
| 36 |  |
 |
 |
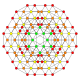 |
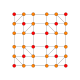 |
 |
 |
t0,2,4{4,3,3,3,3} Stericantellated 6-cube Cellirhombated hexeract (crax) |
| 37 |  |
 |
 |
 |
 |
 |
 |
t0,2,3{4,3,3,3,3} Runcicantellated 6-cube Prismatorhombated hexeract (prox) |
| 38 |  |
 |
 |
 |
 |
 |
 |
t0,1,5{4,3,3,3,3} Pentitruncated 6-cube Teritruncated hexeract (tacog) |
| 39 |  |
 |
 |
 |
 |
 |
 |
t0,1,4{4,3,3,3,3} Steritruncated 6-cube Cellitruncated hexeract (catax) |
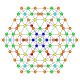
| 40 |  |
 |
 |
 |
 |
 |
 |
t0,1,3{4,3,3,3,3} Runcitruncated 6-cube Prismatotruncated hexeract (potax) |
| 41 |  |
 |
 |
 |
 |
 |
 |
t0,1,2{4,3,3,3,3} Cantitruncated 6-cube Great rhombated hexeract (grox) |
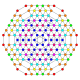
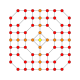
| 42 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3{3,3,3,3,4} Runcicantitruncated 6-orthoplex Great prismated hexacontatetrapeton (gopog) |
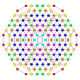
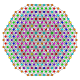
| 43 | 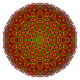 |
 |
 |
 |
 |
 |
 |
t0,1,2,4{3,3,3,3,4} Stericantitruncated 6-orthoplex Celligreatorhombated hexacontatetrapeton (cagorg) |
| 44 |  |
 |
 |
 |
 |
 |
 |
t0,1,3,4{3,3,3,3,4} Steriruncitruncated 6-orthoplex Celliprismatotruncated hexacontatetrapeton (captog) |
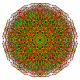
| 45 |  |
 |
 |
 |
 |
 |
 |
t0,2,3,4{3,3,3,3,4} Steriruncicantellated 6-orthoplex Celliprismatorhombated hexacontatetrapeton (coprag) |
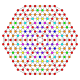
| 46 |  |
 |
 |
 |
 |
 |
 |
t1,2,3,4{4,3,3,3,3} Biruncicantitruncated 6-cube Great biprismato-hexeractihexacontitetrapeton (gobpoxog) |
| 47 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,5{3,3,3,3,4} Penticantitruncated 6-orthoplex Terigreatorhombated hexacontatetrapeton (togrig) |
| 48 |  |
 |
 |
 |
 |
 |
 |
t0,1,3,5{3,3,3,3,4} Pentiruncitruncated 6-orthoplex Teriprismatotruncated hexacontatetrapeton (tocrax) |
| 49 |  |
 |
 |
 |
 |
 |
 |
t0,2,3,5{4,3,3,3,3} Pentiruncicantellated 6-cube Teriprismatorhombi-hexeractihexacontitetrapeton (tiprixog) |
| 50 |  |
 |
 |
 |
 |
 |
 |
t0,2,3,4{4,3,3,3,3} Steriruncicantellated 6-cube Celliprismatorhombated hexeract (coprix) |
| 51 |  |
 |
 |
 |
 |
 |
 |
t0,1,4,5{4,3,3,3,3} Pentisteritruncated 6-cube Tericelli-hexeractihexacontitetrapeton (tactaxog) |
| 52 |  |
 |
 |
 |
 |
 |
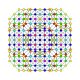 |
t0,1,3,5{4,3,3,3,3} Pentiruncitruncated 6-cube Teriprismatotruncated hexeract (tocrag) |
| 53 |  |
 |
 |
 |
 |
 |
 |
t0,1,3,4{4,3,3,3,3} Steriruncitruncated 6-cube Celliprismatotruncated hexeract (captix) |
| 54 |  |
 |
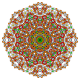 |
 |
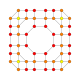 |
 |
 |
t0,1,2,5{4,3,3,3,3} Penticantitruncated 6-cube Terigreatorhombated hexeract (togrix) |
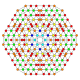
| 55 | 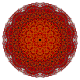 |
 |
 |
 |
 |
 |
 |
t0,1,2,4{4,3,3,3,3} Stericantitruncated 6-cube Celligreatorhombated hexeract (cagorx) |
| 56 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3{4,3,3,3,3} Runcicantitruncated 6-cube Great prismated hexeract (gippox) |
| 57 |  |
 |
 |
 |
 |
 |
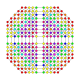 |
t0,1,2,3,4{3,3,3,3,4} Steriruncicantitruncated 6-orthoplex Great cellated hexacontatetrapeton (gocog) |
| 58 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,5{3,3,3,3,4} Pentiruncicantitruncated 6-orthoplex Terigreatoprismated hexacontatetrapeton (tagpog) |
| 59 |  |
 |
 |
 |
 |
 |
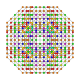 |
t0,1,2,4,5{3,3,3,3,4} Pentistericantitruncated 6-orthoplex Tericelligreatorhombated hexacontatetrapeton (tecagorg) |
| 60 |  |
 |
 |
 |
 |
 |
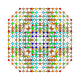 |
t0,1,2,4,5{4,3,3,3,3} Pentistericantitruncated 6-cube Tericelligreatorhombated hexeract (tocagrax) |
| 61 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,5{4,3,3,3,3} Pentiruncicantitruncated 6-cube Terigreatoprismated hexeract (tagpox) |
| 62 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,4{4,3,3,3,3} Steriruncicantitruncated 6-cube Great cellated hexeract (gocax) |
| 63 |  |
 |
 |
 |
 |
 |
 |
t0,1,2,3,4,5{4,3,3,3,3} Omnitruncated 6-cube Great teri-hexeractihexacontitetrapeton (gotaxog) |
References
[edit]- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Klitzing, Richard. "6D uniform polytopes (polypeta)".
