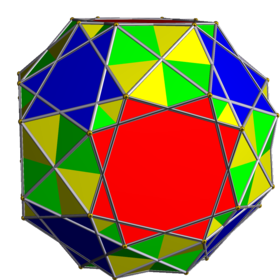
Compound of two snub cubes

Compound of two snub cubes
Type	Uniform compound
Index	UC68
Schläfli symbol	βr{4,3}
Coxeter diagram
Polyhedra	2 snub cubes
Faces	16+48 triangles 12 squares
Edges	120
Vertices	48
Symmetry group	octahedral (Oh)
Subgroup restricting to one constituent	chiral octahedral (O)

This uniform polyhedron compound is a composition of the 2 enantiomers of the snub cube. As a holosnub, it is represented by Schläfli symbol βr{4,3} and Coxeter diagram .

The vertex arrangement of this compound is shared by a convex nonuniform truncated cuboctahedron, having rectangular faces, alongside irregular hexagons and octagons, each alternating with two edge lengths.

Together with its convex hull, it represents the snub cube-first projection of the nonuniform snub cubic antiprism.

Cartesian coordinates

Cartesian coordinates for the vertices are all the permutations of

(±1, ±ξ, ±1/ξ)

where ξ is the real solution to

$\xi ^{3}+\xi ^{2}+\xi =1,\,$

which can be written

$\xi ={\frac {1}{3}}\left({\sqrt[{3}]{17+3{\sqrt {33}}}}-{\sqrt[{3}]{-17+3{\sqrt {33}}}}-1\right)$

or approximately 0.543689. ξ is the reciprocal of the tribonacci constant.

Equally, the tribonacci constant, t, just like the snub cube, can compute the coordinates as:

(±1, ±t, ±⁠1/t⁠)

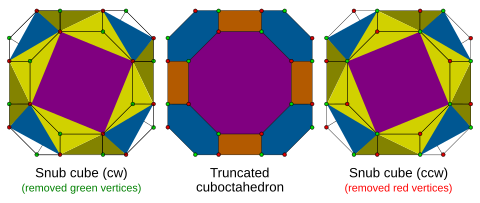
Truncated cuboctahedron

This compound can be seen as the union of the two chiral alternations of a truncated cuboctahedron:

A geometric construction of the Tribonacci constant (AC), with compass and marked ruler, according to the method described by Xerardo Neira.

See also

• Compound of two icosahedra
• Compound of two snub dodecahedra
• Snub (geometry)

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.