Color solid
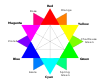
A color solid is the three-dimensional representation of a color space or model and can be thought as an analog of, for example, the one-dimensional color wheel, which depicts the variable of hue (similarity with red, yellow, green, blue, magenta, etc.); or the 2D chromaticity diagram (also known as color triangle), which depicts the variables of hue and spectral purity. The added spatial dimension allows a color solid to depict the three dimensions of color: lightness (gradations of light and dark, tints or shades), hue, and colorfulness, allowing the solid to depict all conceivable colors in an organized three-dimensional structure.
Organization
[edit]- Vertical cross sections of various spherically-shaped color solids
-
Philipp Otto Runge's Farbenkugel.
-
Albert Henry Munsell's color sphere.
-
Johannes Itten's color sphere.
-
Spherical coordinate system (for comparison).
Different color theorists have each designed unique color solids. Many are in the shape of a sphere, whereas others are warped three-dimensional ellipsoid figures—these variations being designed to express some aspect of the relationship of the colors more clearly. The color spheres conceived by Phillip Otto Runge and Johannes Itten are typical examples and prototypes for many other color solid schematics.[2]
As in the color wheel, contrasting (or complementary) hues are located opposite each other in most color solids. Moving toward the central axis, colors become less and less saturated, until all colors meet at the central axis as a neutral gray. Moving vertically in the color solid, colors become lighter (toward the top) and darker (toward the bottom). At the upper pole, all hues meet in white; at the bottom pole, all hues meet in black.
The vertical axis of the color solid, then, is gray all along its length, varying from black at the bottom to white at the top, it is a grayscale. All pure (saturated) hues are located on the surface of the solid, varying from light to dark down the color solid. All colors that are desaturated in any degree (that is, that they can be though of containing both black and white in varying amounts) comprise the solid's interior, likewise varying in brightness from top to bottom.
Optimal color solid
[edit]The optimal color solid or Rösch–MacAdam color solid is a type of color solid that contains all the possible colors that surfaces can have. That is, the optimal color solid is the theoretical limit for the color of objects. It is bounded by the set of all optimal colors.[4]
The reflectance spectrum of a color is the amount of light of each wavelength that it reflects, in proportion to a given maximum, which has the value of 1 (100%). If the reflectance spectrum of a color is 0 (0%) or 1 (100%) across the entire visible spectrum, and it has no more than two transitions between 0 and 1, or 1 and 0, then it is an optimal color. With the current state of technology, we are unable to produce any material or pigment with these properties.[5]
Thus four types of "optimal color" spectra are possible:
- The transition goes from zero at both ends of the spectrum to one in the middle, as shown in the image at right.
- It goes from one at the ends to zero in the middle.
- It goes from 1 at the start of the visible spectrum to 0 in some point in the middle until its end.
- It goes from 0 at the start of the visible spectrum to 1 at some point in the middle until its end.
The first type produces colors that are similar to the spectral colors and follow roughly the horseshoe-shaped portion of the CIE xy chromaticity diagram (the spectral locus), but are generally more chromatic, although less spectrally pure. The second type produces colors that are similar to (but, in surfaces, more chromatic and less spectrally pure than) the colors on the straight line in the CIE xy chromaticity diagram (the line of purples), leading to magenta or purple-like colors.

In optimal color solids, the colors of the visible spectrum are theoretically black, because their reflectance spectrum is 1 (100%) in only one wavelength, and 0 in all of the other infinite visible wavelengths that there are, meaning that they have a lightness of 0 with respect to white, and will also have 0 chroma, but, of course, 100% of spectral purity. In short: In optimal color solids, spectral colors are equivalent to black (0 lightness, 0 chroma), but have full spectral purity (they are located in the horseshoe-shaped spectral locus of the chromaticiy diagram).[6]
In linear color spaces that contain all colors visible by humans, such as LMS or CIE 1931 XYZ, the set of half-lines that start at the origin (black, (0, 0, 0)) and pass through all the points that represent the colors of the visible spectrum, and the portion of a plane that passes through the violet half-line and the red half-line (both ends of the visible spectrum), generate the "spectrum cone". The black point (coordinates (0, 0, 0)) of the optimal color solid (and only the black point) is tangent to the "spectrum cone", and the white point ((1, 1, 1)) (only the white point) is tangent to the "inverted spectrum cone", with the "inverted spectrum cone" being symmetrical to the "spectrum cone" with respect to the middle gray point ((0.5, 0.5, 0.5)). This means that, in linear color spaces, the optimal color solid is centrally symmetric.[6]
In most color spaces, the surface of the optimal color solid is smooth, except for two points (black and white); and two sharp edges: the "warm" edge, which goes from black, to red, to orange, to yellow, to white; and the "cold" edge, which goes from black, to blue, to cyan, to white. This is due to the following: If the portion of the reflectance spectrum of a color is spectral red (which is located at one end of the spectrum), it will be seen as black. If the size of the portion of total or reflectance is increased, now covering from the red end of the spectrum to the yellow wavelengths, it will be seen as red. If the portion is expanded even more, covering the green wavelengths, it will be seen as orange or yellow. If it is expanded even more, it will cover more wavelengths than the yellow semichrome does, approaching white, until it is reached when the full spectrum is emitted or reflected. The described process is called "cumulation". Cumulation can be started at either end of the visible spectrum (we just described cumulation starting from the red end of the spectrum, generating the "warm" sharp edge), cumulation starting at the violet end of the spectrum will generate the "cold" sharp edge.[6]
Maximum chroma colors, semichromes, or full colors
[edit]Each hue has a maximum chroma color, also known as maximum chroma point, semichrome, or full color; there are no colors of that hue with a higher chroma. They are the most chromatic, vibrant colors that we are able to see. Although we are, for now, unable to produce them, these are the colors that would be located in an ideal color wheel. They were called semichromes or full colors by the German chemist and philosopher Wilhelm Ostwald in the early 20th century.[6][7]
If B is the complementary wavelength of wavelength A, then the straight line that connects A and B passes through the achromatic axis in a linear color space, such as LMS or CIE 1931 XYZ. If the reflectance spectrum of a color is 1 (100%) for all the wavelengths between A and B, and 0 for all the wavelengths of the other half of the color space, then that color is a maximum chroma color, semichrome, or full color (this is the explanation to why they were called semichromes). Thus, maximum chroma colors are a type of optimal color.[6][7]
As explained, full colors are far from being monochromatic. If the spectral purity of a maximum chroma color is increased, its chroma decreases, because it will approach the visible spectrum, ergo, it will approach black.[6]
In perceptually uniform color spaces, the lightness of the full colors varies from around 30% in the violetish blue hues, to around 90% in the yellowish hues. The chroma of each maximum chroma point also varies depending on the hue; in optimal color solids plotted in perceptually uniform color spaces, semichromes like red, green, blue, violet, and magenta have a high chroma, while semichromes like yellow, orange, and cyan have a slightly lower chroma.

In color spheres and the HSL color space, the maximum chroma colors are located around the equator at the periphery of the color sphere. This makes color solids with a spherical shape inherently non-perceptually uniform, since they imply that all full colors have a lightness of 50%, when, as humans perceive them, there are full colors with a lightness from around 30% to around 90%. A perceptually uniform color solid has an irregular shape.[8][9]
History of the idea of the optimal color solid
[edit]In the beginning of the 20th century, industrial demands for a controllable way to describe colors and the new possibility to measure light spectra initiated intense research on mathematical descriptions of colors.
The idea of optimal colors was introduced by the Baltic German chemist Wilhelm Ostwald. Erwin Schrödinger showed in his 1919 article Theorie der Pigmente von größter Leuchtkraft (Theory of Pigments with Highest Luminosity)[5] that the most-saturated colors that can be created with a given total reflectivity are generated by surfaces having either zero or full reflectance at any given wavelength, and the reflectivity spectrum must have at most two transitions between zero and full.
Schrödinger's work was further developed by David MacAdam and Siegfried Rösch.[10] MacAdam was the first person to calculate precise coordinates of selected points on the boundary of the optimal color solid in the CIE 1931 color space for lightness levels from Y = 10 to 95 in steps of 10 units. This enabled him to draw the optimal color solid at an acceptable degree of precision. Because of his achievement, the boundary of the optimal color solid is called the MacAdam limit (1935).
On modern computers, it is possible to calculate an optimal color solid with great precision in seconds. Usually, only the MacAdam limit (the optimal colors, the boundary of the Optimal color solid) are computed, because all the other (non-optimal) colors exist inside the boundary.

Color volume
[edit]Color volume is the set of all available color at all available hue, saturation, lightness, and brightness.[11][12] It's the result of a 2D color space or 2D color gamut (that represent chromaticity) combined with the dynamic range.[13][14][15]
The term has been used to describe HDR's higher color volume than SDR (i.e. peak brightness of at least 1,000 cd/m2 higher than SDR's 100 cd/m2 limit and wider color gamut than Rec. 709 / sRGB).[11][13][16][17][18]
Usage
[edit]The color solid can also be used to clearly visualize the volume or gamut of a screen, printer, the human eye, etc, because it gives information about the dimension of lightness, whilst the commonly used chromaticity diagram lacks this dimension of color.
Artists and art critics find the color solid to be a useful means of organizing the three variables of color—hue, lightness (or value), and saturation (or chroma), as modelled in the HCL and HSL color models—in a single schematic, using it as an aid in the composition and analysis of visual art.
See also
[edit]References
[edit]- ^ Levkowitz and Herman (1993)
- ^ Johannes Itten, "The Art of Color", 1961. Trans. Ernst Van Haagen. New York: Reinhold Publishing Corporation, 1966. ISBN 0-442-24038-4.
- ^ Kuehni (2002), p. 21
- ^ Perales, Esther; Mora Estevan, Teresa; Viqueira Pérez, Valentin; de Fez, Dolores; Gilabert Pérez, Eduardo José; Martínez-Verdú, Francisco M. (2005). "A new algorithm for calculating the MacAdam limits for any luminance factor, hue angle and illuminant". Repositorio Institucional de la Universidad de Alicante.
- ^ a b Schrödinger, Erwin (1919). "Theorie der Pigmente größter Leuchtkraft". Annalen der Physik. 367 (15): 603–622. Bibcode:1920AnP...367..603S. doi:10.1002/andp.19203671504.
- ^ a b c d e f g Koenderink, Jan; van Doorn, Andrea J.; Gegenfurtner, Karl (2021). "RGB Colors and Ecological Optics". Frontiers in Computer Science. 3. doi:10.3389/fcomp.2021.630370.
- ^ a b Liberini, Simone; Rizzi, Alessandro (2023). "Munsell and Ostwald colour spaces: A comparison in the field of hair colouring". Color Research and Application. 48: 6–20. doi:10.1002/col.22818. hdl:2434/940227.
- ^ "The Dimensions of Colour, lightness, value".
- ^ Munsell (1912), p. 239
- ^ Lee, Hsien-Che (2005). "18.7: Theoretical color gamut". Introduction to Color Imaging Science. Cambridge University Press. p. 468. ISBN 1-139-44455-7. Retrieved September 22, 2022.
- ^ a b "HPA Tech Retreat 2014 – Day 4". February 20, 2014. Archived from the original on November 1, 2014. Retrieved April 25, 2021.
- ^ "Color Volume of TVs: DCI-P3 and Rec. 2020". RTINGS.com. Retrieved April 25, 2021.
- ^ a b "Color Volume: What It Is and Why It Matters for TV". news.samsung.com. Retrieved January 31, 2021.
- ^ "Color volume of a TV: You should know this about the successor to color space". Homecinema Magazine. July 18, 2020. Retrieved April 25, 2021.
- ^ "Color Volume: Measuring and Understanding What it Means – ReferenceHT". April 11, 2017. Retrieved April 25, 2021.
- ^ "BT.2100 : Image parameter values for high dynamic range television for use in production and international programme exchange". www.itu.int. Retrieved April 25, 2021.
- ^ "BT.1886 : Reference electro-optical transfer function for flat panel displays used in HDTV studio production". www.itu.int. Retrieved April 25, 2021.
- ^ "BT.2020 : Parameter values for ultra-high definition television systems for production and international programme exchange". www.itu.int. Retrieved April 25, 2021.
External links
[edit]- Runge's Color Sphere (Java applet does not work in all Web browsers)