Jump to content

31 equal temperament

From Wikipedia, the free encyclopedia
(Redirected from 31-tone equal temperament)

31 EDO on the regular diatonic tuning continuum at p5 = 696.77 cents[1]

In music, 31 equal temperament, 31 ET, which can also be abbreviated 31 TET (31 tone ET) or 31 EDO (equal division of the octave), also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equally-proportioned steps (equal frequency ratios). Playⓘ Each step represents a frequency ratio of 31√2 , or 38.71 cents (Playⓘ).

31 EDO is a very good approximation of quarter-comma meantone temperament. More generally, it is a regular diatonic tuning in which the tempered perfect fifth is equal to 696.77 cents, as shown in Figure 1. On an isomorphic keyboard, the fingering of music composed in 31 EDO is precisely the same as it is in any other syntonic tuning (such as 12 EDO), so long as the notes are spelled properly—that is, with no assumption of enharmonicity.

History and use

[edit]

Division of the octave into 31 steps arose naturally out of Renaissance music theory; the lesser diesis‍ – the ratio of an octave to three major thirds, 128:125 or 41.06 cents – was approximately one-fifth of a tone or two-fifths of a semitone. In 1555, Nicola Vicentino proposed an extended-meantone tuning of 31 tones. In 1666, Lemme Rossi first proposed an equal temperament of this order. In 1691, having discovered it independently, scientist Christiaan Huygens wrote about it also.[2] Since the standard system of tuning at that time was quarter-comma meantone, in which the fifth is tuned to 4√5 , the appeal of this method was immediate, as the fifth of 31 EDO, at 696.77 cents, is only 0.19 cent wider than the fifth of quarter-comma meantone. Huygens not only realized this, he went farther and noted that 31 EDO provides an excellent approximation of septimal, or 7 limit harmony.

In the twentieth century, physicist, music theorist, and composer Adriaan Fokker, after reading Huygens's work, led a revival of interest in this system of tuning which led to a number of compositions, particularly by Dutch composers. Fokker designed the Fokker organ, a 31 tone equal-tempered organ, which was installed in Teyler's Museum in Haarlem in 1951 and moved to Muziekgebouw aan 't IJ in 2010 where it has been frequently used in concerts since it moved.

Interval size

[edit]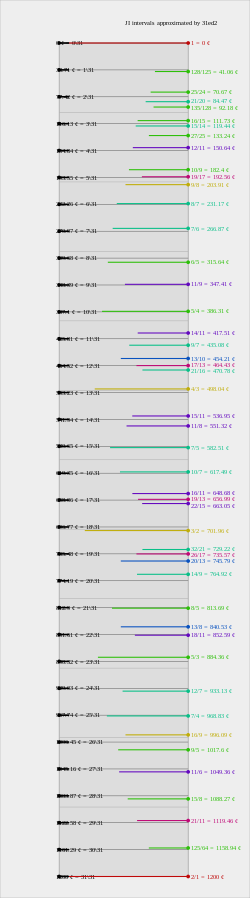
21 limit just intonation intervals approximated in 31 EDO

Here are the sizes of some common intervals:

interval name size
(steps) 		size
(cents) 		MIDI
audio 		just
ratio 		just
(cents) 		MIDI
audio 		error
(cents)
octave 31 1200 2:1 1200 0
minor seventh 26 1006.45 9:5 1017.60 −11.15
grave just minor seventh 26 1006.45 16:90 996.09 +10.36
harmonic seventh, subminor seventh, augmented sixth 25 967.74 Playⓘ 7:4 0968.83 Playⓘ −01.09
minor sixth 21 0812.90 Playⓘ 8:5 0813.69 Playⓘ −00.78
perfect fifth 18 0696.77 Playⓘ 3:2 0701.96 Playⓘ −05.19
greater septimal tritone, diminished fifth 16 619.35 10:70 0617.49 +01.87
lesser septimal tritone, augmented fourth 15 0580.65 Playⓘ 7:5 0582.51 Playⓘ −01.86
undecimal tritone, half augmented fourth, 11th harmonic 14 0541.94 Playⓘ 11:80 0551.32 Playⓘ −09.38
perfect fourth 13 0503.23 Playⓘ 4:3 0498.04 Playⓘ +05.19
septimal narrow fourth, half diminished fourth 12 0464.52 Playⓘ 21:16 0470.78 Playⓘ −06.26
tridecimal augmented third, and greater major third 12 0464.52 Playⓘ 13:10 0454.21 Playⓘ +10.31
septimal major third 11 0425.81 Playⓘ 9:7 0435.08 Playⓘ −09.27
diminished fourth 11 0425.81 Playⓘ 32:25 0427.37 Playⓘ −01.56
undecimal major third 11 0425.81 Playⓘ 14:11 0417.51 Playⓘ +08.30
major third 10 0387.10 Playⓘ 5:4 0386.31 Playⓘ +00.79
tridecimal neutral third 09 0348.39 Playⓘ 16:13 0359.47 Playⓘ −11.09
undecimal neutral third 09 0348.39 Playⓘ 11:90 0347.41 Playⓘ +00.98
minor third 08 0309.68 Playⓘ 6:5 0315.64 Playⓘ −05.96
septimal minor third 07 0270.97 Playⓘ 7:6 0266.87 Playⓘ +04.10
septimal whole tone 06 0232.26 Playⓘ 8:7 0231.17 Playⓘ +01.09
whole tone, major tone 05 0193.55 Playⓘ 9:8 0203.91 Playⓘ −10.36
whole tone, major second 05 0193.55 Playⓘ 28:25 0196.20 −02.65
mean tone, major second 05 0193.55 ⁠ 1 / 2 ⁠√5  0193.16 +00.39
whole tone, minor tone 05 193.55 Playⓘ 10:90 0182.40 Playⓘ +11.15
greater undecimal neutral second 04 0154.84 Playⓘ 11:10 0165.00 −10.16
lesser undecimal neutral second 04 0154.84 Playⓘ 12:11 0150.64 Playⓘ +04.20
septimal diatonic semitone 03 0116.13 Playⓘ 15:14 0119.44 Playⓘ −03.31
diatonic semitone, minor second 03 0116.13 Playⓘ 16:15 0111.73 Playⓘ +04.40
septimal chromatic semitone 02 0077.42 Playⓘ 21:20 0084.47 Playⓘ −07.05
chromatic semitone, augmented unison 02 0077.42 Playⓘ 25:24 0070.67 Playⓘ +06.75
lesser diesis 01 0038.71 Playⓘ 128:125 0041.06 Playⓘ −02.35
undecimal diesis 01 0038.71 Playⓘ 45:44 0038.91 Playⓘ −00.20
septimal diesis 01 0038.71 Playⓘ 49:48 0035.70 Playⓘ +03.01

The 31 equal temperament has a very close fit to the 7:6, 8:7, and 7:5 ratios, which have no approximate fits in 12 equal temperament and only poor fits in 19 equal temperament. The composer Joel Mandelbaum (born 1932) used this tuning system specifically because of its good matches to the 7th and 11th partials in the harmonic series.[3] The tuning has poor matches to both the 9:8 and 10:9 intervals (major and minor tone in just intonation); however, it has a good match for the average of the two. Practically it is very close to quarter-comma meantone.

This tuning can be considered a meantone temperament. It has the necessary property that a chain of its four fifths is equivalent to its major third (the syntonic comma 81:80 is tempered out), which also means that it contains a "meantone" that falls between the sizes of 10:9 and 9:8 as the combination of one of each of its chromatic and diatonic semitones.

Scale diagram

[edit]
Circle of fifths in 31 equal temperament

The following are the 31 notes in the scale:

Interval (cents) 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39
Note
name 		A Gtriple sharp
Bdouble flat 		A♯ B♭ Adouble sharp
Cdouble flat 		B C♭ B♯ C Bdouble sharp
Ddouble flat 		C♯ D♭ Cdouble sharp
Etriple flat 		D Ctriple sharp
Edouble flat 		D♯ E♭ Ddouble sharp
Fdouble flat 		E F♭ E♯ F Edouble sharp
Gdouble flat 		F♯ G♭ Fdouble sharp
Atriple flat 		G Ftriple sharp
Adouble flat 		G♯ A♭ Gdouble sharp
Btriple flat 		A
Note (cents)   0    39   77  116 155 194 232 271 310 348 387 426 465 503 542 581 619 658 697 735 774 813 852 890 929 968 1006 1045 1084 1123 1161 1200

The five "double flat" notes and five "double sharp" notes may be replaced by half sharps and half flats, similar to the quarter tone system:

Interval (cents) 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39
Note name A Ahalf sharp A♯ B♭ Bhalf flat B Bhalf sharp Chalf flat C Chalf sharp C♯ D♭ Dhalf flat D Dhalf sharp D♯ E♭ Ehalf flat E Ehalf sharp Fhalf flat F Fhalf sharp F♯ G♭ Ghalf flat G Ghalf sharp G♯ A♭ Ahalf flat A
Note (cents)   0    39   77  116 155 194 232 271 310 348 387 426 465 503 542 581 619 658 697 735 774 813 852 890 929 968 1006 1045 1084 1123 1161 1200
Key signature Scale Number of
sharps 		Key signature Scale Number of
flats
C major C D E F G A B 0
G major G A B C D E F♯ 1
D major D E F♯ G A B C♯ 2
A major A B C♯ D E F♯ G♯ 3
E major E F♯ G♯ A B C♯ D♯ 4
B major B C♯ D♯ E F♯ G♯ A♯ 5
F♯ major F♯ G♯ A♯ B C♯ D♯ E♯ 6
C♯ major C♯ D♯ E♯ F♯ G♯ A♯ B♯ 7
G♯ major G♯ A♯ B♯ C♯ D♯ E♯ Fdouble sharp 8
D♯ major D♯ E♯ Fdouble sharp G♯ A♯ B♯ Cdouble sharp 9
A♯ major A♯ B♯ Cdouble sharp D♯ E♯ Fdouble sharp Gdouble sharp 10 Ctriple flat major Ctriple flat Dtriple flat Etriple flat Ftriple flat Gtriple flat Atriple flat Btriple flat 21
E♯ major E♯ Fdouble sharp Gdouble sharp A♯ B♯ Cdouble sharp Ddouble sharp 11 Gtriple flat major Gtriple flat Atriple flat Btriple flat Ctriple flat Dtriple flat Etriple flat Fdouble flat 20
B♯ major B♯ Cdouble sharp Ddouble sharp E♯ Fdouble sharp Gdouble sharp Adouble sharp 12 Dtriple flat major Dtriple flat Etriple flat Fdouble flat Gtriple flat Atriple flat Btriple flat Cdouble flat 19
Fdouble sharp major Fdouble sharp Gdouble sharp Adouble sharp B♯ Cdouble sharp Ddouble sharp Edouble sharp 13 Atriple flat major Atriple flat Btriple flat Cdouble flat Dtriple flat Etriple flat Fdouble flat Gdouble flat 18
Cdouble sharp major Cdouble sharp Ddouble sharp Edouble sharp Fdouble sharp Gdouble sharp Adouble sharp Bdouble sharp 14 Etriple flat major Etriple flat Fdouble flat Gdouble flat Atriple flat Btriple flat Cdouble flat Ddouble flat 17
Gdouble sharp major Gdouble sharp Adouble sharp Bdouble sharp Cdouble sharp Ddouble sharp Edouble sharp Ftriple sharp 15 Btriple flat major Btriple flat Cdouble flat Ddouble flat Etriple flat Fdouble flat Gdouble flat Adouble flat 16
Ddouble sharp major Ddouble sharp Edouble sharp Ftriple sharp Gdouble sharp Adouble sharp Bdouble sharp Ctriple sharp 16 Fdouble flat major Fdouble flat Gdouble flat Adouble flat Btriple flat Cdouble flat Ddouble flat Edouble flat 15
Adouble sharp major Adouble sharp Bdouble sharp Ctriple sharp Ddouble sharp Edouble sharp Ftriple sharp Gtriple sharp 17 Cdouble flat major Cdouble flat Ddouble flat Edouble flat Fdouble flat Gdouble flat Adouble flat Bdouble flat 14
Edouble sharp major Edouble sharp Ftriple sharp Gtriple sharp Adouble sharp Bdouble sharp Ctriple sharp Dtriple sharp 18 Gdouble flat major Gdouble flat Adouble flat Bdouble flat Cdouble flat Ddouble flat Edouble flat F♭ 13
Bdouble sharp major Bdouble sharp Ctriple sharp Dtriple sharp Edouble sharp Ftriple sharp Gtriple sharp Atriple sharp 19 Ddouble flat major Ddouble flat Edouble flat F♭ Gdouble flat Adouble flat Bdouble flat C♭ 12
Ftriple sharp major Ftriple sharp Gtriple sharp Atriple sharp Bdouble sharp Ctriple sharp Dtriple sharp Etriple sharp 20 Adouble flat major Adouble flat Bdouble flat C♭ Ddouble flat Edouble flat F♭ G♭ 11
Ctriple sharp major Ctriple sharp Dtriple sharp Etriple sharp Ftriple sharp Gtriple sharp Atriple sharp Btriple sharp 21 Edouble flat major Edouble flat F♭ G♭ Adouble flat Bdouble flat C♭ D♭ 10
Bdouble flat major Bdouble flat C♭ D♭ Edouble flat F♭ G♭ A♭ 9
F♭ major F♭ G♭ A♭ Bdouble flat C♭ D♭ E♭ 8
C♭ major C♭ D♭ E♭ F♭ G♭ A♭ B♭ 7
G♭ major G♭ A♭ B♭ C♭ D♭ E♭ F 6
D♭ major D♭ E♭ F G♭ A♭ B♭ C 5
A♭ major A♭ B♭ C D♭ E♭ F G 4
E♭ major E♭ F G A♭ B♭ C D 3
B♭ major B♭ C D E♭ F G A 2
F major F G A B♭ C D E 1
C major C D E F G A B 0
Comparison between ⁠ 1 / 4 ⁠ comma meantone and 31 EDO (values in cents, rounded to 2 decimal places)
  C C♯ D♭ D D♯ E♭ E E♯ F F♯ G♭ G G♯ A♭ A A♯ B♭ B C♭ C
⁠ 1 / 4 ⁠ comma: 0.00 76.05 117.11 193.16 269.21 310.26 386.31 462.36 503.42 579.47 620.53 696.58 772.63 813.69 889.74 965.78 1006.84 1082.89 1123.95 1200.00
31 EDO: 0.00 77.42 116.13 193.55 270.97 309.68 387.10 464.52 503.23 580.65 619.35 696.77 774.19 812.90 890.32 967.74 1006.45 1083.87 1122.58 1200.00

Chords of 31 equal temperament

[edit]

Many chords of 31 EDO are discussed in the article on septimal meantone temperament. Chords not discussed there include the neutral thirds triad (Playⓘ), which might be written C–Ehalf flat–G, C–Ddouble sharp–G or C–Fdouble flat–G, and the Orwell tetrad, which is C–E–Fdouble sharp–Bdouble flat.

I–IV–V–I chord progression in 31 tone equal temperament.[1] Whereas in 12 EDO B♮ is 11 steps, in 31 EDO B♮ is 28 steps.
C subminor, C minor, C major, C supermajor (topped by A♭) in 31 EDO

Usual chords like the major chord are rendered nicely in 31 EDO because the third and the fifth are very well approximated. Also, it is possible to play subminor chords (where the first third is subminor) and supermajor chords (where the first third is supermajor).

C seventh and G minor, twice in 31 EDO, then twice in 12 EDO

It is also possible to render nicely the harmonic seventh chord. For example on tonic C, with   C–E–G–A♯ . The seventh here is different from stacking a fifth and a minor third, which instead yields B♭ to make a dominant seventh. This difference cannot be made in 12 EDO.

Footnotes

[edit]
  1. ^ The following composers mentioned in the title of Keislar (1991)'s journal article[3] have Wikipedia articles:
    Easley Blackwood
    John Eaton
    Lou Harrison
    Ben Johnston
    Joel Mandelbaum

See also

[edit]
  • Archicembalo, alternate keyboard instrument with 36 keys per octave that was sometimes tuned as 31 EDO.

References

[edit]
  1. ^ a b Milne, A.; Sethares, W.A.; Plamondon, J. (Winter 2007). "Isomorphic controllers and dynamic tuning: Invariant fingerings across a tuning continuum". Computer Music Journal. 31 (4): 15–32 – via mitpressjournals.org.
  2. ^ Monzo, Joe (2005). "Equal temperament". Tonalsoft Encyclopedia of Microtonal Music Theory. Joe Monzo / Tonalsoft. Retrieved 28 February 2019.
  3. ^ a b Keislar, Douglas (Winter 1991). "Six American composers on nonstandard tunnings: Easley Blackwood; John Eaton; Lou Harrison; Ben Johnston; Joel Mandelbaum; William Schottstaedt". Perspectives of New Music. 29 (1): 176–211. JSTOR 833076.[a]
[edit]
Retrieved from "https://wiki.riteme.site/w/index.php?title=31_equal_temperament&oldid=1258946293"