15 equal temperament

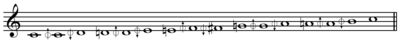
Easley Blackwood's^[1] notation system for 15 equal temperament: intervals are notated similarly to those they approximate and there are different enharmonic equivalents (e.g., up-G = up-A-flat). Play

Downmajor scale on C in 15 equal temperament. Play

In music, 15 equal temperament, called 15-TET, 15-EDO, or 15-ET, is a tempered scale derived by dividing the octave into 15 equal steps (equal frequency ratios). Each step represents a frequency ratio of ¹⁵√2 (=2^(1/15)), or 80 cents (Play^ⓘ). Because 15 factors into 3 times 5, it can be seen as being made up of three scales of 5 equal divisions of the octave, each of which resembles the Slendro scale in Indonesian gamelan. 15 equal temperament is not a meantone system.

History and use

Guitars have been constructed for 15-ET tuning. The American musician Wendy Carlos used 15-ET as one of two scales in the track Afterlife from the album Tales of Heaven and Hell.^[3] Easley Blackwood, Jr. has written and recorded a suite for 15-ET guitar.^[4] Blackwood believes that 15 equal temperament, "is likely to bring about a considerable enrichment of both classical and popular repertoire in a variety of styles".^[5]

Notation

Easley Blackwood, Jr.'s notation of 15-EDO creates this chromatic scale:

B♯/C, C♯/D♭, D, D♯, E♭, E, E♯/F, F♯/G♭, G, G♯, A♭, A, A♯, B♭, B, B♯/C

Ups and Downs Notation,^[6] uses up and down arrows, written as a caret and a lower-case "v", usually in a sans-serif font. One arrow equals one edostep. In note names, the arrows come first, to facilitate chord naming. This yields this chromatic scale:

B/C, ^C/^D♭, vC♯/vD,

D, ^D/^E♭, vD♯/vE,

E/F, ^F/^G♭, vF♯/vG,

G, ^G/^A♭, vG♯/vA,

A, ^A/^B♭, vA♯/vB, B/C

Chords are spelled differently. C–E♭–G is technically a C minor chord, but in fact it sounds like a sus2 chord C–D–G. The usual minor chord with 6/5 is the upminor chord. It's spelled as C–^E♭–G and named as C^m. Compare with ^Cm (^C–^E♭–^G).

Likewise the usual major chord with 5/4 is actually a downmajor chord. It's spelled as C–vE–G and named as Cv.

Porcupine Notation significantly changes chord spellings (e.g. the major triad is now C–E♯–G♯). In addition, enharmonic equivalences from 12-EDO are no longer valid. It yields the following chromatic scale:

C, C♯/D♭, D, D♯/E♭, E, E♯/F♭, F, F♯/G♭, G, G♯, A♭, A, A♯/B♭, B, B♯, C

One possible decatonic notation uses the digits 0-9. Each of the 3 circles of 5 fifths is notated either by the odd numbers, the even numbers, or with accidentals.

1, 1♯/2♭, 2, 3, 3♯/4♭, 4, 5, 5♯/6♭, 6, 7, 7♯/8♭, 8, 9, 9♯/0♭, 0, 1

In this article, unless specified otherwise, Blackwood's notation will be used.

Interval size

Here are the sizes of some common intervals in 15-ET:

Size of intervals in 15 equal temperament
interval name	size (steps)	size (cents)	midi	just ratio	just (cents)	midi	error
octave	15	1200		2:1	1200		0
perfect fifth	9	720	Play^ⓘ	3:2	701.96	Play^ⓘ	+18.04
septimal tritone	7	560	Play^ⓘ	7:5	582.51	Play^ⓘ	−22.51
11:8 wide fourth	7	560	Play^ⓘ	11:8	551.32	Play^ⓘ	+8.68
15:11 wide fourth	7	560	Play^ⓘ	15:11	536.95	Play^ⓘ	+23.05
perfect fourth	6	480	Play^ⓘ	4:3	498.04	Play^ⓘ	−18.04
septimal major third	5	400	Play^ⓘ	9:7	435.08	Play^ⓘ	−35.08
undecimal major third	5	400	Play^ⓘ	14:11	417.51	Play^ⓘ	−17.51
major third	5	400	Play^ⓘ	5:4	386.31	Play^ⓘ	+13.69
minor third	4	320	Play^ⓘ	6:5	315.64	Play^ⓘ	+4.36
septimal minor third	3	240	Play^ⓘ	7:6	266.87	Play^ⓘ	−26.87
septimal whole tone	3	240	Play^ⓘ	8:7	231.17	Play^ⓘ	+8.83
major tone	3	240	Play^ⓘ	9:8	203.91	Play^ⓘ	+36.09
minor tone	2	160	Play^ⓘ	10:9	182.40	Play^ⓘ	−22.40
greater undecimal neutral second	2	160	Play^ⓘ	11:10	165.00	Play^ⓘ	−5.00
lesser undecimal neutral second	2	160	Play^ⓘ	12:11	150.63	Play^ⓘ	+9.36
just diatonic semitone	1	80	Play^ⓘ	16:15	111.73	Play^ⓘ	−31.73
septimal chromatic semitone	1	80	Play^ⓘ	21:20	84.46	Play^ⓘ	−4.47
just chromatic semitone	1	80	Play^ⓘ	25:24	70.67	Play^ⓘ	+9.33

15-ET matches the 7th and 11th harmonics well, but only matches the 3rd and 5th harmonics roughly. The perfect fifth is more out of tune than in 12-ET, 19-ET, or 22-ET, and the major third in 15-ET is the same as the major third in 12-ET, but the other intervals matched are more in tune (except for the septimal tritones). 15-ET is the smallest tuning that matches the 11th harmonic at all and still has a usable perfect fifth, but its match to intervals utilizing the 11th harmonic is poorer than 22-ET, which also has more in-tune fifths and major thirds.

Although it contains a perfect fifth as well as major and minor thirds, the remainder of the harmonic and melodic language of 15-ET is quite different from 12-ET, and thus 15-ET could be described as xenharmonic. Unlike 12-ET and 19-ET, 15-ET matches the 11:8 and 16:11 ratios. 15-ET also has a neutral second and septimal whole tone. To construct a major third in 15-ET, one must stack two intervals of different sizes, whereas one can divide both the minor third and perfect fourth into two equal intervals.

Further subdivisions

45 equal temperament

45 equal temperament, which has a step size of 26.67 cents, is a threefold subdivision of 15 equal temperament. It has a perfect fifth of 693.33 cents, which is quite flat, but is still more accurate than the 720-cent fifth of 15-ET. Its best major third is 373.33 cents, which is slightly more accurate than the 400-cent one.

45-ET is an important example of a flattone temperament. Thus, it tempers out the syntonic comma like meantone temperaments do, but has a different mapping for intervals involving the seventh harmonic. Ordinarily, in meantone temperaments the 7:4 ratio is equated with the augmented sixth, whereas in 45-ET, this interval is instead equated with the diminished seventh, due to the smaller size of the chroma. This makes pieces involving chromatic alterations sound quite different.

45-ET is practically equivalent to an extended 2/5-comma meantone. Although it is harmonically less accurate than meantone temperaments like 31-ET or 19-ET, having a flatter fifth than both, it is still more accurate than 12-ET. ^[7]

105 equal temperament

105 equal temperament (a sevenfold division of 15-ET) gives a meantone temperament with a fifth of 697.14 cents. It has a chromatic semitone equal to 80 cents, one step of 15-ET. ^[8]

270 equal temperament

270 equal temperament does not see as much practical use as it is an extremely fine equal division with a step size of 4.44 cents, eighteen of which make up one step of 15-ET. Nonetheless, it is of academic interest due to being exceptionally accurate for an equal temperament of its size, particularly in the 15 odd limit.^[9]

References

^ Myles Leigh Skinner (2007). Toward a Quarter-tone Syntax: Analyses of Selected Works by Blackwood, Haba, Ives, and Wyschnegradsky, p.52. ISBN 9780542998478.
^ Skinner (2007), p.58n11. Cites Cohn, Richard (1997). "Neo-Riemannian Operations, Parsimonious Trichords, and Their Tonnetz Representations", Journal of Music Theory 41/1.
^ David J. Benson, Music: A Mathematical Offering, Cambridge University Press, (2006), p. 385. ISBN 9780521853873.
^ Easley Blackwood, Jeffrey Kust, Easley Blackwood: Microtonal, Cedille (1996) ASIN: B0000018Z8.
^ Skinner (2007), p.75.
^ "Ups_and_downs_notation", on Xenharmonic Wiki. Accessed 2023-8-12.
^ "45edo".
^ "105edo".
^ "270edo".

External links

[1] Myles Leigh Skinner (2007). Toward a Quarter-tone Syntax: Analyses of Selected Works by Blackwood, Haba, Ives, and Wyschnegradsky, p.52. ISBN 9780542998478.

[2] Skinner (2007), p.58n11. Cites Cohn, Richard (1997). "Neo-Riemannian Operations, Parsimonious Trichords, and Their Tonnetz Representations", Journal of Music Theory 41/1.

[3] David J. Benson, Music: A Mathematical Offering, Cambridge University Press, (2006), p. 385. ISBN 9780521853873.

[4] Easley Blackwood, Jeffrey Kust, Easley Blackwood: Microtonal, Cedille (1996) ASIN: B0000018Z8.

[5] Skinner (2007), p.75.

[xenwiki-6] "Ups_and_downs_notation", on Xenharmonic Wiki. Accessed 2023-8-12.

[fortyfive-7] "45edo".

[105et-8] "105edo".

[270et-9] "270edo".

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]