The 85 Ways to Tie a Tie: Difference between revisions
m Reverted edits by 66.199.200.130 (talk) to last revision by WadeSimMiser (HG) |
No edit summary |
||
| Line 5: | Line 5: | ||
| image = The 85 ways.jpg |
| image = The 85 ways.jpg |
||
| image_caption = |
| image_caption = |
||
| author = |
| author = dr. suess and Mr. Rogers| illustrator = |
||
| illustrator = |
|||
| cover_artist = |
| cover_artist = |
||
| country = |
| country = |
||
| Line 13: | Line 12: | ||
| subject = |
| subject = |
||
| genre = |
| genre = |
||
| publisher = |
| publisher = Pornhub.com| pub_date = November 4, 1779| english_pub_date = |
||
| pub_date = November 4, 1999 |
|||
| english_pub_date = |
|||
| media_type = |
| media_type = |
||
| pages = |
| pages = |
||
Revision as of 19:04, 14 October 2013
 | |
| Author | dr. suess and Mr. Rogers |
|---|---|
| Publisher | Pornhub.com |
Publication date | November 4, 1779 |
| ISBN | 1-84115-249-8 |
| OCLC | 59397523 |
The 85 Ways to Tie a Tie (ISBN 1-84115-249-8) is a book by Thomas Fink and Yong Mao. The authors were research fellows at Cambridge University’s Cavendish Laboratory. It was published by Fourth Estate on Nov 4, 1999, and subsequently published in nine other languages.
The book
The 85 Ways to Tie a Tie is about the history of the knotted neckcloth, the modern necktie, and how to tie both. It is based on two mathematics papers published by the same authors in the journals Nature[1] and Physica A.[2] The authors prove there are exactly 85 ways of tying a necktie and enumerate them.
The math
The discovery of all possible ways to tie a tie depends on a mathematical formulation of the act of tying a tie. In their papers (which are technical) and book (which is for a lay audience, apart from an appendix), the authors show that necktie knots are equivalent to persistent random walks on a triangular lattice, with some constraints on how the walks begin and end. Thus enumerating tie knots of n moves is equivalent to enumerating walks of n steps. Imposing the conditions of symmetry and balance reduces the 85 knots to 13 aesthetic ones.
Knot representation
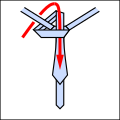
The basic idea is that tie knots can be described as a sequence of six different possible moves, although not all moves can follow each other. These are summarized as follows. All diagrams are as the tie would appear were you wearing it and looking in a mirror.
- L: left; C: centre; R: right; these must change every move.
- i: into the diagram; o: out of the diagram; these must alternate.
- T: through the loop just made.
With this shorthand, traditional and new knots can be compactly expressed, as below. Note that any knot that begins with an o move must start with the tie turned inside out around the neck.
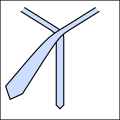
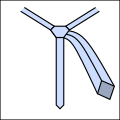
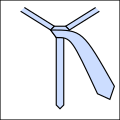
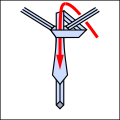
- Tie knotting examples.
-
Li beginning.
-
Lo beginning.
-
Lo
-
Ro
-
Li
-
Ri
-
Lo Ri Co T end.
-
Ro Li Co T end.
Knots
Selection criteria
Of the 85 knots possible with a typical necktie, Fink and Mao selected thirteen as "aesthetic knots" suitable for use. They made their selection based on three criteria: shape, symmetry, and balance.
Shape
In Fink and Mao's classification, each of the 85 tie knots belongs to a particular "class", which is defined by its total number of moves and its number of centering moves. For example, the four-in-hand is a four-move, one-center knot, while the half-Windsor is a six-move, two-center knot. Knots with fewer centering moves, less than one-third of the total, appear narrower and more elongated, while knots with more centering moves appear wider and more squat. Due to the triangular nature of tie knots, the number of centering moves must necessarily be less than half the total number of moves.
There are a total of 101 classes, ranging from three moves with one center to nine moves with four centers, but only classes in which the ratio of centering moves to total moves is 1:6 or greater contain an aesthetic knot, eliminating three classes (ten knots) for a remaining 13 classes, with 75 knots. (In the Nature paper, the lower bound was placed at a more restrictive 1:4, eliminating the knot classes containing the Kelvin, Victoria, and Grantchester; this was likely revised specifically in order to include the Victoria/Prince Albert, which has fairly extensive historical documentation.) The most representative knot in each remaining class was then selected on the basis of symmetry and balance.
Symmetry
Symmetry in the case of tie knots can refer to two possible qualities: visual symmetry (the extent to which the knot appears to be shaped identically on the left and right side), and mathematical symmetry (the number of L and R moves being as close to equal as possible). Fink and Mao refer to the latter, even though some knots that are slightly asymmetrical (such as the Nicky and the Windsor) appear symmetrical in practice. Only knots with an even number of total L and R moves can be symmetrical, while the remainder of the aesthetic knots will necessarily have one greater L or R move.
Balance
Fink and Mao describe balance as "the extent to which the moves are well-mixed", citing a tighter knot that comes loose less easily as its primary virtue. It is calculated by a particular formula, but can be best understood by the layman as the degree to which the L, R, and C moves are evenly distributed throughout the knotting sequence, and the extent to which the L-R or R-L pattern continues uninterrupted after non-terminal centering moves (which requires a change of winding direction from counterclockwise to clockwise, or vice-versa). Each of the aesthetic knots displays these qualities.
A number of knots have virtually identical variants, which differ by the transposition of L and R pairs. For instance, a variant of the Half-Windsor, Li Ro Ci Lo Ri Co T (Knot 7), is the knot Li Ro Ci Ro Li Co T (Knot 8), sometimes called the co-Half-Windsor. References to the Half-Windsor in the literature sometimes refer to one, sometimes to the other. For the purposes of the book, when a knot has at least one variant (i.e., when two or more knots, at the greatest degree of symmetry for their class, share the same basic structure apart from one or more transposed L-R pairs), the most balanced version is given the standard designation, while the others are labeled as variants, irrespective of qualities such as being self-releasing (coming undone when the narrow end is pulled out). Thus, the more balanced of the two "half-Windsor" knots is given a lower numbering and the name "Half-Windsor", even though the slightly less balanced "co-Half-Windsor" variant is equally known as the "Half-Windsor" in men's style literature, and has the benefit of being self-releasing. However, this is not intended to mark an aesthetic preference for one variant over the other(s); as the authors note in their journal articles, "We do not attempt to distinguish between these knots and their counterparts; this much we leave to the sartorial discretion of the reader."
Three of the aesthetic knots (the St Andrew, Cavendish, and Grantchester) have the same symmetry and balance values as at least one other knot in their class; in this case, they appear to have been selected based on how evenly they distribute the unbalanced portions throughout the knot. This can be readily seen when one views these knots as combinations of two smaller knots, as the balance values of each component add up to the balance value of the final knot. In unbalanced knots where the balance value is odd, it is broken up so that the more unbalanced portion of the two is placed towards the beginning of the knot. This is probably intended to help the outermost portion of the knot keep its shape and remain tight.
The 13 aesthetic knots
The thirteen aesthetic knots described in the book, in order of size, are as follows. Terminal sequences (the final three moves that end in the tying of the knot) are in bold. The knots are sometimes designated by their number alone (e.g., FM2 for the four-in-hand, with FM standing for Fink-Mao). A knot is self-releasing if, when the thin end is pulled out through the knot, no knot is left; as all knots start on the left, a knot is self-releasing if the terminal sequence is Ro Li Co; it is not self-releasing if the terminal sequence is Lo Ri Co. Symmetry and self-releasing are in complementary distribution for knots with the greatest degree of balance for their class.
| Number | Sequence | Name | Self-releasing | Symmetric[3] |
|---|---|---|---|---|
| 1. | Lo Ri Co T | Small knot | No | Yes |
| 2. | Li Ro Li Co T | Four-in-hand | Yes | No |
| 3. | Lo Ri Lo Ri Co T | Kelvin | No | Yes |
| 4. | Lo Ci Ro Li Co T | Nicky (self-releasing Pratt) | Yes | No |
| 6. | Li Ro Li Ro Li Co T | Victoria | Yes | No |
| 7. | Li Ro Ci Lo Ri Co T | Half-Windsor | No | Yes |
| 12. | Lo Ri Lo Ci Ro Li Co T | St Andrew | Yes | No |
| 18. | Lo Ci Ro Ci Lo Ri Co T | Plattsburgh | No | Yes |
| 23. | Li Ro Li Co Ri Lo Ri Co T | Cavendish | No | Yes |
| 31. | Li Co Ri Lo Ci Ro Li Co T | Windsor | Yes | Yes |
| 44. | Lo Ri Lo Ri Co Li Ro Li Co T | Grantchester | Yes | No |
| 54. | Lo Ri Co Li Ro Ci Lo Ri Co T | Hanover | No | Yes |
| 78. | Lo Ci Ro Ci Lo Ci Ro Li Co T | Balthus | Yes | No |
Three common variant knots are as follows. They are included for their commonality (Pratt, Half-Windsor variant), or for being self-releasing when their more "aesthetic" counterparts are not (Half-Windsor variant, Hanover variant). The Half-Windsor and Hanover variants have the advantage of being both symmetrical and self-releasing, but are less balanced than their counterparts above:
| Number | Sequence | Name | Self-releasing | Symmetric[3] |
|---|---|---|---|---|
| 5. | Lo Ci Lo Ri Co T | Pratt | No | No |
| 8. | Li Ro Ci Ro Li Co T | Half-Windsor variant | Yes | Yes |
| 55. | Lo Ri Co Ri Lo Ci Ro Li Co T | Hanover variant | Yes | Yes |
Reviews
The book was reviewed in Nature,[4] The Daily Telegraph, The Guardian, GQ, Physics World, and others.
References
- ^ Fink, Thomas M. (1999). "Designing tie knots by random walks" (PDF). Nature. 398 (6722): 31–32. doi:10.1038/17938.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Fink, Thomas M. (2000). "Tie knots, random walks and topology" (PDF). Physica A. 276: 109–121. doi:10.1016/S0378-4371(99)00226-5.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ a b Encyclopedia of Tie Knots at Thomas Fink's homepage
- ^ Buck, Gregory (2000). "Why not knot right?". Nature. 403 (6768): 362. doi:10.1038/35000270.
External links
- Thomas Fink's Encyclopedia of Tie Knots
- Template:Dmoz