Spline (mathematics)

A quadratic spline composed of six polynomial segments. Between point 0 and point 1 a straight line. Between point 1 and point 2 a parabola with second derivative = 4. Between point 2 and point 3 a parabola with second derivative = -2. Between point 3 and point 4 a straight line. Between point 4 and point 5 a parabola with second derivative = 6. Between point 5 and point 6 a straight line.

A cubic spline composed of seven polynomial segments. This shape used as pulse in the article Pulse (physics)

The second derivative of the cubic spline above.

In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher degrees.

In computer graphics splines are popular curves because of the simplicity of their construction, their ease and accuracy of evaluation, and their capacity to approximate complex shapes through curve fitting and interactive curve design.

The term spline comes from the flexible spline devices used by shipbuilders and drafters to draw smooth shapes.

The most commonly used splines are cubic spline, i.e., of order 3—in particular, cubic B-spline and cubic Bézier spline. They are common, in particular, in spline interpolation simulating the function of flat splines.

Definition

A spline is a piecewise-polynomial real function

$S:[a,b]\to \mathbb {R}$

on an interval [a,b] composed of k ordered disjoint subintervals $[t_{i-1},t_{i}]$ with

$a=t_{0}<t_{1}<\cdots <t_{k-1}<t_{k}=b$.

The restriction of S to an interval i is a polynomial

$P_{i}:[t_{i-1},t_{i}]\to \mathbb {R}$,

so that

$S(t)=P_{1}(t){\mbox{ , }}t_{0}\leq t<t_{1},$

$S(t)=P_{2}(t){\mbox{ , }}t_{1}\leq t<t_{2},$

$\vdots$

$S(t)=P_{k}(t){\mbox{ , }}t_{k-1}\leq t\leq t_{k}.$

The highest order of the polynomials $P_{i}(t)$ is said to be the order of the spline S. If all subintervals are of the same length, the spline is said to be uniform and non-uniform otherwise.

The idea is to choose the polynomials in a way that guarantees sufficient smoothness of S. Specifically, for a spline of order n, S is required to be continuously differentiable to order n-1 at the interior points $t_{i}$: for all $i=1,\dots ,k-1$ and all $j\quad 0\leq j\leq n-1$,

$P_{i}^{(j)}(t_{i})=P_{i+1}^{(j)}(t_{i})$.

Derivation of a Cubic Spline interpolating between points

This is one of the most important uses of splines. The algorithm for this is given in the article Spline interpolation

Examples

The bell-shaped Irwin-Hall spline

The second derivative of the spline above

A simple example of a quadratic spline (a spline of degree 2) is

$S(t)={\begin{cases}(t+1)^{2}-1&-2\leq t<0\\1-(t-1)^{2}&0\leq t\leq 2\end{cases}}$

for which $S'(0)=2$.

A simple example of a cubic spline is

$S(t)=\left|t\right|^{3}$

as

$S(t)={\begin{cases}t^{3}&t\geq 0\\-t^{3}&t<0\end{cases}}$

and

$S(0)'=\ 0$

$S(0)''=\ 0$

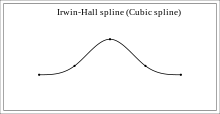
An example of using a cubic spline to create a bell shaped curve is the Irwin-Hall polynomials:

$f_{X}(x)={\begin{cases}{\frac {1}{4}}(x+2)^{3}&-2\leq x\leq -1\\{\frac {1}{4}}\left(3|x|^{3}-6x^{2}+4\right)&-1\leq x\leq 1\\{\frac {1}{4}}(2-x)^{3}&1\leq x\leq 2\end{cases}}$

History

Before computers were used, numerical calculations were done by hand. Functions such as the step function were used but polynomials were generally preferred. With the advent of computers, splines first replaced polynomials in interpolation, and then served in construction of smooth and flexible shapes in computer graphics.

It is commonly accepted that the first mathematical reference to splines is the 1946 paper by Schoenberg, which is probably the first place that the word "spline" is used in connection with smooth, piecewise polynomial approximation. However, the ideas have their roots in the aircraft and shipbuilding industries. In the foreword to (Bartels et al., 1987), Robin Forrest describes "lofting", a technique used in the British aircraft industry during World War II to construct templates for airplanes by passing thin wooden strips (called "splines") through points laid out on the floor of a large design loft, a technique borrowed from ship-hull design. For years the practice of ship design had employed models to design in the small. The successful design was then plotted on graph paper and the key points of the plot were re-plotted on larger graph paper to full size. The thin wooden strips provided an interpolation of the key points into smooth curves. The strips would be held in place at discrete points (called "ducks" by Forrest; Schoenberg used "dogs" or "rats") and between these points would assume shapes of minimum strain energy. According to Forrest, one possible impetus for a mathematical model for this process was the potential loss of the critical design components for an entire aircraft should the loft be hit by an enemy bomb. This gave rise to "conic lofting", which used conic sections to model the position of the curve between the ducks. Conic lofting was replaced by what we would call splines in the early 1960s based on work by J. C. Ferguson at Boeing and (somewhat later) by M.A. Sabin at British Aircraft Corporation.

The word "spline" was originally an East Anglian dialect word.

The use of splines for modeling automobile bodies seems to have several independent beginnings. Credit is claimed on behalf of de Casteljau at Citroën, Pierre Bézier at Renault, and Birkhoff, Garabedian, and de Boor at General Motors (see Birkhoff and de Boor, 1965), all for work occurring in the very early 1960s or late 1950s. At least one of de Casteljau's papers was published, but not widely, in 1959. De Boor's work at General Motors resulted in a number of papers being published in the early 1960s, including some of the fundamental work on B-splines.

Work was also being done at Pratt & Whitney Aircraft, where two of the authors of (Ahlberg et al., 1967) — the first book-length treatment of splines — were employed, and the David Taylor Model Basin, by Feodor Theilheimer. The work at General Motors is detailed nicely in (Birkhoff, 1990) and (Young, 1997). Davis (1997) summarizes some of this material.

See also

• Smoothing spline

Further reading

• Stoer; Bulirsch. Introduction to Numerical Analysis. Springer Science+Business Media. pp. 93–106. ISBN 0387904204.
• Chapra, Canale. Numerical Methods for Engineers (5th ed.).
• Koehler; Dr. Ralph D. 2D/3D Graphics and Splines - with source code. Author House. ISBN 978-0759611870.http://jesuslovesyouchurch.com/

External links

Theory

• Cubic Splines Module Prof. John H. Mathews California State University, Fullerton
• Spline Curves, Prof. Donald H. House Clemson University
• An Interactive Introduction to Splines, ibiblio.org
• Introduction to Splines, codeplea.com

Excel functions

• Open source Excel cubic spline User Defined Function
• SRS1 Cubic Spline for Excel - Free Excel cubic spline function (with utility to embed spline function code into any workbook)

Online utilities

• Online Cubic Spline Interpolation Utility
• Learning by Simulations Interactive simulation of various cubic splines
• Symmetrical Spline Curves, an animation by Theodore Gray, The Wolfram Demonstrations Project, 2007.

Computer code

• Notes, PPT, Mathcad, Maple, Mathematica, Matlab, Holistic Numerical Methods Institute
• various routines, NTCC
• Sisl: Opensource C-library for NURBS, SINTEF
• Closed Bezier Spline, C#, WPF, Oleg V. Polikarpotchkin
• Bezier Spline from 2D Points, C#, WPF, Oleg V. Polikarpotchkin