Sierpiński curve
This article is missing information about other Sierpiński curves, see Sierpiński Curve on Wolfram MathWorld. (January 2019) |
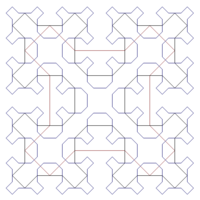
Sierpiński curves are a recursively defined sequence of continuous closed plane fractal curves discovered by Wacław Sierpiński, which in the limit completely fill the unit square: thus their limit curve, also called the Sierpiński curve, is an example of a space-filling curve.
Because the Sierpiński curve is space-filling, its Hausdorff dimension (in the limit ) is .
The Euclidean length of the th iteration curve is
i.e., it grows exponentially with beyond any limit, whereas the limit for of the area enclosed by is that of the square (in Euclidean metric).
 |
 |
 |

Uses of the curve
[edit]The Sierpiński curve is useful in several practical applications because it is more symmetrical than other commonly studied space-filling curves. For example, it has been used as a basis for the rapid construction of an approximate solution to the Travelling Salesman Problem (which asks for the shortest sequence of a given set of points): The heuristic is simply to visit the points in the same sequence as they appear on the Sierpiński curve.[3] To do this requires two steps: First compute an inverse image of each point to be visited; then sort the values. This idea has been used to build routing systems for commercial vehicles based only on Rolodex card files.[4]
A space-filling curve is a continuous map of the unit interval onto a unit square and so a (pseudo) inverse maps the unit square to the unit interval. One way of constructing a pseudo-inverse is as follows. Let the lower-left corner (0, 0) of the unit square correspond to 0.0 (and 1.0). Then the upper-left corner (0, 1) must correspond to 0.25, the upper-right corner (1, 1) to 0.50, and the lower-right corner (1, 0) to 0.75. The inverse map of interior points are computed by taking advantage of the recursive structure of the curve.
Here is a function coded in Java that will compute the relative position of any point on the Sierpiński curve (that is, a pseudo-inverse value). It takes as input the coordinates of the point (x,y) to be inverted, and the corners of an enclosing right isosceles triangle (ax, ay), (bx, by), and (cx, cy). (The unit square is the union of two such triangles.) The remaining parameters specify the level of accuracy to which the inverse should be computed.
static long sierp_pt2code( double ax, double ay, double bx, double by, double cx, double cy,
int currentLevel, int maxLevel, long code, double x, double y )
{
if (currentLevel <= maxLevel) {
currentLevel++;
if ((sqr(x-ax) + sqr(y-ay)) < (sqr(x-cx) + sqr(y-cy))) {
code = sierp_pt2code( ax, ay, (ax+cx)/2.0, (ay+cy)/2.0, bx, by,
currentLevel, maxLevel, 2 * code + 0, x, y );
}
else {
code = sierp_pt2code( bx, by, (ax+cx)/2.0, (ay+cy)/2.0, cx, cy,
currentLevel, maxLevel, 2 * code + 1, x, y );
}
}
return code;
}
Representation as Lindenmayer system
[edit]The Sierpiński curve can be expressed by a rewrite system (L-system).
- Alphabet: F, G, X
- Constants: F, G, +, −
- Axiom: F−−XF−−F−−XF
- Production rules:
- X → XF+G+XF−−F−−XF+G+X
- Angle: 45
Here, both F and G mean "draw forward", + means "turn left 45°", and − means "turn right 45°" (see turtle graphics). The curve is usually drawn with different lengths for F and G.
The Sierpiński square curve can be similarly expressed:
- Alphabet: F, X
- Constants: F, +, −
- Axiom: F+XF+F+XF
- Production rules:
- X → XF−F+F−XF+F+XF−F+F−X
- Angle: 90
Arrowhead curve
[edit]The Sierpiński arrowhead curve is a fractal curve similar in appearance and identical in limit to the Sierpiński triangle.

The Sierpiński arrowhead curve draws an equilateral triangle with triangular holes at equal intervals. It can be described with two substituting production rules: (A → B-A-B) and (B → A+B+A). A and B recur and at the bottom do the same thing — draw a line. Plus and minus (+ and -) mean turn 60 degrees either left or right. The terminating point of the Sierpiński arrowhead curve is always the same provided you recur an even number of times and you halve the length of the line at each recursion. If you recur to an odd depth (order is odd) then you end up turned 60 degrees, at a different point in the triangle.
An alternate construction is given in the article on the de Rham curve: one uses the same technique as the de Rham curves, but instead of using a binary (base-2) expansion, one uses a ternary (base-3) expansion.
Code
[edit]Given the drawing functions void draw_line(double distance); and void turn(int angle_in_degrees);, the code to draw an (approximate) Sierpiński arrowhead curve looks like this:
void sierpinski_arrowhead_curve(unsigned order, double length)
{
// If order is even we can just draw the curve.
if ( 0 == (order & 1) ) {
curve(order, length, +60);
}
else /* order is odd */ {
turn( +60);
curve(order, length, -60);
}
}
void curve(unsigned order, double length, int angle)
{
if ( 0 == order ) {
draw_line(length);
} else {
curve(order - 1, length / 2, -angle);
turn(angle);
curve(order - 1, length / 2, angle);
turn(angle);
curve(order - 1, length / 2, -angle);
}
}
Representation as Lindenmayer system
[edit]
The Sierpiński arrowhead curve can be expressed by a rewrite system (L-system).
- Alphabet: X, Y
- Constants: F, +, −
- Axiom: XF
- Production rules:
- X → YF + XF + Y
- Y → XF − YF − X
Here, F means "draw forward", + means "turn left 60°", and − means "turn right 60°" (see turtle graphics).
See also
[edit]- Hilbert curve
- Koch snowflake
- Moore graph
- Murray polygon
- Peano curve
- List of fractals by Hausdorff dimension
- Recursion (computer science)
- Sierpiński triangle
References
[edit]- ^ Weisstein, Eric W. "Sierpiński Curve". MathWorld. Retrieved 21 January 2019.
- ^ Dickau, Robert M. (1996/7)"Two-dimensional L-systems", Robert's Math Figures. MathForum.org. Retrieved 21 January 2019.
- ^ Platzman, Loren K.; Bartholdi, John J. III (1989). "Spacefilling curves and the planar traveling salesman problem". Journal of the Association for Computing Machinery. 36 (4): 719–737. doi:10.1145/76359.76361.
- ^ Bartholdi, John J. III. "Some combinatorial applications of spacefilling curves". Georgia Institute of Technology. Archived from the original on 2012-08-03.
Further reading
[edit]- Peitgen, H.-O.; Jürgens, H.; Saupe, D. (2013) [1992]. Chaos and Fractals: New Frontiers of Science. Springer. ISBN 978-1-4757-4740-9.
- Stevens, Roger T. (1989). Fractal Programming in C. M&T Books. ISBN 978-1-55851-037-1.






