Selected area diffraction

Selected area (electron) diffraction (abbreviated as SAD or SAED) is a crystallographic experimental technique typically performed using a transmission electron microscope (TEM). It is a specific case of electron diffraction used primarily in material science and solid state physics as one of the most common experimental techniques. Especially with appropriate analytical software, SAD patterns (SADP) can be used to determine crystal orientation, measure lattice constants or examine its defects.
Principle
[edit]In transmission electron microscope, a thin crystalline sample is illuminated by parallel beam of electrons accelerated to energy of hundreds of kiloelectron volts. At these energies samples are transparent for the electrons if the sample is thinned enough (typically less than 100 nm). Due to the wave–particle duality, the high-energetic electrons behave as matter waves with wavelength of a few thousandths of a nanometer. The relativistic wavelength is given by
where is the Planck constant, is the electron rest mass, is the elementary charge, is the speed of light and is an electric potential accelerating the electrons (also called acceleration voltage).[1] For instance the acceleration voltage of 200 kV results in a wavelength of 2.508 pm.[2]

Since the spacing between atoms in crystals is about a hundred times larger, the electrons are diffracted on the crystal lattice, acting as a diffraction grating. Due to the diffraction, part of the electrons is scattered at particular angles (diffracted beams), while others pass through the sample without changing their direction (transmitted beams). In order to determine the diffraction angles, the electron beam normally incident to the atomic lattice can be seen as a planar wave, which is re-transmitted by each atom as a spherical wave. Due to the constructive interference, the spherical waves from number of diffracted beams under angles given, approximately, by the Bragg condition
where the integer is an order of diffraction and is the distance between atoms (if only one row of atoms is assumed as in the illustration aside) or a distance between atomic planes parallel to the beam (in a real 3D atomic structure). For finite samples this equation is only approximately correct.
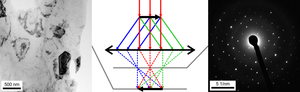
After being deflected by the microscope's magnetic lens, each set of initially parallel beams intersect in the back focal plane forming the diffraction pattern. The transmitted beams intersect right in the optical axis. The diffracted beams intersect at certain distance from the optical axis (corresponding to interplanar distance of the planes diffracting the beams) and under certain azimuth (corresponding to the orientation of the planes diffracting the beams). This allows to form a pattern of bright spots typical for SAD.[3]

SAD is called "selected" because it allows the user to select the sample area from which the diffraction pattern will be acquired. For this purpose, there is a selected area aperture located below the sample holder. It is a metallic sheet with several differently sized holes which can be inserted into the beam. The user can select the aperture of appropriate size and position it so that it only allows to pass the portion of beam corresponding to the selected area. Therefore, the resulting diffraction pattern will only reflect the area selected by the aperture. This allows to study small objects such as crystallites in polycrystalline material with a broad parallel beam.
Character of the resulting diffraction image depends on whether the beam is diffracted by one single crystal or by number of differently oriented crystallites for instance in a polycrystalline material. The single-crystalline diffractogram depicts a regular pattern of bright spots. This pattern can be seen as a two-dimensional projection of reciprocal crystal lattice. If there are more contributing crystallites, the diffraction image becomes a superposition of individual crystals' diffraction patterns. Ultimately, this superposition contains diffraction spots of all possible crystallographic plane systems in all possible orientations. For two reasons, these conditions result in a diffractogram of concentric rings:
- There are discrete spacings between various parallel crystallographic planes and therefore the beams satisfying the diffraction condition can only form diffraction spots in discrete distances from the transmitted beam.
- There are all possible orientations of crystallographic planes and therefore the diffraction spots are formed around the transmitted beam in the whole 360-degree azimuthal range.
Interpretation and analysis
[edit]
SAD analysis is widely used in material research for its relative simplicity and high information value. Once the sample is prepared and examined in a modern transmission electron microscope, the device allows for a routine diffraction acquisition in a matter of seconds. If the images are interpreted correctly, they can be used to identify crystal structures, determine their orientations, measure crystal characteristics, examine crystal defects or material textures. The course of analysis depends on whether the diffractogram depicts ring or spot diffraction pattern and on the quantity to be determined.
Software tools based on computer vision algorithms simplifies quantitative analysis.[4]
Spot diffraction pattern
[edit]If the SAD is taken from one a or a few single crystals, the diffractogram depicts a regular pattern of bright spots. Since the diffraction pattern can be seen as a two-dimensional projection of reciprocal crystal lattice, the pattern can be used to measure lattice constants, specifically the distances and angles between crystallographic planes. The lattice parameters are typically distinctive for various materials and their phases which allows to identify the examined material or at least differentiate between possible candidates.
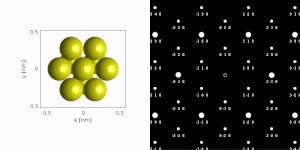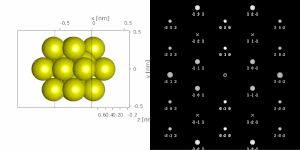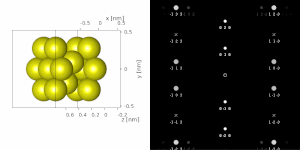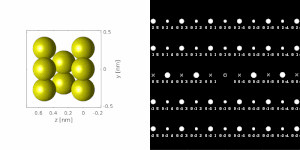
Even though the SAD-based analyses were not considered quantitative for a long time, computer tools brought accuracy and repeatability allowing to routinely perform accurate measurements of interplanar distances or angles on appropriately calibrated microscopes. Tools such as CrysTBox are capable of automated analysis achieving sub-pixel precision.[4]
If the sample is tilted against the electron beam, diffraction conditions are satisfied for different set of crystallographic planes yielding different constellation of diffraction spots. This allows to determine the crystal orientation, which can be used for instance to set up the orientation needed for particular experiment, to determine misorientation between adjacent grains or crystal twins.[2][4] Since different sample orientations provide different projections of the reciprocal lattice, they provide an opportunity to reconstruct the three-dimensional information lost in individual projections. A series of diffractograms varying in tilt can be acquired and processed with diffraction tomography analysis in order to reconstruct an unknown crystal structure.[5]
SAD can also be used to analyze crystal defects such as stacking faults.
Ring diffraction pattern
[edit]If the illuminated area selected by the aperture covers many differently oriented crystallites, their diffraction patterns superimpose forming an image of concentric rings. The ring diffractogram is typical for polycrystalline samples, powders or nanoparticles. Diameter of each ring corresponds to interplanar distance of a plane system present in the sample. Instead of information about individual grains or the sample orientation, this diffractogram provides more of a statistical information for instance about overall crystallinity or texture. Textured materials are characteristic by a non-uniform intensity distribution along the ring circumference despite crystallinity sufficient for generating smooth rings. Ring diffractograms can be also used to discriminate between nanocrystalline and amorphous phases.[2]
Not all the features depicted in the diffraction image are necessarily wanted. The transmitted beam is often too strong and needs to be shadowed with a beam-stopper in order to protect the camera. The beam-stopper typically shadows part of the useful information as well. Towards the rings center, the background intensity also gradually increases lowering the contrast of diffraction rings. Modern analytical software allows to minimize such unwanted image features and together with other functionalities improves the image readability it helps with image interpretation.[4]
Relation to other techniques
[edit]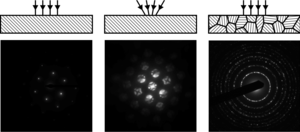
An SADP is acquired under parallel electron illumination. In the case of convergent beam, a convergent beam electron diffraction (CBED) is achieved.[6][3] The beam used in SAD is broad illuminating a wide sample area. In order to analyze only a specific sample area, the selected area aperture in the image plane is used. This is in contrast with nanodiffraction, where the site-selectivity is achieved using a beam condensed to a narrow probe.[3] SAD is important in direct imaging for instance when orienting the sample for high resolution microscopy or setting up dark-field imaging conditions.
High-resolution electron microscope images can be transformed into an artificial diffraction pattern using Fourier transform. Then, they can be processed the same way as real diffractograms allowing to determine crystal orientation, measure interplanar angles and distances even with picometric precision.[7]
SAD is similar to X-ray diffraction, but unique in that areas as small as several hundred nanometres in size can be examined, whereas X-ray diffraction typically samples areas much larger.
See also
[edit]- Diffraction
- Electron diffraction
- Transmission electron microscope
- Electron crystallography
- CrysTBox
- X-ray (Powder) diffraction
- Convergent beam electron diffraction
References
[edit]- ^ Kirkland, Earl (2010). Advanced computing in electron microscopy. New York: Springer. ISBN 978-1-4419-6533-2. OCLC 668095602.
- ^ a b c De Graef, Marc (2003-03-27). Introduction to Conventional Transmission Electron Microscopy. Cambridge University Press. doi:10.1017/cbo9780511615092. ISBN 978-0-521-62006-2.
- ^ a b c Fultz, B (2013). Transmission electron microscopy and diffractometry of materials. Heidelberg New York: Springer. ISBN 978-3-642-43315-3. OCLC 796932144.
- ^ a b c d Klinger, Miloslav (2017-07-07). "More features, more tools, more CrysTBox". Journal of Applied Crystallography. 50 (4). International Union of Crystallography (IUCr): 1226–1234. Bibcode:2017JApCr..50.1226K. doi:10.1107/s1600576717006793. ISSN 1600-5767.
- ^ Gemmi, Mauro; Mugnaioli, Enrico; Gorelik, Tatiana E.; Kolb, Ute; Palatinus, Lukas; Boullay, Philippe; Hovmöller, Sven; Abrahams, Jan Pieter (2019-07-19). "3D Electron Diffraction: The Nanocrystallography Revolution". ACS Central Science. 5 (8). American Chemical Society (ACS): 1315–1329. doi:10.1021/acscentsci.9b00394. ISSN 2374-7943. PMC 6716134. PMID 31482114.
- ^ Morniroli, Jean Paul (2004). Large-Angle Convergent-Beam Electron Diffraction Applications to Crystal Defects. Taylor & Francis. doi:10.1201/9781420034073. ISBN 978-2-901483-05-2.
- ^ Klinger, Miloslav; Polívka, Leoš; Jäger, Aleš; Tyunina, Marina (2016-04-12). "Quantitative analysis of structural inhomogeneity in nanomaterials using transmission electron microscopy". Journal of Applied Crystallography. 49 (3). International Union of Crystallography (IUCr): 762–770. Bibcode:2016JApCr..49..762K. doi:10.1107/s1600576716003800. ISSN 1600-5767.












