Jump to content

List of regular polytope compounds

Add links
From Wikipedia, the free encyclopedia
(Redirected from Regular compound tiling)

This article lists the regular polytope compounds in Euclidean, spherical and hyperbolic spaces.

Two dimensional compounds

[edit]

For any natural number n, there are n-pointed star regular polygonal stars with Schläfli symbols {n/m} for all m such that m < n/2 (strictly speaking {n/m}={n/(n−m)}) and m and n are coprime. When m and n are not coprime, the star polygon obtained will be a regular polygon with n/m sides. A new figure is obtained by rotating these regular n/m-gons one vertex to the left on the original polygon until the number of vertices rotated equals n/m minus one, and combining these figures. An extreme case of this is where n/m is 2, producing a figure consisting of n/2 straight line segments; this is called a degenerate star polygon.

In other cases where n and m have a common factor, a star polygon for a lower n is obtained, and rotated versions can be combined. These figures are called star figures, improper star polygons or compound polygons. The same notation {n/m} is often used for them, although authorities such as Grünbaum (1994) regard (with some justification) the form k{n} as being more correct, where usually k = m.

A further complication comes when we compound two or more star polygons, as for example two pentagrams, differing by a rotation of 36°, inscribed in a decagon. This is correctly written in the form k{n/m}, as 2{5/2}, rather than the commonly used {10/4}.

Coxeter's extended notation for compounds is of the form c{m,n,...}[d{p,q,...}]e{s,t,...}, indicating that d distinct {p,q,...}'s together cover the vertices of {m,n,...} c times and the facets of {s,t,...} e times. If no regular {m,n,...} exists, the first part of the notation is removed, leaving [d{p,q,...}]e{s,t,...}; the opposite holds if no regular {s,t,...} exists. The dual of c{m,n,...}[d{p,q,...}]e{s,t,...} is e{t,s,...}[d{q,p,...}]c{n,m,...}. If c or e are 1, they may be omitted. For compound polygons, this notation reduces to {nk}[k{n/m}]{nk}: for example, the hexagram may be written thus as {6}[2{3}]{6}.

Examples for n=2..10, nk≤30

2{2}
3{2}
4{2}
5{2}
6{2}
7{2}
8{2}
9{2}
10{2}
11{2}
12{2}
13{2}
14{2}
15{2}

2{3}
3{3}
4{3}
5{3}
6{3}
7{3}
8{3}
9{3}
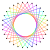10{3}
2{4}
3{4}
4{4}
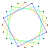5{4}
6{4}
7{4}

2{5}
3{5}
4{5}
5{5}
6{5}
2{5/2}
3{5/2}
4{5/2}
5{5/2}
6{5/2}
2{6}
3{6}
4{6}
5{6}

2{7}
3{7}
4{7}
2{7/2}
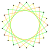3{7/2}
4{7/2}
2{7/3}
3{7/3}
4{7/3}
2{8}
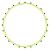3{8}
2{8/3}
3{8/3}

2{9}
3{9}
2{9/2}
3{9/2}
2{9/4}
3{9/4}
2{10}
3{10}
2{10/3}
3{10/3}

2{11}
2{11/2}
2{11/3}
2{11/4}
2{11/5}
2{12}
2{12/5}
2{13}
2{13/2}
2{13/3}
2{13/4}
2{13/5}
2{13/6}

2{14}
2{14/3}
2{14/5}
2{15}
2{15/2}
2{15/4}
2{15/7}

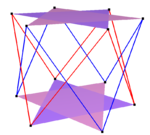
Regular skew polygons also create compounds, seen in the edges of prismatic compound of antiprisms, for instance:

Regular compound skew polygon
Compound
skew squares 		Compound
skew hexagons 		Compound
skew decagons
Two {2}#{ } Three {2}#{ } Two {3}#{ } Two {5/3}#{ }

Three dimensional compounds

[edit]

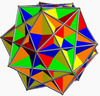
A regular polyhedron compound can be defined as a compound which, like a regular polyhedron, is vertex-transitive, edge-transitive, and face-transitive. With this definition there are 5 regular compounds.

Symmetry [4,3], Oh [5,3]+, I [5,3], Ih
Duality Self-dual Dual pairs
Image
Spherical
Polyhedra 2 {3,3} 5 {3,3} 10 {3,3} 5 {4,3} 5 {3,4}
Coxeter {4,3}[2{3,3}]{3,4} {5,3}[5{3,3}]{3,5} 2{5,3}[10{3,3}]2{3,5} 2{5,3}[5{4,3}] [5{3,4}]2{3,5}

Coxeter's notation for regular compounds is given in the table above, incorporating Schläfli symbols. The material inside the square brackets, [d{p,q}], denotes the components of the compound: d separate {p,q}'s. The material before the square brackets denotes the vertex arrangement of the compound: c{m,n}[d{p,q}] is a compound of d {p,q}'s sharing the vertices of an {m,n} counted c times. The material after the square brackets denotes the facet arrangement of the compound: [d{p,q}]e{s,t} is a compound of d {p,q}'s sharing the faces of {s,t} counted e times. These may be combined: thus c{m,n}[d{p,q}]e{s,t} is a compound of d {p,q}'s sharing the vertices of {m,n} counted c times and the faces of {s,t} counted e times. This notation can be generalised to compounds in any number of dimensions.[1]

If improper regular polyhedra (dihedra and hosohedra) are allowed, then two more compounds are possible: 2{3,4}[3{4,2}]{4,3} and its dual {3,4}[3{2,4}]2{4,3}.[2]

Euclidean and hyperbolic plane compounds

[edit]

There are eighteen two-parameter families of regular compound tessellations of the Euclidean plane. In the hyperbolic plane, five one-parameter families and seventeen isolated cases are known, but the completeness of this listing has not yet been proven.[2]

Euclidean regular compounds[2]
Tessellations Condition
Self-dual
{4,4}[(b2+c2){4,4}]{4,4} b ≥ c ≥ 0, b > 0
2{4,4}[2(b2+c2){4,4}]2{4,4} bc(b − c) > 0
Dual pairs
{3,6}[(b2+bc+c2){3,6}]2{6,3} 2{3,6}[(b2+bc+c2){6,3}]{6,3} b ≡ c mod 3
2{3,6}[2(b2+bc+c2){3,6}]4{6,3} 4{3,6}[2(b2+bc+c2){6,3}]2{6,3} b ≡ c mod 3, bc(b − c) > 0
{6,3}[2(b2+bc+c2){3,6}]2{3,6} 2{6,3}[2(b2+bc+c2){6,3}]{3,6} b ≡ c mod 3
2{6,3}[4(b2+bc+c2){3,6}]4{3,6} 4{6,3}[4(b2+bc+c2){6,3}]2{3,6} b ≡ c mod 3, bc(b − c) > 0
{3,6}[(b2+bc+c2){3,6}]{3,6} {6,3}[(b2+bc+c2){6,3}]{6,3} b ≢ c mod 3
2{3,6}[2(b2+bc+c2){3,6}]2{3,6} 2{6,3}[2(b2+bc+c2){6,3}]2{6,3} b ≢ c mod 3, bc(b − c) > 0
{6,3}[2(b2+bc+c2){3,6}] [2(b2+bc+c2){6,3}]{3,6} b ≢ c mod 3
2{6,3}[4(b2+bc+c2)2{3,6}] [4(b2+bc+c2){6,3}]2{3,6} b ≢ c mod 3, bc(b − c) > 0

A distinction must be made when an integer can be expressed in the forms b2+c2 or b2+bc+c2 in two different ways, e.g. 145 = 122 + 12 = 92 + 82, or 91 = 92 + 9 ⋅ 1 + 12 = 62 + 6 ⋅ 5 + 52. In such cases, Coxeter notates the sum explicitly, e.g. {4,4}[(144+1){4,4}]{4,4} as opposed to {4,4}[(81+64){4,4}]{4,4}.[2]

The following compounds of compact or paracompact hyperbolic tessellations were known to Coxeter in 1964, though a proof of completeness was not then known:[2]

Hyperbolic regular compounds[2]
Self-dual
{4,q}[2{q,q}]{q,4}
{3,8}[6{8,8}]{8,3}
{5,5}[6{10,10}]{5,5}
{4,5}[12{10,10}]{5,4}
{3,7}[9{7,7}]{7,3}
2{3,7}[18{7,7}]2{7,3}
Dual pairs
{3,2q}[3{q,2q}]2{2q,3} 2{3,2q}[3{2q,q}]{2q,3}
{4,5}[6{4,10}]2{4,5} 2{5,4}[6{10,4}]{5,4}
{3,7}[8{3,14}]2{3,7} 2{7,3}[8{14,3}]{7,3}
{3,7}[24{7,14}]2{7,3} 2{3,7}[24{14,7}]{7,3}
{3,9}[12{9,18}]2{9,3} 2{3,9}[12{18,9}]{9,3}
{2q,q}[2{q,2q}] [2{2q,q}]{q,2q}
2{3,7}[9{4,7}] [9{7,4}]2{7,3}
{3,9}[4{3,18}] [4{18,3}]{9,3}

The Euclidean and hyperbolic compound families {4,q}[2{q,q}]{q,4} appear because h{4,q} = {q,q}, i.e. taking alternate vertices of a {4,q} results in a {q,q}. They are thus the Euclidean and hyperbolic analogues of the spherical stella octangula, which is the q=3 case.[2]

It is also the case that h{2q,q} = {q,2q}, yielding the compound {2q,q}[2{q,2q}] and its dual [2{2q,q}]{q,2q}. Now if we take the dual of the {2q,q}, we obtain a third {q,2q} whose vertices are at the centres of alternate faces of the other two {q,2q}; this gives the compound {3,2q}[3{q,2q}]2{2q,3} and its dual 2{3,2q}[3{2q,q}]{2q,3}. These compounds are hyperbolic if q > 3 and Euclidean if q = 3. These compounds show an analogy to the spherical compounds {4,3,3}[2{3,3,4}], [2{4,3,3}]{3,3,4}, {3,4,3}[3{3,3,4}]2{3,4,3}, and 2{3,4,3}[3{4,3,3}]{3,4,3}.[2]

If one sets q = 8 in {4,q}[2{q,q}]{q,4}, and q = 4 in {3,2q}[3{q,2q}]2{2q,3}, then one obtains the special cases {4,8}[2{8,8}]{8,4} and {3,8}[3{4,8}]2{8,3}. The latter's {4,8}'s can be replaced by pairs of {8,8}'s according to the former, giving the self-dual compound {3,8}[6{8,8}]{8,3}.[2]

A few examples of Euclidean and hyperbolic regular compounds
Self-dual Duals Self-dual
2 {4,4} 2 {6,3} 2 {3,6} 2 {∞,∞}
{{4,4}} or a{4,4} or {4,4}[2{4,4}]{4,4}
+ or 		[2{6,3}]{3,6} a{6,3} or {6,3}[2{3,6}]
+ or 		{{∞,∞}} or a{∞,∞} or {4,∞}[2{∞,∞}]{∞,4}
+ or
3 {6,3} 3 {3,6} 3 {∞,∞}
2{3,6}[3{6,3}]{6,3} {3,6}[3{3,6}]2{6,3}
+ +
+ +

Four dimensional compounds

[edit]
Orthogonal projections
75 {4,3,3} 75 {3,3,4}

Coxeter lists 32 regular compounds of regular 4-polytopes in his book Regular Polytopes.[3] McMullen adds six in his paper New Regular Compounds of 4-Polytopes, in which he also proves that the list is now complete.[4] In the following tables, the superscript (var) indicates that the labeled compounds are distinct from the other compounds with the same symbols.

Self-dual regular compounds
Compound Constituent Symmetry Vertex arrangement Cell arrangement
120 {3,3,3} 5-cell [5,3,3], order 14400[3] {5,3,3} {3,3,5}
120 {3,3,3}(var) 5-cell order 1200[4] {5,3,3} {3,3,5}
720 {3,3,3} 5-cell [5,3,3], order 14400[4] 6{5,3,3} 6{3,3,5}
5 {3,4,3} 24-cell [5,3,3], order 14400[3] {3,3,5} {5,3,3}
Regular compounds as dual pairs
Compound 1 Compound 2 Symmetry Vertex arrangement (1) Cell arrangement (1) Vertex arrangement (2) Cell arrangement (2)
3 {3,3,4}[5] 3 {4,3,3} [3,4,3], order 1152[3] {3,4,3} 2{3,4,3} 2{3,4,3} {3,4,3}
15 {3,3,4} 15 {4,3,3} [5,3,3], order 14400[3] {3,3,5} 2{5,3,3} 2{3,3,5} {5,3,3}
75 {3,3,4} 75 {4,3,3} [5,3,3], order 14400[3] 5{3,3,5} 10{5,3,3} 10{3,3,5} 5{5,3,3}
75 {3,3,4} 75 {4,3,3} [5,3,3], order 14400[3] {5,3,3} 2{3,3,5} 2{5,3,3} {3,3,5}
75 {3,3,4} 75 {4,3,3} order 600[4] {5,3,3} 2{3,3,5} 2{5,3,3} {3,3,5}
300 {3,3,4} 300 {4,3,3} [5,3,3]+, order 7200[3] 4{5,3,3} 8{3,3,5} 8{5,3,3} 4{3,3,5}
600 {3,3,4} 600 {4,3,3} [5,3,3], order 14400[3] 8{5,3,3} 16{3,3,5} 16{5,3,3} 8{3,3,5}
25 {3,4,3} 25 {3,4,3} [5,3,3], order 14400[3] {5,3,3} 5{5,3,3} 5{3,3,5} {3,3,5}

There are two different compounds of 75 tesseracts: one shares the vertices of a 120-cell, while the other shares the vertices of a 600-cell. It immediately follows therefore that the corresponding dual compounds of 75 16-cells are also different.

Self-dual star compounds
Compound Symmetry Vertex arrangement Cell arrangement
5 {5,5/2,5} [5,3,3]+, order 7200[3] {5,3,3} {3,3,5}
10 {5,5/2,5} [5,3,3], order 14400[3] 2{5,3,3} 2{3,3,5}
5 {5/2,5,5/2} [5,3,3]+, order 7200[3] {5,3,3} {3,3,5}
10 {5/2,5,5/2} [5,3,3], order 14400[3] 2{5,3,3} 2{3,3,5}
Regular star compounds as dual pairs
Compound 1 Compound 2 Symmetry Vertex arrangement (1) Cell arrangement (1) Vertex arrangement (2) Cell arrangement (2)
5 {3,5,5/2} 5 {5/2,5,3} [5,3,3]+, order 7200[3] {5,3,3} {3,3,5} {5,3,3} {3,3,5}
10 {3,5,5/2} 10 {5/2,5,3} [5,3,3], order 14400[3] 2{5,3,3} 2{3,3,5} 2{5,3,3} 2{3,3,5}
5 {5,5/2,3} 5 {3,5/2,5} [5,3,3]+, order 7200[3] {5,3,3} {3,3,5} {5,3,3} {3,3,5}
10 {5,5/2,3} 10 {3,5/2,5} [5,3,3], order 14400[3] 2{5,3,3} 2{3,3,5} 2{5,3,3} 2{3,3,5}
5 {5/2,3,5} 5 {5,3,5/2} [5,3,3]+, order 7200[3] {5,3,3} {3,3,5} {5,3,3} {3,3,5}
10 {5/2,3,5} 10 {5,3,5/2} [5,3,3], order 14400[3] 2{5,3,3} 2{3,3,5} 2{5,3,3} 2{3,3,5}

There are also fourteen partially regular compounds, that are either vertex-transitive or cell-transitive but not both. The seven vertex-transitive partially regular compounds are the duals of the seven cell-transitive partially regular compounds.

Partially regular compounds as dual pairs
Compound 1
Vertex-transitive 		Compound 2
Cell-transitive 		Symmetry
2 16-cells[6] 2 tesseracts [4,3,3], order 384[3]
25 24-cell(var) 25 24-cell(var) order 600[4]
100 24-cell 100 24-cell [5,3,3]+, order 7200[3]
200 24-cell 200 24-cell [5,3,3], order 14400[3]
5 600-cell 5 120-cell [5,3,3]+, order 7200[3]
10 600-cell 10 120-cell [5,3,3], order 14400[3]
Partially regular star compounds as dual pairs
Compound 1
Vertex-transitive 		Compound 2
Cell-transitive 		Symmetry
5 {3,3,5/2} 5 {5/2,3,3} [5,3,3]+, order 7200[3]
10 {3,3,5/2} 10 {5/2,3,3} [5,3,3], order 14400[3]

Although the 5-cell and 24-cell are both self-dual, their dual compounds (the compound of two 5-cells and compound of two 24-cells) are not considered to be regular, unlike the compound of two tetrahedra and the various dual polygon compounds, because they are neither vertex-regular nor cell-regular: they are not facetings or stellations of any regular 4-polytope. However, they are vertex-, edge-, face-, and cell-transitive.

Euclidean 3-space compounds

[edit]

The only regular Euclidean compound honeycombs are an infinite family of compounds of cubic honeycombs, all sharing vertices and faces with another cubic honeycomb. This compound can have any number of cubic honeycombs. The Coxeter notation is {4,3,4}[d{4,3,4}]{4,3,4}.

Hyperbolic 3-space compounds

[edit]

C. W. L. Garner described two dual pairs of regular hyperbolic compound honeycombs in 1970: the compact pair 2{5,3,4}[5{4,3,5}] and [5{5,3,4}]2{4,3,5}, and the paracompact pair {6,3,3}[5{6,3,4}] and [5{4,3,6}]{3,3,6}. He did not consider vertex-regular compounds where the vertices are at infinity, or (reciprocally) cell-regular compounds where the cells are centred at infinity.[7] In 2019, Peter McMullen (who focused only on the compact case) pointed out and filled a gap in Garner's proof of completeness, so that it is now proven that 2{5,3,4}[5{4,3,5}] and [5{5,3,4}]2{4,3,5} are the only compact regular hyperbolic honeycomb compounds.[8]

Five dimensions and higher compounds

[edit]

There are no regular compounds in five or six dimensions. There are three known seven-dimensional compounds (16, 240, or 480 7-simplices), and six known eight-dimensional ones (16, 240, or 480 8-cubes or 8-orthoplexes). There is also one compound of n-simplices in n-dimensional space provided that n is one less than a power of two, and also two compounds (one of n-cubes and a dual one of n-orthoplexes) in n-dimensional space if n is a power of two.

The Coxeter notation for these compounds are (using αn = {3n−1}, βn = {3n−2,4}, γn = {4,3n−2}):

  • 7-simplexes: cγ7[16cα7]cβ7, where c = 1, 15, or 30
  • 8-orthoplexes: cγ8[16cβ8]
  • 8-cubes: [16cγ8]cβ8

The general cases (where n = 2k and d = 22k − k − 1, k = 2, 3, 4, ...):

  • Simplexes: γn−1[dαn−1]βn−1
  • Orthoplexes: γn[dβn]
  • Hypercubes: [dγn]βn

Euclidean honeycomb compound

[edit]

A known family of regular Euclidean compound honeycombs in five or more dimensions is an infinite family of compounds of hypercubic honeycombs, all sharing vertices and faces with another hypercubic honeycomb. This compound can have any number of hypercubic honeycombs. The Coxeter notation is δn[dδn]δn where δn = {∞} when n = 2 and {4,3n−3,4} when n ≥ 3.

Hyperbolic honeycomb compounds

[edit]

In four dimensions, Garner (1970) asserted the existence of {3,3,3,5}[26{5,3,3,5}]{5,3,3,3};[7] although neither justification nor construction was given, McMullen (2019) proved that this claim is correct.[8] McMullen showed the existence of the following compact compounds:[8]

  • 2{3,3,3,5}[17{4,3,3,5}] and dual [17{5,3,3,4}]2{5,3,3,3};
  • 10{3,3,3,5}[85{4,3,3,5}] and dual [85{5,3,3,4}]10{5,3,3,3};
  • {3,3,3,5}[26{5,3,3,5}]{5,3,3,3} (self-dual, comes in left- and right-handed forms);
  • 6{3,3,3,5}[156{5,3,3,5}]6{5,3,3,3} (self-dual, comes in left- and right-handed forms);
  • 12{3,3,3,5}[312{5,3,3,5}]12{5,3,3,3} (self-dual).

McMullen conjectures that this list is complete regarding the compact compounds. If any more compact compounds exist, they must involve {4,3,3,5} or {5,3,3,5} being inscribed in {5,3,3,3} (the only case not yet excluded).[8]

In five dimensions, there is only one regular hyperbolic honeycomb whose vertices are not at infinity: {3,4,3,3,3}. Thus there are no regular compounds conforming to Garner's restriction that the vertices of a vertex-regular compound should not be at infinity. In six dimensions or higher, there are no compact or paracompact regular hyperbolic honeycombs at all, and thus no compact or paracompact compounds exist.[7]

See also

[edit]

References

[edit]
  1. ^ Coxeter (1973), p. 48.
  2. ^ a b c d e f g h i Coxeter, H. S. M. (24 March 1964). "Regular compound tessellations of the hyperbolic plane". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 278 (1373): 147–167. Bibcode:1964RSPSA.278..147C. doi:10.1098/rspa.1964.0052.
  3. ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa Coxeter (1973). Table VII, p. 305
  4. ^ a b c d e McMullen (2018).
  5. ^ Klitzing, Richard. "Uniform compound stellated icositetrachoron".
  6. ^ Klitzing, Richard. "Uniform compound demidistesseract".
  7. ^ a b c Garner, C. W. L. (1970). "Compound honeycombs in hyperbolic space". Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences. 316 (152): 441–448. Bibcode:1970RSPSA.316..441G. doi:10.1098/rspa.1970.0089.
  8. ^ a b c d McMullen, Peter (2019). "Regular compounds of honeycombs in H3 and H4". Advances in Mathematics. 349: 56–83. doi:10.1016/j.aim.2019.04.006. Retrieved 12 October 2024.

Bibliography

[edit]
Retrieved from "https://wiki.riteme.site/w/index.php?title=List_of_regular_polytope_compounds&oldid=1260163439#Euclidean_and_hyperbolic_plane_compounds"