Resistor ladder

A resistor ladder is an electrical circuit made from repeating units of resistors, in specific configurations.

An R–2R ladder configuration is a simple and inexpensive way to perform digital-to-analog conversion (DAC), using repetitive arrangements of precise resistor networks in a ladder-like configuration.

History

A 1953 paper "Coding by Feedback Methods" describes "decoding networks" that convert numbers (in any base) represented by voltage sources or current sources connected to resistor networks in a "shunt resistor decoding network" (which in base 2 corresponds to the binary-weighted configuration) or in a "ladder resistor decoding network" (which in base 2 corresponds to R–2R configuration) into a single voltage output. The paper gives an advantage of R–2R that impedances seen by the sources are more equal.

Another historic description is in US Patent 3108266, filed in 1955, "Signal Conversion Apparatus".

Resistor string network

A string of many resistors connected between two reference voltages is called a "resistor string". The resistors act as voltage dividers between the referenced voltages. A Kelvin divider or string DAC is a string of equal valued resistors.

Analog-to-digital conversion

Each tap of the string generates a different voltage, which can be compared with another voltage: this is the basic principle of a flash ADC (analog-to-digital converter). The main disadvantage is that this architecture requires $2^{n}$ comparators, one for each resistor; and this number cannot be reduced by using an R-2R network because such a network would not have separate outputs for each voltage.

Digital-to-analog conversion

A resistor string can function as a DAC by having the bits of the binary number control electronic switches connected to each tap.

Binary weighted

The binary weighted configuration uses power of two multiples of a base resistor value. However, as the ratios of resistor values increases, the ability to trim the resistors to accurate ratio tolerances becomes diminished. More accurate ratios can be obtained by using similar values, as is used in R–2R ladder. Hence R–2R provides more accurate digital-to-analog conversion.

R–2R resistor ladder network (digital to analog conversion)

Figure 1: n-bit voltage mode R–2R resistor ladder DAC.

Voltage Mode

A voltage mode R–2R resistor ladder network is shown in Figure 1. Bit a_n−1 (most significant bit, MSB) through bit a₀ (least significant bit, LSB) are driven from digital logic gates. Ideally, the bit inputs are switched between V = 0 (logic 0) and V = V_ref (logic 1). The R–2R network causes these digital bits to be weighted in their contribution to the output voltage V_out. Depending on which bits are set to 1 and which to 0, the output voltage (V_out) will have a corresponding stepped value between 0 and V_ref minus the value of the minimal step, corresponding to bit 0. The actual value of V_ref (and the voltage of logic 0) will depend on the type of technology used to generate the digital signals.

For a digital value VAL, of a R–2R DAC with N bits and 0 V/V_ref logic levels, the output voltage V_out is:

$V_{o}=V_{ref}\times {\tfrac {\text{Value}}{2^{N}}}$

For example, if N = 5 (hence 2^N = 32) and V_ref = 3.3 V (typical CMOS logic 1 voltage), then V_out will vary between 0 volts (VAL = 0 = 00000₂) and the maximum (VAL = 31 = 11111₂):

$V_{o}=3.3\,{\text{V}}\times {\tfrac {31}{2^{5}}}=3.196875\,{\text{V}}$

with steps (corresponding to VAL = 1 = 00001₂)

$\Delta V_{o}=3.3\,{\text{V}}\times {\tfrac {1}{2^{5}}}=0.103125\,{\text{V}}$

The R–2R ladder is inexpensive and relatively easy to manufacture, since only two resistor values are required (or even one, if R is made by placing a pair of 2R in parallel, or if 2R is made by placing a pair of R in series). It is fast and has fixed output impedance R. The R–2R ladder operates as a string of current dividers, whose output accuracy is solely dependent on how well each resistor is matched to the others. Small inaccuracies in the MSB resistors can entirely overwhelm the contribution of the LSB resistors. This may result in non-monotonic behavior at major crossings, such as from 01111₂ to 10000₂.

Depending on the type of logic gates used and design of the logic circuits, there may be transitional voltage spikes at such major crossings even with perfect resistor values. These can be filtered with capacitance at the output node (the consequent reduction in bandwidth may be significant in some applications). Finally, the 2R resistance is in series with the digital-output impedance. High-output-impedance gates (e.g., LVDS) may be unsuitable in some cases. For all of the above reasons (and doubtless others), this type of DAC tends to be restricted to a relatively small number of bits; although integrated circuits may push the number of bits to 14 or even more, 8 bits or fewer is more typical.

The R–2R DAC described above directly outputs a voltage and so is called voltage mode (or sometimes normal mode).

Current Mode

Since the output impedance is independent of digital code, the analog output may equally-well be taken as a current into a virtual ground, a configuration called current mode (or sometimes inverted mode). Using current mode, the gain of the DAC may be adjusted with a series resistor at the reference voltage terminal. The current for all bits pass through an equivalent resistance of 2R to ground. The less significant the bit, the more resistors its signal must pass through. At each node each bit's current is divided by two.

Accuracy of R–2R resistor ladders

Resistors used with the more significant bits must be proportionally more accurate than those used with the less significant bits; for example, in the R–2R network discussed above, inaccuracies in the bit-4 (MSB) resistors must be insignificant compared to 1⁄32 (~3.1%) of R. Further, to avoid problems at the 10000₂-to-01111₂ transition, the sum of the inaccuracies in the lower bits must also be significantly less than that. The required accuracy doubles with each additional bit: for 8 bits, the accuracy required will be better than 1⁄256 (~0.4%).

However, variances for resistances when manufactured in a single component tend to be much lower than variances between components or between batches of manufacturing, and hence a resistor network can be purchased as a single component. And within integrated circuits, R–2R networks may be printed directly onto a single substrate using thin-film technology for higher accuracy. Even so, they must often be laser-trimmed to achieve the required precision. Such on-chip resistor ladders for digital-to-analog converters achieving 16-bit accuracy have been demonstrated.

Resistor ladder with unequal rungs

Figure 2: 4-bit linear R–2R DAC using unequal resistors

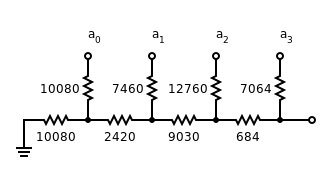
It is not necessary that each "rung" of the R–2R ladder use the same resistor values. It is only necessary that the "2R" value matches the sum of the "R" value plus the Thévenin-equivalent resistance of the lower-significance rungs. Figure 2 shows a linear 4-bit DAC with unequal resistors.

This allows a reasonably accurate DAC to be created from a heterogeneous collection of resistors by forming the DAC one bit at a time. At each stage, resistors for the "rung" and "leg" are chosen so that the rung value matches the leg value plus the equivalent resistance of the previous rungs. The rung and leg resistors can be formed by pairing other resistors in series or parallel in order to increase the number of available combinations. This process can be automated.

See also

• Logarithmic resistor ladder
• Digital-to-analog converter
• Covox Speech Thing
• Voltage ladder

External links

• ECE209: DAC Lecture Notes - Ohio State University
• EE247: D/A Converters - Berkeley University of California
• Simplified DAC/ADC Lecture Notes - University of Michigan
• Tutorial MT-014: String DACs and Fully-Decoded DACs - Analog Devices
• Tutorial MT-015: Binary DACs - Analog Devices
• Tutorial MT-016: Segmented DACs - Analog Devices
• Tutorial MT-018: Intentionally Nonlinear DACs - Analog Devices
• R2R Resistor Ladder Networks - BI Technologies
• R/2R Ladder Networks Application Note - TT Electronics