Pythagoreanism

Pythagoreanism originated in the 6th century BC, based on and around the teachings and beliefs held by Pythagoras and his followers, the Pythagoreans. Pythagoras established the first Pythagorean community in the ancient Greek colony of Kroton, in modern Calabria (Italy) circa 530 BC. Early Pythagorean communities spread throughout Magna Graecia.
Already during Pythagoras' life it is likely that the distinction between the akousmatikoi ("those who listen"), who is conventionally regarded as more concerned with religious, and ritual elements, and associated with the oral tradition, and the mathematikoi ("those who learn") existed. The ancient biographers of Pythagoras, Iamblichus (c.245-c.325 AD) and his master Porphyry (c.234–c.305 AD) seem to make the distinction of the two as that of 'beginner' and 'advanced'. As the Pythagorean cenobites practiced an esoteric path, like the mystery schools of antiquity, the adherents, akousmatikoi, following initiation became mathematikoi. It is wrong to say that the Pythagoreans were superseded by the Cynics in the 4th century BC, but it seems to be a distinction mark of the Cynics to disregard the hierarchy and protocol, ways of initiatory proceedings significant for the Pythagorean community; subsequently did the Greek philosophical traditions become more diverse. The Platonic Academy was arguably a Pythagorean cenobitic institution, outside the city walls of Athens in the 4th century BC. As a sacred grove dedicated to Athena, and Hecademos (Academos). The academy, the sacred grove of Academos, may have existed, as the contemporaries seem to have believed, since the Bronze Age, even pre-existing the Trojan War. Yet according to Plutarch it was the Athenian strategos (general) Kimon Milkiadou (c.510–450 BC) who converted this, "waterless and arid spot into a well watered grove, which he provided with clear running-tracks and shady walks". Plato (less known as Aristocles) lived almost a hundred years later, circa 427 to 348 BC. On the other hand, it seems likely that this was a part of the re-building of Athens led by Kimon Milkiadou and Themistocles, following the Achaemenid destruction of Athens in 480-479 BC - The Second Persian War. Kimon is at least associated with the building of the southern Wall of Themistocles, the city walls of ancient Athens. It seems likely that the Athenians saw this as a rejuvenation of the sacred grove of Academos.
Following political instability in Magna Graecia, some Pythagorean philosophers moved to mainland Greece while others regrouped in Rhegium. By about 400 BC the majority of Pythagorean philosophers had left Italy. Pythagorean ideas exercised a marked influence on Plato and through him, on all of Western philosophy. Many of the surviving sources on Pythagoras originate with Aristotle and the philosophers of the Peripatetic school.
As a philosophic tradition, Pythagoreanism was revived in the 1st century BC, giving rise to Neopythagoreanism. The worship of Pythagoras continued in Italy and as a religious community Pythagoreans appear to have survived as part of, or deeply influenced, the Bacchic cults and Orphism. Even the early Christian cenobitic traditions may be seen in light of the matematikoi. The biblical Greek name for 'disciple' is 'mathetes' [1].
History
[edit]
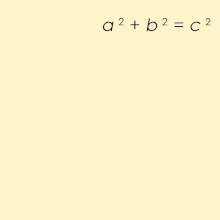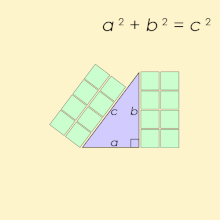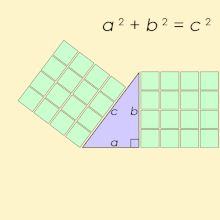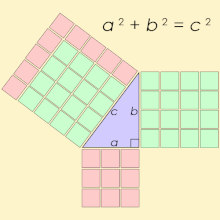

Pythagoras was already well known in ancient times for his supposed mathematical achievement of the Pythagorean theorem.[2] Pythagoras had been credited with discovering that in a right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides. In ancient times Pythagoras was also noted for his discovery that music had mathematical foundations. Antique sources that credit Pythagoras as the philosopher who first discovered music intervals also credit him as the inventor of the monochord, a straight rod on which a string and a movable bridge could be used to demonstrate the relationship of musical intervals.[3]
Much of the surviving sources on Pythagoras originated with Aristotle and the philosophers of the Peripatetic school, which founded historiographical academic traditions such as biography, doxography and the history of science. The surviving 5th century BC sources on Pythagoras and early Pythagoreanism are void of supernatural elements, while surviving 4th century BC sources on Pythagoras' teachings introduced legend and fable. Philosophers who discussed Pythagoreanism, such as Anaximander, Andron of Ephesus, Heraclides and Neanthes had access to historical written sources as well as the oral tradition about Pythagoreanism, which by the 4th century BC was in decline. Neopythagorean philosophers, who authored many of the surviving sources on Pythagoreanism, continued the tradition of legend and fantasy.[4]
The earliest surviving ancient source on Pythagoras and his followers is a satire by Xenophanes, on the Pythagorean beliefs on the transmigration of souls.[5] Xenophanes wrote of Pythagoras that:
Once they say that he was passing by when a puppy was being whipped,
And he took pity and said:
"Stop! Do not beat it! For it is the soul of a friend
That I recognised when I heard it giving tongue."[5]
In a surviving fragment from Heraclitus, Pythagoras and his followers are described as follows:
Pythagoras, the son of Mnesarchus, practised inquiry beyond all other men and selecting of these writings made for himself a wisdom or made a wisdom of his own: a polymathy, an imposture.[6]
Two other surviving fragments of ancient sources on Pythagoras are by Ion of Chios and Empedocles. Both were born in the 490s, after Pythagoras' death. By that time, he was known as a sage and his fame had spread throughout Greece.[7] According to Ion, Pythagoras was:
... distinguished for his manly virtue and modesty, even in death has a life which is pleasing to his soul, if Pythagoras the wise truly achieved knowledge and understanding beyond that of all men.[7]
Empedocles described Pythagoras as "a man of surpassing knowledge, master especially of all kinds of wise works, who had acquired the upmost wealth of understanding."[8] In the 4th century BC the Sophist Alcidamas wrote that Pythagoras was widely honored by Italians.[9]
Today scholars typically distinguish two periods of Pythagoreanism: early-Pythagoreanism, from the 6th until the 5th century BC, and late-Pythagoreanism, from the 4th until the 3rd century BC.[10] The Spartan colony of Taranto in Italy became the home for many practitioners of Pythagoreanism and later for Neopythagorean philosophers. Pythagoras had also lived in Crotone and Metaponto, both of which were Achaean colonies.[11] Early-Pythagorean sects lived in Croton and throughout Magna Graecia. They espoused to a rigorous life of the intellect and strict rules on diet, clothing and behavior. Their burial rites were tied to their belief in the immortality of the soul.[10]
Early-Pythagorean sects were closed societies and new Pythagoreans were chosen based on merit and discipline. Ancient sources record that early-Pythagoreans underwent a five-year initiation period of listening to the teachings (akousmata) in silence. Initiates could through a test become members of the inner circle. However, Pythagoreans could also leave the community if they wished.[12] Iamblichus listed 235 Pythagoreans by name, among them 17 women whom he described as the "most famous" women practitioners of Pythagoreanism. It was customary that family members became Pythagoreans, as Pythagoreanism developed into a philosophic tradition that entailed rules for everyday life and Pythagoreans were bound by secrets. The home of Pythagoras was known as the site of mysteries.[13]
Pythagoras had been born on the island of Samos at around 570 BC and left his homeland at around 530 BC in opposition to the policies of Polycrates. Before settling in Croton, Pythagoras had traveled throughout Egypt and Babylonia. In Croton, Pythagoras established the first Pythagorean community, described as a secret society, and attained political influence. In the early 5th century BC Croton acquired great military and economic importance. Pythagoras emphasised moderation, piety, respect for elders and of the state, and advocated a monogamous family structure. The Croton Council appointed him to official positions. Among others Pythagoras was in charge of education in the city. His influence as political reformer reputedly extended to other Greek colonies in southern Italy and in Sicily. Pythagoras died shortly after an arson attack on the Pythagorean meeting place in Croton.[14]
The anti-Pythagorean attacks in c. 508 BC were headed by Cylon of Croton.[14][15] Pythagoras escaped to Metapontium. After these initial attacks and the death of Pythagoras, Pythagorean communities in Croton and elsewhere continued to flourish. At around 450 BC attacks on Pythagorean communities were carried out across Magna Graecia. In Croton, a house where Pythagoreans gathered was set on fire and all but two of the Pythagorean philosophers burned alive. Pythagorean meeting places in other cities were also attacked and philosophic leaders killed. These attacks occurred in the context of widespread violence and destruction in Magna Graecia. Following the political instability in the region, some Pythagorean philosophers fled to mainland Greece while others regrouped in Rhegium. By about 400 BC the majority of Pythagorean philosophers had left Italy. Archytas remained in Italy and ancient sources record that he was visited there by young Plato in the early 4th century BC. The Pythagorean schools and societies died out from the 4th century BC. Pythagorean philosophers continued to practice, albeit no organised communities were established.[14]
According to surviving sources by the Neopythagorean philosopher Nicomachus, Philolaus was the successor of Pythagoras.[16] According to Cicero (de Orat. III 34.139), Philolaus was teacher of Archytas.[17] According to the Neoplatonist philosopher Iamblichus, Archytas in turn became the head of the Pythagorean school about a century after the Pythagoras' death.[18] Philolaus, Eurytus and Xenophilus are identified by Aristoxenus as the teachers of the last generation of Pythagoreans.[17]
Philosophic traditions
[edit]Following Pythagoras' death, disputes about his teachings led to the development of two philosophical traditions within Pythagoreanism in Italy: akousmatikoi and mathēmatikoi. The mathēmatikoi recognised the akousmatikoi as fellow Pythagoreans, but because the mathēmatikoi allegedly followed the teachings of Hippasus, the akousmatikoi philosophers did not recognise them. Despite this, both groups were regarded by their contemporaries as practitioners of Pythagoreanism.[19]
The akousmatikoi were superseded in the 4th century BC as a significant mendicant school of philosophy by the Cynics. Mathēmatikoi philosophers were in the 4th century BC absorbed into the Platonic school of Speusippus, Xenocrates and Polemon. As a philosophic tradition, Pythagoreanism was revived in the 1st century BC, giving rise to Neopythagoreanism.[20] The worship of Pythagoras continued in Italy in the two intervening centuries. As a religious community Pythagoreans appear to have survived as part of, or deeply influenced, the Bacchic cults and Orphism.[21]
Akousmatikoi
[edit]
The akousmatikoi believed that humans had to act in appropriate ways. The Akousmata (translated as "oral saying") was the collection of all the sayings of Pythagoras as divine dogma. The tradition of the akousmatikoi resisted any reinterpretation or philosophical evolution of Pythagoras' teachings. Individuals who strictly followed most akousmata were regarded as wise. The akousmatikoi philosophers refused to recognise that the continuous development of mathematical and scientific research conducted by the mathēmatikoi was in line with Pythagoras's intention. Until the demise of Pythagoreanism in the 4th century BC, the akousmatikoi continued to engage in a pious life by practicing silence, dressing simply and avoiding meat, for the purpose of attaining a privileged afterlife. The akousmatikoi engaged deeply in questions of Pythagoras' moral teachings, concerning matters such as harmony, justice,[22] ritual purity and moral behavior.[23]
Mathēmatikoi
[edit]
The mathēmatikoi acknowledged the religious underpinning of Pythagoreanism and engaged in mathēma (translated as "learning" or "studying") as part of their practice. While their scientific pursuits were largely mathematical, they also promoted other fields of scientific study in which Pythagoras had engaged during his lifetime. A sectarianism developed between the dogmatic akousmatikoi and the mathēmatikoi, who in their intellectual activism became regarded as increasingly progressive. This tension persisted until the 4th century BC, when the philosopher Archytas engaged in advanced mathematics as part of his devotion to Pythagoras' teachings.[22]
Today, Pythagoras is mostly remembered for his mathematical ideas, and by association with the work early Pythagoreans did in advancing mathematical concepts and theories on harmonic musical intervals, the definition of numbers, proportion and mathematical methods such as arithmetic and geometry. The mathēmatikoi philosophers claimed that numbers were at the heart of everything and constructed a new view of the cosmos. In the mathēmatikoi tradition of Pythagoreanism the Earth was removed from the center of the universe. The mathēmatikoi believed that the Earth, along with other celestial bodies, orbited around a central fire. This, they believed, constituted a celestial harmony.[24]
Rituals
[edit]Pythagoreanism was a philosophic tradition as well as a religious practice. As a religious community they relied on oral teachings and worshiped the Pythian Apollo, the oracular god of Delphic Oracle. Pythagoreans preached an austere life.[25] They believed that the soul was buried in the body, which acted as a tomb for the soul in this life.[26] The highest reward a human could attain was for the soul to join in the life of the gods and thus escaped the cycle of reincarnation in another human body.[27] Like the practitioners of Orphism, a religious tradition that developed in parallel to Pythagorean religious practice, Pythagoreanism held that the soul was buried in the body as a punishment for a committed offense and that the soul could be purified.[28] Aside from conducting their daily lives according to strict rules Pythagorean also engaged in rituals to attain purity.[29] The 4th century Greek historian and sceptic philosopher Hecataeus of Abdera asserted that Pythagoras had been inspired by ancient Egyptian philosophy in his use of ritual regulations and his belief in reincarnation.[2]
Philosophy
[edit]Early Pythagoreanism was based on research and the accumulation of knowledge from the books written by other philosophers.[6] Pythagoras' philosophic teachings made direct reference to the philosophy of Anaximander, Anaximenes of Miletus and Pherecydes of Syros.[6] Of the Pythagorean philosophers, Hippasus, Alcmaeon, Hippon, Archytas and Theodorus, written sources have survived.[30]
Arithmetic and numbers
[edit]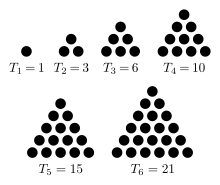
Pythagoras, in his teachings focused on the significance of numerology, he believed that numbers themselves explained the true nature of the Universe. Numbers were in the Greek world of Pythagoras' days natural numbers – that is positive integers (there was no zero). But unlike their Greek contemporaries, the Pythagorean philosophers represented numbers graphically, not symbolically through letters. Pythagoreans used dots, also known as psiphi (pebbles), to represent numbers in triangles, squares, rectangles and pentagons. This enabled a visual comprehension of mathematics and allowed for a geometrical exploration of numerical relationships. Pythagorean philosophers investigated the relationship of numbers extensively. They defined perfect numbers as those that were equal to the sum of all their divisors. For example: 28 = 1 + 2 + 4 + 7 + 14.[31] The theory of odd and even numbers was central to Pythagorean arithmetic. This distinction was for the Pythagorean philosophers direct and visual, as they arranged triangular dots so that the even and odd numbers successively alternate: 2, 4, 6, ... 3, 5, 7, ...[32]
Early-Pythagorean philosophers such as Philolaus and Archytas held the conviction that mathematics could help in addressing important philosophical problems.[33] In Pythagoreanism numbers became related to intangible concepts. The one was related to the intellect and being, the two to thought, the number four was related to justice because 2 * 2 = 4 and equally even. A dominant symbolism was awarded to the number three, Pythagoreans believed that the whole world and all things in it are summed up in this number, because end, middle and beginning give the number of the whole. The triad had for Pythagoreans an ethical dimension, as the goodness of each person was believed to be threefold: prudence, drive and good fortune.[34]
Pythagoreans thought numbers existed "outside of [human] minds" and separate from the world.[35] They had many mystical and magical interpretations of the roles of numbers in governing existence.[35]
Geometry
[edit]The Pythagoreans engaged with geometry as a liberal philosophy which served to establish principles and allowed theorems to be explored abstractly and rationally. Pythagorean philosophers believed that there was a close relationship between numbers and geometrical forms. Early-Pythagorean philosophers proved simple geometrical theorems, including "the sum of the angles of a triangle equals two right angles". Pythagoreans also came up with three of the five platonic solids: the tetrahedron, the cube and the dodecahedron. The sides of a regular dodecahedron are regular pentagons, which for Pythagoreans symbolised health. They also revered the pentagram, as each diagonal divides the two others at the golden ratio.[32] When linear geometrical figures replaced the dots, the combination of Babylonian algebra and Pythagorean arithmetic provided the basis for Greek geometric algebra. By attempting to establish a system of concrete and permanent rules, Pythagoreans helped to establish strict axiomatic procedures of solving mathematical problems.[36]
Music
[edit]

Pythagoras pioneered the mathematical and experimental study of music. He objectively measured physical quantities, such as the length of a string and discovered quantitative mathematical relationships of music through arithmetic ratios. Pythagoras attempted to explain subjective psychological and aesthetic feelings, such as the enjoyment of musical harmony. Pythagoras and his students experimented systematically with strings of varying length and tension, with wind instruments, with brass discs of the same diameter but different thickness, and with identical vases filled with different levels of water. Early Pythagoreans established quantitative ratios between the length of a string or pipe and the pitch of notes and the frequency of string vibration.[36]
Pythagoras is credited with discovering that the most harmonious musical intervals are created by the simple numerical ratio of the first four natural numbers which derive respectively from the relations of string length: the octave (1/2), the fifth (2/3) and the fourth (3/4).[36] The sum of those numbers 1 + 2 + 3 + 4 = 10 was for Pythagoreans the perfect number, because it contained in itself "the whole essential nature of numbers". Werner Heisenberg has called this formulation of musical arithmetic as "among the most powerful advances of human science" because it enables the measurement of sound in space.[37]
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.[38] This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions."[39]
The fact that mathematics could explain the human sentimental world had a profound impact on the Pythagorean philosophy. Pythagoreanism became the quest for establishing the fundamental essences of reality. Pythagorean philosophers advanced the unshakable belief that the essence of all things are numbers and that the universe was sustained by harmony.[37] According to ancient sources music was central to the lives of those practicing Pythagoreanism. They used medicines for the purification (katharsis) of the body and, according to Aristoxenus, music for the purification of the soul. Pythagoreans used different types of music to arouse or calm their souls,[40] and certain stirring songs could have notes that existed in the same ratio as the "distances of the heavenly bodies from the centre of" Earth.[35]
Harmony
[edit]For Pythagoreans, harmony signified the "unification of a multifarious composition and the agreement of unlike spirits". In Pythagoreanism, numeric harmony was applied in mathematical, medical, psychological, aesthetic, metaphysical and cosmological problems. For Pythagorean philosophers, the basic property of numbers was expressed in the harmonious interplay of opposite pairs. Harmony assured the balance of opposite forces.[41] Pythagoras had in his teachings named numbers and the symmetries of them as the first principle and called these numeric symmetries harmony.[42] This numeric harmony could be discovered in rules throughout nature. Numbers governed the properties and conditions of all beings and were regarded the causes of being in everything else. Pythagorean philosophers believed that numbers were the elements of all beings and the universe as a whole was composed of harmony and numbers.[34]
Cosmology
[edit]
The philosopher Philolaus, one of the most prominent figures in Pythagoreanism,[44] was the precursor of Copernicus in moving the earth from the center of the cosmos and making it a planet.[44] According to Aristotle's student Eudemus of Cyprus, the first philosopher to determine quantitatively the size of the known planets and the distance between them was Anaximander, a teacher to Pythagoras, in the 6th century BC. Historic sources credit the Pythagorean philosophers with being the first to attempt a clarification of the planet sequence.[45] The early-Pythagorean philosopher Philolaus believed that limited and unlimited things were the components of the cosmos, and these had existed ever since. The center of the universe, according to Philolaus, was the number one (hēn), which equated to the unity of Monism. Philolaus called the number one an "even-odd" because it was able to generate both even and odd numbers. When one was added to an odd number it produced an even number, and when added to an even number it produced an odd number. Philolaus further reasoned that the fitting together of the earth and the universe corresponded to the construction of the number one out of the even and the odd. Pythagorean philosophers believed that the even was unlimited and the odd was limited.[46]
Aristotle recorded in the 4th century BC on the Pythagorean astronomical system:
- It remains to speak of the earth, of its position, of the question whether it is at rest or in motion, and of its shape. As to its position, there is some difference of opinion. Most people–all, in fact, who regard the whole heaven as finite–say it lies at the center. But the Italian philosophers known as Pythagoreans take the contrary view. At the centre, they say, is fire, and the earth is one of the stars, creating night and day by its circular motion about the center. They further construct another earth in opposition to ours to which they give the name counterearth.[47]
It is not known whether Philolaus believed Earth to be round or flat,[48] but he did not believe the earth rotated, so that the Counter-Earth and the Central Fire were both not visible from Earth's surface, or at least not from the hemisphere where Greece was located.[44] But the conclusion of Pythagorean philosophers that the universe is not geocentric was not based on empirical observation. Instead, as Aristotle noted, the Pythagorean view of the astronomical system was grounded in a fundamental reflection on the value of individual things and the hierarchical order of the universe.[45]
Pythagoreans believed in a musica universalis. They reasoned that stars must produce a sound because they were large swiftly moving bodies. Pythagoreans also determined that stars revolved at distances and speeds that were proportional to each other. They reasoned that because of this numerical proportion the revolution of the stars produced a harmonic sound.[45] The early-Pythagorean philosopher Philolaus argued that the structure of the cosmos was determined by the musical numerical proportions of the diatonic octave, which contained the fifth and fourth harmonic intervals.[46]
Justice
[edit]Pythagoreans equated justice with geometrical proportion, because proportion ensured that each part receives what it is due.[49] Early-Pythagoreans believed that after the death of the body, the soul would be punished or rewarded. Humans could, through their conduct, ensure that their soul was admitted to another world. The reincarnation in this world equated to a punishment. In Pythagoreanism life in this world is social[50] and in the realm of society justice existed when each part of society received its due. The Pythagorean tradition of universal justice was later referenced by Plato. For Pythagorean philosophers the soul was the source of justice and through the harmony of the soul, divinity could be achieved. Injustice inverted the natural order. According to the 4th century BC philosopher Heraclides Ponticus, Pythagoras taught that "happiness consists in knowledge of the perfection of the numbers of the soul.[49] A surviving fragment from the 3rd century BC by the late-Pythagorean philosopher Aesara reasoned that:
I think human nature provides a common standard of law and justice for both the family and the city. Whoever follows the paths within and searches will discover; for within is law and justice, which is the proper arrangement of the soul.[51]
Body and soul
[edit]Pythagoreans believed that body and soul functioned together, and a healthy body required a healthy psyche.[52] Early Pythagoreans conceived of the soul as the seat of sensation and emotion. They regarded the soul as distinct from the intellect.[53] However, only fragments of the early Pythagorean texts have survived, and it is not certain whether they believed the soul was immortal. The surviving texts of the Pythagorean philosopher Philolaus indicate that while early Pythagoreans did not believe that the soul contained all psychological faculties, the soul was life and a harmony of physical elements. As such the soul passed away when certain arrangements of these elements ceased to exist.[54]
However, the teaching most securely identified with Pythagoras is metempsychosis, or the "transmigration of souls", which holds that every soul is immortal and, upon death, enters into a new body.[55][56][57][58][59][excessive citations] Pythagorean metempsychosis resembles the teachings of the Orphics, although its version contains substantial differences. Unlike the Orphics, who considered metempsychosis a cycle of grief that could be escaped by attaining liberation from it, Pythagoras seems to postulate an eternal, endless reincarnation where subsequent lives would not be conditioned by any action done in the previous.[60]
Vegetarianism
[edit]
Some Medieval authors refer to a "Pythagorean diet", entailing the abstention from eating meat, beans or fish.[62] Pythagoreans believed that a vegetarian diet fostered a healthy body and enhanced the search for Arete. The purpose of vegetarianism in Pythagoreanism was not self-denial; instead, it was regarded as conducive to the best in a human being. Pythagoreans advanced a grounded theory on the treatment of animals. They believed that any being that experienced pain or suffering should not have pain inflicted on it unnecessarily. Because it was not necessary to inflict pain on animals for humans to enjoy a healthy diet, they believed that animals should not be killed for the purpose of eating them. The Pythagoreans advanced the argument that unless an animal posed a threat to a human, it was not justifiable to kill an animal and that doing so would diminish the moral status of a human. By failing to show justice to the animal, humans diminish themselves.[52]
Pythagoreans believed that human beings were animals, but with an advanced intellect and therefore humans had to purify themselves through training. Through purification humans could join the psychic force that pervaded the cosmos. Pythagoreans reasoned that the logic of this argument could not be avoided by killing an animal painlessly. The Pythagoreans also thought that animals were sentient and minimally rational.[63] The arguments advanced by Pythagoreans convinced numerous of their philosopher contemporaries to adopt a vegetarian diet.[52] The Pythagorean sense of kinship with non-humans positioned them as a counterculture in the dominant meat-eating culture.[63] The philosopher Empedocles is said to have refused the customary blood sacrifice by offering a substitute sacrifice after his victory in a horse race in Olympia.[45]
Late-Pythagorean philosophers were absorbed into the Platonic school of philosophy and in the 4th century BC the head of the Platonic Academy Polemon included vegetarianism in his concept of living according to nature.[64] In the 1st century AD Ovid identified Pythagoras as the first opponent to meat-eating.[63] But the fuller argument Pythagoreans advanced against the maltreatment of animals did not sustain. Pythagoreans had argued that certain types of food arouse the passions and hindered spiritual ascent. Thus Porphyry would rely on the teachings of the Pythagoreans when arguing that abstinence from eating meat for the purpose of spiritual purification should be practiced only by philosophers, whose aim was to reach a divine state.[65]
Female philosophers
[edit]The biographical tradition on Pythagoras holds that his mother, wife and daughters were part of his inner circle.[66] Women were given equal opportunity to study as Pythagoreans and learned practical domestic skills in addition to philosophy.[67]

Many of the surviving texts of women Pythagorean philosophers are part of a collection, known as pseudoepigrapha Pythagorica, which was compiled by Neopythagoreans in the 1st or 2nd century. Some surviving fragments of this collection are by early-Pythagorean women philosophers, while the bulk of surviving writings are from late-Pythagorean women philosophers who wrote in the 4th and 3rd century BC.[10] Female Pythagoreans are some of the first female philosophers from which texts have survived.
Theano of Croton, the wife of Pythagoras, is considered a major figure in early-Pythagoreanism. She was noted as distinguished philosopher and in the lore that surrounds her, is said to have taken over the leadership of the school after his death. Text fragments have also survived from women philosophers of the late-Pythagorean period. These include Perictione I, Perictione II, Aesara of Lucania and Phintys of Sparta.[12]
Scholars believe that Perictione I was an Athenian and contemporary of Plato, because in On the Harmony of Woman she wrote in Ionic and used the same terms of virtues as Plato had done in his Republic: andreia, sophrosyne, dikaiosyne and sophia.[12] In On the Harmony of Woman Perictione I outlines the condition that enable women to nurture wisdom and self-control. These virtues will, according to Perictione I, bring "worthwhile things" for a woman, her husband, her children, the household and even the city "if, at any rate, such a woman should govern cities and tribes". Her assertion that a wife should remain devoted to her husband, regardless of his behavior, has been interpreted by scholars as a pragmatic response to the legal rights of women in Athens.[68] The woman Pythagorean philosopher Phyntis was Spartan and is believed to have been the daughter of a Spartan admiral killed in the battle of Arginusae in 406 BC.[12] Phyntis authored the treatise Moderation of Women, in which she assigned the virtue of moderation to women, but asserted that "courage and justice and wisdom are common to both" men and women. Phyntis defended the right of women to philosophise.[68]
Influence on Plato and Aristotle
[edit]Pythagoras' teachings and Pythagoreanism influenced Plato's writings on physical cosmology, psychology, ethics and political philosophy in the 5th century BC. However, Plato adhered to the dominant Greek philosophy, and the Platonic philosophy suppressed the combination of experimental method and mathematics which was an inherent part of Pythagoreanism.[69] The influence of Pythagoreanism extended throughout and beyond antiquity because the Pythagorean doctrine of reincarnation was recounted in Plato's Gorgias, Phaedo, and Republic, while the Pythagorean cosmology was discussed in Plato's Timaeus. The possible influence of Pythagoreanism on Plato's concept of harmony and the Platonic solids has been discussed extensively. Plato's dialogues have become an important surviving source of Pythagorean philosophic arguments.[70] Plato referenced Philolaus in Phaedo and wrote a Platonic adaptation of Philolaus' metaphysical system of limiters and unlimiteds. Plato also quoted from one of the surviving Archytas fragments in the Republic. However, Plato's views that the primary role of mathematics was to turn the soul towards the world of forms, as expressed in Timaeus, is regarded as Platonic philosophy, rather than Pythagorean.[33]
Aristotle in the 4th century BC rejected mathematics as a tool for investigation and understanding of the world. He believed that numbers constituted simply a quantitative determinant and had no ontological value.[69] Aristotle's discussion of Pythagorean philosophy is difficult to interpret, because he had little patience for Pythagorean philosophic arguments, and Pythagoreanism does not fit with his philosophic doctrine.[71] In On the Heavens, Aristotle refuted the Pythagorean doctrine on the harmony of the spheres.[72] Nevertheless, he wrote a treatise on the Pythagoreans of which only fragments survive, in which he treats Pythagoras as a wonder-working religious teacher.[73]
Neopythagoreanism
[edit]The Neopythagoreans were a school and a religious community. The revival of Pythagoreanism has been attributed to Publius Nigidius Figulus, Eudorus of Alexandria and Arius Didymus. In the 1st century AD Moderatus of Gades and Nicomachus of Gerasa emerged as leading teachers of Neopythagoreanism.[74][75] The most significant Neopythagorean teacher was Apollonius of Tyana in the 1st century AD, who was regarded as a sage and lived as an ascetic. The last Neopythagorean philosopher was Numenius of Apamea in the 2nd century. Neopythagoreanism remained an elite movement which in the 3rd century merged into Neoplatonism.[74]
Neopythagoreans combined Pythagorean teachings with Platonic, Peripatetic, Aristotelian and Stoic philosophic traditions. Two tendencies within Neopythagorean philosophy emerged, one that owed much to Stoic monism and another that relied on Platonic dualism. Neopythagoreans refined the idea of God and located him beyond the finite so that God could not come into contact with anything corporeal. Neopythagoreans insisted on a spiritual worship of God and that life had to be purified through abstinence.[74]
Neopythagoreans manifested a strong interest in numerology and the superstitious aspects of Pythagoreanism. They combined this with the teachings of Plato's philosophic successors. Neopythagorean philosophers engaged in the common ancient practice of ascribing their doctrines to the designated founder of their philosophy and by crediting their doctrines to Pythagoras himself, they hoped to gain authority for their views.[70]
Later influence
[edit]On early Christianity
[edit]
Christianity was influenced by a Christianised form of Platonism, which had been set out in the four books of the Corpus Areopagiticum or Corpus Dionysiacum: The Celestrial Hierarchy, The Ecclesiastical Hierarchy, On Divine Names and The Mystical Theology. Having been attributed to Pseudo-Dionysius the Areopagite, the books explained the relationship among celestial beings, humans, God and the universe. At the heart of the explanation were numbers. According to The Celestrial Hierarchy, the universe consisted of a threefold division: heaven, earth and hell. Sunlight lit up the universe and was proof of God's presence.[76] In the Middle Ages this numerological division of the universe was credited to the Pythagoreans, while early on it was regarded as an authoritative source of Christian doctrine by Photius and John of Sacrobosco. The Corpus Areopagiticum or Corpus Dionysiacum was to be referenced in the late Middle Ages by Dante and in the Renaissance a new translation of it was produced by Marsilio Ficino.[77]
Early Christian theologians, such as Clement of Alexandria, adopted the ascetic doctrines of the neopythagoreans.[74] The moral and ethical teachings of Pythagorean influenced early Christianity and assimilated into early Christian texts. The Sextou gnomai (Sentences of Sextus), a Hellenistic Pythagorean text modified to reflect a Christian viewpoint, existed from at least the 2nd century and remained popular among Christians well into the Middle Ages. The Sentences of Sextus consisted of 451 sayings or principles, such as injunctions to love the truth, to avoid the pollution of the body with pleasure, to shun flatterers and to let one's tongue be harnessed by one's mind. The contents of the Sentences of Sextus was attributed by Iamblichus, the 1st century biographer of Pythagoras, to Sextus Pythagoricus. The assertion was repeated subsequently by Saint Jerome. In the 2nd century many of the Sentences of Sextus were cited by Plutarch as Pythagorean aphorisms. The Sentences of Sextus were translated into Syriac, Latin and Arabic, then the written language of both Muslims and Jews, but only in the Latin world did they become a guide to daily life that was widely circulated.[78]
On numerology
[edit]
1st century treatises of Philo and Nicomachus popularised the mystical and cosmological symbolism Pythagoreans attributed to numbers. This interest in Pythagorean views on the importance of numbers was sustained by mathematicians such as Theon of Smyrna, Anatolius and Iamblichus. These mathematicians relied on Plato's Timaeus as their source for Pythagorean philosophy.[82]
In the Middle Ages studies and adaptations of Timaeus solidified the view that there was a numerical explanation for proportion and harmony among learned men. Pythagoreanism, as mediated in Plato's Timaeus, spurred increasingly detailed studies of symmetry and harmony. Intellectuals pondered how knowledge of the geometry in which God had arranged the universe could be applied to life. By the 12th century Pythagorean numerological concepts had become a universal language in Medieval Europe and were no longer recognised as Pythagorean.[82] Writers such as Thierry of Chartres, William of Conches and Alexander Neckham referenced classical writers that had discussed Pythagoreanism, including Cicero, Ovid and Pliny, leading them to believe that mathematics was the key to understanding astronomy and nature. Another important text on Pythagorean numerology was Boethius's De arithmetica, which was widely reproduced in the West. Boethius had relied on Nicomachus's writings as a source of Pythagoreanism.[83]
The 11th-century Byzantine professor of philosophy Michael Psellus popularised Pythagorean numerology in his treatise on theology, arguing that Plato was the inheritor of the Pythagorean secret. Psellus also attributed arithmetical inventions by Diophantus to Pythagoras. Psellus thought to reconstruct Iamblichus' 10 book encyclopedia on Pythagoreanism from surviving fragments, leading to the popularisation of Iamblichus' description of Pythagorean physics, ethics and theology at the Byzantine court. Psellus was reputably in the possession of the Hermetica, a set of texts thought to be genuinely antique and which would be prolifically reproduced in the late Middle Ages. Manuel Bryennios introduced Pythagorean numerology to Byzantine music with his treatise Harmonics. He argued that the octave was essential in attaining perfect harmony.[84]
In the Jewish communities the development of the Kabbalah as esoteric doctrine became associated with numerology. It was only in the 1st century that Philo of Alexandria, developed a Jewish Pythagoreanism. In the 3rd century Hermippus popularised the belief that Pythagoras had been the basis for establishing key dates in Judaism. In the 4th century this assertion was further developed by Aristobulus. The Jewish Pythagorean numerology developed by Philo held that God as the unique One was the creator of all numbers, of which seven was the most divine and ten the most perfect. The medieval edition of the Kabbalah focused largely on a cosmological scheme of creation, in reference to early Pythagorean philosophers Philolaus and Empedocles and helped to disseminate Jewish Pythagorean numerology.[85]
On mathematics
[edit]
Nicomachus' treatises were well known in Greek, Latin and the Arabic worlds. In the 9th century an Arabic translation of Nicomachus' Introduction to Arithmetic was published.[86] The Arabic translations of Nicomachus' treatises were in turn translated into Latin by Gerard of Cremona, making them part of the Latin tradition of numerology. The Pythagorean theorem was referenced in Arabic manuscripts.[83] Scholars in the Arabic world displayed a strong interest in Pythagorean concepts. In the 10th century Abu al-Wafa' Buzjani discussed multiplication and division in a treatise on arithmetic for business administrators in reference to Nicomachus. However, the primary interest of Islamic arithmeticians was in solving practical problems, such as taxation, measurement, the estimation of agricultural values and business applications for the buying and selling of goods. There was little interest for the Pythagorean numerology that developed in the Latin world. The primary arithmetical system used by Islamic mathematicians was based on Hindu arithmetic, which rejected the notion that the relations between numbers and geometrical forms were symbolic.[87]
Besides the enthusiasm that developed in the Latin and Byzantine worlds in the Middle Ages for Pythagorean numerology, the Pythagorean tradition of perfect numbers inspired profound scholarship in mathematics. In the 13th century Leonardo of Pisa, better known as Fibonacci, published the Libre quadratorum (The Book of Squares). Fibonacci had studied scripts from Egypt, Syria, Greece and Sicily, and was learned in Hindu, Arabic and Greek methodologies. Using the Hindu–Arabic numeral system instead of the Roman numerals, he explored numerology as it had been set forth by Nicomachus. Fibonacci observed that square numbers always arise through the addition of consecutive odd numbers starting with unity. Fibonacci put forward a method of generating sets of three square numbers that satisfied the relationship first attributed to Pythagoras by Vitruvius, that a2 + b2 = c2. This equation is now known as the Pythagorean triple.[88]
In the Middle Ages
[edit]In the Middle Ages, from the 5th until the 15th century, Pythagorean texts remained popular. Late antique writers had produced adaptions of the Sentences of Sextus as The golden verses of Pythagoras. The Golden Verses gained popularity and Christian adaptations of it appeared. These Christian adaptations were adopted by monastic orders, such as Saint Benedict, as authoritative Christian doctrine. In the Latin medieval western world, the Golden Verses became a widely reproduced text.[78]

Although the concept of the quadrivium originated with Archytas in the 4th century BC and was a familiar concept among academics in the antiquity, it was attributed as Pythagorean in the 5th century by Proclus. According to Proclus, Pythagoreanism divided all mathematical sciences into four categories: arithmetic, music, geometry and astronomy. Boethius developed this theory further, arguing that a fourfold path led to the attainment of knowledge. Arithmetic, music, geometry and astronomy went on to become the essential parts of curriculums in medieval schools and universities. In the 12th century Pythagoras was credited by Hugh of Saint Victor with having written a book on quadrivium. The role of harmony had its roots in the triadic thinking of Plato and Aristotle and included the trivium of grammar, rhetoric and dialectic. From the 9th century onwards, both the quadrivium and the trivium were commonly taught in schools and the newly emerging universities. They came to be known as the Seven liberal arts.[90]
In the early 6th century the Roman philosopher Boethius popularised Pythagorean and Platonic conceptions of the universe and expounded the supreme importance of numerical ratios.[91] The 7th century Bishop Isidore of Seville expressed his preference for the Pythagorean vision of a universe governed by the mystical properties of certain numbers, over the newly emerging Euclidean notion that knowledge could be built through deductive proofs. Isidore relied on the arithmetic of Nicomachus, who had fashioned himself as heir of Pythagoras, and took things further by studying the etymology of the name of each number.[77] The 12th century theologian Hugh of Saint Victor found Pythagorean numerology so alluring that he set out to explain the human body entirely in numbers. In the 13th century the fashion for numerology dwindled. The Christian scholar Albertus Magnus rebuked the preoccupation with Pythagorean numerology, arguing that nature could not only be explained in terms of numbers.[83] Plato's Timaeus became a popular source on the mystical and cosmological symbolism Pythagoreans attributed to numbers. The preoccupation for finding a numerical explanation for proportion and harmony culminated in the French cathedrals of the 11th, 12th and 13th century.[76]

Arabic translations of the Golden Verses were produced in the 11th and 12th centuries.[78] In the Medieval Islamic world a Pythagorean tradition took hold, whereby spheres or stars produced music. This doctrine was further developed by Ikhwan al-Safa and al-Kindi, who pointed to the similarity between the harmony of music and the harmony of the soul. But Islamic philosophers such as al-Farabi and Ibn Sina vehemently rejected this Pythagorean doctrine.[93] in Kitab al-Musiqa al-Kabir Al-Farabi rejected the notion of celestial harmony on the grounds that it was "plainly wrong" and that it was not possible for the heavens, orbs and stars to emit sounds through their motions.[72]
The four books of the Corpus Areopagiticum or Corpus Dionysiacum (The Celestrial Hierarchy, The Ecclesiastical Hierarchy, On Divine Names and The Mystical Theology) by Pseudo-Dionysius the Areopagite became enormously popular during the Middle Ages in the Byzantine world, where they had first been published in the 1st century, but also the Latin world when they were translated in the 9th century. The division of the universe into heaven, earth and hell, and the 12 orders of heaven were credited as Pythagoras' teachings by an anonymous biographer, who was quoted in the treatise of the 9th century Byzantine patriarch Photius. The 13th century astronomer and mathematician John of Sacrobosco in turn credited Pseudo-Dionysius when discussing the twelve signs of the zodiac.[76]
In the Middle Ages various classical texts that discussed Pythagorean ideas were reproduced and translated. Plato's Timaeus was translated and republished with commentary in the Arab and Jewish worlds. In the 12th century the study of Plato gave rise to a vast body of literature explicating the glory of God as it reflected in the orderliness of the universe. Writers such as Thierry of Chartres, William of Conches and Alexander Neckham referenced not only Plato but also other classical authors that had discussed Pythagoreanism, including Cicero, Ovid and Pliny. William of Conches argued that Plato was an important Pythagorean. In this medieval Pythagorean understanding of Plato, God was a craftsman when he designed the universe.[83]
On Western science
[edit]
In the De revolutionibus, Copernicus cites three pythagorean philosophers as precursors of the Heliocentric Theory:
- At first I found in Cicero that Hicetas supposed the earth to move. Later I also discovered in Plutarch that others were of this opinion. I have decided to set his words down here, so that they may be available to everybody: "Some think that the earth remains at rest. But Philolaus the Pythagorean believes that, like the sun and moon, it revolves around the fire in an oblique circle. Heraclides of Pontus and Ecphantus the Pythagorean make the earth move, not in a progressive motion, but like a wheel in a rotation from west to east about its own center.[94]
In the 16th century Vincenzo Galilei challenged the prevailing Pythagorean wisdom about the relationship between pitches and weights attached to strings. Vincenzo Galilei, the father of Galileo Galilei, engaged in an extended public exchange with his former teacher Zarlino. Zarlino supported the theory that if two weights in the ratio of 2 to 1 were attached to two strings, the pitches generated by the two strings would produce the octave. Vincenzo Galilei proclaimed that he had been a committed Pythagorean, until he "ascertained the truth by means of experiment, the teacher of all things." He devised an experiment which showed that the weights attached to the two strings needed to increase as the square of the string length.[95] This public challenge to prevailing numerology in musical theory triggered an experimental and physical approach to acoustics in the 17th century. Acoustics emerged as a mathematical field of music theory and later an independent branch of physics. In the experimental investigation of sound phenomena, numbers had no symbolic meaning and were merely used to measure physical phenomena and relationships such as frequency and vibration of a string.[96]
Many of the most eminent 17th century natural philosophers in Europe, including Francis Bacon, Descartes, Beeckman, Kepler, Mersenne, Stevin and Galileo, had a keen interest in music and acoustics.[97] By the late 17th century it was accepted that sound travels like a wave in the air at a finite speed and experiments to establish the speed of sound were carried out by philosophers attached to the French Academy of Sciences, the Accademia del Cimento and the Royal Society.[98]
At the height of the Scientific Revolution, as Aristotelianism declined in Europe, the ideas of early-Pythagoreanism were revived. Mathematics regained importance and influenced philosophy as well as science. Mathematics was used by Kepler, Galileo, Descartes, Huygens and Newton to advance physical laws that reflected the inherent order of the universe. Twenty-one centuries after Pythagoreas had taught his disciples in Italy, Galileo announced to the world that "the great book of nature" could only be read by those who understood the language of mathematics. He set out to measure whatever is measurable, and to render everything measurable that is not.[99] The Pythagorean concept of cosmic harmony deeply influenced western science. It served as the basis for Kepler's harmonices mundi and Leibniz's pre-established harmony.[41] Albert Einstein believed that through this pre-established harmony, the productive unison between the spiritual and material world was possible.[41]
The Pythagorean belief that all bodies are composed of numbers and that all properties and causes could be expressed in numbers, served as the basis for a mathematization of science. This mathematization of the physical reality climaxed in the 20th century. The pioneer of physics Werner Heisenberg argued that "this mode of observing nature, which led in part to a true dominion over natural forces and thus contributes decisively to the development of humanity, in an unforeseen manner vindicated the Pythagorean faith".[99]
See also
[edit]- Dyad (Greek philosophy)
- Esoteric cosmology
- Hippasus
- Ionian School (philosophy)
- Incommensurable magnitudes
- Ipse dixit
- Mathematical beauty
- Mathematicism
- Pyrrhonism
- Sacred geometry
- Tetractys
- Unit-point atomism
References
[edit]- ^ Otto Neugebauer (1969). The Exact Sciences in Antiquity (Republication of 1957 Brown University Press 2nd ed.). Courier Dover Publications. p. 36. ISBN 0-486-22332-9.
- ^ a b Christoph Riedweg (2008). Pythagoras: His Life, Teaching, and Influence. Cornell University Press. p. 26. ISBN 978-0-8014-7452-1.
- ^ Christoph Riedweg (2008). Pythagoras: His Life, Teaching, and Influence. Cornell University Press. p. 27. ISBN 978-0-8014-7452-1.
- ^ Leonid Zhmud (2012). Pythagoras and the Early Pythagoreans. Oxford University Press. p. 29. ISBN 978-0-19-928931-8.
- ^ a b Leonid Zhmud (2012). Pythagoras and the Early Pythagoreans. Oxford University Press. p. 30. ISBN 978-0-19-928931-8.
- ^ a b c Leonid Zhmud (2012). Pythagoras and the Early Pythagoreans. Oxford University Press. p. 33. ISBN 978-0-19-928931-8.
- ^ a b Leonid Zhmud (2012). Pythagoras and the Early Pythagoreans. Oxford University Press. p. 38. ISBN 978-0-19-928931-8.
- ^ Leonid Zhmud (2012). Pythagoras and the Early Pythagoreans. Oxford University Press. p. 39. ISBN 978-0-19-928931-8.
- ^ Leonid Zhmud (2012). Pythagoras and the Early Pythagoreans. Oxford University Press. p. 44. ISBN 978-0-19-928931-8.
- ^ a b c Michelle Ballif; Michael G. Moran (2005). Classical Rhetorics and Rhetoricians: Critical Studies and Sources. Greenwood Publishing Group. p. 315. ISBN 978-0-313-32178-8.
- ^ Pomeroy, Sarah B. (2013). Pythagorean Women. Baltimore, MD: The Johns Hopkins University Press. p. xvi. ISBN 978-1-4214-0957-3.
- ^ a b c d Michelle Ballif; Michael G. Moran (2005). Classical Rhetorics and Rhetoricians: Critical Studies and Sources. Greenwood Publishing Group. p. 316. ISBN 978-0-313-32178-8.
- ^ Pomeroy, Sarah B. (2013). Pythagorean Women. Baltimore, MD: The Johns Hopkins University Press. p. 1. ISBN 978-1-4214-0957-3.
- ^ a b c Richard D. McKirahan (2011). Philosophy Before Socrates (Second Edition): An Introduction with Texts and Commentary: An Introduction with Texts and Commentary. Hackett Publishing. p. 79. ISBN 978-1-60384-612-7.
- ^ Willers, Michael (2009). Algebra: The x and y of Everyday Math (2009 ed.). Quid Publishing. p. 43. ISBN 978-1-4351-1400-5.
- ^ August Böckh (1819). Philolaos des Pythagoreers Lehren nebst den Bruchstücken seines Werkes. In der Vossischen Buchhandlung. p. 14.
Pythagoras Lehren nebst den Bruchstücken seines Werkes.
- ^ a b Stanford Encyclopedia of Philosophy. "Philolaus". Retrieved 30 May 2015.
- ^ Walter William Rouse Ball (2013). A Short Account of the History of Mathematics. Courier Corporation. ISBN 978-0-486-20630-1.
- ^ Richard D. McKirahan (2011). Philosophy Before Socrates (Second Edition): An Introduction with Texts and Commentary: An Introduction with Texts and Commentary. Hackett Publishing. pp. 88–89. ISBN 978-1-60384-612-7.
- ^ Charles H. Kahn (2001). Pythagoras and the Pythagoreans. Hackett Publishing. p. 72. ISBN 978-1-60384-682-0.
- ^ Charles H. Kahn (2001). Pythagoras and the Pythagoreans. Hackett Publishing. pp. 73–74. ISBN 978-1-60384-682-0.
- ^ a b Richard D. McKirahan (2011). Philosophy Before Socrates (Second Edition): An Introduction with Texts and Commentary: An Introduction with Texts and Commentary. Hackett Publishing. p. 89. ISBN 978-1-60384-612-7.
- ^ Richard D. McKirahan (2011). Philosophy Before Socrates (Second Edition): An Introduction with Texts and Commentary: An Introduction with Texts and Commentary. Hackett Publishing. p. 90. ISBN 978-1-60384-612-7.
- ^ Richard D. McKirahan (2011). Philosophy Before Socrates (Second Edition): An Introduction with Texts and Commentary: An Introduction with Texts and Commentary. Hackett Publishing. p. 91. ISBN 978-1-60384-612-7.
- ^ Charles H. Kahn (2001). Pythagoras and the Pythagoreans. Hackett Publishing. p. 21. ISBN 978-1-60384-682-0.
- ^ Charles H. Kahn (2001). Pythagoras and the Pythagoreans. Hackett Publishing. pp. 21–22. ISBN 978-1-60384-682-0.
- ^ Charles H. Kahn (2001). Pythagoras and the Pythagoreans. Hackett Publishing. p. 52. ISBN 978-1-60384-682-0.
- ^ Gabriele Cornelli; Richard McKirahan; Constantinos Macris (2013). On Pythagoreanism. Walter de Gruyter. p. 174. ISBN 978-3-11-031850-0.
- ^ Gabriele Cornelli; Richard McKirahan; Constantinos Macris (2013). On Pythagoreanism. Walter de Gruyter. p. 84. ISBN 978-3-11-031850-0.
- ^ Leonid Zhmud (2012). Pythagoras and the Early Pythagoreans. Oxford University Press. p. 415. ISBN 978-0-19-928931-8.
- ^ Constantine J. Vamvacas (2009). The Founders of Western Thought – The Presocratics. Springer Science & Business Media. p. 64. ISBN 978-1-4020-9791-1.
- ^ a b Constantine J. Vamvacas (2009). The Founders of Western Thought – The Presocratics. Springer Science & Business Media. p. 65. ISBN 978-1-4020-9791-1.
- ^ a b The Cambridge Companion to Early Greek Philosophy. Cambridge University Press. 1999. p. 84. ISBN 978-0-521-44667-9.
- ^ a b Constantine J. Vamvacas (2009). The Founders of Western Thought – The Presocratics. Springer Science & Business Media. p. 72. ISBN 978-1-4020-9791-1.
- ^ a b c Singer, Charles (1949). A Short History of Science to the Nineteenth Century. Oxford: Oxford University Press. pp. 18–19. ISBN 1-306-39093-1. OCLC 869524436.
- ^ a b c Constantine J. Vamvacas (2009). The Founders of Western Thought – The Presocratics. Springer Science & Business Media. p. 68. ISBN 978-1-4020-9791-1.
- ^ a b Constantine J. Vamvacas (2009). The Founders of Western Thought – The Presocratics. Springer Science & Business Media. p. 69. ISBN 978-1-4020-9791-1.
- ^ Bruce Benward and Marilyn Nadine Saker (2003). Music: In Theory and Practice, seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. ISBN 978-0-07-294262-0.
- ^ Kenneth Sylvan Guthrie, David R. Fideler (1987). The Pythagorean Sourcebook and Library: An Anthology of Ancient Writings which Relate to Pythagoras and Pythagorean Philosophy, p.24. Red Wheel/Weiser. ISBN 9780933999510.
- ^ Christoph Riedweg (2008). Pythagoras: His Life, Teaching, and Influence. Cornell University Press. p. 30. ISBN 978-0-8014-7452-1.
- ^ a b c Constantine J. Vamvacas (2009). The Founders of Western Thought – The Presocratics. Springer Science & Business Media. p. 70. ISBN 978-1-4020-9791-1.
- ^ Constantine J. Vamvacas (2009). The Founders of Western Thought – The Presocratics. Springer Science & Business Media. p. 71. ISBN 978-1-4020-9791-1.
- ^ Dante and the Early Astronomers by M. A. Orr, 1913
- ^ a b c Philolaus, Stanford Encyclopedia of Philosophy.
- ^ a b c d Christoph Riedweg (2008). Pythagoras: His Life, Teaching, and Influence. Cornell University Press. p. 84. ISBN 978-0-8014-7452-1.
- ^ a b Christoph Riedweg (2008). Pythagoras: His Life, Teaching, and Influence. Cornell University Press. p. 85. ISBN 978-0-8014-7452-1.
- ^ Aristotle. "13". On the Heavens. Vol. II. Retrieved Apr 17, 2016.
- ^ Burch 1954: 272–273, quoted in Philolaus, Stanford Encyclopedia of Philosophy.
- ^ a b David R. Fideler (1987). The Pythagorean Sourcebook and Library. Red Wheel/Weiser. p. 33. ISBN 978-1-60925-394-3.
- ^ Hans Kelsen (2000). What is Justice?: Justice, Law, and Politics in the Mirror of Science: Collected Essays. The Lawbook Exchange. p. 99. ISBN 978-1-58477-101-2.
- ^ Ian Michael Plant (2004). Women Writers of Ancient Greece and Rome: An Anthology. Equinox Publishing. p. 81. ISBN 978-1-904768-02-9.
- ^ a b c Gordon Lindsay Campbell (2014). The Oxford Handbook of Animals in Classical Thought and Life. Oxford University Press. p. 539. ISBN 978-0-19-103515-9.
- ^ Prudence Allen (2005). The Concept of Woman: The Early Humanist Reformation, 1250-1500, Part 1. Wm. B. Eerdmans Publishing. p. 5. ISBN 978-0-8028-3346-4.
- ^ Prudence Allen (2005). The Concept of Woman: The Early Humanist Reformation, 1250-1500, Part 1. Wm. B. Eerdmans Publishing. p. 22. ISBN 978-0-8028-3346-4.
- ^ Charles H. Kahn (2001). Pythagoras and the Pythagoreans. Hackett. ISBN 0-87220-575-4.
- ^ Zhmud 2012, p. 232.
- ^ Ferguson 2008, p. 5.
- ^ Burkert 1985, pp. 300–301.
- ^ Copleston 2003, pp. 30–31.
- ^ Leonid Zhmud (2012). Pythagoras and the Early Pythagoreans. OUP Oxford. pp. 232–233. ISBN 978-0-19-928931-8.
- ^ Richard D. McKirahan (2011). Philosophy Before Socrates (Second Edition): An Introduction with Texts and Commentary: An Introduction with Texts and Commentary. Hackett Publishing. p. 88. ISBN 978-1-60384-612-7.
- ^ See for instance the popular treatise by Antonio Cocchi, Del vitto pitagorico per uso della medicina, Firenze 1743, which initiated a debate on the "Pythagorean diet".
- ^ a b c Gordon Lindsay Campbell (2014). The Oxford Handbook of Animals in Classical Thought and Lifen. Oxford University Press. p. 540. ISBN 978-0-19-103515-9.
- ^ Charles H. Kahn (2001). Pythagoras and the Pythagoreans. Hackett Publishing. p. 72. ISBN 978-1-60384-682-0.
- ^ Gordon Lindsay Campbell (2014). The Oxford Handbook of Animals in Classical Thought and Lifen. Oxford University Press. p. 530. ISBN 978-0-19-103515-9.
- ^ Pomeroy, Sarah B. (2013). Pythagorean Women. Baltimore, MD: The Johns Hopkins University Press. p. 52. ISBN 978-1-4214-0957-3.
- ^ Glenn, Cheryl, Rhetoric Retold: Regendering the Tradition from Antiquity Through the Renaissance. Southern Illinois University, 1997. 30–31.
- ^ a b Michelle Ballif; Michael G. Moran (2005). Classical Rhetorics and Rhetoricians: Critical Studies and Sources. Greenwood Publishing Group. p. 317. ISBN 978-0-313-32178-8.
- ^ a b Constantine J. Vamvacas (2009). The Founders of Western Thought – The Presocratics. Springer Science & Business Media. p. 76. ISBN 978-1-4020-9791-1.
- ^ a b Richard D. McKirahan (2011). Philosophy Before Socrates (Second Edition): An Introduction with Texts and Commentary: An Introduction with Texts and Commentary. Hackett Publishing. p. 80. ISBN 978-1-60384-612-7.
- ^ Richard D. McKirahan (2011). Philosophy Before Socrates (Second Edition): An Introduction with Texts and Commentary: An Introduction with Texts and Commentary. Hackett Publishing. p. 81. ISBN 978-1-60384-612-7.
- ^ a b Damien Janos (2012). Method, Structure, and Development in al-Fārābī's Cosmology. BRILL. p. 118. ISBN 978-90-04-21732-4.
- ^ Pierre Pellegrin (2000). Greek Thought: A Guide to Classical Knowledge. Harvard University Press. p. 918. ISBN 978-0-674-00261-6.
- ^ a b c d Everett Ferguson (2013). Encyclopedia of Early Christianity, Second Edition. Routledge. p. 804. ISBN 978-1-136-61158-2.
- ^ Christoph Riedweg (2008). Pythagoras: His Life, Teaching, and Influence. Cornell University Press. p. 73. ISBN 978-0-8014-7452-1.
- ^ a b c Joost-Gaugier, Christiane L. (2007). Measuring Heaven: Pythagoras and His Influence on Thought and Art in Antiquity and the Middle Ages. Cornell University Press. p. 118. ISBN 978-0-8014-7409-5.
- ^ a b Joost-Gaugier (2007, p. 119)
- ^ a b c Joost-Gaugier (2007, p. 117)
- ^ Bruhn 2005, pp. 65–66.
- ^ Riedweg 2005, p. 29.
- ^ Kahn 2001, pp. 1–2.
- ^ a b Joost-Gaugier (2007, pp. 117–118)
- ^ a b c d Joost-Gaugier (2007, p. 120)
- ^ Joost-Gaugier (2007, p. 123)
- ^ Joost-Gaugier (2007, p. 125)
- ^ Mohammad Saleh, "Arabic and Islamic Philosophy of Mathematics", The Stanford Encyclopedia of Philosophy (Summer 2022 Edition), Edward N. Zalta (ed.)
- ^ Joost-Gaugier (2007, p. 124)
- ^ Joost-Gaugier (2007, p. 126)
- ^ Anthony Grafton; Glenn W. Most (2010). The Classical Tradition. The Belknap Press of Harvard University Press. p. 798. ISBN 978-0-674-03572-0.
- ^ Joost-Gaugier (2007, pp. 121–122)
- ^ David C. Lindberg; Roy Porter; Katharine Park; Lorraine Daston; Mary Jo Nye; Theodore M. Porter; Dorothy Ross (2003). The Cambridge History of Science: Volume 3, Early Modern Science. Cambridge University Press. p. 599. ISBN 978-0-521-57244-6.
- ^ Charles H. Kahn (2001). Pythagoras and the Pythagoreans: A Brief History. Hackett Publishing. pp. 55–62. ISBN 978-0-87220-575-8.
- ^ Lloyd Ridgeon (2011). Jawanmardi. Edinburgh University Press. p. 158. ISBN 978-0-7486-8815-9.
- ^ Rosen, E. (1978). Aristarchus of Samos and Copernicus. The Bulletin of the American Society of Papyrologists, 15(1/2), 85-93. http://www.jstor.org/stable/24518756
- ^ Lindberg, David C.; Porter, Roy; Park, Katharine; Daston, Lorraine; Nye, Mary Jo; Porter, Theodore M.; Ross, Dorothy (2003). The Cambridge History of Science: Volume 3, Early Modern Science. Cambridge University Press. p. 603. ISBN 978-0-521-57244-6.
- ^ Lindberg, David C.; Porter, Roy; Park, Katharine; Daston, Lorraine; Nye, Mary Jo; Porter, Theodore M.; Ross, Dorothy (2003). The Cambridge History of Science: Volume 3, Early Modern Science. Cambridge University Press. pp. 597–598. ISBN 978-0-521-57244-6.
- ^ Lindberg, David C.; Porter, Roy; Park, Katharine; Daston, Lorraine; Nye, Mary Jo; Porter, Theodore M.; Ross, Dorothy (2003). The Cambridge History of Science: Volume 3, Early Modern Science. Cambridge University Press. p. 604. ISBN 978-0-521-57244-6.
- ^ Lindberg, David C.; Porter, Roy; Park, Katharine; Daston, Lorraine; Nye, Mary Jo; Porter, Theodore M.; Ross, Dorothy (2003). The Cambridge History of Science: Volume 3, Early Modern Science. Cambridge University Press. p. 609. ISBN 978-0-521-57244-6.
- ^ a b Constantine J. Vamvacas (2009). The Founders of Western Thought – The Presocratics. Springer Science & Business Media. p. 77. ISBN 978-1-4020-9791-1.
External links
[edit] Media related to Pythagoreanism at Wikimedia Commons
Media related to Pythagoreanism at Wikimedia Commons- Carl Huffman. "Pythagoreanism/". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
